一元线性回归模型在经济预测中的应用
线性回归在经济中的应用

本 文只介绍直线相关系数 , 它是衡量两个变量之 间线性相 关关系的重
要指 标 。它 是 在 线 性 相 关条 件 下 , 明两 个 现 象 之 间相 关 关 系 的 方 向 和 密 说 切程 度 的统 计 分 析 指 标 , 常用 r 示 。 通 表
线性 回归 模 型 通 常应 满 足 以下 几个 基 本 假 设 :
测 中的 应 用 。 【 关键 词 l线 性 回 归 经济
建模
任何一个 数学模 型的运 用都 是有 条件的 , 元线 性回 归模型也 不例 一 () 1 两种变量之间确实存在直线关系。当两种变量 的成对 数值绘 成散 () 2 两种变量之间确 实存在显著的相关关系。如果两种 变量之 间没有
如 粜变 精 , 啦的概 率分布 之对廊 。随机变 髓Y与辛 关变鼙 1 … 便 。 f j
l, 2, … ,
零, ∑O一 )= ’。因 有 即 , m m 而最 代表性, 佳的 直 型。 是最 回归 线模
3 相 关 图 的绘 制 . 相 关 图 又 称 散点 图 、 布 图 , 是 将 相 关 表 中 的 观 测 值 在 平 面 直 角 坐 散 它 标 系 中用 坐 标 点 描绘 出 来 , 表 明相 关 点 的 分 布 状 况 。 通 过 相 关 图 , 以 以 可 大致 看 出两 个 变 量 之 间 有 无 相 关 关 系 以 及 相 关 的 形 态 、 向 和 密 切 程 度 。 方
之 问的概率模型 为
’ ’l 2 , ) s =/ , + ( …
(. ) 1 1
中,随机变 髓 称为闽变 髓r^. … t, 称 为 自变齄, / ,:…, ) 、 、 为 (
般 变精 ,2 , 的确定性 必系, 为随机误 麓。 X, … J 足因为随机变 量误蓑项 的
基于一元线性回归模型预测工程项目的造价

(3)进行线性回归分析:利用最小二乘法对自变量和因变量进行线性回归分 析,得到回归模型的参数a和b。
(4)验证模型:利用历史数据对模型进行训练和预测,并计算预测误差,以 验证模型的准确性和可靠性。
2、提取影响工程项目造价的关 键因素
工程项目造价受到多种因素的影响,包括工程量、材料价格、人工成本、市场 环境等。在一元线性回归模型中,我们需要根据历史数据和实际情况,提取对 工程项目造价影响最为显著的关键因素作为自变量。
(3)地区差异性:不同地区的工程项目造价可能存在较大差异,因此模型的 适用范围可能受到限制。未来可以考虑建立地区特定的模型,以提高模型的适 用性。
结论
本次演示基于一元线性回归模型预测工程项目的造价,通过提取影响工程项目 造价的关键因素,建立回归模型并利用历史数据进行训练和预测。结果表明, 一元线性回归模型在工程项目造价预测中具有较好的准确性,但同时也存在一 定的局限性。未来可以进一步完善模型结构,考虑更多影响因素,提高模型的 预测精度和适用范围。
接下来,利用得到的模型参数,我们对测试集进行预测。对于每个测试项目, 我们根据其工程量、材料价格和人工成本等数据,代入回归模型计算出预测的 工程造价。将预测值与实际值进行比较,可得到模型的预测误差。
4、分析预测结果及模型局限性
通过计算,我们得到了模型的预测误差为10%,表明一元线性回归模型在工程 项目造价预测中具有较好的准确性。但同时我们也发现模型的预测结果存在一 定的偏差,这可能与以下因素有关:
谢谢观看
结论与展望
一元线性回归模型在经济预测中具有广泛的应用价值,其能够通过对历史数据 的分析,揭示变量之间的线性关系,并以此为依据对未来趋势进行预测。然而, 需要注意的是,这种模型的应用也存在一定的局限性。例如,它无法处理非线 性关系和复杂因素的影响,对于一些不确定性和变化性较大的经济现象可能无 法得出准确的预测结果。
【文献综述】一元线性回归在经济预测中的应用

文献综述信息与计算科学一元线性回归在经济预测中的应用经济预测是指用可靠的方法进行对未来经济的分析,是与未来有关的旨在减少不确定性对经济活动影响的一种经济分析.它是对将来经济发展的科学认识活动.经济预测是以科学的理论和方法、可靠的资料、精密的计算及对客观规律性的认识所作出的分析和判断。
这样的预测是一种分析的程序,它可以重复地连续进行下去。
目的是为未来问题的经济决策服务.为了提高决策的正确性,需要由预测提供有关未来的情报,使决策者增加对未来的了解,把不确定性或无知程度降到最低限度,并有可能从各种备选方案中作出最优决策.因此,经济预测是各级领导机关和经济管理工作者展望经济发展前景,制定政策,编制计划,做出决策,以及进行科学管理的重要依据,在计划经济中有着重要的作用.预测是一门实用学科,它有科学基础,包括理论、资料、方法、计算等因素,依赖于对客观经济规律的认识和掌握。
它还依赖于预测者提出假设、选择方法、利用资料的技巧,和运用他自己的学识、经验、获得的情报进行判断的能力.经济预测有它的哲学基础、经济学基础、统计学基础,同时在多数情况下还以经济数学模型的建立与运用为基础。
一种实用模型根据一定的理论和事实,考虑到种种条件的假设和政策变化的影响,就可以用来预测经济的发展.经济预测的方法一般分为质的预测方法与量的预测方法两大类。
第一类方法,如专家调查法、民意调查法等.后一种方法是向消费者、生产者调查他们对未来发展的意见或意向,考虑他们的心理因素的预测方法.它适用于了解居民的消费需求和购买意图、市场的动向以及投资的趋向等问题.第二类方法,如时间数列法、指标分析法、因素分析法等。
时间数列法是通过分析时间数列的组成要素来研究其变化形态,把过去的发展趋势延续下去和外推未来的预测方法.它的主要方法有移动平均法、加权移动平均法、指数平滑法、最小平方法等等。
指标分析法是通过分析反映经济变动的互有联系的指标或指标组,研究那些预示经济转折的“动向”指标和预报经济可能出现严重问题的“警戒”指标,来确定经济形势变化的迹象的预测方法。
一元回归模型在市场预测中的应用

各 时期产 品需 求量 的平均 值 , _ _
;
的冰淇淋 消 费量 。 设冰淇淋消费量的线性回归模 型为Y e , = -  ̄t 为选定 t
收 稿 日期 : 0 9 1 — 3 2 0 — 2 1 基 金 项 目: 西华 师范 大 学 校 级 基 金 项 目( 9 0 7 0A 1 ) 作 者 简 介 : 艳 梅 (9 7 )女 , 杨 1 7 一 , 讲师 , 理 学硕 士 , 管 研究 方 向为 技 术 经 济 管理 、 策 管理 、 济 预 测 。 决 经
果 关 系的模 型对 因变量进 行预 测 。
一
量, 以及 冰淇 淋消 费各 月份波 动情况 等数 据 。 各 年度 冰淇淋 消费量 的历史记 录见 表 1 。
表 1 各 年 度 的冰 淇 淋 消 费 量 99 9
元 线性 回归模 型 如下 :
2 一 元 回归 模 型 在 市 场 预 测 中的 应 用 实 例
以 四川 某纸杯 公 司为例 ,介绍 一元 回归 模型在
市场预 测 中的运用 。
据调 查该 纸杯 公 司的计 划缺少 科学 预测 ,而 回 归模型 能恰 到好处 地用 于预测 方 面。 于是针 对每种
1 一 元 回归 分 析 方 法 简 介
回归分 析是用 于处 理变量 间相关 关 系 的一 种数
不 同类 型 的产 品。 建立各 自的预测模 型 。 对于 相似 的 产 品 。 通过 统计 学 的方 法发 现它们 之 间 的相 关性 , 则
通过调 整相关 系数 来进 行预 测 。 据重要 性原 则 , 根 首
先 选择 了公 司 目前 销 售量 最 大 的5 司纸 杯 为 主要 盎
6 一趋 势 直线 的斜率 。
线性回归分析及其在经济预测中的应用

线性回归分析及其在经济预测中的应用线性回归分析是一种常用的统计方法,用于研究自变量与因变量之间的关系。
它假设自变量与因变量之间存在线性关系,并通过拟合一条直线来描述这种关系。
线性回归分析在经济学领域有着广泛的应用,可以用于预测经济指标、分析经济政策的效果等。
首先,线性回归分析可以用于预测经济指标。
经济指标是评估经济状况和发展趋势的重要依据,例如国内生产总值(GDP)、消费者物价指数(CPI)等。
通过收集历史数据,我们可以建立一个线性回归模型,将过去的自变量与因变量进行拟合,然后利用这个模型来预测未来的因变量。
例如,我们可以利用过去几年的GDP增长率和其他相关因素,来预测未来一年的GDP增长率。
这样的预测对政府决策、企业投资等具有重要的指导作用。
其次,线性回归分析可以用于分析经济政策的效果。
在经济学中,政府的经济政策往往会对经济指标产生影响,例如降低利率可以刺激投资,提高税收可以增加政府财政收入等。
通过线性回归分析,我们可以将政策变量与经济指标进行拟合,从而判断政策对经济的影响程度。
例如,我们可以将货币供应量与通货膨胀率进行回归分析,来评估货币政策对通胀的影响。
这样的分析有助于政府制定更有效的经济政策,提高经济运行的稳定性和可持续性。
除了经济预测和政策分析,线性回归分析还可以用于经济学理论的验证和发展。
经济学理论通常会提出一些假设和关系,例如供给与需求之间的关系、劳动力市场的决定因素等。
通过线性回归分析,我们可以将理论中的变量与实际数据进行拟合,从而验证理论的有效性。
如果理论与实际数据拟合较好,那么就可以认为该理论在一定程度上解释了经济现象。
如果理论与实际数据拟合较差,那么就需要对理论进行修正或者寻找其他解释。
这样的研究有助于推动经济学理论的发展,提高其解释和预测能力。
然而,线性回归分析也存在一些限制和局限性。
首先,线性回归分析假设自变量与因变量之间存在线性关系,但实际情况往往更为复杂。
如果变量之间存在非线性关系,那么线性回归模型的拟合效果可能较差。
线性回归模型在社会科学中的应用

线性回归模型在社会科学中的应用在社会科学领域,线性回归模型是一种经济、心理学、社会学等学科中常用的统计分析工具。
线性回归模型能够提供变量之间的关联性和预测能力,对于研究人类行为和社会现象具有重要的应用。
下面将介绍线性回归模型在社会科学中的应用,并探讨其局限性和改进方向。
一、经济领域中的线性回归模型应用在经济学中,线性回归模型被广泛运用于经济现象的解释和预测。
例如,通过构建家庭收入与教育水平的线性回归模型,可以分析收入与教育之间的关系。
该模型可以帮助政府了解教育资源的投入效果,制定有针对性的教育政策。
此外,线性回归模型还可以用于研究物价与供求关系、经济增长与人口因素之间的关系等。
二、心理学中的线性回归模型应用心理学家常常使用线性回归模型来探索人类行为和心理现象之间的关系。
例如,通过构建社会支持与幸福感的线性回归模型,可以了解社会支持对个体幸福感的影响程度。
此外,线性回归模型还可以用于研究人格特征与工作表现之间的关系、家庭环境对儿童心理发展的影响等。
三、社会学中的线性回归模型应用社会学研究中,线性回归模型被广泛应用于社会现象的解释和预测。
例如,通过构建收入与社会阶层的线性回归模型,可以研究社会阶层对个体经济状况的影响。
此外,线性回归模型还可以用于研究种族、性别对职业选择和收入差距的影响等。
尽管线性回归模型在社会科学中具有广泛的应用,但也存在一些局限性。
首先,线性回归模型假设自变量和因变量之间的关系是线性的,但实际情况往往更为复杂。
其次,线性回归模型对数据的要求较高,需要满足一系列假设条件,如自变量和误差项之间应独立、误差项应服从正态分布等。
此外,线性回归模型容易受到离群值(outliers)的影响,进而导致模型拟合效果不佳。
为了克服线性回归模型的局限性,研究者们提出了一系列改进方法。
例如,非线性回归模型可以用于处理自变量与因变量之间的非线性关系。
加权最小二乘法和岭回归等方法可用于处理数据不满足线性回归模型的假设条件的情况。
线性回归模型在金融领域中的应用探讨

线性回归模型在金融领域中的应用探讨一、引言随着金融市场的不断发展和金融数据的快速增长,如何从海量数据中提取有效的信息成为金融领域研究的热点问题之一。
线性回归模型作为一种重要的统计分析工具,已经被广泛应用于金融领域中的数据分析和预测,如股票价格预测、信用评级、风险控制等。
本文将从金融市场分析的角度,探讨线性回归模型在金融领域中的应用情况及其优缺点。
二、线性回归模型的基本原理线性回归模型是一种用于描述自变量与因变量之间关系的数学模型。
简单线性回归模型可以表示为:$Y_i = \beta_0 + \beta_1 X_i + \epsilon_i$其中,$Y_i$是因变量,$X_i$是自变量,$\beta_0$和$\beta_1$是待求系数,$\epsilon_i$是误差项。
通过对样本数据的拟合,可以得到模型的系数估计值,从而进行预测和分析。
三、线性回归模型在金融领域中的应用1. 股票价格预测股票价格预测一直是金融领域中的热点问题。
通过构建一个合理的模型,可以对未来的股票价格进行预测,为投资者提供决策依据。
线性回归模型可以结合资本市场理论,考虑到影响股票价格的各种因素,如宏观经济环境、公司业绩、市场情况等,来进行股票价格的预测。
2. 信用评级信用评级是金融领域中的重要工作之一。
应用线性回归模型,可以将不同的客户的历史信用数据作为自变量,将客户当前的信用水平作为因变量,从而构建出一个评级模型。
评级模型可以根据客户的信用等级,给出相应的贷款利率或者借款额度等信息,对于银行和其他金融机构来说,可以进行更为准确的风险控制。
3. 风险控制风险控制是金融机构必须考虑的问题。
线性回归模型可以通过对历史数据进行分析,推断出不同的因素对风险的影响程度,从而建立出相应的模型。
模型可以预测未来的风险水平,为金融机构的风险控制提供决策依据。
四、线性回归模型的优缺点线性回归模型具有简单易懂、操作便捷、可解释性强的优点。
此外,线性回归模型还可以通过引入新的解释变量,来不断改进和修正模型。
一元线性回归模型在经济预测中的应用
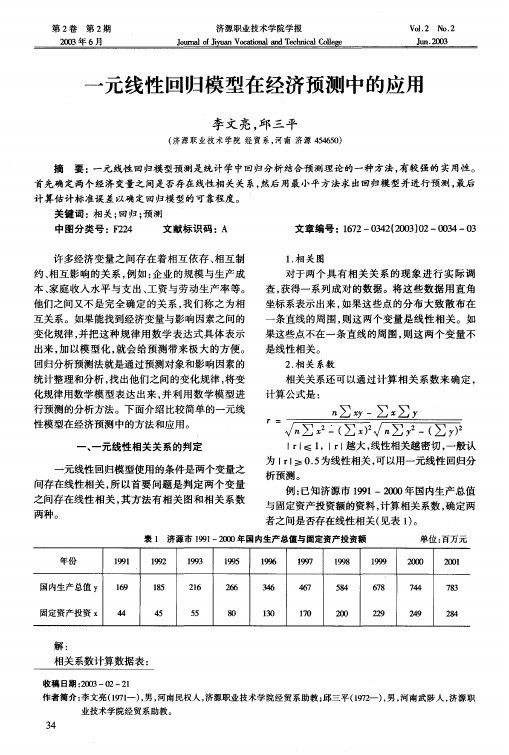
1.相关图 对于两个具有相关关系的现象进行实际调
互关系。如果能找到经济变量与影响因素之间的
变化规律, 并把这种规律用数学表达式具体表示
Q = 习(, Y 一c)2= 习(, 。 b = 最 一 一x)
小值
根据微积分知识, Q值要达到最小, 必要条件 是Q对a 和b 的一阶偏导数等于零:
碧=一 1 , b =” 2}7( 一 x) ,
整理得 :
。 +。 习: 习x2= 习。 na + b艺二 艺, =
解之得:
: = / -一 二Yc夕 “ V AL臼}y
(Jiyuan V ocational and T echnical College, Jiyuan 454650, Henan ,hina ) C
A b str a ct :
One variable linear r gr ssive e e is an anticipating method which combines the r gr ssive analysis e e in statistics with anticipation theor . It ' s ver practical . Firstly, we should see if ther exist l near r lations among y y e i e the econom ic should get the r gr ssive equation to anticipate parameters with the method of e e the standard estimated 二 to make sure the degr e of r gressive model ’ e e s OLS. Final y l
