二次函数的图像和性质课件下载
合集下载
26.2二次函数的图象与性质(第2课时)课件(共12张PPT)

为0 。
3.函数y=3x2+5与y=3x2的图象的不同之处是( C
)
A.对称轴
B.开口方向
C.顶点
D.形状
4.已知抛物线y=2x2-<1上有两点(x1,y1 ) ,(x1,y1 ) 且x1<x2<0,则y1 y2(填“<”或“>”)
5.已知一个二次函数图像的顶点在y轴上,并 且离原点1个单位,图像经过点(–1,0),求该 二次函数解析式。
1.5
1
0.5
y3x2 1
1
2
-0.5
-1
在同一直角坐标系中
画出函数 y 1 x2 y 1x2 2 3
5 4
y
3 y 1 x2 2
3
3 2
的图像
1
x
–5 –4 –3 –2 –1O –1
–2
y 1x2 2
–3
3
–4
–5
12345
y 1 x2 2 3
y 1 x2 3
试说出函数y=ax2+k(a、k是常数,a≠0)的图 象的开口方向、对称轴和顶点坐标,并填写下 表.
1
-6 -4 -2
2
4
6
x y=3x2 y=3x2–1
… –1 –0.6
…3
1.08
…2
0.08
(2)二次函数 y=3x²-1 的图 象与二次函数
y=3x²的图象有 什么关系?
-2
-1
–0.3
0
0.3
0.27
0
0.27
–0.73 – 1 –0.73
y 3x2
2
0.6 1 … 1.08 3 … 0.08 2 …
谢谢观赏
You made my day!
《二次函数的图像与性质》PPT课件

(2)抛物线y=x2+1,y=x2-1与抛物线y=x2的异同点:
相同点: ①形状大小相同 ②开口方向相同 ③对称轴相同
不同点:顶点的位置不同, 抛物线的位置也不 同.
y y=x2+1
10
9
y=x2
8
7
6
5
4
3 2
y=x2-1
1●
-5 -4 -3 -2 -1●o 1 2 3 4 5 x ●
抛物线y=x2+1,y=x2-1与抛物线
二次函数的图像与性质
学习目标
• 1、能画出y=ax2+ k;y=a(x-h)2的图象,并 能根据图象探索出它的性质。
• 2、能灵活应用y=ax2+ k;y=a(x-h)2的性质 解决相关问题。
二次函数y=x2的图象是____,它的开口向 _____,顶点坐标是_____;对称轴是______, 在对称轴的左侧,y随x的增大而______,在 对称轴的右侧,y随x的增大而______,函数y =x2当x=______时, y有最______值,其最 ______值是______。
后,得到抛物线y=(x-3)2
5、把抛物线y=x2+mx+n向左平移4个单位,得到抛
物线y=(x-1)2,则m= -10 ,n= 25 .
6.已知二次函数y=8(x -2)2 当 x>2 时,y随x的增大而增大, 当 x<2 时,y随x的增大而减小.
7.抛物线y=3(x-8)2最小值 0 .
8.抛物线y=-3(x+2)2与x轴y轴的交点坐标分别为 (-2,0) (0,-12).
大值,这个最大值等
-6
于 c。
-8
总结: 函数y=ax2 (a≠0)和函数y=ax2+c (a≠0)的 图象形状 相,同只是位置不同;当c>0时,函数 y=ax2+c的图象可由y=ax2的图象向 上平移c 个单位
二次函数y=ax2的图象和性质ppt课件

例4 如图, 四个二次函数的图象分别对应 ① y=ax2 ;② y=bx2;
③ y=cx2;④ y=dx2,且①与③,②与④分别关于x 轴对称.
(1)比较a,b,c,d 的大小; (2)说明a 与c,b 与d 的数量关系.
解:(1)由抛物线的开口方向,知 a > 0,b > 0,c < 0,d < 0,
由抛物线的开口大小,知 |a| > |b|,|c| > |d|, 因此a > b,c < d. ∴ a > b > d > c. (2)∵①与③,②与④分别关于x 轴对称,
∴①与③,②与④的开口大小相同,方向相反. ∴ a+c=0,b+d=0.
课堂练习
1、下列函数中,y总随x增大而减小的是( B )
归纳总结
位置开 开口向上,在x轴上方 开口向下,在x轴下方
口方向
a的绝对值越大,开口越小
对称性 顶点最值
关于y轴对称,对称轴方程是直线x=0 顶点坐标是原点(0,0)
当x=0时,y最小值=0 当x=0时,y最大值=0
增减性
在对称轴左侧递减 在对称轴左侧递增 在对称轴右侧递增 在对称轴右侧递减
1、如右图,观察函数y=( k-1)x2的图象, 则k的取值范围是 k>1 .
复习引入
1.二次函数的一般形式是怎样的? y=ax²+bx+c(a,b,c是常数,a≠ 0)
2.下列函数中,哪些是二次函数?
①
②
③
④
⑤
3.一次函数的图象是一条 直线.
4.通常怎样画一个函数的图象? 列表、描点、连线
那么,二次函数的图象会是什么样的图形呢?这节课我们 来学习最简单的二次函数y=ax2的图像
不同点: a的值越大,开口越小.
二次函数的图像和性质ppt课件

二次函数的图像和性质ppt课件
contents
目录
• 引言 • 二次函数的定义和公式 • 二次函数的图像 • 二次函数的性质 • 二次函数的实际应用 • 总结与回顾 • 课后作业与思考题
01 引言
课程背景介绍
01
二次函数是数学中基础知识之一 ,掌握好二次函数的图像和性质 对于后续学习代数、几何等数学 领域都有重要的意义。
二次函数的定义
01
02
03
定义
一般地,形如$y = ax^2 + bx + c$($a$、$b$、 $c$是常数,$a \neq 0$ )的函数叫做二次函数。
解释
二次函数是包含未知数的 二次多项式的函数,其未 知数的最高次数为2。
示例
$y = 2x^2 + 3x - 4$是 一个二次函数。
二次函数的公式
01
02
03
04
当x增大时,如果a>0,y值会 随之增大;如果a<0,y值会
随之减小。
当x增大时,如果a>1,y值会 快速增大;如果0<a<1,y值
会缓慢增大。
当x减小时,如果a>0,y值会 随之减小;如果a<0,y值会
随之增大。
当x减小时,如果a>1,y值会 快速减小;如果0<a<1,y值
会缓慢减小。
减。
当$\Delta = 0$时,函
数有一个实根;当
$\Delta < 0$时,函数
没有实根。
极值:当$a > 0$时,二 次函数在区间$(-\infty, -b/2a)$上单调递增,在 区间$(-b/2a,+\infty)$ 上单调递减,此时$b/2a$为极小值点;当 $a < 0$时,二次函数在 区间$(-\infty, -b/2a)$ 上单调递减,在区间$(b/2a,+\infty)$上单调递 增,此时$-b/2a$为极 大值点。
contents
目录
• 引言 • 二次函数的定义和公式 • 二次函数的图像 • 二次函数的性质 • 二次函数的实际应用 • 总结与回顾 • 课后作业与思考题
01 引言
课程背景介绍
01
二次函数是数学中基础知识之一 ,掌握好二次函数的图像和性质 对于后续学习代数、几何等数学 领域都有重要的意义。
二次函数的定义
01
02
03
定义
一般地,形如$y = ax^2 + bx + c$($a$、$b$、 $c$是常数,$a \neq 0$ )的函数叫做二次函数。
解释
二次函数是包含未知数的 二次多项式的函数,其未 知数的最高次数为2。
示例
$y = 2x^2 + 3x - 4$是 一个二次函数。
二次函数的公式
01
02
03
04
当x增大时,如果a>0,y值会 随之增大;如果a<0,y值会
随之减小。
当x增大时,如果a>1,y值会 快速增大;如果0<a<1,y值
会缓慢增大。
当x减小时,如果a>0,y值会 随之减小;如果a<0,y值会
随之增大。
当x减小时,如果a>1,y值会 快速减小;如果0<a<1,y值
会缓慢减小。
减。
当$\Delta = 0$时,函
数有一个实根;当
$\Delta < 0$时,函数
没有实根。
极值:当$a > 0$时,二 次函数在区间$(-\infty, -b/2a)$上单调递增,在 区间$(-b/2a,+\infty)$ 上单调递减,此时$b/2a$为极小值点;当 $a < 0$时,二次函数在 区间$(-\infty, -b/2a)$ 上单调递减,在区间$(b/2a,+\infty)$上单调递 增,此时$-b/2a$为极 大值点。
二次函数的图像与性质-完整版课件

二次函数与一元二次方程关系
一元二次方程 $ax^2 + bx + c = 0$($a neq 0$)的解即为二次函数 $y = ax^2 + bx + c$ 与 $x$ 轴交点的横坐标。
当 $Delta = b^2 - 4ac > 0$ 时,二次函数与 $x$ 轴有两个交点;当 $Delta = 0$ 时,有 一个交点;当 $Delta < 0$ 时,没有交点。
• 分析:根据题意设交点坐标为$(-1, y_1)$和$(3, y_2)$,代入直线方程可得两个方程。又因为这两个点也在抛 物线上,所以代入抛物线方程也可得两个方程。联立这四个方程即可求出二次函数的解析式。
• 示例2:已知二次函数$y = ax^2 + bx + c (a • eq 0)$的图像与直线$y = x + m (m • eq 0)$相交于两点,且这两点关于原点对称,求二次函数的解析式。 • 分析:根据题意设交点坐标为$(x_1, y_1)$和$(x_2, y_2)$,由于两点关于原点对称,所以有$x_1 = -x_2$和
BIG DATA EMPOWERS TO CREATE A NEW ERA
二次函数的图像与性质-完
整版课件
汇报人:XXX
2024-01-29
• 二次函数基本概念 • 二次函数图像特征 • 二次函数性质探讨 • 典型例题分析与解答 • 实际应用场景举例说明 • 总结回顾与拓展延伸
目录
CONTENTS
零点存在性及个数判断方法
零点定义
二次函数零点存在 性判断方法
对于函数f(x),若存在x0∈D, 使得f(x0)=0,则称x0为函数 f(x)的零点。
通过判别式Δ=b^2-4ac来判断 。当Δ>0时,二次函数有两个 不相等的零点;当Δ=0时,二 次函数有两个相等的零点(即 一个重根);当Δ<0时,二次 函数无零点。
二次函数 的图象和性质--PPT课件
点(h,k)坐标 Nhomakorabea对
称
x=h
轴
最 值
最小值为k
最大值为k
新知应用-----基础知识
新知应用-----拓展提高
这节课你学到了什么
图像及性质 合作、分享 类比、化归
知识 方法 思想
作业布置
• 课后习题 • 练习册
送给大家
函数是纲 纲举目张 数形结合 相得益彰
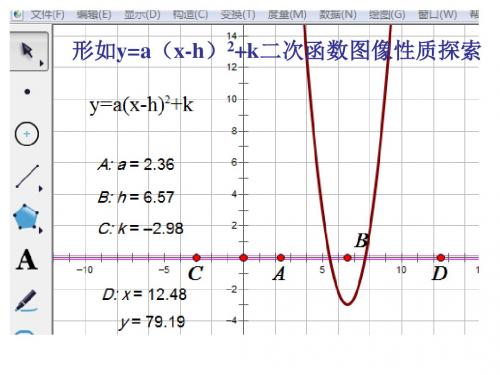
形如y=a(x-h)2+k二次函数图像性质探索
文件名
抛物 线
开口 方向
顶点 坐标
对称 轴
y=ax2(a>0) y=ax2(a<0)
向上
向下
(0,0) y轴
最值 最小值为0 最大值为0
温馨提示:鼠标拖动点A
文件名
抛物 线
开口 方向
顶点 坐标
对称 轴
y=ax2+k y=ax2+k (a>0) (a<0)
向上
向下
(0,K)
y轴
最值 最小值为k 最大值为k
文件名
抛物 线
开口 方向
顶点 坐标
对称 轴
最值
y=a(x-h)2 y=a(x-h)2
(a>0)
(a<0)
向上
向下
(h,0)
x=h
最小值为0
最大值为0
文件名
抛
物 y=a(x-h)2+k
线
(a>0)
y=a(x-h)2+k (a<0)
开
口
向上
方
向
向下
顶
二次函数的图像和性质PPT课件(共21张PPT)
相同点
相同点:开口都向下,顶点是
原点而且是抛物线的最高点,
对称轴是 y 轴.
不同点
不同点:|a|越大,抛物线的
开口越小.
x
O
y
-4 -2
2
4
-2
-4
-6
y 1 x2 2
-8
y x2
y 2x2
尝试应用
1、函数y=2x2的图象的开向口上 ,对称轴y轴 ,顶点是(0,0;)
2、函数y=-3x2的图象的开口向下 ,对称轴y轴 ,顶点是(0,0;) 3、已知抛物线y=ax2经过点A(-2,-8).
不在此抛物线上。
小结
1. 二次函数的图像都是什么图形?
2. 抛物线y=ax2的图像性质: (1) 抛物线y=ax2的对称轴是y轴,顶点是原点.
(2)当a>0时,抛物线的开口向上,顶点是抛物 线的最低点;
当a<0时,抛物线的开口向下,顶点是抛物 线的最高点;
(3)抛物线的增减性
(4)|a|越大,抛物线的开口越小;
得到y=-x2的图像.
y 1
-5 -4 -3 -2 -1-1 o 1 2 3 4 5 x
-2
-3 -4
-5
-6
y=-x2
-7
-8 -9
-10
二次函数的图像
从图像可以看出,二次函数y=x2和y=-x2的图像都是一条
曲线,它的形状类似于投篮球或投掷ห้องสมุดไป่ตู้球时球在空中所经过
的路线.
这样的曲线叫做抛物线.
y=x2的图像叫做抛物线y=x2.
解:分别填表,再画出它们的图象,如图 当a<0时,抛物线的开口向下,顶点是抛物线的最高点;
在同一直角坐标系中画出函数y=-x2、y=-2x2、y=- x2的图象,有什么共同点和不同点? -8=a(-2)2,解出a= -2,所求函数解析式为y= -2x2.
二次函数的图像与性质(第一课时)优质课件
对称轴与抛物 线的交点叫做 抛物线的顶点.
抛物线y=x2在x轴的上方(除顶点外), 顶点是它的最低点,开口向上, 当x=0 时,函数y的值最小,最小值是0.
【内容】独立完成探究点一的针对练习、 探究点二。(5min)
【要求】1.独立思考,认真分析总结; 2.标记好自己的疑难问题,以便讨论 探究; 3.自主独立做题,2min时间到后学 科组长组织组员针对疑难问题及 小组任务进行讨论交流。
2.2 二次函数的图像与性质(一)
我们把物体抛射时所经过的路线叫做抛物线.
1.经历探索二次函数y=x2 的图像的作法
和性质的过程,获得利用图像研究函数性质 的经验;
2.能够利用描点法作出二次函数y=x2的图 像,并能根据图像认识和理解二次函数y=x2 的性质;
3.能够作出二次函数 y=-x2的图像,并能 够y=x2比较出与 的图像的异同,初步建立二 次函数表达式与图像之间的联系.
【内容】快速、独立完成训练案“自测反馈”(8min) 【要求】1.独立思考,认真分析总结
2.标记好自己的疑难问题,以便课后讨论探究
探究内容 展示小组
14组小2源自2组组 合3
6组
作
4
5组
能力提升1
1组
能力提升2
3组
【要求】1.独立完成训练案的填空题;2.标记好自己的疑难
问题,以便讨论 ;3.针对疑难,自由探讨,互帮互助.
2、剩余时间思考探究案中其他问题,并把你认为正确的答 案写在学案上。
1.列表时注意自变量X的取值是否有意义.
(1)反比例函数: y
2
x
(x≠0)
(2)圆的面积公式:S r 2 (r≥0)
(3)二次函数: y=-x2 (x取全体实数)
抛物线y=x2在x轴的上方(除顶点外), 顶点是它的最低点,开口向上, 当x=0 时,函数y的值最小,最小值是0.
【内容】独立完成探究点一的针对练习、 探究点二。(5min)
【要求】1.独立思考,认真分析总结; 2.标记好自己的疑难问题,以便讨论 探究; 3.自主独立做题,2min时间到后学 科组长组织组员针对疑难问题及 小组任务进行讨论交流。
2.2 二次函数的图像与性质(一)
我们把物体抛射时所经过的路线叫做抛物线.
1.经历探索二次函数y=x2 的图像的作法
和性质的过程,获得利用图像研究函数性质 的经验;
2.能够利用描点法作出二次函数y=x2的图 像,并能根据图像认识和理解二次函数y=x2 的性质;
3.能够作出二次函数 y=-x2的图像,并能 够y=x2比较出与 的图像的异同,初步建立二 次函数表达式与图像之间的联系.
【内容】快速、独立完成训练案“自测反馈”(8min) 【要求】1.独立思考,认真分析总结
2.标记好自己的疑难问题,以便课后讨论探究
探究内容 展示小组
14组小2源自2组组 合3
6组
作
4
5组
能力提升1
1组
能力提升2
3组
【要求】1.独立完成训练案的填空题;2.标记好自己的疑难
问题,以便讨论 ;3.针对疑难,自由探讨,互帮互助.
2、剩余时间思考探究案中其他问题,并把你认为正确的答 案写在学案上。
1.列表时注意自变量X的取值是否有意义.
(1)反比例函数: y
2
x
(x≠0)
(2)圆的面积公式:S r 2 (r≥0)
(3)二次函数: y=-x2 (x取全体实数)
《二次函数》ppt课件
判别式意义
当 $Delta > 0$ 时,方程有两个不相等 的实根,抛物线与 $x$ 轴有两个交点。
02
二次函数与一元二次方程 关系
一元二次方程求解方法
01
02
03
公式法
对于一般形式的一元二次 方程,可以使用求根公式 进行求解。
配方法
通过配方将一元二次方程 转化为完全平方形式,从 而求解。
因式分解法
首先,通过配方将二次函数转 化为顶点式f(x) = a(x - h)^2 + k,其中(h, k)为顶点坐标。然后, 根据二次函数的性质,对称轴 为x = h,顶点坐标为(h, k)。最 后,代入具体的a、b、c值求解。
已知二次函数f(x) = x^2 - 2x, 求在区间[-1, 3]上的最值。
首先,将二次函数配方为f(x) = (x - 1)^2 - 1,确定对称轴为x = 1。然后,根据二次函数的单 调性,在区间[-1, 1]上单调递减, 在[1, 3]上单调递增。因此,在x = 1处取得最小值f(1) = -1,在 x = 3处取得最大值f(3) = 3。
04
根的判别式Δ=b²-4ac可 以用于判断二次函数与x 轴交点的个数。
当Δ>0时,二次函数与x 轴有两个不同的交点。
当Δ=0时,二次函数与x 轴有一个重根,即一个 交点。
当Δ<0时,二次函数与x 轴无交点。
03
二次函数图像变换与性质 分析
平移变换对图像影响
平移方向
二次函数图像在平面直角坐标系中可 沿x轴或y轴方向进行平移。
04
二次函数在实际问题中应 用举例
利润最大化问题建模与求解
1 2 3
问题描述
某公司生产一种产品,其成本和销售价格与产量 之间存在一定的关系。公司希望通过调整产量来 实现利润最大化。
《二次函数的图象与性质》二次函数PPT教学课件(第2课时)
B.抛物线y=-3x2向左平移1个单位得到
C.抛物线y=3x2向上平移1个单位得到
D.抛物线y=-3x2向上平移1个单位得到
新知讲解
在同一坐标系中,画出二次函数 = − ,y=− + ,
y=−
− 的图象,并分别指出它们的开口方向,对称轴和顶
点坐标,指明抛物线y=− + 通过怎样的平移可得到抛物线
来,|a|越大,抛物线的开口就越小.
新知讲解
做一做:在同一直角坐标系中,画出二函数 y=2x2+1与y=2x2-1的图象.
解:先列表,
9
5.5
3
1
3
5.5
9
7
3.5
1
-1
1
3.5
7
新知讲解
然后描点画图,
y
y = 2x2+1
8
y = 2x2 -1
6
4
抛物线y = 2x2+1 , y = 2x2 -1 的
a<0,开口向下
=
−
-4
− .
如图所示
y
y=− +2
1
y x 2 -2
2
y=−
-2 O
-2
-4
-6
2
4 x
归纳总结
二次函数y = ax2 +c的图象和性质:
a的符号
图
象
a>0
a<0
c>0
c<0
开口方向
对称轴
顶点坐标
向上
向下
C.抛物线y=3x2向上平移1个单位得到
D.抛物线y=-3x2向上平移1个单位得到
新知讲解
在同一坐标系中,画出二次函数 = − ,y=− + ,
y=−
− 的图象,并分别指出它们的开口方向,对称轴和顶
点坐标,指明抛物线y=− + 通过怎样的平移可得到抛物线
来,|a|越大,抛物线的开口就越小.
新知讲解
做一做:在同一直角坐标系中,画出二函数 y=2x2+1与y=2x2-1的图象.
解:先列表,
9
5.5
3
1
3
5.5
9
7
3.5
1
-1
1
3.5
7
新知讲解
然后描点画图,
y
y = 2x2+1
8
y = 2x2 -1
6
4
抛物线y = 2x2+1 , y = 2x2 -1 的
a<0,开口向下
=
−
-4
− .
如图所示
y
y=− +2
1
y x 2 -2
2
y=−
-2 O
-2
-4
-6
2
4 x
归纳总结
二次函数y = ax2 +c的图象和性质:
a的符号
图
象
a>0
a<0
c>0
c<0
开口方向
对称轴
顶点坐标
向上
向下
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
直线x=3
2) ( 3 , 7)
向下 直线x=2 ( 2 , 6)
画出函数 y
1 x2 x 2
函数具有哪些性质.
5的图像,并说明这个
2
分析 因为 1 x2 x 5
2
2
1 ( x 1)2 2, 2
所以函数即为
y
1 ( x 1)2 2,
2
因此这个函数的图像开口向下,对称轴为直线
x=1,顶点坐标(1,-2).
Ⅱ、当a<0时
当
x
=
-b 2a
最大值=
4ac - b2 4a
例2 求抛物线y=x2+2x-1的对称轴和顶点坐标,并 画出它的图像.
解:∵y=x2+2x-1=(x+1)2-2, ∴抛物线的对称轴为x=-1,顶点坐标为(-1,-2). (1)列表:
(2)在直角坐标系中,描点,连线,即得二次函 数y=x2+2x-1的图像,如图30-2-7.
二次函数的图像和性质
PPT教学课件
1、抛物线y=a(x-h)2+k的图像与性质:
1.当a﹥0时,开口 向上 , 当a﹤0时,开口 向下 , 2.对称轴是 直线x=h; 3.顶点坐标是 (h,k.)
2、一般地,抛物线y=a(x-h)2+k与 y=ax2的 形状 相同,位置 不同
y=ax2
y=a(x-h)2+k
的交点坐标是
;与
x轴的交点坐标是
;
2.抛物线y=-6x2-x+2与y轴的
交点坐标是
;与x轴
的交点坐标是
;
已知二次函数
y x2 2x 3
1.求它的图像的顶点坐标. 2. x取何值时,y随x增大而增大? 3. x取何值时,y随x增大而减小?
4.x取何值时,y>0? x取何值时,y<0?
怎样画出函数 y= ax2+bx+c的图像?
根据这些特点,我们容易画出它的图像.
解
列表:
画出的图像如图26.2.4所示.
一般地,我们可以用配方法求 抛物线y=ax2+bx+c(a≠0)的顶点 与对称轴.
y= ax2+bx+c
= a( x2 + b x) + c
a
=
a
轾轾轾轾( x
+
b )2 2a
-
b2 4a2
+c
=
a( x
+
b )2 2a
PPT素材:./sucai/ PPT图表:./tubiao/ PPT教程: ./powerpoint/ 范文下载:./fanwen/ 教案下载:./jiaoan/
PPT 课件:./k ejian/ 数学课件:./kejian/shuxue/ 美术课件:./kejian/meishu/ 物理课件:./kejian/wuli/ 生物课件:./kejian/shengwu/ 历史课件:./kejian/lishi/
例3 根据下列条件,确定抛物线的表达式.
(1)抛物线y=-2x2+px+q的顶点坐标为(-3,
5).
(2)抛物线y=ax2+bx-6经过点A(-1,3)和
B(2,-6).
解:(1)∵
y 2x2 px q (2 x p )2 p2 8q ,
4
8
∴ p 3,p2 8q 5,
4
8
∴ p 12,q 13.
(1) y=2x2+4x;
(2) y=-2x2-3x;
(3)y=-3x2+6x-7; (4) y=x2-4x+5.
2求下列函数的最大值或最小值:
(1)y=x2-3x+4;
(2) y=1-2x-x2;
(3) y=7 x2
2 7x
3; 2
(4) y=100-5x2;
练习:
1.抛物线y=4x2-11x-3与y轴
+
k
y = a(x – h )2
上下平移 y = ax2 左右平移
二次函数 y=2(x+3)2+5 y = -3x(x-1)2 -2 y = 4(x-3)2 +7 y = -5(2-x)2 - 6
开口方向 对称轴 顶点坐标
向上 向下 向上
直对线称x轴=-3 顶( -点3,坐标
直线x=1 (51), -
x<-
b 2a
x>-
b 2a
a>0
向 下
x<-
b 2a
x>-
b 2a
当x=
-
b 2a
时,
y有最小值:4a4ca-b2
当x=
-
b 2a
时,
y有最大值:4a4ca-b2
谢谢大家
所以该抛物线的表达式为y=-2x2-12x-13.
(2)点A(-1,3)和B(2,-6)的坐标满足抛
物线的表达式,即
解得
a b 6 3, 4a 2b 6 6.
a 3, b 6.
所以该抛物线的表达式为y=3x2-6x-6.
例. 通过配方,写出下列抛物线的 开口方向、对称轴和顶点坐标.
-
b2 4a
+c
=
a( x
+
b )2 2a
+
4ac 4a
b2
1、函数y= ax2+bx+c的图像 的顶点坐标:
(- b , 2a
4ac - b2 ) 4a
对称轴:直线
x
=
-
b 2a
函数y= ax2+bx+c Ⅰ、当a>0时:
当
x
=
-
b 2a
最小值=
4ac - b2 4a
函数y= ax2+bx+c
画二次函数的图像取点时先确定顶 点,再在顶点的两旁对称地取相同 数量的点,一般取5-7个点即可.
函数y=ax²+bx+c的图像和性质:
顶点坐标:(-2ba ,4a4ca-b2)对称轴: 直线x=-2ba
与y轴交点:(0,c) 与x轴交点(:-b± b2-4ac
2a
,0)
开口 增减性
最值
向 a>0 上
y = a( x – h )2 + k
平左 移右
平上 移下
y
= ax2 PPT模板:./moban/ PPT背景:./beijing/ PPT下载:./xiazai/ 资料下载:./ziliao/ 试卷下载:./shiti/ PPT论坛: 语文课件:./kejian/yuwen/ 英语课件:./kejian/yingyu/ 科学课件:./kejian/kexue/ 化学课件:./kejian/huaxue/ 地理课件:./kejian/dili/
