一种微带准椭圆函数带通滤波器的研制
椭圆滤波器的仿真研究
计 。综合设计 出的电路经 Ｅ Ａ仿真可 以方便 地观察滤波 Ｄ 器 的各种 特性 ， 根据仿 真结果适 当调整 电路各参 数 ， 直至 滤波器各项参数指标达到设计要求。
例 如 ：设 计 一 个 带 通 椭 圆 数 字 滤 波 器 ，通 带 为 １０～ ０
０ 引言
数字信号处理的主要组成部分就是数 字滤波器 。滤
—
∑ｂ ｋ Ｚ
Ｈ（ ） 一 ：
ｘ ＺＪ 【
：
ｋ ＝０
（ ２）
［ ，］ｅ ｉ（ ， ｐ Ｒ ， ） ｂ ａ ｌｐ ｎ Ｒ ， ｓ Ｗｎ ； ＝ ｌ ｆ ｑ（ ，， １ ， ） ｒ ｚｂ ａ ５ ２ｆ ｅ ｓ
１∑ａ 一 Ｚ
由（ ） １式可 以知道 ， 加法器 、 单位延迟器和常数乘法器 是实现数字滤波器需要 三种基本运算单元 。 然椭 圆函数 虽 滤波器的幅度响应在通带和阻带 内均有波 动 ， 但是 由于在 给定 阶数 和容许 的通带 、 阻带 波动指标 下 ， 圆函数滤波 椭 器具有最 窄的过渡带 ， 阻带 衰减较 大 ， 以其综合 性能最 所
波器在许多科学技术领域 中广泛使用 ， 其功能 是把 输入序
列通 过 一 定 的运 算 ， 换 成 输 出序 列 。数 字 滤 波 器 可 以 用 变 差分方程来表示 ， ： 即
Ｍ
２ ０ ｚ过渡带 均为 ５ Ｈ ， ５Ｈ， ０ ｚ 通带波 纹小于 ３ｂ 阻带 衰减为 ｄ， ３ｄ ， ０ ｂ 采样频率 ｆ ｌ０ Ｈｚ ｓ Ｏ ０ 。其程序为： ＝
垩一０ …＿ 十一 寸…… …＿－一■ … … … … ３ ｛ ０ ． … ｝－ － － … ｛
． 口 ４０
Ｉ
： ： ｌ ｌ ； ； ； ； ； ； ； ｊ ： Ｉ ・ ・ ： 一 ：
LC椭圆函数带通滤波器的设计及仿真
LC椭圆函数带通滤波器的设计及仿真第13卷第5期2008年10月哈尔滨理工大学J0URNALHARBINUNIV.SCI.&TECH.V01.13No.5Oct.,2008LC椭圆函数带通滤波器的设计及仿真常会敏,张礼勇,蒋辉雄(哈尔滨理工大学测控技术与通信工程学院,黑龙江哈尔滨150040)摘要:椭圆滤波器在各种滤波器中具有其自身独特的优点,但设计过程往往比较复杂.本文给出了一种简易的计算方法.这种方法需要的初始值数据较少,设计步骤简练,计算量小.并用PSPICE仿真软件分别对椭圆函数低通,高通,带通滤波器进行设计和仿真分析,仿真结果证明了这种滤波器设计方法的有效性.关键词:椭圆函数滤波器;PSPICE仿真;传输特性;耦合器中图分类号:TN713文献标识码:A文章编号:1007—2683(2008)05—0021—04 TheDesignandSimulationofLCEllipticBand——passFilterCHANGHui—min,ZHANGLi—yong,JIANGHui—xiong(SchoolofMe~ure—controlTechnologyandCommunicationEngineering,HarbinUniversityofScienceandTec hnology,Harbin150040,China)Abstract:Throughallkindsoffilters,theellipticoneshaveparticularadvantages,buttheirdes ignprocessesaremorecomplicated.Thisthesismakesuseofaneasycalculationmethodwithsampledesigningsteps,lowcom—putationalcomplexityandneedinglessoriginalvaluedata.PSPICEsimulationsoftwareisus edtodesignandsimu—lateellipticlow—pass,high—passandband—passfilters,andthesimulationresultsshowtheeffectivenessofthescheme.Keywords:ellipticfilter;PSPICESimulation;transmissioncharacteristic;coupler带通滤波器的应用非常广泛,涉及到各个领域.带通滤波器性能的优劣,对提高接收机信噪比,防止邻近信道干扰,提高设备的技术指标,具有十分重要的意义.滤波器的设计技术已比较成熟,根据设计要求,首先确定滤波器的曲线和类型,以及滤波器的阶数,根据设计参数确定具体曲线和归一化元件值,再根据实际去归一化得到实际的元件值.1一种模拟带通滤波器本文通过设计一个1M到30M的【C模拟带通滤波器来表述一种设计方法,如图1所示.设计指标收稿日期:2007—04—29基金项目:国家自然科学基金(60372104)作者简介:常会敏(1980一),女,哈尔滨理工大学硕士研究生确定如下:1)3dB截止频率分别为950k和30.5M;2)30dB截止频率分别为500k和40M;3)lM到30M之间的通带波纹小于0.2dB./\图1带通滤波器曲线由以上截止频率可知,这是一个宽带带通滤波22哈尔滨理工大学第l3卷器,故可以通过设计一个截止频率为30M的低通滤波器和一个截止频率为1M的高通滤波器级联而成.2椭圆函数低通滤波器的设计第一步:计算没计波彤参数,陡度系数为:_1.33(1)出现A…的最低阻带频率,即'=_1_3模角为sin-I1:sin南50.(3)第二步:选择归一化低通滤波器.在阻带端点以内的最小衰减至少为30dB,选择反射系数P:20%,由文[1]可知,它对应的通带波纹为0.18d13;由罔2可知,与P=20%对应的反射损耗分贝数A=13.9dB.故有/l.+A.=30dB+13.9dB=43.9dB(4)图2所示为估算椭圆函数滤波器阶数用的曲线表明,在:1.3时,n=5的滤波器可满足设计要求,具体编号为CO520,0=50..满足设计要求的归一化低通滤波器有两种形式,如图2a,和图2b所示.但考虑到在实际电路的调试过程中,一般用手工制作的电感和从市面上购买的电容相比,手制电感本身的衰减往往比电容衰减大,冈此,使用电感的总数应尽量少.在这里,低通滤波器的设计选择使用图2a形式. .工工L3￡一'～;(b)另一种形图2两种归～化低通滤波器形式第三步:查表得到归一化的元件值.即:Ci=0.12031,C2=0.23421,Lz=1.12513,C3=1.61339,C4=0.71418,L4=0.76973,C5=0.81771第四步:对归一化低通滤波器进行频率和阻抗标度.将所有的电抗元件都除上一个频率标度系数(FSF),就可把一个已知滤波器响应标度到不同频率范围,即=㈤只进行频率标度后的滤波器的元件值很不实际,电容值太大,而1n的电阻值也不适宜,这种情况可以刚阻抗标度来解决.任何线性有源或无源网络,如果所有电阻和电感值乘阻抗标度系数z,而所有电容除以同样的系数z,其传递函数维持不变. 在这里,用FSF=2,rrf~=2'rr×30×10.和Z=50,对归一化低通滤波器进行频率和阻抗标度.去归一化数值的计算式为R=RZ(6)L=而L~Z(7)C=—FSF一~Z一(8)得到去归一化元件值,如图3的滤波电路所示.n图330M低通滤波电路采用PSPICE仿真软件,对30M低通滤波器电路仿真,仿真后可得到滤波器的传输特性如图4所示.3椭圆函数高通滤波器的设计弟一步:计算设计波彤参数.陡度系数为争==2(9)Ⅲ现Ai的最低阻带频率,即=丽950k=1.9(10)模角为6f=sin～1=sl~n-11=31.(11)第二步:洗择归一化高诵滤波器.第5期常会敏等:LC椭圆函数带通滤波器的设计及其仿真23 O—lo0ll.十一-'.一'.+1.O1030loo频率/MHz(a)幅频特性曲线,\,;,,.1频率/MHz(b)相频特性曲线图430M低通滤波器幅频,相频特性曲线如果1/s代替归一化低通传递函数中的,可以获得高通滤波器,低通衰减值将在等于低通频率倒数的高通频率上出现.简单地用电容替换每个电感或用电感替换每个电容,且利用元件值的倒数可以将归一化LC低通滤波器变换为相应的高通滤波器,表示为C高通=1/低通,￡高通=1/C低通(12)信号源内阻和端接电阻不变.首先选择归一化低通滤波器,在阻带端点以内的最小衰减Ai至少为30dB,依然选择反射系数P=20%,由文[1]中图2—86所示的估算椭圆函数滤波器阶数用的曲线表明,在=1.9时,/I=5的滤波器可满足设计要求,具体编号为C05200:31..为使高通滤波器中电感总数最少,通常选择图2b的归一化低通滤波电路进行变换.查表得归一化低通元件值为L】=0.5773,L2=0.0834,C2=1.2413,L=1.4579,L:0.1788,C4=1.3610,L5=1.2945根据变换规则:C高通=1/L低通和L高通=1/Cf~通, 将归一化低通滤波器变换为归一化高通滤波器,变换结果如图5所示.第三步:计算得到归一化高通滤波器的元件值.C1=1.7322,C2=11.9904,L2=0.8056,图5低通到高通归一化滤波电路的变换C3=0.6859,C4=5.5928,L4=0.7348,第四步:对归一化高通滤波器进行频率和阻抗标度.低通到高通变换之后,把归一化的高通滤波器根据要求的截止频率和阻抗进行标度.这里,FSF= 2=21T×1×10,Z=50.然后同样根据计算公式(1),(2),(3)对归一化高通滤波器进行频率和阻抗标度,标度后的去归一化元件值如图6所示.1V2n图61M高通滤波电路采用PSPICE仿真软件对1M高通滤波器电路仿真,仿真后可得到滤波器的传输特性,如图7所示. O—loo||L』,一f,,VfI.1IrlrO.1lOl0o频率/MHz(a)幅频特性曲线I|lI………一,\\\-～1.01030频率/MHz(h)相频特性曲线图71M高通滤波器幅频特性和相频特性曲线删一一24哈尔滨理工大学第13卷4椭圆函数带通滤波器的设计宽带带通滤波器可通过级联一个低通滤波器和一个高通滤波器得到.这种方法的有效性是基于这样的假设:即这些滤波器即使级联,仍然保持它们自己的响应不变.如果低通和高通滤波器级联,且两个滤波器设计成具有相等的信号源阻抗和端接阻抗,它们的截止频率至少相距一个或两个倍频程,那么,每个滤波器在其通带内将有合适的端接阻抗.如果通带间隔不够, 由于阻抗变化,滤波器将相互影响,这时候常用一衰减器将两个滤波器隔离,使这种影响减至最小.1M到30M的宽带带通滤波器可通过级联一个截止频率为1M的低通滤波器和一个截止频率为30M的高通滤波器得到.两个滤波器通带间隔比较大,故不需要使用衰减器,而直接级联即可.级联成的带通滤波器电路如图8所示.5结语一l00f,|l,:—rI川I●●●●●图81M到30M带通滤波电路同样,采用PSPICE仿真软件对1M到30M的带通滤波器电路进行仿真,可得到滤波器的传输特性, 如图9所示.由文[1]知,设计滤波器时要综合考虑截止特性和相位失真的要求.截止特性好的,相位失真就严重,两者不可兼得.由图4,图7,图9的仿真特性曲线可以看出,在滤波器阻带内有零点出现(毛刺现象),这是由椭圆函数滤波器的特性决定的.根据对滤波器衰减特性的要求,此椭圆函数带通滤波器设计折中了截止特性和相位失真度,符合设计要求.同时这种方法同文[5]的方法相比较,不但克服了其繁杂性,且极大地节省计算量,设计过程非常简练. ,'\\,\,\.0.31.010301001.01030频率/MHz频率/MHz(a)幅频特性曲线(b)相频特性曲线图9IM到30M带通滤波器幅频特性和相频特性曲线电力线为非理想的随机参数通信信道,本身具有高噪声,高衰减,高畸变等特性.利用低压配电线进行高速数据通信,所使用的频段一般在1—30MHz之间.本文设计的1M到3oM带通滤波器通常用于低压电力线通信系统研究中,通常与耦合器联用,在发送端使高频信号经过滤波后耦合到低压电力线上进行传输,同时将电力线上的50Hz工频信号隔离;在接收端也同样起耦合,强电隔离,滤波作用.本文采用一种新的计算方法,用PSPICE仿真软件分别对1M到30M低通,高通,带通滤波器进行了设计和仿真分析,仿真结果与滤波器性能吻合,证明这种滤波器的设计方法是有效的.上述方法也适用于其他频段的椭圆函数低通,高通,带通滤波器的设计及仿真过程,具有一定的灵活性.为设计人员提供了一种参考,也可缩短滤波器设计时间和减少设计人员的劳动强度.参考文献:[1](美)阿瑟.B.威廉斯.电子滤波器设计手册[M].喻春轩,译.北京:电子工业出版社,1986.[2]熊俊俏,卢容德.模拟椭圆低通滤波器的设计与仿真[J].华jE航天工业学院.2001(11):66—67.[3]李秀人.用PSPICE实现电子电路的设计与分折[J].微电子与基础产品.2001(3):51—53.[4]王田,CELESTINOA.Corral,杨士中.椭圆滤波器边带优化设计方法研究[J].仪器仪表.2005(6):562—586.【5JANSARIR.EllipticFilterDesignforaClassofGeneralizedHalf- bandFilters[J].IEEETrans.1985,33(44):1146—1150.,(编辑:付长缨)。
基于ADS的准椭圆函数带通滤波器的设计
＝００２４ － ． ３ ３
ｋ３ ００１２ ２ － ３ ６
ｋ ４ ０ ０１ ７ ｌｋ１ 一 ・ １ ７ ３ 一 ． ９１ ４ ０ ０ ０ １
ｋ ５ ＋ ． ２ ５ ４ ＝ ０ ０ １８
ｋ ６ 一 ． ２ ２ ｋ ７ ＋ ． ２ ４ ｋ ８ 一 ． ３ ２ ５ ＝ ０ ０６ ４ ５＝ ０ ０ ｉ ７ ６ ＝ ０ ０ ８４ ７＝ ０ ０ ５ ２ ｌｋ ８ 一 ．０ ８
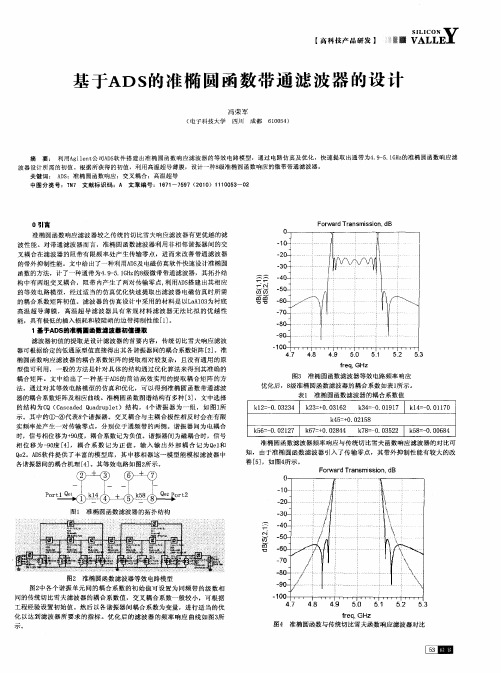
器 的耦 合系数 矩 阵及相 应 曲线 。准椭 圆 函数 图谱 结构 有多种 ［］ ３ ，文 中选择
的结 构 为Ｃ （ａ ｃｄ ｄ Ｑａ ｒｐ ｅ ）结 构 ，４ Ｏ Ｃｓ ａｅ ｕ ｄ ｕｌ ｔ 个谐 振 器 为 一 组 ， 如 图 １ 所
示 。其 中 的①— 代表 ８ ⑧ 个谐 振 器 。交叉 耦 合 与主 耦合 极 性相 反 时会 在有 限 实频 率 处产 生一 对传 输 零 点 ，分别 位 于通 频 带 的两侧 。谐振 器 间为 电耦 合 时 ，信号 相位 移为＋ ０ ，耦合 系数 记 为负值 。谐 振器 间 为磁耦 合 时，信 号 ９度 相 位 移 为 一Ｏ ［］ ９度 ４ ，耦 合 系 数 记 为 正 值 。输 入 输 出 外 部 耦 合 记 为 Ｏ ｌ ｅ 和 Ｑ ２ Ｄ软 件 提供 了 丰 富的模 型 库 ，其 中移 相 器这 一模 型 能模 拟 滤 波器 中 ｅ。Ａ Ｓ 各谐振 器 间的耦 合机 理 ［］ ４ 。其 等效 电路 如 图２ 示 。 所
４７ ４． ８ ４． ９ ５． ０ ５１ ５２ ５． ３
型值 可利 用 ，一般 的方法 是 针对 具体 的结构 通 过优 化 算法 来得 到 其准 确 的
耦 合 矩 阵 。文 中给 出 了一种 基 于Ａ Ｓ 简 洁高 效 实 用 的提 取 耦合 矩 阵 的 方 Ｄ的
椭圆函数LC带通滤波器的应用设计
椭圆函数LC带通滤波器的应用设计
滤波器类型的选择可根据滤波器设计的带宽等指标和具体的应用场合来选择。
相对带宽在20%以下的为窄带滤波器，应选用窄带滤波器的设计方法来设计；相对带宽在40%以上的为宽带滤波器，应选用宽带滤波器的设计方法来设计；而介于两者之间的为中等带宽滤波器。
由上面的指标可以看出本滤波器是窄带带通滤波器。
采用巴特沃斯滤波器来设计可以使通带内具有最大平坦的幅频响应；而切比雪夫滤波器的好处是：带外抑制好，但是带内有一定的波动；本文设计的滤波器要求带外近端抑制良好（可以用切比雪夫滤波器或椭圆函数滤波器来实现，但是从后面的分析看要使用LC滤波器，而用LC滤波器的话，使用切比雪夫形式电路元件的值过于小，很难实现，这个可以用软件仿真来说明），以此可以看出，用椭圆函数滤波器更适合。
微带滤波器通过采用不同的衬底材料可以在很大的频率范围内应用（从几百MHz到几十GHz）；同轴滤波器由于其微小的尺寸，制作精度很难达到；波导滤波器在小信号电平上，它的频率基本是8~100 GHz;陶瓷介质滤波器体积大，形状因子与品质因数较小；LC滤波器适用于本滤波器频段，且较容易制作和调试。
一种微带准椭圆函数带通滤波器的研制
函数多项式进 行多种 处理产生初 始耦合矩 阵 ， 然后 多次旋 转耦合矩 阵 ， 消去 不易实现 的耦合 单元 ， 最终 达 到所需形式 的耦合矩 阵 由于上述耦 合 系数 综合 方 法过 于 繁难 ， 便 于Ｔ 程实践 。 本 文采 用 Ｌ ｖ 不 ｅｙ等人
ｇａ ・ ｒｍ
Ｋｅ ｒ ：ｑ ｓ —ｅｌｐ ｉ ｕ ｃｉ ｎ；ｆｌｅ ；ｔａ ｓ ｓｉ ｎ ｚ ｒ ｙ ｗｏ ｄｓ ｕａ ｉ ｌｉ ｔ ｆ ｎ ｔ ｃ ｏ ｉｔｒ ｒ ｎ ｍｉｓｏ ｅ ｏ；ｓ ｌ ｃｉｉ ｅｅ ｔｖｔ ｙ
Ｏ 引 言
带有一 对传输零点 的准椭 网函数滤波 器相 比切 比雪 夫型 滤波 器具 备更 好 的选 择性 。在进 行准 椭 网 函数滤波器 的设 计时 ， 须首先 完成耦 合系数 的计 算 ， Ｊ 耦合系数 是滤波器设 计 中的一个 重要参 数 ， 必 Ｌ为 大 同
申 凯 王 光 明 谷 国栋 。齐立 辉 ， ， ，
（ ． 军 Ｉ 大学 导 弹学 院 ， 两 原 ７ ３０ ；． 周人 民 解 放 军驻 ７６厂 军 代 室 ， 安 ７０ ３ ） Ｊ空 ： 程 陕 １８０ ２ 巾 ８ 两 １０８
摘要 ： 带有…对传输零点的准椭网 函数滤波器相 比切 比雪 夫型滤波器具备更好的选择性
文章 编 号 ：１０ ７ ６ （０ ８ ０ ０ ４ ０ ０９— ９ １ ２０ ）５— ０ ３— ４
Ｄｅｅｏ ｍｅ ｔ ｆａＱｕ ｓ —Ｅ ｌ ｔ ｕ ｃｉｎＢ ｎ — ａｓＦｌ ｒ ｖｌｐ ｎ ａｉ— ｌｐｉ Ｆ ｎ ｔ ａ ｄ—Ｐ ｓ ｉｅ ｏ ｉ ｃ ｏ ｔ
椭圆带通滤波器的设计(matlab)
燕山大学课程设计说明书题目：椭圆带通滤波器的设计学院（系）：电气工程学院年级专业： 12级学号：学生姓名：指导教师：教师职称：电气工程学院《课程设计》任务书课程名称：数字信号处理课程设计基层教学单位：仪器科学与工程系指导教师：说明：1、此表一式四份，系、指导教师、学生各一份，报送院教务科一份。
2、学生那份任务书要求装订到课程设计报告前面。
电气工程学院教务科摘要所谓数字滤波器，是指输入输出均为数字信号，通过数值运算处理改变输入信号所含频率成分的相对比例，或者滤除某些频率成分的数字器件或程序。
数字滤波器处理精度高、稳定、体积小、重量轻、灵活、不存在阻抗匹配问题。
典型的模拟滤波器有巴特沃斯滤波器、切比雪夫滤波器和椭圆滤波器和贝塞尔滤波器，其中椭圆滤波器具有较好的性能。
Matlab是一套集数值计算、符号运算及图形处理等强大功能于一体的科学计算软件。
作为强大的科学计算平台，它几乎能够满足所有的计算需求。
本课结合MATLAB设计模拟椭圆滤波器。
目录第一章概论------------------------------------------------------ 1第二章信号处理原理---------------------------------------------- 22.1椭圆滤波器的基本理论-------------------------------------- 22.2采样定理-------------------------------------------------- 3第三章软件仿真设计---------------------------------------------- 43.1椭圆滤波器设计结构图-------------------------------------- 43.2设计椭圆模拟带通滤波器的步骤------------------------------ 43.3 MATLAB相关函数介绍--------------------------------------- 4第四章程序和仿真结果分析---------------------------------------- 84.1带通通滤波器设计程序-------------------------------------- 84.2仿真结果KK及分析----------------------------------------- 9参考文献-------------------------------------------------------- 13第一章概论椭圆滤波器又称考尔滤波器。
椭圆带通滤波器的设计.doc
椭圆带通滤波器的设计燕山大学课程设计说明:椭圆带通滤波器设计学院(系)名称:电气工程学院年级专业:12年级学校编号:学生姓名:讲师:教师职称:电气工程学院《课程设计》作业课程名称:数字信号处理课程设计基础教学单元；仪器科学与工程系讲师；学生姓名(专业)课程设计主题2椭圆带通滤波器技术参数的设计采样频率100赫兹，采样数100，低频、中频和高频信号频率分别为5Hz、15Hz和30Hz。
设计要求对连续信号进行采样和频谱分析，包括低频、中频和高频分量。
设计一个高通滤波器对信号进行滤波，观察滤波后信号的频谱。
(熟悉函数freqz，ellip，filter，fft)参考数据数字信号处理数据MATLAB 数据内容采集消化数据，学习MATLAB软件，计算相关参数，编写仿真程序，签署调试指导，签署基层教学单位主任在上半年的指令:1.本表一式四份，系、讲师、学生各一份，学院教务处一份。
2.学生的作业书需要装订在课程设计报告的前面。
电气工程学院教务处概要中的所谓数字滤波器，是指输入和输出都是数字信号，并且输入信号中包含的频率分量的相对比例通过数值计算处理而改变，或者某些频率分量被滤除的数字设备或程序。
该数字滤波器具有处理精度高、稳定、体积小、重量轻、灵活、无阻抗匹配问题的优点。
典型的模拟滤波器包括巴特沃斯滤波器、切比雪夫滤波器、椭圆滤波器和贝塞尔滤波器，其中椭圆滤波器具有更好的性能。
Matlab是一套集数值计算、符号计算和图形处理等强大功能于一体的科学计算软件。
作为一个强大的科学计算平台，它可以满足几乎所有的计算需求。
本课结合MATLAB设计一个模拟椭圆滤波器。
文字数据目录第1章简介第1章信号处理原理第2章椭圆滤波器基本理论第22.2章采样定理第3章软件仿真设计第43.1章椭圆滤波器设计结构图第43.2章设计椭圆模拟带通滤波器的步骤第43.3章MATLAB相关函数简介第4章程序和仿真结果分析第84.1章带通滤波器设计程序第84.2章仿真结果KK和分析第9章参考文献第13章文字数据简介椭圆滤波器又称考尔滤波器。
matlab设计椭圆带通滤波器
椭圆带通滤波器是一种数字信号处理中常用的滤波器，具有在指定频率范围内实现带通滤波的特点。
Matlab作为一种强大的科学计算软件，可以方便地对椭圆带通滤波器进行设计和实现。
本文将介绍使用Matlab设计椭圆带通滤波器的基本原理和方法，并给出相应的实例演示。
1. 椭圆带通滤波器的基本原理椭圆带通滤波器是一种数字信号处理滤波器，其设计依据是数字信号的频域特性和滤波器的传递函数。
在滤波器设计中，一般需要确定滤波器的通带、阻带以及过渡带的频率范围，以及滤波器在这些频率范围内的增益特性。
椭圆带通滤波器相比于其他常见的滤波器如Butterworth滤波器和Chebyshev滤波器，其具有更为陡峭的通带与阻带边缘、更小的过渡带宽度、更高的阻带衰减等优点，适用于对信号频率精确要求较高的应用场景。
2. 椭圆带通滤波器的设计步骤椭圆带通滤波器的设计主要包括两个方面：确定滤波器的频率响应特性和实现滤波器的传递函数。
在Matlab中，可以利用信号处理工具箱提供的相关函数和工具进行滤波器设计和分析，以下是椭圆带通滤波器设计的基本步骤：(1) 确定滤波器的通带、阻带与过渡带频率范围；(2) 根据设计要求选择椭圆带通滤波器的滤波器类型、阶数和指定通带和阻带的最大允许波纹；(3) 使用Matlab中的ellipord函数计算椭圆带通滤波器的阶数和截止频率；(4) 利用ellip函数设计滤波器的传递函数，并计算其零极点信息；(5) 可视化滤波器的频率响应曲线和幅度响应曲线，评估滤波器的设计效果。
3. Matlab实例演示以下是使用Matlab进行椭圆带通滤波器设计的简单实例演示：(1) 确定椭圆带通滤波器的设计参数，包括通带频率范围、阻带频率范围及其对应的最大允许波纹等；(2) 使用Matlab中的ellipord函数计算椭圆带通滤波器的阶数和截止频率，例如：```matlab[order, cutoff] = ellipord(wp, ws, Rp, Rs, 's');```(3) 利用ellip函数设计滤波器的传递函数，并计算其零极点信息，例如：```matlab[num, den] = ellip(order, Rp, Rs, cutoff, 's');zplane(num, den);```(4) 绘制滤波器的频率响应曲线和幅度响应曲线，例如：```matlabfreqz(num, den);```(5) 评估滤波器的设计效果，包括通带波纹、阻带衰减、相位特性等。
基于椭圆球面波函数的数字带通滤波器设计
基于椭圆球面波函数的数字带通滤波器设计数字信号处理中的数字滤波器在信号处理中扮演着至关重要的角色，其中数字带通滤波器是其中的一种。
数字带通滤波器可以帮助我们过滤掉不需要的高频信号，同时保留在我们希望保留的频率范围内的信号。
在这篇文章中，我们将讨论基于椭圆球面波函数的数字带通滤波器设计。
椭圆球面波函数是一种特殊的函数，它在数学和工程中都有广泛的应用。
在数字信号处理领域中，椭圆球面波函数被用于数字滤波器设计中，特别是在设计带通和陷波滤波器中。
这是因为椭圆球面波函数具有可控的、高阶的滤波特性，这使得它成为设计数字带通滤波器的一种有力工具。
在使用椭圆球面波函数设计数字带通滤波器时，我们需要确定一些设计参数，例如通带和阻带边缘频率、通带和阻带最大衰减以及滤波器的阶数等。
确定这些参数的方法是基于所需的应用和滤波器性能的具体要求而定的。
例如，在通信系统中，我们可能需要设计一个数字带通滤波器，以仅通过特定频率的信号，以及阻止频率范围外的其他信号。
因此，在这种情况下，我们需要根据特定的通信系统来确定所需的滤波器特性。
在确定设计参数之后，我们可以利用椭圆球面波函数来设计数字带通滤波器。
这可以通过一些计算和优化技术来实现。
例如，我们可以使用著名的Parks-McClellan算法来设计数字滤波器。
该算法可以根据所需的滤波特性，通过优化椭圆球面波函数来生成数字带通滤波器。
在数字带通滤波器被设计和实现之后，我们可以将其应用于所需的数字信号处理应用中。
例如，在音频处理中，我们可以应用数字带通滤波器来滤除噪声信号，以便我们更好地听到音频信号的细节和细微之处。
在图像处理中，数字带通滤波器可以提高图像的清晰度和质量，以便我们更好地识别和分析图像。
总之，基于椭圆球面波函数的数字带通滤波器是数字信号处理领域中的一个强大和有用的工具。
通过确定滤波器的设计参数，我们可以使用椭圆球面波函数来生成数字带通滤波器，并将其应用于不同的数字信号处理应用中。
基于SIR的准椭圆函数微带带通滤波器设计
基于SIR的准椭圆函数微带带通滤波器设计刘凯正;刘仕琴;向天宇;郑晓缘;雷涛【摘要】A microstrip bandpass filter with quasi-elliptic function response based on SIR was proposed for the first time. With two opened half-wavelength SIRs side-coupled to I/O feed lines, the realized filter response possesses two transmission zeros in stopband which improve the stopband rejection, first spurious rejection and selectivity, but the circuit size is almost not increased. The effective overall circuit only occupies 16 mm×3.32 mm, about 0.45λg×0.093λg, where λgis the guided wavelength at the passband centre frequency. The simulated and measured results show that the bandstop filter has a centre frequency of 4.95 GHz. The minimum insertion loss is 1.6 dB. The two transmission zeros are located at 2.34 GHz and 6.3 GHz. The stopband rejections are better than 40 dB and 35 dB near the lower stopband and upper stopband, respectively. The first spurious rejection is better than 25 dB. The bandwidth of upper stopband better than 20 dB is 9 GHz.%首次提出一种基于SIR(Stepped Impendence Resonator)的准椭圆函数微带带通滤波器.两阶SIR与I/O馈线之间采用边缘耦合的方式,在上下阻带各产生一个传输零点,在几乎不增加滤波器尺寸的情况下,有效提高了滤波器的带外抑制度与选择性,并且有效抑制了阻带的一次杂散.滤波器的有效尺寸为16 mm×3.32 mm,等于0.45λg×0.093λg(λg为通带中心频率的波导波长),中心频率位于4.95 GHz,带内最小插损为1.6 dB,两个传输零点分别位于2.34 GHz,6.3 GHz,下阻带边缘抑制度大于40 dB,上阻带边缘抑制度大于35 dB,阻带一阶杂散抑制度大于25 dB,大于20 dB上阻带宽度为9 GHz.【期刊名称】《电子元件与材料》【年(卷),期】2018(037)005【总页数】4页(P73-76)【关键词】SIR;边缘耦合;滤波器;准椭圆函数;高选择性;高阻带抑制【作者】刘凯正;刘仕琴;向天宇;郑晓缘;雷涛【作者单位】贵州师范大学机械与电气工程学院,贵州贵阳 550025;吉安职业技术学院机械与电子工程学院,江西吉安 343000;贵州师范大学机械与电气工程学院,贵州贵阳 550025;贵州师范大学机械与电气工程学院,贵州贵阳 550025;贵州师范大学机械与电气工程学院,贵州贵阳 550025【正文语种】中文【中图分类】TN713现代无线通信系统对射频滤波器的小型化、高性能方面的要求越来越高，而提高滤波器的选择性与带外抑制度是提高射频滤波器性能的主要发展方向之一。
一种椭圆函数微带低通滤波器的设计与实现
一种椭圆函数微带低通滤波器的设计与实现李婵娟;傅世强;孙爽【摘要】为克服传统微带低通滤波器结构尺寸大和过渡带衰减慢的缺点,基于椭圆函数低通滤波器原型,设计了一款结构紧凑、插损小、过渡带陡峭的高低阻抗线微带低通滤波器.给出了该滤波器结构尺寸的计算公式,并通过仿真软件ADS和HFSS 对其进行了仿真优化,采用微波材料板制作出滤波器实物并进行了测试验证,实测结果与仿真结果具有较好的一致性,且验证了该设计方案的可行性.【期刊名称】《电子科技》【年(卷),期】2015(028)011【总页数】3页(P69-70,74)【关键词】低通滤波器;微带线;高低阻抗;椭圆函数【作者】李婵娟;傅世强;孙爽【作者单位】大连海事大学信息科学技术学院,辽宁大连116026;大连海事大学信息科学技术学院,辽宁大连116026;大连海事大学信息科学技术学院,辽宁大连116026【正文语种】中文【中图分类】TN713微波滤波器是现代通信系统中重要部件之一，其的主要作用是抑制不需要的信号，让需要的信号通过。
滤波器的优劣直接影响到整个系统的性能。
高性能的微带低通滤波器常被用来抑制系统的谐波输出。
基于Richards 变换与Kuroda 法则的微带低通滤波器设计［1－2］和高低阻抗微带低通滤波器的设计［3－4］是两种常用的方法。
然而，上述方法设计的滤波器一方面电路尺寸较大，过渡带较宽;另一方面由于相邻耦合线线宽不同产生不连续性，使带内插入损耗较大。
为此，文献［5］和文献［6］采用DGS 技术，使滤波器电路结构更加紧凑;文献［7］运用分形结构设计成阶跃阻抗微带滤波器，改善通带特性;文献［8］采用扇形短截线结构设计微带滤波器，缩小尺寸的同时提升了性能。
但以上设计方法复杂，对于加工精度要求较高。
为克服传统微带滤波器结构不紧凑，阻带衰减较慢，寄生通带抑制不充分等缺点，本文采用微带滤波器中比较成熟的高低阻抗线结构，设计并实现了一款截止频率为1 GHz 的椭圆函数微带低通滤波器。
带DGS结构的宽带微带线准椭圆函数滤波器设计
带DGS结构的宽带微带线准椭圆函数滤波器设计
刘丹丹;肖高标
【期刊名称】《信息技术》
【年(卷),期】2007(31)3
【摘要】准椭圆滤波器体积小,重量轻,结构紧凑,比契比雪夫滤波器有更好的过渡特性,更高的带外抑制,在卫星通信和移动通信中有广泛的应用前景.但在用准椭圆滤波器实现宽带滤波器时,有时会遇到耦合间隙过小难以加工的问题.在准椭圆滤波器的谐振器底板加入缺陷接地结构(DGS),可以增强谐振器之间的耦合.应用DGS结构,用较宽的耦合间隙实现较强的耦合,从而使宽带滤波器物理上更容易实现.应用三维电磁场仿真软件,设计了一种带DGS结构的宽带微带线准椭圆函数滤波器.
【总页数】5页(P51-55)
【作者】刘丹丹;肖高标
【作者单位】上海交通大学电子工程系,上海,200240;上海交通大学电子工程系,上海,200240
【正文语种】中文
【中图分类】TN713
【相关文献】
1.基于共面波导/微带线耦合结构的超宽带滤波器设计 [J], 徐姣姣;姜弢
2.基于DGS结构的超宽带高通滤波器设计 [J], 张山杉
3.基于准椭圆函数响应的超宽带介质滤波器设计 [J], 李明
4.DGS微带线滤波器设计 [J], 林强;张祖荫;郭伟
5.基于平行耦合微带线和DGS结构的超宽带滤波器 [J], 王章静
因版权原因，仅展示原文概要，查看原文内容请购买。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
ｒｅａｌ ａｎｄ
ｉｍａｇｉｎａｒｙ ｆｒｅｑｕｅｎｃｉｅｓ［Ｊ］．ＩＥＥＥ
ｒｙ
Ｔｒａｎｓ．Ｍｉｃｒｏｗａｖｅ Ｔｈｅｏ－
ａｎｄ Ｔｅｃｈ。１９７６，２４：１７２—１８１． ａｎｄ
图５
传输特性测试曲线
［３］Ｊ．Ｓ．Ｈｏｎｇ
Ｍ．Ｊ．Ｌａｎｃａｓｔｅｒ．Ｄｅｓｉｇｎ ｏｆ ｈｉｇｈｌｙ ａｅｌｅｅ・
ａ
ｔｉｖｅ ｍｉｅｒｏｓｔｒｉｐ ｂａｎｄｐａｓｓ ｆｉｌｔｅｒｓ ｗｉｔｈ ｕａｔｉｏｎ ｐｏｌｅｓ
—６３．
■ 位
Ｊ
舶
『
ｌ ．｝
／
＼
［５］申凯，王光明，郑武团．微带阶跃阻抗谐振器小型化滤
枷
－
Ｉ
Ｉ
波器的精确设计［Ｊ］．中国电子科学研究院学报，
Ｉ
囊取ＯＳｚ） 图６设计仿真曲线
。、
２００８．３（２）：１９５—１９８． ［６］Ｍ．Ｍａｋｉｍｏｔｏ，Ｓ．Ｙａｍａｓｈｉｔａ．无线通信中的微波谐振器 与滤波器［Ｍ】．赵宏锦，译．北京：国防Ｔ业出版社，
２．Ｍｉｌｉｔａｒｙ Ｒｅｐｒｅｓｅｎｔａｔｉｖｅ Ｏｆｆｉｃｅ ｏｆ ＰＬＡ ｉｎ Ｎｏ．７８６ Ｏｐｅｒａｔｉｏｎ，Ｘｉｈｎ Ｓｈａｎｘｉ Ａｂｓｔｒａｃｔ：Ｔｈｅ ｑｕａｓｉ—・ｅｌｌｉｐｔｉｃ ｆｕｎｃｔｉｏｎ ｆｉｌｔｅｒ ｗｉｔｈ Ｃｈｅｂｙｓｈｅｖ ｆｉｌｔｅｒ．Ｂａｓｅｄ
ｏｎ ｏｎｅ
万方数据
淮
阴工学院学报
２００８笠
图１ ，‘：＿
７
准椭圆函数滤波器低通原型等效电路
由式（２）给出
ｇＩ
２ｓｉ凡五７１＂ ２——
ｇｌｇｉ—Ｉ：譬囊譬㈦．１五
一
“＝瓦≯玄
即
㈩
＝———————了■—了■＿ｔｌ＝ Ｖ‘＋Ｓｌ，ｌ‘３————ｏ
＿，川的引入使滤波器发生失谐，为了满足通频 带内所要求的回波损耗，必须对Ｌ的值进行修正，
２．２
‰。＝半
‰相＝罨≥
２
２．１
耦合系数和外部品质因数的计算
为了满足指定的阻带，衰减极点应该被放置
（４）
在垃＝±１。２６４５处。将晓＝１．２６４５带人式 （１）（２）（３）可以得到低通原型滤波器的元件值， 即ｇＩ＝１．０２７６１，９２＝１．４６５６１，９３＝１．９９１８４，９４ ＝１．８６４４１，Ｊ３＝－０。３３６８１，＾＝１．３０１３。准椭圆函 数滤波器的电参数由式（４）解得：
八阶准椭圆函数带通滤波器的设计
滤波器设计指标：
中心频率：９８５ＭＨｚ
Ｍ１２＝Ｍ７Ｂ＝０．０８４４１，Ｍ２，＝％＝０．０６０６３，
Ｍ３４＝纸＝０．０５３７５，犯５＝０．０７２３，纸＝一０．
万方数据
第５期
申凯。王光明，谷国栋，等：一种微带准椭圆函数带通滤波器的研制
４５
０１７５２，Ｑ“＝Ｑ。＝９．９２０２７ 滤波器谐振器对级间耦合系数和输入输出谐 振器的外部品质因数的计算参照文献中的计算方 法。 滤波器可由２６ｍｍ
万方数据
Ⅲ∞Ｉ，∞‘Ｉ‘：■：∞
标和实测结果．发现二者吻合比较好。其中，中心 频率的设计结果比指标偏高１３ＭＨｚ（１．３２％），带 宽减小了１３．０３６２ＭＨｚ。此方法设计精度较高，可以 满足Ｔ程要求。
∞●ｔｈ
』
１、
１ Ｌ
Ｉ‘Ｍ●●■ 酊Ｉ
ＩＩ
ｎｍｈ
乱－ｔ●¨●■
参考文献：
＾
【１］Ｒ．Ｍ．Ｋｕｒｚｏｋ．Ｇｅｎｅｒａｌ
Ｄｅｖｅｌｏｐｍｅｎｔ ｏｆ
（１．Ｓｃｈｏｏｌ
ａ
Ｑｕａｓｉ—・Ｅｌｌｉｐｔｉｃ
Ｆｕｎｃｔｉｏｎ Ｂａｎｄ——Ｐａｓｓ Ｆｉｌｔｅｒ Ｇｕｏ—ｄｏｎ９１。ＱＩ
Ｌｉ—ｈｕｉ２
ＳＨＥＮ Ｋａｉ‘，ＷＡＮＧ Ｇｕａｎｇ—ｍｉｎｇ。，ＧＵ
ｏｆ Ｍｉｓｓｉｌｅ，Ａｉｒ Ｆｏｒｃｅ Ｅｎｇｉｎｅｅｒｉｎｇ Ｕｎｉｖｅｒｓｉｔｙ，Ｓａｎｙｕａｎ Ｓｈａｎｘｉ ７ １ ３８００，Ｃｈｉｎａ；
Ｘ
曲线。
２．３
滤波器的设计仿真与实测结果
如图３所示。可得微带八阶准椭圆函数滤波器
的几何结构： ２６ｒａｍ的方形开环谐振器
Ｓ１２
２
５７８＝０。３ｒａｍ，Ｓ２３
２
Ｓ６７＝０．４ｒａｍ，Ｓ＿＝
来实现。采用相对介电常数为３．３８，厚度为０．８１３ｒａｍ 的介质基片。采用Ｓｏｎｎｅｔ仿真软件拟合出谐振器的 级间耦合系数和外部品质因数与其物理结构的关系
Ｊ。＝１／，Ｉｓ
Ｊ。一ｌ＝０
为了在１－１＝±ｎ处引入传输零点，Ｌ一。的值可
７
＇
ｒ
＇ｒ
７７
～Ｌ．
Ｊ■
－ｈ．
Ｊ１
图２
具有一对衰减极点滤波器的一般耦合结构
带内插损：≤３．５ｄＢ
ｑ“＝口。＝而ｇ丽ｌ
Ｍｉ．ｉ＋。＝：Ｍ。一ｊ．。一ｉ＋。＝＝婴（ｉ：１，２，３，，ｎ
～／ｇｉｇｉ＋１
通带带宽：１０５ＭＨｚ ４０ｄＢ阻带带宽：１２９ＭＨｚ 通带回波损耗：一２０ｄＢ
７１００３８，Ｃｈｉｎａ）
ｔｒａｎｓｍｉｓｓｉｏｎ
ｚｅｒｏ
ｈａｓ ｔｈｅ ｂｅｔｔｅｒ ｓｅｌｅｃｔｉｖｉｔｙ ｔｈａｎ ｔｈｅ ｇｅｎｅｒａｌ
ｔｈｅ ｄｅｓｉｇｎ ａｐｐｒｏａｃｈ ｐｒｅｓｅｎｔｅｄ ｂｙ Ｌｅｖｙ ｅｔｃ．ａｎｄ ｔｈｅ ｍｉｃｒｏｗａｖｅ ｆｉｌｅｄ ｓｉｍｕｌａｔｉｏｎ ｓｏｆｔ－
ｆｏｕｒ—ｒｅｓｏｎａｔｏｒ ｆｉｌｔｅｒｓ
ａｔ
ｍｉｃｒｏ－
∥
／
｜ ｛
ｗａｖｅ
ｆｒｅｑｕｅｎｃｉｅｓ［Ｊ】．ＩＥＥＥ
Ｔｒａｎｓ．Ｍｉｃｒｏｗａｖｅ
Ｔｈｅｏｒｙ
ａｎｄ Ｔｅｅｈ，１９６６，１４：２９５—２９６．
【２］Ｒ．Ｌｅｖｙ，Ｆｉｌｔｅｒｓ
ｗｉｔｈ ｓｉｎｇｌｅ ｔｒａｎｓｍｉｓｓｉｏｎ
ｚｅｒｏ￥ａｔ
滤波器的综合及电参数的求取
准椭圆函数滤波器的传输零点可以通过滤波器的不相邻谐振器之间增加交叉耦合来实现。Ｌｅｖｙ等
人提出了一种基于图ｌ所示的低通原型结构的滤波器近似综合方法。图中的矩形框代表理想的导纳变 换器，低通原型的元件值可由公式（１）求出：
收稿日期：２００８—０５—２５ 作者简介：申凯（１９７９一），男，山西运城人，在读博士，主要研究方向为微波电路与系统。
Ｓ５６＝０．７ｍｍ，Ｓ＂＝０．６ｍｍ，Ｓ２３＝Ｉ．３ｒａｍ，ｔＩ＝ｔ２＝ １４．Ｏｍｍ
－Ⅻ
ｔｍ
●Ⅻ
●《 “∞
ａ．Ｄｌ｜
Ｅ．ｍ．
Ⅷ●
口Ｊ１ｌ ●ＪＩ●
＾∞●
Ｅ
ｔ（ｍｍｌ
图３
耦合系数和外部品质因数曲线
ｔ，ｌ
图４
八阶准椭圆函数滤波器
万方数据
４６
淮
阴工学院学报
２００８年
图５和图６分别为加丁样品的测试结果与设 计结构的Ｓｏｎｎｅｔ仿真结果。
第１７卷第５期
２００８年１０月
淮
阴
Ｔ学院学报
Ｖ０１．１７ Ｎｏ．５ ０ｃｔ．２００８
Ｊｏｕｒｎａｌ ｏｆ Ｈｕａｉｙｉｎ Ｉｎｓｔｉｔｕｔｅ ｏｆ Ｔｅｃｈｎｏｌｏｇｙ
一种微带准椭圆函数带通滤波器的研制
申
凯１，王光明１，谷国栋１，齐立辉２
（１．空军Ｔ程大学导弹学院，陕西ｉ原７１３８００；２．中国人民解放军驻７８６厂军代室，西安７１００３８） 摘要：带有一对传输零点的准椭网函数滤波器相比切比雪夫型滤波器具备更好的选择性。采用ｋｖｙ等人提Ｈ｛的一种滤 波器近似综合方法，结合微波场仿真软件，实现ｒ对８阶准椭圆函数滤波器的精确设计，加－１ｊ和实测结果表明丫该方法的 有效性，完全可以满足下程需求。 关键词：准椭圆甬数；滤波器；传输零点；选择性 分类号：ＴＮ８１４ 文献标识码：Ａ 文章编号：１００９—７９６１（２００８）０５—００４３—０４
Ｏ
引言
带有一对传输零点的准椭网函数滤波器相比切比雪夫型滤波器具备更好的选择性。在进行准椭圆
函数滤波器的设计时，必须首先完成耦合系数的计算，因为耦合系数是滤波器设计中的一个重要参数，同 时又有较大的难度，它的计算精确与否直接关系到滤波器设计是否成功。椭圆甬数滤波器的设计过程一 般是根据滤波器设计指标，如中心频率、带宽、带内插损等，采用适当的方法，综合优化ｍ相应的耦合矩 阵。需说明的是，由指标获取耦合矩阵的过程相当复杂且难度较大。就综合手段而言，目前还没有一个 非常好的方法，其通用的过程是：由指标构造传递函数，其分子和分母均为有理函数多项式，通过对有理 函数多项式进行多种处理产生初始耦合矩阵，然后多次旋转耦合矩阵，消去不易实现的耦合单元，最终达 到所需形式的耦合矩阵。由于上述耦合系数综合方法过于繁难，不便于工程实践。本文采用Ｌｅｖｙ等人 提ｍ的相对较为简单近似综合方法，完成了８阶准椭圆函数滤波器的设计。 ｌ
，
，ｚ，
…，ｍ），ｍ＝ｎ／２ ７：ｓｉ，ｌＩＩｌ（』１ｉ，ｌ＾一－ｊ一）
（１）
－，二＝＿ｊ产广 “
１＋．，。．，。一ｌ
（３）
”７
ห้องสมุดไป่ตู้
由式（１）得出初始值，再由式（２）和（３）循环 解出修正值，其他元件值保持不变。 准椭圆函数滤波器的电参数（即图２所示的外 部品质因数和耦合系数），由下列公式确定：
Ｓ＝（√１＋占２＋占）２（通带驻波比）
ｗａｒｅ，ｔｈｅ ｐｒｅｃｉｓｅ ｄｅｓｉｇｎ ｏｆ ８一ｏｒｄｅｒ ｑｕａｓｉ—ｅｌｌｉｐｔｉｃ ｆｕｎｃｔｉｏｎ ｆｉｌｔｅｒｓ ｗａｓ ｍａｄｅ．Ｔｈｅ ａｖａｉｌａｂｉｌｉｔｙ ａｎｄ ｔｈｅ ａｃｃｕｒａｃｙ ｏｆ ｔｈｅ ｍｅｔｈｏｄ ｗｅｒｅ ｐｒｏｖｅｄ ｂｙ ｔｈｅ ｔｅｓｔ ｒｅｓｕｌｔｓ．Ｔｈｅ ｍｅｔｈｏｄ ｉｓ ａｌｓｏ ａｂｓｏｌｕｔｅｌｙ ａｐｐｌｉｃａｂｌｅ ｔｏ ｔｈｅ ｇｅｎｅｒａｌ ｄｅｓｉｇｎ ｐｒｏ— ｇｒａｍ－ Ｋｅｙ ｗｏｒｄｓ：ｑｕａｓｉ—ｅｌｌｉｐｔｉｃ ｆｕｎｃｔｉｏｎ；ｆｉｌｔｅｒ；ｔｒａｎｓｍｉｓｓｉｏｎ ｚｅｒｏ；ｓｅｌｅｃｔｉｖｉｔｙ