组合图形的惯性矩.
惯性矩
1、静矩（求形心）⎰=AZ ydA S⎰=Ay zdA SSz 、Sy 分别定义为图形对z 轴和y 轴的静矩，也称为图形对z 轴和y 轴的一次矩。
平面图形的静矩是对某一坐标而言的，同一图形对不同的坐标轴，其静矩也就不同。
静矩的数值可能为正值，可能为负值，也可能为零。
静矩的量纲是长度的三次方。
静矩用来求平面图形的形心坐标：A zdAz A ydAy AA⎰⎰==对于规则的形状，可以将其划分为若干个规则的简单图形，通过组合求的形心。
212211212211A A z A z A z A A y A y A y ++=++=注：A 为简单图形的面积（空心面积可以为负值），y 、z 为简单图形的形心坐标值2、惯性矩⎰⎰==Ay AZ dAz I dAy I 22Iz 、Iy 分别定义为图形对z 轴和y 轴的惯性矩，也称为图形对z 轴和y 轴的二次轴矩。
惯性矩始终为正值，惯性矩的量纲是长度的四次方。
计算步骤123222332202202bh bx dx x b x bdx dA z I h h Ay =⨯=⨯=⨯⨯==⎰⎰⎰左图三角形面积对z轴的惯性矩1243)()(44322hyhydyyyhydyyhI hhz=-=-=⨯-=⎰⎰右图关于z轴的惯性矩为左图的四倍34hIz=惯性距的平行移轴定理：有了它规则形状的物体就不用通过积分来求惯性矩了，省时省力(但精准度差了一些)截面图形对某轴的惯性矩，等于它对该轴平行的形心轴的惯性矩，加上两轴间距离的平方乘以截面面积。
A a I I xc x 2+=Ix ——截面图形对目标轴的惯性矩（目标轴：组合图形的形心轴） Ixc ——截面图形对形心轴的惯性矩（注意理解：此处的形心轴是指划分的规则截面的形心轴）a ——两轴之间的距离 A ——截面图形的面积3、极惯性矩图形对于任意一对互相垂直的轴的惯性矩之和，等于它对该两轴交点的极惯性矩。
I p=I z+I y4、惯性积在平面图形的坐标（x ，y ）处，取微面积dA ，遍及整个图形面积的积分⎰=AyzyzdA I ，定义为图形对y ，z 轴的惯性积。
惯性矩基础知识
ah a
dz
by ybdy 2
b
2 ah
a
h bh(a ) AyC 2
2 b
z
S y zdA zhdz A
0
S zc ydA
A
h 2
hz 2
0 h
b bh AzC 2
2 h 2
ybdy
h 2
by 2 2
0
4
二、简单图形的形心
1、形心坐标公式：
S z A ydA yc A A S y AzdA zc A A
E
C D
z1
z
O
z
B
I z1 I y1 I z I y
上式表明，截面对于通过同一点的任意一对相互垂直 的坐标轴的惯性矩之和为一常数，并等于截面对该坐标原 点的极惯性矩
22
I z1 I y1
Iz Iy 2 Iz Iy 2 2
Iz Iy 2 Iz Iy 2
cos 2 I zy sin 2 cos 2 I zy sin 2
i ci
Az
120
z
yc
A y
i
ci
A
A1 y c1 A2 y c 2 A1 A2
60 1100 34.7(mm) 10 110 80 10 8
y
10 10
解法三：负面积法
A1 9600mm 2 , z c1 40mm, y c1 60mm A2 70 110mm 2 , z c 2 45mm, y c 2 65mm
2
y
z
yc zc
b
c
a
y
dA yc
zc
I zy I zcyc abA
——平行移轴公式
惯性矩的计算方法
I等． I等是从不同角度反映了截S，其数学表达式(4 -1a )(4-1b)(4 -2a )(4-2b)式中 y、 z 为截面图形形心的坐标值．若把式 (4-2) 改写成(4-3)性质：•若截面图形的静矩等于零，则此坐标轴必定通过截面的形心．•若坐标轴通过截面形心，则截面对此轴的静矩必为零．•由于截面图形的对称轴必定通过截面形心，故图形对其对称轴的静矩恒为零。
4 ）工程实际中，有些构件的截面形状比较复杂，将这些复杂的截面形状看成是由若干简单图形 ( 如矩形、圆形等 ) 组合而成的．对于这样的组合截面图形，计算静矩 (S) 与形心坐标 (y、 z ) 时，可用以下公式(4-4)(4-5)式中 A， y ， z 分别表示第个简单图形的面积及其形心坐标值， n 为组成组合图形的简单图形个数．即：组合图形对某一轴的静矩等于组成它的简单图形对同一轴的静矩的代数和．组合图形的形心坐标值等于组合图形对相应坐标轴的静矩除以组合图形的面积．组合截面图形有时还可以认为是由一种简单图形减去另一种简单图形所组成的．例 4-1 已知 T 形截面尺寸如图 4-2 所示，试确定此截面的形心坐标值．、两个矩形，则设任一截面图形 ( 图 4 — 3) ，其面积为 A ．选取直角坐标系 yoz ，在坐标为 (y 、 z) 处取一微小面积 dA ，定义此微面积 dA 乘以到坐标原点o的距离的平方，沿整个截面积分，为截面图形的极惯性矩 I．微面积 dA 乘以到坐标轴 y 的距离的平方，沿整个截面积分为截面图形对 y 轴的惯性矩 I．极惯性矩、惯性矩常简称极惯矩、惯矩．数学表达式为极惯性矩 (4-6)对 y 轴惯性矩 (4 -7a )同理，对 z 轴惯性矩 (4-7b)由图 4-3 看到所以有即(4-8) 式 (4 — 8) 说明截面对任一对正交轴的惯性矩之和恒等于它对该两轴交点的极惯性矩。
在任一截面图形中 ( 图 4 —3) ，取微面积 dA 与它的坐标 z 、 y 值的乘积，沿整个截面积分，定义此积分为截面图形对 y 、z 轴的惯性积，简称惯积．表达式为(4-9)惯性矩、极惯性矩与惯性积的量纲均为长度的四次方． I,I,I恒为正值．而惯性积 I其值能为正，可能为负，也可能为零．若选取的坐标系中，有一轴是截面的对称轴，则截面图形对此轴的惯性积必等于零．当截面图形对某一对正交坐标轴的惯性积等于零时，称此对坐标轴为截面图形的主惯性轴．对主惯性轴的惯性矩称为主惯性矩．而通过图形形心的主惯性轴称为形心主惯性轴 ( 或称主形心惯轴 ) ．截面对形心主惯性轴的惯性矩称为形心主惯性矩 ( 或称主形心惯矩 ) ．例如，图 4-4 中若这对 yz 轴通过截面形心，则它们就是形心主惯性轴．对这两个轴的惯性矩即为形心主惯性矩．工程应用中 ( 如压杆稳定中 ) ，有时将惯性矩表示成截面面积与某一长度平方的乘积，即,或写成, （ 4-10 ）式中 i分别称为截面图形对 y 轴、 z 轴的惯性半径．其量纲为长度的一次方．例 4-2 已知矩形截面的尺寸 b,h( 图 4-5) ，试求它的形心主惯性矩．解：取形心主惯性轴 ( 即对称轴 )y,z ，及 dA=dy，代入公式 (I— 7a ,) 得同理：例 4-3 设圆的直径为 D( 图 4-6) ，试求图形对其形心轴的惯性矩及惯性半径值．解： (1) 求惯性矩因为图形对称， y,z 为对称轴，所以 I＝ I这是较简单的解法．本例也可取出图 4-6 上的微面积 dA ，按积分法来求得。
材料力学附录I 平面图形的几何性质2形心主轴和形心主惯性矩
i1
i1
i1
材料力学 附录I 平面图形的几何性质
例I-4-1：已知三角形对底边(x1轴)的惯性矩为bh3/12，
求其对过顶点的与底边平行的x2轴的惯性矩。
解：由于x1、x2轴均非形心轴，所以不
x2
能直接使用平行移轴公式，需先求出 三角形对形心轴xC的惯性矩，再求对
h xC
h/3
x1
x2轴的惯性矩，即进行两次平行移轴
3.求截面形心主惯性矩的方法
①建立坐标系
②计算面积和面积矩 ③求形心位置
x
Sy A
xi Ai A
y
Sx A
yi Ai A
④建立形心坐标系；求：IyC ， IxC ， IxCyC
⑤求形心主轴方向 — 0
tg2
0
2I xCyC I xC I yC
⑥求形心主惯性矩
I I
xC0 yC0
I
x
C
I 2
b
：
I xC
I x1
a12 A
bh3 12
h 2 3
bh 2
bh3 36
I x2
I xC
a22 A
bh3 36
2h 2 3
bh 2
bh3 4
材料力学 附录I 平面图形的几何性质
例I-4-2：求图示T型截面对形心轴的惯性矩。
30
5
30
5
材料力学 附录I 平面图形的几何性质
30
求T形截面对形心轴的惯性矩
C O
10 150yC x1
x
由于对称知： xC=0
材料力学 附录I 平面图形的几何性质
§I-2 惯性矩和惯性半径
一、惯性矩
最新惯性矩总结(含常用惯性矩公式)
惯性矩是一个物理量，通常被用作描述一个物体抵抗扭动，扭转的能力。
惯性矩的国际单位为(m^4)。
工程构件典型截面几何性质的计算2.1面积矩1．面积矩的定义图2-2.1任意截面的几何图形如图2-31所示为一任意截面的几何图形(以下简称图形)。
定义：积分和分别定义为该图形对z轴和y轴的面积矩或静矩，用符号S z和S y，来表示，如式(2—2.1)(2—2.1)面积矩的数值可正、可负，也可为零。
面积矩的量纲是长度的三次方，其常用单位为m3或mm3。
2．面积矩与形心平面图形的形心坐标公式如式(2—2.2)(2—2.2)或改写成，如式(2—2.3)(2—2.3)面积矩的几何意义：图形的形心相对于指定的坐标轴之间距离的远近程度。
图形形心相对于某一坐标距离愈远，对该轴的面积矩绝对值愈大。
图形对通过其形心的轴的面积矩等于零；反之，图形对某一轴的面积矩等于零，该轴一定通过图形形心。
3．组合截面面积矩和形心的计算组合截面对某一轴的面积矩等于其各简单图形对该轴面积矩的代数和。
如式(2—2.4)(2—2.4)式中，A和y i、z i分别代表各简单图形的面积和形心坐标。
组合平面图形的形心位置由式(2—2.5)确定。
(2—2.5)2.2极惯性矩、惯性矩和惯性积1．极惯性矩任意平面图形如图2-31所示，其面积为A。
定义：积分称为图形对O点的极惯性矩，用符号I P，表示，如式(2—2.6)(2—2.6)极惯性矩是相对于指定的点而言的，即同一图形对不同的点的极惯性矩一般是不同的。
极惯性矩恒为正，其量纲是长度的4次方，常用单位为m4或mm4。
(1)圆截面对其圆心的极惯性矩，如式(2—7)(2—2.7)(2)对于外径为D、内径为d的空心圆截面对圆心的极惯性矩，如式(2—2.8)(2—2.8)式中，d/D为空心圆截面内、外径的比值。
2．惯性矩在如图6-1所示中，定义积分，如式(2—2.9)(2—2.9)称为图形对z轴和y轴的惯性矩。
惯性矩是对一定的轴而言的，同一图形对不同的轴的惯性矩一般不同。
各种截面下极惯性矩
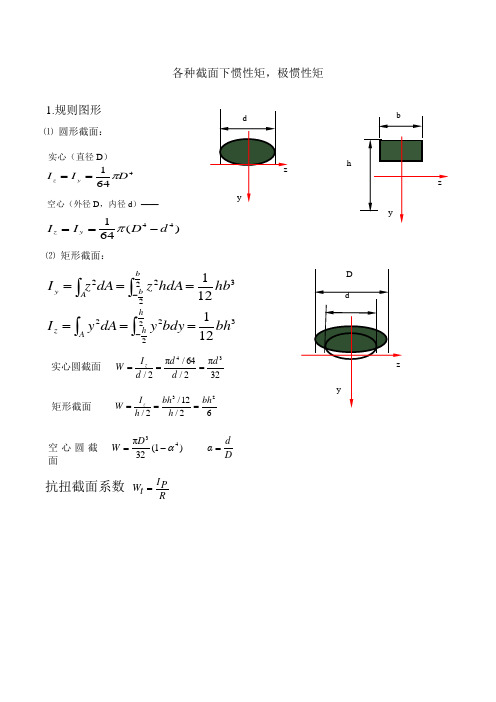
y
dA
y2dA z2dA I z I y
o
A
A
z
y
图形对任一对相互垂直的坐标系的惯性矩之和恒等于此图形对该两轴交点的极惯性矩。
四、惯性半径(Radius of gyration of the area)
iy
Iy A
iz
Iz A
I y I yi
I z I zi
I yz I yizi
（1）两平行轴中，必须有一轴为形心轴,截面对任意两平行轴 的惯性矩间的关系,应通过平行的形心轴惯性矩来换算;
（2）截面图形对所有平行轴的惯性矩中,以对通过形心轴的惯 性矩最小.
6、惯性矩与极惯性矩的关系：
z
I p
2dA
A
( y2 z2 )dA
各种截面下惯性矩，极惯性矩
1.规则图形
d
⑴ 圆形截面：
实心（直径 D）
Iz
Iy
1 D4
64
空心（外径 D，内径 d）——
Iz
Iy
1 (D4
64
d 4)
⑵ 矩形截面：
z y
I y
z2dA
A
b
2 b
2
z 2 hdA
1 12
hb3
Iz
y2dA
A
h
2 h
2
y 2bdy
1 bh3 12
实心圆截面 W I z πd 4 / 64 πd 3 d / 2 d / 2 32
矩形截面
W I z bh3 /12 bh2 h/2 h/2 6
空 心 圆 截 W πD3 (1 4 )
面
32
抗扭截面系数
Wt
材料力学第五章
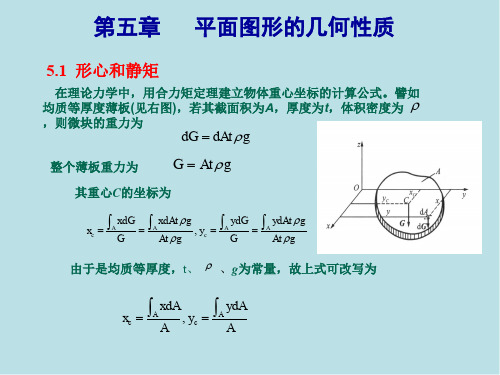
xC
Sy A
n
x C
Ai
i 1
n
Ai
i 1
n
yC
Sx A
i 1 n
y C
Ai
Ai
i 1
第五章 平面图形的几何性质
270
30
y [例1] 已知：图形尺寸如图
Ⅱ
所示。
求：图形的形心。
50
C2
Ⅰ
C C1
yc
z
解：1、将图形分解为 简单图形的组合
第五章 平面图形的几何性质
静矩与形心坐标之间的关系
S y
zdA
A
S z
ydA
A
Sy AzC
Sz AyC
yC
Sz A
ydA
A
A
zC
Sy A
zdA
A
A
已知静矩可以确定图形的形心坐标 已知图形的形心坐标可以确定静矩
第五章 平面图形的几何性质
构件截面的图形往往是由矩形、圆形等简单图形 组成，称为组合图形。
xc
A
G
A At g
, yc
A
G
A At g
由于是均质等厚度，t、 、g为常量，故上式可改写为
xdA
ydA
xc
A
A
, yc
A
A
第五章 平面图形的几何性质
1. 静矩的定义
对 z 轴静矩 对 y 轴静矩
Sz
ydA
A
Sy
极惯性矩常用计算公式[精华]
![极惯性矩常用计算公式[精华]](https://img.taocdn.com/s3/m/fc9d50e976c66137ef061951.png)
极惯性矩常用计算公式[精华]极惯性矩常用计算公式:Ip=?Aρ^2dA矩形对于中线(垂直于h边的中轴线)的惯性矩:b*h^3/12三角形:b*h^3/36圆形对于圆心的惯性矩:π*d^4/64环形对于圆心的惯性矩:π*D^4*(1-α^4)/64;α=d/D?16-1 静矩和形心平面图形的几何性质一般与杆件横截面的几何形状和尺寸有关，下面介绍的几何性质表征量在杆件应力与变形的分析与计算中占有举足轻重的作用。
静矩:平面图形面积对某坐标轴的一次矩，如图?-1所示。
定义式:， (?-1)量纲为长度的三次方。
由于均质薄板的重心与平面图形的形心有相同的坐标和。
则由此可得薄板重心的坐标为同理有所以形心坐标， (?-2) 或，由式(?-2)得知，若某坐标轴通过形心，则图形对该轴的静矩等于零，即，;，则;反之，若图形对某一轴的静矩等于零，则该轴必然通过图形的形心。
静矩与所选坐标轴有关，其值可能为正，负或零。
如一个平面图形是由几个简单平面图形组成，称为组合平面图形。
设第i块分图形的面积为，形心坐标为，则其静矩和形心坐标分别为， (?-3)， (?-4)【例I-1】求图?-2所示半圆形的及形心位置。
【解】由对称性，，。
现取平行于轴的狭长条作为微面积所以读者自己也可用极坐标求解。
【例I-2】确定形心位置，如图?-3所示。
【解】将图形看作由两个矩形?和?组成，在图示坐标下每个矩形的面积及形心位置分别为矩形?:mm2mm，mm矩形?:mm2mm，mm 整个图形形心的坐标为?16-2 惯性矩和惯性半径惯性矩:平面图形对某坐标轴的二次矩，如图?-4所示。
， (?-5)量纲为长度的四次方，恒为正。
相应定义， (?-6)为图形对轴和对轴的惯性半径。
组合图形的惯性矩设为分图形的惯性矩，则总图形对同-轴惯性矩为， (?-7)若以表示微面积到坐标原点的距离,则定义图形对坐标原点的极惯性矩(?-8) 因为所以极惯性矩与(轴)惯性矩有关系(?-9) 式(?-9)表明，图形对任意两个互相垂直轴的(轴)惯性矩之和，等于它对该两轴交点的极惯性矩。
建筑力学6第六章
学习目标：
1. 理解静矩、惯性矩、极惯性矩、惯性半径和惯性积的概 念。
2. 熟练掌握组合图形形心位置的计算。 3. 会应用平行移轴公式计算组合图形对形心轴的惯性矩。 4. 熟记矩形、圆形等简单图形对其形心轴的惯性矩。
重点：
组合图形形心位置的确定及组合图形对形心轴的惯性矩的 计算。
平面图形的几何性质
若平面图形对某轴的静矩为零，则该轴必通过平面图形的形 心。
• 如果平面图形具有对称轴，对称轴必然是平面图形的 形心轴。故平面图形对其对称轴的静矩必等于零。 二、组合图形的静矩
在工程实际中，经常遇到工字形、T形、环形等横截面的 构件，这些构件的截面图形是由几个简单的几何图形组合而 成的，称为组合图形。
单位为m或mm。
为了便于查用，表6-1列出了几种常见截面图形的面积、 形心和惯性矩。
平面图形的几何性质
平面图形的几何性质
第三节 组合图形的惯性矩
第一节 静矩
一、静矩的概念
微面积dA与坐标 y（或坐标 z） 的乘积称为微面积dA对z轴（或y轴）
的静矩 .
这些微小乘积在整个面积 A内 的总和，称为该平面图形对z轴（或 y轴）的静矩。
用Sz（或Sy）表示。即
Sz
A dSz
A
ydA
Sy
A dS y
zdA
A
Ai zCi
i1
式中 yCi 、zCi 及 Ai 分别为各简单图形的形心坐标和面积 ，n 为组成组合图形的简单图形的个数。
平面图形的几何性质
例6-1 矩形截面尺寸如图所示。试求该矩形对 z1轴的 静矩 Sz1和对形心轴 z 的静矩 Sz 。
理论力学 第五章 平面图形的几何性质
y
2)、求形心
xc
Ax
A
i ci
A1 xc1 A2 xc 2 A1 A2
C2
c(-20.3;34.7)
C1 80
35 1100 20.3(mm) 10 110 80 10
i ci
x
yc
A y
A
A1 y c1 A2 y c 2 A1 A2
60 1100 34.7(mm) 10 110 80 10
§5-3
极惯性矩
y
dA
定义：I p dA
2 A
I p：极惯性矩
极惯性矩恒为正 单位：长度4
x
O
圆截面
d
2
I p A dA
1、实心圆截面——
O
d
I P dA 2 d
2 2 A A
d 2 0
1 4 2 d d 32
y 10
A2 1200mm2 , xc 2 5mm, yc 2 60mm
2)、求形心
C2
120
c(19.7;39.7)
C1
A1 xc1 A2 xc 2 zc A A1 A2 45 700 5 1200 19.7mm) 700 1200
i ci
Ax
80
2 2 A A 2 A c 2 2 A A
y
I x I xc a 2 A I y I yc b A
2
yc xc
x
b
c
a
y
dA yc
xc
——平行移轴公式
o
x
•图形对任意轴的惯性矩，等于图形对于与该轴平 行的形心轴的惯性矩加上图形面积与两平行轴间距 平方的乘积；
惯性矩总结(含常用惯性矩公式).docx
惯性矩是一个物理量，通常被用作描述一个物体抵抗扭动，扭转的能力惯性矩的国际单位为(m^4) O工程构件典型截面几何性质的计算2.1面积矩1.面积矩的定义别定义为该图形对Z轴和y轴的面积矩或静矩，用符号S Z和S y,来表示，如式(2 —2.1)面积矩的数值可正、可负，也可为零。
面积矩的量纲是长度的三次方，其常用单3 3位为m或mm>2.面积矩与形心平面图形的形心坐标公式如式(2 —2.2)乩(2 — 2.2)或改写成，如式(2 —2.3)S2= A-y i(2 —2.3)面积矩的几何意义：图形的形心相对于指定的坐标轴之间距离的远近程度。
图形如图2-31所示为一任意截面的几何图形(以下简称图形)。
定义:积分川和J 分(2 —2.1)图2-2.1任意截面的几何图形S Z= I Z ydA形心相对于某一坐标距离愈远，对该轴的面积矩绝对值愈大。
图形对通过其形心的轴的面积矩等于零；反之，图形对某一轴的面积矩等于零, 该轴一定通过图形形心。
3 •组合截面面积矩和形心的计算组合截面对某一轴的面积矩等于其各简单图形对该轴面积矩的代数和。
如式 (2 — 2.4)Σ¾ =Σj ⅛z J (2 — 2.4)式中，A 和y i 、Z i 分别代表各简单图形的面积和形心坐标。
组合平面图形的形心位 置由式(2 — 2.5)确定2.2极惯性矩、惯性矩和惯性积1 •极惯性矩任意平面图形如图2-31所示，其面积为A 。
定义：积分丨「’川称为图形对O 点的 极惯性矩，用符号I P ，表示，如式(2 — 2.6)'[ 」(2 — 2.6)极惯性矩是相对于指定的点而言的，即同一图形对不同的点的极惯性矩一般是不同的。
极惯性矩恒为正，其量纲是长度的4次方，常用单位为m 4或mr ⅛(1)圆截面对其圆心的极惯性矩，如式(2 — 7)IP- 32 (2 — 2.7)(2)对于外径为D 内径为d 的空心圆截面对圆心的极惯性矩，如式(2 — 2.8)_(1 —況)P 32(2 — 2.8)式中，：二d/D 为空心圆截面内、外径的比值。
组合图形的惯性矩 PPT
=8a2·a+(-1/2πa2) 4a/3π =1.98×105mm3
图8.3
惯性矩和惯性半径
◆ 惯性矩定义
如图8.4所示，在平面图形上取一微面积dA, dA与其坐标平方的乘积y2dA、z2dA分别称为 该微面积dA对z轴和y轴的惯性矩，它们在整 个图形范围内的定积分
S Z
ydA
A
S y
根据图形静矩的定义，组合图形对某轴的静矩 等于各个简单图形对同一轴静矩的代数和，即
n
SyzC 1A 1zC 2A 2...zCA n n zCA ii i 1
n
SZyC 1A 1yC 2A 2.. .yCA n n yCA ii i 1
大家学习辛苦了，还是要坚持
继续保持安静
【例8.2】试计算图8.3所示截面对z轴和y轴的静 矩。已知a=30mm
S Z
ydA
A
(a)
S y
zdA
A
分别称为整个平面图形对于z轴和y轴的静矩。
◆简单图形静矩的计算
在静力学的第３章中，已经导出平面图形的形
ydA
yC
AБайду номын сангаас
A
zdA
zC
A
A
(8.1)
将公式(8.1)代入式(a)，平面图形的形心坐标 公式可写为
惯性矩计算方法及常用截面惯性矩计算公式
惯性矩的计算方法及常用截面惯性矩计算公式截面图形的几何性质一.重点及难点：(一).截面静矩和形心1.静矩的定义式如图1所示任意有限平面图形，取其单元如面积dA ，定义它对任意轴的一次矩为它对该轴的静矩，即ydAdSx xdA dS y == 整个图形对y 、z 轴的静矩分别为⎰⎰==AAy ydASx xdAS （I-1） 2.形心与静矩关系 图I-1设平面图形形心C 的坐标为C C z y , 则 0AS y x=， A S x y = （I-2）推论1 如果y 轴通过形心（即0=x ），则静矩0=y S ；同理，如果x 轴通过形心（即0=y ），则静矩0=Sx ；反之也成立。
推论2 如果x 、y 轴均为图形的对称轴，则其交点即为图形形心；如果y 轴为图形对称轴，则图形形心必在此轴上。
3.组合图形的静矩和形心设截面图形由几个面积分别为n A A A A ⋯⋯321,,的简单图形组成，且一直各族图形的形心坐标分别为⋯⋯332211,,,y x y x y x ；；，则图形对y 轴和x 轴的静矩分别为∑∑∑∑========ni ni ii xi x ni ii n i yi y y A S S x A S 1111S （I-3）截面图形的形心坐标为∑∑===ni ini ii AxA x 11 ， ∑∑===ni ini ii AyA y 11 （I-4）4.静矩的特征(1) 界面图形的静矩是对某一坐标轴所定义的，故静矩与坐标轴有关。
(2) 静矩有的单位为3m 。
(3) 静矩的数值可正可负，也可为零。
图形对任意形心轴的静矩必定为零，反之，若图形对某一轴的静矩为零，则该轴必通过图形的形心。
(4) 若已知图形的形心坐标。
则可由式（I-1）求图形对坐标轴的静矩。
若已知图形对坐标轴的静矩，则可由式（I-2）求图形的形心坐标。
组合图形的形心位置，通常是先由式（I-3）求出图形对某一坐标系的静矩，然后由式（I-4）求出其形心坐标。
惯性矩ppt
VIP有效期内享有搜索结果页以及文档阅读页免广告特权，清爽阅读没有阻碍。
知识影响格局，格局决定命运！ 多端互通
抽奖特权
VIP有效期内可以无限制将选中的文档内容一键发送到手机，轻松实现多端同步。 开通VIP后可以在VIP福利专区不定期抽奖，千万奖池送不停！
福利特权
开通VIP后可在VIP福利专区定期领取多种福利礼券。
b dy
Iz
bh3 12
Iz
y2dA 2 h/2by2dy
A
0
2 by3 3
h/2 0
1 bh3 12
[练习] 求图示矩形截面对z轴的惯性矩。
dA y z h
dy
b
解：
Iz
y2dA h by2dy
A
0
1 by3 3
h 0
1 bh3 3
2
2. 圆形截面的惯性矩
dA dd
dA
C d
年VIP
月VIP
连续包月VIP
VIP专享文档下载特权
享受60次VIP专享文档下载特权，一 次发放，全年内有效。
VIP专享文档下载特权自VIP生效起每月发放一次， 每次发放的特权有效期为1个月，发放数量由您购买 的VIP类型决定。
每月专享9次VIP专享文档下载特权， 自VIP生效起每月发放一次，持续有 效不清零。自动续费，前往我的账号 -我的设置随时取消。
服务特 权
共享文档下载特权
VIP用户有效期内可使用共享文档下载特权下载任意下载券标价的文档（不含付费文档和VIP专享文档），每下载一篇共享文
档消耗一个共享文档下载特权。
年VIP
月VIP
连续包月VIP
享受100次共享文档下载特权，一次 发放，全年内有效
组合图形的惯性矩.
在计算组合图形对z、y轴的惯性矩时，应先将组合图形分成若干个简单图形，并计算出每一简单图形对平行于y、z轴的自身形心轴的惯性矩，然后利用平行移轴公式计算出各简单图形对y、z轴的惯性矩，最后利用上式求总和。
惯性矩的计算方法
第1节静矩和形心4.1静矩和形心任何受力构件的承载能力不仅与材料性能和加载方式有关.而口与构件截面的几何形状和尺寸有关.如：计算杆的拉伸与压缩变形时用到截面而积A ,计算圆轴扭转变形时用到横截面的极惯性矩I?等.A、1?等是从不同角度反映了截而的几何特性，因此称它们为截而图形的几何性质.4.1静矩和形心设有一任意截而图形如图4 一1所示，其面积为A .选収直角坐标系yoz ,在坐标为（y,z）处取一微小而积dA ,定义微而积dA乘以到y轴的距离z ,沿整个截面的积分，为图形对y轴的静矩S?,其数学表达式(4 -la )同理，图形对z轴的静矩为□4-1图41截面静矩与坐标轴的选取有关•它随坐标轴y、z的不同而不同.所以静矩的数值可能足正，也可能足负或定零.静矩的虽纲为长度的三次方.确定截面图形的形心位置（图4-1中C点）:A (4-2b)第1页共30页式中T、"为截而图形形心的坐标值.若把式（4-2）改写成心"•儿，為"•乙（4 3）性质：・若截面图形的静矩等于零，则此坐标轴必定通过截面的形心.・若坐标轴通过截而形心，则截而对此轴的静矩必为零.・山于截而图形的对称轴必定通过截而形心，故图形对其对称轴的静矩恒为零。
4 ）工程实际中，有些构件的截面形状比较复杂，将这些复杂的截面形状看成是山若干简单图形（如矩形、圆形等）组合g而成的.对于这样的组合截而图形，计算静矩（S»‘ r）与形心坐标（y*、z '）时，可用以下公式1-1 2-1式中A— y i , z i分别表示第，个简单图形的面积及其形心坐标值，n为组成组合图形的简单图形个数.即：组合图形对某一轴的静矩等于组成它的简单图形对同一轴的静矩的代数和.组合图形的形心坐标值等于组合图形对相应坐标轴的静矩除以组合图形的面积.组合截面图形有时还可以认为是山一种简单图形减去另一种简单图形所组成的.例4J己知T形截面尺寸如图4-2所示，试确定此截面的形心坐标值.i-1 i-1 (4-5)图4-2解：(1)选参考轴为y 轴，z 轴为对称轴,(2)将图形分成I 、口两个矩形，则= 20 x 100加朋 S 右=(10 + 140)^^34 = 2Q X 14%/,22 二注型(3)代入公式(4・5)20x100x150+20x140x70 20x100 + 20x140此=°4.2惯性矩、惯性积和惯性半径设任一截面图形(图4-3),其而积为A ・选取直角坐标系yoz ,在坐标为(y 、z)处取一微小面积dA ,定义此微2面积dA 乘以到坐标原点o 的距离的平方Q ,沿整个截面积分，为截而图形的极惯性矩I?.做而积dA 乘以到坐标轴y 的2距离的平方2 ,沿整个截而积分为截面图形对y 轴的惯性矩I 》•极惯性矩、惯性矩常简称极惯矩、惯矩.j.l ~2Z4数学表达式为打=f p^dA极惯性矩“俎（4-6）对y轴惯性矩图4-3山图4-3看到“ =y +Z 9所以有打=\A^dA= £cy2 +/）曲二必+加必即；? （4-8）式（4-8）说明截面对任一对正交轴的惯性矩之和恒等于它对该两轴交点的极惯性矩。
惯性矩基础知识
ybdy
h
by2 2 0 2 h
2
2
z
dz
z
4
二、简单图形的形心
1、形心坐标公式： 2、形心确定的规律：
yc
Sz A
ydA
A
A
zc
Sy A
zdA
A
A
（1）图形有对称轴时，形心必在此对称轴上。
（2）图形有两个对称轴时，形心必在此两对称轴的交点处。
5
三、组合图形（由若干个基本图形组合而成的图形）的静矩：
8
y
10
解法三：负面积法
10
A1 9600mm2 , zc1 40mm, yc1 60mm A2 70 110mm2 , zc2 45mm, yc2 65mm
120 10
求形心：
80
y
C2 C0 C1
z
zc
Ai zci A1 zc1 A2 zc2
A
A1 A2
40 96 45 (77) 19.7(mm)
z
图形对z轴的惯性矩: I z y2dA, A
图形对y轴的惯性矩: I y z 2dA
2 z2 y2
2、量纲：m4、mm4。
A
3、惯性矩是对轴而言（轴惯性矩）。
4、惯性矩的取值恒为正值。
5、极惯性矩：（对o点而言）
Io
2dA
A
Ip
10
6、惯性矩与极惯性矩的关系：
y
I p
2dA
2
I zy
cos 2 )
2I z1y1
令 0
dI z1
0
d 0
23
dIz1
d
2
0
Iz
惯性矩的算法
截面图形的几何性质一.重点及难点：(一).截面静矩和形心1.静矩的定义式如图1所示任意有限平面图形，取其单元如面积dA ，定义它对任意轴的一次矩为它对该轴的静矩，即ydAdSx xdA dS y == 整个图形对y 、z 轴的静矩分别为⎰⎰==AAy ydASx xdAS （I-1） 2.形心与静矩关系 图I-1设平面图形形心C 的坐标为C C z y , 则 0A S y x= ， AS x y = （I-2）推论1 如果y 轴通过形心（即0=x ），则静矩0=y S ；同理，如果x 轴通过形心（即0=y ），则静矩0=Sx ；反之也成立。
推论2 如果x 、y 轴均为图形的对称轴，则其交点即为图形形心；如果y 轴为图形对称轴，则图形形心必在此轴上。
3.组合图形的静矩和形心设截面图形由几个面积分别为n A A A A ⋯⋯321,,的简单图形组成，且一直各族图形的形心坐标分别为⋯⋯332211,,,y x y x y x ；；，则图形对y 轴和x 轴的静矩分别为∑∑∑∑========ni ni ii xi x ni ii n i yi y y A S S x A S 1111S （I-3）截面图形的形心坐标为∑∑===ni ini ii AxA x 11 ， ∑∑===ni ini ii AyA y 11 （I-4）4.静矩的特征(1) 界面图形的静矩是对某一坐标轴所定义的，故静矩与坐标轴有关。
(2) 静矩有的单位为3m 。
(3) 静矩的数值可正可负，也可为零。
图形对任意形心轴的静矩必定为零，反之，若图形对某一轴的静矩为零，则该轴必通过图形的形心。
(4) 若已知图形的形心坐标。
则可由式（I-1）求图形对坐标轴的静矩。
若已知图形对坐标轴的静矩，则可由式（I-2）求图形的形心坐标。
组合图形的形心位置，通常是先由式（I-3）求出图形对某一坐标系的静矩，然后由式（I-4）求出其形心坐标。
（二）.惯性矩 惯性积 惯性半径1. 惯性矩定义 设任意形状的截面图形的面积为A （图I-3），则图形对O 点的极惯性矩定义为⎰=Ap dA I 2ρ （I-5）图形对y 轴和x 轴的光性矩分别定义为⎰=Ay dA x I 2 ， dA y I Ax ⎰=2 （I-6）惯性矩的特征（1） 界面图形的极惯性矩是对某一极点定义的；轴惯性矩是对某一坐标轴定义的。
3.3惯性矩-单元教学设计
《惯性矩》单元教学设计一、教案头二、教学内容（一）建筑结构中的杆件，其截面都是具有一定几何形状的平面图形。
与平面图形形状及尺寸有关的几何量统称为平面图形的几何性质。
杆件的强度、刚度、稳定性都与杆件横截面图形的几何性质密切相关，因此，必须明确这些几何性质的概念和几何量的计算方法。
（二）相关高等数学知识（例如积分）（三）1、明白惯性矩的定义；2、明白惯性矩的几何意义；惯性半径的概念；3、掌握几种平面图形形心惯性矩的公式；4、会应用平行移轴公式计算组合截面的惯性矩 （四）任务实施 （五）检查评价2. 教学实施【步骤l 】复习巩固和引入新课⑵ 引入新课（案例）：1）何谓惯性矩平行移轴公式是什么【步骤2】课程介绍及知识讲授1. 惯性矩的定义图3-5所示任意形状的平面图形，在坐标为(,)z y 处取微面积dA ，则可求得下述积分⎪⎭⎪⎬⎫==⎰⎰A y AdA I dA y I 22z z (3-9)式（3-9）中Z I 称平面图形对z 轴的二次矩（惯性矩），y I 称平面图形对y 轴的二次矩（惯性矩）。
由上述定义可以看出，图形对轴的惯性矩恒为正，其单位是长度单位的四次方，即4m 或4mm 。
由图3-5可以看出，222y z +=ρ，将此式代入式（3-6）中可得y P I I I +=z (3-10)式（3-10）表明图形对任一点的极惯性矩，恒等于此图形对过该点的任一对直角坐标轴的两个惯性矩之和。
图3-5例题3-3 例题3-3图所示矩形，高度为h ，宽度为b ，z 轴和y 轴为图形的形心轴，且z 轴平行矩形底边。
求矩形截面对形心轴z 、y 的惯性矩。
解：取宽为b 、高为dy 且平行于z 轴的狭长矩形的微面积为bdy dA =由式(3-9)得矩形图形对z 轴的惯性矩为123222z bh bdy y I hh ==⎰- 同理，可得矩形图形对y 轴的惯性矩为123hb I y =例题3-2图 例题3-4图例题3-4 例题3-4图所示圆图形，半径为R ，z 轴和y 轴为其形心轴。