管理统计学3 第三章 数据特征的描述
合集下载
第3章 统计数据的特征描述

n 4
3n QU组位置= 4
②根据各组的累积频数确定四分位数的具体值。 (1) 对单项式分组数据,该组的变量值就是四分位数。 (2) 对于组距式分组数据,通过下面的公式来计算:
n S M 1 1 Q L L1 4 d f Q1
3n S M 3 1 QU L3 4 d f Q3
3.3.2 峰度 峰度(kurtosis):一组数据分布的陡缓程度,它是 与标准正态分布相比较而言的。 其计算公式为:
Ku
n 1
1
i 1
ห้องสมุดไป่ตู้
n
4 4 ( xi x ) / s 3
正态分布
尖峰态分布
平峰态分布
normal
leptokurtic
platykurtic
(1) 当数据分布与标准正态分布的陡缓程度相同 时,则峰度值等于零。 (2) 当数据分布的形状比标准正态分布更尖时,则 峰度值Ku>0,称为尖峰态分布。尖峰分布表明集
s
2
n n 2 1 2 2 ( xi nx ) ( xi x ) n 1 i 1 n 1 i 1 1
1 2 s ( xi x ) n 1 i 1
n
分组数据资料计算公式:
s2
( xi x ) f i
2 i 1
k
f
i 1
n
xi f i nx 2
计算公式:
Vr
f
i 1 n
n
i
fm
i
f
i 1
100%
fm:众数所在组的频数 fi:各分组的频数
§3.3 分布形态的描述
数据分布的形态:指数据分布的形状是否对称, 偏斜的程度以及分布的扁平程度等。
统计学第3章数据分布特征描述

xi fi i1
xf
f1 f2 ... fn
n
fi
f
x x f
i 1
f
举例
表3-3 节能灯泡使用寿命数据
使用寿命 组中 数量 (小时) 值x f
xf
频率 f /Σf
xf/Σf
1000以下 900 2 1800 0.020 18
1000-1200 1100 8 8800 0.080 88
n(xi x) 0
i1
(3)各变量值与算术平均数的离差平方之总和最小。 (从全 部数据看,算术平均数最接近所有变量值)
n(xi x)2 min
i1
性质(3)证明:
(三)调和平均数(Harmonic mean)
➢ 调和平均数,也称倒数平均数。 ➢ 各变量值倒数(1/xi)的算术平均数的倒数。 ➢ 计算公式为:
➢由一组数据的总和(总体标志总量)除以 该组数据的项数(总体单位总量)得到; 算术平均数=总体标志总量/总体单位总量
➢是最常用的数值平均数;
➢根据掌握资料不同,其有多种计算公式。
1.简单算术平均数 ➢对未分组数据,采用简单算术平均数公式。即 把各项数据直接加总,然后除以总项数。 ➢计算公式:
N
xi x i1
例如,改变教师职称结构,而不改变各种职 称教师课时费标准,会改变平均课时费水平。
权数实质
➢权数的实质在于其结构,即结构比例形式(比重 权数)。
➢其更能清晰表明权数之权衡轻重的作用。
权数形式有2种:
➢ 绝对数形式
Mp
➢ 结构比例形式
k
N
xik wi
i 1
N
wi
i 1
k
N
i 1
统计学 3数据分布特征的描述_OK
26
2、顺序数据----分位数
(1)四分位数
1)分位数有二分位数(中位数)、四分位数、十 分位数和百分位数等。其中主要有四分位数。 2)排序后处于25%和75%位置上的值即四分位数
25% 25% 25% 25%
QL
QM
QU
3)不受极端值的影响
4)主要用于顺序数据,也可用于数值型数据,但
不能用于分类数据
2021/7/2
33
3.1.4 数值型数据---平均数 STAT 一.算术平均数
平均数(average )的定义----变量值的一般水平,通常 也称为均值(mean) 。有算术均值、调和均值和几何均 值。
算术平均数定义:全部变量值之 和与变量值个数相除所得到的结果。 按其计算形式又有简单算术平均数和 加权算术平均数之分。
一个众数 原始数据: 6 5 9 8 5 5
多于一个众数 原始数据: 25 28 28 36 42 42
2021/7/22
10
有时众数是一个合适的代表值
比如在服装行业中,生产商、批发商和 零售商在做有关生产或存货的决策时, 更感兴趣的是最普遍的尺寸而不是平均 尺寸。
2021/7/2
11
1、分类数据的众数
身高 人数
(CM) (人)
152 1
154 2
155 2
156 4
157 1
158 2
159 2
160 12
161 7
162 8
2021/7/21263
4
身高 人数
(CM) (人) 164 3 165 8 166 5 167 3 168 7 169 1 170 5 171 2 172 3 174 1
2021/7/22
2、顺序数据----分位数
(1)四分位数
1)分位数有二分位数(中位数)、四分位数、十 分位数和百分位数等。其中主要有四分位数。 2)排序后处于25%和75%位置上的值即四分位数
25% 25% 25% 25%
QL
QM
QU
3)不受极端值的影响
4)主要用于顺序数据,也可用于数值型数据,但
不能用于分类数据
2021/7/2
33
3.1.4 数值型数据---平均数 STAT 一.算术平均数
平均数(average )的定义----变量值的一般水平,通常 也称为均值(mean) 。有算术均值、调和均值和几何均 值。
算术平均数定义:全部变量值之 和与变量值个数相除所得到的结果。 按其计算形式又有简单算术平均数和 加权算术平均数之分。
一个众数 原始数据: 6 5 9 8 5 5
多于一个众数 原始数据: 25 28 28 36 42 42
2021/7/22
10
有时众数是一个合适的代表值
比如在服装行业中,生产商、批发商和 零售商在做有关生产或存货的决策时, 更感兴趣的是最普遍的尺寸而不是平均 尺寸。
2021/7/2
11
1、分类数据的众数
身高 人数
(CM) (人)
152 1
154 2
155 2
156 4
157 1
158 2
159 2
160 12
161 7
162 8
2021/7/21263
4
身高 人数
(CM) (人) 164 3 165 8 166 5 167 3 168 7 169 1 170 5 171 2 172 3 174 1
2021/7/22
统计学基础 第3章 统计数据的描述

• 第三步:点击右键,在所列菜单中单击【选择数据】,在【图表数据 区域(D)】方框中数据区域(如本例为A2:B6);
• 第四步:点击【确定】,系统绘制出条形图。其他各项格式可以通过 单击右键,进行各种选择。
统计学
STATISTICS
条形图
• 常见的几种条形图:
各品牌电脑销售频数分布
a 横置条形图
b
• Excel提供了两种排序的方法,一种是直接根据一个变量 按升序或降序排序,另一种是根据多个变量排序,下面仍 以上例职工工资资料为例说明在Excel中数据排序的基本 步骤:
第1步:先选中排序变量,然后单击工具栏中的【排 序和筛选】按钮,出现下拉菜单,如图3.1所示。
第2步:如果仅按照一个变量排序,直接单击下拉菜 单中的【升序】或【降序】命令即可完成排序。如根据基 本工资按升序将职工排序,其结果如图3.12所示:
统计学
STATISTICS
饼图
• 饼图是在圆形中以不同颜色或不同修饰条纹的扇形表示不同类型的数 据,以各种扇形的面积大小表示各类型数据的多少,以反映分类数据 的结构。饼图主要用于反映样本数据或总体数据在某一方面的构成情 况,同样适用于顺序数据和数值型数据等所有类型数据。
• Excel 提供了非常方便的饼图绘制功能,可以选择平面图形,也可以绘 制三维饼图,还可以选择是否标示数据,数据标示可以选择频数或频 率。
图3.24
图形绘制过程3—选择功能
统计学
STATISTICS
饼图
• 第四步:输入数据,在主对话框【图表数据区域(D)】中输入数据 区域(数据区域为各类型的频数,本例为各品牌电脑的销售量)输入 方法是点击【图表数据区域(D)】后方框内工作表图标,用鼠标左 键将数据区域拉入方框内,再点击工作表图标确认,本例为 $A$2:$B$6),如图3.25所示:
• 第四步:点击【确定】,系统绘制出条形图。其他各项格式可以通过 单击右键,进行各种选择。
统计学
STATISTICS
条形图
• 常见的几种条形图:
各品牌电脑销售频数分布
a 横置条形图
b
• Excel提供了两种排序的方法,一种是直接根据一个变量 按升序或降序排序,另一种是根据多个变量排序,下面仍 以上例职工工资资料为例说明在Excel中数据排序的基本 步骤:
第1步:先选中排序变量,然后单击工具栏中的【排 序和筛选】按钮,出现下拉菜单,如图3.1所示。
第2步:如果仅按照一个变量排序,直接单击下拉菜 单中的【升序】或【降序】命令即可完成排序。如根据基 本工资按升序将职工排序,其结果如图3.12所示:
统计学
STATISTICS
饼图
• 饼图是在圆形中以不同颜色或不同修饰条纹的扇形表示不同类型的数 据,以各种扇形的面积大小表示各类型数据的多少,以反映分类数据 的结构。饼图主要用于反映样本数据或总体数据在某一方面的构成情 况,同样适用于顺序数据和数值型数据等所有类型数据。
• Excel 提供了非常方便的饼图绘制功能,可以选择平面图形,也可以绘 制三维饼图,还可以选择是否标示数据,数据标示可以选择频数或频 率。
图3.24
图形绘制过程3—选择功能
统计学
STATISTICS
饼图
• 第四步:输入数据,在主对话框【图表数据区域(D)】中输入数据 区域(数据区域为各类型的频数,本例为各品牌电脑的销售量)输入 方法是点击【图表数据区域(D)】后方框内工作表图标,用鼠标左 键将数据区域拉入方框内,再点击工作表图标确认,本例为 $A$2:$B$6),如图3.25所示:
管理统计学:第三章:样本数据特征

• 样本均值(Sample Mean) • 样本均值仅适用于刻度级的数据。 • 样本数据集合的样本均值定义为:
• 式中,Xi为样本观察值。
第3.4节 样本数据的离散特征
• 描述数据集合的离散特征的两种方法: • 一、点状描述,如明确样本数据集合中的最小 值和最大值等; • 二、区间描述(基于差值的描述),如样本数 据集合中的最大值与最小值之差。
3.4.1 对样本数据离散特征的点状描述: 极值、四分点与百分位点
• 1.极大值(Maximum)与极小值 (Minimum)
• 极大值与极小值,从一定视角反映了样本 数据集合中样本的离散情况。 • 问:极大值、极小值适用于什么测度? • 另一个位与数的问题:
• 2.下四分点(Lower quartile)与上四分点 (Upper quartile) • 1)上、下四分点的概念 • 下四分点使由小到大排序后的数据集合的左 边部分,包含25%的样本总个数,右边部分 包含75%的样本总个数。 • 上四分点使由小到大排序后的数据集合的左 边部分,包含75%的样本总个数,右边部分 包含25%的样本总个数。 • 上、下四分点在一定意义上反映了样本数据 的离散情况。
• 基于排序,能够简单统计频次:
• 价格(元)9.93 9.94 9.95 9.96 9.97 9.98 9.99 10.00 • 次数: 1 0 1 1 2 3 4 4 • 频率% 3.33 0 3.33 3.33 6.67 10.00 13.33 13.33 • 价格(元)10.01 10.02 10.03 10.04 10.05 10.06 • 次数: 4 2 3 2 2 1 • 频率% 13.33 6.67 10.0 6.67 6.67 3.33
第 3章 样本数据特征的初步 分析
• 式中,Xi为样本观察值。
第3.4节 样本数据的离散特征
• 描述数据集合的离散特征的两种方法: • 一、点状描述,如明确样本数据集合中的最小 值和最大值等; • 二、区间描述(基于差值的描述),如样本数 据集合中的最大值与最小值之差。
3.4.1 对样本数据离散特征的点状描述: 极值、四分点与百分位点
• 1.极大值(Maximum)与极小值 (Minimum)
• 极大值与极小值,从一定视角反映了样本 数据集合中样本的离散情况。 • 问:极大值、极小值适用于什么测度? • 另一个位与数的问题:
• 2.下四分点(Lower quartile)与上四分点 (Upper quartile) • 1)上、下四分点的概念 • 下四分点使由小到大排序后的数据集合的左 边部分,包含25%的样本总个数,右边部分 包含75%的样本总个数。 • 上四分点使由小到大排序后的数据集合的左 边部分,包含75%的样本总个数,右边部分 包含25%的样本总个数。 • 上、下四分点在一定意义上反映了样本数据 的离散情况。
• 基于排序,能够简单统计频次:
• 价格(元)9.93 9.94 9.95 9.96 9.97 9.98 9.99 10.00 • 次数: 1 0 1 1 2 3 4 4 • 频率% 3.33 0 3.33 3.33 6.67 10.00 13.33 13.33 • 价格(元)10.01 10.02 10.03 10.04 10.05 10.06 • 次数: 4 2 3 2 2 1 • 频率% 13.33 6.67 10.0 6.67 6.67 3.33
第 3章 样本数据特征的初步 分析
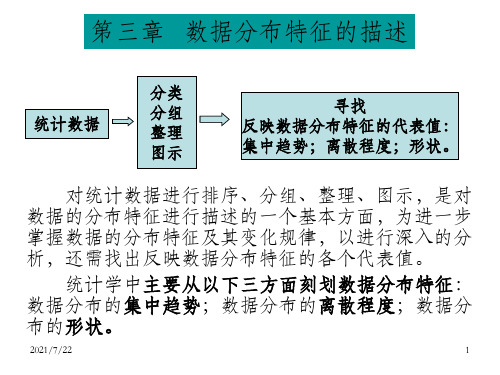
统计学第三章 数据分布特征的描述

(二)意义
1.为人们深入认识事物发展的质量与状况提供客观 依据。(例如2010年我国GDP总量构成:第一产业占 10.16%,第二产业占46.86%,第三产业占42.98%。)
2.可以使不能直接对比的现象找到可以对比的基础, 进行更为有效的分析。(例如:2010年我国农民年人均 纯收入5919元。) 统计学课程建设小组
求支出中,食品支出占相当大的比例,其次是居住、衣着、家庭设备用品及服
务。衣着基本需求支出为107.3元,家庭设备用品及服务基本需求支出为75.3。
从实际情况来看,随着农村居民收入的增加,对衣、食、住、行方面的消费需
求,已由追求数量过渡到讲究质量。对于农村居民而言,衣、食、住、行是最
为基本的要求也是最低层次的,在并未达到富裕水平的农村居民而言,这些方
三峡大学
经济与管理学院
第三章 数据分布特征的描述
本章教学目的:本章要求掌握①总量指标的概 念、作用和种类;②相对指标的概念、作用、 常见相对指标的性质、特点和计算方法;③平 均指标的概念、作用、常见的几种平均数的特 点和计算方法;④变异指标的概念、计算。
本章教学重点:时期指标、时点指标、相对指 标、平均指标及变异指标的计算。
本章教学难点:时期与时点指标区别及变异指 标的计算。
本章教学学时:10学时
统计学课程建设小组
三峡大学
经济与管理学院
第一节 总量指标
一、总量指标的概念、作用
(一)概念
又称绝对数。它是表明一定时间、地点和条件下某种
社会经济现象总体规模或水平的统计指标。(如2009年年
末全国就业人员77995万人;2009年年末国家外汇储备
面的增长更加依赖于收入的增加,因此会在相当大的程度上受到收入变动的影
第03章管理统计学

0 10 20
虚拟的 外推组 30 40 50 60
中点
管理统计学
Management statistics
3.累积折线图
累计 % 100%
虚拟的 外推组
组别 15 ~ 25 25 ~ 35 35 ~ 45 > 45
75% 50%
25% 0%
0 15 25 35 下界 45
累计 % 0% 30% 80% 100%
茎叶图类似横置 的直方图
图 某车间工人日加工零件数的茎叶图
数据个数
3 13 24 10
Management statistics
管理统计学
茎叶图
树茎 树叶
10* 10. 11* 11. 12* 12. 13* 13. 788 02234 57778889 00122223333444 5566777889 013344 5799
管理统计学
时间序列数据实例
【例】已知 1991~1998年 我国城乡居民 家庭的人均收 入数据如表311。试绘制线 图
表 1991~1998年城乡居民家庭人均收入
年份
1991 1992 1993 1994 1995 1996 1997 1998
城镇居民 1700.6 2026.6 2577.4 3496.2 4283.0 4838.9 5160.3 5425.1
管理统计学
3.2.1 定量数据整理
统计分组 根据统计研究的目的和客观现象的内在特点, 按某个标志(或几个标志)把被研究的总体划 分为若干个不同性质的组。 例:收集到某班所有同学的英语考试成绩,为了 研究需要划分高、中、低三个成绩段,每个成绩 段的范围分别是85-100,70-85,0-70,然后将每 个成绩归入到相应的组中。
虚拟的 外推组 30 40 50 60
中点
管理统计学
Management statistics
3.累积折线图
累计 % 100%
虚拟的 外推组
组别 15 ~ 25 25 ~ 35 35 ~ 45 > 45
75% 50%
25% 0%
0 15 25 35 下界 45
累计 % 0% 30% 80% 100%
茎叶图类似横置 的直方图
图 某车间工人日加工零件数的茎叶图
数据个数
3 13 24 10
Management statistics
管理统计学
茎叶图
树茎 树叶
10* 10. 11* 11. 12* 12. 13* 13. 788 02234 57778889 00122223333444 5566777889 013344 5799
管理统计学
时间序列数据实例
【例】已知 1991~1998年 我国城乡居民 家庭的人均收 入数据如表311。试绘制线 图
表 1991~1998年城乡居民家庭人均收入
年份
1991 1992 1993 1994 1995 1996 1997 1998
城镇居民 1700.6 2026.6 2577.4 3496.2 4283.0 4838.9 5160.3 5425.1
管理统计学
3.2.1 定量数据整理
统计分组 根据统计研究的目的和客观现象的内在特点, 按某个标志(或几个标志)把被研究的总体划 分为若干个不同性质的组。 例:收集到某班所有同学的英语考试成绩,为了 研究需要划分高、中、低三个成绩段,每个成绩 段的范围分别是85-100,70-85,0-70,然后将每 个成绩归入到相应的组中。
《管理统计学》焦建玲 第03章 描述性统计分析

第三章 描述性统计分析
3.1 统计数据整理与显示
频数分布
【例3-1】以下是一个班级60名学生数学期末考试成绩,请编制 组距式变量数列。 90 78 81 64 83 75 78 79 81 82 91 93 95 94 84 64 61 87 70 60 20 65 77 73 78 92 88 73 86 73 64 76 71 67 63 69 70 89 90 83 74 79 76 99 75 38 55 82 93 98 85 78 89 66 71 84 70 68 72 80
第三章 描述性统计分析
3.1 统计数据整理与显示
统计分组
统计分组是根据统计研究的任务的要求和现象总体的内 在特点,按照一定的标志,将统计总体区分为不同类型或 不同性质的若干组成部分。这些组成部分中的每一个部分 就叫做一个分组,通过分组把总体内部不同性质的单位分 开,把性质相同的单位归并在一个组内,说明总体内部各 组之间的相互关系及其特征。
下限公式: 上限公式:
Me L
fi 2 Sm1 h fm
Me U
fi 2 Sm1 h fm
第三章 描述性统计分析
3.1 统计数据整理与显示
【例3-2】某高校随机抽取300名学生的身高样本资料,
并根据研究需求对样本进行分组,数据如表3-4所示,试
计算该校学生身高的中位数。
表3-4 某高校学生身高样本数据
第三章 描述性统计分析
3.1 统计数据整理与显示
频数分布
组限的具体形式有间断组限和重合组限,开口组限和闭口组限。 例如:企业职工按年龄分组,其 组限可表示为:30岁以下,30~39 岁,40~49岁,50~59岁,60岁以 上。
间断组限是每一组的组限与邻组的组限都是间断设置的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
被工作组收容的时间记录数据,该样本反映了病人被收容后1~185天内住院时长
的变化情况。
平均数:35.7天 中位数:17天 众 数:1天
利用这些信息,可以提高制定收容计划的科学性。
常见的频数分布曲线
(1)正态分布:如农作物的单位面积产量、零件的公差、纤维强度
(2)偏态分布:如上例中病人被收容的时间分布
5 1 1.70%
1
1.70%
5
-25
625
10 2 3.40%
3
5.10%
20
-20
800
15 4 6.80%
7
11.90%
60
-15
900
20 7 11.90%
14
23.70%
140
-10
700
25 10 16.90%
24
40.70%
250
-5
250
30 11 18.60%
35
59.30%
330
星蓝海学习网
学习目标
本章学习数据分布的集中趋势特征和离中趋势特征的描述方法。重点要掌握 众数、中位数、均值、标准差、变异系数和相关系数等指标的计算和应用问题。
星蓝海学习网
3.1 描述统计
3.1.1 描述统计
描述统计的内容包括频数分布,但主要是关于集中趋势和离中趋势的描述问
题。
例如,BND医院为了制定一个收容计划,工作人员搜集了一个含有67个病人
(3)J型分布:如经济学中的供给曲线和需求曲线
(4)U型分布:如人和动物的死亡率分布
星蓝海学习网
3.1 描述统计
3.1.2 集中趋势和离中趋势
我们可以从两个方面对正态分布的特征进行描述:一是数据分布的集中趋势, 二是数据分布的离散程度 集中趋势特征指标
(1)众数 (2)中位数 (3)均值 离中趋势特征指标 (1)极差 (2)四分位差 (3)标准差 (4)变异系数
3.2 正态分布特征的描述
3.2.2 极差、四分位差、标准差和变异系数
标准差 标准差等于离差平方平均数的平方根,记为σ,则有
σ = (������ − ������ҧ)2������ / ������
在表3-1中,σ = σ (������ − ������ҧ)2������ / σ ������ = 6550/59=10.54
3.2.2 极差、四分位差、标准差和变异系数
表3-2 A、B、C三组数据分布状况比较
A
组
B
组
C
X������
������������
X������
������������
X������
5151源自25102
10
1
30
15
4
15
3
35
20
7
20
7
40
25
10
25
11
45
30
11
30
13
50
35
10
35
11
管理统计学 [第四版]
星蓝海学习网
第三章 数据特征的描述
星蓝海学习网
案例导入
某互联网公司人力资源部主管为了解本公司员工通勤情况,随机抽查20位员 工每日上下班平均时长(分钟):
120 80 80 50 140 100 90 100 80 50 60 90 140 80 80 60 50 70 100 80 通过以上抽样数据,请问本公司员工平均需要花费多长时间上下班?员工通 勤时长的分布情况如何?通过本章的学习,你将学会如何分析和描述数据,如何 从数据中掌握事件的动态发展。
在适度偏态条件下,均值、众数和中位数之间的关系可以估算为: 均值-众数=3×(均值-中位数)
表3-3中, 均值 ≈ (3×中位数-众数)/2= (3×25-20.83)/ 2 = 27.09 中位数 ≈ (众数+2×均值) / 3= (20.83 + 2×26.08) / 3 = 24.33
星蓝海学习网
������0 = ������ + ������ × ∆1 /(∆1+∆2) 在表3-3中,������0 = 17.5 + 5×2 / ( 2 + 1) = 17.5 + 3.33 = 20.83 在组距分组条件下,中位数的计算要考虑频数的全部排序,其计 算公式如下:
������������ = ������ + ������ × ( ������ / 2 -������������ )/ ������������ 在表3-3中,������������ = 22.5 + 5×(69/2-29)/11 = 22.5 + 2.5 = 25
(������ − ������ҧ)2 425756.3 305256.3 232806.3 124256.3 41006.3 41006.3
SK = (均值-中位数)/标准差 在表3-3中,SK=(26.083-25)/11.95 = 0.091 在正态分布条件下,由于均值等于众数所以偏度系数等于0。当偏度系数 大于0时,称为正偏态;当偏度系数小于0时,称为负偏态。
星蓝海学习网
3.4 双变量交叉分布特征的描述
3.4.1 相关关系与协方差
25
625
—
6550
图3-1 正态分布图
根据表3-1可得: 众数=30 中位数=30 平均数=30
星蓝海学习网
3.2 正态分布特征的描述
3.2.2 极差、四分位差、标准差和变异系数
极差 极差等于数据分布中最大值与最小值之差,记为R。表3-1中R=55-5=50。
四分位差 四分位差等于第3个四分位数( ������3 )与第1个四分位数( ������1 )之差,记为RQ。
变量x
图3-2 三组分布状况比较
星蓝海学习网
3.3 偏态分布特征的描述
3.3.1 偏态分布:正偏态和负偏态
表3-3 偏态频率分布表
组别
组中值
频数
累计频数
组中值×频数
2.5 ~7.5
5
1
1
5
7.5 ~12.5
10
6
7
60
12.5 ~ 17.5
15
10
17
150
17.5 ~ 22.5
20
12
29
240
0
0
35 10 16.90%
45
76.30%
350
5
250
40 7 11.90%
52
88.10%
280
10
700
45 4 6.80%
56
94.90%
180
15
900
50 2 3.40%
58
98.30%
100
20
800
55 1 合计 59
1.70% 100%
59 ——
100.00% ——
55 1770
则有 ������������ = ������3 − ������1
在表3-1中,������������ = ������3 − ������1 = 35−25=10 与极差相比,四分位差不受极端值的影响,对数据分布的离散趋势的描述比 较客观。但中间部分数据的离散状况也无法反映出来。
星蓝海学习网
星蓝海学习网
3.3 偏态分布特征的描述
3.3.3 分组下的均值及其与众数和中位数的关系
分组下的均值 在组距分组条件下计算均值,其公式与单变量分组情况相同,则有
������ҧ = ������������ / ������
表3-3中,从均值(26.087)大于众数(20.833)可知,数据分布为正偏 态。 分组下的均值与众数、中位数的关系
22.5 ~ 27.5
25
11
40
275
27.5 ~ 32.5
30
10
50
300
32.5 ~ 37.5
35
8
58
280
37.5 ~ 42.5
40
5
63
200
42.5 ~ 47.5
45
3
66
135
47.5 ~ 52.5
50
2
68
100
52.5 ~ 57.5
55
1
69
55
合计
—
69
—
1800
离差平方×频数 444.7 1552.7 1229.2 444.6 13.0 153.1 635.5 967.9 1073.1 1143.7 836.0 8493.5
55
40
7
40
7
60
45
4
45
3
65
50
2
50
1
70
55
1
55
1
75
合计
59
合计
59
合计
组 ������������ 1 2 4 7 10 11 10 7 4 2 1 59
星蓝海学习网
3.2 正态分布特征的描述
3.2.2 极差、四分位差、标准差和变异系数
反映数据分布的两大数量特征为均值和标准差。但在比较表3-2中A、B、
y − ������ -1145.8 -1035.8 -915.8 -665.8 -525.8 -465.8 -265.8
-65.8 534.2 934.2 1584.2 2034.2
0
������ − ������ҧ -652.5 -552.5 -482.5 -352.5 -202.5 -202.5
表3-4 居民家庭的人均食品支出(X)与家庭人均收入(Y)相关计算表
