湘教版八年级数学下册2.1多边形(含答案)
湘教版2019八年级数学下册第2章2.1多边形第1课时多边形的内角和练习含答案

课时作业(九)[2.1 第1课时 多边形的内角和] 一、选择题1.从一个七边形的某个顶点出发,分别连接这个点与其余各顶点,可以把这个七边形分割成的三角形的个数为( )A.6 B.5 C.8 D.72.正八边形的每一个内角的度数为( )链接听课例2归纳总结A.120° B.135°C.140° D.144°3.多边形的边数由7增加到8,它的内角和增加( )A.360° B.270° C.180° D.90°4.2017·苏州如图K-9-1,在正五边形ABCDE中,连接BE,则∠ABE的度数为( )图K-9-1A.30° B.36°C.54° D.72°5.2017·宜昌如图K-9-2,将一张四边形纸片沿直线剪开,如果剪开后的两个图形的内角和相等,那么图K-9-2四种剪法中,符合要求的是( )图K-9-2 图K-9-3A.①② B.①③C.②④ D.③④二、填空题6.如果一个多边形的所有内角从小到大排列起来,恰好依次增加相同的度数,设最小角的度数为100°,最大角的度数为140°,那么这个多边形是________边形.链接听课例2归纳总结7.2018·邵阳如图K-9-4,在四边形ABCD中,AD⊥AB,∠C=110°,它的一个外角∠ADE=60°,则∠B的大小是________.图K-9-4三、解答题8.小贝在进行多边形内角和的计算时,求得一个多边形的内角和为1500°,当她发现计算错了之后,重新检查,发现少加了一个内角,你知道她少加的这个内角是多少度吗?她求的这个多边形是几边形?链接听课例2归纳总结一题多变在四边形ABCD中,∠A=140°,∠D=80°.(1)如图K-9-5①,若∠B=∠C,试求∠C的度数;(2)如图②,若∠ABC的平分线BE交DC于点E,且BE∥AD,试求∠C的度数;(3)如图③,若∠ABC和∠BCD的平分线交于点E,试求∠BEC的度数.图K-9-5详解详析课堂达标1.[解析] B 从一个七边形的某个顶点出发,分别连接这个点与其余各顶点,可以把一个七边形分割成7-2=5(个)三角形.2.B3.[解析] C (8-2)×180°-(7-2)×180°=180°.4.[解析] B 在正五边形ABCDE 中,∠A=×(5-2)×180°=108°.15∵AB=AE ,∴△ABE 是等腰三角形,∴∠ABE=×(180°-108°)=36°.12故选B.5.[解析] B ∵①剪开后的两个图形是四边形,它们的内角和都是360°,③剪开后的两个图形都是三角形,它们的内角和都是180°,∴①③剪开后的两个图形的内角和分别相等.故选B.6.[答案] 六[解析] 设该多边形的边数为n ,则=180·(n -2),(100+140)n 2解得n =6.故这个多边形为六边形.7.[答案] 40°[解析] 根据邻补角的性质可得∠CDA=180°-60°=120°.又因为四边形的内角和为360°,所以∠B=360°-110°-120°-90°=40°.8.解:1500°÷180°=8,则边数n =8+2+1=11.则少加的内角是(11-2)×180°-1500°13=120°.答:她少加的这个内角是120°,这个多边形是十一边形.素养提升[解析] (1)根据四边形的内角和是360°,结合已知条件就可求解;(2)根据平行线的性质得到∠ABE 的度数,再根据角平分线的定义得到∠ABC 的度数,进一步根据四边形的内角和定理进行求解;(3)根据四边形的内角和定理以及角平分线的概念求得∠EBC+∠ECB 的度数,再进一步求得∠BEC 的度数.解:(1)∵∠A+∠B+∠C+∠D=360°,∠B=∠C,∴∠C=∠B==360°-∠A -∠D 2=70°.360°-140°-80°2(2)方法一:∵BE∥AD,∴∠BEC=∠D=80°,∠ABE=180°-∠A=180°-140°=40°.又∵BE 平分∠ABC,∴∠EBC=∠ABE=40°,∴∠C=180°-∠EBC-∠BEC=180°-40°-80°=60°.方法二:∵BE∥AD,∴∠ABE=180°-∠A=180°-140°=40°.又∵BE 平分∠ABC,∴∠ABC=2∠ABE=80°,∴∠C=360°-∠ABC-∠A-∠D=60°.(3)∵∠A+∠ABC+∠BCD+∠D=360°,∴∠ABC+∠BCD=360°-∠A-∠D=360°-140°-80°=140°.∵∠EBC=∠ABC,∠BCE=∠BCD,1212∴∠BEC=180°-∠EBC-∠BCE=180°-(∠ABC+∠BCD)=180°-×140°=110°.1212。
湘教版数学八年级下册2.1 多边形(共2课时)精品课件

D
4
E
5
F6
3C
2
B
1
A
六边形
6 个外角与跟它相邻的内角之和 加起来是__6_×__1_8_0_°__. 六边形的内角和是__(6_-_2_)_×__1_8_0_°_.
六边形的外角和是 _6_×__1_8_0_°__-_(6_-_2_)_×__1_8_0_°__=__3_6_0_°_.
【教材P38】
伸缩晾衣杆
衣架
1. 如图,在五边形 ABCDE 中, AB ∥CD ,∠1,∠2,∠3
分别是与∠BAE,∠AED ,∠EDC 相邻的外角, 则
∠1+∠2+∠3等于( B )
A. 90°
B. 180°
C. 210°
D. 270°
2. 如图,工人师傅做了一个长方形窗框ABCD ,E,F,G,H 分别是四条边上的中点,为了使它稳固,需要在窗框上 钉一根木条,这根木条不应钉在( B ) A. A,C两点之间 B. E,G两点之间 C. B,F两点之间 D. G,H两点之间
18
18
∵ n 为整数 , ∴n = 9. ∴ 这个多边形的边数是 9.
课后作业
1.从课后习题中选取; 2.完成练习册本课时的习题.
学法指导
新课程标准有以下几项变化,一是理念变化:确立核心素养导向的课 程目标;二是结构变化:明确学业要求与学业质量标准;三是内容变化: 调整教学要求和增加教学内容。最终是要结合学生认知水平和生活经验, 设计合理的生活情境、数学情境、科学情境。关注情境的真实性,适当引 入数学文化,真正让学生感受数学与生活的密切关系和对生活的影响以及 作用。培养学生的核心素养目标,从本质上提升教学质量。
湘教版八年级下册2.1多边形课件(共17张PPT)

2.1 多边形
锦囊妙计
在解决较复杂的多边形问题时, 常通过作辅 助线将多边 形问题转化为三角形问题.
2.1 多边形
题型四 与正多边形镶嵌有关的问题
例题4 小王到瓷砖店购买一种正多边形瓷 砖铺设地面(瓷砖间
要求无缝隙), 则他购买的瓷砖 形状不可以是( D ).
A.正三角形
B.正方形
C.正六边形
D.正八边形
∠H+∠I+∠J的值为( B).
A.180°
B.360°
C.540°
D.720°
2.1 多边形
分析 如图2-1-10.
三角形 的 外角 性质
∠1=∠A+∠B, ∠2=∠C+∠D, ∠3=∠E+∠F, ∠4=∠G+∠H, ∠5=∠I+∠J
∠1+∠2+ ∠3+∠4+ ∠5=360°
∠1, ∠2, ∠3, ∠4, ∠5是五 边形的五 个外角
例题2 一个正多边形的每个内角比与它相邻 的外角大60°, 求
这个正多边形的边数及内角和.
解:设这个正多边形为正n边形,则它的每 一个外角为 , 与它相邻的内角为180°-
.
根据题意, 得(180°- )- =60°, 解得n=6,
故这个正多边形的边数为6, 所以其内角和为 (6-2)×180°=720°.
2.1 多边形
2.1 多边形
锦囊妙计 判断图形平面镶嵌的依据
判断图形是否能够平面镶嵌, 只需看拼在同一 顶点处的几 个角的和是否等于360°, 若等于360°, 则说明图形能够平面 镶嵌, 否则, 图形不能平面镶嵌.
2.1 多边形
题型五 运用多边形内(外)角和求不规则图形的角度之和
湘教版八年级数学下册_2.1 多边形

2.1 多边形
学习目标
1 课时讲解 2 课时流程
多边形及其相关概念 多边形的内角和 多边形的外角和 四边形的不稳定性
逐点 导讲练
课堂 小结
作业 提升
感悟新知
知识点 1 多边形及其相关概念
知1-讲
1.多边形的定义: 在平面内,由一些线段首尾顺次相接组成的封闭图形
叫作多边形. 分类: 多边形根据边数可以分为三角形、四边形、五
知4-练
方法点拨 将不稳定的多边形转化为稳定图形的方法就是
让转化的图形的每一个组成部分都成为三角形,常 用的转化方法是作多边形从同一顶点出发的对角线 .
课堂小结
多边形
定义
内角 多
内角和
边 对角线
正多边形 形 外角
外角和
知3-讲
1.外角: 多边形的内角的一边与另一边的反向延长线所组成 的角叫作这个多边形的一个外角 .
感悟新知
2. 外角和: 在多边形的每个顶点处取一个外角,它们 知3-讲 的和叫作这个多边形的外角和 .
3. 定理: 任意多边形的外角和等于 360° . 多边形的外角和是由多边形内、外角的关系推导出的,
感悟新知
知识点 4 四边形的不稳定性
知4-讲
和三角形不同,即使四边形的边长确定,它的形状也不 能确定,我们把四边形的这个性质称为四边形的不稳定性 .
感悟新知
知4-讲
注意:(1)四边形的不稳定性即其形状的不确定性,有它 有利的一面,也有它不利的一面,我们应充分利用它有利的 一面为生活服务 .
(2)生活中四边形的不稳定性有着广泛的应用,如电动伸 缩门、伸缩衣架等 .
知2-练
感悟新知
特别提醒 一个多边形(除三角形外)截去
2019年精选初中八年级下册数学2.1 多边形湘教版课后辅导练习[含答案解析]第三十九篇
![2019年精选初中八年级下册数学2.1 多边形湘教版课后辅导练习[含答案解析]第三十九篇](https://img.taocdn.com/s3/m/dbb6ac2b14791711cc7917e4.png)
2019年精选初中八年级下册数学2.1 多边形湘教版课后辅导练习[含答案解析]第三十九篇第1题【单选题】一个多边形的外角和与它的内角和相等,则多边形是( )A、六边形B、五边形C、四边形D、三角形【答案】:【解析】:第2题【单选题】用下列一种正多边形可以拼地板的是( )A、正五边形B、正六边形C、正八边形D、正十二边形【答案】:【解析】:第3题【单选题】正六边形的每个内角都是( )A、60°B、80°C、100°D、120°【答案】:【解析】:第4题【单选题】如图所示,小华从A点出发,沿直线前进10米后左转24°,再沿直线前进10米,又向左转24°,……,照这样走下去,他第一次回到出发地A点时,一共走的路程是( )A、140米B、150米C、160米D、240米【答案】:【解析】:第5题【单选题】用下列图形不能进行平面镶嵌的是( )A、正三角形和正四边形B、正三角形和正六边形C、正四边形和正八边形D、正四边形和正十二边形【答案】:【解析】:第6题【填空题】一个多边形每个外角都是60°,这个多边形是______边形,它的内角和是______度,外角和是______度.【答案】:【解析】:第7题【填空题】小燕偶然发现爸爸手机有软件可用来测量方位,于是她来到小区一处广场上.如图,小燕从P点向西直走12米后,向左转,转动的角度为α=40度,再走12米,再左转40度,如此重复,最终小燕又回到点P,则小燕一共走了______米.【答案】:【解析】:第8题【填空题】六边形共有______条对角线,它的内角和是______,外角和______.【答案】:【解析】:第9题【填空题】用正三角形和正方形作覆盖平面,在拼接点处有m个正三角形和n个正方形,则m=______,n=______.【答案】:【解析】:第10题【解答题】动手操作,探究:探究一:三角形的一个内角与另两个内角的平分线所夹的钝角之间有何种关系?已知:如图(1),在△ADC中,DP、CP分别平分∠ADC和∠ACD,试探究∠P与∠A的数量关系.探究二:若将△ADC改为任意四边形ABCD呢?已知:如图(2),在四边形ABCD中,DP、CP分别平分∠ADC和∠BCD,试利用上述结论探究∠P与∠A+∠B的数量关系.(写出说理过程)探究三:若将上题中的四边形ABCD改为六边形ABCDEF(图(3))呢?请直接写出∠P与∠A+∠B+∠E+∠F 的数量关系.【答案】:【解析】:第11题【解答题】已知一个多边形的内角和是这个多边形外角和的2倍,求这个多边形的边数?【答案】:【解析】:第12题【综合题】四边形ABCD中,∠BAD的角平分线与边BC交于点E,∠ADC的角平分线交直线AE于点O.若点O在四边形ABCD的内部,如图1,若AD∥BC,∠B=40°,∠C=70°,则∠DOE=______°;如图2,试探索∠B、∠C、∠DOE之间的数量关系,并将你的探索过程写下来.如图3,若点O在四边形ABCD的外部,请你直接写出∠B、∠C、∠DOE之间的数量关系.【答案】:【解析】:第13题【综合题】如图,点M、N分别是正五边形ABCDE的边BC、CD上的点,且BM=CN,AM交BN于点P.求证:△ABM≌△BCN;求∠APN的度数.【答案】:【解析】:。
2019年精选湘教版初中数学八年级下册第2章 四边形2.1 多边形课后辅导练习[含答案解析]三十五
![2019年精选湘教版初中数学八年级下册第2章 四边形2.1 多边形课后辅导练习[含答案解析]三十五](https://img.taocdn.com/s3/m/b7bf1c5bbb68a98271fefa90.png)
2019年精选湘教版初中数学八年级下册第2章四边形2.1 多边形课后辅导练习[含答案解析]三十五第1题【单选题】一个多边形的外角和与它的内角和相等,则多边形是( )A、六边形B、五边形C、四边形D、三角形【答案】:【解析】:第2题【单选题】正八边形的每个外角为( )A、60°B、45°C、35°D、36°【答案】:【解析】:第3题【单选题】如果一个多边形的内角和等于720°,这个多边形是( )A、四边形B、五边形C、六边形D、七边形【答案】:【解析】:第4题【单选题】一个多边形的每个外角都等于60°,则这个多边形的边数为( )A、8B、7C、6D、5【答案】:【解析】:第5题【单选题】在①正三角形、②正方形、③正六边形中能密铺平面的是( )A、①②③B、②③C、①③D、以上都不对【答案】:【解析】:第6题【填空题】正八边形的每个外角的度数为______.【答案】:【解析】:第7题【填空题】已知一个多边形的内角和与它的外角和正好相等,则这个多边形是______边形. 【答案】:【解析】:第8题【填空题】已知正n边形的一个内角为135°,则边数n的值是______.【答案】:【解析】:第9题【填空题】我们知道:n边形从一个顶点出发可画(n﹣3)条对角线,那么十二边形共有______条对角线.【答案】:【解析】:第10题【填空题】如图,五边形ABCDE是一块草地.小明从点S出发,沿着这个五边形的边步行一周,最后仍回到起点S处,小明在各拐弯处转过的角度之和是______【答案】:【解析】:第11题【解答题】已知:如图,在四边形ABCD中,∠A=∠C=90°,BE平分∠ABC,DF平分∠ADC.BE与DF有怎样的位置关系?为什么?【答案】:【解析】:第12题【综合题】如图,已知△BAD和△BCE均为等腰直角三角形,∠BAD=∠BCE=90°,点M为DE的中点,过点E与AD平行的直线交射线AM于点N.当A,B,C三点在同一直线上时(如图1),求证:M为AN的中点;将图1中的△BCE绕点B旋转,当A,B,E三点在同一直线上时(如图2),求证:△ACN为等腰直角三角形;将图1中△BCE绕点B旋转到图3位置时,(2)中的结论是否仍成立?若成立,试证明之,若不成立,请说明理由.【答案】:【解析】:。
八年级数学下册 第2章 四边形2.1 多边形习题课件(新版)湘教版

【教材P39】
解(1)(n-2)·180°-(n-3)·180°=180°即相差 180°. (2)因为任意多边形的外角和为 360°,所以这两个 多边形外角和相等.
【教材P39】
解 ∵ ∠BPC = 120°, ∴∠PBC =∠PCB = 30° n×30°= 360° n = 12
复习课件
八年级数学下册 第2章 四边形2.1 多边形习题课件(新版)湘教版
【教材P39】
解 (1)(n-2)·180°= 1440° n = 10
(2)(n-2)·180°= n×108° n=5
【教材P39】
解 (1)n×36°= 360° n = 10
(2)(n-2)·180°= 360°×2 n=6
【教材P39】
解 5x = 360° x = 72°
【教材P39】
解 设这个多边形的每一个外角为a, 则与它相邻的内角为180°-a, 根据题意,可得a=180°-a,解得a=90°, 所以这个多边形的每一个外角为90°, 这个多边形的边数是360°÷90°=4,所以这个多边 形下册 第2章 四边形2.1 多边 形习题课件(新版)湘教版
同学们,下课休息十分钟。现在是休 息时间,你们休息一下眼睛,
看看远处,要保护好眼睛哦~站起来 动一动,久坐对身体不好哦~
结束语
八年级数学下册 第2章 四边形2.1 多边形习题课 件(新版)湘教版
湘教版八年级数学下册2.1多边形(含答案)
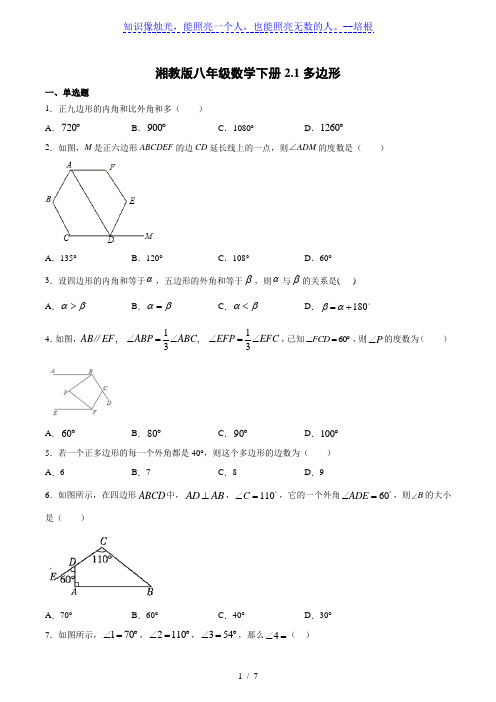
湘教版八年级数学下册2.1多边形一、单选题1.正九边形的内角和比外角和多( )A .720︒B .900︒C .1080︒D .1260︒2.如图,M 是正六边形ABCDEF 的边CD 延长线上的一点,则∠ADM 的度数是( )A .135°B .120°C .108°D .60°3.设四边形的内角和等于α,五边形的外角和等于β,则α与β的关系是( )A .αβ>B .αβ=C .αβ<D .180βα=+ 4.如图,11,,33AB EF ABP ABC EFP EFC ∠=∠∠=∠∥,已知60FCD ∠=︒,则P ∠的度数为( )A .60︒B .80︒C .90︒D .100︒5.若一个正多边形的每一个外角都是40°,则这个多边形的边数为( )A .6B .7C .8D .96.如图所示,在四边形ABCD 中,AD AB ⊥,110C ︒∠=,它的一个外角60ADE ︒∠=,则B 的大小是( )A .70°B .60°C .40°D .30°7.如图所示,170∠=︒,2110∠=︒,354∠=︒,那么4∠=( )A .126︒B .116︒C .146︒D .106︒8.下列命题中: ①长为5cm 的线段AB 沿某一方向平移10cm 后,平移后线段AB 的长为10cm ;②三角形的高在三角形内部;③六边形的内角和是外角和的两倍;④平行于同一直线的两直线平行;⑤两个角的两边分别平行,则这两个角相等,真命题个数有( )A .1B .2C .3D .4 二、填空题9.一个长方形的长为12a+b ,它的周长为 3a+2b ,则它的宽为________. 10.一个多边形的内角和是 1440°,则这个多边形是__________边形.11.在五边形ABCDE 中,若440A B C D ∠+∠+∠+∠=︒,则E ∠=______︒.12.如图,∠1,∠2,∠3是多边形的三个外角,边CD ,AE 的延长线交于点F ,如果∠1+∠2+∠3=225°,那么∠ABC 的度数是______.13.如图,ABCDE 是正五边形,△OCD 是等边三角形,则∠COB =_____°.14.如图所示是三个边长相等的正多边形拼成的无缝隙、不重叠的图形的一部分,正多边形①和②的内角都是108°,则正多边形③的边数是______.15.将边长相等的一个正方形与一个正五边形,按如图重叠放置,则∠1度数=______.16.如图,Rt ABC 的两条直角边AC BC ,分别经过正八边形的两个顶点,则图中12∠+∠的度数是________.三、解答题17.如图,五边形ABCDE 的每个内角都相等,已知EF BC ⊥,求证:EF 平分AED ∠.18.如图,求x的值.19.如图,在四边形ABCD中,∠A=∠C=90°,BE平分∠ABC,DF平分∠CDA.(1)求证:BE∥DF;(2)若∠ABC=56°,求∠ADF的大小.20.(1)已知一个多边形的内角和是它的外角和的3 倍,求这个多边形的边数.(2)如图,点F 是△ABC 的边BC 延长线上一点.DF⊥AB,∠A=30°,∠F=40°,求∠ACF 的度数.21.让我们一起来探究“边数大于或等于3的多边形的内角和问题”.规定:连接多边形不相邻的两个顶点的线段叫做多边形的对角线.尝试:从多边形某一个顶点出发的对角线可以把一个多边形分成若干个三角形,…….这样,就把“多边形内角和问题”转化为“三角形内角和问题”了.……(1)请你在下面表格中,试一试,做一做,并将表格补充完整:(2)根据上面的表格,请你猜一猜,七边形的内角和等于;…….如果一个多边形有n条边,请你用含有n的代数式表示这个多边形的内角和.(3)如果一个多边形的内角和是1260°,请判断这个多边形是几边形.22.如图1所示,称“对顶三角形”,其中,∠A+∠B=∠C+∠D利用这个结论,完成下列填空.(1)如图(2),∠A+∠B+∠C+∠D+∠E=;(2)如图(3),∠A+∠B+∠C+∠D+∠E=;(3)如图(4),∠1+∠2+∠3+∠4+∠5+∠6=;(4)如图(5),∠1+∠2+∠3+∠4+∠5+∠6+∠7=.知识像烛光,能照亮一个人,也能照亮无数的人。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
知识像烛光,能照亮一个人,也能照亮无数的人。--培根
21.让我们一起来探究“边数大于或等于 3 的多边形的内角和问题”. 规定:连接多边形不相邻的两个顶点的线段叫做多边形的对角线. 尝试:从多边形某一个顶点出发的对角线可以把一个多边形分成若干个三角形,…….这样,就把“多边形 内角和问题”转化为“三角形内角和问题”了.…… (1)请你在下面表格中,试一试,做一做,并将表格补充完整:
A.1
B. 2
C. 3
D. 4
二、填空题
9.一个长方形的长为 1 a+b,它的周长为 3a+2b,则它的宽为________. 2
10.一个多边形的内角和是 1440°,则这个多边形是__________边形.
11.在五边形 ABCDE 中,若 A + B + C + D = 440 ,则 E = ______ .
知识像烛光,能照亮一个人,也能照亮无数的人。--培根
湘教版八年级数学下册 2.1 多边形
一、单选题 1.正九边形的内角和比外角和多( )
A.ห้องสมุดไป่ตู้720
B. 900
C.1080
D.1260
2.如图,M 是正六边形 ABCDEF 的边 CD 延长线上的一点,则∠ADM 的度数是( )
A.135°
B.120°
名称
图形
内角和
三角形
180°
四边形
2 180°=360°
五边形
六边形
...
...
……
(2)根据上面的表格,请你猜一猜,七边形的内角和等于
;…….如果一个多边形有 n 条边,请你用
含有 n 的代数式表示这个多边形的内角和
.
(3)如果一个多边形的内角和是 1260°,请判断这个多边形是几边形.
22.如图 1 所示,称“对顶三角形”,其中,∠A+∠B=∠C+∠D
.
6/7
知识像烛光,能照亮一个人,也能照亮无数的人。--培根
参考答案 1.B2.B3.B4.B5.D6.C7.A8.A
9. a
10.十 11.100 12.45° 13.66° 14.10. 15.18°.
16.180
17.略. 18.x=60 19.(1)证明略;(2)∠ADF=62°. 20.(1)8;(2)80°.
2/7
知识像烛光,能照亮一个人,也能照亮无数的人。--培根
15.将边长相等的一个正方形与一个正五边形,按如图重叠放置,则∠1 度数=______.
16.如图, Rt ABC 的两条直角边 AC,BC 分别经过正八边形的两个顶点,则图中 1+ 2 的度数是
________.
三、解答题
17.如图,五边形 ABCDE 的每个内角都相等,已知 EF ⊥ BC ,求证: EF 平分 AED .
3/7
知识像烛光,能照亮一个人,也能照亮无数的人。--培根
18.如图,求 x 的值.
19.如图,在四边形 ABCD 中,∠A=∠C=90°,BE 平分∠ABC,DF 平分∠CDA. (1)求证:BE∥DF; (2)若∠ABC=56°,求∠ADF 的大小.
20.(1)已知一个多边形的内角和是它的外角和的 3 倍,求这个多边形的边数. (2)如图,点 F 是△ABC 的边 BC 延长线上一点.DF⊥AB,∠A=30°,∠F=40°,求∠ACF 的度数.
12.如图,∠1,∠2,∠3是多边形的三个外角,边 CD,AE 的延长线交于点 F,如果∠1 + ∠2 + ∠3 = 225°,
那么∠ABC的度数是______.
13.如图,ABCDE 是正五边形,△OCD 是等边三角形,则∠COB=_____°.
14.如图所示是三个边长相等的正多边形拼成的无缝隙、不重叠的图形的一部分,正多边形①和②的内角 都是 108°,则正多边形③的边数是______.
1/7
知识像烛光,能照亮一个人,也能照亮无数的人。--培根
A.126
B.116
C.146
D.106
8.下列命题中:
①长为 5cm 的线段 AB 沿某一方向平移10cm 后,平移后线段 AB 的长为10cm ;
②三角形的高在三角形内部;
③六边形的内角和是外角和的两倍;
④平行于同一直线的两直线平行;
⑤两个角的两边分别平行,则这两个角相等,真命题个数有( )
C.108°
D.60°
3.设四边形的内角和等于 ,五边形的外角和等于 ,则 与 的关系是( )
A.
B. =
C.
D. = +180
4.如图,AB∥EF, ABP = 1 ABC, EFP = 1 EFC ,已知 FCD = 60 ,则 P 的度数为( )
3
3
A. 60
B. 80
C. 90
21.(1)3 180°=540°,4 180°=720°;(2)900°,(n-2) 180°;(3)这个多边形为九边形
22.(1)180°,(2)180°,(3)360°,(4)540°
1/7
D.100
5.若一个正多边形的每一个外角都是 40°,则这个多边形的边数为( )
A.6
B.7
C.8
D.9
6.如图所示,在四边形 ABCD 中, AD ⊥ AB , C = 110 ,它的一个外角 ADE = 60 ,则ÐB 的大小
是( )
A.70°
B.60°
C.40°
D.30°
7.如图所示, 1 = 70 , 2 = 110 , 3 = 54 ,那么 4 = ( )
5/7
知识像烛光,能照亮一个人,也能照亮无数的人。--培根
利用这个结论,完成下列填空.
(1)如图 (2),∠A+∠B+∠C+∠D+∠E=
;
(2)如图(3),∠A+∠B+∠C+∠D+∠E=
;
(3)如图(4),∠1+∠2+∠3+∠4+∠5+∠6=
;
(4)如图(5),∠1+∠2+∠3+∠4+∠5+∠6+∠7=
