(完整版)一元一次方程的应用等积变形问题
完整版)一元一次方程应用题及答案

完整版)一元一次方程应用题及答案1.某商店开业,为了吸引顾客,所有商品均以八折优惠出售。
已知某种皮鞋进价为60元一双,商家以40%的利润率出售。
问这种皮鞋的标价和优惠价分别是多少元?2.某商品在加价20%后的价格为120元,求它的进价是多少?3.一家商店将某种服装的标价提高40%,并以八折优惠卖出。
结果每件服装仍可获得15元的利润。
问这种服装每件的进价是多少?4.一家商店将一种自行车的标价提高45%,并以八折优惠卖出。
结果每辆自行车仍可获得50元的利润。
问这种自行车每辆的进价是多少元?5.某商品的进价为800元,出售时标价为1200元。
由于该商品积压,商店准备打折出售。
但要保持利润率不低于5%,则至多可以打几折?6.一家商店将某种型号的彩电先按原售价提高40%,然后在广告中写上“大酬宾,八折优惠”。
经顾客投诉后,拆迁部门按已得非法收入的10倍处以每台2700元的罚款。
求每台彩电的原售价是多少?7.甲乙两件衣服的成本共500元,商店老板为获取利润,决定将甲服装按50%的利润定价,乙服装按40%的利润定价。
在实际销售时,两件服装均按9折出售。
这样商店共获利157元。
求甲乙两件服装的成本各是多少元?8.某同学在A、B两家超市发现他看中的随身听和书包的单价和为452元,且随身听的单价比书包的单价的4倍少8元。
某天该超市打折,A超市所有商品打8折出售,B超市购物每满100元返购物券30元。
但他只带了400元钱,如果他只在一家超市购买看中的两件物品,你能说明他可以选择哪一家吗?若两家都可以选择,哪家更省钱?知识点2:方案选择问题1.某蔬菜公司有一种绿色蔬菜,直接销售每吨利润为1000元,经粗加工后销售每吨利润可达4500元,经精加工后销售每吨利润涨至7500元。
当地一家公司收购这种蔬菜140吨,该公司的加工生产能力是:如果对蔬菜进行精加工,每天可加工16吨,如果进行粗加工,每天可加工6吨。
但两种加工方式不能同时进行,受季度等条件限制,公司必须在15天将这批蔬菜全部销售或加工完毕。
一元一次方程的应用等积变化问题

一元一次方程的应用等积变化问题等积变化问题是一元一次方程应用题中的一种常见题型,其基本特点是涉及到体积、面积、长度等量的变化,而这种变化是等积的,即变化前后的量是相等的。
解决等积变化问题的关键在于理解“等积”的含义,即体积、面积、长度等量在变化过程中保持不变。
因此,我们需要根据题目描述,建立等量关系,然后列出方程求解。
下面是一个具体的例子:题目:有一个长方体,它的长增加了2cm,宽和高不变,体积增加了40立方厘米;宽增加了2cm,长和高不变,体积增加了60立方厘米;高增加了2cm,长和宽不变,体积增加了48立方厘米。
求原来长方体的体积是多少?解:设原长方体的长为l cm,宽为w cm,高为h cm。
根据题目描述,我们可以建立以下方程:1. 长增加2cm后,体积增加了40立方厘米:(l + 2) × w × h - l × w × h = 402. 宽增加2cm后,体积增加了60立方厘米:l × (w + 2) × h - l ×w × h = 603. 高增加2cm后,体积增加了48立方厘米:l × w × (h + 2) - l × w × h = 48将以上三个方程整理为一元一次方程组:1) (l + 2) × w × h - l × w × h = 402) l × (w + 2) × h - l × w × h = 603) l × w × (h + 2) - l × w × h = 48通过解这个方程组,我们可以得到原长方体的长、宽、高分别为:l = 5 cm, w = 4 cm, h = 3 cm。
因此,原来长方体的体积是:l × w × h = 5 × 4 × 3 = 60 立方厘米。
5.3 一元一次方程的应用(2) 等积变形--

2、用一根15cm长的铁丝围成一个三角形,然后 把它围成长方形;
解:围成的图形的面积发生了变化,但铁丝的长度不变
3、用一块橡皮泥先做成一个立方体,源自把它改 变成球。解:形状改变,体积不变
一纪念碑建筑的底面呈正方形,其四周 铺上花岗石,形成一个宽为3米的正方形 边框(如图中阴影部分),已知铺这个边 框恰好用了192块边长为0.75米的正方形 花岗石(接缝忽略不计),问纪念碑建筑 底面的边长是多少米?
4 3 x 3 0.75 0.75 192
解这个方程,得x=6
答:纪念碑建筑底面的边长为6米. 方案二
本题还有哪些解法?
1、在应用方程解决问有关实际问题时,清楚地分辨量之间的 关系,尤其相等关系是建立方程的关键。 2、对于等积变形(面积)问题,它的基本数量关系是相关的 面积公式,相等关系的特征是存在不变量,也就是用不同的 方法来计算阴影部分的面积,面积不变。
3
x
3
阴影部分的面积= 192块边长为0.75正方形花岗岩的面积 阴影部分的面积= 4个长为(x+3)米、宽为3米的长方形 解: 设纪念碑建筑底面的边长为米,根据题意,得
4 3 x 3 0.75 0.75 192
解这个方程,得x=6 答:纪念碑建筑底面的边长为6米.
2x 5 x 2 x3
例2、学校组织植树活动,已知在甲处植树的有23人, 在乙处植树的有 17 人,现调 20 人去支援,使在甲处 植树的人数是乙处植树人数的2倍,应调往甲、乙两 处各多少人? 分析 : 设应调往甲处 x 人,题目中涉及的有关数量 及其关系能用表格去表示吗?
例2、学校组织植树活动,已知在甲处植树的有23人, 在乙处植树的有 17 人,现调 20 人去支援,使在甲处 植树的人数是乙处植树人数的2倍,应调往甲、乙两 处各多少人? 分析 : 设应调往甲处 x 人,题目中涉及的有关数量 及其关系能用表格去表示吗? 原有人数 甲 处 23 乙 17 处
一元一次方程实际应用题之等积变形问题
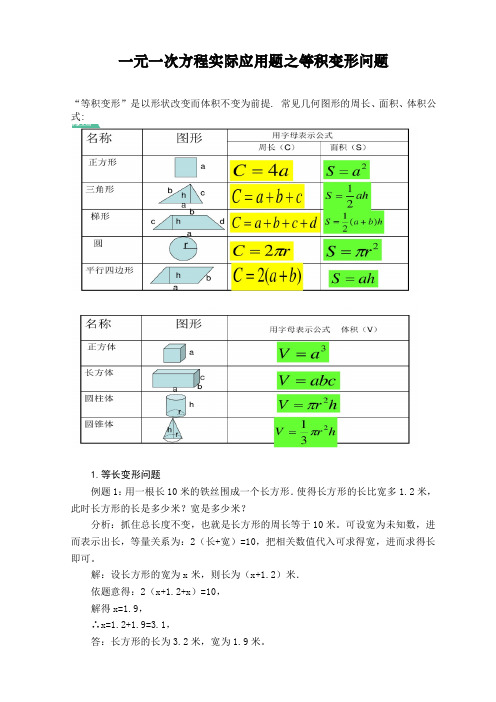
一元一次方程实际应用题之等积变形问题“等积变形”是以形状改变而体积不变为前提. 常见几何图形的周长、面积、体积公式:1.等长变形问题例题1:用一根长10米的铁丝围成一个长方形.使得长方形的长比宽多1.2米,此时长方形的长是多少米?宽是多少米?分析:抓住总长度不变,也就是长方形的周长等于10米。
可设宽为未知数,进而表示出长,等量关系为:2(长+宽)=10,把相关数值代入可求得宽,进而求得长即可。
解:设长方形的宽为x米,则长为(x+1.2)米.依题意得:2(x+1.2+x)=10,解得x=1.9,∴x=1.2+1.9=3.1,答:长方形的长为3.2米,宽为1.9米。
2.等体积变形问题例题2:要锻造直径为60mm,高为30mm的圆柱形毛坯,需截取直径为40mm的圆钢长是多少毫米?分析:抓住锻造前后的体积不变,此题的等量关系为:锻造前的体积=锻造后的体积.据此列方程求解。
要注意的是,题目中已知直径,需要转化为半径。
解:设需截取直径为40mm的圆钢长xmm,60÷2=30(mm)、40÷2=20(mm);依题意得:π×30^2×30=π×20^2×x解得:x=67.5例题3:有一段钢材可作一个底面直径 8 厘米,高 9 厘米的圆柱形零件。
如果把它改制成高是 12 厘米的圆锥形零件,零件的底面积是多少平方厘米?分析:根据“底面直径8厘米,高9厘米的圆柱形零件”,利用圆柱体积公式,可以求出圆柱的体积,又因为把圆柱形的零件改制成圆锥形零件时,此段钢的体积不变,根据体积不变列出方程求解。
解:零件的底面积是x平方厘米。
8÷2=4(厘米)依题意得:3×π×4^2×9=x×12解得:x=36π答:零件的底面积是36π平方厘米。
3.等面积变形问题例题4:如图,某小学将一块梯形空地改成宽为30m的长方形运动场地,要求面积不变.若在改造后的运动场地,小王、小李两人同时从点A出发,小李沿着长方形边顺时针跑,小王则是逆时针跑,并且小王每秒比小李多跑2m,经过10秒钟他们相遇.(1)求长方形的长;(2)求小王、小李两人的速度分析:(1)求得原梯形的面积,利用面积不变和长方形的面积求得长方形的长即可;(2)设小李的速度是xm/s,则小王的速度是(x+2)m/s,利用10秒钟他们相遇所走的路程为长方形的周长列出方程解决问题。
一元一次方程的应用+第1课时等积变形问题+ 课件 +2024-—2025学年北师大版数学七年级上册

新知小结 2. 常见图形的周长、面积及体积计算公式.
(1)长方体的体积= 长×宽×高 ;
(2)圆柱的体积= 底面积×高 ;
(3)长方形的周长= 2×(长+宽) ;
(4)长方形的面积= 长×宽 .
3. 列一元一次方程解决实际问题的基本步骤.
典例精析 例1 用一根长为10m的铁丝围成一个长方形。
课堂总结
等积变 形问题
关 键 根据等量关系列方程.
解应用题步骤
①审; ②设; ③列; ④解; ⑤检; ⑥答.
情境导入 教师让学生拿出课前准备好的橡皮泥,先捏出一个“瘦长”的圆
柱体,然后再让这个“瘦长”的圆柱“变矮”,变成一个又矮又胖的 圆柱,请同学们边操作边思考下列几个问题:
(1)在你操作的过程中,圆柱由“高”变“矮”,圆柱的底面直 径是否变化?还有哪些量改变了?
(2)在这个变化过程中,什么量没有变化呢? 解:(1)圆柱的底面直径发生了变化;
因此,易拉罐的高度变为__1_4_._5_2__cm.
新知小结
1. 常见的几种情形列方程. (1)物体的锻压等应用题,抓住体积不变建立方程; (2)周长一定,围成不同形状的图形,图形的面积可能变了, 抓住周长不变列方程; (3)图形的拼接、割补、平移、旋转等类型的应用题,抓住图 形变化前后的面积、周长不变列方程. 注:应学会“变中找不变”和“不变中找变”的数学思想方法.
随针堂对检练测习
设小明的爸爸设计的养鸡场的宽为 y m, 则长为(y +2)m. 由题意,得 y+y+(y+2)=35, 解得 y=11,则 y+2=13. 所以小明爸爸设计的养鸡场长为13m,小于墙长,宽为11m, 面积为13×11=143(m2). 所以小明爸爸的设计合理,这时养鸡场的面积为143m2.
一元一次方程应用-等积变形、行程问题1

(x+40)km/t
根据题意可得:10(x+4)=1100
考考你
1、某工厂锻造直径为60毫米,高20毫米的圆柱形 瓶内装水,再将瓶内的水倒入一个底面直径6厘米、 高10厘米的圆柱形玻璃杯中,能否完全装下?若 装不下,那么瓶内水面还有多高? 若未能装满, 求杯内水面离杯口的距离。
解:设应截取的圆柱体钢长为xmm 根据题意得
200 x 300 300 90 2
2
解方程得 x≈258 答:应截取约258mm长的圆柱体钢 列方程解应用题的关键就是审 题,弄清题意,分清类型,熟悉 题中所用的数量关系;找出题中 已知量和未知量,明确它们之间 的关系,找出题中的变量和不变 量就,即等量关系。 列方程解应 用题的步骤: 1、审题
注意: 1、单位的统一; 2、两个瓶的底面直径的关系; 3、等量关系是高的关系。 能否装下是什么 意思?有哪几种 情况?
解:未能装满。设杯内水面离杯口的距离为x厘米。 根据题意得:10-x=2 解得:x=8 答:杯内水面离杯口的距离为8厘米。
2、甲、乙两地相距180km,一人骑自行车从甲地出发每小 时走15km;另一人骑摩托车从乙地同时出发,两人相向 而行,已知摩托车速度是自行车的3倍,问多少小时后两 车相遇? 180km 分析: 甲行驶的距离 乙行驶的距离 等量关系是: 甲行驶的距离 + 乙行驶的距离 =108
试一试
1、如图:用直径为200mm的圆柱体钢,锻造一个长、宽、 高分别为300mm,300mm和90mm的长方体毛坯,应 截取多少mm的圆柱体钢。
○200 300 90
把圆柱体锻造成长方体毛 坯,虽然形状改变了,但 前后的体积是相等的。
一元一次方程应用题(6)(等长变形、等积变形)

一元一次方程应用题(6)(等长变形、等积
变形)
1.假设原长方形的长为x,宽为y,则根据周长公式
2(x+y)=26,可得x+y=13.将长减少1,宽增加2后得到的正方
形的边长为y+2,因此有y+2=x-1.将这两个方程联立解得x=9,y=4,所以原长方形的长为9cm,宽为4cm。
2.圆锥体的体积为1/3πr^2h,圆柱体的体积为πr^2h,两
者相等,因此可得圆柱体的高为8×(30/10)^2=72cm,所以圆
柱体内的水高为8cm。
3.设新的长方形宽为x,则根据折叠后周长不变可得
2x+10=18,解得x=4,因此新的长方形的长为9cm,宽为4cm。
4.正方体的体积为20^3=8000cm^3,盛水量筒的容积为
12×h,其中h为水面升高的高度,因此有12h=8000,解得
h=666.67cm,所以水面升高了666.67/12≈55.56cm。
5.设大长方形面积为S,则重叠部分面积为S/6,小长方
形面积为S/4,阴影部分面积为224cm^2,因此有S/6-S/4=224,解得S=1344,所以重叠部分面积为S/6=224cm^2.
6.(1) 第一个中的水体积为π(4^2)×16=256π,第二个的底
面积为π(8^2)=64π,因此第二个中的水高为256π/64π=4cm。
2) 将1插入2后,1中的水体积为π(4^2)×10=160π,2中的水体积为π(8^2)×10=640π,因此水位上升了640π-
256π=384π,所以水面升高了384π/(π(8^2))≈1.5cm。
一元一次方程应用题(6)(等长变形、等积变形)

一元一次方程应用题1.一个长方形的周长为26㎝,这个长方形的长减少1㎝,宽增加2㎝,就可成为一个正方形,则原长方形的长和宽各为多厘米?2.在一个底面直径为30厘米,高为8厘米的圆锥体容器中倒满水,然后将水倒入一个底面直径为10厘米的圆柱体空容器内,圆柱体容器内的水有多高?3.已知一个用铁丝折成的长方形,它的长为9cm ,宽为6cm ,把它重新折成一个宽为5cm 的长方形,则新的长方形的宽是多少?4.将棱长为20cm 的正方体铁块没入盛水量筒中,已知量筒底面积为12cm 2,问量筒中水面升高了多少cm ?5.如图所示,两个长方形重叠部分的面积相当于大长方形面积的六分之一,相当于小长方形面积的四分之一,阴影部分的面积为224cm 2,求重叠部分面积。
6.如图是两个圆柱体的容器,它们的半径分别是4cm 和8cm ,高分别为16cm 和10cm ,先在第一个容器中倒满水,然后将其全部倒入第二个容器中。
(1)问倒完后,第二个容器水面的高度是多少?(2)如右图把容器1口朝上插入容器2水位又升高多少?一元一次方程应用题1.一个长方形的周长为26㎝,这个长方形的长减少1㎝,宽增加2㎝,就可成为一个正方形,则原长方形的长和宽各为多厘米?2.在一个底面直径为30厘米,高为8厘米的圆锥体容器中倒满水,然后将水倒入一个底面直径为10厘米的圆柱体空容器内,圆柱体容器内的水有多高?3.已知一个用铁丝折成的长方形,它的长为9cm ,宽为6cm ,把它重新折成一个宽为5cm 的长方形,则新的长方形的宽是多少?4.将棱长为20cm 的正方体铁块没入盛水量筒中,已知量筒底面积为12cm 2,问量筒中水面升高了多少cm ?5.如图所示,两个长方形重叠部分的面积相当于大长方形面积的六分之一,相当于小长方形面积的四分之一,阴影部分的面积为224cm 2,求重叠部分面积。
6.如图是两个圆柱体的容器,它们的半径分别是4cm 和8cm ,高分别为16cm 和10cm ,先在第一个容器中倒满水,然后将其全部倒入第二个容器中。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一元一次方程的应用等积变形问题
【学习目标】
1.知识与技能:会找等积变形问题类型应用题的相等关系设未知数列方程
2.过程与方法:通过学生观察、独立思考等过程,培养学生分析解决问题的能力;
3.情感态度价值观:激发学生浓厚的学习兴趣,使学生有独立思考、勇于创新的精神,养成按客观规律办事的良好习惯;
重点:找相等关系,设未知数列方程.
难点:分析题意,找等积变形问题类型应用题的相等关系设未知数列方程。
一.自主探究(前置性学习)
探究活动(一)
本课内容必备:
圆柱体积公式:
长方体体积公式:
如图,已知圆柱(2)的体积是圆柱(1)的体积的3倍,求圆柱(1)的高(图中φ40表示直径为40毫米)
(二)知识盘点:(三)学习中还有哪些疑问没有解决?
二.合作探究
(一)交流展示
1、用直径为4cm的圆钢(截面为圆形的实心长条钢材)铸造3个直径为2cm,高为16cm的圆柱形零件,则需要截取多长的圆钢?
2、某铜铁厂要锻造长、宽、高分别为260mm、150 mm、130 mm的长方体毛坯,需要截取截面积为 130 mm2的方钢多长?
(二)体验成功
1、用直径为4厘米的圆钢,铸造三个直径为2厘米,高为16厘米的圆柱形零件,问需要截取多长的圆钢?
2、某机器加工厂要锻造一个毛胚,上面是一个直径为20毫米,高为40毫米的圆柱,下面也是一个圆柱,直径为60毫米,高为20毫米,问需要直径为40毫米的圆钢多长?
小结:解决此类问题中的等量关系是:
跟踪训练:
1、某工厂锻造直径为60毫米,高20毫米的圆柱形瓶内装水,再将瓶内的水倒入一个底面直径6厘米、高10厘米的圆柱形玻璃杯中,能否完全装下?若装不下,那么瓶内水面还有多高?若未能装满,求杯内水面离杯口的距离。
课后思考:
1、将一罐满水的直径为40厘米,高为60厘米的圆柱形水桶里的水全部灌于另一半径为30厘米的圆柱形水桶里,问这时水的高度是多少?。
