七年级数学上册有理数知识点、重点、难点、易错点归纳总结

合集下载

七年级数学上册有理数知识点、重点、难点、易错点归纳总结(20200708145801)

七年级数学上册有理数知识点、重点、难点、易错点归纳总结一、知识框架图知识点详列：1、正数和负数：数0既不是正数也不是负数。

正数和负数是表示两种具有相反意义的量。

2、有理数分类（1）按定义分类：（2）按性质符号分类：负分数正分数分数负整数正整数整数有理数负分数负整数负有理数正分数正整数正有理数有理数03、数轴：通常，用一条直线上的点表示数，这条直线叫做数轴。

它满足以下要求：（1）在直线上任取一个点表示数0，这个点叫做原点；（2）通常规定直线上从原点向右（或上）为正方向，从原点向左（或下）为负方向；（3）选取适当的长度为单位长度。

4、相反数：绝对值相等，只有符号不同的两个数叫做互为相反数。

0的相反数仍是0.5、绝对值：一般地，数轴上表示数a的点与原点的距离叫做数a的绝对值，记做|a|。

由绝对值的定义可得：|a-b|表示数轴上a点到b点的距离。

一个正数的绝对值是它本身；一个负数的绝对值是它的相反数；0的绝对值是0.6、有理数比较大小正数大于0，0大于负数，正数大于负数；两个负数，绝对值大的反而小。

7、有理数的四则运算（1）有理数的加法加法法则：①同号两数相加，取相同的符号，并把绝对值相加。

②绝对值不相等的异号两数相加，取绝对值较大的加数的符号，并用较大的绝对值减去较小的绝对值。

互为相反数的两个数相加得0.③一个数同0相加，仍得这个数。

运算律：加法交换律：a+b=b+a加法结合律:（a+b）+c=a+（b+c）(2)有理数的减法可转化为加法进行，减去一个数等于加上这个数的相反数，即a-b=a+(-b)。

正-正=正+负；正-负=正+正；负-正=负+负；负-负=负+正。

（4）有理数的乘法乘法法则：①两数相乘，同号得正，异号得负，并把绝对值相乘。

②任何数同0相乘，都得0.③乘积是1的两个数互为倒数。

④几个不是0的数相乘，负因数的个数是偶数时，积是正数；负因数的个数是奇数时，积为负。

运算律：乘法交换律：ab=ba乘法结合律：（ab）c=ab+ac(5)有理数的除法除以一个不为0的数，等于乘这个数的倒数，即。

初一有理数知识点总结及易错点

稿子一嘿，小伙伴们！咱们一起来瞅瞅初一有理数的那些事儿哈。

先说知识点，有理数包括正整数、零、负整数和正分数、负分数。

整数和分数统称有理数哟。

数轴可重要啦，它像一条带方向的线，上面的点能表示有理数。

正数在原点右边，负数在原点左边，越往右数越大，越往左数越小。

相反数也得知道，只有符号不同的两个数叫相反数，零的相反数还是零。

绝对值呢，就是一个数到原点的距离，正数的绝对值是它本身，负数的绝对值是它的相反数，零的绝对值是零。

有理数的加法，同号相加符号不变，把绝对值相加；异号相加取绝对值大的符号，用大的绝对值减小的绝对值。

减法可以变成加法，减去一个数等于加上它的相反数。

乘法就简单啦，同号得正，异号得负，再把绝对值相乘。

除法也类似，除以一个数等于乘以它的倒数。

再来说说易错点。

哎呀，符号问题可容易出错啦，比如计算的时候一不注意符号就错啦。

还有绝对值，别搞混了正数和负数的绝对值算法。

运算顺序也得注意，先乘除后加减，有括号先算括号里的。

小伙伴们，有理数不难，只要咱们细心，都能学好哒！加油哟！稿子二亲爱的小伙伴们，今天来聊聊初一有理数哈。

有理数的概念得清楚，整数分数都在有理数的大家庭里。

数轴这个工具可好用啦，能帮咱们直观地看到有理数的位置。

说到加法，同号相加别慌张，异号相加要小心，符号可别弄错啦。

减法的时候，记住变成加法来算，这样就不容易出错。

乘法和除法里，正负号的判断要准确，不然答案就跑偏喽。

还有相反数，就是符号相反的一对数，像 3 和 3 就是相反数。

绝对值呢，不管是正数负数还是 0，都要算对距离。

易错点来啦！计算的时候，千万别马虎，一不留神符号就错啦，那可就惨喽。

做混合运算时，一定要按照顺序来，先算乘除后算加减，有括号先算括号里面的。

还有哦，绝对值的计算要细心，别把正数负数的算法搞混。

有时候，分数的运算也容易出错，约分通分要认真。

小伙伴们，有理数的世界很有趣，只要咱们用心学，就一定能搞定它！一起加油吧！。

初一数学上册必考知识点及重难点

初一数学上册必考知识
点及重难点
Document serial number【NL89WT-NY98YT-NC8CB-NNUUT-NUT108】
初一数学上册必考知识点及重难点第一章有理数
1.正数和负数
2.有理数
3.有理数的加减
4.有理数的乘除
5.有理数的乘方
重点：数轴、相反数、绝对值、有理数计算、科学计数法、有效数字
难点：绝对值
易错点：绝对值、有理数计算
中考必考：科学计数法、相反数(选择题)
第二章整式的加减
1.整式
2.整式的加减
重点：单项式与多项式的概念及系数和次数的确定、同类项、整式加减
难点：单项式与多项式的系数和次数的确定、合并同类项易错点：合并同类项、计算失误、整数次数的确定
中考必考：同类项、整数系数次数的确定、整式加减
第三章一元一次方程
1.从算式到方程
2.解一元一次方程----合并同类项与移项
3.解一元一次方程----去括号去分母
4.实际问题与一元一次方程
重点：一元一次方程(定义、解法、应用)
难点：一元一次方程的解法(步骤)
易错点：去分母时，不含有分母项易漏乘、解应用题时，不知道如何找等量关系
第四章图形认识实步
1.多姿多彩的图形
2.直线、射线、线段
3.角
4.课题实习----设计制作长方形形状的包装纸盒
重点：直线、射线、线段、角的认识、中点和角平分线的相关计算、余角和补角，方位角等
难点：中点和角平分线的相关计算、余角和补角的应用易错点：等量关系不会转化、审题不清。

初一数学上册必考知识点及重难点

初一数学上册必考知识点及重难点第一章有理数1.正数和负数2.有理数3.有理数的加减4.有理数的乘除5.有理数的乘方重点：数轴、相反数、绝对值、有理数运算、科学计数法、有效数字难点：绝对值易错点：绝对值、有理数运算中考必考：科学计数法、相反数(选择题)第二章整式的加减1.整式2.整式的加减重点：单项式与多项式的概念及系数和次数的确定、同类项、整式加减难点：单项式与多项式的系数和次数的确定、合并同类项易错点：合并同类项、运算失误、整数次数的确定中考必考：同类项、整数系数次数的确定、整式加减第三章一元一次方程1.从算式到方程2.解一元一次方程----合并同类项与移项3.解一元一次方程----去括号去分母4.实际问题与一元一次方程重点：一元一次方程(定义、解法、应用)难点：一元一次方程的解法(步骤)易错点：去分母时，不含有分母项易漏乘、解应用题时，不明白如何找等量关系第四章图形认识实步1.多姿多彩的图形2.直线、射线、线段3.角4.课题实习----设计制作长方形形状的包装纸盒要练说，得练听。

听是说的前提，听得准确，才有条件正确仿照，才能不断地把握高一级水平的语言。

我在教学中，注意听说结合，训练幼儿听的能力，课堂上，我专门重视教师的语言，我对幼儿说话，注意声音清晰，高低起伏，抑扬有致，富有吸引力，如此能引起幼儿的注意。

当我发觉有的幼儿不用心听别人发言时，就随时夸奖那些静听的幼儿，或是让他重复别人说过的内容，抓住教育时机，要求他们用心听，用心记。

平常我还通过各种趣味活动，培养幼儿边听边记，边听边想，边听边说的能力，如听词对词，听词句说意思，听句子辩正误，听故事讲述故事，听谜语猜谜底，听智力故事，动脑筋，出主意，听儿歌上句，接儿歌下句等，如此幼儿学得生动爽朗，轻松愉快，既训练了听的能力，强化了经历，又进展了思维，为说打下了基础。

重点：直线、射线、线段、角的认识、中点和角平分线的相关运算、余角和补角，方位角等难点：中点和角平分线的相关运算、余角和补角的应用我国古代的读书人,从上学之日起,就日诵不辍,一样在几年内就能识记几千个汉字,熟记几百篇文章,写出的诗文也是字斟句酌,琅琅上口,成为满腹经纶的文人。

七年级数学上册有理数知识点归纳总结

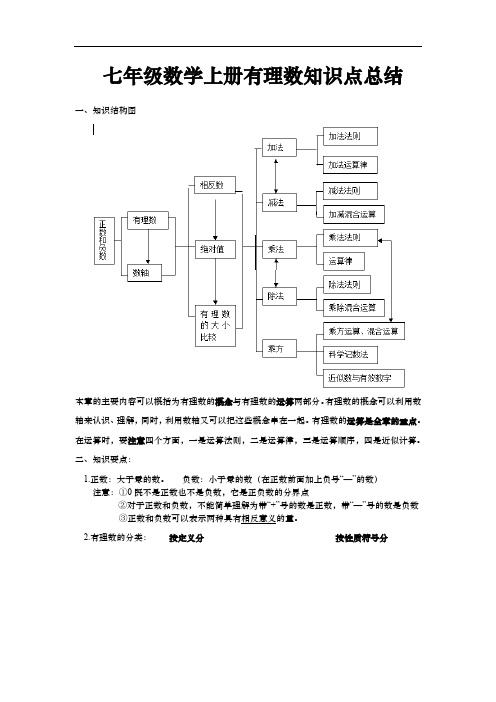
七年级数学上册有理数知识点总结一、知识结构图本章的主要内容可以概括为有理数的概念与有理数的运算两部分。

有理数的概念可以利用数轴来认识、理解，同时，利用数轴又可以把这些概念串在一起。

有理数的运算是全章的重点。

在运算时，要注意四个方面，一是运算法则，二是运算律，三是运算顺序，四是近似计算。

二、知识要点：1.正数：大于零的数。

负数：小于零的数（在正数前面加上负号“—”的数）注意：①0既不是正数也不是负数，它是正负数的分界点②对于正数和负数，不能简单理解为带“+”号的数是正数，带“—”号的数是负数③正数和负数可以表示两种具有相反意义的量。

2.有理数的分类：按定义分按性质符号分⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧⎪⎪⎩⎪⎪⎨⎧⎪⎩⎪⎨⎧⎭⎬⎫⋅⋅⋅⋅⋅⋅），，，负分数（如，如正分数分数），，负整数（如自然数）正整数（如整数有理数 ...506.0-529.0-71-)3.0,238.0,117(2-1-03,2,1 ⎪⎪⎪⎪⎪⎨⎧⎩⎨⎧⎩⎨⎧负分数负整数负有理数正分数正整数正有理数0 注意：①两种分类方法不同，但都包含了所有的有理数。

②零既不是正数也不是负数，但它是整数。

③常见的不是有理数的数有π和有规律的但不循环的小数。

如：0.0100100010001000010000010000001……3.数轴及有理数的大小比较要点：①画数轴时，要注意数轴的三要素：原点，正方向，单位长度。

②所有的有理数都可以用数轴上的一个点表示，但数轴上还有些点不代表有理数，如π。

③数轴上右边点表示的数总比左边点表示的数大。

即：负数小于0，0小于正数，负数小于正数。

④两个负数比较大小，绝对值大的反而小。

例：-1>-24.相反数数轴上在两侧且到的距离相等的两个点表示的两个数互为相反数(几何定义)，只有符号不同的两个数互为相反数(代数定义)，0的相反数是0。

a 的相反数是。

求一个数的相反数就是在这个数前添“ - ”号后再化简。

5.倒数乘积等于1的两个数互为倒数。

七年级数学上册“有理数”知识点梳理

七年级上册数学“有理数”知识点导图知识点一、正数和负数（1）大于0的数叫作正数，正数有时在数字前面加“﹢”号，读作“正”例：1，2，3，+4，+5，+6，+7都是正数（2）正数前面加上“﹣”的数叫作负数，“﹣”读作“负”例：﹣1，﹣2，﹣3，﹣4，﹣5，﹣6，﹣7都是负数（3）正数和负数可以表示“相反”的意思例：向前走5米记为﹢5米，则向后走5米记为﹣5米；向右走5米记为﹢5米，则向左走5米记为﹣5米；（4）0既不是正数，也不是负数，它是正数和负数的分界，0不止是表示“没有”例：0℃所表示的是一个确定的温度，不是表示没有温度习题1：指出下列数哪些是正数，哪些是负数1；3；﹣5；﹣7；﹢9；﹣2；﹢4；6；﹣8；0知识点二、有理数（1）可以写成分数形式的数称为有理数；例：11，﹣12，13，2，﹣3，4都是有理数（2）可以写成正分数形式的数为正有理数；例：11，13，2，4都是正有理数（3）可以写成负分数形式的数为负有理数；例：﹣12，﹣3，都是负有理数习题2：指出下列数哪些是有理数，哪些是正有理数，哪些是负有理数1；2；﹣3；﹣5；π；7；﹣9；13；﹣15知识点三、数轴（1）规定了原点、正方向和单位长度的直线叫作数轴（2）在直线上任取一个点表示数０，这个点叫作原点（3）通常规定直线上从原点向右（或上）为正方向，从原点向左（或下）为负方向（4）选取适当的长度为单位长度，直线上从原点向右，每隔一个单位长度取一个点，依次表示１２，３，...；从原点向左，用类似方法依次表示－１，－２，－３，...例：习题3：用数轴表示下列各点A （1）；B （﹣2）；C （1）；D （2.5）；E （﹣3）知识点四、相反数（1）仅有符号不同的两个数，称这两个数互为相反数。

0的相反数是0例：1和﹣1；12和﹣12；0和0互为相反数习题4：写出下列个数的相反数2；4；﹣6；﹣8；﹣110；0知识点五、绝对值（1）数轴上表示数α的点与原点的距离叫作数α的绝对值，记作|α|（2）一个正数的绝对值是它本身；例：|1|＝1；|2|=2；|3|=3（3）一个负数的绝对值是它的相反数；例：|﹣1|＝1；|﹣2|＝2；|﹣3|＝3（4）0的绝对值是０例：|0|＝0习题5：写出下列各数的绝对值10；﹣11；112；﹣113；0知识点六、有理数的大小比较（1）正数大于０，０大于负数，正数大于负数例：1＞0；0＞﹣1；1＞﹣1（2）两个负数，绝对值大的反而小例：|﹣1|＝1，|﹣2|＝2，2＞1，所以﹣1＞﹣2；|﹣3|＝3，|﹣4|＝4，4＞3，所以﹣3＞﹣4习题6：比较下列各数的大小7与8；9与﹣10；﹣11和﹣12；0与13；0与﹣14习题参考答案习题1：指出下列数哪些是正数，哪些是负数1；3；﹣5；﹣7；﹢9；﹣2；﹢4；6；﹣8；0正数：1；3；﹢9；﹢4；6负数：﹣5；﹣7；﹣2；﹣8习题2：指出下列数哪些是有理数，哪些是正有理数，哪些是负有理数 1；2；﹣3；﹣5；π；7；﹣9；13；﹣15有理数：1；2；﹣3；﹣5；7；﹣9；13；﹣15正有理数：1；2； 7； 13；负有理数：﹣3；﹣5；﹣9；﹣15习题3：用数轴表示下列各点A （1）；B （﹣2）；C （1）；D （2.5）；E （﹣3）习题4：写出下列个数的相反数2；4；﹣6；﹣8；﹣110；0 2和﹣2；4和﹣4；﹣6和6；﹣8和8；﹣110和110；0和0习题5：写出下列各数的绝对值10；﹣11；112；﹣113；0 |10|＝10；|﹣11|＝11；|112|=112；|﹣113|=113；|0|＝0习题6：比较下列各数的大小7与8；9与﹣10；﹣11和﹣12；0与13；0与﹣14 7＞8；9＞﹣10；﹣11＞﹣12；0＜13；0＞﹣14。

初一上学期数学有理数知识总结

初一上学期数学有理数知识总结
初一上学期数学有理数知识总结：
1. 有理数是整数和分数的统称。

有理数可以表示为有限小数、循环小数或不可能化为有限小数或循环小数的无理数。

2. 有理数的加法：对于两个有理数a和b，可以通过以下步骤进行加法运算：
- 如果a和b的符号相同，那么将它们的绝对值相加，并保留相同的符号。

- 如果a和b的符号不同，那么将它们的绝对值相减，并使用绝对值较大数的符号。

3. 有理数的减法：对于两个有理数a和b，可以通过将b取相反数，然后进行加法运算来实现减法。

4. 有理数的乘法：对于两个有理数a和b，可以通过以下步骤进行乘法运算：
- 将a和b的绝对值相乘，并确定结果的符号。

- 如果一个有理数是0，则乘积为0。

5. 有理数的除法：对于两个有理数a和b（b不等于0），可以通过以下步骤进行除法运算：
- 将a和b的绝对值相除，并确定结果的符号。

- 如果b是0，则除法无效。

6. 对于有理数的大小比较：
- 当两个有理数的符号相同时，绝对值较大的数较大。

- 当两个有理数的符号不同时，正数大于负数。

7. 有理数的绝对值：对于一个有理数a，它的绝对值表示为|a|，即a的去除符号的值。

8. 有理数的相反数：对于一个有理数a，它的相反数表示为-b，即a的符号取反。

9. 有理数的倒数：对于一个非零有理数a，它的倒数表示为1/a或a的倒数。

10. 有理数的化简：可以通过约分的方法将一个有理数化简为最简形式。

这些是初一上学期数学有理数的基本知识点总结，掌握了这些知识，可以更好地理解
和应用有理数的概念和运算规则。

七年级上册数学《有理数》知识要点整理

《有理数》知识要点一、有理数的概念1、正数和负数： (1）、大于0的数叫做正数. （2）、在正数前面加上负号“—”的数叫做负数.（3）、数0既不是正数,也不是负数 .(4）、在同一个问题中,分别用正数与负数表示具有相反的量 .2、有理数：(1）凡能写成分数形式的数，都是有理数。

整数和分数统称有理数.注意：0既不是正数，也不是负数；—a 不一定是负数，如：—（-2）=4，这个时候的a=—2. π不是有理数；(2)有理数的分类:①按定义分：⎪⎪⎪⎩⎪⎪⎪⎨⎧⎩⎨⎧⎩⎨⎧负分数负整数负有理数零正分数正整数正有理数有理数②按性质分：⎪⎪⎪⎩⎪⎪⎪⎨⎧⎩⎨⎧⎪⎩⎪⎨⎧负分数正分数分数负整数零正整数整数有理数（3)自然数＜====＞0和正整数；a ＞0 ＜====＞a 是正数； a ＜0 ＜====＞a 是负数；a ≥0＜====＞a 是正数或0＜====＞a 是非负数; a ≤0＜====＞a 是负数或0＜====＞a 是非正数。

3、数轴【重点】：（1)、规定原点、正方向和单位长度的直线叫做数轴。

它满足以下要求:（1)、数轴的三要素：原点、正方向、单位长度。

（2）、画数轴的步骤:一画（画直线）；二取（取原点和正反向）；三选（选取单位长度)；四标（标数字）。

数轴的规范画法:是条直线,数字在下,字母在上.注意:（1）所有的有理数都可以用数字上的点表示，但是数轴上的所有点并不都表示有理数。

原点表示数0.(2）、正数在原点的右边，与原点的距离是|a|个单位长度；负数在原点的左边，与原点的距离是|a ｜个单位长度。

4、相反数：（1）、只有符号不同的两个数叫做互为相反数。

注意：① a —b 的相反数是b —a ；a+b 的相反数是—a —b ；② 相反数的商为-1; ③ 相反数的绝对值相等。

（3）、a 和-a 互为相反数。

0的相反数是0,正数的相反数是负数，负数的相反数是正数。

相反数是它本身的数只有0。

(4）、在任意一个数前面添上“-”号，表示原数的相反数。

七年级数学上册有理数知识点、重点、难点、易错点归纳总结

七年级数学上册有理数知识点、重点、难点、易错点归纳总结一、知识框架图知识点详列：1、正数和负数：数0既不是正数也不是负数。

正数和负数是表示两种具有相反意义的量。

2、有理数分类（1）按定义分类：（2）按性质符号分类： ⎪⎪⎪⎩⎪⎪⎪⎨⎧⎩⎨⎧⎪⎩⎪⎨⎧负分数正分数分数负整数正整数整数有理数0 ⎪⎪⎪⎩⎪⎪⎪⎨⎧⎩⎨⎧⎩⎨⎧负分数负整数负有理数正分数正整数正有理数有理数0 3、数轴：通常，用一条直线上的点表示数，这条直线叫做数轴。

4、相反数：绝对值相等，只有符号不同的两个数叫做互为相反数。

0的相反数仍是0.5、绝对值：一般地，数轴上表示数a的点与原点的距离叫做数a的绝对值，记做|a|。

由绝对值的定义可得：|a-b|表示数轴上a点到b点的距离。

7、有理数的四则运算（1）有理数的加法加法法则：①同号两数相加，取相同的符号，并把绝对值相加。

②绝对值不相等的异号两数相加，取绝对值较大的加数的符号，并用较大的绝对值减去较小的绝对值。

互为相反数的两个数相加得0.③一个数同0相加，仍得这个数。

运算律：加法交换律：a+b=b+a加法结合律:（a+b）+c=a+（b+c）(2)有理数的减法可转化为加法进行，减去一个数等于加上这个数的相反数，即a-b=a+(-b)。

正-正=正+负；正-负=正+正；负-正=负+负；负-负=负+正。

（4）有理数的乘法乘法法则：①两数相乘，同号得正，异号得负，并把绝对值相乘。

②任何数同0相乘，都得0.③乘积是1的两个数互为倒数。

④几个不是0的数相乘，负因数的个数是偶数时，积是正数；负因数的个数是奇数时，积为负。

小升初：初一数学上册《有理数》知识点总结,硬货,带走不谢

小升初：初一数学上册《有理数》知识点总结，硬货，带走不谢暑假开始了，大家的预习热情也变得逐渐高涨，小升初的同学，恭喜你们即将成为初中生！下面给各位分享的就是数学第一章《有理数》部分的知识点~正数和负数知识点1 正数和负数的概念(1) 像3、1.5、1/2、584等大于0的数，叫做正数，在小学学过的数，除0以外都是正数，正数比0大。

(2) 像－3、－1.5、-1/2、－584等在正数前面加“－”(读作负)号的数，叫做负数。

负数比0小。

(3) 零即不是正数也不是负数，零是正数和负数的分界。

注意：(1) 为了强调，正数前面有时也可以加上“＋”（读作正）号，例如：3、1.5也可以写作＋3、＋1.5。

(2) 对于正数和负数的概念，不能简单理解为：带“＋”号的数是正数，带“－”号的数是负数。

例如：－a一定是负数吗？答案是不一定。

因为字母a可以表示任意的数，若a表示的是正数，则－a是负数；若a 表示的是0，则－a仍是0；当a表示负数时，－a就不是负数了（此时－a是正数）。

正数、负数表示正数和负数是根据实际需要而产生的，随着社会的发展，小学学过的自然数、分数和小数已不能满足实际的需要，比如一些有相反意义的量：收入200元和支出100元、零上6和零下等等，它们不但意义相反，而且表示一定的数量，怎样表示它们呢？我们把一种意义的量规定为正的，把另一种和它意义相反的的量规定为负的，这样就产生了正数和负数。

用正数和负数表示具有相反意义的量时，哪种意义为正，是可以任意选择的，但习惯把“前进、上升、收入、零上温度”等规定为正，而把“后退、下降、支出、零下温度”等规定为负。

有理数知识点1 有理数的有关概念有理数：整数和分数统称为有理数。

注：(1)有时为了研究的需要，整数也可以看作是分母为1的数，这时的分数包括整数。

但是本讲中的分数不包括分母是1的分数。

(2)因为分数与有限小数和无限循环小数可以互化，上述小数都可以用分数来表示，所以我们把有限小数和无限循环小数都看作分数。

人教版七年级数学上册学生重点、难点必学常识

人教版七年级数学上册学生重点、难点必学常识1.有理数：1) 任何能写成 p/q (p,q为整数且p≠0) 形式的数都是有理数，整数和分数都属于有理数。

注意：有理数不一定是正数或负数；-a不一定是负数，+a 也不一定是正数；π不是有理数。

正整数、正分数、零、负分数、负整数都属于有理数。

2) 有理数可以分为两类：①零和正有理数；②负有理数。

正有理数包括正整数和正分数；负有理数包括负整数和负分数。

3) 注意：有理数中，1、0、-1是三个特殊的数，它们有自己的特性；这三个数把数轴上的数分成四个区域，这四个区域的数也有自己的特性。

4) 自然数等于正整数；a>0 等价于 a 是正数；a<0 等价于a 是负数；a≥0 等价于 a 是正数或零；a≤0 等价于 a 是负数或零。

2.数轴：数轴是一条直线，规定了原点、正方向和单位长度。

3.相反数：1) 只有符号不同的两个数，其中一个是另一个的相反数；0 的相反数还是 0.2) 注意：a-b+c 的相反数是 -a+b-c；a-b 的相反数是 b-a；a+b 的相反数是 -a-b。

3) 相反数的和为 0 等价于 a+b=0 等价于 a、b 互为相反数。

4) 相反数的商为 -1.5) 相反数的绝对值相等。

4.绝对值：1) 正数的绝对值等于它本身，0 的绝对值是 0，负数的绝对值等于它的相反数。

注意：绝对值的意义是数轴上表示某数的点离开原点的距离。

a>0 时，|a|=a；a≤0 时，|a|=-a。

2) 绝对值可以表示为：|a|=a (a≥0) 或 |a|=-a (a<0)。

3) a/|a|=1 等价于 a>0；a/|a|=-1 等价于 a<0.4) |a| 是重要的非负数，即|a|≥0.5.有理数比大小：1) 正数永远比负数大，负数永远比正数小。

2) 正数大于一切负数。

3) 两个负数比较，绝对值大的反而小。

4) 数轴上的两个数，右边的数总比左边的数大。

七年级上册数学知识点归纳

二、直线、射线、线段
6
1.两点确定一条直线 2.当两条不同的直线有一个公共点时�我们就称这两条直线相交� 这个公共点叫做它们的交点。 3. 两点之间�线段最短。 4. 连接两点间的线段的长度�叫做这两点的距离。三、角 1.有且只有一个角 2.把一个周角 360 等分�每一份就是一度的角�记做 1°�把 1 度的角 60 等分�每一份叫做 1 分的角�记作 1†�把 1 分的角 60 等分�每一份叫做 1 秒的角�记作 1‡。 3.角的运算�1 周角=360°�1 平角=180°,1°=60†,1†=60‡ 4.角的平分线�A. 从一个角的顶点引出一条射线�把这个角分成两个相等的角�这条射线叫做这个角的角平分线。
B.角平分线上的一点到角的两边距离相等。四、线段、射线和直线的联系与区别
联系�线段、射线、直线是部分与整体的关系.线段向一方无限延长形成了射线,向两个方向无限延长得到了直线.直线上的两点和它们之间的部分组成线段,直线上的一点及其一旁的部分是射线,射线反向延长得直线.
ห้องสมุดไป่ตู้
10.整式单项式和多项式统称整式。 11.同类项所含字母相同�并且相同字母的次数也相同的项�叫做同类项�常数项都是同类项� 12.合并同类项把多项式中的同类项合并成一项�叫做合并同类项� 合并同类项的法则是�
3
同类项的系数相加�所得的结果作为系数�字母和字母的指数不变� 13.去括号法则括号前是“+”号�把括号和它前面的“+”号去掉�括号里各项都不变符号� 括号前是“�”号�把括号和它前面的“�”号去掉�括号里各项都改变符号� 例�a+(b-2c)-(e-2d)=a+b-2c-e+2d 14.添括号法则添括号后�括号前面是“+”号�括到括号里的各项都不变符号�

七年级上数学有理数知识点

七年级上数学有理数知识点在七年级上数学学习中，有理数是一个重要的知识点。

有理数包括整数、正数、负数、零以及它们的运算。

下面将介绍有理数的基本概念、加减乘除运算以及应用。

一、有理数的基本概念有理数是可以表示为两个整数的比的数，包括正有理数、负有理数和零。

其中，正有理数是大于零的有理数，负有理数是小于零的有理数，零是既不是正有理数也不是负有理数的有理数。

二、有理数的加减乘除运算1. 加法运算：有理数的加法运算满足交换律、结合律和零元素。

即对于任意的有理数a、b和c，有a+b=b+a，(a+b)+c=a+(b+c)，a+0=a。

2. 减法运算：有理数的减法可以转化为加法，即a-b=a+(-b)。

其中，-b表示b的相反数。

有理数的减法运算满足a+(-a)=0。

3. 乘法运算：有理数的乘法运算满足交换律、结合律和单位元素。

即对于任意的有理数a、b和c，有a×b=b×a，(a×b)×c=a×(b×c)，a×1=a。

4. 除法运算：有理数的除法可以转化为乘法，即a÷b=a×(1/b)，其中1/b表示b的倒数。

有理数的除法运算满足a÷a=1。

三、有理数的应用有理数在生活中的应用非常广泛。

以下列举了一些常见的应用场景：1. 温度计：温度既可以是正数，也可以是负数，用有理数来表示。

正数表示高温，负数表示低温。

2. 海拔高度：海拔高度也可以是正数和负数，正数表示高于海平面，负数表示低于海平面。

3. 账户余额：银行账户的余额可以是正数，表示存款金额；也可以是负数，表示欠款金额。

4. 游戏得分：游戏得分可以是正数，表示得分；也可以是负数，表示失分或扣分。

总结：有理数是包括整数、正数、负数和零的集合。

有理数的加减乘除运算满足一定的运算规律。

有理数在生活中有着广泛的应用，可以用来表示温度、海拔高度、账户余额和游戏得分等。

通过学习有理数的概念和运算规律，我们可以更好地理解和应用数学知识。

七年级上册数学有理数知识点总结

七年级上册数学有理数知识点总结有理数是整数和分数的统称，包括正整数、负整数、零，以及各种形式的分数。

在七年级上册数学中，有理数是一个非常重要的知识点。

本文将对七年级上册数学有理数知识点进行总结和介绍。

1.有理数的定义有理数指的是一切可以表示为分子、分母都是整数且分母不为零的数。

可以用有理数的准确分数表示及有理数的小数表示两种方式予以表示。

2.有理数的四则运算有理数的加法、减法、乘法和除法依然遵循相同的规律。

加法和乘法满足交换律和结合律，除法满足相反数的乘法性质。

3.数轴数轴是一个非常重要的概念，它能够帮助我们直观地理解有理数之间的大小关系。

正数在数轴上位于原点的右侧，负数在数轴上位于原点的左侧。

4.绝对值绝对值表示一个数到原点的距离，用符号|a|表示，其中a是一个数。

当a为正数时，其绝对值等于a；当a为负数时，其绝对值等于-a。

5.有理数的比较在数轴上，我们可以通过有理数的大小关系来比较两个有理数的大小。

绝对值大的数较大，同号数相减取绝对值来比较，异号数按照绝对值大小来比较。

6.约分和通分约分是指将一个分数化为最简分数，通分是指寻找多个分数的最小公倍数，使它们的分母相等。

7.有理数的加减混合运算有理数的加减混合运算需要按照运算法则进行，可以先化为同号数进行加减运算，再根据结果的正负进行具体的计算。

8.有理数的乘法和除法有理数的乘法和除法也需要遵循相同的规律，同号数相乘为正，异号数相乘为负；同号数相除为正，异号数相除为负。

在乘法和除法的计算中，可以先化为同号数进行运算，根据结果的正负进行具体的计算。

9.有理数的应用有理数在生活中有很多实际应用，例如温度变化、海拔高度变化等都可以用有理数来表示和计算。

在学习七年级上册数学有理数知识点时，我们需要掌握有理数的定义、四则运算、数轴、绝对值、有理数的比较、约分和通分、有理数的加减混合运算、有理数的乘法和除法以及有理数的应用。

通过深入学习这些知识点，并进行大量的练习，可以帮助我们更好地掌握有理数的相关知识，并在日常生活中灵活运用。

七年级数学上册必考重点知识点有理数43个知识点

七年级数学上册必考重点知识点有理数43个知识点七年级数学上册必考重点知识点有理数总共有43个知识点。

今天我们将全面梳理这些知识点，确保每一个知识点都得到了深入的理解。

1.有理数的概念有理数是指可以表示为分数的数字，分子和分母都是整数的数称为有理数。

有理数包括整数和分数两种形式。

2.整数的概念整数包括正整数、负整数和零，记作：……，-3，-2，-1，0，1，2，3……3.分数的概念分数是指一个整数除以另一个整数所得到的数，分子为分数线上面的数，分母为分数线下面的数。

4.有理数的比较有理数的比较可以通过大小比较符号（<、>、=）来表示，根据数轴上的位置进行比较。

绝对值大的数较大。

5.有理数的加法有理数的加法满足交换律和结合律，同号两数相加取数的绝对值相加，异号两数相加取绝对值大的减去绝对值小的。

6.有理数的减法有理数的减法可以转化为加法运算，即加上减数的相反数。

7.有理数的乘法有理数的乘法满足交换律和结合律，同号相乘得正，异号相乘得负。

8.有理数的除法有理数的除法可以转化为乘法运算，即用除数的倒数来乘。

9.有理数的运算律有理数的运算满足分配律，即乘法对加法的分配律和乘法对减法的分配律。

10.有理数的混合运算有理数的混合运算就是同时包含加法、减法、乘法、除法的综合运算。

11.数轴及有理数的表示数轴是一个水平线段，通过在上面规定一个原点O和一个正方向，既可以表示正数也可以表示负数。

12.绝对值一个数a的绝对值，记作|a|，是a到原点的距离。

13.有理数的绝对值有理数的绝对值是该有理数到原点的距离，绝对值为非负数。

14.加法逆元有理数a的加法逆元是一个有理数b，使得a+b=0。

15.数轴上两点的位置关系两个数在数轴上的相对位置可以通过它们的大小关系来确定。

16.有理数的应用有理数在日常生活中有很广泛的应用，比如温度计、债务和财务等。

17.有理数的乘方和乘方根有理数的乘方是指一个有理数多次相乘，乘方根是指一个数的指定次数的开方。

初一上学期数学有理数知识点总结

初一上学期数学有理数知识点总结
初一上学期数学有理数知识点总结如下：
1. 有理数的概念：有理数包括整数、分数，可以用分数形式、小数形式表示。

2. 有理数的四则运算：加、减、乘、除。

加法和乘法具有交换律和结合律，减法和除法不具有交换律和结合律。

3. 有理数的加减运算：同号相加、异号相减。

4. 有理数的乘除运算：同号得正、异号得负。

5. 有理数的乘方运算：正数的乘方仍是正数，负数的偶数次幂是正数，负数的奇数次幂是负数，零的非零次幂是零。

6. 有理数的数轴表示：数轴上的点与有理数一一对应，数轴上右边的数比左边的大，两个数之间的距离等于它们的差的绝对值。

7. 有理数的比较：两个有理数相比较时，可以化为相同的分数形式进行比较。

8. 有理数的绝对值：一个数的绝对值表示该数与零的距离，如果是正数，绝对值就是它本身；如果是负数，绝对值就是它的相反数。

9. 有理数的倒数：一个数的倒数是指与它乘积等于1的数。

以上是初一上学期数学有理数的知识点总结，希望对你有帮助！。

人教版数学七年级上册第一章知识点总结

人教版数学七年级上册第一章知识点总结第一章有理数知识点总结正数：大于的数叫做正数。

01.概念负数：在正数前面加上负号“—”的数叫做负数。

注：0既不是正数也不是负数，是正数和负数的分界线，是整数，一、正数和负数自然数，有理数。

（不是带“—”号的数都是负数，而是在正数前加“—”的数。

）2.意义：在同一个问题上，用正数和负数表示具有相反意义的量。

有理数：整数和分数统称有理数。

1.概念整数：正整数、0、负整数统称为整数。

分数：正分数、负分数统称分数。

（有限小数与无限循环小数都是有理数。

）注：正数和零统称为非负数，负数和零统称为非正数，正整数和零统称为非负整数，负整数和零统称为非正整数。

π是正数但不是有理数！2.分类：两种二、有理数⑴按正、负性质分类：⑵按整数、分数分类：正有理数正整数正整数有理数正分数整数0零有理数负整数负有理数负整数分数正分数负分数负分数3.数集内容了解1.概念：规定了原点、正方向、单位长度的直线叫做数轴。

三要素：原点、正方向、单位长度2.对应关系：数轴上的点和有理数是一一对应的。

三、数轴比较大小：在数轴上，右边的数总比左边的数大。

3.应用求两点之间的距离：两点在原点的同侧作减法，在原点的两侧作加法。

“—”号）（注意不带“+”代数：只有符号不同的两个数叫做相反数。

1.概念（0的相反数是0）几何：在数轴上，离原点的距离相等的两个点所表示的数叫做相反数。

2.性质：若a与b互为相反数，则a＋b=0，即a=-b；反之，若a＋b=0，则a与b互为相反数。

四、相反数两个符号：符号相同是正数，符号不同是负数。

3.多重符号的化简多个符号：三个或三个以上的符号的化简，看负号的个数，当“—”号的个数是偶数个时，结果取正号当“—”号的个数是奇数个时，结果取负号1.概念：乘积为1的两个数互为倒数。

（倒数是它本身的数是±1；0没有倒数）五、倒数2.性质若a与b互为倒数，则a·b=1；反之，若a·b=1，则a与b 互为倒数。

初中七年级上册数学重难点

初中七年级上册数学重难点一、有理数。

1. 重点。

- 有理数的概念：整数和分数统称为有理数。

要能准确区分正有理数、负有理数和0。

例如， -3是负有理数，2是正有理数，0既不是正数也不是负数。

- 数轴：理解数轴的三要素（原点、正方向、单位长度），会用数轴上的点表示有理数，并且能根据数轴比较有理数的大小。

在数轴上，右边的数总比左边的数大。

- 相反数：互为相反数的两个数之和为0。

如3和 -3是相反数，它们满足3+( -3)=0。

- 绝对值：正数的绝对值是它本身，负数的绝对值是它的相反数，0的绝对值是0。

例如，5 = 5， - 5=5。

会计算有理数的绝对值，并且能利用绝对值比较两个负数的大小，两个负数比较大小，绝对值大的反而小。

- 有理数的四则运算：- 加法法则：同号两数相加，取相同的符号，并把绝对值相加；异号两数相加，取绝对值较大的符号，并用较大的绝对值减去较小的绝对值；互为相反数的两个数相加得0；一个数同0相加，仍得这个数。

- 减法法则：减去一个数，等于加上这个数的相反数。

- 乘法法则：两数相乘，同号得正，异号得负，并把绝对值相乘；任何数同0相乘都得0。

- 除法法则：除以一个不等于0的数，等于乘以这个数的倒数；两数相除，同号得正，异号得负，并把绝对值相除；0除以任何一个不等于0的数都得0。

2. 难点。

- 绝对值概念的理解：绝对值的几何意义（表示数在数轴上的点到原点的距离）和代数意义的结合运用。

例如，当a<0时，| a|=-a，这里的-a是正数，学生容易混淆。

- 有理数混合运算的顺序：先算乘方，再算乘除，最后算加减；如果有括号，先算括号里面的。

在计算过程中，要注意符号的变化，很多学生在这方面容易出错。

例如，计算2 - 3×(-2)^2，要先算乘方(-2)^2 = 4，再算乘法3×4 = 12，最后算减法2-12=-10。

二、整式的加减。

1. 重点。

- 单项式、多项式的概念：由数与字母的乘积组成的代数式叫做单项式，单独的一个数或一个字母也是单项式；几个单项式的和叫做多项式。

七年级上册数学《有理数》有理数的概念知识点整理

有理数是数学中重要的概念之一，它包括了正整数、负整数、零以及分数。

在七年级上册数学教材中，学生会学习有关有理数的基本概念、整数的加减乘除运算、分数的加减乘除运算、有理数的比较大小以及实际问题的应用等知识点。

下面是对这些知识点进行整理和总结：一、基本概念：1.数轴的介绍：数轴是一条直线，用于表示数的大小关系。

正数在数轴的右侧，负数在数轴的左侧，零位于数轴的原点。

2.整数：包括正整数、负整数和零。

正整数表示数轴上原点右侧的整数，负整数表示数轴上原点左侧的整数，零表示数轴上的原点。

3.分数：包括真分数和假分数。

真分数的分子小于分母，假分数的分子大于等于分母。

4.有理数：包括整数和分数。

有理数可以用分数形式表示为a/b（b≠0），其中a为整数而b为非零的整数。

二、整数的加减乘除运算：1.加法：同号相加得正，异号相加得负。

2.减法：减去一个整数等于加上它的相反数，即a-b=a+(-b)。

3.乘法：同号相乘得正，异号相乘得负。

4.除法：除以一个非零整数等于乘以它的倒数，即a/b=a*(1/b)。

三、分数的加减乘除运算：1.加法：当分母相同时，直接对分子进行加法运算；当分母不同时，需要找到最小公倍数，并转化为通分后进行加法运算。

2.减法：与加法类似，分别对分子进行减法运算或通分后进行减法运算。

3.乘法：将两个分数的分子相乘得到新分子，分母相乘得到新分母，再进行约分。

4.除法：将被除数乘以除数的倒数，再进行约分。

四、有理数的比较大小：1.整数的比较：不同整数之间，绝对值大的数较小，正数大于零，负数小于零。

2.分数的比较：分子相等，分母大的数较小；分母相等，分子大的数较大；分子分母同时相等，两个分数相等。

3.整数与分数的比较：可以将整数转化为分数形式进行比较。

五、实际问题的应用：1.温度的表示：正数表示温度高于一些参考温度，负数表示温度低于一些参考温度。

2.海拔的表示：正数表示高于海平面的高度，负数表示低于海平面的深度。

七年级上册有理数知识点归纳

七年级上册有理数知识点归纳金子塔七年级数学上册第一章有理数知识点归纳一、正数和负数正数和负数是数学中的基本概念。

负数是比小的数，正数则是比大的数。

需要注意的是，字母a可以表示任意数，当a 表示正数时，-a是负数；当a表示负数时，-a是正数；当a表示0时，-a仍是0.此外，带正号的数不一定是正数，带负号的数不一定是负数。

具有相反意义的量若正数表示某种意义的量，则负数可以表示具有与该正数相反意义的量。

在数学中，我们惯把“前进、上升、收入、零上温度”等规定为正，“后退、下降、支出、零下温度”等规定为负。

二、有理数有理数包括正整数、负整数、正分数和负分数。

其中，正整数、负整数统称为整数，正整数和0统称为自然数。

整数和分数统称为有理数。

需要注意的是，π是无限不循环小数，不能写成分数形式，不是有理数。

有限小数和无限循环小数都可化成分数，都是有理数。

数轴数轴是一种表示有理数的工具。

它是一条向两端无限延伸的直线，规定了原点、正方向和单位长度。

所有的有理数都可以用数轴上唯一的点来表示。

正有理数可用原点正方向的点表示，负有理数可用原点负方向的点表示，用原点表示0.相反数只有符号不同的两个数叫做互为相反数。

任何一个有理数都有相反数。

互为相反数的两数的和为0，即：若a、b互为相反数，则a+b=0；互为相反数的两个点在数轴上分别位于原点两侧，并且与原点的距离相等。

在一个数的前面加上负号“-”，就得到了这个数的相反数。

例如，a的相反数是-a。

绝对值绝对值是一个数的大小，与符号无关。

数轴上表示数a的点与原点的距离，叫做a的绝对值，记作：｜a｜。

正数的绝对值是它本身，负数的绝对值是它的相反数。

可用字母表示为：①如果a>0，那么|a|=a；②如果a<0，那么|a|=-a；③如果a=0，那么|a|=0.多重符号的化简多重符号的化简规律：“+”号的个数不影响化简的结果，可以直接省略；“-”号的个数决定最后化简结果；即：“-”的个数是奇数时，结果为负，“-”的个数是偶数时，结果为正。