【管理资料】机械原理第四章作业.汇编
合集下载
机械原理第四章4-1
凸轮机构的命名： 凸轮机构的命名
一般凸轮机构的名称应表明凸轮、从动件的端部形状 和从动件的运动形式及从动件轴线相对凸轮轴心的布置形 式等，通常凸轮机构的命名是上述几种类型的综合。
对心尖顶直 动从动件盘 形凸轮机构
偏置尖顶直 动从动件盘 形凸轮机构
对心滚子直 动从动件盘 形凸轮机构
摆动滚子从动件 盘形凸轮机构
( f ) ( c )
二、凸轮机构的分类
曲底从动件
克服了尖底易磨损的缺点。
二、凸轮机构的分类
3. 按从动件的运动形式分类 直动从动件 (Translating follower) ：
从动件作往复直线运动
摆动从动件 (Oscillating follower )：
从动件作往复摆动
二、凸轮机构的分类
第四章 凸轮机构及其设计
§4.1 凸轮机构的应用和分类 §4.2 从动件的运动规律 §4.3 图解法设计凸轮廓线 §4.4 解析法设计凸轮廓线 §4.5 凸轮机构的压力角及基本尺寸的设计 §4.6 凸轮机构的计算机辅助设计
§4.1 凸轮机构的应用和分类
一、凸轮机构的组成和应用 二、凸轮机构的分类 三、凸轮机构的特点
O ω A
e
二、凸轮机构的分类
4. 按从动件与凸轮维持高副接触的方式分类
封闭（锁合）方式－使从动件与凸轮廓线始终保 持接触而不脱离的方式。
力封闭（锁合） 力封闭（锁合）型凸轮机构
利用重力、弹簧力或其他外力使从动件与凸轮轮 廓始终保持接触。
二、凸轮机构的分类
形封闭（锁合） 形封闭（锁合）型凸轮机构
二、凸轮机构的分类
2. 按从动件端部形状分类 尖底从动件 (Knife-edge follower)
机械原理第四章
FR21= -FR23
FR21
B
Md l’ ω14 A
FR41 c
FR43
FR23
G
ω43
FR43
FR23
b
G
从图上量得： Md＝G(cb/ab)×l’ a
力分析解题步骤小结：
①从二力杆入手，初步判断杆2受拉。 ②由γ、β增大或变小来判断各构件的相对角速度。 ③依据总反力判定准则得出FR12和FR32切于摩擦圆的
三、机构力分析的方法
对于低速机械，因为惯性力的 影响不大，可忽略不计算。高速机 静力分析 械，进行动态静力分析。
方法
动态静力分 析
设计新机械时，机构的尺寸、 假设分析 质量和转动惯量等都没有确
定，因此可在静力分析的基 础上假定未知因素进行动态 静力分析、最后再修正，直 至机构合理。
简化分析
进行力分析时，可假定原动件 按理论运动规律运动，根据实 际情况忽略摩擦力或者重力进 行分析，使得问题简化。
MI1＝－JS1α1
FI1
α1 1
A
B S1MI1
aS1
构件惯性力的确定(3/5) 2．质量代换法 质量代换法 是指设想把构件的质量按一定条件集
中于构件上某几个选定点上的假想集中质量来代替的方
法。假想的集中质量称为代换质量； 代换质量所在的位置称为代换点。
（1）质量代换的参数条件
代换前后构件的质量不变； 代换前后构件的质心位置不变； 代换前后构件对质心轴的转动惯量不变。
一般分析 考虑各种影响因素进行力分析
§4-2 构件惯性力的确定
1．一般力学方法 以曲柄滑块机构为例
B
1 A
1 A
2
3
α2
C 4
FR21
B
Md l’ ω14 A
FR41 c
FR43
FR23
G
ω43
FR43
FR23
b
G
从图上量得： Md＝G(cb/ab)×l’ a
力分析解题步骤小结：
①从二力杆入手，初步判断杆2受拉。 ②由γ、β增大或变小来判断各构件的相对角速度。 ③依据总反力判定准则得出FR12和FR32切于摩擦圆的
三、机构力分析的方法
对于低速机械，因为惯性力的 影响不大，可忽略不计算。高速机 静力分析 械，进行动态静力分析。
方法
动态静力分 析
设计新机械时，机构的尺寸、 假设分析 质量和转动惯量等都没有确
定，因此可在静力分析的基 础上假定未知因素进行动态 静力分析、最后再修正，直 至机构合理。
简化分析
进行力分析时，可假定原动件 按理论运动规律运动，根据实 际情况忽略摩擦力或者重力进 行分析，使得问题简化。
MI1＝－JS1α1
FI1
α1 1
A
B S1MI1
aS1
构件惯性力的确定(3/5) 2．质量代换法 质量代换法 是指设想把构件的质量按一定条件集
中于构件上某几个选定点上的假想集中质量来代替的方
法。假想的集中质量称为代换质量； 代换质量所在的位置称为代换点。
（1）质量代换的参数条件
代换前后构件的质量不变； 代换前后构件的质心位置不变； 代换前后构件对质心轴的转动惯量不变。
一般分析 考虑各种影响因素进行力分析
§4-2 构件惯性力的确定
1．一般力学方法 以曲柄滑块机构为例
B
1 A
1 A
2
3
α2
C 4
《机械原理》第4章
若质心位于回转中心： MI1 =- Js1α1
青岛科技大学专用 作者： 潘存云教授
2.质量代换法 一般力学方法的缺陷： ▲质心位置难以精确测定； B ▲求解各构件质心加速度较繁琐。 mB S2 质量代换法的思路： B 2 将各构件的质量，按一 S2 定条件用集中于某些特 1 S 1 定点的假象质量来替代， A as1 as2 只需求集中质量的惯性 力，而无需求惯性力偶 矩。从而将问题简化。 质量代换的条件： 1）代换前后各构件质量不变； 2）质心位置不变； 3）对质心轴的转动惯量不便。 青岛科技大学专用
Q θ N’21
1 v21 作者：潘存云教授 F G2
N21
θ θ N’21 N”21 1 2
作者：潘存云教授
N’21 = N”21 = G / (2sinθ) F21 = f N’21 + f N”21
= ( f / sinθ)• G = fv G fv－称为当量摩擦系数
G
青岛科技大学专用
作者： 潘存云教授
柱面接触： 矢量和：N21=Σ △N21 =-G 代数和：N’21= Σ |△N21| =kG >|N21|
2 △N21 G 1
N21
作者：潘存云教授
理论分析和实验结果有： k =1~π /2 F21 = f N’21 = f k G = fv G 同理，称 fv为当量摩擦系数。 结论：不论何种运动副元素，有计算通式： F21= f N21 = fv G 非平面接触时 ，摩擦力增大了，为什么？ 是 f 增大了？ 原因：是由于N21 分布不同而导致的。
θ
θ
φ 1 v21
2 G
2.移动副中总反力的确定 总反力为法向反力与摩擦力的合成： FR21=N21+F21 tgφ= F21 / N21 = f N21 / N21 = f φ － 摩 擦 角 ， 方向:∠FR21 V12 ＝(90°+φ) 摩擦锥----以FR21为母线所作圆锥。 结论：移动副中总反力恒切于摩擦锥。
机械原理课件第四章
代换点：上述的选定点。
代换质量：集中于代换点上的假想质量。
二、质量代换法（续）
3. 质量代换时必须满足的三个条件： 1）代换前后构件的质量不变；
m
i 1
n
i
m
2）代换前后构件的质心位置不变； 以原构件的质心为坐标原点时，应满足：
m i x i 0 i 1 n m i y i 0 i 1
PI ma S
一、一般力学方法（续）
3. 绕定轴转动的构件 1）绕通过质心的定轴转动的构件
等速转动：PI =0，MI=0；
变速运动：只有惯性力偶 M I J S s
2）绕不通过质心的定轴转动，
等速转动：产生离心惯性力 变速转动：
PI ma S ,
PI m a n S
12 C M 0
-----摩擦圆半径
Fy 0
F R 21 G
总反力作用线位置的确定
摩擦圆
rFR 21
FN 21
FR 21
F f 21
M d FR 21 G M f Gf v r
摩擦力矩
结论
转动副中，总反力FR21与外载荷G大小相等，方向相反； 总反力FR21切于摩擦圆； 摩擦力矩Mf阻止轴颈转动，与12方向相反。
M I J S
可以用总惯性力PI’来代替PI和MI ，PI’ = PI，作用线
由质心S 偏移 lh
lh MI PI
二、质量代换法
1. 质量代换法 按一定条件，把构件的质量假想地用集中于某几 个选定的点上的集中质量来代替的方法。 简化惯性力的确定，即只需求集中质量的惯性力， 无需求惯性力偶矩。 2. 代换点和代换质量
机械原理作业集
机械原理作业集1. 弹簧的工作原理。
弹簧是一种储存和释放能量的装置，它的工作原理是利用弹性变形来储存能量。
当外力作用在弹簧上时，弹簧会发生形变，将外力储存在其中。
当外力消失时，弹簧会释放储存的能量，将形变恢复原状。
弹簧的工作原理在机械原理中有着广泛的应用，例如弹簧悬挂系统、弹簧减震系统等。
2. 齿轮传动的优势。
齿轮传动是一种常见的机械传动方式，它的优势在于传动效率高、传动比稳定、传动精度高等特点。
齿轮传动可以将动力从一个轴传递到另一个轴，同时可以改变转速和转矩。
在机械原理中，齿轮传动被广泛应用于各种机械设备中，如汽车变速箱、工业机械等。
3. 杠杆原理及应用。
杠杆是一种简单机械，它的作用是将力量或运动转换成另一种形式。
杠杆原理是利用杠杆的支点和力臂的长度差异来增大或减小力的作用效果。
在实际应用中，杠杆被广泛应用于各种机械装置中，如千斤顶、剪刀、门锁等。
4. 摩擦力的影响。
摩擦力是一种阻碍物体相对运动的力，它的大小取决于物体间的接触面积和摩擦系数。
在机械原理中，摩擦力对机械装置的运动有着重要的影响。
合理利用摩擦力可以增加机械装置的稳定性和安全性，同时也可以减小能量损耗，提高机械效率。
5. 原动机的选择。
在机械装置中，原动机的选择是非常重要的。
不同的原动机适用于不同的工作环境和工作要求。
例如，电动机适用于需要稳定转速和精确控制的场合，而内燃机适用于需要大功率输出和移动性的场合。
正确选择原动机可以提高机械装置的效率和可靠性。
6. 机械传动的维护。
机械传动在长时间工作后需要进行维护保养，以确保其正常运行。
常见的维护工作包括润滑、紧固、清洁等。
定期的维护保养可以延长机械传动的使用寿命，减小故障率，提高工作效率。
7. 机械原理的应用。
机械原理在现代工程中有着广泛的应用，涉及到机械设计、机械制造、机械维护等方面。
了解和掌握机械原理对于工程师和技术人员来说是非常重要的，它可以帮助他们更好地设计和制造机械装置，解决实际工程中的问题。
机械原理习题及答案
(2) 当取杆1为机架，将演化成何种机构？这时C、D是整转副还是摆动副；
(3) 当取杆3为机架，将演化成何种机构？这时A、B是整转副还是摆动副
解： (1) 28+72≤52+50且l1=28；曲柄摇杆机构； θ=19； φ=71；γmin={51，23}=23； K=1.236；
C2
2
C
B
1
3
A4
D
虚约束
局部自由度
复合铰链
a)
b)
c)
d)
机械原理 作业
第2章 平面机构的结构分析
2-8：计算自由度；确定机构所含杆组的数目与级别；确定机构级别。画出 瞬时替代机构； 解：自由度：
a) F=3n-2PL-PH=3*7-2*10=1；Ⅱ级 b) F=3n-2PL-PH=3*6-2*8-1=1；Ⅲ级
机械原理 作业
尖顶从动件：h= R lO2 A e 2R lO2 A e 2 2.4 1 ，基圆半径r0=R-lOA=20；
平底从动件：h=2lOA=20，基圆半径r0=R-lOA=20；
(2) 最大压力角αmax数值和位置。 尖顶从动件：sinαmax=(lOA+e)/R=0.667，αmax=41.80 平底从动件：αmax =0；
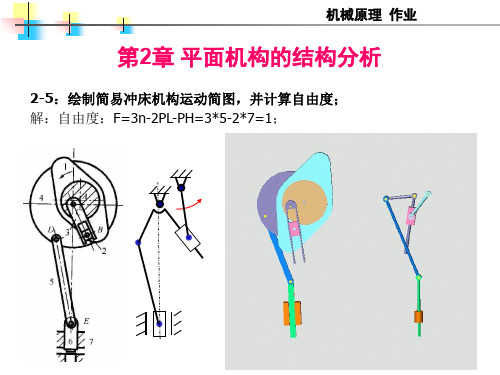
第2章 平面机构的结构分析
2-9：如图所示一简易冲床的初步设计方案， 解：自由度：F=3n-2PL-PH=3*3-2*4-1=0；
机构不能动； 增加一个构件一个低副；
移动副比转动副结构复杂
机械原理 作业
第3章 平面连杆机构
3-11：已知铰链四杆机构各杆长l1=28，l2=52，l3=50，l4=72mm，试求： (1) 取杆4为机架，该机构的极位夹角θ、杆3的最大摆角φ、最小传动角γmin 和行程速比系数K；
机械原理第四章作业
分度圆: d1= mz1 = 14*16 = 224mm d2= mz2 = 14*63 = 882mm 齿顶圆:
d a1 d1 2ha cos δ1 d 12mz 2 / z z
2 1
2 2
224 28 63 162 632 251.14mm
2 2 d a 2 d 2 2ha cos 2 d 22mz1 / z1 z2
题4-14：（1）
L r 32 mm v r , 1 16 0.0625 rad / s
（2）
L r xm 36.8mm v r , 1 16 0.0625 rad / s
rb r cos 30 .07 mm r f r h f xm 31 .8mm ra r ha xm 40 .8mm
《齿轮机构》作业
第1次：4-3、4-6、4-9、4-11、4-14 第2次： 4-18、4-19、 4-21、4-23、(4-32、4-35)
4-3 已知两个渐开线直齿圆柱齿轮的齿数z1=20，z2=40， 它们都是标准齿轮，而且m、、ha*、c*均相同。试用渐 开线齿廓的性质，说明这两个齿轮的齿顶厚度哪一个大， 基圆上的齿厚哪一个大。
延伸：m=2mm，z1=20，z2=40，a=61时,可有几种 办法实现无侧隙啮合? 1 解: 标准中心距 a= (z1+z2)=60mm 2
a=61>a
(1)采用正传动;
r1 =20.33mm, r2 =40.67mm
= arccos(acos/a) =22.44° (2)采用标准斜齿轮传动,
a mn ( z1 z2 ) / 2 cos 231 .9mm
机械原理作业答案(含相对运动图解法)
F
E D
A
C B 图7
以 EF 为原动件时，其基本杆组及驱动杆组如图 8 所示，为 II 级机构。
E
C
B
D
F
A 图8
16c 以 AB 为原动件和以 EF 为原动件时，均为 II 级机构，其基本杆组及驱动杆组分别如图 9、图
10 所示。
B
E
C
C
F
A
D
图9
B
D
C
C A
F E
图 10
16d 除去机构中局部自由度，高副低代后的机构示意图和其基本杆组及驱动杆组如图 11 所示，II 级 机构。
当 AB 为最长杆时，有 lAB+lAD>lBC+lCD，即 lAB+30>50+35，得到 lAB>55 mm；由于 AB 杆的最大长度不
能大于其余三杆长度之和，即 lAB< lBC+lCD+lAD=50+35=30=115 mm，得到 55 mm< lAB<115 mm。
综合以上分析，得到 AB 杆的取值为：15 mm<lAB<45 mm 或 55 mm< lAB<115 mm
图9
2.20 习题
2.21 习题
221 解 设计步骤为（参见图 11）： 1）=180(K1)/(K+1)=180(1.51)/(1.5+1)=36 2）选择长度比例尺l，根据已知条件，作出机架 AD 和摇杆的一个极限位置 DC1，并以 D 为圆心， CD1 为半径画圆弧。连接 AC1；代表摇杆的一个极限位置； 3）根据极位夹角定义，作与 AC1 夹角为 的射线 AC，其与圆弧分别交于 C2 和 C2，则 DC2 和 DC2 均可作为摇杆 CD 的两个极限位置。 4）若将 AC2 视为连杆与曲柄拉伸共线位置，AC1 视为连杆与曲柄重叠共线位置，则 lAB=0.5l(AC2AC1)49.3 mm，lBC=0.5l(AC2+AC1)120 mm 若将 AC1 视为连杆与曲柄拉伸共线位置，AC2 视为连杆与曲柄重叠共线位置，则
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
m=2mm,z=20
a=60 a=61
a=61mm时,
m=2mm,z=40
r1 = a /(1+i12)=20.33mm, r2 =40.67mm
= arccos(acos/a’) =22.44°
c=c*m+(a–a) 为有侧隙传动
还有: 顶隙
延伸：m=2mm，z1=20，z2=40，a=61时,可有几种 办法实现无侧隙啮合?
cosa1rb1/ra1, a13.18 cosa2rb2/ra2, a22.62
（3）啮合角 '
a 2 1z 1 (tg a 1 tg ') z 2 (tg a 2 tg ') 1
23.2
（4）两轮节圆半径r1', r2'
co sr r b 1 1 r r b 2 2 , r1 3.8 8m 6,r2 m 8.8 5m 9 m
vr, 11 60.06r2a/5 sd
（2） （3）
Lrxm 3.8 6mm
vr, 11 60.06r2a/5 sd rb rcos 30.07mm
rf r hf xm31.8mm ra r ha xm40.8mm
vrm 2z, zm 2 v24
4-18 一对外啮合渐开线标准斜齿轮，已知：z1=16、
z2=40、mn=8mm，螺旋角=15o，齿宽b=30mm，试求其无 侧隙啮合的中心距a和轴向重合度，并说明齿轮1是否发
生根切，并根据渐开线标准直齿轮不发生根切的最少齿数 公式，导出斜齿轮不发生根切的最少齿数的公式。
a m n (z 1 z2 )/2 co s 2.3 9 m 1m
bsm inn33 .10 s4i1n 158 591.153
（5）两分度圆在连心线O1O2的距离Δy
O1O2 r1 r2 12.745mm yO1O2(r1r2)2.75mm
4-14
• 用齿条型刀具加工一个齿数为z=16的齿轮,刀具参数
m具=的4m移m动, 速(度=v2刀0°=2，mmha/*s=.试1，求c:*=0.25),在加工齿轮时,刀
（1）欲加工成标准齿轮时,刀具中线与轮坯中心的距离L 为多少?轮坯转动的角速度为多少?
d1=mz1=120mm; d2=mz2=240mm; a=(d1+d2)/2=180mm;
db1 =d1*cosα=112.8mm; db2 =225.5mm; da1=d+2ha*m=128mm; da2=248mm.
B1B2 pn
B1B2
mcos
o1
ra1
rb1
N1
B1
B2
a
N2
rb2
ra2
已知z1=30,z2=60,m=4mm,α=20°，ha*=1，
试按比例精确作图画出无侧隙啮合时的
实际啮合线B1B2的长度，根据量得的B1B2
计算重合度，并用重合度计算公式计算 进行对比校核。
题4-9：（1）画图：计算出标准中心距a、分 度圆直径d1（ d2）、基圆直径db1 （db2）、齿 顶圆直径da1（ da2）
机械原理第四章作业.
4-6 一对已切制好的渐开线外啮合直齿圆柱标准齿轮，z1=20、
Z2=40、m=2mm、 =20o、ha*=1、c*=0.25。试说明在中心
距a=60mm、a’=61mm两种情况下，哪些尺寸不同。
a=60mm时,
r2 =r2 =
r1 =r1
C=c*m
标准中心距: a= m(z1+z2)/2=60mm
此长度时；刚(好2)能齿保顶证圆连周续上传的动压，力试角求αa：1 ,(α1a)2；实(3际) 啮啮合合角线B1‘B2；的
(4) 两轮节圆半径r 离Δy。
’1,
r‘2；(5)
两分度圆在连心线O1O2的距
（1） 因:为 B1B2/pn1 所:以 B1B2pnmcos1.18mm
（2）d1=76mm， d2=168mm， db1 =71.42mm，db2 =157.87mm, da1=84mm， da2=176mm
（2）欲加工出x=1.2的变位齿轮时,刀具中线与轮坯中心 的距离L为多少?轮坯转动的角速度为多少?并计算所加 工ra；出的齿轮的齿根圆半径rf，基圆半径rb和齿顶圆半径
（3）若轮坯转动的角速度不变,而刀具的移动速度改为V 刀=3mm/s,则加工出的齿轮齿数z为多少?
题4-14：（1）
Lr3m 2 m
z V 1 z 1/c3 o s 1/c 63 o 1 s 5 1.7 75
由于Zv1少于17,斜齿轮将发生根切,则有
z 1 z v 1 * c3 o s 1* c 73 o 1 s 5 1.3 52
4-19 一对渐开线外啮合圆柱齿轮,已知z1=21, z2=22，
模数m=2mm，中心距为44mm。若不采用变位齿
解:
标准中心距
a=
1 2
(z1+z2)=60mm
a=61>a
(1)采用正传动;
r1 =20.33mm, r2 =40.67mm
= arccos(acos/a) =22.44°
(2)采用标准斜齿轮传动,
a=
mn 2cos
(z1+z2)=61mm
=10.38º
4-9
一对外啮合渐开线直齿圆柱标准齿轮，
轮，而用标准斜齿圆柱齿轮凑中心距，求斜齿圆柱齿
轮的螺旋角β应为多少?
解: 根据题意, 斜齿轮的法面模数mn即为2mm
由公 :a1 2式 m n(z1z2)/co ,有 s:
cos
1 2
mn ( z1
z2) / a
1 * 2(21 22 ) / 44 2
0.9773
所:以 1.224
4-21 一个标准圆柱斜齿轮减速器，已知z1=22、z2=77、 mn=2mm 、 han*=1 、 =8°6’34” 、 n=20° 、 cn*=0.25。
o2
（2）用公式计算：
a1
rb1 ra1
,
a1
28 .2
cos a2
rb 2 ra 2
,
a2
24 .6
a21z1(tg a1tg ')z2(tg a2tg ')
1.73
4-11 若已知一对齿轮机构的安装位置，当采用一对标准直
齿圆柱齿轮，其z1=19, z2=42, m=4 mm, =20°，ha*=1,
(1) 试述螺旋角取=8°6’34”的理由； (2解) 计: （算1）小若齿螺轮旋的角尺太小寸，（对r、斜齿ra、轮的rf、优r点b）（如及平中稳心、距无。噪声
和冲击、重合度高等）不突出；若太大，则轴向推力太 大，一般取8~15度，因此本题的取值合理。