2016届高考数学理新课标A版一轮总复习开卷速查 必修部分67 离散型随机变量及其分布列
《状元之路》2016届高考数学理新课标A版一轮总复习 6-3

若 z=2x+y 的
第32页
返回导航
第六章
第三节
高考进行时 一轮总复习 · 数学(新课标通用A版 · 理)
解析:(1)由约束条件作出可行域,如图所示的阴影△ABC 区域 (包括边界).
x=-2, 由 x+2y=2
x=-2, 得 y=2.
故 C(-2,2).
第33页
返回导航
考点二
线性目标函数的最值问题
y≥x, 【例 2】 (1)设变量 x,y 满足约束条件:x+2y≤2, x≥-2. =x-3y 的最小值为( A.-2 ) C.-6 D.- 8
则 z
B.-4
第31页
返回导航
第六章
第三节
高考进行时 一轮总复习 · 数学(新课标通用A版 · 理)
x≥1, (2)已知 a>0,x,y 满足约束条件x+y≤3, y≥ax-3. 最小值为 1,则 a=( 1 1 A. 4 B.2 C.1 ) D.2
第六章
第三节
高考进行时 一轮总复习 · 数学(新课标通用A版 · 理)
1 作出直线 l0:y=3x,平移直线 l0,当直线 l0 经过点 C(-2,2)时, z 取得最小值,且 zmin=-2-3×2=-8,故选 D.
x≥1, (2)由题意作出 x+y≤3
所表示的区域如图阴影部分所示,
第12页
返回导航
第六章
第三节
高考进行时 一轮总复习 · 数学(新课标通用A版 · 理)
z z (1)若 b>0,则截距 取最大值时,z 也取最大值;截距 取最小 b b 值时,z 也取最小值. z z (2)若 b<0,则截距 取最大值时,z 取最小值;截距 取最小值 b b 时,z 取最大值.
2016届高考数学理新课标A版一轮总复习课件 第10章 计数原理、概率、随机变量及其分布列-8

第十章
计数原理、概率、随机变量及其分布列
第1页
返回导航
第十章 计数原理、概率、随机变量及其 第一页,编辑于星期五:二十一点 十四分。
高考进行时 一轮总复习 ·数学(新课标通用A版 ·理)
第八节 n次独立重复试验与二项分布
课前学案 基础诊断
课堂学案 考点通关
高考进行时 一轮总复习 ·数学(新课标通用A版 ·理)
►名师点拨 条件概率的两种求解方法 (1)定义法:先求P(A)和P(AB),再由P(B|A)=PPAAB求P(B|A). (2)基本事件法:借助古典概型概率公式,先求事件A包含的基 本事件数n(A),再求事件AB所包含的基本事件数n(AB),得P(B|A) =nnAAB.
2
答案:A
第14页
返回导航
第十章 第八节 第十四页,编辑于星期五:二十一点 十四分。
高考进行时 一轮总复习 ·数学(新课标通用A版 ·理)
4.一个箱子里装有4个白球和3个黑球,一次摸出2个球,在已 知它们的颜色相同的条件下,该颜色是白色的概率为__________.
解析:设颜色相同为事件A,颜色都是白色为事件B,则P(B|A) =nnAAB=C42+C42C23=23.
为P(B|A)=□1 ______________________.
在古典概型中,若用n(A)表示事件A中基本事件的个数,则 P(B|A)=nnAAB.
第5页
返回导航
第十章 第八节 第五页,编辑于星期五:二十一点 十四分。
高考进行时 一轮总复习 ·数学(新课标通用A版 ·理)
(2)条件概率具有的性质:
第26页
返回导航
第十章 第八节 第二十六页,编辑于星期五:二十一点 十四分。
《状元之路》2016届高考数学理新课标A版一轮总复习 3-2

3-1 答案: 2
第16页
返回导航
第三章
第二节
高考进行时 一轮总复习 · 数学(新课标通用A版 · 理)
课堂学案
考点通关
考点例析 通关特训
第17页
返回导航
第三章
第二节
高考进行时 一轮总复习 · 数学(新课标通用A版 · 理)
考点一
同角三角函数基本关系式的应用
1 【例1】 已知α是三角形的内角,且sinα+cosα=5. (1)求tanα的值; (2)把 1 2 2 用tanα表示出来,并求其值. cos α-sin α
第21页
返回导航
第三章
第二节
高考进行时 一轮总复习 · 数学(新课标通用A版 · 理)
sin2α+cos2α sin2α+cos2α tan2α+1 cos2α 1 (2) 2 = = = . cos α-sin2α cos2α-sin2α cos2α-sin2α 1-tan2α cos2α 4 ∵tanα=- , 3
第6页
返回导航
第三章
第二节
高考进行时 一轮总复习 · 数学(新课标通用A版 · 理)
8 ________,tan(π 公式四:sin(π-α)=sinα,cos(π-α)= □ -α)=-tanα.
第7页
返回导航
第三章
第二节
高考进行时 一轮总复习 · 数学(新课标通用A版 · 理)
答案: 1 sin2α+cos2α=1 □ sinα 2 □tanα=cosα 3 cosα □
2.三角函数的诱导公式 3 ____,tan(α 公式一:sin(α+2kπ)=sinα,cos(α+2kπ)= □ +2kπ)=tanα,其中k∈Z. 4 ______,cos(π+α)= □ 5 ____, 公式二:sin(π+α)= □ tan(π+α)=tanα. 6 ______,cos(-α)= □ 7 ______, 公式三:sin(-α)= □ tan(-α)=-tanα.
《状元之路》2016届高考数学理新课标A版一轮总复习 2-7

返回导航
第二章
第七节
高考进行时 一轮总复习 · 数学(新课标通用A版 · 理)
考点二
识图与辨图
【例 2】 (1)小明骑车上学,开始时匀速行驶,途中因交 通堵塞停留了一段时间后,为了赶时间加快速度行驶,与以上事件 吻合得最好的图像是( )
A
B
C
D
第32页
返回导航
第二章
第七节
高考进行时 一轮总复习 · 数学(新课标通用A版 · 理)
第27页
返回导航
第二章
第七节
高考进行时 一轮总复习 · 数学(新课标通用A版 · 理)
通关特训 1 分别画出下列函数的图像: (1)y=|lgx|; (2)y=2x+2;
x+2 (3)y= ; (4)y=|log2x-1|. x+3
第28页
返回导航
第二章
第七节
高考进行时 一轮总复习 · 数学(新课标通用A版 · 理)
x0≤x≤1, f(x)= 11<x≤2. 10≤x≤1, f(2-x)= 2-x1<x≤2,
当 x∈[0,2]时,2-x∈[0,2],所以
-10≤x≤1, y=-f(2-x)= x-21<x≤2.
故
故其对应的图像应为 B.
第38页
返回导航
第二章
第七节
高考进行时 一轮总复习 · 数学(新课标通用A版 · 理)
1. 描点法作图 方法步骤:(1)确定函数的定义域;(2)化简函数的解析式;(3) 讨论函数的性质即奇偶性、周期性、单调性、最值(甚至变化趋 势);(4)描点连线,画出函数的图像.
第5页
返回导航
第二章
第七节
高考进行时 一轮总复习 · 数学(新课标通用A版 · 理)
《状元之路》2016届高考数学理新课标A版一轮总复习3-5
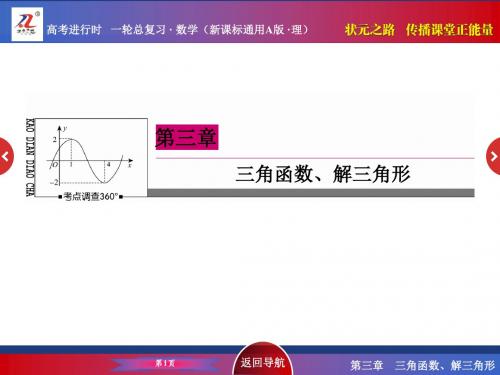
3.已知tanα-π6=37,tanπ6+β=25,则tan(α+β)的值为(
)
29
1
A.41
B.29
1 C.41
D.1
第16页
返回导航
第三章 第五节
高考进行时 一轮总复习 ·数学(新课标通用A版 ·理)
第13页
返回导航
第三章 第五节
高考进行时 一轮总复习 ·数学(新课标通用A版 ·理)
1.若sinα2= 33,则cosα=(
)
A.-23
B.-13
1
2
C.3
D.3
解析:因为sinα2= 33,所以cosα=1-2sin2α2=1-2× 332=13.
答案:C
第14页
返回导航
第三章 第五节
第11页
返回导航
第三章 第五节
高考进行时 一轮总复习 ·数学(新课标通用A版 ·理)
(2)互余与互补关系 π4+α+π4-α=2π;π3+α+6π-α=π2; 34π-α+π4+α=π;π6+α+56π-α=π;…
第5页
返回导航
第三章 第五节
高考进行时 一轮总复习 ·数学(新课标通用A版 ·理)
2.二倍角的正弦、余弦、正切公式
sin2α=□4 ____________, cos2α=□5 __________=□6 ________=□7 ________, tan2α=□8 __________
第6页
返回导航
高考进行时 一轮总复习 ·数学(新课标通用A版 ·理)
第三章
三角函数、解三角形
第1页
返回导航
第三章 三角函数、解三角形
高考进行时 一轮总复习 ·数学(新课标通用A版 ·理)
2016届高考数学新课标A版理科一轮复习习题10-7离散型随机变量及其分布列

自主园地 备考套餐加固训练 练透考点1.随机变量X 的概率分布规律为P (X =n )=a n (n +1)(n =1,2,3,4),其中a 是常数,则P ⎝ ⎛⎭⎪⎫12<X <52的值为( ) A.23 B.34 C.45 D.56解析:由题意得a 1·2+a 2·3+a 3·4+a 4·5=1,a ⎝ ⎛⎭⎪⎫1-12+12-13+…+14-15=4a 5=1,a =54, P ⎝ ⎛⎭⎪⎫12<X <52=P (X =1)+P (X =2)=a 1·2+a 2·3=2a 3=56. 答案:D2.一盒中有12个乒乓球,其中9个新的,3个旧的,从盒中任取3个球来用,用完后装回盒中,此时盒中旧球个数X 是一个随机变量,其分布列为P (X ),则P (X =4)的值为( )A.1220B.2755C.27220D.2125 解析:由题意知取出的3个球必为2个旧球1个新球,故P (X =4)=C 23C 19C 312=27220. 答案:C3.在15个村庄中有7个村庄交通不方便,现从中任意选10个村庄,而X 表示这10个村庄中交通不方便的村庄数,下列概率中等于C 47C 68C 1015的是( )A .P (X =2)B .P (X ≤2)C .P (X =4)D .P (X ≤4)解析:X 服从超几何分布P (X =k )=C k 7C 10-k 8C 1015,故k =4. 答案:C4.随机变量ξ的分布列如下:若a 、b 、c 解析:∵a 、b 、c 成等差数列,∴2b =a +c ,又a +b +c =1.∴b =13.∴P (|ξ|=1)=a +c =23.答案:235.由于电脑故障,使得随机变量X 的分布列中部分数据丢失(以“x 、y ”代替),其表如下:解析:由于0.20+0.10+(0.1x +0.05)+0.10+(0.1+0.01y )+0.20=1,得10x +y =25,于是两个数据分别为2,5.答案:2,5。
《状元之路》2016届高考数学理新课标A版一轮总复习开卷速查必修部分7二次函数与幂函数

开卷速查(七)二次函数与幂函数A级基础巩固练1.函数y=x-x 13的图像大致为()ABCD解析:函数y=x-x 13为奇函数.排除C、D;当x>0时,由x-x 13>0,即x3>x可得x2>1,即x>1,结合选项,选A.答案:A 2.幂函数y =x m 2-4m(m ∈Z )的图像如图所示,则m 的值为( )A .0B .1C .2D .3解析:∵y =x m 2-4m(m ∈Z )的图像与坐标轴没有交点, ∴m 2-4m <0,即0<m <4.又∵函数的图像关于y 轴对称,且m ∈Z , ∴m 2-4m 为偶数,因此m =2. 答案:C3.已知函数y =ax 2+bx +c ,如果a >b >c 且a +b +c =0,那么它的图像可能是( )ABCD解析:∵a >b >c ,且a +b +c =0,∴a >0,c <0.∴图像开口向上与y 轴交于负半轴. 答案:D4.已知f (x )=x12,若0<a <b <1,则下列各式中正确的是( )A .f (a )<f (b )<f ⎝ ⎛⎭⎪⎫1a <f ⎝ ⎛⎭⎪⎫1bB .f ⎝ ⎛⎭⎪⎫1a <f ⎝ ⎛⎭⎪⎫1b <f (b )<f (a )C .f (a )<f (b )<f ⎝ ⎛⎭⎪⎫1b <f ⎝ ⎛⎭⎪⎫1aD .f ⎝ ⎛⎭⎪⎫1a <f (a )<f ⎝ ⎛⎭⎪⎫1b <f (b ) 解析:因为函数f (x )=x 12在(0,+∞)上是增函数,又0<a <b <1b <1a ,故f (a )<f (b )<f ⎝ ⎛⎭⎪⎫1b <f ⎝ ⎛⎭⎪⎫1a .答案:C5.已知f (x )=x 2+bx +c 且f (-1)=f (3),则( )A .f (-3)<c <f ⎝ ⎛⎭⎪⎫52B .f ⎝ ⎛⎭⎪⎫52<c <f (-3)C .f ⎝ ⎛⎭⎪⎫52<f (-3)<cD .c <f ⎝ ⎛⎭⎪⎫52<f (-3)解析:由已知可得二次函数图像关于直线x =1对称,则f (-3)=f (5),c =f (0)=f (2),二次函数在区间(1,+∞)上单调递增,故有f (-3)=f (5)>f ⎝ ⎛⎭⎪⎫52>f (2)=f (0)=c .答案:D6.已知f (x )是定义在R 上的奇函数,当x ≥0时,f (x )=x 2+2x ,若f (2-a 2)>f (a ),则实数a 的取值范围是( )A .(-∞,-1)∪(2,+∞)B .(-1,2)C .(-2,1)D .(-∞,-2)∪(1,+∞)解析:∵f(x)是奇函数,∴当x<0时,f(x)=-x2+2x,作出f(x)的大致图像如图中实线所示,结合图像可知f(x)是R上的增函数,由f(2-a2)>f(a),得2-a2>a,即-2<a<1.答案:C7.已知幂函数f(x)=(m2-5m+7)x m-2为奇函数,则m=__________.解析:由f(x)=(m2-5m+7)x m-2为幂函数得:m2-5m+7=1,解得m=2或m=3,又因为该函数为奇函数,所以m=3.答案:38.若函数f(x)=(x+a)(bx+2a)(常数a,b∈R)是偶函数,且它的值域为(-∞,4],则该函数的解析式f(x)=__________.解析:由f(x)的定义域为R,值域为(-∞,4],可知b≠0,∴f(x)为二次函数,f(x)=(x+a)(bx+2a)=bx2+(2a+ab)x+2a2.∵f(x)为偶函数,∴其对称轴为x=0,∴-(2a+ab)=0,解得a=0或b=-2.若a=0,则f(x)=bx2,与值域是(-∞,4]矛盾,∴a≠0,b =-2,又f(x)的最大值为4,∴2a2=4,∴f(x)=-2x2+4.答案:-2x 2+49.二次函数f (x )的二次项系数为正,且对任意x 恒有f (2+x )=f (2-x ),若f (1-2x 2)<f (1+2x -x 2),则x 的取值范围是__________.解析:由f (2+x )=f (2-x ),知x =2为对称轴,由于二次项系数为正的二次函数中距对称轴较近的点的纵坐标较小,∴|1-2x 2-2|<|1+2x -x 2-2|,即|2x 2+1|<|x 2-2x +1|,∴2x 2+1<x 2-2x +1,∴-2<x <0.答案:(-2,0)10.已知函数f (x )=ax 2+(b -8)x -a -ab (a ≠0),当x ∈(-3,2)时,f (x )>0;当x ∈(-∞,-3)∪(2,+∞)时,f (x )<0.(1)求f (x )在[0,1]内的值域;(2)若不等式ax 2+bx +c ≤0在[1,4]上恒成立,求c 的取值范围. 解析:由题意,得x =-3和x =2是函数f (x )的零点,且a <0,则⎩⎨⎧0=a ×(-3)2+(b -8)×(-3)-a -ab ,0=a ×22+(b -8)×2-a -ab .解得⎩⎨⎧a =-3,b =5.∴f (x )=-3x 2-3x +18.(1)由图像知,函数在[0,1]内单调递减, ∴当x =0时,y =18; 当x =1时,y =12.∴f (x )在[0,1]内的值域为[12,18]. (2)令g (x )=-3x 2+5x +c .∵g (x )在⎝ ⎛⎭⎪⎫56,+∞上单调递减,要使g (x )≤0在[1,4]上恒成立,则需要g (1)≤0.即-3+5+c ≤0,解得c ≤-2.∴当c ≤-2时,不等式ax 2+bx +c ≤0在[1,4]上恒成立.B 级 能力提升练11.已知x ∈[-1,1]时,f (x )=x 2-ax +a2>0恒成立,则实数a 的取值范围是( )A .(0,2)B .(2,+∞)C .(0,+∞)D .(0,4)解析:二次函数图像开口向上,对称轴为x =a2,又x ∈[-1,1]时,f (x )=x 2-ax +a2>0恒成立,即f (x )最小值>0.①当a 2≤-1,即a ≤-2时,f (-1)=1+a +a 2>0,解得a >-23,与a ≤-2矛盾;②当a 2≥1,即a ≥2时,f (1)=1-a +a2>0, 解得a <2,与a ≥2矛盾;③当-1<a 2<1,即-2<a <2时,Δ=(-a )2-4·a2<0,解得0<a <2.综上得实数a 的取值范围是(0,2). 答案:A12.已知函数f (x )=x 2-2x ,g (x )=ax +2(a >0),对任意的x 1∈[-1,2]都存在x 0∈[-1,2],使得g (x 1)=f (x 0),则实数a 的取值范围是________.解析:当x 0∈[-1,2]时,由f (x )=x 2-2x 得f (x 0)∈[-1,3],又对任意的x 1∈[-1,2]都存在x 0∈[-1,2],使得g (x 1)=f (x 0),∴当x 1∈[-1,2]时,g (x 1)∈[-1,3].当a >0时,⎩⎨⎧-a +2≥-1,2a +2≤3,解得a ≤12.综上所述,实数a 的取值范围是⎝ ⎛⎦⎥⎤0,12. 答案:⎝ ⎛⎦⎥⎤0,12 13.已知函数f (x )=ax 2-2ax +2+b (a ≠0),若f (x )在区间[2,3]上有最大值5,最小值2.(1)求a ,b 的值;(2)若b <1,g (x )=f (x )-mx 在[2,4]上单调,求m 的取值范围. 解析:(1)f (x )=a (x -1)2+2+b -a . 当a >0时,f (x )在[2,3]上为增函数,故⎩⎨⎧ f (3)=5,f (2)=2,⇒⎩⎨⎧ 9a -6a +2+b =5,4a -4a +2+b =2,⇒⎩⎨⎧a =1,b =0.当a <0时,f (x )在[2,3]上为减函数,故⎩⎨⎧f (3)=2,f (2)=5,⇒⎩⎨⎧9a -6a +2+b =2,4a -4a +2+b =5,⇒⎩⎨⎧a =-1,b =3.(2)∵b <1,∴a =1,b =0,即f (x )=x 2-2x +2. g (x )=x 2-2x +2-mx =x 2-(2+m )x +2, ∵g (x )在[2,4]上单调,∴2+m 2≤2或m +22≥4. ∴m ≤2或m ≥6.故m 的取值范围为(-∞,2]∪[6,+∞).14.[2015·“江淮十校”联考]设二次函数f (x )=x 2-ax +b ,集合A ={x |f (x )=x }.(1)若A ={1,2},求函数f (x )的解析式;(2)若F (x )=f (x )+2-a -a 2且f (1)=0,且|F (x )|在[0,1]上单调递增,求实数a 的取值范围.解析:(1)由f (x )=x ,得x 2-(a +1)x +b =0.∵A ={x |f (x )=x }={1,2},∴1,2是关于x 的一元二次方程x 2-(a +1)x +b =0的两个实数根.∴⎩⎨⎧a +1=3,b =2.⇒⎩⎨⎧a =2,b =2.∴f (x )=x 2-2x +2.(2)∵f (1)=0,∴1-a +b =0,b =a -1. ∴F (x )=f (x )+2-a -a 2=x 2-ax +(1-a 2).①当Δ≤0,即(-a )2-4(1-a 2)≤0,-255≤a ≤255时,应满足⎩⎨⎧a2≤0,-255≤a ≤255⇒-255≤a ≤0.②当Δ>0,即a <-255或a >255时,设方程F (x )=0的两个实数根分别为x 1,x 2(x 1<x 2).若a2≥1,则x 1≤0,即⎩⎪⎨⎪⎧ a 2≥1,F (0)=1-a 2≤0⇒a ≥2;若a2≤0,则x 2≤0,即⎩⎪⎨⎪⎧a 2≤0,F (0)=1-a 2≥0.⇒-1≤a <-255.综上,实数a的取值范围是-1≤a≤0或a≥2.。
《状元之路》2016届高考数学理新课标A版一轮总复习 1-1
第10页
返回导航
第一章
第一节
高考进行时 一轮总复习 · 数学(新课标通用A版 · 理)
4.集合的基本运算 并集 符号 表示 图形 表示 意义 22 ______ □ 23 ______ □ 24 ______________ □ A∪B 交集 A∩B 补集 若全集为U,A⊆U, 则集合A的补集为∁UA
(2)已知集合 A={x|-2≤x≤7},B={x|m+1< x<2m-1}.若 B⊆A,则实数 m 的取值范围是( A.-3≤m≤4 C.2<m≤4
第29页
)
B.-3<m<4 D.m≤4
返回导航
第一章 第一节
高考进行时 一轮总复习 · 数学(新课标通用A版 · 理)
解析:(1)由 x2-3x+2=0 得 x=1 或 x=2,故 A={1,2}.由题 意知 B={1,2,3,4},因此满足条件的 C 可为{1,2},{1,2,3},{1,2,4}, {1,2,3,4},故选 D. (2)当 B=∅时,有 m+1≥2m-1,则 m≤2. 当 B≠∅时,若 B⊆A,如图.
答案:B
第21页
返回导航
第一章
第一节
高考进行时 一轮总复习 · 数学(新课标通用A版 · 理)
课堂学案
考点通关
考点例析 通关特训
第22页
返回导航
第一章
第一节
高考进行时 一轮总复习 · 数学(新课标通用A版 · 理)
考点一
集合的基本概念
【例 1】 (1)已知集合 A={1,2,3,4,5},B= {(x,y)|x∈ A, y∈ A, x-y∈ A},则 B 中所含元素的个数为( A.3 个 B.6 个 C.8 个 ) D.10 个
第25页
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
开卷速查(六十七)离散型随机变量及其分布列
A级基础巩固练
1.某食品厂为了检查一条自动包装流水线的生产情况,随机抽取该流水线上40件产品作为样本称出它们的质量(单位:克),质量的分组区间为(490,495],(495,500],…,(510,515].由此得到样本的频率分布直方图,如图所示.
(1)根据频率分布直方图,求质量超过505克的产品数量;
(2)在上述抽取的40件产品中任取2件,设Y为质量超过505克的产品数量,求Y的分布列.
解析:(1)根据频率分布直方图可知,质量超过505克的产品数量为40×(0.05×5+0.01×5)=40×0.3=12.
(2)Y的可能取值为0,1,2,且Y服从参数为N=40,M=12,n=2的超几何分布,故
P(Y=0)=C012C228
C240=
63
130,
P(Y=1)=C112C128
C240=
28
65,
P(Y=2)=C212C028
C240=
11
130.
所以Y的分布列为
2.每一件一等品都能通过检测,每一件二等品通过检测的概率为2
3.现有10件产品,其中6件是一等品,4件是二等品.
(1)随机选取1件产品,求能够通过检测的概率;
(2)随机选取3件产品,其中一等品的件数记为X ,求X 的分布列; (3)随机选取3件产品,求这3件产品都不能通过检测的概率. 解析:(1)设随机选取一件产品,能够通过检测的事件为A ,事件A 等于事件“选取一等品都通过检测或者是选取二等品通过检测”,
∴P(A)=610+410×23=1315.
(2)由题可知X 的可能取值为0,1,2,3.
P(X =0)=C 34C 06C 310=130,P(X =1)=C 24C 16
C 310=310,
P(X =2)=C 14C 26
C 310=12,P(X =3)=C 04C 36C 310
=16.
∴X 的分布列如下:
(3)设“随机选取的事件为B ,事件B 等于事件“随机选取3件产品都是二等品且都不能通过检测”,
所以,P(B)=130·⎝ ⎛⎭
⎪⎫133=1810. B 级 能力提升练
3.一次考试共有12道选择题,每道选择题都有4个选项,其中
有且只有一个是正确的.评分标准规定:“每题只选1个选项,答对得5分,不答或答错得0分”.某考生已确定有8道题的答案是正确的,其余题中:有2道题都可判断2个选项是错误的,有1道题可以判断1个选项是错误的,还有1道题因不理解题意只好乱猜.请求出该考生:
(1)得60分的概率; (2)所得分数X 的分布列.
解析:(1)设“选对可判断2个选项是错误的2道题之一”为事件A ,“选对可判断1个选项是错误的1道题”为事件B ,“选对不理解题意的1道题”为事件C.
则P(A)=12,P(B)=13,P(C)=1
4, 所以得60分的概率P =12×12×13×14=1
48.
(2)依题意得,所得分数X 可能的取值为40,45,50,55,60. P(X =40)=12×12×23×34=1
8;
P(X =45)=C 1
2×12×12×23×34+12×12×13×34+12×12×23×14=1748
;
P(X =50)=12×12×23×34+C 12×12×12×13×34+C 1
2×12×12×23×14+12×12×13×14=1748;
P(X =55)=C 12
×12×12×13×14+12×12×23×14+12×12×13×34=7
48; P(X =60)=12×12×13×14=1
48. 所以所得分数X 的分布列为:
4.2014年1065周年,来自北京大学和清华大学的6名大学生志愿者被随机平均分配到天安门广场运送矿泉水、打扫卫生、维持秩序这三个岗位服务,且运送矿泉水岗位至少有1名北京大学志愿者的概率是3
5.
(1)求打扫卫生岗位恰好有北京大学、清华大学志愿者各1名的概率;
(2)设随机变量ξ为在维持秩序岗位服务的北京大学志愿者的人数,求ξ的分布列.
解析:(1)记“至少有1名北京大学志愿者被分到运送矿泉水岗位”为事件A ,则事件A 的对立事件为“没有北京大学志愿者被分到运送矿泉水岗位”,设有北京大学志愿者x 名,1≤x<6,那么P(A)=1
-C 26-x
C 26
=35,解得x =2,即来自北京大学的志愿者有2名,来自清华大
学的志愿者有4名.
记“打扫卫生岗位恰好有北京大学、清华大学志愿者各1名”为
事件B ,则P(B)=C 12C 14
C 26
=815,
所以打扫卫生岗位恰好有北京大学、清华大学志愿者各1名的概率是815.
(2)在维持秩序岗位服务的北京大学志愿者的人数ξ服从超几何分布,其中N =6,M =2,n =2,于是
P(ξ=k)=C k 2C 2-k 4
C 26
,k =0,1,2,
∴P(ξ=0)=C 02C 24C 26=2
5,
P(ξ=1)=C 12C 14C 26=8
15,
P(ξ=2)=C 22C 04C 26
=1
15.
所以ξ的分布列为。
