柱下条形基础简化计算及其设计步骤-清晰版
柱下条形基础计算书
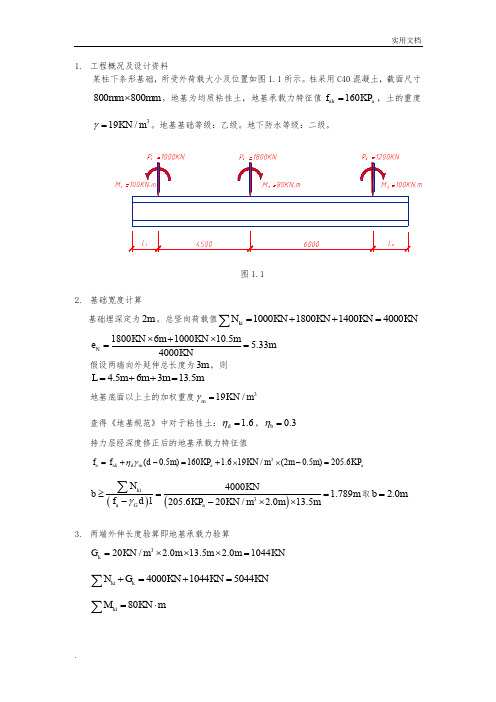
1. 工程概况及设计资料某柱下条形基础,所受外荷载大小及位置如图1.1所示。
柱采用C40混凝土,截面尺寸800800mm mm ⨯。
地基为均质粘性土,地基承载力特征值160ak a f KP =,土的重度319/KN m γ=。
地基基础等级:乙级。
地下防水等级:二级。
图1.12. 基础宽度计算基础埋深定为2m 。
总竖向荷载值1000180014004000kiNKN KN KN KN =++=∑180********.5 5.334000N KN m KN me m KN⨯+⨯==假设两端向外延伸总长度为3m ,则 4.56313.5L m m m m =++= 地基底面以上土的加权重度319/m KN m γ=查得《地基规范》中对于粘性土: 1.6d η=,0.3b η= 持力层经深度修正后的地基承载力特征值3(0.5)160 1.619/(20.5)205.6a ak d m a af f d m KP KN m m m KP ηγ=+-=+⨯⨯-=()()34000 1.789205.620/ 2.013.5kia G a NKNb m f d lKP KN m m mγ≥==--⨯⨯∑取 2.0b m =3. 两端外伸长度验算即地基承载力验算320/ 2.013.5 2.01044k G KN m m m m KN =⨯⨯⨯=400010445044kik NG KN KN KN +=+=∑ 80kiMKN m =⋅∑800.0155244N G KN me m KN+⋅==113.5 5.445 1.3052l m m ⎛⎫=-= ⎪⎝⎭213.5 5.055 1.6952l m m ⎛⎫=-= ⎪⎝⎭5244194.22205.62.013.5kikk a a a NG KNp KP f KP blm m +===<=⨯∑,max ,min6195.58 1.2246.7524460.015(1)(1)2.013.513.5192.860kikk N G a a ak a NG p e KP f KP KN p bll m m KP ++>=⨯=±=±=⨯>∑图1.24. 计算基础内力(倒梁法)(1)求基地净反力基础高度定为1.5m ,1.516.04i h l ==,满足要求。
柱下条形基础

柱下条形基础1)构造要求1、 基础梁高 l h )81~41(=,使梁具有较大的抗弯刚度以调整不均匀沉降; 2、 翼板厚度通过计算确定,但一般不小于200mm,当介于200到250之间时,取等厚翼板;当大于250mm时,取变厚度翼板,3:1≤i 。
3、 端部宜挑出一定长度,以增大面积并调整形心位置,长度为边跨的31~41; 4、 现浇柱与条形基础梁交接处,梁二侧比柱至少宽出50mm;5、 砼强度等级不低于20C ;6、 基础梁纵向受力钢筋、弯起筋应按M 、V 图配置,考虑整体弯曲,顶部纵向受力钢筋宜全部通长布置,底部通长钢筋不应小于底部受力钢筋总面积的1/3。
7、 梁内箍筋:✓ 当梁腹板高度大于450mm应沿高度配置纵向构造钢筋(腰筋),每侧不少于0.1%A ,间距不宜大于200mm;✓ 梁两侧纵向构造钢筋宜用拉筋连接(拉筋),直径同箍筋,间距500~700;✓ 梁内箍筋形式应采用封闭式,直径6~12,一般大于8mm⏹当梁宽mm b 350≤ 采用双肢箍; ⏹当梁宽]800,350(∈b ,采用四肢箍; ⏹ 当梁宽mm b 800>,采用六肢箍。
8、 底板配筋要求⏹ 横向受力钢筋,由计算确定,但直径不能小于10mm,间距为100~200;⏹ 纵向受力钢筋,直径为8~10,间距不超过300mm。
⏹ 纵横向交接处连接见规范。
2)内力计算:基础梁和底板1、计算方法:简化计算法和弹性地基梁法简化法:一般假定基底反力按直线分布。
实践中采用二种计算方法,静定梁法和倒梁法。
为满足基底反力按直线分布,一般要求基础梁有足够的相对刚度。
⏹ 静定梁法计算时先安直线分布假定,求出基底净反力,然后将柱荷载直接作用于基础梁上,分析受力(简图见教材),故可按静力平衡条件求出任意截面M 、V 。
当上部结构刚度很小时(如单层排架)宜采用静定分析法。
⏹ 倒梁法当上部结构刚度很大时,各柱之间没有沉降差异,因而可把柱脚视为条形基础铰支座,将基础梁按倒置普通连续梁计算。
柱下条形基础计算方法与步骤

柱下条形基础简化计算及其设计步骤提要:本文对常用的静力平衡法和倒梁法的近似计算及其各自的适用范围和相互关系作了一些叙述,提出了自己的一些看法和具体步骤,并附有柱下条基构造表,目的是使基础设计工作条理清楚,方法得当,既简化好用,又比较经济合理。
一、适用范围:柱下条形基础通常在下列情况下采用:1、多层与高层房屋无地下室或有地下室但无防水要求,当上部结构传下的荷载较大,地基的承载力较低,采用各种形式的单独基础不能满足设计要求时。
2、当采用单独基础所需底面积由于邻近建筑物或构筑物基础的限制而无法扩展时。
3、地基土质变化较大或局部有不均匀的软弱地基,需作地基处理时。
4、各柱荷载差异过大,采用单独基础会引起基础之间较大的相对沉降差异时。
5、需要增加基础的刚度以减少地基变形,防止过大的不均匀沉降量时。
其简化计算有静力平衡法和倒梁法两种,它们是一种不考虑地基与上部结构变形协调条件的实用简化法,也即当柱荷载比较均匀,柱距相差不大,基础与地基相对刚度较件下梁的计算。
二、计算图式1、上部结构荷载和基础剖面图2、静力平衡法计算图式3. 倒梁法计算图式三、设计前的准备工作1. 确定合理的基础长度为使计算方便,并使各柱下弯矩和跨中弯矩趋于平衡,以利于节约配筋,一般将偏心地基净反力(即梯形分布净反力)化成均布,需要求得一个合理的基础长度.当然也可直接根据梯形分布的净反力和任意定的基础长度计算基础.基础的纵向地基净反力为:j j i p F bL MbL min max=±∑∑62式中 P jmax ,P jmin —基础纵向边缘处最大和最小净反力设计值.∑F i —作用于基础上各竖向荷载合力设计值(不包括基础自重和其上覆土重,但包括其他局部均布q i ).∑M—作用于基础上各竖向荷载(F i ,q i ),纵向弯矩(M i )对基础底板纵向中点产生的总弯矩设计值.L —基础长度,如上述.B —基础底板宽度.先假定,后按第2条文验算.当P jmax 与P jmin 相差不大于10%,可近似地取其平均值作为均布地基反力,直接定出基础悬臂长度a 1=a 2(按构造要求为第一跨距的1/4~1/3),很方便就确定了合理的基础长度L ;如果P jmax 与P jmin 相差较大时,常通过调整一端悬臂长度a 1或a 2,使合力∑F i 的重心恰为基础的形心(工程中允许两者误差不大于基础长度的3%),从而使∑M 为零,反力从梯形分布变为均布,求a 1和a 2的过程如下:先求合力的作用点距左起第一柱的距离:式中, ∑M i —作用于基础上各纵向弯矩设计值之和.x i —各竖向荷载F i 距F 1的距离.当x≥a/2时,基础长度L=2(x+a 1), a 2=L-a-a 1.当x<a/2时,基础长度L=2(a-x+a 2), a 1=L-a-a 2.按上述确定a 1和a 2后,使偏心地基净反力变为均布地基净反力,其值为:式中, p j —均布地基净反力设计值.由此也可得到一个合理的基础长度L.2. 确定基础底板宽度b.由确定的基础长度L 和假定的底板宽度b,根据地基承载力设计值f,一般可按两个方向分别进行如下验算,从而确定基础底板宽度b.基础底板纵向边缘地基反力:应满足基础底板横向边缘地基反力:x F x M F i iii =+∑∑∑j i p F bL =∑2max min 6bL M bL G F i p ∑∑±+=()fp p f p≤+≤22.1min max max min 及应满足式中, pmax, pmin —基础底板纵向边缘处最大和最小地基反力设计值 p'max, p'min —基础底板横向边缘处最大和最小地基反力设计值G —基础自重设计值和其上覆土重标准值之和,可近似取G=20bLD,D 为基础埋深,但在地下水位以下部分应扣去浮力.∑M'—作用于基础上各竖向荷载、横向弯矩对基础底板横向中点产生的总弯矩设计值.其余符号同前述当∑M'=0时,则只须验算基础底板纵向边缘地基反力当∑M=0时,则只须验算基础底板横向边缘地基反力.当∑M=0且∑M'=0时(即地基反力为均布时),则按下式验算,很快就可确定基础底板宽度b:式中, p —均布地基反力设计值.3.求基础梁处翼板高度并计算其配筋先计算基础底板横向边缘最大地基净反力pmax 和最小地基净反力pmin,求出基础梁边处翼板的地基净反力pj1,如图,再计算基础梁边处翼板的截面弯矩和剪力,确定其厚度h1和抗弯钢筋面积.右图中, p —翼板悬挑长度, b1 =(b- b0)/2h1—基础梁边翼板高度b0,h —基础梁宽和梁高基础底板横向边缘处地基净反力式中, S —从基础纵向边缘最大地基反力处开始到任一截面的距离. 其余符号同前述基础梁边处翼板地基净反力p F G bL f b F L f D ii=+≤⇒≥-∑∑()20()2min max max maxmin '6'bL M p p L S p j j j j j p ∑±⎥⎦⎤⎢⎣⎡--=()min max 1max 1''''j j j j p p b b p p --=2max min '6'bL M bL G F i p ∑∑±+=()f p p f p ≤+≤2''2.1min max max '及基础梁边处翼板每米宽弯矩基础梁边处翼板每米宽剪力若∑M'=0时,则上述M,V 表达式为若∑M=0时,则上述M,V 表达式为但p'j1和p'j2公式中的p'jmax 和p'jmin 可简化为若∑M=0和∑M'=0时,则上述M,V 表达式为基础梁边处翼板有效高度基础梁边处翼板截面配筋 式中, f c —混凝土轴心抗压强度设计值.f y —钢筋抗拉强度设计值.其余符号同前述4. 抗扭当上述∑M'≠0时,对于带有翼板的基础梁,一般可以不考虑抗扭计算,仅从构造上将梁的箍筋做成闭合式;反之,则应进行抗扭承载力计算.四、静力平衡法和倒梁法的应用在采用净力平衡法和倒梁法分析基础梁内力时,应注意以下六个问题:第一,由于基础自重和其上覆土重将与它产生的地基反力直接抵消,不会引起基础梁1max 22112''2'3''j j j j j p p b p p M p -=⎪⎪⎭⎫ ⎝⎛+=112'2'b p p V j j ⎪⎪⎭⎫ ⎝⎛+=()()1min max max 21min max ,21b p p L S p V b p p L S p M j j j j j jnax ⎥⎦⎤⎢⎣⎡--=⎥⎦⎤⎢⎣⎡--=1122112'2',2'3'b p P V b p p M j j j j ⎪⎪⎭⎫ ⎝⎛+=⎪⎪⎭⎫ ⎝⎛+=2max min '6'bL M bL F i j j p ∑∑±=b p V b p M j j ==,2121bLF i j p ∑=()mm f V c h ⨯⨯≥100007.001()2019.0mm f h M y s A =内力,故基础梁的内力分析用的是地基净反力.第二,对a1和a2悬臂段的截面弯矩可按以下两种方法处理: 1.考虑悬臂段的弯矩对各连续跨的影响,然后两者叠加得最后弯矩; 2.倒梁法中可将悬臂段在地基净反力作用下的弯矩,全由悬臂段承受,不传给其它跨.第三,两种简化方法与实际均有出入,有时出入很大,并且这两种方法同时计算的结果也不相同.建议对于介于中等刚度之间且对基础不均匀沉降的反应很灵敏的结构,应根据具体情况采用一种方法计算同时,采用另一种方法复核比较,并在配筋时作适当调整.第四,由于建筑物实际多半发生盆形沉降,导至柱荷载和地基反力重新分布.研究表明:端柱和端部地基反力均会加大.为此,宜在边跨增加受力纵筋面积,并上下均匀配置.第五,为增大底面积及调整其形心位置使基底反力分布合理,基础的端部应向外伸出,即应有悬臂段.第六,一般计算基础梁时可不考虑翼板作用.(一)静力平衡法静力平衡法是假定地基反力按直线分布不考虑上部结构刚度的影响根据基础上所有的作用力按静定梁计算基础梁内力的简化计算方法1. 静力平衡法具体步骤:❶先确定基础梁纵向每米长度上地基净反力设计值,其最大值为p jmax*b,最小值为p jmin*b,若地基净反力为均布则为p j*b,如图中虚线所示:❷对基础梁从左至右取分离体,列出分离体上竖向力平衡方程和弯矩平衡方程,求解梁纵向任意截面处的弯矩M S和剪力V S,一般设计只求出梁各跨最大弯矩和各支座弯矩及剪力即可.2.地基压缩性和基础荷载分布都比较均匀,基础高度大于柱距的1/6或平均柱距满足l,≤1.75/λ,且上部结构为柔性结构时的柱下条形基础和联合基础,用此法计算比较接近实际.上式中:l m —基础梁上的平均柱距其中: k s —基床系数,可按k s = p 0/S 0计算(p 0为基础底面平均附加压力标准值,S 0为以p 0计算的基础平均沉降量),也可参照各地区性规范按土类名称及其状态已给出的经验值. b 0,I L —基础梁的宽度和截面惯性矩.E c —混凝土的弹性模量.3. 对静力平衡法的一些看法(仅供参考评议):(1)由于静力平衡法不考虑基础与上部结构的相互作用,因而在荷载和直线分布的基底反力作用下可能产生整体弯曲.与其它方法比较,这样计算所得的基础梁不利截面的弯矩绝对值一般还是偏大.(2)上述适用条件中要求上部结构为柔性结构.如何判断上部结构为柔性结构,从绝大多数建筑的实际刚度来看均介于绝对刚性和完全柔性之间,目前还难以定量计算.在实践中往往只能定性地判断其比较接近哪一种极端情况,例如,剪力墙体系的高层建筑是接近绝对刚性的,而以屋架--柱--基础为承重体系的排架结构和木结构以及一般静定结构,是接近完全柔性的.具体应用上,对于中等刚度偏下的建筑物也可视为柔性结构,如中、低层轻钢结构;柱距偏大而柱断面不大且楼板开洞又较多的中、低层框架结构以及体型简单,长高比偏大(一般大于5以上)的结构等等.(二) 倒梁法倒梁法是假定上部结构完全刚性,各柱间无沉降差异,将柱下条形基础视为以柱脚作为固定支座的倒置连续梁,以线性分布的基础净反力作为荷载,按多跨连续梁计算法求解内力的计算方法.1. 倒梁法具体步骤:(1) 先用弯矩分配法或弯矩系数法计算出梁各跨的初始弯矩和剪力.弯矩系数法比弯矩分配法简便,但它只适用于梁各跨度相等且其上作用均布荷载的情况,它的计算内力表达式为:M=弯矩系数 * p j * b * l ;V=剪力系数 * p j * b * l 。
柱下条形基础内力计算(zhang)

一、柱下条形基础的计算1. 倒梁法倒梁法假定上部结构是刚性的,柱子之间不存在差异沉降,柱脚可以作为基础的不动铰支座,因而可以用倒连续梁的方法分析基础内力。
这种假定在地基和荷载都比较均匀、上部结构刚度较大时才能成立。
此外,要求梁截面高度大于1/6柱距,以符合地基反力呈直线分布的刚度要求。
倒梁法的内力计算步骤如下:(1).按柱的平面布置和构造要求确定条形基础长度L ,根据地基承载力特征值确定基础底面积A ,以及基础宽度B=A/L 和截面抵抗矩6/2BL W =。
(2).按直线分布假设计算基底净反力n p :minmaxn n p p W M A F ii ∑±∑=(4-12)式中 ∑i F 、∑i M −相应于荷载效应标准组合时,上部结构作用在条形基础上的竖向力(不包括基础和回填土的重力)总和,以及对条形基础形心的力矩值总和。
当为轴心荷载时,nn n p p p ==min max 。
(3).确定柱下条形基础的计算简图如图4-13,系为将柱脚作为不动铰支座的倒连续梁。
基底净线反力B p n 和除掉柱轴力以外的其它外荷载(柱传下的力矩、柱间分布荷载等)是作用在梁上的荷载。
(4).进行连续梁分析,可用弯矩分配法、连续梁系数表等方法。
(5).按求得的内力进行梁截面设计。
(6).翼板的内力和截面设计与扩展式基础相同。
倒连续梁分析得到的支座反力与柱轴力一般并不相等,这可以理解为上部结构的刚度对基础整体挠曲的抑制和调整作用使柱荷载的分布均匀化,也反映了倒梁法计算得到的支座反力与基底压力不平衡的缺点。
为此提出了“基底反力局部调整法”,即将不平衡力(柱轴力与支座反力的差值)均匀分布在支座附近的局部范围(一般取1/3的柱跨)上再进行连续梁分析,将结果叠加到原先的分析结果上,如此逐次调整直到不平衡力基本消除,从而得到梁的最终内力分布。
由图4-14,连续梁共有n 个支座,第i 支座的柱轴力为i F ,支座反力为i R ,左右柱跨分别为1-i l 和i l ,则调整分析的连续梁局部分布荷载强度i q 为:边支座)1(n i i ==或 3/)(1)1(0)(1)(1)(1n n n n n l l R F q +-=+ (4-13a )中间支座)1(n i <<i i i i i l l R F q +-=-1)(3 (4-13b ) 当i q 为负值时,表明该局部分布荷载应是拉荷载,例如图4-14中的2q 和3q 。
柱下条形基础课程设计指导书2016

柱下条形基础课程设计指导书一、设计计算步骤:(一)确定柱下条形基础底面尺寸,并验算持力力层和软弱下卧层的承载力⒈ 绘出条形基础梁的计算简图,包括荷载、尺寸等,如图。
F AX CM ⒉ 求荷载合力重心位置。
设合力作用点与边柱A的距离为xc ,据合力矩定理,以A点为参考点,则有: ∑Fik xi + ∑Mikxc = ────────── ∑Fik⒊ 确定基础梁的长度和外伸尺寸。
设基础梁两端外伸的长度为a1、a2,两边柱之间的轴线距离为a。
为使其合力作用点与基底形心相重合或接近,基础梁两端可有适当的长度伸出边柱外。
但伸出长度也不宜太大,一般宜取第一跨距的0.25倍。
当xc 确定后,可按合力作用点与基底形心相重合的原则,定出基础梁的长度L。
若巳选定a1,则有:L = 2(xc + a1 ), a2 = L-a -a1 ⒋ 按地基持力层的承载力确定基础梁的宽度b。
初定基础的埋置深度d,若d>0.5m ,应对持力层承载力进行深度修正,即: f a '= f ak +ηd ·γm (d- 0.5 )。
则有:∑Fikb≥ ───────── L(f a '- 20d)若b>3m时,还应进行地基承载力的宽度修正后,再代入上式确定基础宽度。
若b≤3m时,则持力层的地基承载力设计值f a =f a '。
⒌ 当地基有软弱下卧层时,还应进行软弱下卧层的强度验算。
作用于软弱下卧层顶部的附加应力与自重应力之和不超过软弱下卧层顶面处经深度修正后的地基承载力特征值,即:pcz + pz ≤f az其中: pcz = ∑γi hib(pk -pc )pz = ──────── b + 2ztan θf az =f ak + ηd γm (d+z -0.5 )⒍ 考虑Mmax 时的荷载组合,验算持力层的地基承载力(梁长方向)。
初设基础高度H0,验算:pkmax =( ∑Fik + Gk )/bL+ 6∑Mk /bL2 ≤ 1.2f apkmin =( ∑Fik + Gk )/bL- 6∑Mk /bL2 > 0式中:∑Fik ─── 相应于荷载效应标准组合时,上部结构传至基顶的竖向力值之和(kN ); Gk ─── 基础及其台阶上土的重量(kN );∑Mk = ∑Mik + ∑Vk ·H0 +∑F ik i x;∑Mik ───相应于荷载效应标准组合时,上部结构传至基础顶面的力矩(kN ·m ); ∑Vik ───相应于荷载效应标准组合时,上部结构传至基础顶面的剪力(kN );的1/6;f a ─── 持力层经深宽修正后的地基承载力特征值;i x─── 各柱轴力至基底形心的距离。
柱下条形基础设计

-1164582 -582-566 –1471 1471 566735.51 -735.5-228 -507.5 507.5 228 253.8 253.8A 截面左边的剪力为:Va l =bP j L 0=638×1.1=701.8KN取OB 段作脱离体,计算A 截面的支座反力。
R A =1/L 1(1/2bP j (L 0+ L 1)²-M B )=1/5.4×(1/2×638×6.5²-1259.3)=2262.8KN A 截面右边的剪力为:Va r =bP j L 0- R A =638×1.1-2262.8=-1561KNξ=0.01A s =ξα1fcbf´h=0.01×1.0×16.7×2560×1465/360=1740mm2实配钢筋7Ф28(4310 mm2)P=4310/(1000×1465)=0.29%>0.25%,满足要求。
因BC跨为下部受拉,故上部仅需按构造配筋,取3Ф28,As=1847 mm2P=1847/(1000×1465)=0.13支座下部截面配筋按双筋矩形截面计算,比较M=800 KN·m,这时As′=1847mm2则:αs =M/(αsfcbf´h)=-0.004说明As′富裕,且达不到屈服,可近似取:A s =M/fy(h-αs′)=2454.8 mm2故取5Ф28(3079 mm2)按照构造钢筋要求,尚应有1/2~1/3的支座钢筋贯通全跨,故通常钢筋可取3Ф28(2)基础梁斜截面受剪承载力计算AB跨与BC跨间的最大剪力相同,故取γRE V =1601.57 KN<0.25βcfcbh 0=6116.38KN故截面尺寸满足要求。
梁端加密区箍筋取6肢Ф10@130,箍筋用HPB235钢筋(fyv=210N/mm2),则0.7 fc bh+1.25 fyvAsv/s h=2213.8KN>1601.57KN加密区长度取0.85m,非加密区取6肢Ф10@400,因BC非加密区长度较小,故全跨均可按加密区配置,箍筋设置满足要求。
10-4 柱下条形基础设计步骤

柱下条形基础的柱荷载分布如图所示,其合力作用点距N 1的距离为:选定左侧外伸长度a 1,并设最外侧两柱之间的距离为a ,则总长度L 和从右侧外伸长度a 2分别为如此处理后,则荷载重心与基础形心重合,计算简图也相应调整。
∑∑∑+=i
i i i N M x N x 121 , )(2a a L a a x L --=+=三、柱下条形基础的设计计算步骤
(1) 求荷载合力重心位置(2) 确定基础梁的长度和悬臂尺寸
(4) 按墙下条形基础设计方法确定翼板厚度及横向钢筋的配筋。
(5) 基础梁的纵向内力计算。
(6) 根据纵向内力计算结果,按受弯构件进行基础梁纵向
截面高度验算与配筋计算,同时应满足设计构造要求。
(3) 按地基承载力要求计算所需的条形基础底面积A ,进而确定底板宽度b 。
柱下条型基础设计程序

单位
N/mm m 2 N/mm N/mm2 kN kN kN kN m m m m m N/mm2 2 N/mm kN kN.m m2 m m kN m kpa kpa kpa kpa kN m kN.m mm mm
3 2
JC1
175.0 2.0 16.5 310 868.1 21.5 917.4 6.6 5.10 1.15 1.15 0.4 0.4 192.5 152.5 1785.5 28.1 12.9 7.4 1.7 515.16 3.74 186.2 满足要求 171.1 满足要求 138.64 0.67 31.14 600 555 0.006 0.006 182 Φ 10-180 500 900 855 241.28 159.55 159.55 159.55 624.93 0.026 0.027 610.14 0.104本 几 何 信 息
地 基 承 载 力 2 验 W=L*B /6 算 fmax=(F+G)/A+M/W
fmax<1.2fd fmin=(F+G)/A-M/W fmin<fd P净=(F+G)/A-ro*d L1=(B-bc)/2
基 M=P净*L12/2 基础底板厚度h 础 ho=h-45 底 板 α s=M/(fcm*b*ho2) 计 ξ =1-SQRT(1-2*α s) 算 As=ξ *b*ho*fcm/fy
mm2 mm2 mm2 mm mm mm kN/m kN.m kN.m kN.m kN.m
mm2
mm2 mm2 mm2
单跨条型基础计算表
算简图
单跨条型基础计算表
计算
fk 埋深d fcm fy F1 M1(绕X轴方向) F2 M2(绕Y轴方向) 柱距Lo 肋梁悬挑长度b1 肋梁悬挑长度b2 柱沿基础短边向宽bc 柱沿基础短边向宽hc fd=1.1fk f净=fd-ro*d F=F1+F2 M=M1+M2 A=1.1*F/f净 基础总长L 基础宽度B G=ro*d*A
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
柱下条形基础简化计算及其设计步骤论文上传:yujie2001_0论文作者:摘抄您是本文第1770位读者摘要:本文对常用的静力平衡法和倒梁法的近似计算及其各自的适用范围和相互关系作了一些叙述,提出了自己的一些看法和具体步骤,并附有柱下条基构造表,目的是使基础设计工作条理清楚,方法得当,既简化好用,又比较经济合理.关键词:柱下条形基础简化计算设计步骤一.适用范围:柱下条形基础通常在下列情况下采用:1.多层与高层房屋无地下室或有地下室但无防水要求,当上部结构传下的荷载较大,地基的承载力较低,采用各种形式的单独基础不能满足设计要求时.2.当采用单独基础所需底面积由于邻近建筑物或构筑物基础的限制而无法扩展时.3.地基土质变化较大或局部有不均匀的软弱地基,需作地基处理时.4.各柱荷载差异过大,采用单独基础会引起基础之间较大的相对沉降差异时.5.需要增加基础的刚度以减少地基变形,防止过大的不均匀沉降量时.其简化计算有静力平衡法和倒梁法两种,它们是一种不考虑地基与上部结构变形协调条件的实用简化法,也即当柱荷载比较均匀,柱距相差不大,基础与地基相对刚度较大,以致可忽略柱下不均匀沉降时,假定基底反力按线性分布,仅进行满足静力平衡条件下梁的计算.二.计算图式1.上部结构荷载和基础剖面图2.静力平衡法计算图式3.倒梁法计算图式三.设计前的准备工作在采用上述两种方法计算基础梁之前,需要做好如下工作:1.确定合理的基础长度为使计算方便,并使各柱下弯矩和跨中弯矩趋于平衡,以利于节约配筋,一般将偏心地基净反力(即梯形分布净反力)化成均布,需要求得一个合理的基础长度.当然也可直接根据梯形分布的净反力和任意定的基础长度计算基础.基础的纵向地基净反力为:式中Pjmax,Pjmin—基础纵向边缘处最大和最小净反力设计值.∑Fi—作用于基础上各竖向荷载合力设计值(不包括基础自重和其上覆土重,但包括其它局部均布qi).∑M—作用于基础上各竖向荷载(Fi ,qi),纵向弯矩(Mi)对基础底板纵向中点产生的总弯矩设计值.L—基础长度,如上述.B—基础底板宽度.先假定,后按第2条文验算.当Pjmax与Pjmin相差不大于10%,可近似地取其平均值作为均布地基反力,直接定出基础悬臂长度a1=a2(按构造要求为第一跨距的1/4~1/3),很方便就确定了合理的基础长度L;如果Pjmax与Pjmin相差较大时,常通过调整一端悬臂长度a1或a2,使合力∑Fi的重心恰为基础的形心(工程中允许两者误差不大于基础长度的3%),从而使∑M为零,反力从梯形分布变为均布,求a1和a2的过程如下:先求合力的作用点距左起第一柱的距离:式中,∑Mi—作用于基础上各纵向弯矩设计值之和.xi—各竖向荷载Fi距F1的距离.当x≥a/2时,基础长度L=2(X+a1), a2=L-a-a1.当x<a/2时,基础长度L=2(a-X+a2), a1=L-a-a2.按上述确定a1和a2后,使偏心地基净反力变为均布地基净反力,其值为:式中, pj—均布地基净反力设计值.由此也可得到一个合理的基础长度L.2.确定基础底板宽度b.由确定的基础长度L和假定的底板宽度b,根据地基承载力设计值f,一般可按两个方向分别进行如下验算,从而确定基础底板宽度b.基础底板纵向边缘地基反力:应满足基础底板横向边缘地基反力:应满足式中, pmax, pmin—基础底板纵向边缘处最大和最小地基反力设计值p'max, p'min—基础底板横向边缘处最大和最小地基反力设计值G—基础自重设计值和其上覆土重标准值之和,可近似取G=20bLD,D为基础埋深,但在地下水位以下部分应扣去浮力.∑M'—作用于基础上各竖向荷载、横向弯矩对基础底板横向中点产生的总弯矩设计值.其余符号同前述当∑M'=0时,则只须验算基础底板纵向边缘地基反力当∑M=0时,则只须验算基础底板横向边缘地基反力.当∑M=0且∑M'=0时(即地基反力为均布时),则按下式验算,很快就可确定基础底板宽度b:式中, p—均布地基反力设计值.3.求基础梁处翼板高度并计算其配筋先计算基础底板横向边缘最大地基净反力pmax和最小地基净反力pmin,求出基础梁边处翼板的地基净反力pj1,如图,再计算基础梁边处翼板的截面弯矩和剪力,确定其厚度h1和抗弯钢筋面积.图中, p—翼板悬挑长度, b1 =(b- b0)/2h1—基础梁边翼板高度b0,h—基础梁宽和梁高基础底板横向边缘处地基净反力式中, S—从基础纵向边缘最大地基反力处开始到任一截面的距离.其余符号同前述基础梁边处翼板地基净反力基础梁边处翼板每米宽弯矩基础梁边处翼板每米宽剪力若∑M'=0时,则上述M,V表达式为若∑M=0时,则上述M,V表达式为但p'j1和p'j2公式中的p'jmax和p'jmin可简化为若∑M=0和∑M'=0时,则上述M,V表达式为基础梁边处翼板有效高度基础梁边处翼板截面配筋式中, fc—混凝土轴心抗压强度设计值.fy—钢筋抗拉强度设计值.其余符号同前述4.抗扭当上述∑M'≠0时,对于带有翼板的基础梁,一般可以不考虑抗扭计算,仅从构造上将梁的箍筋做成闭合式;反之,则应进行抗扭承载力计算.四.静力平衡法和倒梁法的应用在采用净力平衡法和倒梁法分析基础梁内力时,应注意以下六个问题: 第一,由于基础自重和其上覆土重将与它产生的地基反力直接抵消,不会引起基础梁内力,故基础梁的内力分析用的是地基净反力.第二,对a1和a2悬臂段的截面弯矩可按以下两种方法处理: 1.考虑悬臂段的弯矩对各连续跨的影响,然后两者叠加得最后弯矩; 2.倒梁法中可将悬臂段在地基净反力作用下的弯矩,全由悬臂段承受,不传给其它跨.第三,两种简化方法与实际均有出入,有时出入很大,并且这两种方法同时计算的结果也不相同.建议对于介于中等刚度之间且对基础不均匀沉降的反应很灵敏的结构,应根据具体情况采用一种方法计算同时,采用另一种方法复核比较,并在配筋时作适当调整.第四,由于建筑物实际多半发生盆形沉降,导至柱荷载和地基反力重新分布.研究表明:端柱和端部地基反力均会加大.为此,宜在边跨增加受力纵筋面积,并上下均匀配置.第五,为增大底面积及调整其形心位置使基底反力分布合理,基础的端部应向外伸出,即应有悬臂段.第六,一般计算基础梁时可不考虑翼板作用.(一)静力平衡法静力平衡法是假定地基反力按直线分布不考虑上部结构刚度的影响根据基础上所有的作用力按静定梁计算基础梁内力的简化计算方法1.静力平衡法具体步骤:先确定基础梁纵向每米长度上地基净反力设计值,其最大值为pjmax*b,最小值为pjmin*b,若地基净反力为均布则为pj*b,如图中虚线所示:对基础梁从左至右取分离体,列出分离体上竖向力平衡方程和弯矩平衡方程,求解梁纵向任意截面处的弯矩MS和剪力VS,一般设计只求出梁各跨最大弯矩和各支座弯矩及剪力即可.2.静力平衡法适用条件:地基压缩性和基础荷载分布都比较均匀,基础高度大于柱距的1/6或平均柱距满足l,£1.75/l,且上部结构为柔性结构时的柱下条形基础和联合基础,用此法计算比较接近实际.上式中lm—基础梁上的平均柱距其中ks—基床系数,可按ks= p0/S0计算(p0为基础底面平均附加压力标准值,S0为以p0计算的基础平均沉降量),也可参照各地区性规范按土类名称及其状态已给出的经验值.b0,IL—基础梁的宽度和截面惯性矩.Ec—混凝土的弹性模量.3.对静力平衡法的一些看法(仅供参考评议):由于静力平衡法不考虑基础与上部结构的相互作用,因而在荷载和直线分布的基底反力作用下可能产生整体弯曲.与其它方法比较,这样计算所得的基础梁不利截面的弯矩绝对值一般还是偏大.上述适用条件中要求上部结构为柔性结构.如何判断上部结构为柔性结构,从绝大多数建筑的实际刚度来看均介于绝对刚性和完全柔性之间,目前还难以定量计算.在实践中往往只能定性地判断其比较接近哪一种极端情况,例如,剪力墙体系的高层建筑是接近绝对刚性的,而以屋架--柱--基础为承重体系的排架结构和木结构以及一般静定结构,是接近完全柔性的.具体应用上,对于中等刚度偏下的建筑物也可视为柔性结构,如中、低层轻钢结构;柱距偏大而柱断面不大且楼板开洞又较多的中、低层框架结构以及体型简单,长高比偏大(一般大于5以上)的结构等等.(二)倒梁法倒梁法是假定上部结构完全刚性,各柱间无沉降差异,将柱下条形基础视为以柱脚作为固定支座的倒置连续梁,以线性分布的基础净反力作为荷载,按多跨连续梁计算法求解内力的计算方法.1.倒梁法具体步骤:先用弯矩分配法或弯矩系数法计算出梁各跨的初始弯矩和剪力.弯矩系数法比弯矩分配法简便,但它只适用于梁各跨度相等且其上作用均布荷载的情况,它的计算内力表达式为:M=弯矩系数* pj * b * lª ; V=剪力系数* pj * b * l如前述,pj*b即是基础梁纵向每米长度上地基净反力设计值。
其中弯矩系数和剪力系数按所计算的梁跨数和其上作用的均布荷载形式,直接从建筑结构静力计算手册中查得,l为梁跨长度,其余符号同前述。
调整不平衡力:由于倒梁法中的假设不能满足支座处静力平衡条件,因此应通过逐次调整消除不平衡力.首先,由支座处柱荷载Fi和求得的支座反力Ri计算不平衡力△Ri:△Ri= Fi - Ri ; Ri= V左i –V右i式中△Ri—支座i处不平衡力,V左i ,V右i —支座i处梁截面左,右边剪力.其次,将各支座不平衡力均匀分布在相邻两跨的各1/3跨度范围内,如图C(实际上是调整地基反力使其成阶梯形分布,更趋于实际情况,这样各支座上的不平衡力自然也就得到了消除),△qi按下式计算:对于边跨支座: △qi = △R1 /(a1 +l1/3)对于中间支座: △qi = △Ri / (li-1 /3 + li/3)式中△qi—支座i处不平衡均布力.li-1 ,li —支座i左右跨长度.继续用弯矩分配法或弯矩系数法计算出此情况的弯矩和剪力,并求出其支座反力与原支座反力叠加,得到新的支座反力.重复步骤,直至不平衡力在计算容许精度范围内.一般经过一次调整就基本上能满足所需精度要求了(不平衡力控制在不超过20%).将逐次计算结果叠加即可得到最终弯矩和剪力.a)柱荷载Fi和柱距图:b)计算简图和支座反力Ri:c)调整不平衡力荷载△qi:2.倒梁法适用条件:地基压缩性和基础荷载分布都比较均匀,基础高度大于柱距的1/6或平均柱距满足lm£1.75/l(符号同静力平衡法所述),且上部结构刚度较好时的柱下条形基础,可按倒梁法计算.基础梁的线刚度大于柱子线刚度的3倍,即:式中EC—混凝土弹性模量..IL—基础梁截面惯性矩.H ,IZ—分别为上部结构首层柱子的计算高度和截面惯性矩.同时,各柱的荷载及各柱柱距相差不多时,也可按倒梁法计算.3.对倒梁法的一些看法(仅供参考评议):满足上述适用条件之一的条形基础一般都能迫使地基产生比较均匀的下沉,与假定的地基反力按直线分布基本吻合.由于假定中忽略了各支座的竖向位移差且反力按直线分布,因此在采用该法时,相邻柱荷载差值不应超过20%,柱距也不宜过大,尽量等间距.另外,当基础与地基相对刚度愈小,柱荷载作用点下反力会过于集中成―钟形‖,与假定的线性反力不符;相反,如软弱地基上基础的刚度较大或上部结构刚度大,由于地基塑性变形,反力重分布成―马鞍形‖,趋于均匀,此时用倒梁法计算内力比较接近实际.实际工程中,有一些不需要算得很精很细,有时往往粗略地将第一步用弯矩分配法或弯矩系数法计算出的弯矩和剪力直接作为最终值,不再进行调整不平衡力,这对于中间支座及其中间跨中来说是偏于安全的,而对于边跨及其支座是偏于不安全,从几个等跨梁算例来看,一般情况下,多次调整不平衡力(此项较繁琐),结果使中间支座的内力(指弯矩,剪力)及其跨中弯矩有所减小,边跨支座剪力及其跨中弯矩有所增加,但增减幅度都不大.因此,若不进行调整平衡力,建议根据地区设计经验适当增大边跨纵向抗弯钢筋,其幅度5%左右,这在某些精度范围内一般可以满足设计要求,另外,由于各支座剪力值相差不大(除边支座外),也可取各支座最大剪力值设计抗剪横向钢筋,当然每跨的中间可以放宽.附:基础梁的高跨比选用参考表注:1.选用时应注意梁高不致于过大,同时尚应综合考虑地基与上部结构对基础抗弯刚度的要求.2.反力大时取上限.柱下条形基础构造表注:1.翼板根部厚度及其横向受力钢筋,梁高及其纵向受力钢筋,还须满足计算要求.2.其它要求见图例.参考文献[1] 中华人民共和国国家标准,《建筑地基基础设计规范》(GBJ7-89)中国建筑工业出版社,1989北京[2] 沈杰编《地基基础设计手册》上海科学技术出版社,1988[3] 高大钊主编《岩土工程标准规范实施手册》中国建筑工业出版社,1997[4] 北京市建筑设计研究院编《结构专业技术措施》华北地区建筑设计标准化办公室,1991[5] 中华人民共和国行业标准《机械工厂结构设计规范》(JBJ8-97)北京机械工业出版社,1997。
