2019秋八年级数学上册解题技巧专题勾股定理与面积问题习题课件(新版)华东师大版
合集下载
八年级上华东师大版14.1勾股定理课件

勾股定理的逆定理指出:如果三角形的三边长a、b、c满足a² + b² = c²,那么这 个三角形一定是直角三角形。
逆定理为我们提供了一个判断三角形是否为直角三角形的方法,即验证三边是否 满足勾股定理的关系式。
02
勾股定理证明方法
拼图法证明
将两个直角三角形的斜边作为拼 图的两个边,通过拼接可以形成
05
拓展与延伸:费马大定理简介
费马大定理内容
费马大定理是指一个整数幂不可能被 分解为两个大于1的整数幂的和。
例如,费马猜想了不存在整数a、b和 c,使得a3=b3+c3(这被称为费马最 后定理)。
具体来说,费马猜想了以下三个情形 :对于任何大于2的整数n,不存在三 个大于1的整数a、b和c,使得 an=bn+cn。
例如,对于形如$a^2+b^2>c^2$的不等式,可以通过 构造直角三角形并应用勾股定理来证明或求解该不等式。
辅助角公式推导
勾股定理在三角函数中有重要应用, 特别是在推导辅助角公式时。
利用勾股定理和三角函数的定义,可 以推导出诸如$sin(A+B)$和 $cos(A+B)$等辅助角公式,从而简化 三角函数的计算和证明过程。
02
公式表示为:a² + b² = c²,其中 a和b是直角三角形的两个直角边 ,c是直角三角形的斜边。
勾股数及性质
勾股数是指满足勾股定理的三个正整 数,即a² + b² = c²中的a、b、c为 正整数。
勾股数的性质包括:任意两个勾股数 一定是互质的;一组勾股数中,必有 一个数是偶数等。
勾股定理逆定理
04
勾股定理在代数中的应用
求解代数式最值问题
利用勾股定理,可以将某些代数式转化为直角三角形中的边 长关系,进而利用三角形的性质求解最值问题。
逆定理为我们提供了一个判断三角形是否为直角三角形的方法,即验证三边是否 满足勾股定理的关系式。
02
勾股定理证明方法
拼图法证明
将两个直角三角形的斜边作为拼 图的两个边,通过拼接可以形成
05
拓展与延伸:费马大定理简介
费马大定理内容
费马大定理是指一个整数幂不可能被 分解为两个大于1的整数幂的和。
例如,费马猜想了不存在整数a、b和 c,使得a3=b3+c3(这被称为费马最 后定理)。
具体来说,费马猜想了以下三个情形 :对于任何大于2的整数n,不存在三 个大于1的整数a、b和c,使得 an=bn+cn。
例如,对于形如$a^2+b^2>c^2$的不等式,可以通过 构造直角三角形并应用勾股定理来证明或求解该不等式。
辅助角公式推导
勾股定理在三角函数中有重要应用, 特别是在推导辅助角公式时。
利用勾股定理和三角函数的定义,可 以推导出诸如$sin(A+B)$和 $cos(A+B)$等辅助角公式,从而简化 三角函数的计算和证明过程。
02
公式表示为:a² + b² = c²,其中 a和b是直角三角形的两个直角边 ,c是直角三角形的斜边。
勾股数及性质
勾股数是指满足勾股定理的三个正整 数,即a² + b² = c²中的a、b、c为 正整数。
勾股数的性质包括:任意两个勾股数 一定是互质的;一组勾股数中,必有 一个数是偶数等。
勾股定理逆定理
04
勾股定理在代数中的应用
求解代数式最值问题
利用勾股定理,可以将某些代数式转化为直角三角形中的边 长关系,进而利用三角形的性质求解最值问题。
初中数学华东师大八年级上册勾股定理勾股定理的应用 PPT

你会吗?
例题1、在直角三角形ABC中,∠C = 90° AB = c,BC = a ,AC= b
(1)a=3 ,b=4,求 c (2)a=5, c=13 求 b (3)如果∠A = 90°, a=10, c=16 求 c
例题2、国旗杆的绳子垂到地面时,还多了1m ,拉着绳子下端离开旗杆5m时,绳子被拉直且 下端刚好接触地面,试求旗杆的高.
例题3、有一个水池,水面是一个边长为10尺的正方 形,在水池正中央有一根新生的芦苇,它高出水面1尺. 如果把这根芦苇拉向岸边,它的顶端恰好到达岸边的 水面,请问这个水池的深度和这根芦苇的长度各是多 少?
1尺 水池
5尺
x尺
x2 + 52 = (x+1)2
x = 12
练一练
1、若一个三角形的一个角等于其他两个角的 差,那么这个三角形是____________三角形。
北
乙 甲
东
作业:
课本第十四章第四节 练习 1、2、3题。
再见
2、在△ABC中,∠A: ∠B: ∠C=1:2:3,则 BC:AC:AB=_________。
3、设直角三角形的三条边长为连续自然数, 则这个直角三角形的面积是____,甲往东 走了4km,乙往南走了6km,这时甲、乙两人 相距__________km.
5、想一想:我 怎么走会最近呢
B
C
一?圆柱体的底面周长为20cm, 高AB为4cm,BC是上底面的直 径.一只蚂蚁从点A出发,沿着 圆柱的侧面爬行到点C,试求 出爬行的最短路程. (精确到
0.01cm)
A
D
6、甲、乙两位探险者到沙漠进行探险.某日早晨 8:00 甲先出发,他以6千米/小时的速度向东行走,1小时 后乙出发,他以5千米/小时的速度向北行进,上午 10:00,甲、乙二人相距多远?
八年级数学上册第14章勾股定理本章复习课件新版华东师大版

在 Rt△DEB中,根据勾股定理,得
BE2=BD2-DE222=4 ∴ BE=2
在Rt△ACD和 Rt△AED中,
x
∵CD=DE , AD=AD
∴ Rt△ACD Rt△AED
1
∴ AC=AE
2 A
令AC=x,则AB=x+2
在 Rt△ABC中,根据勾股定理,得 AC2+BC2=AB2
即:x2+42=(x+2)2 ∴ x=3
提示: 先运用勾股定理证明中线AD⊥BC, 再利用等腰三角形的判定方法就可以说明了.
8.已知,如图,在Rt△ABC中,∠C=90°, ∠1=∠2,CD=1.5, BD=2.5, 求AC的长.
提示:作辅助线DE⊥AB,利用平分线的性 质和勾股定理。
C
1 2 A
D B
过D点做DE⊥AB ∵ ∠1=∠2, ∠C=90°
2.已知一个Rt△的两边长分别为3和4,则第三
边长的平方是( D )
A、25 B、14 C、7
D、7或25
3.下列各组数中,以a,b,c为边的三角形不是Rt△
的是( A )
A、,b=2,c=3
B、a=7,b=24,c=25
C、a=6,b=8,c=10
D、a=3,b=4,c=5
4.若线段a,b,c组成Rt△,则它们的比为( C )
那么这个三角形是直角三角形
勾股数
满足a2 +b2=c2的三个正整数,称为勾股数
巩固提升
1、在Rt△ABC中,∠C=90°,
①若a=5,b=12,则c=____1_3______; ②若a=15,c=25,则b=____2_0______; ③若c=61,b=60,则a=___1_1______; ④若a∶b=3∶4,c=10则SRt△ABC=___2_4____。
初中数学华东师大八年级上册勾股定理勾股定理复习PPT

针对训练
4.如图,在矩形纸片ABCD中,AB=12,
BC=5,点E在AB上,将△DAE沿DE折
叠,使点A落在对角线BD上的点A′
10
处,则AE的长为 3
.
课堂小结
勾股定理
勾股定理 及逆定理
勾股数
a2+b2=c2 勾股定理的验证
勾股定理 的应用
图形的面积与周长的计算
利用勾股定理和逆定理解 决实际问题
考点四 本章数学思想和解题方法
方程思想 例4 如图,有一张直角三角形纸片,两直角边AC=6 cm,BC= 8 cm,将△ABC折叠,使B与A重合,折痕是DE,求CD的长. 【解析】 欲求的线段CD在Rt△ACD中,但 此三角形只知一边,可设法找出另两边的关 系,然后用勾股定理求解. 解:由折叠知:DA=DB,△ACD为直角三角形.
课后作业
教材 复习题第4,6,7题
在Rt△ACD中,AC2+CD2=AD2①,
设CD=x cm,则AD=BD=(8-x)cm,
代入①式,得62+x2=(8-x)2,
化简,得36=64-16x,
所以x= =1.75,即CD的长为1.75 cm.
方法总结
勾股定理可以直接解决直角三角形中已知两边求第三边 的问题;如果只知一边和另两边的关系时,也可用勾股定 理求出未知边,这时往往要列出方程求解.
(1)确定最大边; (2)算出最大边的平方与另两边的 平方和 ; (3)比较最大边的平方与另两边的平方和是否相等,若相等 ,则说明这个三角形是直角 三角形.
3.勾股定理的应用 应用勾股定理及其逆定理可解决如下问题: (1)已知直角三角形的任意两边,求第三边长或图形周长、 面积的问题; (2)说明线段的平方关系问题; (3)在 数轴 上作表示 2、3、5 等数的点的问题; (4)解决实际问题.一些实际问题,如解决圆柱侧面两点间 距离问题、航海问题、折叠问题、梯子下滑问题等,常直接 或间接运用勾股定理及其逆定理.
华东师大版八年级数学上册1勾股定理课件

练习
5.如图,将矩形ABCD沿EF折叠,使点D与点B重合,己知AB=3,AD=9,求BE的长。
【答案】BE=5
【解析】设BE=x,则DE=BE=x,AE=AD-DE=9-x.在Rt△ABE中,AB2+AE2=BE2
∴32+(9-x)2=x2,解得x=5.
练习
6.如图,有两棵树,一棵高8米,另一棵高2米,两树相距8米,一只小鸟从
结论
勾股定理:如果直角三角形两直角边分别
为a,b,斜边为c,有
a2 + b 2 = c 2
反过来
逆定理:如果三角形的三边长a、b、c满
足 a2
+
2
b
=
直角三角形。
2
c ,那么这个三角形是
趁热打铁
判断由线段a,b,c组成的三角形是不是直角 三角形?
(1) a=15,b=17,c=8; (2) a=13,b=15,c=14
A.14 cm2
B.13 cm2
C.12 cm2
D.8 cm2
练习
4.如图,在Rt△ABC中,∠C=90°,若a+b=14,c=10,求Rt△ABC的面积.
解:∵∠C=90°,
∴a2+b2=c2=100.
∴(a+b)2-2ab=100.
∴142-2ab=100.
∴ab=48.
∴S△ABC=ab=24.
C
b
图甲
B
SA+SB=SC
3.猜想a、b、c 之间的关系?
a2 +b2 =c2
02
章节
PART
探究与证明
• 合作探究
• 趁热打铁
• 理论证明
合作探究
小组活动:请你利用自己准备的四个全等的直角三角形拼出
华师版数学八年级上册 14.2勾股定理的应用 课件(共19张ppt)

B NhomakorabeaA
新知探究
(1)自己做一个圆柱,尝试从点A到点B沿圆柱侧面画 几条路线,你觉得哪条路线最短?
B
B
B
A 方案①
A 方案②
A 方案③
(2)如图,将圆柱侧面剪开展成一个长方形,点A到
点B的最短路线是什么?你画对了吗?
B
B
A B
A
A
因为两点之间线段最短, 所以方案③的路线最短.
(3)蚂蚁从点A出发,想吃到B点上的食物,它沿圆柱 侧面爬行的最短路程是多少?
第14章 勾股定理
14.2 勾股定理的应用
学习目标
➢ 能解决与勾股定理有关的问题:立体图形中最 短路径问题、网格问题等.
➢ 能将实际问题转化为直角三角形的数学模型, 并能用勾股定理解决简单的实际问题,培养数 学应用意识.
情境引入
如图,有一个圆柱,它的高等于12 cm,底面圆的周长 为18 cm,在圆柱下底面的点A处有一只蚂蚁,它想吃 到上底面上与点A相对的点B处的食物,沿圆柱侧面爬 行的最短路程是多少?
解:设滑道AC的长度为x m,则AB的 长也为x m,AE的长度为(x-1)m.
CD
在Rt△ACE中,∠AEC=90°,
由勾股定理得AE2+CE2=AC2,
即(x-1)2+32=x2,
A
解得x=5.
EB
故滑道AC的长度为5 m.
感谢观看!
例2 如图,在公路AB旁有一危楼 C需要爆破,已知点C与公路上的 停靠站A的距离为300米,与公路 上另一停靠站B的距离为400米, 且CA⊥CB,为了安全起见,爆破点C周围250米范 围内不得进入,问:在进行爆破时,公路AB段是否 因有危险而需要暂时封锁?
新知探究
(1)自己做一个圆柱,尝试从点A到点B沿圆柱侧面画 几条路线,你觉得哪条路线最短?
B
B
B
A 方案①
A 方案②
A 方案③
(2)如图,将圆柱侧面剪开展成一个长方形,点A到
点B的最短路线是什么?你画对了吗?
B
B
A B
A
A
因为两点之间线段最短, 所以方案③的路线最短.
(3)蚂蚁从点A出发,想吃到B点上的食物,它沿圆柱 侧面爬行的最短路程是多少?
第14章 勾股定理
14.2 勾股定理的应用
学习目标
➢ 能解决与勾股定理有关的问题:立体图形中最 短路径问题、网格问题等.
➢ 能将实际问题转化为直角三角形的数学模型, 并能用勾股定理解决简单的实际问题,培养数 学应用意识.
情境引入
如图,有一个圆柱,它的高等于12 cm,底面圆的周长 为18 cm,在圆柱下底面的点A处有一只蚂蚁,它想吃 到上底面上与点A相对的点B处的食物,沿圆柱侧面爬 行的最短路程是多少?
解:设滑道AC的长度为x m,则AB的 长也为x m,AE的长度为(x-1)m.
CD
在Rt△ACE中,∠AEC=90°,
由勾股定理得AE2+CE2=AC2,
即(x-1)2+32=x2,
A
解得x=5.
EB
故滑道AC的长度为5 m.
感谢观看!
例2 如图,在公路AB旁有一危楼 C需要爆破,已知点C与公路上的 停靠站A的距离为300米,与公路 上另一停靠站B的距离为400米, 且CA⊥CB,为了安全起见,爆破点C周围250米范 围内不得进入,问:在进行爆破时,公路AB段是否 因有危险而需要暂时封锁?
1勾股定理(第2课时)教学PPT课件(华师大版)
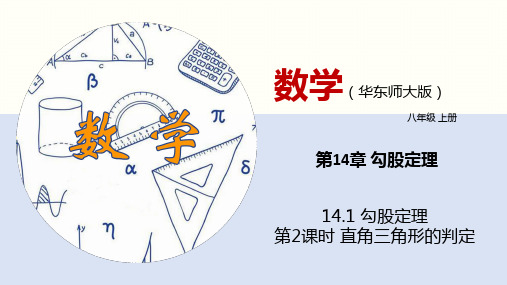
C. a 1, 2a,a 1
D. a 1, 2a,a 1
当堂检测
5.若三角形ABC的三a,b,c满足a2+b2+c2+50=6a+8b+10c. 试判断
△ABC的形状.
解:∵ a2+b2+c2+50=6a+8b+10c ∴ a2-6a+9+b2-8b+16+c2-10c+25=0. 即 (a-3)²+ (b-4)²+ (c-5)²=0. ∴ a=3, b=4, c=5 即 a2+b2+c2.
“直角三角形”为条件,数量关系a2+ b2= c2 数量关系a2+ b2= c2为条件,“直角三角形”
为结论. 是直角三角形的性质.
为结论. 是直角三角形的判定.
联系
都与直角三角形有关,都与三边数量关系a2 + b2 = c2有关
讲授新课
典例精析
【例1】下面以a、b、c为边长的三角形是不是直角三角形?若是,请指
∴△ABC直角三角形.
当堂检测
6.一艘在海上朝正北方向航行的轮船,在航行240海里时方位仪坏了,凭经
验,船长指挥船左传90°,继续航行70海里,则距出发地250海里,你能判
断船转弯后,是否沿正西方向航行?
解:由题意画出相应的图形AB=240海里,BC=70海里,AC=250 海里; 在△ABC中AC2-AB2=2502-2402 =4900=702 =BC2 即AB2+BC2=AC2 ∴△ABC是Rt△ 答:船转弯后,是沿正西方向航行的。
解:因为a2=c2-b2,所以a2+b2=c2,所以这个三角形是直角三角形.
