第6讲 函数的三要素(二)(必修1)第6讲 讲义
高中数学必修1函数讲义--函数的三要素

高一函数讲义一、求函数定义域1、使得x 在实数范围内让解析式可以正常运算的x 的范围。
① 分式的分母不等于0;② 偶次根式被开方式大于等于0;③ 对数式的真数大于0,底数大于0且不等于1;④ 指数为0时,底数不等于0【例1】求下列函数的定义域(1)21x y += (2)lgcos y x (3)y=lg(a x -kb x ) (a,b>0且a,b≠1,k ∈R)[解析](1)依题有1021021032403241x x x x ≠+>⎪⎪+≠⎨⎪->⎪⎪-≠⎩ 4112052log 31x x x x x ≠±⎧⎪⎪>-⎪⎪⇒≠⎨⎪⎪<⎪⎪≠⎩ ∴函数的定义域为415{|0,1,log 31}22x x x -<<≠且 (2)依题意有2250cos 0x x ⎧-≥⎨>⎩ 5522()22x k x k k z ππππ-≤≤⎧⎪⇒⎨-<<+∈⎪⎩∴函数的定义域为33[5,)(,)(,5]2222ππππ--⋃-⋃ (3)要使函数有意义,则a x -kb x >0,即xa kb ⎛⎫> ⎪⎝⎭①当k≤0时,定义域为R②当k>0时,(Ⅰ)若a>b>0,则log a b x k > 定义域为{x|log a b x k >}(Ⅱ)若0<a<b ,则log a b x k <, 定义域为{x|log a bx k <}(Ⅲ)若a=b>0,则当0<k<1时定义域为R ;当k≥1时,定义域为空集[评析]把求定义域的问题等价转化为关于x 的不等式(组)的求解问题,其关键是列全限制条件(组)。
2、抽象函数的定义域:(1)已知)(x f 的定义域,求))((x g f 的定义域。
例:已知)(x f 定义域为[0,1],求函数)32(-=xf y 的定义域 (2)已知))((xg f 的定义域,求)(x f 的定义域。
高考数学专题讲座 第6讲 三角函数的图象与性质

π 高考数学专题讲座 第6讲 三角函数的图象与性质一、考纲要求1.理解任意角的概念、弧度的意义,能正确地进行弧度与角度的换算.2.掌握任意角的正弦、余弦、正切的定义,了解余切、正割、余割的定义,掌握同角三角函数的基本关系式,掌握正弦、余弦的诱导公式,理解周期函数与最小正周期的意义.3.了解正弦函数、余弦函数、正切函数的图象和性质,会用“五点法”画正弦函数、余弦函数和函数)sin(ϕω+=x A y )的简图,理解A 、ω、ϕ的物理意义. 二、基础过关1.函数||sin x x y +=,],[ππ-∈x 的大致图象是( ).y y y yπ π π -πo π x -π o π x -π o π x -π o π x-π -π -πA B C D2.(2002北京)已知)(x f 是定义在)3,3(-上的奇函数,当30<<x 时,)(x f 的图象如图所示,那么不等式0cos )(<x x f 的解集是( ).A . )3,2()1,0(2,3(ππ --B . )3,2()1,0()1,2(ππ --C . )3,1()1,0()1,3( -- 0 1 2 3 xD .)3,1()1,0(2,3( π--3.定义在R 上的函数)(x f 既是偶函数又是周期函数,若)(x f 的最小正周期是π,且当]2,0[π∈x 时,x x f sin )(=,则)35(πf 的值为( ). A .21-B .21 C .23-D .23 4.给定性质: ①最小正周期为π;②图象关于直线x=3π对称,则下列四个函数中,同时具有性质①、②的是( ).A .y = sin(2x +6π) B .y = sin(2x+6π) C .y = sin|x| D .y = sin(2x -6π)5.下列四个结论中正确的个数有 ( ).①y = sin|x|的图象关于原点对称;②y = sin(|x|+2)的图象是把y = sin|x|的图象向左平移2个单位而得;③y = sin(x+2)的图象是把y = sinx 的图象向左平移2个单位而得;④y = sin(|x|+2)的图象是由y = sin(x+2)( x ≥0)的图象及y = -sin(x-2) ( x<0)的图象组成的. A .1个 B .2个 C .3个 D .4个y6.把函数y = cos(x+3π)的图象向左平移m 个单位(m>0), 所得图象关于y 轴对称, 则m 的最小值是 . 7.函数y = 2sin(4π+2x )cos(4π+2x )+asinx (x ∈R)的图象关于x=8π对称, 则g(x)= asin(a+1)x 的最小正周期是 . 三、典型例题例1 已知函数f(x)=tan(3πsinx). (1)求f(x)的定义域和值域;(2)在(-π,π)中,求f(x)的单调区间; (3)判定方程f(x)=tan 32π在区间(-π,π)上解的个数.例2 已知函数()b a x x a x a x f++--=2cos sin 322cos 的定义域为⎥⎦⎤⎢⎣⎡20π,,值域为 [ -5,1 ],求常数a 、b 的值.例3 已知函数3cos 33cos 3sin )(2x x x x f +=. (1)将)(x f 写成)sin(φω+x A 的形式,并求其图象对称中心的横坐标; (2)函数的图象可由)(sin R x x y ∈=的图象经过怎样的变换得到?(3)如果△ABC 的三边a 、b 、c 满足b 2=ac ,且边b 所对的角为x ,试求x 的范围及此时函数f(x)的值域.例4 设二次函数),()(2R c b c bx x x f ∈++=,已知不论βα,为何实数恒有)(sin αf ≥0,)cos 2(β+f ≤0.(1)求证:1-=+c b ; (2)求证:c ≥3;(3)若函数)(sin αf 的最大值为8,求b ,c 的值.四、 热身演练1.在)2,0(π内,使x x cos sin >成立的x 取值范围为( ).A .)45,()2,4(ππππ B .),4(ππ C .)45,4(ππ D .)23,45(),4(ππππ2.已知sin α>sin β,那么下列命题成立的是( ).A .若α、β是第一象限角,则cos α>cos βB .若α、β是第二象限,则tan α>tan βC .若α、β是第三象限角,则cos α>cos βD .若α、β是第四象限角,则tan α>tan β 3.下列命题中正确的是( ).A .x y tan =是增函数B .x y sin =在第一象限是增函数C .x y arccos 2-=π是奇函数 D .x y sin =的反函数是x y arcsin =4.要得到函数⎪⎭⎫ ⎝⎛-=42cos 3πx y 的图象,可以将函数x y 2sin 3=的图象( ).A .沿x 轴向左平移8π单位 B .沿x 轴向右平移8π单位 C .沿x 轴向左平移4π单位 D .沿x 轴向右平移4π单位5.若2sin 2α+sin 2β-2sin α=0则cos 2α+cos 2β的取值范围是( ).A .[1,5]B .[1,2]C .[1,49] D .[-1,2]6.在∆ABC 中,已知A 、B 、C 成等差数列,求 2tan 2tan 32tan 2tan CA C A ⋅++的值 为 .7.设直角三角形ABC 的内切圆半径与外接圆半径分别为r 的R ,则Rr的最大值为 .8.设函数)sin()(ϕω+=x x f ,(0>ω,22πϕπ<<-)给出下列四个论断:(1)它的周期为π; (2)它的图象关于直线x =12π对称;(3)它的图象关于点(3π,0)对称; (4)在区间(-6π,0)上是增函数.以其中两个论断为条件,另两个论断为结论,写出你认为正确的一个命题: . 9.(1)已知sin(4π+α)·sin(4π-α)=61, α∈(2π,π),求sin4α;(2)已知 cos(x+4π)=53,45π<x<47π,求x x x tan 1sin 22sin 2-+的值.10.如下图,某地一天从6时到14时的温度变化曲线近似满足函数y=A sin(ωx+φ)+b.(1)求这段时间的最大温差;(2)写出这段曲线的函数解析式.11.已知函数f(x)是定义域为一切实数且图象关于x=3对称的奇函数,f(1)=1且 523sin cos =-x x . 求证:(1)函数)(x f 是周期函数;(2)求])4cos(2sin 15[π+x xf 的值.12.已知⊙O 的半径为2,在它的内接三角形ABC 中,有()()B b a C A sin sin sin 2222-=-成立,求△ABC面积S 的最大值.π 三角函数的图象与性质一、考纲要求1.理解任意角的概念、弧度的意义,能正确地进行弧度与角度的换算.2.掌握任意角的正弦、余弦、正切的定义,了解余切、正割、余割的定义,掌握同角三角函数的基本关系式,掌握正弦、余弦的诱导公式,理解周期函数与最小正周期的意义.3.了解正弦函数、余弦函数、正切函数的图象和性质,会用“五点法”画正弦函数、余弦函数和函数)sin(ϕω+=x A y )的简图,理解A 、ω、ϕ的物理意义. 二、基础过关1.函数||sin x x y +=,],[ππ-∈x 的大致图象是( C ).y y y yπ π π -πo π x -π o π x -π o π x -π o π x-π -π -πA B C D2.(2002北京)已知)(x f 是定义在)3,3(-上的奇函数,当30<<x 时,)(x f 的图象如图所示,那么不等式0cos )(<x x f 的解集是( B ).A . )3,2()1,0(2,3(ππ --B . )3,2()1,0()1,2(ππ --C . )3,1()1,0()1,3( -- 0 1 2 3 xD .)3,1()1,0(2,3( π--3.定义在R 上的函数)(x f 既是偶函数又是周期函数,若)(x f 的最小正周期是π,且当]2,0[π∈x 时,x x f sin )(=,则)35(πf 的值为( D ). A .21-B .21 C .23-D .23 4.给定性质: ①最小正周期为π;②图象关于直线x=3π对称,则下列四个函数中,同时具有性质①、②的是( D ).A .y = sin(2x +6π) B .y = sin(2x+6π) C .y = sin|x| D .y = sin(2x -6π)5.下列四个结论中正确的个数有( B ).①y = sin|x|的图象关于原点对称;②y = sin(|x|+2)的图象是把y = sin|x|的图象向左平移2个单位而得;③y = sin(x+2)的图象是把y = sinx 的图象向左平移2个单位而得;④y = sin(|x|+2)的图象是由y = sin(x+2)( x ≥0)的图象及y = -sin(x-2) ( x<0)的图象组成的. A .1个 B .2个 C .3个 D .4个y6.把函数y = cos(x+3π)的图象向左平移m 个单位(m>0), 所得图象关于y 轴对称, 则m 的 最小值是 .32π 7.函数y = 2sin(4π+2x )cos(4π+2x )+asinx (x ∈R)的图象关于x=8π对称, 则g(x)= asin(a+1)x 的最小正周期是 .π2三、典型例题: 例1 已知函数f(x)=tan(3πsinx). (1)求f(x)的定义域和值域;(2)在(-π,π)中,求f(x)的单调区间; (3)判定方程f(x)=tan32π在区间(-π,π)上解的个数. 解:(1)∵-1≤sinx ≤1 ∴ -3π≤3πsinx ≤3π. 又函数y=tanx 在x=k π+2π(k ∈Z)处无定义,且(-2π,2π)[-3π,3π](-π, π),∴令3πsinx=±2π,则sinx=±23解之得:x=k π±3π(k ∈Z)∴f(x)的定义域是A={x|x ∈R ,且x ≠k π±3π,k ∈Z}∵tanx 在(-2π,2π)内的值域为(-∞,+∞),而当x ∈A 时,函数y=13πsinx 的值域B 满足(-2π,2π) B∴f(x)的值域是(-∞,+∞).(2)由f(x)的定义域知,f(x)在[0,π]中的x=3π和x=32π处无定义.设t=3πsinx ,则当x ∈[0, 3π)∪(3π,32π)∪(32π,π)时,t ∈[0, 2π)∪(2π,3π],且以t 为自变量的函数y=tant 在区间(0,2π),(2π,3π]上分别单调递增.又∵当x ∈[0,3π]时,函数t=3πsinx 单调递增,且t ∈[0, 2π),当x ∈(3π,2π]时,函数t=3πsinx 单调递增,且t ∈(2π, 3π]当x ∈[2π,32π)时,函数t=3πsinx 单调递减,且t ∈(2π, 3π]当x ∈(32π,π)时,函数t=3πsinx 单调递减,且t ∈(0,2π) ∴f(x)=tan(13πsinx)在区间[0,3π),(3π,2π]上分别是单调递增函数;在),32(),32,2[ππππ上是单调递减函数.又f(x)是奇函数,所以区间(-3π,0],[-2π,-3π)也是f(x)的单调递增区间]2,32(),32,[ππππ----是f(x)的递减区间. 故在区间(-π,π)中,f(x)的单调递增区间为:[-2π,-3π),(-3π,3π),(3π,2π]单调递减区间为),32(),32,32(),32,[ππππππ---. (3)由f(x)=tan 32π得:tan(3πsinx)=tan(32π)⇔3πsinx=k π+32π (k ∈Z )⇔sinx=k 3+36(k ∈Z)① 又∵-1≤sinx ≤1,∴323323-≤≤--k ∴k=0或k= -1当k=0时,从①得方程sinx=36 当k=1时,从①得方程sinx= -3+36 显然方程sinx=36,sinx= -3+36,在(-π, π)上各有2个解,故f(x)=tan 32π在区间(-π,π)上共有4个解.例2 已知函数()b a x x a x a x f++--=2cos sin 322cos 的定义域为⎥⎦⎤⎢⎣⎡20π,,值域为 [ -5,1 ],求常数a 、b 的值.解:∵ ()b a x a x a x f ++--=22sin 32cos ,b a x a ++⎪⎭⎫ ⎝⎛--=232cos 2π .∵ 20π≤≤x ,∴ 32323πππ≤-≤-x ,∴ 1 32cos 21≤⎪⎭⎫ ⎝⎛-≤-πx .当a > 0时,b ≤ f ( x ) ≤ 3a + b ,∴ ⎩⎨⎧-==+.513b b a , 解得 ⎩⎨⎧-==.52b a ,当a < 0时,3a + b ≤ f ( x ) ≤ b .∴ ⎩⎨⎧=-=+.153b b a , 解得 ⎩⎨⎧=-=.12b a ,故a 、b 的值为 ⎩⎨⎧-==52b a 或 ⎩⎨⎧=-=12b a例3 已知函数3cos 33cos 3sin )(2xx xx f +=. (1)将)(x f 写成)sin(φω+x A 的形式,并求其图象对称中心的横坐标; (2)函数的图象可由)(sin R x x y ∈=的图象经过怎样的变换得到?(3)如果△ABC 的三边a 、b 、c 满足b 2=ac ,且边b 所对的角为x ,试求x 的范围及此时函数f(x)的值域.解:(1)23)332sin(2332cos2332sin21)32cos1(2332sin21)(++=++=++=πx x x x x x f 由)332sin(π+x =0即z k k x z k k x ∈-=∈=+πππ213)(332得即对称中心的横坐标为z k k ∈-,π213(2)将函数x y sin =的图象依次进行如下变换:① 把函数x y sin =的图象向左平移3π,得到函数)3sin(π+=x y 的图象; ② 把得到的图象上各点横坐标伸长到原来的23倍(纵坐标不变),得到函数)632sin(π+=x y 的图象;③把得到的图象向上平移23个单位长度,得到函数)632sin(π+=x y +23的图象;(3)由已知b 2=a c,,,,,,231)332sin(31)332sin(3sin |295||23|953323301cos 21212222cos 22222+≤+<∴≤+<∴->-≤+<≤<<≤∴=-≥-+=-+=πππππππππππx x x x x ac ac ac ac ac c a ac b c a x 即)(x f 的值域为]231,3(+. 综上所述,]3,0(π∈x , )(x f 值域为]231,3(+.例4 设二次函数),()(2R c b c bx x x f ∈++=,已知不论βα,为何实数恒有)(sin αf ≥0,)cos 2(β+f ≤0.(1)求证:1-=+c b ; (2)求证:c ≥3;(3)若函数)(sin αf 的最大值为8,求b ,c 的值.解: (1) ]1,1[sin -∈α , ]3,1[cos 2∈β+, 0)(sin f ≥α 又 , 0)cos 2(f ≤β+ 恒成立.0)1(f ≥∴ , 0)1(f ≤, 即 0)1(f = 恒成立. ∴01=++c b , 即 1c b -=+.(2)0)3(f ≤ , 0c b 39≤++∴, ∴0)1(39≤+--+c c , ∴3≥c .(3)由题意可知: 上为减函数,在]11[)x (f -,∴c b f +-=-=1)1(8 ①, 1c b -=+ ② ,由 ① ,② 可得 b = 4- ,c = 3 .四、热身演练:1.在)2,0(π内,使x x cos sin >成立的x 取值范围为( C ).A .)45,()2,4(ππππ B .),4(ππ C .)45,4(ππ D .)23,45(),4(ππππ2.已知sin α>sin β,那么下列命题成立的是( D ).A .若α、β是第一象限角,则cos α>cos βB .若α、β是第二象限,则tan α>tan βC .若α、β是第三象限角,则cos α>cos βD .若α、β是第四象限角,则tan α>tan β 3.下列命题中正确的是( C ).A .x y tan =是增函数B .x y sin =在第一象限是增函数C .x y arccos 2-=π是奇函数 D .x y sin =的反函数是x y arcsin =4.要得到函数⎪⎭⎫ ⎝⎛-=42cos 3πx y 的图象,可以将函数x y 2sin 3=的图象( A ).A .沿x 轴向左平移8π单位 B .沿x 轴向右平移8π单位 C .沿x 轴向左平移4π单位 D .沿x 轴向右平移4π单位5.若2sin 2α+sin 2β-2sin α=0则cos 2α+cos 2β的取值范围是( A ).A .[1,5]B .[1,2]C .[1,49] D .[-1,2]6.在∆ABC 中,已知A 、B 、C 成等差数列,求 2tan 2tan 32tan 2tan CA C A ⋅++的值 为 .37.设直角三角形ABC 的内切圆半径与外接圆半径分别为r 的R ,则Rr的最大值为 .12-8.设函数)sin()(ϕω+=x x f ,(0>ω,22πϕπ<<-)给出下列四个论断:(1)它的周期为π; (2)它的图象关于直线x =12π对称;(3)它的图象关于点(3π,0)对称; (4)在区间(-6π,0)上是增函数.以其中两个论断为条件,另两个论断为结论,写出你认为正确的一个命题: . (1)(2)→(3)(4)或(1)(3)→(2)(4)9.(1)已知sin(4π+α)·sin(4π-α)=61, α∈(2π,π),求sin4α;(2)已知 cos(x+4π)=53,45π<x<47π,求x x x tan 1sin 22sin 2-+的值.解 (1)∵α+4π+4π-α=2π∴sin(4π-α)=cos(4π+α)∴sin(4π+α)·sin(4π-α)=sin(4π+α)·cos(4π+α)=21sin(2π+2α)= 21cos2α= 61又∵π<2α<2π,cos2α=31,∴sin2α= -322,∴sin4α=2sin2α·cos2α= -924.(2)原式=xx x x x sin cos )sin (cos cos sin 2-+α=)4cos(2)4sin(22sin ππ++⋅x x x=-cos(2x+2π)tan(x+4π) =[1-2cos 2(x+4π)]tan(x+4π)而cos(x+4π)=53,tan(x+4π)= -34,代入得:原式= -7528.10.如下图,某地一天从6时到14时的温度变化曲线近似满足函数y =A sin(ωx +φ)+b .(1)求这段时间的最大温差; (2)写出这段曲线的函数解析式.解:(1)由图示,这段时间的最大温差是30-10=20(℃);(2)图中从6时到14时的图象是函数y =A sin(ωx +φ)+b 的半个周期的图象. ∴ωπ221⋅=14-6,解得ω=8π,由图示A =21(30-10)=10,b =21(30+10)=20, 这时y =10sin(8πx +φ)+20,将x =6,y =10代入上式可取φ=43π.综上所求的解析式为y =10sin(8πx +43π)+20,x ∈[6,14].11.已知函数f(x)是定义域为一切实数且图象关于x=3对称的奇函数,f(1)=1且 523sin cos =-x x . 求证:(1)函数)(x f 是周期函数;(2)求])4cos(2sin 15[π+x x f 的值.解:∵函数f(x)的图象关于x=3对称,∴f(-x)=f(6+x),∵函数f(x)又是奇函数,∴f(6+x)=f(-x)=—f(x),f(x+12)=-f(x+6)=f(x),∴函数f(x)的周期为1, ∴函数f(x)是周期函数.cosx -sinx=2cos(x+4π)=523,∴cos(x+4π)=53,)4cos(2sin 15π+x x =)4cos()22cos(15ππ++-x x =-)4cos()1)4(cos 2(152ππ+-+x x =7,f[)4cos(2sin 15π+x x ]=f(7)=f(6+1)=f(-1)=-f(1)=-1.12.已知⊙O 的半径为2,在它的内接三角形ABC 中,有()()B b a C A sin sin sin 2222-=-成立,求△ABC面积S 的最大值.解:∵()()B b a C A sin sin sin 2222-=-,又2R=22,由正弦定理得:22[22)2()2(RcR a -]=(a -b )R b 2,∴a 2+b 2-c 2=ab,∴cosC=21 ∴∠C=3π.S=21absinC=B A B R A R sin sin 32sin 2sin 243=⋅⋅=-3[cos(A+B)-cos(A-B)].∵A+B=32π,∴s=23+3cos(A -B), 故当cos(A -B)=1时,即A=B=3π时,△ABC 面积S 的最大值为233.。
高一数学函数的三要素知识点

高一数学函数的三要素知识点在高一数学学习中,函数是一个重要的概念和工具。
理解和掌握函数的三要素是学好数学的基础。
本文将介绍函数的三要素的知识点,包括定义域、值域和图像。
一、定义域定义域是指函数所能接受的自变量的取值范围。
对于一个函数来说,它并不是任意定义的,而是有一定的限制。
在确定定义域时,需要考虑函数中出现的各种运算,比如平方根、分母不能为零等。
例如,对于函数y = √x,由于不能对负数开平方根,因此定义域为x ≥ 0;对于函数y = 1/x,由于分母不能为零,因此定义域为x ≠ 0。
需要注意的是,对于一些复杂的函数,确定定义域可能需要借助一些技巧和方法。
二、值域值域是函数所有可能的输出值的集合。
它是定义域经过函数变换后得到的结果。
确定值域的方法通常有两种:代数方法和图像法。
在使用代数方法确定值域时,可以分析函数的性质和特点,并求出函数的最值。
例如,对于函数y = x^2,在定义域为实数集时,函数的最小值为0,因此值域为y ≥ 0;对于函数y = sinx,在定义域为实数集时,由于正弦函数的取值范围是[-1, 1],因此值域为-1 ≤ y ≤ 1。
图像法是通过作出函数的图像来确定值域。
通过观察函数的图像,我们可以直观地判断函数的值域。
例如,对于函数y = 2x + 1,在作出其图像后,我们可以看到函数的图像是一条直线,它包含了所有的实数,因此值域为实数集。
三、图像函数的图像是函数在坐标系上的表示。
通过观察函数的图像,我们可以了解函数的性质和特点,进而更好地理解函数的三要素。
在绘制函数的图像时,需要根据定义域和值域的情况选择适当的坐标系和标尺。
对于简单的函数,可以通过画出一些特殊点和关键点,再通过描点连线的方法绘制函数的图像;对于复杂的函数,则可以借助计算机绘图工具进行绘制。
无论使用哪种方法,绘制的图像应该准确反映函数的性质,直观地展示函数的变化趋势。
综上所述,函数的三要素——定义域、值域和图像,是理解和掌握高一数学函数的关键知识点。
新高考数学一轮复习考点知识归类讲义 第6讲 函数及其表示
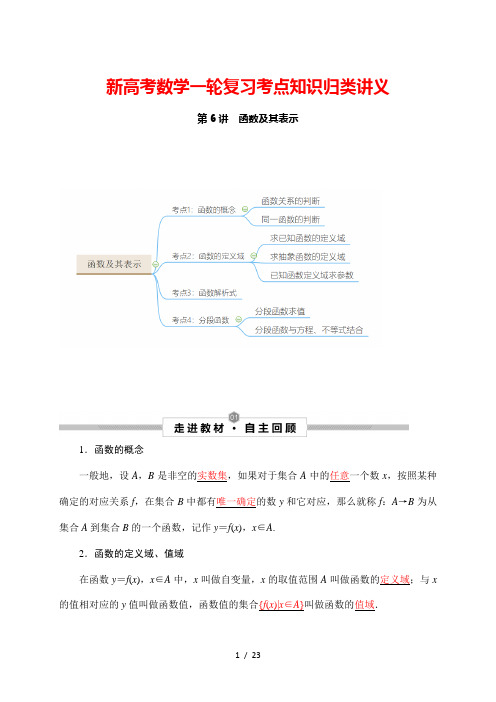
新高考数学一轮复习考点知识归类讲义第6讲函数及其表示1.函数的概念一般地,设A,B是非空的实数集,如果对于集合A中的任意一个数x,按照某种确定的对应关系f,在集合B中都有唯一确定的数y和它对应,那么就称f:A→B为从集合A到集合B的一个函数,记作y=f(x),x∈A.2.函数的定义域、值域在函数y=f(x),x∈A中,x叫做自变量,x的取值范围A叫做函数的定义域;与x 的值相对应的y值叫做函数值,函数值的集合{f(x)|x∈A}叫做函数的值域.3.函数的表示法表示函数的常用方法有解析法、图像法和列表法.4.分段函数(1)若函数在其定义域的不同子集上,因对应关系不同而分别用几个不同的式子来表示,这种函数称为分段函数.(2)分段函数虽由几个部分组成,但它表示的是一个函数.分段函数的定义域等于各段函数的定义域的并集,值域等于各段函数的值域的并集.➢考点1 函数的概念[名师点睛](1)函数的定义要求非空数集A中的任何一个元素在非空数集B中有且只有一个元素与之对应,即可以“多对一”,不能“一对多”,而B中有可能存在与A中元素不对应的元素.(2)构成函数的三要素中,定义域和对应关系相同,则值域一定相同1.(2022·全国·高三专题练习)下列四个图像中,是函数图像的是()A .(1)(2)B .(1)(2)(3)C .(1)(3)(4)D .(1)(2)(3)(4) 【答案】C 【解析】根据函数的定义,一个自变量值对应唯一一个函数值,或者多个自变量值对应唯一一个函数值,显然只有(2)不满足. 故选:C.2.(2021·湖南·雅礼中学高三阶段练习)下列各组函数中,()f x ,()g x 是同一函数的是( )A .()2f x x =,()4g x x =B .()2log a f x x =,()2log a g x x =C .()4121x x f x -=-,()21x g x =+D .()11f x x x --()11g x x x --【答案】D 【解析】解:对于A 选项,()2f x x =的定义域为R ,()4g x x =的定义域为[)0,∞+,故不满足;对于B 选项,()2log a f x x =的定义域为{}0x x ≠,()2log a g x x =的定义域为()0,∞+,故不满足;对于C 选项,()4121x x f x -=-的定义域为{}0x x ≠,()21xg x =+的定义域为R ,故不满足;对于D 选项,()f x ,()g x 的定义域均为{}1,对应关系均为0y =,故是同一函数.故选:D [举一反三]1.(2022·全国·高三专题练习)函数y =f (x )的图象与直线1x =的交点个数( ) A .至少1个B .至多1个C .仅有1个D .有0个、1个或多个 【答案】B 【解析】若1不在函数f (x )的定义域内,y =f (x )的图象与直线1x =没有交点, 若1在函数f (x )的定义域内,y =f (x )的图象与直线1x =有1个交点, 故选:B.2.(2022·天津市西青区张家窝中学高三阶段练习)下列各组函数中,表示同一个函数的是( )A .y =x -1和y =211x x -+B .y =x 0和y =1C .f (x )=x 2和g (x )=(x +1)2D .f (xg (x 【答案】D 【解析】对于A ,函数y =x -1定义域是R ,函数y =211x x -+定义域是(,1)(1,)-∞-⋃-+∞,A 不是;对于B ,0y x =定义域是(,0)(0,)-∞+∞,函数y =1定义域是R ,B 不是;对于C ,()2f x x =和()2(1)g x x =+对应法则不同,C 不是;对于D ,f (x和g (x (0,)+∞,并且对应法则相同,D 是.故选:D3.(2022·全国·高三专题练习)下列各组函数中,表示同一个函数的是( )A .1y =与0y x =B .y x =与2y =C .22log y x =与22log y x =D .1ln 1xy x+=-与()()ln 1ln 1y x x =+-- 【答案】D 【解析】对于A :1y =定义域为R ,0y x =定义域为{}|0x x ≠,定义域不同不是同一个函数,故选项A 不正确;对于B :y x =定义域为R ,2y =的定义域为{}|0x x ≥,定义域不同不是同一个函数,故选项B 不正确;对于C :22log y x =的定义域为{}|0x x >,22log y x =定义域为{}|0x x ≠,定义域不同不是同一个函数,故选项C 不正确; 对于D :由101xx +>-可得()()110x x +-<,解得:11x -<<,所以1ln 1x y x+=-的定义域为{}|11x x -<<,由1010x x +>⎧⎨->⎩可得11x -<<,所以函数()()ln 1ln 1y x x =+--的定义域为{}|11x x -<<且()()1ln 1ln 1ln1xy x x x+=+--=-,所以两个函数定义域相同对应关系也相同是同一个函数,故选项D 正确, 故选:D.➢考点2 函数的定义域[典例]1.(2022·北京·模拟预测)函数()()=-的定义域是_______.lg2f x x【答案】1[,2)2- 【解析】 由题意可得,21020x x +≥⎧⎨->⎩,解之得122x -≤<则函数()()lg 2f x x =-的定义域是1[,2)2- 故答案为:1[,2)2-2.(2022·全国·高三专题练习)若函数()y f x =的定义域是[0,8],则函数()g x =义域是( )A .(1,32)B .(1,2)C .(1,32]D .(1,2] 【答案】D 【解析】因为函数()y f x =的定义域是[0,8], 所以04802,,12101x x x x x ≤≤≤≤⎧⎧∴∴<≤⎨⎨->>⎩⎩.故选:D.3.(2022·全国·高三专题练习)已知函数(1)f x +的定义域为(-2,0),则(21)f x -的定义域为( )A .(-1,0)B .(-2,0)C .(0,1)D .1,02⎛⎫- ⎪⎝⎭【答案】C 【解析】由题设,若1t x =+,则(1,1)t ∈-,∴对于(21)f x -有21(1,1)x -∈-,故其定义域为(0,1). 故选:C4.(2022·全国·高三专题练习)已知函数()f x =的定义域是R ,则实数a 的取值范围是( )A .(12,0)-B .(12,0]-C .1(,)3+∞D .1(,]3-∞ 【答案】B 【解析】∵()f x =的定义域为R ,∴只需分母不为0即可,即230ax ax +-≠恒成立, (1)当0a =时,30恒成立,满足题意,(2)当0a ≠时,24(3)0a a ∆=-⨯-<,解得120a -<<, 综上可得120a -<≤. 故选:B. [举一反三]1.(2022·全国·高三专题练习)函数y =13x -的定义域为( ) A .3,2⎡⎫+∞⎪⎢⎣⎭B .(-∞,3)∪(3,+∞)C .3,32⎡⎫⎪⎢⎣⎭(3,+∞)D .(3,+∞)【答案】C 【解析】要使函数y =13x -有意义,则 所以x x -≥-≠⎧⎨⎩23030,解得32x ≥且3x ≠,所以函数y =13x -的定义域为3,32⎡⎫⎪⎢⎣⎭∪(3,+∞). 故选:C.2.(2022·全国·高三专题练习)函数y 22x ππ-≤≤)的定义域是( )A .,02π⎡⎤-⎢⎥⎣⎦B .,26ππ⎡⎫-⎪⎢⎣⎭C .,02π⎡-⎫⎪⎢⎣⎭D .,26ππ⎡⎤-⎢⎥⎣⎦【答案】A由题意,得512sin 0log (12sin )022x x x ππ⎧⎪->⎪-≥⎨⎪⎪-≤≤⎩,则1sin 212sin 122x x x ππ⎧<⎪⎪-≥⎨⎪⎪-≤≤⎩,即sin 022x x ππ≤⎧⎪⎨-≤≤⎪⎩,∴[,0]2x π∈-.故选:A.3.(2022·全国·高三专题练习)已知函数(1)=-y f x 的定义域为[]1,3,则函数()3log y f x =的定义域为( )A .[]0,1B .[]1,9C .[]0,2D .[]0,9 【答案】B 【解析】由[]1,3x ∈,得[]10,2x -∈, 所以[]3log 0,2x ∈,所以[]1,9x ∈. 故选:B .4.(2022·全国·高三专题练习)定义域是一个函数的三要素之一,已知函数()Jzzx x 定义域为[211,985],则函数 ()shuangyiliu x (2018)(2021)Jzzx x Jzzx x =+的定义域为( )A .211985,20182021⎡⎤⎢⎥⎣⎦B .211985,20212018⎡⎤⎢⎥⎣⎦ C .211985,20182018⎡⎤⎢⎥⎣⎦D .211985,20212021⎡⎤⎢⎥⎣⎦【答案】A 【解析】由抽象函数的定义域可知,21120189852112021985x x ≤≤⎧⎨≤≤⎩,解得21198520182021x, 所以所求函数的定义域为211985,20182021⎡⎤⎢⎥⎣⎦. 故选A.5.(2022·全国·高三专题练习)已知函数()f x =R ,则m 的取值范围是( )A .12m -<<B .12m -<≤C .12m -≤≤D .12m -≤< 【答案】C 【解析】由题意得:()()231104m x m x +-++≥在R 上恒成立.10m +=即1m =-时,()f x =10m +≠时,只需()()2101310m m m +>⎧⎪⎨∆=+-+≤⎪⎩, 解得:12m -<≤, 综上:1,2m ,故选:C .6.(2022·上海市奉贤中学高三阶段练习)函数()f x =___________.【答案】(,0]-∞【解析】解:由1102x⎛⎫-≥ ⎪⎝⎭,得011122⎛⎫⎛⎫≥= ⎪ ⎪⎝⎭⎝⎭x ,所以0x ≤,所以函数的定义域为(,0]-∞,故答案为:(,0]-∞7.(2022·全国·高三专题练习)函数y =的定义域是R ,则a 的取值范围是_________. 【答案】[)0,4【解析】由题意可得210ax ax ++>在R 上恒成立. ①当0a =时,则10>恒成立,0a ∴=符合题意;②当0a ≠时,则2040a a a >⎧⎨-<⎩,解得04a <<.综上可得04a ≤<,∴实数a 的取值范围为[)0,4. 故答案为:[)0,4.8.(2022·全国·高三专题练习)已知函数()f x =R ,则a的范围是________. 【答案】[1,5) 【解析】当1a =时,()1f x =,即定义域为R ;当1a ≠,要使()f x 的定义域为R ,则2()(1)(1)10g x a x a x =-+-+>在x ∈R 上恒成立,∴()()210{1410a a a ->∆=---<,解得15a <<, 综上,有15a ≤<, 故答案为:[1,5)➢考点3 函数解析式[典例]1.(1)已知f(x+1)=x+2x,则f(x)的解析式为________________.(2)若f(x)为二次函数且f(0)=3,f(x+2)-f(x)=4x+2,则f(x)的解析式为________.(3)已知函数f(x)满足2f(x)+f(-x)=2x,则f(x)的解析式为________.【答案】(1)f(x)=x2-1(x≥1)(2)f(x)=x2-x+3(3)f(x)=2x【解析】(1)方法一(换元法):令x+1=t,则x=(t-1)2,t≥1,所以f(t)=(t-1)2+2(t-1)=t2-1(t≥1),所以函数f(x)的解析式为f(x)=x2-1(x≥1).方法二(配凑法):f(x+1)=x+2x=x+2x+1-1=(x+1)2-1.因为x+1≥1,所以函数f(x)的解析式为f(x)=x2-1(x≥1).(2)(待定系数法)设f (x )=ax 2+bx +c (a ≠0), 又f (0)=c =3, 所以f (x )=ax 2+bx +3,所以f (x +2)-f (x )=a (x +2)2+b (x +2)+3-(ax 2+bx +3)=4ax +4a +2b =4x +2. 所以⎩⎨⎧4a =4,4a +2b =2,所以⎩⎨⎧a =1,b =-1,所以函数f (x )的解析式为f (x )=x 2-x +3. (3)(解方程组法)因为2f (x )+f (-x )=2x ,① 将x 换成-x 得2f (-x )+f (x )=-2x ,② 由①②消去f (-x ),得3f (x )=6x , 所以f (x )=2x .2.(2022·全国·高三专题练习)根据下列条件,求函数f (x )的解析式. (1)f (x )是一次函数,且满足f (f (x ))=4x -3;(2)已知f (x )满足2f (x )+f (1x)=3x ,求f (x )的函数解析式.(3)已知f (0)=1,对任意的实数x ,y 都有f (x -y )=f (x )-y (2x -y +1). 【解】(1)因为f (x )是一次函数,所以设()()0f x kx b k =+≠,所以()()()2f f x k kx b b k x kb b =++=++,又因为f (f (x ))=4x -3,所以243k x kb b x ++=-,故243k kb b ⎧=⎨+=-⎩,解得21k b =⎧⎨=-⎩或23k b =-⎧⎨=⎩,所以()21f x x =-或()23f x x =-+;(2)将1x 代入()123f x f x x ⎛⎫+= ⎪⎝⎭,得()132f f x x x ⎛⎫+= ⎪⎝⎭,因此()()123132fx f x x ff x x x ⎧⎛⎫+=⎪⎪⎪⎝⎭⎨⎛⎫⎪+= ⎪⎪⎝⎭⎩,解得()()120f x x x x=-≠. (3)令x =0,得f (-y )=f (0)-y (-y +1)=1+y 2-y=()()21y y -+-+,所以f (y )=y 2+y +1,即f (x )=x 2+x +1.[举一反三]1.(2022·全国·高三专题练习)已知函数221111x xf x x --⎛⎫= ⎪++⎝⎭,则()f x 的解析式为( ) A .()()2211x f x x x =≠-+B .()()2211xf x x x =-≠-+ C .()()211x f x x x =≠-+D .()()211x f x x x =-≠-+ 【答案】A 【解析】令11x t x -=+,则11t x t -=+ ,所以()()222112111111t t t f t t t t t -⎛⎫- ⎪+⎝⎭==≠-+-⎛⎫+ ⎪+⎝⎭, 所以()()2211xf x x x =≠-+,故选:A. 2.(2022·全国·高三专题练习)已知函数f (x ﹣1)=x 2+2x ﹣3,则f (x )=( ) A .x 2+4x B .x 2+4C .x 2+4x ﹣6D .x 2﹣4x ﹣1 【答案】A【解析】()()()22123141f x x x x x -=+-=-+-,所以()24f x x x =+.故选:A3.(2022·全国·高三专题练习)已知函数()f x 的定义域为R ,且2()2()f x f x x x +-=-,则()f x =( )A .223x x +B .223x x +C .2223x x+D .23x x +【答案】D【解析】令x 为x -,则2()2()f x f x x x -+=+, 与2()2()f x f x x x +-=-联立可解得,2()3x f x x =+.故选:D .4.(多选)(2022·全国·高三专题练习)已知函数()f x 是一次函数,满足()()98f f x x =+,则()f x 的解析式可能为( ) A .()32f x x =+B .()32f x x =- C .()34f x x =-+D .()34f x x =-- 【答案】AD 设()f x kx b =+,由题意可知()()()298f f x k kx b b k x kb b x =++=++=+,所以298k kb b ⎧=⎨+=⎩,解得32k b =⎧⎨=⎩或34k b =-⎧⎨=-⎩,所以()32f x x =+或()34f x x =--. 故选:AD.5.(2022·山东济南·二模)已知函数2()23f x x x =--+,则(1)f x +=______. 【答案】24x x -- 【解析】解:因为2()23f x x x =--+,所以()()22(+1)+12+143f x x x x x =--+-=-,(1)f x +=24x x --.故答案为:24x x --.6.(2022·全国·高三专题练习)已知()49f f x x =+⎡⎤⎣⎦,且()f x 为一次函数,求()f x =_________【答案】23x +或29x --. 【解析】因为()f x 为一次函数,所以设()()0f x kx b k =+≠,所以()()()()21f f x f kx b k kx b b k x b k =+=++=++⎡⎤⎣⎦, 因为()49f f x x =+⎡⎤⎣⎦,所以()2149k x b k x ++=+恒成立, 所以()2419k b k ⎧=⎪⎨+=⎪⎩,解得:23k b =⎧⎨=⎩或29k b =-⎧⎨=-⎩,所以()23f x x =+或()29f x x =--, 故答案为:23x +或29x --.7.(2022·全国·高三专题练习)已知函数)25f x =+,则()f x 的解析式为_______【答案】()()212f x x x =+≥【解析】2t +=,则2t ≥,且()22x t =-, 所以()()()2224251f t t t t =-+-+=+,()2t ≥所以()()212f x x x =+≥,故答案为:()()212f x x x =+≥.8.(2022·全国·高三专题练习)设函数f (x )对x ≠0的一切实数都有f (x )+2f (2020x)=3x ,则f (x )=_________. 【答案】4040()f x x x=- 【解析】 因为()202023f x f x x ⎛⎫+=⎪⎝⎭,可得()2020232020x f f x x ⎛⎫+= ⎪⎝⎭,由()()2020232020232020f x f x x x f f x x ⎧⎛⎫+=⎪⎪⎪⎝⎭⎨⎛⎫⎪+= ⎪⎪⎝⎭⎩,解得4040()f x x x=-. 故答案为:4040()f x x x=-. 9.(2022·全国·高三专题练习)已知定义域为R 的函数()f x 满足()()323f x f x x --=,则()f x =___________.【答案】3x【解析】因为()()323f x f x x --=,所以()()323f x f x x --=-,同除以2得()()31322f x f x x --=-,两式相加可得()33322f x x =,即()3f x x =.故答案为:3x .10.(2022·全国·高三专题练习)(1)已知()f x 是二次函数且(0)2f =,(1)()1f x f x x +-=-,求()f x ;(2)已知1()2(0)f x f x x x ⎛⎫+=≠ ⎪⎝⎭,求()f x .【解】(1)∵f (x )为二次函数,∴f (x )=ax 2+bx +c (a ≠0),∵f (0)=c =2,∵f (x +1)﹣f (x )=x ﹣1,∴2ax +a +b =x ﹣1,∴a 12=,b 32=-, ∴f (x )12=x 232-x +2. (2)∵()12f x f x x ⎛⎫+= ⎪⎝⎭,①,∴f (1x )+2f (x )1x=,② ①-②×2得:﹣3f (x )=x 2x-, ∴2()(0)33xf x x x =-≠➢考点4 分段函数1.(2022·广东梅州·二模)设函数()()21log 6,1,2, 1.x x x f x x -⎧-<=⎨≥⎩,则()()22log 6f f -+=( ) A .2B .6C .8D .10 【答案】B 【解析】 解:因为()()21log 6,1,2, 1.x x x f x x -⎧-<=⎨≥⎩,所以()()2log 61222log 83,log 623f f --====,所以()()22log 66f f -+=. 故选:B.2.(2022·山东潍坊·模拟预测)设函数()()()3,104,10x x f x f f x x -≥⎧⎪=⎨+<⎪⎩,则()8f =( )A .10B .9C .7D .6【答案】C 【解析】因为()()()3,104,10x x f x f f x x -≥⎧⎪=⎨+<⎪⎩,则()()()()()()()812913107f f f f f f f =====.故选:C.3.(2022·浙江省江山中学高三期中)已知[]1,1∈-a ,函数()()()22sin 2, 21,π⎧⎡⎤-≤⎪⎣⎦=⎨-++>⎪⎩x a x a f x x a x a x a 若()() 1=f f a ,则=a _______.【答案】1-或34【解析】()()()01f f a f ==,当01a ≤≤时,()()0sin 21π=-=f a ,得14a k =--,故34a =;当10a -≤<时,()201f a ==,故1a =-.故答案为:34a =或1a =-.4.(2022·湖南湘潭·三模)已知0a >,且1a ≠,函数()()2log 21,0,0a xx x f x a x ⎧+≥⎪=⎨<⎪⎩,若()()12f f -=,则=a ___________,()4f x ≤的解集为___________.【答案】∞⎛- ⎝⎦【解析】①由题可知,()()()()121log 212a f f f a a ---==+=,则2221a a -=+,即4220a a --=,解得22a =,故a =②当0x 时,())2214f x x=+,解得602x;当0x <时,()4x f x =恒成立.故不等式的解集为∞⎛- ⎝⎦.∞⎛- ⎝⎦. [举一反三]1.(2022·山东·济南一中高三阶段练习)已知函数()()21,13,1xx f x f x x ⎧+<⎪=⎨-≥⎪⎩,则()9f =( ) A .2B .9C .65D .513 【答案】A 【解析】()09(93)(6)(3)(0)212f f f f f =-====+=,故选:A2.(2022·重庆八中模拟预测)已知函数()()1,221,2xx f x f x x ⎧⎛⎫≤⎪ ⎪=⎨⎝⎭⎪->⎩,则()2log 12f =( )A .13B .6-C .16D .3- 【答案】A 【解析】因为()2log 31,2∈,则()22log 122log 33,4=+∈,所以()()()()22log 31log 322211log 122log 3log 3223f f f -⎛⎫=+==== ⎪⎝⎭,故选:A.3.(2022·安徽安庆·二模)已知函数()()()lg ,10R 10,01axx x f x a x ⎧--≤<=∈⎨≤≤⎩且()12f =,则()41log 310f f ⎛⎫--= ⎪⎝⎭( ) A.1-.1-.1.1【答案】A【解析】∵()1102a f ==,∴lg 2a =,由()()()lg ,10R 10,01ax x x f x a x ⎧--≤<=∈⎨≤≤⎩,知()()lg ,102,01x x x f x x ⎧--≤<=⎨≤≤⎩. 于是()241log 3log log 32411log 3lg 2121211010f f ⎛⎫--=-=--=--=- ⎪⎝⎭故选:A4.(2022·福建三明·模拟预测)已知函数()33,0log ,0x x f x x x ⎧≤=⎨>⎩,则()2f f -=⎡⎤⎣⎦___________. 【答案】-2【解析】因为()33,0log ,0x x f x x x ⎧≤=⎨>⎩,所以()()()22323log 32f f f ---===-⎡⎤⎣⎦ 故答案为:-25.(2022·辽宁·建平县实验中学模拟预测)已知函数()221010,231,2x x x f x x x --⎧-≤⎪=⎨-->⎪⎩,则不等式()()10f x f x +-<的解集为___________. 【答案】9,2⎛⎫-∞ ⎪⎝⎭ 【解析】①当2x ≤时,11x -≤,()221010x x f x --=-在(],2-∞上单调递增, ()()20f x f ∴≤=,又()()()1120f x f f -≤<=, ()()10f x f x ∴+-<恒成立;②当23x <≤时,112x <-≤,()3120f x x x =--=-<,又()()120f x f -≤=,()()10f x f x ∴+-<恒成立; ③当34x <≤时,213x <-≤,()314f x x x =--=-,()1413f x x x -=--=-; ()()110f x f x ∴+-=-<恒成立;④当4x >时,13x ->,()314f x x x =--=-,()1415f x x x -=--=-, ()()1290f x f x x ∴+-=-<,解得:92x <,942x ∴<<; 综上所述:不等式()()10f x f x +-<的解集为9,2⎛⎫-∞ ⎪⎝⎭. 故答案为:9,2⎛⎫-∞ ⎪⎝⎭. 6.(2022·浙江省临安中学模拟预测)设()(),0121,1x x f x x x ⎧<<⎪=⎨-≥⎪⎩,若()()1f a f a =+,则=a __________,1f a ⎛⎫= ⎪⎝⎭__________. 【答案】146 【解析】 若01a <<,则112a <+<,由()()1f a f a =+,得()211a a =+-,即24a a =, 解得:0a =(舍去)或14a =;若1a ≥,由()()1f a f a =+,得()()21211a a -=+-,该方程无解.综上可知,14a =,()()142416f f a =⎛⎫ =⎪-⎝=⎭ 故答案为:14; 67.(2022·浙江·湖州中学高三阶段练习)已知函数,则()()1f f =___________;方程()1f x =的解集为___________. 【答案】 1 {1,e}【解析】()()()()11e e,1e lne 1f f f f =====,()1,1e 10x x f x x ≤=⇒=⇒=, ()1,1ln 1e x f x x x >=⇒=⇒=, {}0,e .x ∴∈故答案为:1;{}0,e .8.(2022·浙江·高三专题练习)已知()23log ,1,,1,x x f x x x ≥⎧=⎨-<⎩则()(2)f f -=______;若()1f x <,则x 的取值范围是______.【答案】 3 ()1,2-【解析】因为()32(2)8f -=--=, ()()()328l g 8o 3f f f ∴-===,当1x <时,()31f x x =-<,得11x -<<,当1≥x 时,()2log 1f x x =<,得12x ≤<, 故x 的取值范围是()1,2-故答案为:3;()1,2-.9.(2022·浙江浙江·二模)设a ∈R ,函数33(0)()log (0)ax x f x x x ⎧≤=⎨>⎩.则(9)f =________;若1273f f ⎛⎫⎛⎫≤ ⎪ ⎪⎝⎭⎝⎭,则实数a 的取值范围是________. 【答案】 2 [)3,∞-+【解析】3(9)log 92f ==, 311log 133f ⎛⎫==- ⎪⎝⎭由()31132733a f f f -⎛⎫⎛⎫=-=≤= ⎪ ⎪⎝⎭⎝⎭,则3a -≤,所以3a ≥- 故答案为:2;[)3,∞-+。
高一数学函数的三要素

高一数学函数的三要素数学中的函数是一种非常重要的概念,它在高中数学课程中占据着极其重要的位置。
作为高一数学的一部分,理解函数的三要素对于学生掌握数学知识和解题能力至关重要。
首先,我们来谈谈函数的定义域和值域。
在数学中,函数是一种特殊的关系,它将一个集合中的每个元素都映射到另一个集合中的唯一元素上。
在函数的定义中,我们需要明确指定函数的定义域和值域。
定义域是指函数能够接受的输入值的集合,而值域则是函数输出的所有可能值的集合。
通过确定函数的定义域和值域,我们可以清晰地了解函数的输入和输出范围,从而进行正确的运算和解题。
其次,讨论函数的图像和性质是不可或缺的。
函数的图像是函数在坐标系中的表示形式,它可以直观地展现函数的随变关系。
通常情况下,我们可以用平面直角坐标系来绘制函数的图像。
图像的性质包括增减性、奇偶性、周期性等等。
通过研究函数的图像和性质,我们可以深入了解函数的规律和特点,并在解决问题时能够更加灵活地运用函数的性质。
最后,要探讨函数的解析式或者定义式。
函数的解析式是用代数表达式来表示函数的一种方式。
通过解析式,我们可以用简洁明了的方式描述函数的规律和特征。
例如,对于一元函数来说,我们可以用y=f(x)的形式来表示函数,其中 f(x)就是函数的解析式,y 表示函数的值。
掌握函数的解析式可以使我们更方便地进行函数运算和问题求解。
综上所述,高一数学的函数概念涉及了函数的三个重要要素:定义域和值域、图像和性质以及解析式。
只有全面理解和掌握了这些要素,我们才能在数学学习和解题中灵活运用函数的知识。
因此,我们应该注重理论学习,结合实际问题进行实践,逐步提升对函数的理解和运用能力。
第6讲函数的概念及其表示方法2023高三数学一轮复习提高版课件共33张PPT

课堂评价
1. (2019·潍坊段测)函数 f (x)=ln(x-1)+ 21-x的定义域为( A )
A. (1,2)
B. [1,2)
C. (1,2]
D. [1,2]
【解析】 由题意得x2--1x> >00, , 解得 1<x<2,所以函数 f (x)的定义域为(1,2).
2. (多选)已知函数 f (x)=legx--1,xx,≥x0<. 0, 若 f (1)+f (a)=2,则 a 的所有可能值为
下列对应法则 f 为 A 上的函数的有_____1___个. ①A=Z,B=N*,f:x→y=x2; ②A=Z,B=Z,f:x→y= x; ③A=[-1,1],B={0},f:x→y=0. 【解析】 对于①,当 0∈A 时,y=0∉B,故①所给的对应法则不是 A 到 B 的映射, 当然它不是 A 上的函数关系;对于②,当 2∈A 时,y= 2∉B,故②所给的对应法则不 是 A 到 B 的映射,当然它不是 A 上的函数关系;对于③,对于 A 中的任一个数,按照 对应法则,在 B 中都有唯一元素 0 和它对应,故③所给的对应法则是 A 到 B 的映射, 这两个数集之间的关系是集合 A 上的函数关系.
(3) f (x)=x,g(x)=3 x3; 【解答】 两个函数的定义域、值域和对应法则都相同,所以它们是同一函数. (4) f (x)=2x,g(x)= 4x2. 【解答】 两个函数的对应法则不同,其中 g(x)=|2x|,所以它们不是同一函数.
函数的定义含有三个要素,即定义域 A、值域 C 和对应法则 f,当且仅当两个函数 的定义域和对应法则都分别相同时,这两个函数才是同一函数.
目标 2 求函数的定义域 (1) 函数 y= x+1+2-1 x的定义域为____[_-__1_,2_)_∪__(2_,__+__∞__)_____.
函数三要素

高中数学函数的三要素函数的三要素是指定义域、值域、对应法则。
每个要素里掌握的方向不一样。
定义域从具体函数和抽象函数两个方向去把握,值域掌握求值域的方法有哪些,对应法则也掌握的是方法有哪些,下面一一介绍。
一、定义域1、具体函数定义域,主要从以下几个方面去掌握:(1)整式函数的定义域是全体实数。
(2)分式函数的定义域是使得分母不为0的自变量的取值。
(3)含有偶次根式是被开放数大于等于0(4)对数函数是真数大于0(5)若f(x)是由几个式子构成的,则函数的定义域要使各个式子都有意义。
2、抽象函数的定义域,此部分只需记住2句话即可:(1)、凡是出现定义域三个字,统统是指的取值范围。
(2)、相同准则条件下,相同位置取值范围一样。
通俗一句话就是括号里的取值范围一样。
3、实际问题,既要使构建的函数解析式有意义,又要考虑实际问题的要求。
二、对应法则函数解析式的求法(1)待定系数法:若已知函数的类型,可用待定系数法(例如一次函数、二次函数)。
(2)换元法:已知复合函数f(g(x))的解析式,可用换元法,此时要注意新元的取值范围。
(3)配凑法:由已知条件f(g(x))=F(x),可将F(x)改写成关于g(x)的表达式,然后以x替代g(x),便得f(x)的解析式。
(4)消去法(构造方程组法):已知f(x)与fx(1)或f(-x)之间的关系式,可根据已知条件再构造出另外一个等式组成方程组,通过解方程组求出f(x)。
三、求值域:求值域的方法:(1)分离常数法:适合分子分母都是一次函数。
(2)反解法。
(3)配方法。
(4)不等式法。
(5)单调性法。
(6)换元法。
(7)数形结合法。
(8)导数法。
函数的概念及其三要素

函数的概念及其三要素
一、什么是函数
函数是指一种映射关系,它把一个或多个输入值映射成输出值,当用
相同的输入值时,可以产生相同的输出值,这种一一映射的关系就是函数。
数学上的函数可以分为普通函数和复合函数,普通函数主要用作表达其中
一种性质随变量而变化的定量关系,复合函数是通过一个函数定义另一个
函数,而满足其中一种定义域和值域的关系,是构成数学理论的基础。
二、函数的三要素
1、定义域
定义域也叫做函数的域,它表示函数的取值范围,即允许函数的输入
取值的范围,它可以是实数的整数、分数、有理数,也可以是复数。
一般
情况下,为了更好地研究函数的特性,会将定义域划分为有限多个区间,
即定义域可以表示为一个有限的集合。
2、值域
值域表示函数的输出取值可以取到的范围,也就是函数的输出值可以
取的范围。
值域可以是实数集、自然数集等,有时也会将值域分为有限多
个区间,以方便函数特性的研究。
3、解析式
解析式是一种表示函数关系的方式,它用数学符号把函数所表示的变
化关系表示出来,如一元函数的解析式一般可以写成y=f(x),其中f(x)
就是函数的解析式,这里的x表示函数的自变量,y表示函数的因变量,
f(x)称为函数式。
