2019届人教B版(文科数学) 第4章 三角函数、解三角形 23 单元测试
2019版高考文科数学大一轮复习人教B版讲义:第四章 三

§4.1 任意角、弧度制及任意角的三角函数1.角的概念(1)角的分类(按旋转的方向)角⎩⎪⎨⎪⎧正角:按照逆时针方向旋转而成的角.负角:按照顺时针方向旋转而成的角.零角:射线没有旋转.(2)象限角(3)终边相同的角所有与α终边相同的角,包括α本身构成一个集合,这个集合可记为S ={β|β=α+k ·360°,k ∈Z }. 2.弧度制(1)定义:长度等于半径长的圆弧所对的圆心角叫做1弧度的角,正角的弧度数是正数,负角的弧度数是负数,零角的弧度数是零.(2)角度制和弧度制的互化:180°=π rad,1°=π180 rad ,1 rad =⎝⎛⎭⎫180π°. (3)扇形的弧长公式:l =|α|r , 扇形的面积公式:S =12lr =12|α|r 2.3.任意角的三角函数的定义α为任意角,α的终边上任意一点P (异于原点)的坐标(x ,y ),它与原点的距离OP =r =x 2+y 2 (r >0),则sin α=y r ;cos α=x r ;tan α=yx ;cot α=x y ;sec α=r x ;csc α=ry.4.三角函数在各象限的符号规律及三角函数线 (1)三角函数在各象限的符号:(2)三角函数线:正弦线 如图,角α的正弦线为MP →. 余弦线 如图,角α的余弦线为OM →. 正切线 如图,角α的正切线为AT →.知识拓展三角函数值的符号规律三角函数值在各象限内的符号:一全正、二正弦、三正切、四余弦.题组一 思考辨析1.判断下列结论是否正确(请在括号中打“√”或“×”) (1)锐角是第一象限的角,第一象限的角也都是锐角.( × ) (2)角α的三角函数值与其终边上点P 的位置无关.( √ ) (3)不相等的角终边一定不相同.( × ) (4)若α为第一象限角,则sin α+cos α>1.( √ ) 题组二 教材改编2.角-225°=弧度,这个角在第象限. 答案 -5π4二3.角α的终边经过点Q ⎝⎛⎭⎫-22,22,则sin α=,cos α=. 答案22 -224.一条弦的长等于半径,这条弦所对的圆心角大小为弧度. 答案 π3题组三 易错自纠5.(2018·秦皇岛模拟)下列与9π4的终边相同的角的表达式中正确的是 ( ) A .2k π+45°(k ∈Z ) B .k ·360°+9π4(k ∈Z ) C .k ·360°-315°(k ∈Z ) D .k π+5π4(k ∈Z )答案 C解析 与9π4的终边相同的角可以写成2k π+9π4(k ∈Z ),但是角度制与弧度制不能混用,所以只有答案C 正确.6.集合⎩⎨⎧⎭⎬⎫α⎪⎪k π+π4≤α≤k π+π2,k ∈Z 中的角所表示的范围(阴影部分)是( )答案 C解析 当k =2n (n ∈Z )时,2n π+π4≤α≤2n π+π2,此时α表示的范围与π4≤α≤π2表示的范围一样;当k =2n +1 (n ∈Z )时,2n π+π+π4≤α≤2n π+π+π2,此时α表示的范围与π+π4≤α≤π+π2表示的范围一样,故选C. 7.(2018·攀枝花质检)已知角α的终边经过点(-4,3),则cos α=. 答案 -45解析 cos α=-4(-4)2+32=-45. 8.(2018·济宁模拟)函数y =2cos x -1的定义域为. 答案 ⎣⎡⎦⎤2k π-π3,2k π+π3(k ∈Z ) 解析 ∵2cos x -1≥0, ∴cos x ≥12.由三角函数线画出x 满足条件的终边范围(如图阴影部分所示),∴x ∈⎣⎡⎦⎤2k π-π3,2k π+π3(k ∈Z ).题型一 角及其表示1.设集合M =⎩⎨⎧⎭⎬⎫x ⎪⎪x =k2·180°+45°,k ∈Z ,N = ⎩⎨⎧⎭⎬⎫x ⎪⎪x =k4·180°+45°,k ∈Z ,那么( )A .M =NB .M ⊆NC .N ⊆MD .M ∩N =∅ 答案 B解析 由于M 中,x =k2·180°+45°=k ·90°+45°=(2k +1)·45°,2k +1是奇数;而N 中,x =k 4·180°+45°=k ·45°+45°=(k +1)·45°,k +1是整数,因此必有M ⊆N ,故选B. 2.若角α是第二象限角,则α2是( )A .第一象限角B .第二象限角C .第一或第三象限角D .第二或第四象限角答案 C解析 ∵α是第二象限角, ∴π2+2k π<α<π+2k π,k ∈Z , ∴π4+k π<α2<π2+k π,k ∈Z . 当k 为偶数时,α2是第一象限角;当k 为奇数时,α2是第三象限角.∴α2是第一或第三象限角. 3.(2017·福州模拟)与-2 015°终边相同的最小正角是. 答案 145°解析 与-2 015°角终边相同的角的集合为{α|α=-2 015°+k ·360°,k ∈Z }, 当k =6时,α=-2 015°+2 160°=145°.思维升华 (1)利用终边相同的角的集合可以求适合某些条件的角,方法是先写出与这个角的终边相同的所有角的集合,然后通过对集合中的参数k 赋值来求得所需的角. (2)确定kα,αk(k ∈N +)的终边位置的方法先写出kα或αk 的范围,然后根据k 的可能取值确定kα或αk 的终边所在位置.题型二 弧度制典例 (1)(2017·珠海模拟)已知扇形的周长是4 cm ,则扇形面积最大时,扇形的圆心角的弧度数是( )A .2B .1 C.12 D .3答案 A解析 设扇形的半径为R ,则弧长l =4-2R , ∴扇形面积S =12lR =R (2-R )=-R 2+2R =-(R -1)2+1,当R =1时,S 最大,此时l =2,扇形圆心角为2弧度.(2)若圆弧长度等于该圆内接正方形的边长,则其圆心角的弧度数是. 答案2解析 设圆半径为r ,则圆内接正方形的对角线长为2r ,∴正方形边长为2r ,∴圆心角的弧度数是2rr= 2. 思维升华 应用弧度制解决问题的方法(1)利用扇形的弧长和面积公式解题时,要注意角的单位必须是弧度. (2)求扇形面积最大值的问题时,常转化为二次函数的最值问题.(3)在解决弧长问题和扇形面积问题时,要合理地利用圆心角所在的三角形.跟踪训练 (1)(2017·太原模拟)已知2弧度的圆心角所对的弦长为2,则这个圆心角所对的弧长是. 答案2sin 1解析 设圆的半径为R ,则R ·sin 1=1,∴R =1sin 1,∴这个圆心角所对弧长为R ×2=2sin 1. (2)已知圆O 与直线l 相切于点A ,点P ,Q 同时从A 点出发,P 沿着直线l 向右,Q 沿着圆周按逆时针以相同的速度运动,当Q 运动到点A 时,点P 也停止运动,连接OQ ,OP (如图),则阴影部分面积S 1,S 2的大小关系是.答案 S 1=S 2解析 设运动速度为m ,运动时间为t ,圆O 的半径为r , 则AQ =AP =tm ,根据切线的性质知OA ⊥AP , ∴S 1=12tm ·r -S 扇形AOB ,S 2=12tm ·r -S 扇形AOB ,∴S 1=S 2恒成立.题型三 三角函数的概念及应用命题点1 三角函数定义的应用典例 (1)已知点P 在角4π3的终边上,且|OP |=4,则点P 的坐标为( )A .(-2,-23) B.⎝⎛⎭⎫-12,-32C .(-23,-2) D.⎝⎛⎭⎫-32,-12 答案 A解析 点P 的坐标为⎝⎛⎭⎫|OP |·cos 4π3,|OP |·sin 4π3,即(-2,-23),故选A. (2)设θ是第三象限角,且⎪⎪⎪⎪cos θ2=-cos θ2,则θ2是( ) A .第一象限角 B .第二象限角 C .第三象限角 D .第四象限角答案 B解析 由θ是第三象限角知,θ2为第二或第四象限角,∵⎪⎪⎪⎪cos θ2=-cos θ2,∴cos θ2<0, 综上知,θ2为第二象限角.命题点2 三角函数线的应用典例 函数y =lg(2sin x -1)+1-2cos x 的定义域为. 答案 ⎣⎡⎭⎫2k π+π3,2k π+5π6(k ∈Z ) 解析 要使原函数有意义,必须有⎩⎪⎨⎪⎧2sin x -1>0,1-2cos x ≥0,即⎩⎨⎧sin x >12,cos x ≤12,如图,在单位圆中作出相应的三角函数线,由图可知,原函数的定义域为⎣⎡⎭⎫2k π+π3,2k π+5π6 (k ∈Z ).思维升华 (1)利用三角函数的定义,已知角α终边上一点P 的坐标可求α的三角函数值;已知角α的三角函数值,也可以求出点P 的坐标.(2)利用三角函数线解不等式要注意边界角的取舍,结合三角函数的周期性写出角的范围. 跟踪训练 (1)已知角α的终边经过点(3a -9,a +2),且cos α≤0,sin α>0.则实数a 的取值范围是( ) A .(-2,3] B .(-2,3) C .[-2,3) D .[-2,3]答案 A解析 ∵cos α≤0,sin α>0,∴角α的终边落在第二象限或y 轴的正半轴上.∴⎩⎪⎨⎪⎧3a -9≤0,a +2>0, ∴-2<a ≤3. (2)(2017·石家庄模拟)若-3π4<α<-π2,从单位圆中的三角函数线观察sin α,cos α,tan α的大小是( )A .sin α<tan α<cos αB .cos α<sin α<tan αC .sin α<cos α<tan αD .tan α<sin α<cos α 答案 C解析 如图,作出角α的正弦线MP ,余弦线OM ,正切线AT , 观察可知sin α<cos α<tan α.数形结合思想在三角函数中的应用典例 (1)如图,在平面直角坐标系xOy 中,一单位圆的圆心的初始位置在(0,1),此时圆上一点P 的位置在(0,0),圆在x 轴上沿正向滚动.当圆滚动到圆心位于C (2,1)时,OP →的坐标为.(2)(2017·合肥调研)函数y =lg(3-4sin 2x )的定义域为.思想方法指导 在坐标系中研究角就是一种数形结合思想,利用三角函数线可直观得到有关三角函数的不等式的解集. 解析 (1)如图所示,过圆心C 作x 轴的垂线,垂足为A ,过P 作x 轴的垂线与过C 作y 轴的垂线交于点B .因为圆心移动的距离为2,所以劣弧P A =2,即圆心角∠PCA =2, 则∠PCB =2-π2,所以PB =sin ⎝⎛⎭⎫2-π2=-cos 2, CB =cos ⎝⎛⎭⎫2-π2=sin 2,设点P (x P ,y P ), 所以x P =2-CB =2-sin 2,yP =1+PB =1-cos 2, 所以OP →=(2-sin 2,1-cos 2).(2)因为3-4sin 2x >0, 所以sin 2x <34,所以-32<sin x <32. 利用三角函数线画出x 满足条件的终边范围(如图阴影部分所示), 所以x ∈⎝⎛⎭⎫k π-π3,k π+π3(k ∈Z ). 答案 (1)(2-sin 2,1-cos 2) (2)⎝⎛⎭⎫k π-π3,k π+π3(k ∈Z )1.角-870°的终边所在的象限是( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限答案 C解析 由-870°=-1 080°+210°,知-870°角和210°角的终边相同,在第三象限. 2.(2017·石家庄模拟)已知点P ⎝⎛⎭⎫32,-12在角θ的终边上,且θ∈[0,2π),则θ的值为( )A.5π6B.2π3C.11π6D.5π3答案 C解析 由已知得tan θ=-33,θ在第四象限且θ∈[0,2π),∴θ=11π6. 3.(2017·福州模拟)已知角θ的终边经过点P (4,m ),且sin θ=35,则m 等于( )A .-3B .3 C.163 D .±3答案 B 解析 sin θ=m 16+m 2=35,且m >0,解得m =3.4.(2018·成都模拟)点P 从(1,0)出发,沿单位圆逆时针方向运动2π3弧长到达Q 点,则Q 点的坐标为 ( ) A.⎝⎛⎭⎫-12,32 B.⎝⎛⎭⎫-32,-12 C.⎝⎛⎭⎫-12,-32D.⎝⎛⎭⎫-32,12 答案 A解析 由三角函数定义可知Q 点的坐标(x ,y )满足 x =cos2π3=-12,y =sin 2π3=32. 5.已知扇形的面积为2,扇形圆心角的弧度数是4,则扇形的周长为( ) A .2 B .4 C .6 D .8 答案 C解析 设扇形的半径为R ,则12×4×R 2=2,∴R =1,弧长l =4,∴扇形的周长为l +2R =6.6.已知α是第二象限的角,其终边上一点为P (x ,5),且cos α=24x ,则tan α等于( ) A.155B.153C .-155D .-153答案 D 解析 ∵x x 2+5=24x 且α在第二象限,∴x =-3,∴tan α=5-3=-153. 7.(2017·怀化模拟)sin 2·cos 3·tan 4的值( )A .小于0B .大于0C .等于0D .不存在答案 A解析 ∵sin 2>0,cos 3<0,tan 4>0,∴sin 2·cos 3·tan 4<0.8.给出下列命题:①第二象限角大于第一象限角;②三角形的内角是第一象限角或第二象限角;③不论是用角度制还是用弧度制度量一个角,它们与扇形的半径的大小无关;④若sin α=sin β,则α与β的终边相同;⑤若cos θ<0,则θ是第二或第三象限的角.其中正确命题的个数是( )A .1B .2C .3D .4答案 A解析 举反例:第一象限角370°不小于第二象限角100°,故①错;当三角形的内角为90°时,其既不是第一象限角,也不是第二象限角,故②错;③正确;由于sin π6=sin 5π6,但π6与5π6的终边不相同,故④错;当cos θ=-1,θ=π时,其既不是第二象限角,也不是第三象限角,故⑤错.综上可知只有③正确.9.(2017·鄂州模拟)已知tan θ<0,且角θ终边上一点为(-1,y ),且cos θ=-12,则y =. 答案 3 解析 由已知得θ在第二象限,∴y >0,∴cos θ=-1y 2+1=-12,∴y = 3. 10.已知扇形的圆心角为π6,面积为π3,则扇形的弧长等于. 答案 π3解析 设扇形半径为r ,弧长为l ,则⎩⎨⎧ l r =π6,12lr =π3, 解得⎩⎪⎨⎪⎧ l =π3,r =2.11.函数y = sin x -32的定义域为. 答案 ⎣⎡⎦⎤2k π+π3,2k π+23π,k ∈Z 解析 利用三角函数线(如图),由sin x ≥32,可知 2k π+π3≤x ≤2k π+23π,k ∈Z . 12.满足cos α≤-12的角α的集合为. 答案 ⎩⎨⎧⎭⎬⎫α⎪⎪2k π+23π≤α≤2k π+43π,k ∈Z解析 作直线x =-12交单位圆于C ,D 两点,连接OC ,OD ,则OC 与OD 围成的区域(图中阴影部分)即为角α终边的范围,故满足条件的角α的集合为⎩⎨⎧⎭⎬⎫α⎪⎪2k π+23π≤α≤2k π+43π,k ∈Z .13.已知sin α>sin β,那么下列命题成立的是( )A .若α,β是第一象限的角,则cos α>cos βB .若α,β是第二象限的角,则tan α>tan βC .若α,β是第三象限的角,则cos α>cos βD .若α,β是第四象限的角,则tan α>tan β答案 D解析 如图,当α在第四象限时,作出α,β的正弦线M 1P 1,M 2P 2和正切线AT 1,AT 2,观察知当sin α>sin β时,tan α>tan β.14.已知点P (sin α+cos α,tan α)在第四象限,则在[0,2π]内α的取值范围是.答案 ⎝⎛⎭⎫π2,34π∪⎝⎛⎭⎫74π,2π 解析 由⎩⎪⎨⎪⎧sin α+cos α>0,tan α<0, 得-1<tan α<0或tan α<-1.又0≤α≤2π,∴π2<α<34π或74π<α<2π.15.(2017·烟台模拟)若角α的终边与直线y =3x 重合,且sin α<0,又P (m ,n )是角α终边上一点,且|OP |=10,则m -n =.答案 2解析 由已知tan α=3,∴n =3m ,又m 2+n 2=10,∴m 2=1.又sin α<0,∴m =-1,∴n =-3.故m -n =2.16.如图,在平面直角坐标系xOy 中,角α的始边与x 轴的非负半轴重合且与单位圆相交于A 点,它的终边与单位圆相交于B 点,始边不动,终边在运动.(1)若点B 的横坐标为-45,求tan α的值; (2)若△AOB 为等边三角形,写出与角α终边相同的角β的集合.(3)若α∈⎝⎛⎦⎤0,2π3,请写出弓形AB 的面积S 与α的函数关系式. 解 (1)根据题意可得B ⎝⎛⎭⎫-45,±35,∴tan α=±34. (2)若△AOB 为等边三角形,则B ⎝⎛⎭⎫12,32或B ⎝⎛⎭⎫12,-32, 当B ⎝⎛⎭⎫12,32时,tan ∠AOB =3,∠AOB =π3; 当B ⎝⎛⎭⎫12,-32时,tan ∠AOB =-3,∠AOB =-π3. ∴与角α终边相同的角β的集合是 ⎩⎨⎧⎭⎬⎫β⎪⎪β=π3+2k π或β=-π3+2k π,k ∈Z . (3)若α∈⎝⎛⎦⎤0,2π3,则S 扇形=12αr 2=12α, 而S △AOB =12×1×1×sin α=12sin α, 故弓形AB 的面积S =12α-12sin α,α∈⎝⎛⎦⎤0,2π3.。
【2019版课标版】高考数学文科精品课件§4.4 解三角形
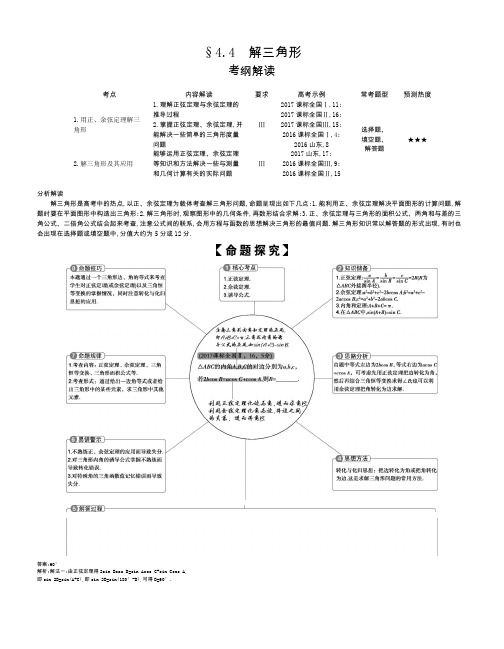
§4.4解三角形考纲解读分析解读解三角形是高考中的热点,以正、余弦定理为载体考查解三角形问题,命题呈现出如下几点:1.能利用正、余弦定理解决平面图形的计算问题,解题时要在平面图形中构造出三角形;2.解三角形时,观察图形中的几何条件,再数形结合求解;3.正、余弦定理与三角形的面积公式、两角和与差的三角公式、二倍角公式结合起来考查,注意公式间的联系,会用方程与函数的思想解决三角形的最值问题.解三角形知识常以解答题的形式出现,有时也会出现在选择题或填空题中,分值大约为5分或12分.答案:60°解析:解法一:由正弦定理得2sin Bcos B=sin Acos C+sin Ccos A,即sin 2B=sin(A+C),即sin 2B=sin(180°-B),可得B=60°.解法二:由余弦定理得2b·-=a·-+c·-,即b·-=b,所以a2+c2-b2=ac,所以cos B=,又0°<B<180°,所以B=60°.五年高考考点一用正、余弦定理解三角形1.(2017课标全国Ⅰ,11,5分)△ABC的内角A,B,C的对边分别为a,b,c.已知sin B+sin A(sin C-cos C)=0,a=2,c=,则C=()A. B. C. D.答案B2.(2016山东,8,5分)△ABC中,角A,B,C的对边分别是a,b,c.已知b=c,a2=2b2(1-sin A).则A=()A. B. C. D.答案C3.(2015广东,5,5分)设△ABC的内角A,B,C的对边分别为a,b,c.若a=2,c=2,cos A=且b<c,则b=()A.3B.2C.2D.答案C4.(2014江西,5,5分)在△ABC中,内角A,B,C所对边的分别是a,b,c.若3a=2b,则-的值为()A.-B.C.1D.答案D5.(2013安徽,9,5分)设△ABC的内角A,B,C所对边的长分别为a,b,c.若b+c=2a,3sin A=5sin B,则角C=()A. B. C. D.答案B6.(2017课标全国Ⅲ,15,5分)△ABC的内角A,B,C的对边分别为a,b,c.已知C=60°,b=则A=.答案75°7.(2016北京,13,5分)在△ABC中,∠A=,a=c,则=.答案 18.(2015重庆,13,5分)设△ABC的内角A,B,C的对边分别为a,b,c,且a=2,cos C=-,3sin A=2sin B,则c=.答案 49.(2016浙江,16,14分)在△ABC中,内角A,B,C所对的边分别为a,b,c.已知b+c=2acos B.(1)证明:A=2B;(2)若cos B=,求cos C的值.解析(1)证明:由正弦定理得sin B+sin C=2sin Acos B,故2sin Acos B=sin B+sin(A+B)=sin B+sin Acos B+cos Asin B,于是sin B=sin(A-B).又A,B∈(0,π),故0<A-B<π,所以,B=π-(A-B)或B=A-B,因此A=π(舍去)或A=2B,所以,A=2B.(2)由cos B=得sin B=,cos 2B=2cos2B-1=-,故cos A=-,sin A=,cos C=-cos(A+B)=-cos Acos B+sin Asin B=.10.(2016四川,18,12分)在△ABC中,角A,B,C所对的边分别是a,b,c,且+=.(1)证明:sin Asin B=sin C;(2)若b2+c2-a2=bc,求tan B.解析(1)证明:根据正弦定理,可设===k(k>0).则a=ksin A,b=ksin B,c=ksin C.代入+=中,有+=,变形可得sin Asin B=sin Acos B+cos Asin B=sin(A+B).在△ABC中,由A+B+C=π,有sin(A+B)=sin(π-C)=sin C,所以sin Asin B=sin C.(2)由已知,b2+c2-a2=bc,根据余弦定理,有cos A=-=.所以sin A==.由(1),sin Asin B=sin Acos B+cos Asin B,所以sin B=cos B+sin B,故tan B==4.11.(2015山东,17,12分)△ABC中,角A,B,C所对的边分别为a,b,c.已知cos B=,sin(A+B)=,ac=2,求sin A和c的值. 解析在△ABC中,由cos B=,得sin B=,因为A+B+C=π,所以sin C=sin(A+B)=.因为sin C<sin B,所以C<B,可知C为锐角,所以cos C=.因此sin A=sin(B+C)=sin Bcos C+cos Bsin C=×+×=.由=,可得a===2c,又ac=2,所以c=1.教师用书专用(12—23)12.(2013辽宁,6,5分)在△ABC中,内角A,B,C的对边分别为a,b,c.若asin Bcos C+csin Bcos A=b,且a>b,则∠B=()A. B. C. D.答案A13.(2013北京,5,5分)在△ABC中,a=3,b=5,sin A=,则sin B=()A. B. C. D.1答案B14.(2013湖南,5,5分)在锐角△ABC中,角A,B所对的边长分别为a,b.若2asin B=则角A等于()A. B. C. D.答案A15.(2015福建,14,4分)若△ABC中,AC=,A=45°,C=75°,则BC=.答案16.(2015安徽,12,5分)在△ABC中,AB=∠A=75°,∠B=45°,则AC=.答案 217.(2015北京,11,5分)在△ABC中,a=3,b=,∠A=,则∠B=.答案18.(2014山东,17,12分)△ABC中,角A,B,C所对的边分别为a,b,c.已知a=3,cos A=,B=A+.(1)求b的值;(2)求△ABC的面积.解析(1)在△ABC中,由题意知,sin A==,因为B=A+,所以sin B=sin=cos A=.由正弦定理可得b===3(2)由B=A+得cos B=cos=-sin A=-.由A+B+C=π,得C=π-(A+B).所以sin C=sin[π-(A+B)]=sin(A+B)=sin Acos B+cos Asin B=×-+×=.因此△ABC的面积S=absin C=×3×3×=.19.(2014课标Ⅱ,17,12分)四边形ABCD的内角A与C互补,AB=1,BC=3,CD=DA=2.(1)求C和BD;(2)求四边形ABCD的面积.解析(1)由题设及余弦定理得BD2=BC2+CD2-2BC·CDcos C=13-12cos C,①BD2=AB2+DA2-2AB·DAcos A=5+4cos C.②由①,②得cos C=,故C=60°,BD=.(2)四边形ABCD的面积S=AB·DAsin A+BC·CDsin C=sin 60°=2.20.(2014陕西,16,12分)△ABC的内角A,B,C所对的边分别为a,b,c.(1)若a,b,c成等差数列,证明:sin A+sin C=2sin(A+C);(2)若a,b,c成等比数列,且c=2a,求cos B的值.解析(1)证明:∵a,b,c成等差数列,∴a+c=2b.由正弦定理得sin A+sin C=2sin B.∵sin B=sin[π-(A+C)]=sin(A+C),∴sin A+sin C=2sin(A+C).(2)由题设有b2=ac,∵c=2a,∴b=a,由余弦定理得cos B=-=-=.21.(2014湖南,19,13分)如图,在平面四边形ABCD中,DA⊥AB,DE=1,EC=,EA=2,∠ADC=,∠BEC=.(1)求sin∠CED的值;(2)求BE的长.解析设∠CED=α.(1)在△CDE中,由余弦定理得EC2=CD2+DE2-2CD·DE·cos∠EDC,得7=CD2+1+CD,即CD2+CD-6=0,解得CD=2(CD=-3舍去). 在△CDE中,由正弦定理得=,得sin α=·==,即sin∠CED=.(2)由题设知,0<α<,于是由(1)知,cos α===.而∠AEB=-α,所以cos∠AEB=cos-=cos cos α+sin sin α=-cos α+sin α=-×+×=.在Rt△EAB中,cos∠AEB==,故BE===4.∠22.(2013湖北,18,12分)在△ABC中,角A,B,C所对应的边分别是a,b,c.已知cos 2A-3cos(B+C)=1.(1)求角A的大小;(2)若△ABC的面积S=5,b=5,求sin Bsin C的值.解析(1)由cos 2A-3cos(B+C)=1,得2cos2A+3cos A-2=0,即(2cos A-1)(cos A+2)=0,解得cos A=或cos A=-2(舍去).因为0<A<π,所以A=.(2)由S=bcsin A=bc·=bc=5,得bc=20.又b=5,所以c=4.由余弦定理得a2=b2+c2-2bccos A=25+16-20=21,故a=由正弦定理得sin Bsin C=sin A·sin A=sin2A=×=.23.(2013天津,16,13分)在△ABC中,内角A,B,C所对的边分别是a,b,c.已知bsin A=3csin B,a=3,cos B=.(1)求b的值;(2)求sin-的值.解析(1)在△ABC中,由=,可得bsin A=asin B,又由bsin A=3csin B,可得a=3c,又a=3,故c=1.由b2=a2+c2-2accos B,cos B=,可得b=.(2)由cos B=,得sin B=,进而得cos 2B=2cos2B-1=-,sin 2B=2sin Bcos B=.所以sin-=sin 2Bcos-cos 2Bsin=.考点二解三角形及其应用1.(2016课标全国Ⅲ,9,5分)在△ABC中,B=,BC边上的高等于BC,则sin A=()A. B. C. D.答案D2.(2014四川,8,5分)如图,从气球A上测得正前方的河流的两岸B,C的俯角分别为75°,30°,此时气球的高是60 m,则河流的宽度BC等于()A.240(-1)mB.180(-1)mC.120(-1)mD.30(+1)m答案C3.(2013课标全国Ⅰ,10,5分)已知锐角△ABC的内角A,B,C的对边分别为a,b,c,23cos2A+cos 2A=0,a=7,c=6,则b=()A.10B.9C.8D.5答案D4.(2013课标全国Ⅱ,4,5分)△ABC的内角A,B,C的对边分别为a,b,c,已知b=2,B=,C=,则△ABC的面积为()A.2+2B.+1C.2-2D.-1答案B5.(2017浙江,14,5分)已知△ABC,AB=AC=4,BC=2.点D为AB延长线上一点,BD=2,连接CD,则△BDC的面积是,cos∠BDC=.答案;6.(2016课标全国Ⅱ,15,5分)△ABC的内角A,B,C的对边分别为a,b,c,若cos A=,cos C=,a=1,则b=.答案7.(2014课标Ⅰ,16,5分)如图,为测量山高MN,选择A和另一座山的山顶C为测量观测点.从A点测得M点的仰角∠MAN=60°,C点的仰角∠CAB=45°以及∠MAC=75°;从C点测得∠MCA=60°.已知山高BC=100 m,则山高MN=m.答案1508.(2017山东,17,12分)在△ABC中,角A,B,C的对边分别为a,b,c.已知b=3,·=-6,S△ABC=3,求A和a.解析因为·=-6,所以bccos A=-6,又S△ABC=3,所以bcsin A=6,因此tan A=-1,又0<A<π,所以A=.又b=3,所以c=2.由余弦定理a2=b2+c2-2bccos A,得a2=9+8-2×3×2×-=29,所以a=.9.(2016天津,15,13分)在△ABC中,内角A,B,C所对的边分别为a,b,c.已知asin 2B=bsin A.(2)若cos A=,求sin C的值.解析(1)在△ABC中,由=可得asin B=bsin A,又由asin 2B=bsin A得2asin Bcos B=bsin A=asin B, 所以cos B=,得B=.(2)由cos A=可得sin A=,则sin C=sin[π-(A+B)]=sin(A+B)=sin=sin A+cos A=.10.(2015课标Ⅰ,17,12分)已知a,b,c分别为△ABC内角A,B,C的对边,sin2B=2sin Asin C.(1)若a=b,求cos B;(2)设B=90°,且a=求△ABC的面积.解析(1)由题设及正弦定理可得b2=2ac.又a=b,所以b=2c,a=2c.由余弦定理可得cos B=-=.(6分)(2)由(1)知b2=2ac.因为B=90°,所以由勾股定理得a2+c2=b2.故a2+c2=2ac,故c=a=.所以△ABC的面积为1.(12分)11.(2015课标Ⅱ,17,12分)△ABC中,D是BC上的点,AD平分∠BAC,BD=2DC.(1)求∠∠;(2)若∠BAC=60°,求∠B.解析(1)由正弦定理得∠=∠,∠=∠.因为AD平分∠BAC,BD=2DC,所以∠==.(2)因为∠C=180°-(∠BAC+∠B),∠BAC=60°,所以sin∠C=sin(∠BAC+∠B)=cos∠B+sin∠B.由(1)知2sin∠B=sin∠C,所以tan∠B=,即∠B=30°.教师用书专用(12—25)12.(2013山东,7,5分)△ABC的内角A,B,C所对的边分别为a,b,c.若B=2A,a=1,b=,则c=()A.2B.2C. D.113.(2013陕西,9,5分)设△ABC的内角A,B,C所对的边分别为a,b,c,若bcos C+ccos B=asin A,则△ABC的形状为()A.直角三角形B.锐角三角形C.钝角三角形D.不确定答案A14.(2017江苏,18,16分)如图,水平放置的正四棱柱形玻璃容器Ⅰ和正四棱台形玻璃容器Ⅱ的高均为32 cm,容器Ⅰ的底面对角线AC的长为10 cm,容器Ⅱ的两底面对角线EG,E1G1的长分别为14 cm和62 cm.分别在容器Ⅰ和容器Ⅱ中注入水,水深均为12 cm.现有一根玻璃棒l,其长度为40 cm.(容器厚度、玻璃棒粗细均忽略不计)(1)将l放在容器Ⅰ中,l的一端置于点A处,另一端置于侧棱CC1上,求l没入水中部分的长度;(2)将l放在容器Ⅱ中,l的一端置于点E处,另一端置于侧棱GG1上,求l没入水中部分的长度.解析(1)由正棱柱的定义,CC1⊥平面ABCD,所以平面A1ACC1⊥平面ABCD,CC1⊥AC.记玻璃棒的另一端落在CC1上点M处.因为AC=10,AM=40,所以MC=-=30,从而sin∠MAC=.记AM与水面的交点为P1,过P1作P1Q1⊥AC,Q1为垂足,则P1Q1⊥平面ABCD,故P1Q1=12,=16.从而AP1=∠答:玻璃棒l没入水中部分的长度为16 cm.(如果将“没入水中部分”理解为“水面以上部分”,则结果为24 cm)(2)如图,O,O1是正棱台的两底面中心.由正棱台的定义,OO1⊥平面EFGH,所以平面E1EGG1⊥平面EFGH,O1O⊥EG.同理,平面E1EGG1⊥平面E1F1G1H1,O1O⊥E1G1.记玻璃棒的另一端落在GG1上点N处.过G作GK⊥E1G1,K为垂足,则GK=OO1=32.因为EG=14,E1G1=62,所以KG1==24,从而GG1===40.设∠EGG1=α,∠ENG=β,则sin α=sin∠=cos∠KGG1=.因为<α<π,所以cos α=-.在△ENG中,由正弦定理可得=,解得sin β=.因为0<β<,所以cos β=.于是sin∠NEG=sin(π-α-β)=sin(α+β)=sin αcos β +cos αsin β=×+-×=.记EN与水面的交点为P2,过P2作P2Q2⊥EG,Q2为垂足,则P2Q2⊥平面EFGH,故P2Q2=12,从而EP2==20.答:玻璃棒l没入水中部分的长度为20 cm.(如果将“没入水中部分”理解为“水面以上部分”,则结果为20 cm)15.(2015陕西,17,12分)△ABC的内角A,B,C所对的边分别为a,b,c.向量m=(a,b)与n=(cos A,sin B)平行.(1)求A;(2)若a=求△ABC的面积.解析(1)因为m∥n,所以asin B-由正弦定理,得sin Asin B-sin Bcos A=0,又sin B≠0,从而tan A=,由于0<A<π,所以A=.(2)解法一:由余弦定理,得a2=b2+c2-2bccos A,而a=,b=2,A=,得7=4+c2-2c,即c2-2c-3=0,因为c>0,所以c=3.故△ABC的面积为bcsin A=.解法二:由正弦定理,得=,从而sin B=,又由a>b,知A>B,所以cos B=.故sin C=sin(A+B)=sin=sin Bcos +cos Bsin =.所以△ABC的面积为absin C=.16.(2015浙江,16,14分)在△ABC中,内角A,B,C所对的边分别为a,b,c.已知tan=2.(1)求的值;(2)若B=,a=3,求△ABC的面积.解析(1)由tan=2,得tan A=,所以==.(2)由tan A=,A∈(0,π),得sin A=,cos A=.又由a=3,B=及正弦定理=,得b=3.由sin C=sin(A+B)=sin得sin C=.设△ABC的面积为S,则S=absin C=9.17.(2015天津,16,13分)在△ABC中,内角A,B,C所对的边分别为a,b,c.已知△ABC的面积为3,b-c=2,cos A=-.(1)求a和sin C的值;(2)求cos的值.解析(1)在△ABC中,由cos A=-,可得sin A=.由S△ABC=bcsin A=3,得bc=24,结合b-c=2,解得b=6,c=4.由a2=b2+c2-2bccos A,可得a=8.由=,得sin C=.(2)cos=cos 2A·cos-sin 2A·sin=(2cos2A-1)-×2sin A·cos A=-.18.(2015四川,19,12分)已知A,B,C为△ABC的内角,tan A,tan B是关于x的方程x2+px-p+1=0(p∈R)的两个实根.(1)求C的大小;(2)若AB=3,AC=,求p的值.解析(1)由已知得,方程x2+px-p+1=0的判别式Δ=(p)2-4(-p+1)=3p2+4p-4≥0.所以p≤-2,或p≥.由韦达定理,有tan A+tan B=-于是1-tan Atan B=1-(1-p)=p≠0,从而tan(A+B)==-=-.所以tan C=-tan(A+B)=,所以C=60°.(2)由正弦定理,得sin B==°=,解得B=45°,或B=135°(舍去).于是A=180°-B-C=75°.则tan A=tan 75°=tan(45°+30°)=°°==2+.所以p=-(tan A+tan B)=-(2++1)=-1-.19.(2014辽宁,17,12分)在△ABC中,内角A,B,C的对边分别为a,b,c,且a>c.已知·=2,cos B=,b=3.求:(1)a和c的值;(2)cos(B-C)的值.解析(1)由·=2得c·acos B=2.又cos B=,所以ac=6.由余弦定理,得a2+c2=b2+2accos B.又b=3,所以a2+c2=9+2×2=13.解得a=2,c=3或a=3,c=2.因为a>c,所以a=3,c=2.(2)在△ABC中,sin B===.由正弦定理,得sin C=sin B=×=.因为a=b>c,所以C为锐角,因此cos C===.于是cos(B-C)=cos Bcos C+sin Bsin C=×+×=.20.(2014大纲全国,18,12分)△ABC的内角A、B、C的对边分别为a、b、c,已知3acos C=2ccos A,tan A=,求B.解析由题设和正弦定理得3sin Acos C=2sin Ccos A.故3tan Acos C=2sin C,因为tan A=,所以cos C=2sin C,tan C=.所以tan B=tan[180°-(A+C)]=-tan(A+C)=-1,=-所以B=135°.21.(2014安徽,16,12分)设△ABC的内角A,B,C所对边的长分别是a,b,c,且b=3,c=1,△ABC的面积为,求cos A与a的值. 解析由三角形面积公式,得×3×1·sin A=,故sin A=.因为sin2A+cos2A=1,所以cos A=±=±=±.①当cos A=时,由余弦定理得a2=b2+c2-2bccos A=32+12-2×1×3×=8,所以a=2.②当cos A=-时,由余弦定理得a2=b2+c2-2bccos A=32+12-2×1×3×-=12,所以a=2.22.(2014重庆,18,13分)在△ABC中,内角A,B,C所对的边分别为a,b,c,且a+b+c=8.(1)若a=2,b=,求cos C的值;(2)若sin Acos2+sin Bcos2=2sin C,且△ABC的面积S=sin C,求a和b的值.解析(1)由题意可知c=8-(a+b)=.由余弦定理得cos C=-=-=-.(2)由sin Acos2+sin Bcos2=2sin C可得sin A·+sin B·=2sin C,化简得sin A+sin Acos B+sin B+sin Bcos A=4sin C.因为sin Acos B+cos Asin B=sin(A+B)=sin C,所以sin A+sin B=3sin C.由正弦定理可知a+b=3c.又因为a+b+c=8,所以a+b=6.由于S=absin C=sin C,所以ab=9,从而a2-6a+9=0,解得a=3,b=3.23.(2013重庆,18,13分)在△ABC中,内角A,B,C的对边分别为a,b,c,且a2=b2+c2+bc.(1)求A;(2)设a=,S为△ABC的面积,求S+3cos Bcos C的最大值,并指出此时B的值.解析(1)由余弦定理得cos A=-=-=-.又因0<A<π,所以A=.(2)由(1)得sin A=,又由正弦定理及a=得S=bcsin A=··asin C=3sin Bsin C,因此,S+3cos Bcos C=3(sin Bsin C+cos Bcos C)=3cos(B-C).所以,当B=C,即B=-=时,S+3cos Bcos C取最大值3.24.(2013浙江,18,14分)在锐角△ABC中,内角A,B,C的对边分别为a,b,c,且2asin B= b.(1)求角A的大小;(2)若a=6,b+c=8,求△ABC的面积.解析(1)由2asin B=b及=,得sin A=.因为A是锐角,所以A=.(2)由a2=b2+c2-2bccos A,得b2+c2-bc=36.又b+c=8,所以bc=.由S=bcsin A,得△ABC的面积为.25.(2013四川,17,12分)在△ABC中,角A,B,C的对边分别为a,b,c,且cos(A-B)cos B-sin(A-B)sin(A+C)=-.(1)求sin A的值;(2)若a=4,b=5,求向量在方向上的投影.解析(1)由cos(A-B)cos B-sin(A-B)sin(A+C)=-,得cos(A-B)cos B-sin(A-B)sin B=-.则cos(A-B+B)=-,即cos A=-.又0<A<π,所以sin A=.(5分)(2)由正弦定理=,得sin B==.由题知a>b,则A>B,故B=.根据余弦定理,有(4)2=52+c2-2×5c×-,解得c=1或c=-7(负值舍去).故向量在方向上的投影为||cos B=.(12分)三年模拟A组2016—2018年模拟·基础题组考点一用正、余弦定理解三角形1.(2018河南中原名校第三次联考,7)△ABC的内角A、B、C的对边分别是a、b、c,若B=2A,a=1,b=,则c=()A.1B.C.2D.2答案C2.(2017湖北黄冈3月质检,6)在△ABC中,角A,B,C的对边分别是a,b,c,若a=b,A=2B,则cos B=()A. B. C. D.答案B3.(2017福建厦门12月联考,6)在锐角△ABC中,a,b,c分别为∠A、∠B、∠C的对边,若向量m=(a-b,1)和n=(c-b,1)平行,且sin B=,当△ABC的面积为时,b=()A. B.C.4D.2+答案A考点二解三角形及其应用4.(2018江西师大附中10月模拟,7)已知△ABC中,满足b=2,B=60°的三角形有两解,则边长a的取值范围是()A.<a<2B.<a<2C.2<a<D.2<a<2答案C5.(2018河南许昌、平顶山联考,8)如图所示,为了测量A,B两处岛屿间的距离,小张以D为观测点,测得A,B分别在D处的北偏西30°、北偏东30°方向,再往正东方向行驶40海里到C处,测得B在C处的正北方向,A在C处的北偏西60°方向,则A,B两处岛屿间的距离为()A.20海里B.40海里C.20(1+)海里D.40海里答案B6.(2018河北衡水中学四调,9)在△ABC中,角A,B,C的对边分别为a,b,c,且2c·cos B=2a+b,若△ABC的面积S=c,则ab的最小值为()A.18B.12C.6D.3答案B7.(2018千校联盟12月模拟,10)在△ABC中,角A,B,C的对边分别为a,b,c.若c=b(cos A+cos B),则△ABC为()A.等腰直角三角形B.直角三角形C.等腰三角形D.等腰三角形或直角三角形答案D8.(2016广东肇庆三模,10)在△ABC中,AB=3,BC=则边AC上的高为()A. B. C. D.3答案B9.(2017江西南昌十校二模,16)在△ABC中,a,b,c分别是内角A,B,C的对边,且B为锐角,若=,sin B=,S△ABC=,则b的值为.答案10.(2017江西六校联考,19)△ABC的内角A、B、C所对的边分别为a,b,c,m=(sin B,5sin A+5sin C)与n=(5sin B-6sin C,sin C-sin A)垂直.(1)求sin A的值;(2)若a=2,求△ABC的面积S的最大值.解析(1)因为m=(sin B,5sin A+5sin C)与n=(5sin B-6sin C,sin C-sin A)垂直,所以m·n=5sin2B-6sin Bsin C+5sin2C-5sin2A=0,即sin2B+sin2C-sin2A=.根据正弦定理得b2+c2-a2=.由余弦定理得cos A=-=.∵角A是△ABC的内角,∴sin A==.(2)由(1)知b2+c2-a2=≥2bc-a2.又∵a=2,∴bc≤10.∵△ABC的面积S==≤4,∴△ABC的面积S的最大值为4.B组2016—2018年模拟·提升题组(满分:70分时间:60分钟)一、选择题(每小题5分,共30分)1.(2018湖南益阳、湘潭9月联考,9)《数书九章》中对“已知三角形三边长求三角形面积”的求法,填补了我国传统数学的一个空白,与著名的海伦公式完全等价,由此可以看出我国古代具有很高的数学水平,其求法是:“以小斜幂并大斜幂减去斜幂,余半之,自乘于上;以小斜幂乘大斜幂,减上,余四约之,为实;一为从隅,开平方得积.”若把这段文字写成公式,即S=--.现有周长为2+的△ABC满足sin A∶sin B∶sinC=(-1)∶∶(+1),用上面给出的公式求得△ABC的面积为()A. B. C. D.答案B2.(2018湖北荆州中学11月模拟,9)在△ABC中,角A,B,C的对边分别为a,b,c,且=-,则角A的最大值为()A. B. C. D.答案A3.(2018四川成都摸底考试,11)△ABC的内角A,B,C的对边分别为a,b,c,且asin A-csin C=(a-b)sin B,c=3,则△ABC的面积的最大值为()A. B. C. D.答案D4.(2017湖南长沙长郡中学12月模拟,6)△ABC的内角A,B,C所对的边分别为a,b,c,已知a=,b=,∠A=,则∠B=()A. B.或 C.或 D.答案B5.(人教A必5,一,1,B2,变式)△ABC中,角A,B,C所对的边分别为a,b,c,若满足c=,acos C=csin A的三角形ABC有两个,则边BC的长度的取值范围是()A.(1,)B.(1,)C.(,2)D.(,2)答案D6.(2016云南昆明三中月考,8)在△ABC中,内角A,B,C的对边分别为a,b,c,若△ABC的面积为S,且2S=(a+b)2-c2,则tan C等于()A. B. C.- D.-答案C二、填空题(共5分)7.(2017山西五校联考,15)已知△ABC的面积为S,三内角A,B,C的对边分别为a,b,c.若4S+a2=b2+c2,则sin C-cos取最大值时,C=. 答案三、解答题(共35分)8.(2018湖北重点高中期中联考,21)在△ABC中,内角A,B,C的对边分别是a,b,c,且-=-.(1)求角B的大小;(2)点D满足=3,且AD=2,求3a+c的取值范围.解析(1)∵-=-,∴由正弦定理得-=-,(2分)∴c(a-c)=(a+b)(a-b),即a2+c2-b2=ac,又∵a2+c2-b2=2accos B,∴cos B=.(4分)∵B∈(0,π),(5分)∴B=.(6分)(2)∵=3,∴BD=3a.在△ABD中,由余弦定理知c2+(3a)2-2·3a·c·cos =22, ∴(3a+c)2-4=3·3ac.(7分)∵a>0,c>0,∴3ac≤,∴(3a+c)2-4≤(3a+c)2,即(3a+c)2≤16,当且仅当3a=c,即a=,c=2时取等号,所以3a+c的最大值为4.(10分)又在△ABD中,3a+c>2,(11分)故3a+c的取值范围是(2,4].(12分)9.(2018河北石家庄摸底考试,17)某学校的平面示意图如图中的五边形区域ABCDE,其中三角形区域ABE为生活区,四边形区域BCDE为教学区,AB,BC,CD,DE,EA,BE为学校的主要道路(不考虑宽度).∠BCD=∠CDE=,∠BAE=,DE=3BC=3CD= km.(1)求道路BE的长度;(2)求生活区△ABE的面积的最大值.解析(1)如图,连接BD,在△BCD中,BD2=BC2+CD2-2BC·CDcos∠BCD=,∴BD= km.∵BC=CD,∠BCD=,∴∠CBD=∠CDB=-=,又∠CDE=,∴∠BDE=.∴在Rt△BDE中,BE===(km). 故道路BE的长度为 km.(6分)(2)设∠ABE=α,∵∠BAE=,∴∠AEB=-α.在△ABE中,∠=∠=∠==,∴AB=sin-km,AE=sin α km.(8分)∴S△ABE=AB·AEsin =sin-sin α=·-km2,∵0<α<, ∴-<2α-<.∴当2α-=,即α=时,S△ABE取得最大值,最大值为×= km2,故生活区△ABE面积的最大值为 km2.(12分)10.(2017山西、河南、河北三省12月联考,17)如图,在△ABC中,sin C=,且<C<π,AB=8,若12sin∠BAC=AB·sin B.(1)求△ABC的面积;(2)已知D在线段BC上,且∠BAD=∠CAD,求sin∠CAD的值以及AD的长.解析(1)记AC=b,BC=a,AB=c,因为sin C=,且<C<π,所以cos C=-=-.因为12sin∠BAC=AB·sin B,且AB=8,所以12sin∠BAC=8sin B,由正弦定理得3a=2b.在△ABC中,c2=a2+b2-2abcos C=a2++2·a··⇒64=4a2,解得a=4,又3a=2b,故b=6.故△ABC的面积S=absin C=×4×6×=3.(2)依(1)得cos∠BAC=-=,又由已知得cos∠BAC=1-2sin2∠CAD,所以sin∠CAD=,故sin∠ADC=sin(∠DAC+∠C)=×-+×=,⇒=⇒AD=.故=∠C组2016—2018年模拟·方法题组方法1正弦定理和余弦定理的应用方法1.(2017广东七校第一次联考,7)在△ABC中,a,b,c是角A,B,C的对边,若a,b,c成等比数列,A=45°,则=()A. B. C. D.答案C2.(2018豫北、豫南精英对抗赛,16)已知锐角△ABC的内角A、B、C的对边分别为a、b、c,其外接圆半径为,b=2,则△ABC的周长的取值范围是.答案(2+2,6]3.(2018河南信阳第一次质检,20)在△ABC中,角A,B,C所对的边分别为a,b,c,且sin A+cos A=2.(1)求角A的大小;(2)现给出三个条件:①a=2;②B=45°;③c=试从中选出两个可以确定△ABC的条件,写出你的选择,并以此为依据求△ABC的面积.(只写出一个方案即可)解析(1)sin A+cos A=2可化为2sin=2,所以sin=1.因为0<A<π,所以A+=,所以A=.(2)方案一:选择①②.在△ABC中,由正弦定理得b==°=2.因为sin C=sin(A+B)=×+×=,所以△ABC的面积为absin C=×2×2×=+1.方案二:选择①③.在△ABC中,由余弦定理得a2=b2+c2-2bccos A=b2+3b2-2·b2cos=b2=4,所以b=2,所以c=2.所以△ABC的面积为bcsin A=×2×2×sin=.说明:若选择②③,则由c=b可得sin C=sin B=>1,故这样的△ABC不存在.4.(2017河北唐山一模,17)已知△ABC的内角A,B,C的对边分别为a,b,c,a2-ab-2b2=0.(1)若B=,求A,C;(2)若C=,c=14,求S△ABC.解析(1)由已知B=,a2-ab-2b2=0结合正弦定理化简整理得2sin2A-sin A-1=0,于是sin A=1或sin A=-(舍).因为0<A<π,所以A=,又A+B+C=π,所以C=π--=.(2)由题意及余弦定理可知a2+b2+ab=196,①由a2-ab-2b2=0得(a+b)(a-2b)=0,因为a+b>0,所以a-2b=0,即a=2b,②联立①②解得b=2,a=4.所以S△ABC=absin C=14.方法2三角形形状的判断方法5.(2018湖南师大附中12月月考,6)在△ABC中,若=,则△ABC的形状是()A.等腰三角形B.直角三角形C.等腰直角三角形D.等腰三角形或直角三角形答案D6.(2017湖北荆州中学12月模拟,9)a,b,c为△ABC三边长,a≠1,b<c,若log(c+b)a+log(c-b)a=2log(c+b)alog(c-b)a,则△ABC的形状为()A.锐角三角形B.直角三角形C.钝角三角形D.无法确定答案B7.(2016江西丰城中学月考,10)在△ABC中,已知2acos B=c,sin Asin B·(2-cos C)=sin2+,则△ABC为()A.等边三角形B.钝角三角形C.锐角非等边三角形D.等腰直角三角形答案D方法3解三角形应用题的方法8.(2017湖北七校联考,16)三国魏人刘徽自撰《海岛算经》,专论测高望远.其中有一题:今有望海岛,立两表齐,高三丈,前后相去千步,令后表与前表相直.从前表却行一百二十三步,人目著地取望岛峰,与表末参合.从后表却行一百二十七步,人目著地取望岛峰,亦与表末参合.问岛高及去表各几何?译文如下:要测量海岛上一座山峰A的高度AH,立两根高均为3丈的标杆BC和DE,前后标杆相距1 000步,使后标杆杆脚D与前标杆杆脚B与山峰脚H 在同一直线上,从前标杆杆脚B退行123步到F,人眼著地观测到岛峰,A、C、F三点共线,从后标杆杆脚D退行127步到G,人眼著地观测到岛峰,A、E、G三点也共线,则岛峰的高度AH=步.(古制:1步=6尺,1里=180丈=1 800尺=300步)答案 1 2559.(2016吉林五校第一次联考,14)2015年8月6日凌晨,马来西亚总理纳吉布在吉隆坡确认,7月29日在法属留尼汪岛发现的飞机残骸来自515天前失联的马航MH370.若一架侦察机以500米/秒的速度在留尼汪岛上空平行于地面匀速飞行时,发现飞机残骸在侦察机前方且俯角为30°的地面上,半分钟后,侦察机发现飞机残骸仍在其前方且俯角为75°的地面上,则侦察机的飞行高度是米.(保留根号)答案 3 750(+1)10.(2018河南商丘九校12月联考,20)如图所示,某公路AB一侧有一块空地△OAB,其中OA=3 km,OB=3 km,∠AOB=90°,当地政府拟在中间开挖一个人工湖△OMN,其中M,N都在边AB上(M,N不与A,B重合,M在A,N之间),且∠MON=30°.(1)若M在距离A点2 km处,求点M,N之间的距离;(2)为节省投入资金,人工湖△OMN的面积要尽可能小,试确定M的位置,使△OMN的面积最小,并求出最小面积.解析(1)在△OAB中,因为OA=3,OB=3∠AOB=90°,所以∠OAB=60°.在△OAM中,由已知及余弦定理得OM2=AO2+AM2-2AO·AM·cos A=7,所以OM=,所以cos∠AOM=-=,在△OAN中,sin∠ONA=sin(∠A+∠AON)=sin(∠AOM+90°)=cos∠AOM=.在△OMN中,由=得MN=×=.故点M,N之间的距离为 km.(2)设∠AOM=θ,0<θ<.在△OAM中,由=得OM=.在△OAN中,由∠=∠得ON==.所以S△OMN=OM·ON·sin∠MON=···====,因为0<θ<,所以2θ+∈,所以当2θ+=,即θ=时,S△OMN取最小值. 所以应设计∠AOM=,可使△OMN的面积最小,最小面积是 km2.。
2019版文科数学讲义:第四章 三角函数 解三角形4.1 含答案

§4.1任意角、弧度制及任意角的三角函数最新考纲考情考向分析1.了解任意角的概念和弧度制的概念.2.能进行弧度与角度的互化.3。
理解任意角三角函数(正弦、余弦、正切)的定义.以理解任意角三角函数的概念、能进行弧度与角度的互化和扇形弧长、面积的计算为主,常与向量、三角恒等变换相结合,考查三角函数定义的应用及三角函数的化简与求值,考查分类讨论思想和数形结合思想的应用意识.题型以选择题为主,低档难度。
1.角的概念(1)角的分类(按旋转的方向)角错误!(2)象限角(3)终边相同的角所有与α终边相同的角,包括α本身构成一个集合,这个集合可记为S={β|β=α+k·360°,k∈Z}.2.弧度制(1)定义:长度等于半径长的圆弧所对的圆心角叫做1弧度的角,正角的弧度数是正数,负角的弧度数是负数,零角的弧度数是零.(2)角度制和弧度制的互化:180°=π rad,1°=错误!rad,1 rad=错误!°. (3)扇形的弧长公式:l=|α|r,扇形的面积公式:S=错误!lr=错误!|α|r2.3.任意角的三角函数的定义α为任意角,α的终边上任意一点P (异于原点)的坐标(x ,y ),它与原点的距离OP =r =错误! (r >0),则sin α=y r ;cos α=错误!;tan α=错误!;cot α=错误!;sec α=错误!;csc α=错误!.4.三角函数在各象限的符号规律及三角函数线(1)三角函数在各象限的符号:象限符号函数Ⅰ Ⅱ Ⅲ Ⅳsin α,csc α + + - -cos α,sec α + - - +tan α,cot α + - + -(2)三角函数线:正弦线 如图,角α的正弦线为错误!。
余弦线 如图,角α的余弦线为错误!。
正切线 如图,角α的正切线为错误!.知识拓展三角函数值的符号规律三角函数值在各象限内的符号:一全正、二正弦、三正切、四余弦.题组一思考辨析1.判断下列结论是否正确(请在括号中打“√"或“×”)(1)锐角是第一象限的角,第一象限的角也都是锐角.(×)(2)角α的三角函数值与其终边上点P的位置无关.(√) (3)不相等的角终边一定不相同.(×)(4)若α为第一象限角,则sin α+cos α〉1。
2019届高考数学一轮复习课件(文科): 第四章 三角函数、解三角形 4.7 解三角形课件 文 新人教A版

(1)√ (2)√ (3)× (4)√ (5)×
答案
-9知识梳理 双基自测 自测点评
1 2 3 4 5
2.△ABC 的内角 A,B,C 的对边分别为 a,b,c.已知 a=√5,c=2,cos
2 A= ,则 3
b=(
) B.√3 C.2 DБайду номын сангаас3
A.√2
关闭
D
答案
-10知识梳理 双基自测 自测点评
1
2
3 4
正弦定理 解 决 的 问 题 (1)已知两角和任一边,求其他 两边和一角; (2)已知两边和其中一边的对 角,求另一边和其他两角
余弦定理 (1)已知三边,求三个角; (2)已知两边和它们的夹 角,求第三边和其他两角
-4知识梳理 双基自测 自测点评
1 2 3 4
2.三角形中的常见结论 (1)在△ABC中,A+B+C=π. (2)在△ABC中,A>B⇔a>b⇔sin A>sin B. (3)任意两边之和大于第三边,任意两边之差小于第三边.
-14考点1 考点2 考点3 考点4
考点 1 利用正弦、余弦定理解三角形
例1在△ABC中,角A,B,C的对边分别是
a,b,c,已知 cos 2A=- ,c=√3,sin A=√6sin C.
(1)求a的值; (2)若角A为锐角,求b的值及△ABC的面积. 思考已知怎样的条件能用正弦定理解三角形?已知怎样的条件能 用余弦定理解三角形?
关闭
由题意和正弦定理,可得 2sin B cos B=sin A cos C+sin Ccos 1 A=sin(A+C)=sin B,即 cos B= . 又因为 B∈(0,π),所以 B= . π
2019届高考数学一轮复习第四章三角函数解三角形4-4三角恒等变换课件文

(2)4cos50°-tan40°=4sin40°-tan40°
=4sin40°ccooss4400°°-sin40°=2sin80°-cossin403°0°+10°
=2cos10°-12ccooss1400°°-
3 2 sin10°
=32cos10c°o-s4023°sin10°
= 3 cosc3o0s°4+0°10°= 3. [答案] (1)1 (2) 3
第
四
三角函数 解三角形
章
第四节
三角恒等变换
高考概览 1.巧变角:三角函数式中往往出现较多的差异角,注意观察 角与角之间的和、差、倍、互补、互余等关系,运用角的变换, 化多角为单角或减少未知角的数目,连接条件角与待求角,使问 题顺利获解.对角变换时:(1)可以通过诱导公式、两角和与差的 三角公式等;(2)注意倍角的相对性;(3)注意拆角、拼角技巧,例 如,2α=(α+β)+(α-β),α=(α+β)-β=(α-β)+β,β=α+2 β- α-2 β=(α+2β)-(α+β),α-β=(α-γ)+(γ-β),15°=45°-30°,
(2)三角函数求值的方法策略
类型
要点
给角 关键是正确地选用公式,以便把非特殊角的三角
求值 函数相约或相消,从而化为特殊角的三角函数
类型
要点
给出某些角的三角函数值,求另外一些角的 给值
三角函数值,解题关键在于“变角”,使其 求值
角相同或具有某种关系
给值 实质是转化为给值求值,关键是变角,把所
求角 求角用含已知角的式子表示,由所得的函数
角度 1:给角求值 (1)化简:sin50°(1+ 3tan10°)=________.
(2)4cos50°-tan40°=________. 化成“一角一
2019高考数学文一轮复习第4章三角函数与解三角形章末总结含解析

❶ 理解同角三角函数的基本关系式:sin 2x +cos 2x =1,sin x=tan x . ❷ 能利用单位圆中的三角函数线推导出 ±α,π±α 的正弦、余弦、正切的诱小值以及与 x 轴的交点等),理解正切函数在区间⎝-2,2⎭内的单调性..A.- B .- 9 9章末总结知识点考纲展示任意角的概念与弧度制、任意角的三角函数同角三角函 数的基本关 系式与诱导公式和与差的三 角函数公式简单的三角 恒等变换三角函数的 图象与性质函数 y = A sin(ω x +φ) 的图象及三 角函数模型 的简单应用正弦定理和 余弦定理解三角形应 用举例❶ 了解任意角的概念.❷ 了解弧度制的概念,能进行弧度与角度的互化.❸ 理解任意角三角函数(正弦、余弦、正切)的定义.cos xπ2导公式.❶ 会用向量的数量积推导出两角差的余弦公式.❷ 能利用两角差的余弦公式导出两角差的正弦、正切公式.❸ 能利用两角差的余弦公式导出两角和的正弦、余弦、正切公式,导出二倍 角的正弦、余弦、正切公式,了解它们的内在联系.能运用公式进行简单的恒等变换(包括导出积化和差、和差化积、半角公式, 但对这三组公式不要求记忆).❶ 能画出 y =sin x ,y =cos x ,y =tan x 的图象,了解三角函数的周期性. ❷ 理解正弦函数、余弦函数在区间[0,2π]上的性质(如单调性、最大值和最⎛ π π⎫❶ 了解函数 y =A sin(ωx +φ)的物理意义;能画出函数 y =A sin(ωx +φ)的图象,了解参数 A ,ω,φ 对函数图象变化的影响.❷ 了解三角函数是描述周期变化现象的重要函数模型,会用三角函数解决一 些简单实际问题.掌握正弦定理、余弦定理,并能解决一些简单的三角形度量问题能够运用正弦定理、余弦定理等知识和方法解决一些与测量和几何计算有关 的实际问题.一、点在纲上,源在本里 考点考题4(2017· 高考全国卷Ⅲ,T 4,5 分)已知 sin α-cos α=3,则 sin 2α=考源三角函数的基本关系( )7 2 9 92 7 C. D.必修 4 P 146A 组T 6(2)(2017· 高考全国卷Ⅱ,T 3,5 分)函数 f (x )=sin ⎝2x +3⎭的最小正周期A.4π B .2π C .πD. A. B .1 C. D. sin ⎝2x + 3 ⎭,则下面结论正确的是( 分别为 a ,b ,c 已知△. ABC 的面积为 .1.(必修 4 P 146A 组 T 6(3)改编)已知 sin 2θ= ,则 sin 4θ+cos 4θ 的值为()3A . 9C . 9三角函数 的周期三角函数 值域三角函数 图象正余弦定理与面积公式 的应用⎛ π⎫为( )π 21 π π(2017· 高考全国卷Ⅲ,T 6,5 分)函数 f (x )=5sin(x +3)+cos(x -6)的最大值为( )6 3 15 5 5(2017·高考全国卷Ⅰ,T 9,5 分)已知曲线 C 1:y =cos x ,C 2:y =⎛ 2π⎫ )A .把 C 1 上各点的横坐标伸长到原来的 2 倍,纵坐标不变,再把π得到的曲线向右平移6个单位长度,得到曲线 C 2B .把C 1 上各点的横坐标伸长到原来的 2 倍,纵坐标不变,再把 π得到的曲线向左平移12个单位长度,得到曲线 C 21C .把 C 1 上各点的横坐标缩短到原来的2倍,纵坐标不变,再把得π到的曲线向右平移6个单位长度,得到曲线 C 21D .把 C 1 上各点的横坐标缩短到原来的2倍,纵坐标不变,再把得π到的曲线向左平移12个单位长度,得到曲线 C 2(2017· 高考全国卷Ⅱ,T 16,5 分△) ABC 的内角 A ,B ,C 的对边分 别为 a ,b ,c ,若 2b cos B =a cos C +c cos A ,则 B =________.(2017· 高考全国卷Ⅲ,T 15,5 分△) ABC 的内角 A ,B ,C 的对边分 别为 a ,b ,c .已知 C =60°,b = 6,c =3,则 A =________.(2017· 高考全国卷Ⅰ,T 17,12 分△) ABC 的内角 A ,B ,C 的对边 a 23sin A(1)求 sin B sin C ;必修 4 P 35 例2(2)必修 4 P 143A 组T 5必修 4 P 55 练习T 2(2)必修 5 P 18 练习T 3 必修 5 P 10A 组 T 2(1)必修 5 P 20B 组T 1(2)若 6cos B cos C =1,a =△3,求 ABC 的周长.二、根置教材,考在变中 一、选择题24 92 35 B.7 D.解析:选D.因为sin2θ=,所以sin4θ+cos4θ=(sin2θ+cos2θ)2-2sin2θcos2θ=1-sin22θ=1-×=.故选D.2.(必修4P147A组T12改编)已知函数f(x)=sin⎝x+6⎭+sin⎝x-6⎭+cos x+a的最大值为解析:选A.f(x)=sin x cos+cos x sin+sin x cos-cos x sin+cos x+a=3sin x+cos x3.(必修4P69A组T8改编)已知tanα=3,则sin⎝2α+4⎭的值为(10B.-2A.2C.D.-sin2α+cos2α1+tan2α1+32522⎛34⎫π⎫cos2α-sin2α1-tan2α1-324=-,所以sin⎝2α+4⎭=-=-⎛52⎝55⎭sin2α+cos2α1+tan2α1+322.选B.4.(必修4P58A组T2(3)改编)如图是y=A sin(ωx+φ)⎝ω>0,-2<φ<2⎭的部分图象,则A.y=2sin⎝x+6⎭B.y=2sin⎝2x-6⎭C.y=2sin⎝x+3⎭D.y=2sin⎝2x+6⎭解析:选D.由题图知=-⎝-12⎭=.所以T=π,所以ω==2.当x=-时,y=0,⎧⎪A sin⎛-π+φ⎫=0,所以φ=,A=2.所以y=2sin⎝2x+6⎭.故选D.⎝6⎭π⎛π⎫当x=0时,y=1.所以⎨⎪⎩A sinφ=12132 147299⎛π⎫⎛π⎫1,则a的值为()A.-1C.1B.0D.2ππππ6666π+a=2sin(x+6)+a,所以f(x)max=2+a=1.所以a=-1.选A.⎛π⎫10)721072102sinαcosα2tanα2×33解析:选B.因为tanα=3,所以sin2α====,cos2α===(sin2α+cos2α)=210⎛ππ⎫其解析式为()⎛π⎫⎛π⎫⎛π⎫⎛π⎫Tπ⎛π⎫π2ππ464T1265.(必修5P18练习T1(1)改编△)在锐角ABC中,a=2,b=3,S△ABC=22,则c=() A.2B.3解析:选 B.由已知得 ×2×3×sin C =2 2,所以 sin C = .由于 C <90°,所以 cos C= 1-sin 2C = .由余弦定理得 c 2=a 2+b 2-2ab cos C =22+32-2×2×3× =9,所以 c =3,A . 3 C . 即 3a cos A =b · +c · =a ,所以 cos A = ,又 0<A <π.所以 sin A = .又 b =2,所以 a sin B =b sin A =2× = .故选 C.cos 80° sin 80° cos 80°sin 80°cos 80°cos 80°- sin 80°⎭ 4sin (60°-80°) 2⎝ 2 1 sin 160° sin 160° =-4sin 20°=-4.( c 4解析:由题意得⎨2 ⎪ C .4D. 171 2 22 31 13 3故选 B.6.(必修 5 P 18 练习 T 3 改编△)已知 ABC 三内角 A 、B 、C 的对边分别为 a ,b ,c ,3a cos A =b cos C +c cos B ,b =2,则 a sin B =()434 2 32 B. 2D .6 2解析:选 C.因为 3a cos A =b cos C +c cos B ,a 2+b 2-c 2 a 2+c 2-b 22ab 2ac1 2 23 32 2 4 23 3二、填空题3 17.(必修 4 P 146A 组 T 5(1)改编)sin 80°- =______.解析:⎛ 3 1 ⎫ 2= =2sin 20°答案:-4 8. 必修 5 P 20A 组 T 11(3)改编△) ABC 的三内角 A ,B ,C 的对边分别为 a ,b , .A =120°,a =7,△S ABC = 153,则 b +c =________.⎧⎪1bc sin 120°=15 34,⎪⎩b 2+c 2-2bc cos 120°=72⎧bc =15即⎨ ,所以 b 2+c 2+2bc =64.所以 b +c =8.⎪⎩b 2+c 2+bc =49答案:82 1 π9.(必修 4 P 56 练习 T 3 改编)关于函数 f (x )=3sin(2x -4)的下列结论:①f (x )的一个周期是-8π;②f (x )的图象关于 x = 对称;③f (x )的图象关于点⎝2,0⎭对称;- ,上单调递增;④f (x )在⎝2 2⎭⑤f (x )的图象可由 g (x )= cos x 向右平移 个单位得到.解析:f (x )的最小正周期 T = =4π.所以 f (x )的一个周期为-8π.①正确.f ⎝2⎭=0,故②错误.③正确.由 2k π- < x - <2k π+ ,k ∈Z ,得4k π- <x <4k π+ π. - , - , .故④正确.令 k =0 得,- <x < π.⎝ 2 2⎭ ⎝ 2 2 ⎭x +g (x )= cos x = sin ⎝2 2⎭x +π) ,(=sin⎦⎣2 x - = sin x -,f (x )= sin ⎝2 4⎭ ⎣2⎝ 2⎭⎦所以 g (x )的图象向右平移 -(-π)= π 即可得到 f (x )的图象.故⑤错误,即①③④正确.(2)将函数 f (x )的图象向左平移 个单位,再将所得图象上各点的横坐标伸长为原来的 3 倍,纵坐标不变,得到函数 y =g (x )的图象,若 α 为锐角,g (α)= - 2,求 cos α.ωx - ·解:(1)f (x )=4sin cos ωx -2 2cos 2ωx = 2(sin 2ωx -cos 4⎭ cos ωx =2 2sin ωx ·⎝ 2ωx - - 2,2ωx )- 2=2sin4⎭⎝由于 f (x )在 x = 处取得最值,因此 2ω· - =k π+ ,k ∈Z ,所以 ω=2k + ,π2⎛π ⎫⎛ π π⎫2 1 π3 2 8其中正确的结论有____________(填上全部正确结论的序号).2π1 2⎛π⎫π 1 π π2 2 4 2π 3 2 2π 3 ⎛ π π⎫ ⎛ π 3π⎫2 22 1 2 ⎛1 π⎫3 2 3 2 ⎡1 ⎤ 3 2 ⎛1 π⎫ 2 ⎡1⎛ π⎫⎤ 3 3 π 32 2答案:①③④三、解答题π π10.(必修 4 P 147A 组 T 10 改编)已知函数 f (x )=4sin(ωx -4)·cos ωx 在 x =4处取得最值,其中 ω∈(0,2).(1)求函数 f (x )的最小正周期;π3643⎛ π⎫⎛ π⎫ π π π π 34 4 4 2 2因为 ω∈(0,2),所以 ω= ,因此,f (x )=2sin ⎝3x -4⎭- 2,所以 T = .个 单 位 , 得 到h (x ) = 2sin ⎣3⎝x +36⎭-4⎦ - 2 = 2sin ⎝3x -6⎭- 2的图象,再将 h (x )图象上各点的横坐标伸长为原来的 3 倍,纵坐标不变,得到 g (x )=2sin ⎝x -6⎭-⎛ 故 g (α)=2sin ⎝α-6⎭- 2= - 2,可得 sin ⎝α-6⎭= ,因为 α 为锐角,所以- <α- < ,因此 cos ⎝α-6⎭=⎛2⎫2= 5, π π⎫ π⎫ π⎫ π π 5 3 2 1 15-2 故 cos α=cos ⎝α-6+6⎭=cos ⎝α-6⎭cos -sin ⎝α-6⎭sin = ⎛ ⎛ ⎛ 6 6 3 2 3 2 6①+②得 m 2= ,所以 m = 6,即 BC = 6.sin ∠ACE sin ∠EAC sin ∠BCE sin ∠CBE 且 BC = ,所以 = = .所以 BE = 6AE ,所以 AE = ( 6-1).32⎛ π⎫ 2π 3(2) 将 函 数 f (x ) 的 图 象 向 左 平 移 π 36 ⎡ ⎛ π ⎫ π⎤⎛ π⎫⎛ π⎫2的图象,π⎫ 4 3⎛ π⎫ 2 3π π π6 6 3⎛ π⎫ 1-⎝3⎭ 3× - × = .11.(必修 5 P 20A 组 T 13 改编)D 为△ABC 的边 BC 的中点.AB =2AC =2AD =2. (1)求 BC 的长;(2)若∠ACB 的平分线交 AB 于 E ,求 △S ACE . 解:(1)由题意知 AB =2,AC =AD =1. 设 BD =DC =m .在△ADB 与△ADC 中, 由余弦定理得AB 2=AD 2+BD 2-2AD · B D cos ∠ADB , AC 2=AD 2+DC 2-2AD · D C cos ∠ADC . 即 1+m 2-2m cos ∠ADB =4,① 1+m 2+2m cos ∠ADB =1.②3 22(2)在△ACE 与△BCE 中,由正弦定理得AE EC BE EC= , = ,由于∠ACE =∠BCE ,AC AE AC 6sin ∠BAC sin ∠CBABE BC 6252AB ·AC 2×2×1=- ,所以 sin ∠BAC = ,= ×1× ( 6-1)× = .AB 2+AC 2-BC 2 22+12-( 6)2又 cos ∠BAC = =1 154 41所以 △S ACE =2AC · AE ·sin ∠BAC1 2 15 3 10- 15 2 5 4 20。
2019高三数学(人教B文)一轮课件:第四章 三角函数、解三角形 4.4

第四章
考点1 考点2 考点3
4.4
函数y=Asin(ωx+φ)的图象及应用
知识梳理 核心考点
-12-
第四章
考点1 考点2 考点3
4.4
函数y=Asin(ωx+φ)的图象及应用
知识梳理 核心考点
-13-
(1)请将上表数据补充完整,并直接写出函数f(x)的解析式; (2)将y=f(x)图象上所有点向左平移θ(θ>0)个单位长度,得到y=g(x) 的图象,若y=g(x)图象的一个对称中心为 ,求θ的最小值. 思考作函数y=Asin(ωx+φ)(A>0,ω>0)的图象有哪些方法?
1 的图象向右平移4个周期后,所得图象
)
π 4
B.y=2sin 2������ + D.y=2sin 2������1 π
π 3
π 3
关闭
由已知周期 T=π,右移4T=4后得 y=2sin 2 ������- 4 + 6 =2sin 2������- 3 的图象,故选 D.
π
Hale Waihona Puke ππD解析
关闭
答案
第四章
4.4
函数y=Asin(ωx+φ)的 图象及应用
第四章
知识梳理 双基自测 自测点评
4.4
函数y=Asin(ωx+φ)的图象及应用
知识梳理 核心考点
-2-
1
2
3
4
1.“五点法”作三角函数图象的五点 作图的五点是三角函数图象在一个周期内的最高点、最低点及 与x轴的三个交点.
第四章
知识梳理 双基自测 自测点评
126 3 5π π π π ∴2× + φ = 2 k π + , k ∈ Z , ∴ φ = 2 k π ,k∈Z. D.4, 12 3 2 3 π π π 又 φ∈ - , ,∴φ=- ,故选 A. 2 2 3
【数学】2019届一轮复习人教B版第4章三角函数解三角形专题探究课2学案

高考导航1.三角函数与解三角形是高考的热点题型,从近五年的高考试题来看,呈现较强的规律性,每年的题量和分值要么三个小题15分,要么一个小题一个大题17分,间隔出现;2.该部分常考查的内容有:(1)三角函数的图象与性质;(2)三角恒等变换与诱导公式;(3)利用正弦定理和余弦定理解三角形;3.在解题过程中,要注意三角恒等变换公式的多样性和灵活性,注意题目中隐含的各种限制条件,选择合理的解决方法,灵活地实现问题的转化.热点一解三角形(教材VS高考)高考对解三角形的考查,以正弦定理、余弦定理的综合应用为主.其命题规律可以从以下两方面看:(1)从内容上看,主要考查正弦定理、余弦定理以及三角函数公式,一般是以三角形或其他平面图形为背景,结合三角形的边角关系考查学生利用三角函数公式处理问题的能力;(2)从命题角度看,主要是在三角恒等变换的基础上融合正弦定理、余弦定理,在知识的交汇处命题.【例1】(满分12分)(2017·全国Ⅰ卷)△ABC的内角A,B,C的对边分别为a,b,c.已知△ABC的面积为a23sin A.(1)求sin B sin C;(2)若6cos B cos C=1,a=3,求△ABC的周长.教材探源本题第(1)问源于教材必修5P20B组1且相似度极高,本题第(2)问在第(1)问的基础上进行拓展,考查正弦定理、余弦定理的应用.满分解答(1)因为△ABC面积S=a23sin A,且S=12bc sin A,1分(得分点1)所以a 23sin A =12bc sin A ,所以a 2=32bc sin 2A .2分 (得分点2)由正弦定理得sin 2A =32sinB sinC sin 2A , 4分 (得分点3)因为sin A ≠0,所以sin B sin C =23. 5分 (得分点4)(2)由(1)得sin B sin C =23,cos B cos C =16. 因为A +B +C =π,所以cos A =cos(π-B -C )=-cos(B +C ) =sin B sin C -cos B cos C =12,7分 (得分点5) 又A ∈(0,π),所以A =π3,sin A =32,cos A =12, 8分 (得分点6)由余弦定理得a 2=b 2+c 2-bc =9, ①9分 (得分点7) 由正弦定理得b =a sin A ·sin B ,c =asin A ·sin C , 所以bc =a 2sin 2A ·sin B sin C =8, ② 10分 (得分点8)由①②得:b +c =33,11分 (得分点9) 所以a +b +c =3+33,即△ABC 周长为3+33. 12分 (得分点10)❶得步骤分:抓住得分点的解题步骤,“步步为赢”.在第(1)问中,写出面积公式,用正弦定理求出结果.第(2)问中,诱导公式→恒等变换→余弦定理→正弦定理→得出结果.❷得关键分:(1)面积公式,(2)诱导公式,(3)恒等变换,(4)正弦定理,(5)余弦定理都是不可少的过程,有则给分,无则没分.❸得计算分:解题过程中的计算准确是得满分的根本保证,如(得分点5),(得分点6),(得分点9),(得分点10).利用正弦定理、余弦定理解三角形的步骤第一步:找条件:寻找三角形中已知的边和角,确定转化方向.第二步:定工具:根据已知条件和转化方向,选择使用的定理和公式,实施边角之间的转化.第三步:求结果:根据前两步分析,代入求值得出结果.第四步:再反思:转化过程中要注意转化的方向,审视结果的合理性.【训练1】 (2018·大连双基测试)已知△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,且满足cos 2B -cos 2C -sin 2A =sin A sin B . (1)求角C ;(2)(一题多解)若c =26,△ABC 的中线CD =2,求△ABC 的面积S 的值. 解 (1)由已知得sin 2A +sin 2B -sin 2C =-sin A sin B ,由正弦定理得a 2+b 2-c 2=-ab ,由余弦定理可得cos C =a 2+b 2-c 22ab =-12.∵0<C <π,∴C =2π3.(2)法一 由|CD→|=12|CA →+CB →|=2,可得CA →2+CB →2+2CA →·CB →=16,即a 2+b 2-ab=16,由余弦定理得a 2+b 2+ab =24,∴ab =4, ∴S =12ab sin C =34ab = 3.法二 延长CD 到M ,使CD =MD ,连接AM ,易证△BCD ≌△AMD ,BC =AM ,∠CAM =π3.由余弦定理得⎩⎨⎧a 2+b 2+ab =24,a 2+b 2-ab =16.∴ab =4,∴S =12ab sin C =34ab = 3. 热点二 三角函数的图象和性质注意对基本三角函数y =sin x ,y =cos x 的图象与性质的理解与记忆,有关三角函数的五点作图、图象的平移、由图象求解析式、周期、单调区间、最值和奇偶性等问题的求解,通常先将给出的函数转化为y =A sin(ωx +φ)的形式,然后利用整体代换的方法求解.【例2】 (2017·山东卷)设函数f (x )=sin ⎝ ⎛⎭⎪⎫ωx -π6+sin ⎝⎛⎭⎪⎫ωx -π2,其中0<ω<3,已知f ⎝ ⎛⎭⎪⎫π6=0.(1)求ω;(2)将函数y =f (x )的图象上各点的横坐标伸长为原来的2倍(纵坐标不变),再将得到的图象向左平移π4个单位,得到函数y =g (x )的图象,求g (x )在⎣⎢⎡⎦⎥⎤-π4,3π4上的最小值.解 (1)因为f (x )=sin ⎝ ⎛⎭⎪⎫ωx -π6+sin ⎝⎛⎭⎪⎫ωx -π2,所以f (x )=32sin ωx -12cos ωx -cos ωx =32sin ωx -32cos ωx =3⎝ ⎛⎭⎪⎫12sin ωx -32cos ωx=3sin ⎝⎛⎭⎪⎫ωx -π3.由题设知f ⎝ ⎛⎭⎪⎫π6=0,所以ωπ6-π3=k π,k ∈ , 故ω=6k +2,k ∈ . 又0<ω<3,所以ω=2.(2)由(1)得f (x )=3sin ⎝⎛⎭⎪⎫2x -π3,所以g (x )=3sin ⎝ ⎛⎭⎪⎫x +π4-π3=3sin ⎝ ⎛⎭⎪⎫x -π12.因为x ∈⎣⎢⎡⎦⎥⎤-π4,3π4,所以x -π12∈⎣⎢⎡⎦⎥⎤-π3,2π3,当x -π12=-π3,即x =-π4时,g (x )取得最小值-32.探究提高 三角函数的图象与性质是高考考查的重点,通常先将三角函数化为y =A sin(ωx +φ)+k 的形式,然后将t =ωx +φ视为一个整体,结合y =sin t 的图象求解.【训练2】 (2018·东北三省联考)已知函数f (x )=4tan x sin ⎝ ⎛⎭⎪⎫π2-x cos ⎝ ⎛⎭⎪⎫x -π3- 3.(1)求f (x )的定义域与最小正周期;(2)讨论f (x )在区间⎣⎢⎡⎦⎥⎤-π4,π4上的单调性.解 (1)f (x )的定义域为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x |x ≠π2+k π,k ∈Z ,f (x )=4tan x cos x cos ⎝⎛⎭⎪⎫x -π3- 3=4sin x cos ⎝⎛⎭⎪⎫x -π3- 3=4sin x ⎝ ⎛⎭⎪⎫12cos x +32sin x - 3=2sin x cos x +23sin 2x - 3 =sin 2x +3(1-cos 2x )- 3 =sin 2x -3cos 2x =2sin ⎝⎛⎭⎪⎫2x -π3,所以f (x )的最小正周期T =2π2=π.(2)令 =2x -π3,函数y =2sin 的单调递增区间是⎣⎢⎡⎦⎥⎤-π2+2k π,π2+2k π,k∈ .由-π2+2k π≤2x -π3≤π2+2k π,k ∈ ,得-π12+k π≤x ≤5π12+k π,k ∈ .设A =⎣⎢⎡⎦⎥⎤-π4,π4,B =⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x |-π12+k π≤x ≤5π12+k π,k ∈Z ,易知A ∩B =⎣⎢⎡⎦⎥⎤-π12,π4.所以,当x ∈⎣⎢⎡⎦⎥⎤-π4,π4时,f (x )在区间⎣⎢⎡⎦⎥⎤-π12,π4上单调递增,在区间⎣⎢⎡⎦⎥⎤-π4,-π12上单调递减.热点三 三角函数与平面向量结合三角函数、解三角形与平面向量的结合主要体现在以下两个方面:(1)以三角函数式作为向量的坐标,由两个向量共线、垂直、求模或求数量积获得三角函数解析式;(2)根据平面向量加法、减法的几何意义构造三角形,然后利用正、余弦定理解决问题.【例3】 已知△ABC 的三内角A ,B ,C 所对的边分别是a ,b ,c ,向量m = (cos B ,cos C ),n =(2a +c ,b ),且m ⊥n . (1)求角B 的大小;(2)若b =3,求a +c 的取值范围.解 (1)∵m =(cos B ,cos C ),n =(2a +c ,b ),且m ⊥n , ∴(2a +c )cos B +b cos C =0,∴cos B (2sin A +sin C )+sin B cos C =0, ∴2cos B sin A +cos B sin C +sin B cos C =0. 即2cos B sin A =-sin(B +C )=-sin A . ∵A ∈(0,π),∴sin A ≠0,∴cos B =-12. ∵0<B <π,∴B =2π3. (2)由余弦定理得b 2=a 2+c 2-2ac cos 23π=a 2+c 2+ac =(a +c )2-ac ≥(a +c )2-⎝⎛⎭⎪⎫a +c 22=34(a +c )2,当且仅当a =c 时取等号. ∴(a +c )2≤4,故a +c ≤2. 又a +c >b =3,∴a +c ∈(3,2]. 即a +c 的取值范围是(3,2].探究提高 向量是一种解决问题的工具,是一个载体,通常是用向量的数量积运算或性质转化成三角函数问题.【训练3】 已知△ABC 中内角A ,B ,C 的对边分别为a ,b ,c ,向量m =(2sin B ,-3),n =(cos 2B ,2cos 2B2-1),B 为锐角且m ∥n . (1)求角B 的大小;(2)如果b =2,求S △ABC 的最大值. 解 (1)∵m ∥n ,∴2sin B ⎝ ⎛⎭⎪⎫2cos 2B 2-1=-3cos 2B ,∴sin 2B =-3cos 2B ,即tan 2B =- 3. 又∵B 为锐角,∴2B ∈(0,π), ∴2B =2π3,∴B =π3.(2)∵B =π3,b =2,由余弦定理b 2=a 2+c 2-2ac cos B , 得a 2+c 2-ac -4=0.又a 2+c 2≥2ac ,代入上式,得ac ≤4, 故S △ABC =12ac sin B =34ac ≤3, 当且仅当a =c =2时等号成立, 即S △ABC 的最大值为 3.1.(2017·济南调研)函数f (x )=3sin ⎝⎛⎭⎪⎫2x +π6的部分图象如图所示.(1)写出f (x )的最小正周期及图中x 0,y 0的值; (2)求f (x )在区间⎣⎢⎡⎦⎥⎤-π2,-π12上最大值和最小值.解 (1)由题得,f (x )的最小正周期为π,y 0=3. 当y 0=3时,sin ⎝⎛⎭⎪⎫2x 0+π6=1,由题干图象可得2x 0+π6=2π+π2,解得x 0=7π6.(2)因为x ∈⎣⎢⎡⎦⎥⎤-π2,-π12,所以2x +π6∈⎣⎢⎡⎦⎥⎤-5π6,0. 于是:当2x +π6=0,即x =-π12时,f (x )取得最大值0;当2x +π6=-π2,即x =-π3时,f (x )取得最小值-3.2.(2017·天津卷)在△ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c .已知a sin A =4b sin B ,ac =5(a 2-b 2-c 2). (1)求cos A 的值; (2)求sin(2B -A )的值.解 (1)由a sin A =4b sin B 及a sin A =bsin B ,得a =2b .由ac =5(a 2-b 2-c 2)及余弦定理,得cos A =b 2+c 2-a 22bc =-55acac =-55.(2)由(1),可得sin A =255,代入a sin A =4b sin B ,得sin B =a sin A 4b =55.由(1)知,A 为钝角,所以cos B =1-sin 2B =255.于是sin 2B =2sin B cos B =45,cos 2B =1-2sin 2B =35,故sin(2B -A )=sin 2B cos A -cos 2B sin A=45×⎝ ⎛⎭⎪⎫-55-35×255=-255.3.(2018·湖南湘中名校联考)已知函数f (x )=cos x (cos x +3sin x ). (1)求f (x )的最小值;(2)在△ABC 中,角A ,B ,C 的对边分别是a ,b ,c ,若f (C )=1,S △ABC =334,c =7,求△ABC 的周长.解 (1)f (x )=cos x (cos x +3sin x )=cos 2x +3sin x cos x =1+cos 2x 2+32sin 2x =12+sin ⎝⎛⎭⎪⎫2x +π6.当sin ⎝⎛⎭⎪⎫2x +π6=-1时,f (x )取得最小值-12.(2)f (C )=12+sin ⎝ ⎛⎭⎪⎫2C +π6=1,∴sin ⎝ ⎛⎭⎪⎫2C +π6=12,∵C ∈(0,π),2C +π6∈⎝ ⎛⎭⎪⎫π6,13π6,∴2C +π6=5π6,∴C =π3. ∵S △ABC =12ab sin C =334,∴ab =3.又(a +b )2-2ab cos π3=7+2ab ,∴(a +b )2=16,即a +b =4,∴a +b +c =4+7, 故△ABC 的周长为4+7.4.(2017·合肥质检)在△ABC 中,内角A ,B ,C 的对边分别是a ,b ,c ,向量m =⎝ ⎛⎭⎪⎫a 2,c 2,n =(cos C ,cos A ),且n ·m =b cos B . (1)求角B 的值;(2)若cos A -C2=3sin A ,且|m |=5,求△ABC 的面积.解 (1)由m ·n =b cos B ,得a 2cos C +c2cos A =b cos B , sin A cos C +sin C cos A =2sin B cos B ,即sin(A +C )=2sin B cos B ,sin B =2sin B cos B , ∵0<B <π,sin B ≠0,∴cos B =12,∴B =π3.(2)C =π-A -B =2π3-A ,cos A -C 2=3sin A ⇒cos ⎝⎛⎭⎪⎫A -π3=3sin A ⇒cos A =3sin A ⇒tan A =33.∵0<A <23π⇒A =π6,∴C =π-π6-π3=π2.在Rt △ABC 中,∵a =c sin π6=12c , 又|m |=5,即a 2+c 2=20, ∴a =2,c =4,b =16-4=23, △ABC 的面积S =12×2×23=2 3.5.(2018·河南天一大联考)已知函数f (x )=a ·b ,其中a =(2cos x ,-3sin 2x ),b = (cos x ,1),x ∈R .(1)求函数y =f (x )的单调递减区间;(2)在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,f (A )=-1,a =7,且向量m =(3,sin B )与n =(2,sin C )共线,求边长b 和c 的值.解 (1)f (x )=2 cos 2x -3sin 2x =1+cos 2x -3sin 2x =1+2cos ⎝⎛⎭⎪⎫2x +π3,令2k π≤2x +π3≤2k π+π(k ∈ ),解得k π-π6≤x ≤k π+π3(k ∈ ),∴函数y =f (x )的单调递减区间为⎣⎢⎡⎦⎥⎤k π-π6,k π+π3(k ∈ ).(2)∵f (A )=1+2cos ⎝⎛⎭⎪⎫2A +π3=-1,∴cos ⎝ ⎛⎭⎪⎫2A +π3=-1,又π3<2A +π3<7π3,∴2A +π3=π,即A =π3.∵a =7,∴由余弦定理得a 2=b 2+c 2-2bc cos A =(b +c )2-3bc =7.① ∵向量m =(3,sin B )与n =(2,sin C )共线, ∴2sin B =3sin C ,由正弦定理得2b =3c ,② 由①②得b =3,c =2.6.(2018·东北三省三校联考)已知在△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c ,且a -c a -b =sin A +sin B sin (A +B ).(1)求角B 的值;(2)(一题多解)若△ABC 的外接圆半径为1,求△ABC 面积S 的最大值. 解 (1)∵A +B +C =π,∴sin(A +B )=sin C , ∴a -c a -b=sin A +sin B sin C , 由正弦定理得a -c a -b =a +bc ,即b 2=a 2+c 2-ac ,结合余弦定理,有cos B =12,B ∈(0,π),∴B =π3.(2)法一 2R =2=b sin π3⇒b =3, 所以b 2=3=a 2+c 2-2ac cos π3≥2ac -ac =ac (当且仅当a =c 时取等号),所以S =12ac sin π3≤334,最大值为334. 法二 S =12ac sin B =34ac =34×2sin A ×2sin C=3sin A sin ⎝ ⎛⎭⎪⎫2π3-A =3sin A ⎝ ⎛⎭⎪⎫32cos A +12sin A =32(3sin A cos A +sin 2A ) =32⎝ ⎛⎭⎪⎫32sin 2A -12cos 2A +12 =32sin ⎝ ⎛⎭⎪⎫2A -π6+34. ∵0<A <2π3,∴-π6<2A -π6<7π6, ∴当2A -π6=π2,即A =π3时,S 取到最大值334.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
23解三角形基础巩固1.(2017安徽马鞍山一模)△ABC的内角A,B,C的对边分别为a,b,c.已知a=,b=2,A=60°,则c=()A. B.1C. D.22.△ABC的内角A,B,C的对边分别为a,b,c,若a,b,c成等比数列,且c=2a,则cos B=()A. B.C. D.3.在△ABC中,B=,BC边上的高等于BC,则sin A=??()A. B.C. D.4.如图,两座相距60 m的建筑物AB,CD的高度分别为20 m,50 m,BD为水平面,则从建筑物AB 的顶端A看建筑物CD的张角为()A.30°B.45°C.60°D.75°5.在△ABC中,角A,B,C的对边分别为a,b,c,若,b=4,则△ABC的面积的最大值为()A.4B.2C.2D.6.在△ABC中,若三边长a,b,c满足a3+b3=c3,则△ABC的形状为()A.锐角三角形B.钝角三角形C.直角三角形D.以上均有可能7.已知△ABC的三个内角A,B,C的对边分别为a,b,c,且满足=sin A-sin B,则角C=.8.在△ABC中,B=120°,AB=,A的角平分线AD=,则AC=.9.如图所示,长为3.5 m的木棒AB斜靠在石堤旁,木棒的一端A在离堤足C处1.4 m的地面上,另一端B在离堤足C处2.8 m的石堤上,石堤的倾斜角为α,则坡度值tan α=.10.已知岛A南偏西38°方向,距岛A 3 n mile的B处有一艘缉私艇.岛A处的一艘走私船正以10 n mile/h的速度向岛北偏西22°方向行驶,问缉私艇朝何方向以多大速度行驶,恰好用0.5 h 能截住该走私船?能力提升11.(2017全国Ⅰ,文11)△ABC的内角A,B,C的对边分别为a,b,c.已知sin B+sin A(sin C-cosC)=0,a=2,c=,则C=()A.B.C.D.12.如图,已知AB是圆O的直径,AB=2,点C在直径AB的延长线上,BC=1,点P是圆O上半圆上的动点,以PC为边作等边三角形PCD,且点D与圆心分别在PC的两侧,记∠POB=x,将△OPC和△PCD的面积之和表示成x的函数f(x),则y=f(x)取最大值时x的值为()A. B. C. D.π13.(2017河南濮阳一模)在△ABC中,D为BC边上的一点,AD=BD=5,DC=4,∠BAD=∠DAC,则AC=??()A.9B.8C.7D.614.在△ABC中,a,b,c分别为内角A,B,C的对边,且b2+c2-a2=bc,(1)求角A的大小;(2)设函数f(x)=sin x+2cos2,a=2,f(B)=+1时,求边长b.高考预测15.(2017辽宁沈阳一模)为了竖一块广告牌,要制造三角形支架,如图,要求∠ACB=60°,BC的长度大于1 m,且AC比AB长0.5 m,为了稳固广告牌,要求AC越短越好,则AC最短为()A.mB.2 mC.(1+) mD.(2+) m16.(2017河南洛阳一模)已知f(x)=sin(π+ωx)·sin-cos2ωx(ω>0)的最小正周期为T=π.(1)求f的值.(2)在△ABC中,角A,B,C所对的边分别为a,b,c,若(2a-c)cos B=b cos C,求角B的大小以及f(A)的取值范围.参考答案23解三角形1.B解析由已知及余弦定理,得3=4+c2-2×2×c×,整理,得c2-2c+1=0,解得c=1.故选B.2.B解析在△ABC中,a,b,c成等比数列,且c=2a,则b=a,cos B=.故选B.3.D解析(方法一)记角A,B,C的对边分别为a,b,c,则由题意,得S△ABC=a·a=ac sin B,即c= a.由正弦定理,得sin C=sin A.∵C=-A,∴sin C=sin sin A,即cos A+sin A=sin A,整理,得sin A=-3cos A.∵sin2A+cos2A=1,∴sin2A+sin2A=1,即sin2A=,解得sin A=(排除负值).故选D.(方法二)记角A,B,C的对边分别为a,b,c,则由题意得S△ABC=a·ac sin B,∴c= a.∴b2=a2+-2a·,即b=.由正弦定理,得sin A=.故选D.4.B解析依题意可得AD=20m,AC=30m,又CD=50m,所以在△ACD中,由余弦定理,得cos∠CAD=,又0°<∠CAD<180°,所以∠CAD=45°,所以从顶端A看建筑物CD的张角为45°.5.A解析∵在△ABC中,,∴(2a-c)cos B=b cos C.∴(2sin A-sin C)cos B=sin B cos C.∴2sin A cos B=sin C cos B+sin B cos C=sin(B+C)=sin A.∴cos B=,即B=.由余弦定理可得16=a2+c2-2ac cos B=a2+c2-ac≥2ac-ac=ac,故ac≤16,当且仅当a=c时取等号,因此,△ABC的面积S=ac sin B=ac≤4,故选A.6.A解析由题意可知c>a,c>b,即角C最大,所以a3+b3=a·a2+b·b2<ca2+cb2,即c3<ca2+cb2,所以c2<a2+b2.根据余弦定理,得cos C=>0,则0<C<,即三角形为锐角三角形.7.解析在△ABC中,∵=sin A-sin B,∴=a-b.∴a2+b2-c2=ab,∴cos C=.∴C=.8.解析由题意及正弦定理,可知,即,故∠ADB=45°.所以A=180°-120°-45°,故A=30°,则C=30°,所以三角形ABC是等腰三角形.所以AC=2sin60°=.9.解析在△ABC中,AB=3.5m,AC=1.4m,BC=2.8m,且α+∠ACB=π.由余弦定理,可得AB2=AC2+BC2-2·AC·BC·cos∠ACB,即3.52=1.42+2.82-2×1.4×2.8×cos(π-α),解得cosα=,则sinα=,所以tanα=.10.解设缉私艇在C处截住走私船,D为岛A正南方向上的一点,缉私艇的速度为x nmile/h, 则BC=0.5x nmile,AC=5nmile,依题意,∠BAC=180°-38°-22°=120°,由余弦定理可得BC2=AB2+AC2-2AB·AC cos120°,解得BC2=49,BC=0.5x=7,解得x=14.又由正弦定理得sin∠ABC=,所以∠ABC=38°.又∠BAD=38°,所以BC∥AD.故缉私艇以14nmile/h的速度向正北方向行驶,恰好用0.5h截住该走私船.11.B解析由题意结合三角形的内角和,可得sin(A+C)+sin A(sin C-cos C)=0,整理得sin A cos C+cos A sin C+sin A sin C-sin A cos C=0,则sin C(sin A+cos A)=0,因为sin C>0,所以sin A+cos A=0,即tan A=-1,因为A∈(0,π),所以A=.由正弦定理,得,即sin C=,所以C=,故选B.12.A解析∵S△OPC=OP·OC·sin x=sin x,PC2=12+22-2·1·2·cos x=5-4cos x,S△PCD=PC2·sin(5-4cos x),∴f(x)=sin x+(5-4cos x)=2sin.故当x-,即x=时,f(x)有最大值,故选A.13.D解析设∠B=θ,则∠ADC=2θ,在△ADC中,由,所以AC=8cosθ,在△ABC中,由,可得,所以16cos2θ=9,可得cosθ=,所以AC=8×=6.故选D.14.解(1)在△ABC中,∵b2+c2-a2=bc,∴cos A=.∵0<A<π,∴A=.(2)∵f(x)=sin x+2cos2=sin x+cos x+1=sin+1,∴f(B)=sin+1=+1,∴B=.∵,即,∴b=.15.D解析设BC的长度为x米,AC的长度为y米,则AB的长度为(y-0.5)米,在△ABC中,依余弦定理得AB2=AC2+BC2-2AC·BC cos∠ACB,即(y-0.5)2=y2+x2-2yx×,化简得y(x-1)=x2-,由x>1,知x-1>0,因此y=,y=(x-1)++2≥+2,当且仅当x-1=时,取“=”号,即x=1+时,y有最小值2+.16.解(1)f(x)=sin(π+ωx)·sin-cos2ωx=sinωx·cosωx-cos2ωx=sin2ωx-cos2ωx-=sin.∵最小正周期为T=π,∴=π,即ω=1.∴f(x)=sin,∴f=sin.(2)∵(2a-c)cos B=b cos C,∴(2sin A-sin C)cos B=sin B cos C,2sin A cos B=sin B cos C+cos B sin C=sin(B+C)=sin A.∵sin A>0,∴cos B=.∵B∈(0,π),∴B=.∴A∈,2A-,∴sin.f(A)的取值范围是.。
