2020年高考理科数学原创专题卷：《三角函数》
2020年高考理科数学及答案解析(全国Ⅲ卷)
2020年普通高等学校招生全国统一考试理科数学（含答案解析）注意事项：1．答卷前，考生务必将自己的姓名和准考证号填写在答题卡上。
2．回答选择题时，选出每小题答案后，用铅笔把答题卡对应题目的答案标号涂黑。
如需改动，用橡皮擦干净后，再选涂其他答案标号。
回答非选择题时，将答案写在答题卡上。
写在本试卷上无效。
3．考试结束后，将本试卷和答题卡一并交回。
一、选择题：本题共12小题，每小题5分，共60分。
在每小题给出的四个选项中，只有一项是符合题目要求的。
1．已知集合2{1,0,1,2}{|1}A B x x =-=≤，，则A B = A ．{}1,0,1-B ．{}0,1C ．{}1,1-D ．{}0,1,2【答案】A 【难度】容易 【点评】本题考查集合之间的运算关系，即包含关系.在高一数学强化提高班上学期课程讲座1，第一章《集合》中有详细讲解，其中第02节中有完全相同类型题目的计算.在高考精品班数学（理）强化提高班中有对集合相关知识的总结讲解. 2．若(1i)2i z +=，则z = A ．1i -- B ．1+i -C ．1i -D ．1+i【答案】D 【难度】容易【点评】本题考查复数的计算。
在高二数学（理）强化提高班下学期，第四章《复数》中有详细讲解，其中第02节中有完全相同类型题目的计算。
在高考精品班数学（理）强化提高班中有对复数相关知识的总结讲解。
3．《西游记》《三国演义》《水浒传》和《红楼梦》是中国古典文学瑰宝，并称为中国古典小说四大名著.某中学为了解本校学生阅读四大名著的情况，随机调查了100位学生，其中阅读过《西游记》或《红楼梦》的学生共有90位，阅读过《红楼梦》的学生共有80位，阅读过《西游记》且阅读过《红楼梦》的学生共有60位，则该校阅读过《西游记》的学生人数与该校学生总数比值的估计值为A ．0.5B ．0.6C ．0.7D ．0.8【答案】C 【难度】容易【点评】本题在高考数学（理）提高班讲座 第十四章《概率》中有详细讲解，在寒假特训班、百日冲刺班中均有涉及。
2020年高考试题：三角函数
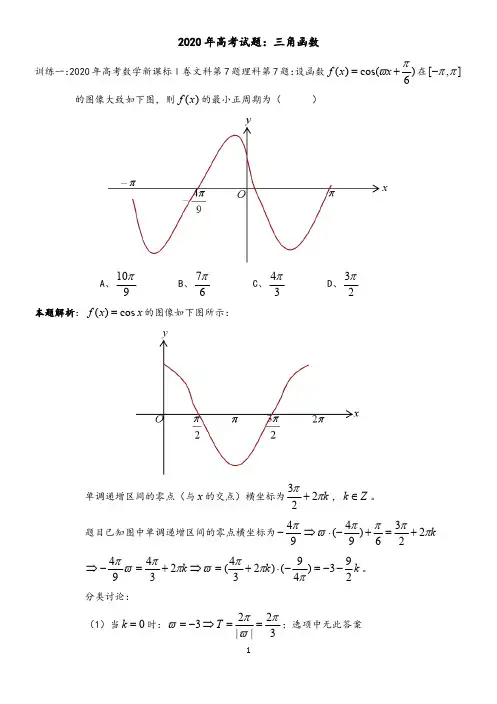
D、 3 2
单调递增区间的零点（与 x 的交点）横坐标为 3 2k ， k Z 。 2
题目已知图中单调递增区间的零点横坐标为 4 ( 4 ) 3 2k
9
9 62
4 9
4 3
2k
( 4 3
2k
)
(
9 4
)
3
9 2
k
。
分类讨论：
（1）当 k
0 时：
3 T
2 | |
2 3
；选项中无此答案
t
t
ymin
1 1 1
2 ；两者综合得到：
ymin
。
y sin x 是奇函数 sin(x) sin x 。
3
f (x) sin x 1 f (x) sin(x) 1 sin x 1
sin x
sin( x)
sin x
(sin x 1 ) f (x) f (x) f (x) 是奇函数 f (x) 关于原点对称。 sin x
2
2
3
3
3( 3 sin 1 cos ) 1 3(cos sin sin cos ) 1
2
2
6
6
3 sin( ) 1 sin( ) 1
3
。
6
6 33
训练六：2020 年高考文科数学新课标Ⅲ卷第 12 题：已知函数 f (x) sin x 1 ，则（
）
sin x
A、 f (x) 的最小值为 2
2 (1800 3600 (1 k),3600 3600 (1 k)) 2 为第三、四象限角
sin 2 0 。
训练五：2020 年高考文科数学新课标Ⅲ卷第 5 题：已知 sin sin( ) 1，则 sin( ) （ ）
2020高考—三角函数(解答+答案)
2020年高考——三角函数1.(20全国Ⅰ文18)ABC △的内角A ，B ，C 的对边分别为a ，b ，c .已知B =150°.（1）若a ，b ABC △的面积；（2）若sin A C ，求C .2. （20全国Ⅱ文17）△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，已知25cos ()cos 24A A π++=． （1）求A ；（2）若b c -=，证明：△ABC 是直角三角形．3.（20全国Ⅱ理 17）ABC △中，sin 2A －sin 2B －sin 2C = sin B sin C ．（1）求A ；（2）若BC =3，求ABC △周长的最大值．4.（20新高考Ⅰ17）在①ac =sin 3c A =，③c =这三个条件中任选一个，补充在下面问题中，若问题中的三角形存在，求c 的值；若问题中的三角形不存在，说明理由．问题：是否存在ABC △，它的内角,,A B C 的对边分别为,,a b c ，且sin A B ，6C π=，________? 注：如果选择多个条件分别解答，按第一个解答计分．5.(20天津16)（本小题满分14分）在ABC △中，角,,A B C 所对的边分别为,,a b c ．已知5,a b c === （Ⅰ）求角C 的大小； （Ⅱ）求sin A 的值； （Ⅲ）求πsin(2)4A +的值．6.(20浙江18)（本题满分14分）在锐角△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ．已知2sin 0b A =． （Ⅰ）求角B 的大小；（Ⅱ）求cos A +cos B +cos C 的取值范围．7.（20江苏16）（本小题满分14分）在△ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，已知3,2,45a c B ===︒． （1）求sin C 的值；（2）在边BC 上取一点D ，使得4cos 5ADC ∠=-，求tan DAC ∠的值．8.（20全国Ⅱ理21）(12分)已知函数f (x )= sin 2x sin2x ．（1）讨论f (x )在区间(0，π)的单调性； （2）证明: 33()f x ≤； （3）设n ∈N *，证明：sin 2x sin 22x sin 24x …sin 22n x ≤34nn ．9.(20北京17)（本小题13分）在ABC 中，11a b +=，再从条件①、条件②这两个条件中选择一个作为己知，求： （Ⅰ）a 的值：（Ⅱ）sin C 和ABC 的面积．条件①：17,cos 7c A ==-； 条件②：19cos ,cos 816A B ==．注：如果选择条件①和条件②分别解答，按第一个解答计分．参考答案：1.解：（1）由题设及余弦定理得2222832cos150c c =+-⨯︒，解得2c =-（舍去），2c =，从而a =ABC △的面积为12sin1502⨯⨯︒=（2）在ABC △中，18030A B C C =︒--=︒-，所以sin sin(30)sin(30)A C C C C =︒-=︒+，故sin(30)C ︒+=而030C ︒<<︒，所以3045C ︒+=︒，故15C =︒.2．解：（1）由已知得25sin cos 4A A +=，即21cos cos 04A A -+=． 所以21(cos )02A -=，1cos 2A =．由于0A <<π，故3A π=．（2）由正弦定理及已知条件可得sin sin B C A -．由（1）知23B C π+=，所以2sin sin()33B B ππ--．即11sin 22B B =，1sin()32B π-=．由于03B 2π<<，故2B π=．从而ABC △是直角三角形．3．解：（1）由正弦定理和已知条件得222BC AC AB AC AB --=⋅，①由余弦定理得2222cos BC AC AB AC AB A =+-⋅，② 由①，②得1cos 2A =. 因为0πA <<，所以2π3A =.（2）由正弦定理及（1）得sin sin sin AC AB BCB C A===从而AC B =，π)3cos AB A B B B =--=-.故π33cos 3)3BC AC AB B B B ++=++=++.又π03B <<，所以当π6B =时，ABC △周长取得最大值3+4．解：方案一：选条件①．由6C π=和余弦定理得2222a b c ab +-=．由sin A B =及正弦定理得a =．222=b c =．由①ac =1a b c ==．因此，选条件①时问题中的三角形存在，此时1c =． 方案二：选条件②．由6C π=和余弦定理得2222a b c ab +-=．由sin A B =及正弦定理得a =．222=b c =，6B C π==，23A π=．由②sin 3c A =，所以6c b a ===．因此，选条件②时问题中的三角形存在，此时c =方案三：选条件③．由6C π=和余弦定理得2222a b c ab +-=．由sin A B =及正弦定理得a =．222=b c =．由③c =，与b c =矛盾．因此，选条件③时问题中的三角形不存在．5．（Ⅰ）解：在ABC △中，由余弦定理及5,a b c ===222cos 22a b c C ab +-==．又因为(0,π)C ∈，所以π4C =．（Ⅱ）解：在ABC △中，由正弦定理及π,4C a c ===，可得sin sin 13a C A c ==．（Ⅲ）解：由a c <及sin A =cos A == 进而2125sin 22sin cos ,cos 22cos 113A A A A A ===-=．所以，πππ125sin(2)sin 2cos cos 2sin 44413213226A A A +=+=⨯+⨯=．6.（Ⅰ）由正弦定理得2sin sin B A A ，故sin B =， 由题意得π3B =. （Ⅱ）由πA B C ++=得2π3C A =-， 由ABC △是锐角三角形得ππ(,)62A ∈.由2π1cos cos()cos 32C A A A =-=-得11π13cos cos cos cos sin()]22622A B C A A A ++++=++∈.故cos cos cos A B C ++的取值范围是3]2.7.解：（1）在ABC △中，因为3,45a c B ===︒，由余弦定理2222cos b a c ac B =+-，得292235b =+-⨯︒=，所以b =在ABC △中，由正弦定理sin sin b cB C=，，所以sin C =（2）在ADC △中，因为4cos 5ADC ∠=-,所以ADC ∠为钝角，而180ADC C CAD ∠+∠+∠=︒,所以C ∠为锐角.故cos C =则sin 1tan cos 2C C C ==. 因为4cos 5ADC ∠=-，所以3sin 5ADC ∠==，sin 3tan cos 4ADC ADC ADC ∠∠==-∠.从而31tan()242tan tan(180)tan()===311tan tan 111()42ADC C ADC ADC C ADC C ADC C -+∠+∠∠=︒-∠-∠=-∠+∠---∠⨯∠--⨯8．解：（1）()cos (sin sin 2)sin (sin sin 2)f x x x x x x x ''=+22sin cos sin 22sin cos2x x x x x =+ 2sin sin3x x =．当(0,)(,)33x π2π∈π时，()0f x '>；当(,)33x π2π∈时，()0f x '<． 所以()f x 在区间(0,),(,)33π2ππ单调递增，在区间(,)33π2π单调递减．（2）因为(0)()0f f =π=，由（1）知，()f x 在区间[0,]π的最大值为()3fπ=，最小值为()3f 2π=．而()f x 是周期为π的周期函数，故|()|f x ≤． （3）由于32222(sin sin 2sin 2)nx xx333|sin sin 2sin 2|n x xx =23312|sin ||sin sin 2sin 2sin 2||sin 2|n n n x x x x x x -= 12|sin ||()(2)(2)||sin 2|n n x f x f x f x x -=1|()(2)(2)|n f x f x f x -≤，所以22223333sin sin 2sin 2()4n nnn x xx ≤=．9.。
2020届山东省新高考高三优质数学试卷分项解析 专题05 三角函数与解三角形(原卷版)
专题5 三角函数与解三角形1.近几年高考在对三角恒等变换考查的同时，对三角函数图象与性质的考查力度有所加强，往往将三角恒等变换与三角函数的图象和性质结合考查，先利用三角公式进行化简，然后进一步研究三角函数的性质.其中三角函数的定义域值域、单调性、奇偶性、周期性、对称性以及图象变换是主要考查对象，难度以中档以下为主.2.高考对正弦定理和余弦定理的考查较为灵活，题型多变，往往以小题的形式独立考查正弦定理或余弦定理，以解答题的形式综合考查定理的综合应用，多与三角形周长、面积有关；有时也会与平面向量、三角恒等变换等结合考查，试题难度控制在中等或以下，主要考查灵活运用公式求解计算能力、推理论证能力、数学应用意识、数形结合思想等．预测2020年将突出考查恒等变换与三角函数图象和性质的结合、恒等变换与正弦定理和余弦定理的结合.一、单选题1．（2020届山东省潍坊市高三上期中）sin 225︒= （ ）A ．12-B ．2-C ．D ．1-2．（2020届山东省泰安市高三上期末）“1a <-”是“0x ∃∈R ，0sin 10+<a x ”的（ ） A ．充分不必要条件 B ．必要不充分条件 C ．充要条件D ．既不充分也不必要条件3．（2020届山东省潍坊市高三上期末）已知345sin πα⎛⎫-= ⎪⎝⎭，0,2πα⎛⎫∈ ⎪⎝⎭，则cos α=（ ）A ．10B ．10C ．2 D ．104．（2020届山东省枣庄市高三上学期统考）设函数2sin cos ()(,0)x x xf x a R a ax +=∈≠，若(2019)2f -=，(2019)f =( )A ．2B ．-2C ．2019D ．-20195．（2020届山东省枣庄市高三上学期统考）已知函数()cos()(0)f x x ωϕω=+>的最小正周期为π，且对x ∈R ，()3f x f π⎛⎫⎪⎝⎭…恒成立，若函数()y f x =在[0,]a 上单调递减，则a 的最大值是（ ） A ．π6 B ．π3C ．2π3D ．5π66．（2020届山东省滨州市三校高三上学期联考）若π1sin 34α⎛⎫-= ⎪⎝⎭，则πcos 23α⎛⎫+= ⎪⎝⎭（ ）．A ．78-B ．14-C ．14 D ．787．（2020届山东省潍坊市高三上期中）已知函数()sin cos f x x x =+，则（ ） A ．()f x 的最小正周期为π B ．()y f x =图象的一条对称轴方程为4x π=C ．()f x 的最小值为2-D ．()f x 的0,2π⎡⎤⎢⎥⎣⎦上为增函数8．（2020届山东省九校高三上学期联考）如图是一个近似扇形的鱼塘，其中OA OB r ==，弧AB 长为l （l r <）.为方便投放饲料，欲在如图位置修建简易廊桥CD ，其中34OC OA =，34OD OB =.已知1(0,)2x ∈时，3sin 3!x x x ≈-，则廊桥CD 的长度大约为（ ）A ．323432r r l - B ．323432l l r - C ．32324l l r-D ．32324r r l-9．（2020·武邑县教育局教研室高三上期末（理））已知()cos 2cos 2παπα⎛⎫-=+ ⎪⎝⎭，且()1tan 3αβ+=，则tan β的值为（） A ．-7B ．7C ．1D ．-110．（2020届山东师范大学附中高三月考）为了得函数23y sin x π⎛⎫=+ ⎪⎝⎭的图象，只需把函数2y sin x =的图象（ ） A ．向左平移6π个单位 B ．向左平移3π单位 C ．向右平移6π个单位 D ．向右平移3π个单位11．（2020届山东省枣庄、滕州市高三上期末）将曲线()cos 2y f x x =上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向右平移4π个单位长度，得到曲线cos 2y x =，则6f π⎛⎫= ⎪⎝⎭（ ）A ．1B ．-1C D ．12．（2020届山东省济宁市高三上期末）在ABC ∆中,1,3,1AB AC AB AC ==⋅=-u u u r u u u r,则ABC ∆的面积为( )A ．12B ．1CD ．213．（2020届山东省潍坊市高三上学期统考）将函数()πsin 23f x x ⎛⎫=+ ⎪⎝⎭的图像向右平移()0a a >个单位得到函数()πcos 24g x x ⎛⎫=+ ⎪⎝⎭的图像，则a 的值可以为（ ）A ．5π12B ．7π12C ．19π24D ．41π2414．（2020届山东省临沂市高三上期末）已知函数2()2cos 12f x x πω⎛⎫=- ⎪⎝⎭(0)>ω的图象关于直线4x π=对称，则ω的最小值为（ ） A ．13B ．16C ．43D ．5615．（2020届山东省潍坊市高三上学期统考）已知△ABC 的内角,,A B C 的对边分别为,,a b c ，若2cos cos cos b B a C c A =+，2b =，则△ABC 面积的最大值是A ．1B C ．2D ．416．（2020届山东省烟台市高三上期末）若x α=时，函数()3sin 4cos f x x x =+取得最小值，则sin α=（ ）A ．35B ．35-C ．45D ．45-17．（2020届山东实验中学高三上期中）在ABC △中，若 13,3,120AB BC C ==∠=o ，则AC =（ ） A ．1B ．2C ．3D ．418．（2020届山东实验中学高三上期中）已知()cos 2cos 2παπα⎛⎫-=+ ⎪⎝⎭，且()1tan 3αβ+=，则tan β的值为（ ） A ．-7B ．7C ．1D ．-119．（2020届山东省济宁市高三上期末）函数22cos cos 1y x x =-++，,22x ππ⎡⎤∈-⎢⎥⎣⎦的图象大致为( ) A ． B ．C ．D ．20．（2020届山东师范大学附中高三月考）泉城广场上矗立着的“泉标”，成为泉城济南的标志和象征．为了测量“泉标”高度，某同学在“泉标”的正西方向的点A 处测得“泉标”顶端的仰角为45︒，沿点A 向北偏东30︒前进100 m 到达点B ，在点B 处测得“泉标”顶端的仰角为30︒，则“泉标”的高度为（ ） A ．50 mB ．100 mC ．120 mD ．150 m21．（2020届山东实验中学高三上期中）已知函数()sin 23f x a x x =的图象关于直线12x π=-对称，若()()124f x f x ⋅=-，则12a x x -的最小值为（ ） A ．4πB ．2π C ．πD ．2π22．（2020届山东省滨州市高三上期末）已知函数()2sin(2)f x x ϕ=+的图象过点,26A π⎛⎫⎪⎝⎭，则( ) A ．把()y f x =的图象向右平移6π个单位得到函数2sin 2y x =的图象B ．函数()f x 在区间,02π⎛⎫- ⎪⎝⎭上单调递减C ．函数()f x 在区间[]0,2π内有五个零点D ．函数()f x 在区间0,3π⎡⎤⎢⎥⎣⎦上的最小值为1 二、多选题23．（2020届山东省滨州市三校高三上学期联考）设函数()sin 23f x x π⎛⎫=- ⎪⎝⎭，则下列结论正确的是（ ） A ．π-是()f x 的一个周期 B ．()f x 的图像可由sin 2y x =的图像向右平移3π得到 C ．()f x π+的一个零点为6x π=D ．()y f x =的图像关于直线1712x π=对称 24．（2020届山东师范大学附中高三月考）在平面直角坐标系xOy 中，角α顶点在原点O ，以x 正半轴为始边，终边经过点()()1,0P m m <，则下列各式的值恒大于0的是（ ） A ．sin tan ααB ．cos sin αα-C ．sin cos ααD ．sin cos αα+25．（2020·蒙阴县实验中学高三期末）关于函数()22cos cos(2)12f x x x π=-+-的描述正确的是（ ）A ．其图象可由2y x =的图象向左平移8π个单位得到 B ．()f x 在(0,)2π单调递增C ．()f x 在[]0,π有2个零点D ．()f x 在[,0]2π-的最小值为26．（2020·山东省淄博实验中学高三上期末）已知函数()sin cos f x x x =-，()g x 是()f x 的导函数，则下列结论中正确的是（ ）A ．函数()f x 的值域与()g x 的值域不相同B ．把函数()f x 的图象向右平移2π个单位长度，就可以得到函数()g x 的图象 C ．函数()f x 和()g x 在区间,44ππ⎛⎫-⎪⎝⎭上都是增函数 D ．若0x 是函数()f x 的极值点，则0x 是函数()g x 的零点27．（2020届山东省枣庄市高三上学期统考）将函数()sin 23f x x π⎛⎫=+ ⎪⎝⎭的图象向右平移2π个单位长度得到()g x 图象，则下列判断正确的是（ ） A ．函数()g x 在区间,122ππ⎡⎤⎢⎥⎣⎦上单调递增 B ．函数()g x 图象关于直线712x π=对称 C ．函数()g x 在区间,63ππ⎡⎤-⎢⎥⎣⎦上单调递减 D ．函数()g x 图象关于点,03π⎛⎫⎪⎝⎭对称28．（2020届山东省潍坊市高三上期末）已知()()22210f x cos x x ωωω=->的最小正周期为π，则下列说法正确的有（ ） A ．2ω= B ．函数()f x 在[0,]6π上为增函数C ．直线3x π=是函数()y f x =图象的一条对称轴D ．5π,012骣琪琪桫是函数()y f x =图象的一个对称中心29．（2020届山东省潍坊市高三上学期统考）在ABC V 中，内角A ，B ，C 所对的边分别为a ，b ，c ，若1tan A ，1tan B ，1tan C依次成等差数列，则下列结论中不一定成立．．．．．的是（ ） A ．a ，b ，c 依次成等差数列B C ．2a ，2b ，2c 依次成等差数列 D ．3a ，3b ，3c 依次成等差数列30．（2020届山东省济宁市高三上期末）将函数()sin 2f x x =的图象向右平移4π个单位后得到函数()g x 的图象,则函数()g x 具有性质( )A ．在0,4π⎛⎫⎪⎝⎭上单调递增,为偶函数 B ．最大值为1,图象关于直线32x π=-对称 C ．在3,88ππ⎛⎫-⎪⎝⎭上单调递增,为奇函数 D ．周期为π,图象关于点3,04π⎛⎫⎪⎝⎭对称 31．（2020届山东实验中学高三上期中）己知函数()()()sin 0,023f x x f x ππωϕωϕ⎛⎫=+><<- ⎪⎝⎭，为的一个零点，6x π=为()f x 图象的一条对称轴，且()()0f x π在，上有且仅有7个零点，下述结论正确．．的是（ ） A ．=6πϕB ．=5ωC ．()()0f x π在，上有且仅有4个极大值点D ．()042f x π⎛⎫⎪⎝⎭在，上单调递增32．（2019·山东师范大学附中高三月考）在平面直角坐标系xOy 中，角α顶点在原点O ，以x 正半轴为始边，终边经过点()()1,0P m m <，则下列各式的值恒大于0的是（ ） A ．sin tan ααB ．cos sin αα-C ．sin cos ααD ．sin cos αα+33．（2020届山东省烟台市高三上期末）已知函数()()sin 322f x x ππϕϕ⎛⎫=+-<< ⎪⎝⎭的图象关于直线4x π=对称，则（ ） A ．函数12f x π⎛⎫+⎪⎝⎭为奇函数 B ．函数()f x 在,123ππ⎡⎤⎢⎥⎣⎦上单调递增 C ．若()()122f x f x -=，则12x x -的最小值为3πD ．函数()f x 的图象向右平移4π个单位长度得到函数cos3y x =-的图象 三、填空题34．（2020届山东省枣庄市高三上学期统考）已知1sin 4x =，x 为第二象限角，则sin 2x =______. 35．（2020届山东省日照市高三上期末联考）已知tan 3α=，则sin cos sin cos αααα-+的值为______.36．（2020届山东师范大学附中高三月考）已知1tan 3α=，则2sin 2sin 1cos 2ααα-+的值为________．37．（2020届山东省枣庄、滕州市高三上期末）在平面直角坐标系xOy 中，角α的顶点是O ，始边是x 轴的非负半轴，02απ<<，点1tan,1tan1212P ππ⎛⎫+- ⎪⎝⎭是α终边上一点，则α的值是________. 38．（2020·全国高三专题练习（文））已知sin cos 11cos 2ααα=-，1tan()3αβ-=，则tan β=________.39．（2020届山东实验中学高三上期中）在ABC ∆中，,,a b c 分别为内角,,A B C 的对边，若32sin sin sin ,cos 5B AC B =+=，且6ABC S ∆=，则b =__________． 40．（2020届山东省日照市高三上期末联考）已知函数()9sin 26f x x π⎛⎫=-⎪⎝⎭，当[]0,10x π∈时，把函数()()6F x f x =-的所有零点依次记为123,,,,n x x x x ⋅⋅⋅，且123n x x x x <<<⋅⋅⋅<，记数列{}n x 的前n 项和为n S ，则()12n n S x x -+=______.41．（2020届山东省德州市高三上期末）已知函数()()sin f x A x =+ωϕ0,0,||2A πωϕ⎛⎫>><⎪⎝⎭的最大值2π，且()f x 的图象关于直线3x π=-对称，则当,66x ππ⎡⎤∈-⎢⎥⎣⎦时，函数()f x 的最小值为______.42．（2020届山东省泰安市高三上期末）在△ABC 中，内角A ，B ，C 的对边分别为,,a b c ，若cos cos sin A B C a b c +=，22265b c a bc +-=，则tan B =______． 四、解答题43．（2020届山东省临沂市高三上期末）在①3cos 5A =，cos C =，②sin sin sin c C A b B =+，60B =o，③2c =，1cos 8A =三个条件中任选一个补充在下面问题中，并加以解答. 已知ABC V 的内角A ，B ，C 的对边分别为a ，b ，c ，若3a =，______，求ABC V 的面积S . 44．（2020届山东省泰安市高三上期末）在①函数()()1sin 20,22f x x πωϕωϕ⎛⎫=+>< ⎪⎝⎭的图象向右平移12π个单位长度得到()g x 的图象，()g x图象关于原点对称；②向量),cos 2m x x ωω=u r，()11cos ,,0,24n x f x m n ωω⎛⎫=>=⋅ ⎪⎝⎭r u r r ；③函数()1cos sin 64f x x x πωω⎛⎫=+- ⎪⎝⎭()0ω>这三个条件中任选一个，补充在下面问题中，并解答．已知_________，函数()f x 的图象相邻两条对称轴之间的距离为2π． （1）若02πθ<<，且sin θ=()f θ的值； （2）求函数()f x 在[]0,2π上的单调递减区间．45．（2020届山东省枣庄市高三上学期统考）ABC ∆的内角A ，B ，C 的对边分别为,,a b c ，已知()2cos cos 0a c B b A ++=.（I ）求B ；（II ）若3,b ABC =∆的周长为3ABC +∆的面积.46．（2020届山东省滨州市三校高三上学期联考）已知函数()sin()f x A x ωϕ=+，其中0A >，0>ω，(0,)ϕπ∈，x ∈R ，且()f x 的最小值为-2，()f x 的图象的相邻两条对称轴之间的距离为2π，()f x 的图象过点,03π⎛-⎫ ⎪⎝⎭.（1）求函数()f x 的解析式和单调递增区间； （2）若[0,2]x πÎ函数()f x 的最大值和最小值.47．（2020届山东省潍坊市高三上期中）在ABC ∆中，内角A ，B ，C 所对的边分别为a ，b ，c ．已知10a b +=，5c =，sin 2sin 0B B +=．（1）求a ，b 的值： （2）求sin C 的值．48．（2020届山东省烟台市高三上期末）在条件①()(sin sin )()sin a b A B c b C +-=-，②sin cos()6a Bb A π=+，③sinsin 2B Cb a B +=中任选一个，补充到下面问题中，并给出问题解答. 在ABC ∆中，角,,A B C 的对边分别为,,a bc ，6b c +=，a =， . 求ABC ∆的面积.49．（2020届山东省泰安市高三上期末）如图所示，有一块等腰直角三角形地块ABC ，90A ∠=o ，BC 长2千米，现对这块地进行绿化改造，计划从BC 的中点D 引出两条成45°的线段DE 和DF ，与AB 和AC 围成四边形区域AEDF ，在该区域内种植花卉，其余区域种植草坪；设BDE α∠=，试求花卉种植面积()S α的取值范围．50．（2020届山东省日照市高三上期末联考）在①ABC ∆面积2ABC S ∆=，②6ADC π∠=这两个条件中任选一个，补充在下面问题中，求AC . 如图，在平面四边形ABCD 中，34ABC π∠=，BAC DAC ∠=∠，______，24CD AB ==，求AC .51．（2020届山东省滨州市三校高三上学期联考）在ABC ∆中，内角A ，B ，C 所对的边分别为a ，b ，c ，23sin 2cos02A CB +-=. （1）求角B 的大小；（2）若2sin 2sin sin B A C =，且ABC ∆的面积为3ABC ∆的周长.52．（2020届山东省德州市高三上期末）已知a ，b ，c 分别为ABC ∆内角A ，B ，C 的对边，若ABC ∆同时满足下列四个条件中的三个：①2633()b a ac c a b -+=+；②2cos 22cos 12A A +=；③6a =④2b =（1）满足有解三角形的序号组合有哪些？（2）在（1）所有组合中任选一组，并求对应ABC ∆的面积. （若所选条件出现多种可能，则按计算的第一种可能计分）53．（20203(cos )sin b C a c B -=；②22cos a c b C +=；③sin 3sin2A Cb A a += 这三个条件中任选一个，补充在下面问题中的横线上，并解答相应的问题.在ABC ∆中，内角A ，B ，C 的对边分别为a ，b ，c ，且满足________________，23,b =4a c +=，求ABC ∆的面积.54．（2020届山东师范大学附中高三月考）ABC V 的内角A ，B ，C 的对边分别为a ，b ，c ，且满足cos cos 2c A a C a +=．（1）求a b的值； （2）若1a =，7c =，求ABC V 的面积． 55．（2020·蒙阴县实验中学高三期末）在非直角ABC ∆中，a ，b ，c 分别是A ，B ，C 的对边.已知4a =，5AB AC ⋅=u u u r u u u r ，求：（1）tan tan tan tan A A B C+的值； （2）BC 边上的中线AD 的长.56．（2020届山东师范大学附中高三月考）设函数5()2cos()cos 2sin()cos 122f x x x x x ππ=++++. （1）设方程()10f x -=在(0,)π内有两个零点12,x x ，求12x x +的值；（2）若把函数()y f x =的图象向左平移6π个单位，再向下平移2个单位，得函数()g x 图象，求函数()g x 在[,]33ππ-上的最值. 57.（2020届山东省潍坊市高三上期末）在①34asinC ccosA =;②252B C bsinasinB +=这两个条件中任选-一个，补充在下面问题中，然后解答补充完整的题.在ABC V 中，角,,A B C 的对边分别为,,a b c ，已知 ，32a =.(1)求sinA ;(2)如图，M 为边AC 上一点，,2MC MB ABM π=∠=，求ABC V 的面积58．（2020·山东省淄博实验中学高三上期末）在ABC ∆中，角A ，B ，C 的对边分别为a ，b ，c ，已知4cos cos cos a A c B b C =+.（1）若4a =，ABC ∆的面积为15，求b ，c 的值； （2）若()sin sin 0B k C k =>，且角C 为钝角，求实数k 的取值范围.59．（2020届山东省潍坊市高三上学期统考）已知函数()()23sin cos sin 10f x x x x ωωωω=-+>图象的相邻两条对称轴之间的距离为2π.（1）求ω的值及函数()f x 的单调递减区间；（2）如图，在锐角三角形ABC 中有()1f B =，若在线段BC 上存在一点D 使得2AD =，且6AC =，31CD =-，求三角形ABC 的面积.60．（2020届山东省济宁市高三上期末）已知()()23sin sin cos 2f x x x x ππ⎛⎫=-+- ⎪⎝⎭. (1)若1210f α⎛⎫= ⎪⎝⎭,求2cos 23πα⎛⎫+ ⎪⎝⎭的值; (2)在△ABC 中,角A ,B ,C 所对应的边分别,,a b c ,若有()2cos cos a c B b C -=,求角B 的大小以及()f A 的取值范围.61．（2020届山东省济宁市高三上期末）如图,某市三地A ,B ,C 有直道互通.现甲交警沿路线AB ､乙交警沿路线ACB 同时从A 地出发,匀速前往B 地进行巡逻,并在B 地会合后再去执行其他任务.已知AB =10km ,AC =6km ,BC =8km ,甲的巡逻速度为5km /h ,乙的巡逻速度为10km /h .(1)求乙到达C 地这一时刻的甲､乙两交警之间的距离;(2)已知交警的对讲机的有效通话距离不大于3km ,从乙到达C 地这一时刻算起,求经过多长时间,甲､乙方可通过对讲机取得联系.62．（2020·全国高三专题练习（文））在ABC V 中，a ，b ，c 分别为内角A ，B ，C 的对边，且满()(sin sin )(3sin sin )b a B A c B C -+=-.（1）求A 的大小；（2）再在①2a =，②4B π=，③3=c b 这三个条件中，选出两个使ABC V 唯一确定的条件补充在下面的问题中，并解答问题.若________，________，求ABC V 的面积.63．（2020届山东实验中学高三上期中）己知函数()23sin cos sin 244f x x x x a ππ⎛⎫⎛⎫=++++ ⎪ ⎪⎝⎭⎝⎭的最大值为1.（1）求实数a 的值；（2）若将()f x 的图象向左平移6π个单位，得到函数()g x 的图象，求函数()g x 在区间0,2π⎡⎤⎢⎥⎣⎦上的最大值和最小值.64．（2020届山东实验中学高三上期中）“我将来要当一名麦田里的守望者，有那么一群孩子在一块麦田里玩，几千万的小孩子，附近没有一个大人，我是说……除了我”《麦田里的守望者》中的主人公霍尔顿将自己的精神生活寄托于那广阔无垠的麦田.假设霍尔顿在一块成凸四边形ABCD 的麦田里成为守望者，如图所示，为了分割麦田，他将BD 连接，设ABD ∆中边BD 所对的角为A ，BCD ∆中边BD 所对的角为C ，经测量已知2AB BC CD ===，23AD =.（1）霍尔顿发现无论BD 3cos A C -为一个定值，请你验证霍尔顿的结论，并求出这个定值；（2）霍尔顿发现麦田的生长于土地面积的平方呈正相关，记ABD ∆与BCD ∆的面积分别为1S 和2S ，为了更好地规划麦田，请你帮助霍尔顿求出2212S S +的最大值.。
2020年高考数学(理)热点专练05三角函数及解三角形(解析版).pdf
对于三角函数有关恒等变换的题目应注重公式的变形。
解三角形类型的大题中， 重点是角边转化， 但是要注意两边必须同时转化， 对于对应的面
积的最大值问题以及周长的最值问题一般转化成基本不等式去求，
但是在用基本不等式的时
候应注意不等式等号成立的条件。
【考查题型】 选择题，填空，（解答题 21 题）（两小一大或者是三小）
3 b 2 a2 c 2 ，则 B 4
A ． 90
B． 60
C ． 45
D． 30
2
【答案】 D
【解析】
【分析】
由正弦定理， 两角和的正弦函数公式化简已知等式可得 三角形面积公式可求角 C，从而得到 B 的值．
sinA＝ 1，即 A＝ 900，由余弦定理、
【详解】
由正弦定理及 ccosB bcosC asinA, 得 sinCcosB sinBcosC sin2 A,
热点 05 三角函数与解三角形
【命题趋势】
新高考环境下，三角函数与解三角形依然会作为一个重点参与到高考试题中，其中对
应的题目的 分布特点与命题规律分析可以看出 , 三角试题每年都考 , 而且文理有别 , 或 " 一大
一小 ", 或 " 三小 ", 或 " 二小 "(" 小 " 指选择题或填空题 ," 大 " 指解答题 ), 解答题以简单题或中档
【限时检测】（建议用时： 90 分钟）
1
1．（ 2019 ·安徽芜湖一中高三开学考试） ABC 的三个内角 A 、B 、C 所对的边分别为 a，b，c ，
asin Asin B
b cos2 A =
2a
b
，则
2020年高考试题分类汇编(三角函数)
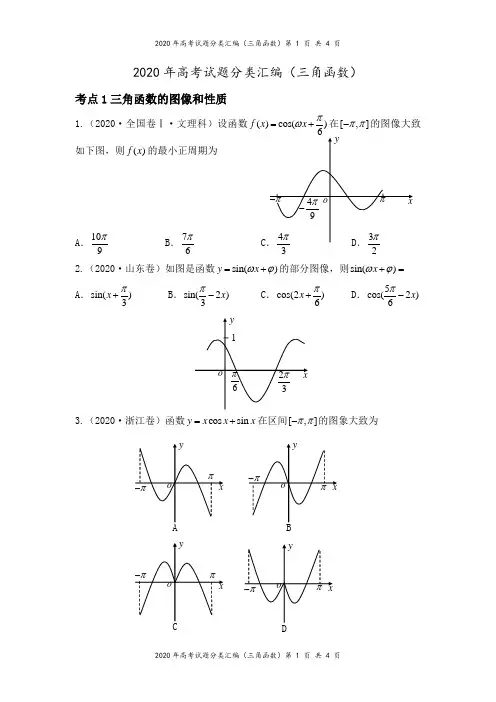
2020年高考试题分类汇编（三角函数）考点1三角函数的图像和性质1.（2020·全国卷Ⅰ·文理科）设函数()cos()f x x πω=+在[,]ππ-的图像大致如下图，则()fx 的最小正周期为 A ．109πB ．76π C 2.（2020·山东卷）如图是函数sin()y x ωϕ=+的部分图像，则sin()x ωϕ+=A．sin()3x π+ B ．sin(2)3x π- C．cos(2)6x π+ D ．5cos(2)6x π-3.（2020·浙江卷）函数cos sin y x x x =+在区间[,]ππ-的图象大致为4.（2020·全国卷Ⅲ·理科）关于函数1()sin sin f x x x=+有如下四个命题： ①()f x 的图像关于y 轴对称； ②()f x 的图像关于原点对称； ③()f x 的图像关于2x π=轴对称； ④()f x 的最小值为2.其中所有真命题的序号是 .5.（2020·全国卷Ⅲ·文科）设函数1()sin sin f x x x=+，则 A ．()f x 有最小值为2 B ．()f x 的图像关于y 轴对称 C ．()f x 的图像关于x π=轴对称 D ．()f x 的图像关于2x π=轴对称6.（2020·上海卷）已知()sin f x x ω=（0ω>）. （Ⅰ）若()f x 的周期是4π，求ω，并求此时1()2f x =的解集；（Ⅱ）已知1ω=，2()()()()2g x f x x f x π=--，[0,]4x π∈，求()g x的值域.7.（2020·天津卷）已知函数()sin()3f x x π=+．给出下列结论： ①()f x 的最小正周期为2π； ②()2f π是()f x 的最大值；③把函数sin y x =的图象上所有点向左平移3π个单位长度，可得到函数()y f x =的图象．其中所有正确结论的序号是A.①B.①③C.②③D.①②③ 8.（2020·北京卷）若函数()sin()cos f x x x ϕ=++的最大值为2，则常数ϕ的一个取值为 ．9.（2020·全国卷Ⅱ·理科）已知函数2()sin sin 2f x x x =. （Ⅰ）讨论()f x 在区间(0,)π的单调性；（Ⅱ）证明：()f x ≤；（Ⅲ）设n N *∈，证明：22223sin sin 2sin 4sin 24nnn x x xx ≤.考点2恒等变换1.（2020·全国卷Ⅰ·理科）已知(0,)απ∈，且3cos28cos 5αα-=，则sin α=A ．23 C ．13D 2.（2020·全国卷Ⅱ·理科）若α为第四象限的角，则A ．cos20α>B ．cos20α<C ．sin 20α>D ．sin 20α<3.（2020·全国卷Ⅱ·文科）2sin 3x =-，则cos2x = .4.（2020·全国卷Ⅲ·理科）已知2tan tan()74πθθ-+=，则tan θ=A ．2-B ．1-C ．1D ．2 5.（2020·全国卷Ⅲ·文科）sin sin()13πθθ++=，则sin()6πθ+=A ．12BC ．23D6.（2020·浙江卷）已知tan 2θ=，则cos2θ= ；tan()4πθ-= ．考点3解三角形1.（2020·全国卷Ⅲ·理科）在ABC ∆中，2cos 3C =，4AC =，3BC =，则cos B = A ．19 B ．13 C ．12 D ．232.（2020·全国卷Ⅲ·文科）在ABC ∆中，2cos 3C =，4AC =，3BC =，则tan B =A B ．．． 3.（2020·全国卷Ⅰ·文科）ABC ∆的内角A ，B ，C 所对的边分别为a ，b ，c .已知150B =.（Ⅰ）若a =，b =ABC ∆的面积；（Ⅱ）若sin 2A C =，求C . 4.（2020·全国卷Ⅱ·理科）ABC ∆中，222sin sin sin sin sin A B C B C --=.（Ⅰ）求A ；（Ⅱ）若3BC =，求ABC ∆周长的最大值.5.（2020·全国卷Ⅱ·文科）ABC ∆的内角A ，B ，C 所对的边分别为a ，b ，c ，已知25cos ()cos 24A A π++=.（Ⅰ）求A ；（Ⅱ）若b c -=，证明：ABC ∆是直角三角形.6.（2020·山东卷）在①ac =，②sin 3c A =，③c =这三个条件中任选一个，补充在下面问题中，若问题中的三角形存在，求c 的值；若问题中的三角形不存在，说明理由．问题：是否存在ABC ∆，它的内角A ，B ，C 所对的边分别为a ，b ，c .且sin AB ，6C π=， ?7.（2020·北京卷）在ABC ∆中，11a b +=，再从条件①、条件②这两个条件中选择一个作为己知，求： （Ⅰ）a 的值：（Ⅱ）sin C 和ABC ∆的面积．条件①：7c =，1cos 7A =-；条件②：1cos 8A =，9cos 16B =．注：如果选择条件①和条件②分别解答，按第一个解答计分．8.（2020·天津卷）在ABC ∆中，角A ，B ，C 所对的边分别为a ，b ，c .已知a =5b =，c =． （Ⅰ）求角C 的大小； （Ⅱ）求sin A 的值； （Ⅲ）求sin(2)4A π+的值． 9.（2020·浙江卷）在锐角ABC ∆中，角A ，B ，C 所对的边分别为a ，b ，c ，且2sin b A =． （Ⅰ）求角B ；（Ⅱ）求cos cos cos A B C ++的取值范围．。
2020高考—三角函数(选择+填空+答案)
2020年高考——三角函数1.(20全国Ⅰ文7)．设函数π()cos()6f x x ω=+在[−π，π]的图像大致如下图，则f （x ）的最小正周期为A ．10π9 B ．7π6 C ．4π3D ．3π22.(20全国Ⅰ理9)．已知 π()0,α∈，且3cos28cos 5αα-=，则sin α= A 5B ．23C ．13D 53.（20全国Ⅱ理2）．若α为第四象限角，则 A ．cos2α>0B ．cos2α<0C ．sin2α>0D ．sin2α<04.（20全国Ⅲ文5）．已知πsin sin=3θθ++（）1，则πsin =6θ+（） A ．12B 3C ．23D 2 5.（20全国Ⅲ文11）．在△ABC 中，cos C =23，AC =4，BC =3，则tan B = A 5B ．5C ．5D ．56.（20全国Ⅲ文12）．已知函数f (x )=sin x +1sin x，则 A ．f (x )的最小值为2B ．f (x )的图像关于y 轴对称C ．f (x )的图像关于直线x =π对称D ．f (x )的图像关于直线2x π=对称 7.（20全国Ⅲ理7）．在△ABC 中，cos C =23，AC =4，BC =3，则cos B = A ．19B ．13C ．12D ．238.（20全国Ⅲ理9）．已知2tan θ–tan(θ+π4)=7，则tan θ=A ．–2B ．–1C ．1D ．29.（20新高考Ⅰ10）．下图是函数y = sin(ωx +φ)的部分图像，则sin(ωx +φ)=A ．πsin(3x +）B ．πsin(2)3x - C ．πcos(26x +） D ．5πcos(2)6x -10.(20天津8)．已知函数π()sin()3f x x =+．给出下列结论： ①()f x 的最小正周期为2π； ②π()2f 是()f x 的最大值；③把函数sin y x =的图象上所有点向左平移π3个单位长度，可得到函数()y f x =的图象．其中所有正确结论的序号是 A ．①B ．①③C ．②③D ．①②③11.(20浙江4)．函数y =x cos x +sin x 在区间[–π，π]上的图象可能是12.(20北京9)．已知,R αβ∈，则“存在k Z ∈使得(1)kk απβ=+-”是“sin sin αβ=”的（ ）．A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件13.(20北京10)．2020年3月14日是全球首个国际圆周率日（π Day ）．历史上，求圆周率π的方法有多种，与中国传统数学中的“割圆术”相似．数学家阿尔·卡西的方法是：当正整数n 充分大时，计算单位圆的内接正6n 边形的周长和外切正6n 边形（各边均与圆相切的正6n 边形）的周长，将它们的算术平均数作为2π的近似值．按照阿尔·卡西的方法，π的近似值的表达式是（ ）．A ．30303sin tan n n n ︒︒⎛⎫+ ⎪⎝⎭B ．30306sin tan n n n ︒︒⎛⎫+ ⎪⎝⎭C ．60603sin tan n n n ︒︒⎛⎫+ ⎪⎝⎭D ．60606sintan n n n ︒︒⎛⎫+ ⎪⎝⎭ 14. （20全国Ⅱ文13）．若2sin 3x =-，则cos2x =__________． 15.（20全国Ⅲ理）16．关于函数f （x ）=1sin sin x x+有如下四个命题： ①f （x ）的图像关于y 轴对称． ②f （x ）的图像关于原点对称． ③f （x ）的图像关于直线x =2π对称． ④f （x ）的最小值为2．其中所有真命题的序号是__________．16.(20浙江13)．已知tan 2θ=，则cos2θ=_______，πtan()4θ-=_______．17.（20江苏8）．已知2sin ()4απ+=23，则sin 2α的值是 ▲ ．18.（20江苏10）．将函数πsin(32)4y x =﹢的图象向右平移π6个单位长度，则平移后的图象中与y 轴最近的对称轴的方程是 ▲ ．19.(20北京14)．若函数()sin()cos f x x x ϕ=++的最大值为2，则常数ϕ的一个取值为________． 参考答案：1．C 2．A 3．D 4．B 5．C 6．D 7．A 8．D 9．BC 10．B 11.A 12. C 13. A14.1915．②③ 16.31,53- 17．13 18．524x π=- 19.2π。
2020年高考试题三角函数汇编【题目+答案版】
2020年高考各地三角函数真题(1)【2020全国高考III卷(文)第5题】已知sin θ+sin (θ+π3)=1，则sin (θ+π6)=()A. 12B. √33C. 23D. √22(2)【2020全国高考（浙江卷）第4题】函数y=xcosx+sinx在区间[−π,π]的图象大致为()A. B.C. D.(3)【2020全国高考III卷(理)第9题】已知2tanθ−tan(θ+π4)=7,则tanθ=()A. −2B. −1C. 1D. 2(4)【2020全国高考（天津）卷第7题】已知函数f(x)=sin(x+π3).给出下列结论：①f(x)的最小正周期为2π；②f(π2)是f(x)的最大值；③把函数y=sinx的图象上的所有点向左平移π3个单位长度，可得到函数y=f(x)的图象．其中所有正确结论的序号是()A. ①B. ①③C. ②③D. ①②③(5)【2020全国高考（浙江卷）第13题】已知tttt=2，则ttt2t=______；tan(t−t4)=______．(6)【2020全国高考（江苏卷）第10题】将函数y=3sin(2x+π4)的图象向右平移π6个单位长度，则平移后的图象中与y轴最近的对称轴的方程是______．(7)【2020全国高考（江苏卷）第18题】在△ttt中，角A、B、C的对边分别为a、b、t.已知t=3，t=√2，t=45°．(1)求sin C的值；(2)在边BC上取一点D，使得cos∠ttt=−45，求tan∠ttt的值．(8)【2020全国高考I卷(理)第16题】如图，在三棱锥t−ttt的平面展开图中，tt=1，tt=tt=，AB AC，AB AD，ttt=，则ttt=__________．(9) 【2020全国高考天津卷第15题】如图，在四边形ABCD 中，∠t =60°，tt =3，tt =6，且tt ⃗⃗⃗⃗⃗⃗⃗⃗⃗ =t tt ⃗⃗⃗⃗⃗⃗⃗⃗⃗ ，tt ⃗⃗⃗⃗⃗⃗⃗⃗⃗ ⋅tt ⃗⃗⃗⃗⃗⃗⃗⃗⃗ =−32，则实数t 的值为______，若M ，N 是线段BC 上的动点，且|tt ⃗⃗⃗⃗⃗⃗⃗⃗⃗ |=1，则tt ⃗⃗⃗⃗⃗⃗⃗⃗⃗ ⋅tt ⃗⃗⃗⃗⃗⃗⃗⃗⃗ 的最小值为______．(10) 【2020全国高考（浙江卷）第18题】在锐角△ttt 中，角t ,t ,t 的对边分别为t ,t ,t .已知2t sin t −√3t =0． (1)求角B ；(2)求cos t +cos t +cos t 的取值范围．(11) 【2020全国高考（上海卷）第18题】已知函数t (t )=sin tt ，t >0．(1)f(x)的周期是4π，求ω，并求f(x)=12的解集；(2)已知ω=1，g(x)=f 2(x)+√3f(−x)f(π2−x)，x ∈[0,π4]，求g(x)的值域．(12) 【2020全国高考（天津卷）第16题】在△ttt 中，角A ，B ，C 所对的边分别为a ，b ，t .已知t =2√2，t =5，t =√13． (1)求角C 的大小； (2)求sin A 的值；(3)求sin (2t +t4)的值．(13) 【2020全国高考I 卷（文）第18题】∆ttt 的内角t ,t ,t 的对边分别为t ,t ,t ，已知t =150∘．（1）若a =√3c ，b =2√7，求∆ABC 的面积；（2）若sinA +√3sinC =√22，求C ．(14) 【2020全国高考II 卷（理）第16题】∆ttt 中，sin 2t −sin 2t −sin 2t =sin t sin t ．(1) 求A ；(2) 若BC =3，求∆ABC 周长的最大值．(15) 【2020全国高考II 卷（文）第17题】△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，已知cos 2(π2+A)+cosA =54．(1)求A ；(2)若b −c =√33a ，证明：△ABC 是直角三角形．（16）【2020全国高考II卷理科21题】已知函数t(t)=sin2t sin2t．(1)讨论t(t)在区间(0,t)的单调性；(2)证明：|t(t)|≤3√3；8(3)设t∈N∗，证明：sin2t sin22t sin24t⋯sin22t t≤3t．4t【答案】2020年高考各地三角函数真题(1)【2020全国高考III卷(文)第5题】已知sin θ+sin (θ+π3)=1，则sin (θ+π6)=()A. 12B. √33C. 23D. √22解：∵sin (t+t3)=12sin t+√32cos t，∴sin t+sin (t+t3)=32sin t+√32cos t=√3sin (t+t6)=1得sin (t+t6)=√33故选：B．(2)【2020全国高考（浙江卷）第4题】函数y=xcosx+sinx在区间[−π,π]的图象大致为()A. B.C. D.【答案】A【解析】解：t=t(t)=ttttt+tttt，则t(−t)=−ttttt−tttt=−t(t)，∴t(t)为奇函数，函数图象关于原点对称，故排除B，D，当t=t时，t=t(t)=ttttt+tttt=−t<0，故排除B，故选：A．先判断函数的奇偶性，再判断函数值的特点．本题考查了函数图象的识别，掌握函数的奇偶性额函数值得特点是关键，属于基础题．(3)【2020全国高考III卷(理)第9题】已知2tanθ−tan(θ+π4)=7,则tanθ=()A. −2B. −1C. 1D. 2解：∵2tan t−tan (t+t4)=2tan t−tan t+11−tan t=7，∴2tan t(1−tan t)−(tan t+1)=7−7tan t，整理得(tan t−2)2=0，∴tan t=2，故选D．(4)【2020全国高考（天津）卷第7题】已知函数f(x)=sin(x+π3).给出下列结论：①f(x)的最小正周期为2π；②f(π2)是f(x)的最大值；③把函数y=sinx的图象上的所有点向左平移π3个单位长度，可得到函数y=f(x)的图象．其中所有正确结论的序号是()A. ①B. ①③C. ②③D. ①②③【答案】B【解析】【分析】本题以命题的真假判断为载体，主要考查了正弦函数的性质的简单应用，属于中档题．由已知结合正弦函数的周期公式可判断①，结合函数最值取得条件可判断②，结合函数图象的平移可判断③．【解答】解：因为f(x)=sin(x+π3)，①由周期公式可得，f(x)的最小正周期T=2π，故①正确；、②f(π2)=sin(π2+π3)=sin5π6=12，不是f(x)的最大值，故②错误；③根据函数图象的平移法则可得，函数y=sinx的图象上的所有点向左平移π3个单位长度，可得到函数y=f(x)的图象，故③正确．故选：B．(5) 【2020全国高考（浙江卷）第13题】已知tttt =2，则ttt2t =______；tan (t −t4)=______． 【答案】−35 13【解析】解：tttt =2，则ttt2t =cos 2t −sin 2t cos 2t +sin 2t=1−tan 2t 1+tan 2t =1−41+4=−35．tan (t −t4)=tttt −tan t41+ttttttt t4=2−11+2×1=13． 故答案为：−35；13．利用二倍角公式以及同角三角函数基本关系式求解第一问，利用两角和与差的三角函数转化求解第二问．本题考查二倍角公式的应用，两角和与差的三角函数以及同角三角函数基本关系式的应用，是基本知识的考查．(6) 【2020全国高考（江苏卷）第10题】将函数y =3sin(2x +π4)的图象向右平移π6个单位长度，则平移后的图象中与y 轴最近的对称轴的方程是______．解：因为函数t =3ttt (2t +t4)的图象向右平移t6个单位长度可得t (t )=t (t −t6)=3ttt (2t −t 3+t 4)=3ttt (2t −t12)，则t =t (t )的对称轴为2t −t12=t2+tt ，t ∈t ，即t =7t 24+tt2，t ∈t ，当t =0时，t =7t24， 当t =−1时，t =−5t24， 所以平移后的图象中与y 轴最近的对称轴的方程是t =−5t24， 故答案为：t =−5t 24．(7) 【2020全国高考（江苏卷）第18题】在△ttt 中，角A 、B 、C 的对边分别为a 、b 、t .已知t =3，t =√2，t =45°． (1)求sin C 的值；(2)在边BC 上取一点D ，使得cos ∠ttt =−45，求tan ∠ttt 的值．【答案】解：(1)因为t =3，t =√2，t =45°.，由余弦定理可得：t =√t 2+t 2−2tttttt =√9+2−2×3×√2×√22=√5，由正弦定理可得t tttt =ttttt ，所以tttt =t t⋅ttt45°=√2√5⋅√22=√55，所以tttt =√55；(2)因为cos ∠ttt =−45，所以sin ∠ttt =√1−cos 2∠ttt =35， 在三角形ADC 中，易知C 为锐角，由(1)可得tttt =√1−sin 2t =2√55，所以在三角形ADC 中，sin ∠ttt =sin (∠ttt +∠t )=sin ∠tttttt ∠t +cos ∠tttttt ∠t =2√525，因为∠ttt ∈(0,t2)，所以cos ∠ttt =√1−sin 2∠ttt =11√525，所以tan ∠ttt =sin ∠ttt cos ∠ttt=211．(8) 【2020全国高考I 卷(理)第16题】如图，在三棱锥t −ttt 的平面展开图中，tt =1，tt =tt =，AB AC ，ABAD ，ttt =，则ttt =__________．解：由已知得tt =√2tt =√6， ∵t 、E 、F 重合于一点，∴tt =tt =√3，tt =tt =√6， ∴ △ttt 中，由余弦定理得，∴tt =tt =1， ∴在△ttt 中，由余弦定理得．故答案为．(9) 【2020全国高考天津卷第15题】如图，在四边形ABCD 中，∠t =60°，tt =3，tt =6，且tt ⃗⃗⃗⃗⃗⃗⃗⃗⃗ =t tt ⃗⃗⃗⃗⃗⃗⃗⃗⃗ ，tt⃗⃗⃗⃗⃗⃗⃗⃗⃗ ⋅tt ⃗⃗⃗⃗⃗⃗⃗⃗⃗ =−32，则实数t 的值为______，若M ，N 是线段BC 上的动点，且|tt ⃗⃗⃗⃗⃗⃗⃗⃗⃗ |=1，则tt ⃗⃗⃗⃗⃗⃗⃗⃗⃗ ⋅tt ⃗⃗⃗⃗⃗⃗⃗⃗⃗ 的最小值为______． (10) 【答案】16 132(11) 【解析】解：以B 为原点，以BC 为x 轴建立如图所示的直角坐标系，∵∠B =60°，AB =3，∴A(32,3√32)， ∵BC =6， ∴C(6,0)， ∵AD ⃗⃗⃗⃗⃗⃗ =λBC ⃗⃗⃗⃗⃗ ， ∴AD//BC ， 设D(x 0,3√32)， ∴AD⃗⃗⃗⃗⃗⃗ =(x 0−32,0)，AB ⃗⃗⃗⃗⃗ =(−32,−3√32)， ∴AD ⃗⃗⃗⃗⃗⃗ ⋅AB ⃗⃗⃗⃗⃗ =−32(x 0−32)+0=−32，解得x 0=52，∴D(52,3√32)， ∴AD ⃗⃗⃗⃗⃗⃗ =(1,0)，BC ⃗⃗⃗⃗⃗ =(6,0)， ∴AD ⃗⃗⃗⃗⃗⃗ =16BC ⃗⃗⃗⃗⃗ ，∴λ=16，∵|MN⃗⃗⃗⃗⃗⃗⃗ |=1， 设M(x,0)，则N(x +1,0)，其中0≤x ≤5，∴DM ⃗⃗⃗⃗⃗⃗⃗ =(x −52,−3√32)，DN ⃗⃗⃗⃗⃗⃗ =(x −32,−3√32)， ∴DM ⃗⃗⃗⃗⃗⃗⃗ ⋅DN ⃗⃗⃗⃗⃗⃗ =(x −52)(x −32)+274=x 2−4x +212=(x −2)2+132，当x =2时取得最小值，最小值为132， 故答案为：16，132．以B 为原点，以BC 为x 轴建立如图所示的直角坐标系，根据向量的平行和向量的数量积即可求出点D 的坐标，即可求出λ的值，再设出点M ，N 的坐标，根据向量的数量积可得关于x 的二次函数，根据二次函数的性质即可求出最小值．本题考查了向量在几何中的应用，考查了向量的共线和向量的数量积，以及二次函数的性质，属于中档题．(12) 【2020全国高考（浙江卷）第18题】在锐角△ttt 中，角t ,t ,t 的对边分别为t ,t ,t .已知2t sin t −√3t =0． (1)求角B ；(2)求cos t +cos t +cos t 的取值范围．【答案】解：(1)∵2t sin t =√3t ， ∴2sin t sin t =√3sin t ， ∵sin t ≠0， ∴sin t =√32， ，∴t =t3，(2)∵△ttt 为锐角三角形，t =t3， ∴t =2t3−t ，，△ttt 为锐角三角形，，，解得， ，，∴cos t+cos t+cos t的取值范围为(√3+12,32 ]．【解析】本题考查了正弦定理，三角函数的化简，三角函数的性质，考查了运算求解能力和转化与化归能力，属于中档题．(1)根据正弦定理可得sin t=√32，结合角的范围，即可求出，(2)根据两角和差的余弦公式，以及利用正弦函数的性质即可求出．(13)【2020全国高考（上海卷）第18题】已知函数t(t)=sin tt，t>0．(1)f(x)的周期是4π，求ω，并求f(x)=12的解集；(2)已知ω=1，g(x)=f2(x)+√3f(−x)f(π2−x)，x∈[0,π4]，求g(x)的值域．【答案】解：(1)由于t(t)的周期是4t，所以t=2t4t =12，所以t(t)=sin12t．令sin12t=12，故12t=2tt+t6或2tt+5t6，整理得t=4tt+t3或t=4tt+5t3．故解集为{t|t=4tt+t3或t=4tt+5t3，t∈t}．(2)由于t=1，所以t(t)=sin t．所以t(t)=sin2t+√3sin(−t)sin(t2−t)=1−cos2t2−√32sin2t=−√32sin2t−12cos2t+12=12−sin(2t+t6)．由于t∈[0,t4]，所以t6≤2t+t6≤2t3．故−1≤−sin(2t+t6)≤−12，故−12≤t(t)≤0．所以函数t(t)的值域为[−12,0]．【解析】本题考查的知识要点：三角函数关系式的恒等变换，正弦型函数的性质的应用，主要考查学生的运算能力和转换能力及思维能力，属于中档题．(1)直接利用正弦型函数的性质的应用求出结果．(2)利用三角函数关系式的变换和正弦型函数的性质的应用求出函数的值域．【2020全国高考（天津卷）第16题】在△ttt中，角A，B，C所对的边分别为a，b，t.已知t=2√2，t=5，t=√13．(1)求角C的大小；(2)求sin A的值；(3)求sin(2t+t4)的值．【答案】解：(1)由余弦定理以及a=2√2，b=5，c=√13，则cosC=a2+b2−c22ab =2×22×5=√22，∵C∈(0,π)，∴C=π4；(2)由正弦定理，以及C=π4，a=2√2，c=√13，可得sinA= asinCc=2√2×√22√13=2√1313；(3)由a<c，及sinA=2√1313，可得cosA=√1−sin2A=3√1313，则sin2A=2sinAcosA=2×2√1313×3√1313=1213，∴cos2A=2cos2A−1=513，∴sin(2A+π4)=√22(sin2A+cos2A)=√22(1213+513)=17√226．【解析】本题考了正余弦定理，同角的三角形函数的关系，二倍角公式，两角和的正弦公式，属于中档题．(1)根据余弦定理即可求出C的大小；(2)根据正弦定理即可求出sin A的值；(3)根据同角的三角形函数的关系，二倍角公式，两角和的正弦公式即可求出．(14)【2020全国高考I卷（文）第18题】∆ttt的内角t,t,t的对边分别为t,t,t，已知t=150∘．（1）若a=√3c，b=2√7，求∆ABC的面积；（2）若sinA+√3sinC=√22，求C．【答案】解：(1)由余弦定理得t2=t2+t2−2tt cos t，即28=3t2+t2−2√3t2cos150∘，解得t=4，所以t=4√3，所以t△ttt=12tt sin t=12×4√3×4×12=4√3．(2)因为t=180∘−t−t=30∘−t，所以sin t+√3sin t=sin(30∘−t)+√3sin t=12cos t+√32sin t=sin(30∘+t)=√22，因为t>0°，t>0°，所以0°<t<30°，所以30°<30°+t<60°，所以30°+t=45°，所以t=15°．【解析】【解析】本题考查余弦定理，三角形面积公式的应用，三角恒等变换的应用，属于中档题．(1)由已知条件结合余弦定理可求得c，从而可根据三角形面积公式求解；(2)由两角差的正弦公式对已知式进行化简，再由辅助角公式根据C的范围求解即可．(15) 【2020全国高考II 卷（理）第17题】∆ttt 中，sin 2t −sin 2t −sin 2t =sin t sin t ．(2) 求A ；(2) 若BC =3，求∆ABC 周长的最大值．【答案】解：(1)在▵ttt 中，设内角A ，B ，C 的对边分别为a ，b ，c ， 因为sin 2t −sin 2t −sin 2t =sin t sin t ，由正弦定理得，t 2−t 2−t 2=tt ，即t 2+t 2−t 2=−tt ， 由余弦定理得，cos t =t2+t 2−t 22tt =−12，因为0<t <t ，所以t =2t 3． (2)由(1)知，t =2t3，因为tt =3，即t =3，由余弦定理得，t 2=t 2+t 2−2tt cos t ，所以9=t 2+t 2+tt =(t +t )2−tt ， 由基本不等式可得tt ≤(t +t )24，所以9=(t +t )2−tt ≥34(t +t )2,所以t +t ≤2√3(当且仅当t =t =√3时取得等号)， 所以▵ttt 周长的最大值为3+2√3．【解析】本题主要考查利用正余弦定理解三角形的问题，属于中档题． (1)直接利用正余弦定理即可求解；(2)利用余弦定理与基本不等式即可求解．(16) 【2020全国高考II 卷（文）第17题】△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，已知cos 2(π2+A)+cosA =54．(1)求A ；(2)若b −c =√33a ，证明：△ABC 是直角三角形．【答案】【解答】解：(1)∵cos2(t2+t)+cos t=54，化简得cos2t−cos t+14=0，解得cos t=12，∵t是tttt的内角，故t=t3．(2)证明：∵t−t=√33t，t=t3，由正弦定理可得sin t−sin t=√33sin t=12，又t=t−t−t=2t3−t，∴sin(2t3−t)−sin t=12，化简可得√32cos t−12sin t=12，即可得cos(t+t6)=12，又t∈(0,2t3)，得t+t6∈(t6,5t6)，故可得t+t6=t3，即t=t6，故t+t=t3+t6=t2，∴tttt是直角三角形．【解析】本题考查了正弦定理的应用以及两角和差的正余弦公式的应用，考查了诱导公式和辅助角公式，属于中档题．(1)利用诱导公式和同角的三角函数关系对已知式进行化简，得到cos t=12，再结合A为三角形的一内角，即可求出角A；(2)利用正弦定理把t−t=√33t中的边化成角，得到sin t−sin t=√33sin t=12，再结合t+t=2t3，对式子进行化简，最后结合辅助角公式以及角C的范围，求出角C，即可证得三角形为直角三角形．（17）【2020全国高考II卷理科21题】已知函数t(t)=sin2t sin2t．(1)讨论t(t)在区间(0,t)的单调性；(2)证明：|t(t)|≤3√38；(3)设t∈N∗，证明：sin2t sin22t sin24t⋯sin22t t≤3t4t．【答案】解：(1)t(t)=sin2t⋅sin2t=2sin2t⋅sin t⋅cos t =2sin3t⋅cos tt′(t)=2[sin2t(3cos2t−sin2t)]=2sin2t⋅(√3cos t+sin t)⋅(√3cos t−sin t)=−8sin2t⋅sin(t+t3)⋅sin(t−t3)所以对于f’(t)有：当t∈(0,t3)时，t′(t)>0；当t∈[t3,23t]时，t′(t)≤0；当t∈(2t3,t)时t′(t)>0。
2020高考—三角函数(选择+填空+答案)
2020年高考——三角函数1.(20全国Ⅰ文7)．设函数π()cos()6f x x ω=+在[−π，π]的图像大致如下图，则f （x ）的最小正周期为A ．10π9 B ．7π6 C ．4π3D ．3π22.(20全国Ⅰ理9)．已知 π()0,α∈，且3cos28cos 5αα-=，则sin α= A 5B ．23C ．13D 53.（20全国Ⅱ理2）．若α为第四象限角，则 A ．cos2α>0B ．cos2α<0C ．sin2α>0D ．sin2α<04.（20全国Ⅲ文5）．已知πsin sin=3θθ++（）1，则πsin =6θ+（） A ．12B 3C ．23D 2 5.（20全国Ⅲ文11）．在△ABC 中，cos C =23，AC =4，BC =3，则tan B = A 5B ．5C ．5D ．56.（20全国Ⅲ文12）．已知函数f (x )=sin x +1sin x，则 A ．f (x )的最小值为2B ．f (x )的图像关于y 轴对称C ．f (x )的图像关于直线x =π对称D ．f (x )的图像关于直线2x π=对称 7.（20全国Ⅲ理7）．在△ABC 中，cos C =23，AC =4，BC =3，则cos B = A ．19B ．13C ．12D ．238.（20全国Ⅲ理9）．已知2tan θ–tan(θ+π4)=7，则tan θ=A ．–2B ．–1C ．1D ．29.（20新高考Ⅰ10）．下图是函数y = sin(ωx +φ)的部分图像，则sin(ωx +φ)=A ．πsin(3x +）B ．πsin(2)3x - C ．πcos(26x +） D ．5πcos(2)6x -10.(20天津8)．已知函数π()sin()3f x x =+．给出下列结论： ①()f x 的最小正周期为2π； ②π()2f 是()f x 的最大值；③把函数sin y x =的图象上所有点向左平移π3个单位长度，可得到函数()y f x =的图象．其中所有正确结论的序号是 A ．①B ．①③C ．②③D ．①②③11.(20浙江4)．函数y =x cos x +sin x 在区间[–π，π]上的图象可能是12.(20北京9)．已知,R αβ∈，则“存在k Z ∈使得(1)kk απβ=+-”是“sin sin αβ=”的（ ）．A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件13.(20北京10)．2020年3月14日是全球首个国际圆周率日（π Day ）．历史上，求圆周率π的方法有多种，与中国传统数学中的“割圆术”相似．数学家阿尔·卡西的方法是：当正整数n 充分大时，计算单位圆的内接正6n 边形的周长和外切正6n 边形（各边均与圆相切的正6n 边形）的周长，将它们的算术平均数作为2π的近似值．按照阿尔·卡西的方法，π的近似值的表达式是（ ）．A ．30303sin tan n n n ︒︒⎛⎫+ ⎪⎝⎭B ．30306sin tan n n n ︒︒⎛⎫+ ⎪⎝⎭C ．60603sin tan n n n ︒︒⎛⎫+ ⎪⎝⎭D ．60606sintan n n n ︒︒⎛⎫+ ⎪⎝⎭ 14. （20全国Ⅱ文13）．若2sin 3x =-，则cos2x =__________． 15.（20全国Ⅲ理）16．关于函数f （x ）=1sin sin x x+有如下四个命题： ①f （x ）的图像关于y 轴对称． ②f （x ）的图像关于原点对称． ③f （x ）的图像关于直线x =2π对称． ④f （x ）的最小值为2．其中所有真命题的序号是__________．16.(20浙江13)．已知tan 2θ=，则cos2θ=_______，πtan()4θ-=_______．17.（20江苏8）．已知2sin ()4απ+=23，则sin 2α的值是 ▲ ．18.（20江苏10）．将函数πsin(32)4y x =﹢的图象向右平移π6个单位长度，则平移后的图象中与y 轴最近的对称轴的方程是 ▲ ．19.(20北京14)．若函数()sin()cos f x x x ϕ=++的最大值为2，则常数ϕ的一个取值为________． 参考答案：1．C 2．A 3．D 4．B 5．C 6．D 7．A 8．D 9．BC 10．B 11.A 12. C 13. A14.1915．②③ 16.31,53- 17．13 18．524x π=- 19.2π。
2020年高考理科数学《三角函数》题型归纳与训练含答案解析
2020年高考理科数学《三角函数》题型归纳与训练【题型归纳】题型一 三角函数的概念、诱导公式及同角关系式例1 （1）点P 从(1,0)出发，沿单位圆x 2＋y 2＝1逆时针方向运动2π3弧长到达Q 点，则Q 点的坐标为( )A ．(－12，32)B ．(－32，－12) C ．(－12，－32)D ．(－32，12) (2)已知角α的顶点与原点重合，始边与x 轴的正半轴重合，终边上一点P(－4,3)，则cos()sin()2119cos()sin()22παπαππαα+---+的值为________． 【答案】（1）A （2）－34【解析】(1)设Q 点的坐标为(x ，y)， 则x ＝cos 2π3＝－12，y ＝sin 2π3＝32.∴Q 点的坐标为(－12，32)．(2)原式＝－sin α·sin α－sin α·cos α＝tan α.根据三角函数的定义， 得tan α＝y x ＝－34，∴原式＝－34.【易错点】诱导公式和三角函数定义不熟练【思维点拨】(1)涉及与圆及角有关的函数建模问题(如钟表、摩天轮、水车等)，常常借助三角函数的定义求解．应用定义时，注意三角函数值仅与终边位置有关，与终边上点的位置无关．(2)应用诱导公式时要弄清三角函数在各个象限内的符号；利用同角三角函数的关系化简过程要遵循一定的原则，如切化弦、化异为同、化高为低、化繁为简等． 题型二 三角函数的图象及应用例1已知曲线1cos C y x =：，22πsin 23C y x ⎛⎫=+⎪⎝⎭：，则下面结正确的是（ ）.A.把1C 上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向右平移π6个单位长度，得到曲线2CB.把1C 上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向左平移π12个单位长度，得到曲线2CC.把1C 上各点的横坐标缩短到原来的12倍，纵坐标不变，再把得到的曲线向右平移π6个单位长度，得到曲线2CD.把1C 上各点的横坐标缩短到原来的12倍，纵坐标不变，再把得到的曲线向左平移π12个单位长度，得到曲线2C 【答案】D【解析】（1） 1:cos C y x =，22π:sin 23⎛⎫=+ ⎪⎝⎭C y x ，首先曲线1C 、2C 统一为一三角函数名，可将1:cos C y x =用诱导公式处理．πππcos cos sin 222⎛⎫⎛⎫==+-=+ ⎪ ⎪⎝⎭⎝⎭y x x x ．横坐标变换需将1=ω变成2=ω，即112πππsin sin 2sin 2224y x y x x ⎛⎫⎛⎫⎛⎫=+−−−−−−−−→=+=+→ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭C 上各坐短它原点横标缩来2ππsin 2sin 233y x x ⎛⎫⎛⎫=+=+ ⎪ ⎪⎝⎭⎝⎭． 注意ω的系数，在右平移需将2=ω提到括号外面，这时π4+x 平移至π3+x ，根据“左加右减”原则，“π4+x ”到“π3+x ”需加上π12，即再向左平移π12．故选D. 【易错点】函数图像水平方向平移容易出错 【思维点拨】平移变换理论 (1)平移变换:①沿x 轴平移,按“左加右减”法则; ②沿y 轴平移,按“上加下减”法则. (2)伸缩变换:①沿x 轴伸缩时,横坐标x 伸长(0<ω<1)或缩短(ω>1)为原来的 倍(纵坐标y 不变); ②沿y 轴伸缩时,纵坐标y 伸长(A>1)或缩短(0<A<1)为原来的A 倍(横坐标x 不变). 2.注意平移前后两个函数的名称是否一致,若不一致,应用诱导公式化为同名函数再平移.例2函数sin 21cos xy x=-的部分图像大致为（ ）.【答案】C【解析】由题意知，函数sin 21cos xy x =-为奇函数，故排除B ；当x =π时，0y =，排除D ；当1x =时，sin 21cos 2y =>-，排除A.故选C.【易错点】函数图形判断通过过排除法 【思维点拨】例3函数f(x)＝2sin(ωx ＋φ)⎝⎛⎭⎫ω>0，－π2<φ<π2的部分图象如图所示，则ω，φ的值分别是( ) A ．2，－π3B ．2，－π6C ．4，－π6D ．4，π3【答案】A【解析】 (1)因为T 2＝11π12－5π12，所以T ＝π.又T ＝2πω(ω>0)，所以2πω＝π，所以ω＝2.又2×5π12＋φ＝π2＋2kπ(k ∈Z )，且－π2<φ<π2，故φ＝－π3.【易错点】求φ时，容易忽略讨论k 【思维点拨】题型三 三角函数性质例1 （1）已知函数f(x)＝sin(ωx ＋φ)＋3cos(ωx ＋φ)(ω>0,0<|φ|<π2)为奇函数，且函数y ＝f(x)的图象的两相邻对称轴之间的距离为π2.(1)求f(π6)的值；(2)将函数y ＝f(x)的图象向右平移π6个单位后，得到函数y ＝g(x)的图象，求函数g(x)的单调递增区间．【答案】（1）f(π6)＝2sin π3＝3（2）[kπ－π12，kπ＋5π12](k ∈Z )．【解析】（1）f(x)＝sin(ωx ＋φ)＋3cos(ωx ＋φ) ＝2[12sin(ωx ＋φ)＋32cos(ωx ＋φ)]＝2sin(ωx ＋φ＋π3)．因为f(x)为奇函数，所以f(0)＝2sin(φ＋π3)＝0，又0<|φ|<π2，可得φ＝－π3，所以f(x)＝2sin ωx ，由题意得2πω＝2·π2，所以ω＝2.故f(x)＝2sin 2x. 因此f(π6)＝2sin π3＝ 3.(2)将f(x)的图象向右平移π6个单位后，得到f(x －π6)的图象，所以g(x)＝f(x －π6)＝2sin[2(x －π6)]＝2sin(2x －π3)．当2kπ－π2≤2x －π3≤2kπ＋π2(k ∈Z )，即kπ－π12≤x≤kπ＋5π12(k ∈Z )时，g(x)单调递增，因此g(x)的单调递增区间为[kπ－π12，kπ＋5π12](k ∈Z )．【易错点】 【思维点拨】题型四三角函数范围问题例1函数()23sin 0,42f x x x x ⎛π⎫⎡⎤=-∈ ⎪⎢⎥⎣⎦⎝⎭的最大值是 ． 【答案】1【解析】()2233πsin 1cos 0442f x x x x x x ⎛⎫⎡⎤=+-=--∈ ⎪⎢⎥⎣⎦⎝⎭，，令cos x t =且[]01t ∈，，214y t =-+21t ⎛=-+ ⎝⎭，则当t =时，()f x 取最大值1． 【易错点】换元之后转化为二次函数在定区间上的定义域及最值 【思维点拨】 例2函数()cos sin =2+fx x x 的最大值为 .【解析】2()21f x +=【易错点】【思维点拨】辅助角公式运用 例3【2017年Ⅲ】函数()1ππsin cos 536f x x x ⎛⎫⎛⎫=++- ⎪ ⎪⎝⎭⎝⎭的最大值为（ ）. A ．65B ．1C ．35D ．15【答案】A 【解析】11()sin sin sin sin 5362533f x x x x x πππππ⎛⎫⎛⎫⎛⎫⎛⎫=++-+=+++= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭ 6sin 53x π⎛⎫+ ⎪⎝⎭.故选A. 【易错点】本题属于中档题，基础差一点的学生在解题思路方面可能会存在一定问题，三角恒等变换中公式的选择对于学生来说是一个难点，对于老师教学来说是一个重点，选择合适的公式能起到事半功倍的效果！【思维点拨】题型五三角函数求值问题 例1已知π0,2α⎛⎫∈ ⎪⎝⎭，tan 2α=，则πcos 4α⎛⎫-= ⎪⎝⎭ .【解析】由tan 2sin 2cos ααα==得 又22sin cos 1αα+=，所以21cos 5α=.因为0,2απ⎛⎫∈ ⎪⎝⎭，所以cos 5α=，sin 5α=.因为cos cos cos sin sin 44αααππ⎛⎫-=π+ ⎪⎝⎭，所以cos 4525210πα⎛⎫-=+⨯= ⎪⎝⎭. 【易错点】【思维点拨】例2（1）若3tan 4α=，则2cos 2sin 2αα+=（ ） (A)6425 (B) 4825 (C) 1 (D)1625（2）sin 20cos10cos160sin10-=（ ）A ．-B C ．12- D ．12【答案】（1）A （2）12【解析】（1）由sin 3tan cos 4ααα==，22cos sin 1αα+=，得3sin 5α=，4cos 5α=或3sin 5α=-， 4cos 5α=-，所以24sin 22sin cos 25ααα==，则2164864cos 2sin 2252525αα+=+=，故选A（2）原式=1sin 20cos10cos 20sin10sin(2010)sin 302+=+==【易错点】 【思维点拨】例3已知函数f(x)＝sin ⎝⎛⎭⎫π2－x sin x －3cos 2x. (1)求f(x)的最小正周期和最大值； (2)讨论f(x)在⎣⎡⎦⎤π6，2π3上的单调性．【答案】（1）f(x)的最小正周期为π，最大值为2－32,（2）f(x)在⎣⎡⎦⎤π6，5π12上单调递增；在⎣⎡⎦⎤5π12，2π3上单调递减【解析】 (1)f(x)＝sin ⎝⎛⎭⎫π2－x sin x －3cos 2x ＝cos xsin x －32(1＋cos 2x)＝12sin 2x －32cos 2x －32＝sin ⎝⎛⎭⎫2x －π3－32， 因此f(x)的最小正周期为π，最大值为2－32.(2)当x ∈⎣⎡⎦⎤π6，2π3时，0≤2x －π3≤π，从而当0≤2x －π3≤π2，即π6≤x≤5π12时， f(x)单调递增，当π2≤2x －π3≤π，即5π12≤x≤2π3时， f(x)单调递减．综上可知，f(x)在⎣⎡⎦⎤π6，5π12上单调递增；在⎣⎡⎦⎤5π12，2π3上单调递减． 【易错点】【思维点拨】解答技巧，方法策略等 题型六 简单的三角恒等变换 例1(2018·新疆第二次适应性检测)cos10(13tan 30)cos50︒+︒︒的值是________．【答案】2【解析】依题意得cos 10°1＋3tan 10°cos 50°＝cos 10°＋3sin 10°cos 50°＝2sin 10°＋30°cos 50°＝2sin 40°sin 40°＝2.【易错点】【思维点拨】解答技巧，方法策略等 例2已知tan α＝2. (1)求tan ⎝⎛⎭⎫α＋π4的值； (2)求sin 2αsin 2α＋sin αcos α－cos 2α－1的值．【答案】（1）-3（2）1【解析】(1)tan ⎝⎛⎭⎫α＋π4＝tan α＋tanπ41－tan αtanπ4＝2＋11－2×1＝－3. (2)sin 2αsin 2α＋sin αcos α－cos 2α－1 ＝2sin αcos αsin 2α＋sin αcos α－2cos 2α＝2tan αtan 2α＋tan α－2＝2×24＋2－2＝1.【易错点】 【思维点拨】解三角函数的给值求值问题的基本步骤 (1)先化简所求式子或所给条件； (2)观察已知条件与所求式子之间的联系； (3)将已知条件代入所求式子，化简求值． 例3若sin 2α＝55，sin(β－α)＝1010，且α∈⎣⎡⎦⎤π4，π，β∈⎣⎡⎦⎤π，3π2，则α＋β的值是( ) A.7π4 B.9π4 C.5π4或7π4 D.5π4或9π4【答案】A【解析】选A ∵α∈⎣⎡⎦⎤π4，π，∴2α∈⎣⎡⎦⎤π2，2π，∵sin 2α＝55，∴2α∈⎣⎡⎦⎤π2，π. ∴α∈⎣⎡⎦⎤π4，π2且cos 2α＝－255，又∵sin(β－α)＝1010，β∈⎣⎡⎦⎤π，3π2，∴β－α∈⎣⎡⎦⎤π2，5π4，cos(β－α)＝－31010， ∴cos(α＋β)＝cos[(β－α)＋2α]＝cos(β－α)cos 2α－sin(β－α)sin 2α＝⎝⎛⎭⎫－31010×⎝⎛⎭⎫－255－1010×55＝22，又α＋β∈⎣⎡⎦⎤5π4，2π，所以α＋β＝7π4. 【易错点】 【思维点拨】对于给值求角问题，通过先求角的某个三角函数值来求角，在选取函数时，遵循以下原则： (1)已知正切函数值，选正切函数．(2)已知正、余弦函数值，选正弦或余弦函数．若角的范围是⎝⎛⎭⎫0，π2，选正弦或余弦函数皆可；若角的范围是(0，π)，选余弦函数较好；若角的范围为⎝⎛⎭⎫－π2，π2，选正弦函数较好．【巩固训练】题型一 三角函数的概念、诱导公式及同角关系式1. 已知角θ的顶点为坐标原点，始边为x 轴的正半轴，若()4,P y 是角θ终边上一点，且sin θ=则y = . 【答案】-8.【解析】由tan ⎝⎛⎭⎫π4－θ＝1－tanθ1＋tanθ＝12，得tanθ＝13，∴sinθcosθ＝sinθcosθsin 2θ＋cos 2θ＝tanθtan 2θ＋1＝1319＋1＝310.故填310. 2. (1)已知tan α＝2，求值： ①2sin α－3cos α4sin α－9cos α；②4sin 2α－3sin αcos α－5cos 2α.(2)已知θ∈(0，π)，且sin θ＋cos θ＝13，求sin θ－cos θ的值．【答案】(1)①-1②1(2)173【解析】(1)①2sin α－3cos α4sin α－9cos α＝2tan α－34tan α－9＝2×2－34×2－9＝－1.②4sin 2α－3sin αcos α－5cos 2α＝4sin 2α－3sin αcos α－5cos 2αsin 2α＋cos 2α＝4tan 2α－3tan α－5tan 2α＋1＝4×4－3×2－54＋1＝1.(2)∵sin θ＋cos θ＝13，∴(sin θ＋cos θ)2＝1＋2sin θcos θ＝19，∴sin θcos θ＝－49.∵θ∈(0，π)，θ∈⎝⎛⎭⎫π2，θ， ∴sin θ>0>cos θ，sin θ－cos θ>0.由(sin θ－cos θ)2＝1－2sin θcos θ＝1＋89＝179，得sin θ－cos θ＝173.3.若cos(π－α)＝53且α∈⎝⎛⎭⎫π2，π，则sin(π＋α)＝( ) A ．－53B ．－23C ．－13D ．±23【答案】B【解析】cos (π－α)＝－cos α＝53，∴cos α＝－53. 又∵α∈⎝⎛⎭⎫π2，π，∴sin α＝1－cos 2α＝1－⎝⎛⎭⎫－532＝23， ∴sin (π＋α)＝－sin α＝－23，故选B ．题型二 三角函数图像1.为了得到函数y ＝sin 3x ＋cos 3x 的图象，可以将函数y ＝2cos 3x 的图象( A ) A ．向右平移π12个单位B ．向右平移π4个单位C ．向左平移 π12个单位 D ．向左平移π4个单位【答案】A【解析】因为y ＝sin 3x ＋cos 3x ＝2cos ⎝⎛⎭⎫3x －π4，所以将y ＝2cos 3x 的图象向右平移π12个单位后可得到y ＝2cos ⎝⎛⎭⎫3x －π4的图象. 2.函数f(x)＝Asin(ωx ＋φ)⎝⎛⎭⎫A>0，ω>0，|φ|<π2的部分图象如图所示，若x 1，x 2∈⎝⎛⎭⎫－π6，π3，且f(x 1)＝f(x 2)，则f(x 1＋x 2)＝( )A ．1B ．12C ．22D ．32【答案】D【解析】 观察图象可知，A ＝1，T ＝π，∴ω＝2，f(x)＝sin(2x ＋φ). 将⎝⎛⎭⎫－π6，0代入上式得sin ⎝⎛⎭⎫－π3＋φ＝0. 由|φ|<π2，得φ＝π3，则f(x)＝sin ⎝⎛⎭⎫2x ＋π3.函数图象的对称轴为x ＝－π6＋π32＝π12.又x 1，x 2∈⎝⎛⎭⎫－π6，π3，且f(x 1)＝f(x 2)，∴x 1＋x 22＝π12， ∴x 1＋x 2＝π6，∴f(x 1＋x 2)＝sin ⎝⎛⎭⎫2×π6＋π3＝32，故选D ． 3.已知函数f(x)＝2sin ⎝⎛⎭⎫2ωx ＋π4(ω>0)的最小正周期为π. (1)求ω的值；(2)讨论f(x)在区间⎣⎡⎦⎤0，π2上的单调性. 【答案】(1) ω＝1(2) f(x)在区间⎣⎡⎦⎤0，π8上单调递增， 在区间⎝⎛⎦⎤π8，π2上单调递减.【解析】 (1)因为f(x)＝2sin ⎝⎛⎭⎫2ωx ＋π4的最小正周期为π，且ω>0.从而有2π2ω＝π，故ω＝1． (2)因为f(x)＝2sin ⎝⎛⎭⎫2x ＋π4. 若0≤x≤π2，则π4≤2x ＋π4≤5π4.当π4≤2x ＋π4≤π2，即0≤x≤π8时，f(x)单调递增； 当π2<2x ＋π4≤5π4，即π8<x≤π2时，f(x)单调递减. 综上可知，f(x)在区间⎣⎡⎦⎤0，π8上单调递增， 在区间⎝⎛⎦⎤π8，π2上单调递减. 题型三 三角函数性质1. 已知ω>0，函数f(x)＝sin ⎝⎛⎭⎫ωx ＋π4在⎝⎛⎭⎫π2，π上单调递减，则ω的取值范围是( ) A ．⎣⎡⎦⎤12，54 B ．⎣⎡⎦⎤12，34 C ．⎣⎡⎦⎤0，12 D ．[0,2]【答案】A【解析】由π2<x<π，ω>0得，ωπ2＋π4<ωx ＋π4<ωπ＋π4.又y ＝sin x 在⎝⎛⎭⎫π2，3π2上递减，所以⎩⎨⎧ωπ2＋π4≥π2，ωπ＋π4≤3π2，解得12≤ω≤54，故选A ．2.设函数f(x)＝cos ⎝⎛⎭⎫x ＋π3，则下列结论错误的是( ) A ．f(x)的一个周期为－2πB ．y ＝f(x)的图象关于直线x ＝8π3对称C ．f(x ＋π)的一个零点为x ＝π6D ．f(x)在⎝⎛⎭⎫π2，π单调递减 【答案】D【解析】根据函数解析式可知函数f(x)的最小正周期为2π，所以函数一个周期为－2π，A 项正确；当x ＝8π3时，x ＋π3＝3π，所以cos ⎝⎛⎭⎫x ＋π3＝－1，所以B 项正确；f(x ＋π)＝cos ⎝⎛⎭⎫x ＋π＋π3＝cos ⎝⎛⎭⎫x ＋4π3，当x ＝π6时，x ＋4π3＝3π2，所以f(x ＋π)＝0，所以C 项正确；函数f(x)＝cos ⎝⎛⎭⎫x ＋π3在⎝⎛⎭⎫π2，23π上单调递减，在⎝⎛⎭⎫23π，π上单调递增，故D 项不正确，故选D ．3.已知函数①y ＝sin x ＋cos x ，②y ＝22sin xcos x ，则下列结论正确的是( ) A ．两个函数的图象均关于点⎝⎛⎭⎫－π4，0中心对称 B ．两个函数的图象均关于直线x ＝－π4对称C ．两个函数在区间⎝⎛⎭⎫－π4，π4上都是单调递增函数 D ．将函数②的图象向左平移π4个单位得到函数①的图象【答案】C【解析】函数①y ＝sin x ＋cos x ＝2sin ⎝⎛⎭⎫x ＋π4，②y ＝22·sin xcos x ＝2sin 2x ，由于①的图象关于点⎝⎛⎭⎫－π4，0中心对称，②的图象不关于点⎝⎛⎭⎫－π4，0中心对称，故A 项不正确；由于函数①的图象不可能关于直线x ＝－π4对称，故B 项不正确；由于这两个函数在区间⎝⎛⎭⎫－π4，π4上都是单调递增函数，故C 项正确；将函数②的图象向左平移π4个单位得到函数y ＝2sin ⎣⎡⎦⎤2⎝⎛⎭⎫x ＋π4的图象，而y ＝2sin ⎣⎡⎦⎤2⎝⎛⎭⎫x ＋π4≠2sin ⎝⎛⎭⎫x ＋π4，故D 项不正确，故选C ．题型四三角函数范围问题1.已知函数f(x)=2sin x+sin 2x,则f(x)的最小值是 .【答案】3√32【解析】由题意可得T=2π是f(x)=2sin x+sin 2x 的一个周期,所以求f(x)的最小值可考虑求f(x)在[0,2π)上的值域.由f(x)=2sin x+sin 2x,得f'(x)=2cos x+2cos 2x=4cos 2x+2cos x -2.令f'(x)=0,可得cos x=12或cos x=-1,x ∈[0,2π)时,解得x=π3或x=5π3或x=π.因为f(x)=2sin x+sin 2x 的最值只能在x=π3,x=5π3,x=π或x=0时取到,且f (π3)=3√32,f (5π3)=-3√32,f(π)=0,f(0)=0,所以函数f(x)的最小值为-3√32.2.已知y ＝3－sin x －2cos 2x ，x ∈⎣⎡⎦⎤π6，7π6，求y 的最大值与最小值之和． 【答案】238【解析】 ∵x ∈⎣⎡⎦⎤π6，7π6，∴sin x ∈⎣⎡⎦⎤－12，1. 又y ＝3－sin x －2cos 2x ＝3－sin x －2(1－sin 2x) ＝2⎝⎛⎭⎫sin x －142＋78， ∴当sin x ＝14时，y min ＝78；当sin x ＝－12或sin x ＝1时，y max ＝2.故函数的最大值与最小值的和为2＋78＝238.3.已知函数f(x)＝sin(ωx ＋φ)(0<ω<1,0≤φ≤π)是R 上的偶函数，其图象关于点M ⎝⎛⎭⎫3π4，0对称. (1)求ω，φ的值； (2)求f(x)的单调递增区间；(3)若x ∈⎣⎡⎦⎤－3π4，π2，求f(x)的最大值与最小值， 【答案】(1)ω＝23.(2) ⎣⎡⎦⎤3kπ－3π2，3kπ，k ∈Z (3) 函数f(x)的最大值为1，最小值为0. 【解析】(1)因为f(x)＝sin(ωx ＋φ)是R 上的偶函数，所以φ＝π2＋kπ，k ∈Z ，且0≤φ≤π，则φ＝π2，即f(x)＝cos ωx.因为图象关于点M ⎝⎛⎭⎫34π，0对称， 所以ω×34π＝π2＋mπ，m ∈Z ，ω＝23＋4m3，又0<ω<1，所以ω＝23.(2)由(1)得f(x)＝cos 23x ，由－π＋2kπ≤23x≤2kπ，且 k ∈Z 得，3kπ－3π2≤x≤3kπ，k ∈Z ，所以函数的递增区间是⎣⎡⎦⎤3kπ－3π2，3kπ，k ∈Z . (3)因为x ∈⎣⎡⎦⎤－3π4，π2，所以23x ∈⎣⎡⎦⎤－π2，π3， 当23x ＝0时，即x ＝0，函数f(x)的最大值为1， 当23x ＝－π2时，即x ＝－3π4，函数f(x)的最小值为0.题型五三角函数求值问题 1.设α，β为钝角，且sin α＝55，cos β＝－31010，则α＋β的值为( ) A ．3π4B ．5π4C ．7π4D ．5π4或7π4【答案】 C【解析】∵α，β为钝角，sin α＝55，cos β＝－31010，∴cos α＝－255，sin β＝1010， ∴cos(α＋β)＝cos αcos β－sin αsin β＝22>0. 又α＋β∈(π，2π)，∴α＋β∈⎝⎛⎭⎫3π2，2π，∴α＋β＝7π4. 2.已知函数f(x)＝2cos 2ωx －1＋23sin ωxcos ωx(0<ω<1)，直线x ＝π3是函数f(x)的图象的一条对称轴.(1)求函数f(x)的单调递增区间；(2)已知函数y ＝g(x)的图象是由y ＝f(x)的图象上各点的横坐标伸长到原来的2倍，然后再向左平移2π3个单位长度得到的，若g ⎝⎛⎭⎫2α＋π3＝65，α∈⎝⎛⎭⎫0，π2，求sin α的值. 【答案】（1）f(x)的单调递增区间为⎣⎡⎦⎤2kπ－2π3，2kπ＋π3(k ∈Z )（2） 【解析】 (1)f(x)＝cos 2ωx ＋3sin 2ωx ＝2sin ⎝⎛⎭⎫2ωx ＋π6，（2）43－310由于直线x ＝π3是函数f(x)＝2sin ⎝⎛⎭⎫2ωx ＋π6的图象的一条对称轴，所以sin ⎝⎛⎭⎫2π3ω＋π6＝±1，因此2π3ω＋π6＝kπ＋π2(k ∈Z )，解得ω＝32k ＋12(k ∈Z )，又0<ω<1，所以ω＝12，所以f(x)＝2sin ⎝⎛⎭⎫x ＋π6.由2kπ－π2≤x ＋π6≤2kπ＋π2(k ∈Z )，得2kπ－2π3≤x≤2kπ＋π3(k ∈Z )， 所以函数f(x)的单调递增区间为⎣⎡⎦⎤2kπ－2π3，2kπ＋π3(k ∈Z ). (2)由题意可得g(x)＝2sin ⎣⎡⎦⎤12⎝⎛⎭⎫x ＋2π3＋π6，即g(x)＝2cos x 2， 由g ⎝⎛⎭⎫2α＋π3＝2cos ⎣⎡⎦⎤12⎝⎛⎭⎫2α＋π3＝2cos ⎝⎛⎭⎫α＋π6＝65，得cos ⎝⎛⎭⎫α＋π6＝35， 又α∈⎝⎛⎭⎫0，π2，故π6<α＋π6<2π3，所以sin ⎝⎛⎭⎫α＋π6＝45， 所以sin α＝sin ⎣⎡⎦⎤⎝⎛⎭⎫α＋π6－π6＝sin ⎝⎛⎭⎫α＋π6cos π6－cos ⎝⎛⎭⎫α＋π6sin π6＝45×32－35×12＝43－310.3.已知cos ⎝⎛⎭⎫π6－α＝33，求cos ⎝⎛⎭⎫5π6＋α－sin 2⎝⎛⎭⎫α－π6的值. 【答案】－3＋23 【解析】 cos ⎝⎛⎭⎫56π＋α－sin 2⎝⎛⎭⎫α－π6 ＝cos ⎣⎡⎦⎤π－⎝⎛⎭⎫π6－α－sin 2⎝⎛⎭⎫π6－α ＝－cos ⎝⎛⎭⎫π6－α－⎣⎡⎦⎤1－cos 2⎝⎛⎭⎫π6－α ＝－33－⎝⎛⎭⎫1－13＝－3＋23. 题型六 简单的三角恒等变换1.已知sin ⎝⎛⎭⎫π6－α＝cos ⎝⎛⎭⎫π6＋α，则cos 2α＝( ) A ．1 B ．－1 C.12D ．0【答案】选D【解析】 ∵sin ⎝⎛⎭⎫π6－α＝cos ⎝⎛⎭⎫π6＋α， ∴12cos α－32sin α＝32cos α－12sin α，即⎝⎛⎭⎫12－32sin α＝－⎝⎛⎭⎫12－32cos α， ∴tan α＝sin αcos α＝－1，∴cos 2α＝cos 2α－sin 2α＝cos 2α－sin 2αsin 2α＋cos 2α＝1－tan 2αtan 2α＋1＝0.2.计算cos 10°－3cos －100°r(1－sin 10°)＝________(用数字作答)．【答案】2【解析】cos 10°－3cos －100°r(1－sin 10°)＝cos 10°＋3cos 80°1－cos 80°＝cos 10°＋3sin 10°2sin 40°＝2sin10°＋30°r(2sin 40°)＝2.3.已知cos α＝17，cos(α－β)＝1314，且0<β<α<π2，则β＝________.【答案】π3【解析】由cos α＝17，0<α<π2，得sin α＝1－cos 2α＝1－⎝⎛⎭⎫172＝437，由0<β<α<π2，得0<α－β<π2，又∵cos(α－β)＝1314，∴sin(α－β)＝1－cos 2α－β＝1－⎝⎛⎭⎫13142＝3314.由β＝α－(α－β)，得cos β＝cos[α－(α－β)] ＝cos αcos(α－β)＋sin αsin(α－β) ＝17×1314＋437×3314＝12. ∴β＝π3.。
2020衡水名师理科数学专题卷：专题六《三角函数》 Word版含答案
2020衡水名师原创理科数学专题卷专题六 三角函数考点16：三角函数的有关概念、同角三角函数关系式及诱导公式（1-4题，13题，17题） 考点17：三角函数的图象及其变换（5,6题，18题）考点18：三角函数的性质及其应用（7-12题，14-16题，19-22题）考试时间：120分钟 满分：150分说明：请将选择题正确答案填写在答题卡上，主观题写在答题纸上第I 卷（选择题）一、选择题（本题共12小题，每小题5分，共60分。
在每小题给出的四个选项中，只有一项是最符合题目要求的。
） 1、考点16 易 如果()1cos π2A +=-,那么sin π2A ⎛⎫+= ⎪⎝⎭( )A.12-B.12C.2-D.22、考点16 易已知sin(π)2cos(3π)0θθ-++-=，则sin cos sin cos θθθθ+=-（ ）A ．-3B ．3C ．13-D ．133、考点16 易已知角θ的终边经过点34(,)55-,则sin θ22的值为( )A.110 B. 15C. 45D. 9104、考点16 中难已知sin cos αα-=()0,πα∈,则tan α=( )A.1B.-D.1-5、考点17 中难设函数()sin()f x A x ωϕ=+（,,A ωϕ是常数，0,0A ω>>），且函数()f x 的部分图象如下图所示，则有（ ）A ．3π5π7π()()()436f f f -<< B ．3π7π5π()()()463f f f -<< C ．5π7π3π()()()364f f f <<- D ．5π3π7π()()()346f f f <-< 6、考点17 中难 为了得到函数sin(2)3πy x =-的图象,只需把函数sin 2y x =的图象( ) A.向左平移π3个单位长度 B.向右平移π3个单位长度C.向左平移π6个单位长度D.向右平移π6个单位长度7、考点18 易 设函数()πsin 23f x x ⎛⎫=+⎪⎝⎭,则下列结论中正确的是( ) A.函数()f x 的图像关于直线π3x =对称 B.函数()f x 的图像关于点π,04⎛⎫⎪⎝⎭对称C.把()f x 的图像向左平移π12个单位长度，得到一个偶函数的图像 D.函数()f x 的最小正周期为π，且在π0,6⎡⎤⎢⎥⎣⎦上为增函数8、考点18 中难将函数)0(cos sin 3)(>+=ωωωx x x f 的图像向左平移π4个单位后与原函数的图像重合，则实数ω的值可能是（ ） A ．6B ．10C ．12D ．169、考点18 中难已知π()2sin()(0)3f x x ωω=+>,若12()()4f x f x ⋅=-,且12||x x -的最小值为π4,则ω=( )A.8B.4C.2D.110、考点18 中难已知函数()sin()f x x ωϕ=+（π0,||2ωϕ><）的零点构成一个公差为π2的等差数列，(0)f =，则()f x 的一个单调递增区间是( ) A. 5ππ(,)1212-B. ππ(,)63-C. π5π(,)1212-D. π7π(,)121211、考点18 难已知函数()sin()f x x ωφ=+在区间4π[0,]3上单调，且π4π()0,()133f f ==，则 (0)f 的值为（ ）A. 1-B. 12- C. 12、考点18 难已知线段AB 的长为6，以AB 为直径的圆有一内接四边形ABCD ，其中//AB CD ，则这个内接四边形的周长的最大值为（ ）A ．15B ．16C ．17D ．18第Ⅱ卷（非选择题）二.填空题（每题5分，共20分） 13、考点16 中难α是第二象限角，(P x 为其终边上一点，且cos 4x α=，则sin α的值为___________. 14、考点18 易若函数2sin cos 1y x x a =++-在区间ππ[,]22-上的最大值是14,则a =____________ 15、考点18中难已知0ω>，函数π()sin()4f x x ω=+在π(,π)2上单调递减，则ω的取值范围是 ． 16、考点18 难 下面有5个命题：①函数44sin cos y x x =-的最小正周期是π． ②终边在y 轴上的角的集合是π{|,Z}2k k αα=∈． ③在同一坐标系中，函数sin y x =的图象和函数y x =的图象有3个公共点． ④把函数π3sin(2)3y x =+的图象向右平移π6得到3sin 2y x =的图象． ⑤函数πsin()2y x =-在[0,π]上是减函数．其中，真命题的编号是__________（写出所有真命题的编号） 三.解答题（共70分）17、（本题满分10分）考点16易如图，在单位圆上，()62AOB ααππ∠=<<，3BOC π∠=，且A O C △．（1）求sin a 的值； （2）求2cos()sin()2326ααππ-+ 18、（本题满分12分）考点17 易设向量1(22sin ,1),(,2cos )2a b αα==，其中π(,π)2α∈. 1.若a b ⊥，求sin 2cos 2sin cos αααα+-的值；2.若|2|22a b -=，求πsin(2)3α+的值. 19、（本题满分12分）考点18 易已知角α终边上一点(1,)P m -(α是第三象限角)，且sin 5α=,求下列各式的值 1.4sin(π)2cos()π35sin()3cos(π)22αααα---+++2.22211sin cos sin 2342ααα++20、（本题满分12分）考点18 中难已知函数2()2sin 22(R)f x x x a x =-+++∈,()f x 有最大值1.求实数a 的值2.函数()f x 向左平移π(0)2ϕϕ<<个单位变为偶函数，求ϕ的值 21、（本题满分12分）考点18 中难 已知函数π()4sin cos()3f x x x =⋅-1.求函数()f x 最小正周期； 2.讨论()f x 在区间ππ[,]44-上的单调性．3.若()20f x a -+=在区间π[0,]2有根，求实数a 的取值范围 22、（本题满分12分）考点18 难已知O 为坐标原点，2(2cos ,1)OA x =，2)(R,R OB x a x a =+∈∈且a 为常数)，若()f x OA OB =⋅.1.求函数()f x 的最小正周期和单调递减区间；2.若π[0,]2x ∈时，函数()f x 的最小值为2，求实数a 的值.答案以及解析1答案及解析： 答案：B 解析：()1cos πcos 2A A +=-=-, 则1π1cos ,sin cos 222A A A ⎛⎫⎪⎝=⎭=+=.2答案及解析： 答案：D 解析：3答案及解析： 答案：C解析：因为点34,55⎛⎫- ⎪⎝⎭在单位圆上，又在角θ的终边上，所以3cos 5θ=-则()cos sin θθ---===2311452215;故选C.4答案及解析： 答案：D 解析：5答案及解析： 答案：D 解析：6答案及解析： 答案：D解析：函数sin 2y x =的图象向右平移π6个单位长度,可得到函数ππsin[2()]sin(2)63y x x =-=-的图象.故选D.7答案及解析： 答案：C 解析：8答案及解析： 答案：D 解析：9答案及解析： 答案：B解析：由12()()4f x f x ⋅=-可知, 12(),()f x f x 分别为函数的最大值与最小值(或最小值与最大值),再由条件可知,该函数的半个周期为π4,故2ππ24ω=⨯,故4ω=,故选B.10答案及解析： 答案：C 解析：11答案及解析： 答案：B 解析：12答案及解析： 答案：D 解析：13答案及解析：解析：14答案及解析： 答案：0 解析：15答案及解析： 答案：]45,21[ 解析：16答案及解析：答案：①④解析：①4422sin cos sin cos cos 2y x x x x x =-=-=-，正确；②错误；③sin ,tan y x y x ==和y x =在第一象限无交点，错误；④正确；⑤错误．17答案及解析：答案：（1）1sin()23AOC S απ=+=△∴sin()3απ+=62αππ<<,∴5236απππ<+<，1cos()37απ∴+=- sin sin()sin()cos cos()sin 333333ααααππππππ=+-=+-+11727214=+⨯=（2）∵cos()cos()sin()2326226αααππππ-=+-=+， ∴282cos()sin()2sin ()1cos()23262637ααααππππ-+=+=-+=. 解析：18答案及解析：答案：1.若a b ⊥0αα=，得tan 1α=-， 所以sin 2cos tan 212sin cos 2tan 13αααααα++==---2.因为1(22sin ,1),(,2cos )2a b αα==，2(22sin 1,1)a b αα-=--， 因为2|2|2,(2)8a b a b -=-=，即228sin118cos 8αααα-++-+=，化简得2αα+=即π8sin()24α+=，所以π1sin()44α+=因为π(,π)2α∈，所以π3π5π(,)444α+∈，πcos()44α+=-,所以πππsin 2()2sin()cos()444ααα+=++= 2ππ7cos 2()12sin ()448αα+=-+=所以πππππππsin(2)sin[2()]sin 2()coscos 2()sin 3464646αααα+=+-=+-+7182=-⨯= 解析：19答案及解析：答案：1.因为(1,)P m -，OP ==∴又sin 5m α==∵ 2m =±∴，又α∵是第三象限角 2m =-∴ tan 2α=∴4sin(π)2cos()4sin 2cos 4sin 2cos π35cos 3sin 5cos 3sin 5sin()3cos(π)22αααααααααααα-----==+++++4tan 2653tan 11αα-==+ 2.原式222221sin cos sin cos 34sin cos αααααα++=+2221tan tan 5934tan 160ααα++=+=++解析：20答案及解析：答案：1.2π()2sin 222sin(2)16f x x x a x a =-+++=+++ ∴1a =- 2.ππ2sin(2())2sin(22)66x x ϕϕ++=++ ππ2π62k ϕ+=+∴ ∴ππ(0)62ϕϕ=<< 解析：21答案及解析：答案：1.∵π()4sin cos()3f x x x =⋅-14sin (cos )2x x x =-22sin cos x x x =+-2sin 22sin )x x =--sin 22x x =π2sin(2)3x =- ∴()f x 的最小正周期2ππ2T ==. 2.由πππ2π22π,Z 232k x k k -+≤-≤+∈， 解得π5πππ,Z 1212k x k k -+≤≤+∈ 当0k =时，增区间为π5π[,]1212-， 由ππ3π2π22π,Z 232k x k k +≤-≤+∈， 解得5π11πππ,Z 1212k x k k +≤≤+∈； 当1k =-时，减区间为7ππ[,]1212--，∴在区间ππ[,]44-上，()f x 的减区间是ππ[,]412--,()f x 的增区间是ππ[,]124- 3.()20f x a -+=在区间π[0,]2有根，即()2f x a =-有根由()f x 的图像知22a ≤-≤24a ≤∴解析：22答案及解析：答案：1.由题意，2(2cos ,1)OA x =，2)(R,R OB x a x a =+∈∈且a 为常数)∴2()2cos 2f x x x a =++cos 221x x a =+++π2sin(2)16x a =+++， ∴()f x 的最小正周期为2ππ2=， 令ππ3π2π22π,Z 262k x k k +≤+≥+∈ 得π2πππ,Z 63k x k k +≤≤+∈， 所以()f x 的单调递减区间为π2π[π+,π],Z 63k k k +∈. 2.当π[0,]2x ∈时，ππ7π2[,]666x +∈， ∴当π7π266x +=，即π2x =时，min 1()2()122f x a a =⨯-++==, 所以2a =.解析：。
专题06 三角函数及解三角形——2020年高考真题和模拟题理科数学分项汇编(解析版).docx
专题06三角函数及解三角形2020年高考真题1. ［2020年高考全国I卷理数】设函数f(x) = cos(®x + -)在［-”，兀］的图像大致如下图，则/(%)的最小正6周期为9 64兀3兀C. —D.兰3 2【答案】C【解析】由图可得：函数图象过点( 4 兀1T \将它代入函数/(兀)可得：cosl一- •<« + —1 = 0,又［-普,o］是函数/(兀)图象与x轴负半轴的第一个交点,十.I 4兀兀兀5 e 3所以-亍0+丁丐,解得r •2K _ 2兀_ 4兀所以函数/(%)最小正周期为=T=T=T2故选C.【点睛】本题主要考查了三角函数的性质及转化能力，还考查了三角函数周期公式，属于中档题.2. [2020 年高考全国I 卷理数】已知cc G (0,7i),且3COS2Q-8COSQ =5 ,贝0 sin^z =A. B.【答案】A又 a e (0, n),.'. sin a = Jl-cos? a =•故选：A. 【点睛】本题考查三角恒等变换和同角间的三角函数关系求值，熟记公式是解题的关键，考查计算求解 能力，属于基础题.3.【2020年高考全国II 卷理数】若a 为第四象限角，则B. cos2a<0D. sin2a<0 【答案】D【解析】方法-：由。
为第四象限角，可得亍2炽“<2卄2炽从Z,所以 3兀 + 4k 兀 < 2a < 4兀 + 4-kn, e Z此时2a 的终边落在第三、四象限及V 轴的非正半轴上，所以sin2a<0,故选：D.兀方法二：当& =——时，cos 2a = cos 由a 在第四象限可得：sin a <0, cos a > 0 ,则由2 a 蕃1 aaz Qz < ，选项C 错误，选项D 正确； 故选：D.【点睛】本题主要考查三角函数的符号，二倍角公式，特殊角的三角函数值等知识，意在考查学生的转 化能力和计算求解能力.C. sin2a>0>0,选项B 错误;<0,选项A 错误;【解析】3cos2a-8cosa = 5 ,得6cos 2tz-8coscr-8 = 0 -【答案】A2【解析】在ABC中，cosC = —, AC = 4, BC = 3, 3根据余弦定理：AB2 =AC2+BC2-2AC BC COS C，7AB- =42+32-2X4X3X-,3可得AB2 = 9，即AB — 3 ,… AB2+BC2-AC2 9 + 9-16 1由cos B = ------------------------- = ------------ =—,2ABBC2x3x3 9故cos B =—.9故选：A.5. [2020年高考全国III卷理数】已知2tan^-tan（0+ —）=7,则tan^=A. -2B. -1【答案】D【解析】2 tan - tan | ^ + — | = 7 , z. 2tan^~ tan^ + ^ =7 ,I 4 丿 1 - tan令/ = tan&,/Hl,则2/—土 = 7,整理得严_4/ + 4 = 0,解得t = 2,即tan6» = 2.故选：D.【点睛】本题主要考查了利用两角和的正切公式化简求值，属于中档题.6.【2020年高考北京】2020年3月14日是全球首个国际圆周率日（兀Day）.历史上，求圆周率兀的方法有多种，与中国传统数学中的“割圆术”相似.数学家阿尔•卡西的方法是：当正整数"充分大时，计算单位圆的内接正6“边形的周长和外切正6“边形（各边均与圆相切的正6“边形）的周长，将它们的算术平均数作为2兀的近似值.按照阿尔•卡西的方法，兀的近似值的表达式是2 71 、［/ — 71 -- 当“一 2571 6 _ 时，y = —1 二 2x^ + ^ = —+ 2^(^ e Z),3n < .30° 30°) 6n < .30° 30°) A. sin —— + tan ----- B. sin —— + tan ----- 1 n n 丿 I n n ) 3n (.60° 60°) 6n (.60° < 60°) c. sin ---- + tan ----- D. sin ----- + tan ----- I nn 丿 I nn ) 【答案】A 360° 60° 30° 【解析】单位圆内接正6〃边形的每条边所对应的圆周角为一 =——，每条边长为2sin —, nx6 n n 30° 所以，单位圆的内接正6〃边形的周长为12nsin ——, n30° 30° 单位圆的外切正6n 边形的每条边长为2tan —,其周长为12〃tan —, n n30° 30° 12nsin ----- 12ntan ---------.・.* 二 ----- n --------------- n _ 2( 30° 30°则 7i = 3n\ sin------ + tan --- I n n故选：A.【点睛】本题考查圆周率兀的近似值的计算，根据题意计算出单位圆内接正6〃边形和外切正6〃边形的 周长是解答的关键，考查计算能力，属于中等题.7. [2020年新高考全国I 卷】下图是函数y 二sin （亦+卩）的部分图像，贝!j sin （亦+卩）=【答案】BC=6“ sin 竺+ tan 竺, I n n ) A. sin(x + f)¥亠)【解析】由函数图像可知：- = -7T —— 2 3 71 _71 6~2 27T 则血=—=—=2,所以不选A, T 71 B.解得：cp 二 Ikn + 彳兀(£ e Z ),即函数的解析式为：y = sin| 2x + —TT + 2A ；7Z - | = sin| 2x + —+ —| = cos| 2x + — | = sin| — -2x I 3 丿(6 2丿(6丿(3 (\5/r而 cos I 2x + — I — - cos( — 2x) 故选：BC.【点睛】已知fix) =Asin(a}x +^)(A>0, e>0)的部分图象求其解析式时，A 比较容易看图得出，困难的 是求待定系数e 和0常用如下两种方法：竺即可求出e ；确定y 时，若能求出离原点最近的右侧图象上升(或下降)的“零点”横坐标xo,则令 exo+0 = O(或 a )xo+<p=7t'),即可求出 <p.(2)代入点的坐标，利用一些已知点(最高点、最低点或“零点”)坐标代入解析式，再结合图形解出co 和<p, 若对A, e 的符号或对°的范围有要求，则可用诱导公式变换使其符合要求.&【2020年高考全国I 卷理数】如图，在三棱锥P ABC 的平面展开图中，AC=1, AB = AD =也,佔丄AC, AB±AD, ZCAE=30°,贝0 cosZFCB= _______________ .【答案】4【解析】 AB 丄AC, AB = j3, AC = E由勾股定理得BC = V A B 2+AC 2 = 2 ‘71 F(P)同理得 BD =品，：.BF = BD = ^，在△4CE 中，AC = 1, AE = AD =运,ZCAE = 30 ，由余弦定理得 CF = 3+^2—240 AEcos30 =l + 3-2xlxV3x —= 1, 2:.CF = CE = 1,在 BCF 中，BC = 2, BF =愿，CF = 1,CF~ + BC 2 -BF 2由余弦定理得cos ZFCB = 七——2CFBC故答案为：—. 4【点睛】本题考查利用余弦定理解三角形，考查计算能力，属于中等题.9.【2020年高考全国III 卷理数】16.关于函数f (x) =sinx ——-—有如下四个命题: sinx®f (%)的图像关于y 轴对称.®f (x)的图像关于原点对称.1T®f (X )的图像关于直线x=3对称.®f (X )的最小值为2.其中所有真命题的序号是 __________ .【答案】②③所以，函数/(x)的图象不关于y 轴对称，命题①错误；对于命题②，函数/(X )的定义域为[x\x^kn,k^Z^ ,定义域关于原点对称, / ( -x) = sin (-%) + —r = - sin x - -— = -fsinx + -^―] = -/(%),sin (—兀) sinx I sinx)所以，函数/(x)的图象关于原点对称，命题②正确;1 + 4-6 2x1x2 【解析】对于命题①,A 7C \ . (7C ] 1(2 丿(2 ) .(7i' 7' 7 sm —+ x12所以，函数/(x)的图象关于直线x = |对称，命题③正确;对于命题④，当一7i<x<0时，sinx<0,贝J f(x} = sinx + — <0< 2 , sinx命题④错误.故答案为：②③.【点睛】本题考查正弦型函数的奇偶性、对称性以及最值的求解，考查推理能力与计算能力，属于中等题.JT 210.【2020年高考江苏】已知sin2(-+ <?) = -,则sin2a 的值是▲.4 3【解析】Qsin2(—+ cr) = (-^cosa-\——sin a)2 = —(1 + sin 2a)4 2 2 21 2 1— (1 + sin 2a) = —sin 2a =—2 3 3故答案为：-3【点睛】本题考查两角和正弦公式、二倍角正弦公式，考查基本分析求解能力，属基础题.11.【2020年高考北京】若函数/(x) = sin(x+^) + cosx的最大值为2,则常数0的一个取值为 _______________IT TT【答案辽(2唸+亍心均可)【解析】因为 (兀)=cos ©sin 兀 +(sin 0 + 1)cos 兀=Jcos? 0 +(sin 0 + 1)2 sin (兀+ 0), 所以Jcos?(p + (sin(p +1『=2,解得sin0 = l,故可取^ = ~-7T7T故答案为：-(2^ + -,^eZ 均可). 2 2【点睛】本题主要考查两角和的正弦公式，辅助角公式的应用，以及平方关系的应用，考查学生的数 学运算能力，属于基础题.1T12. [2020 年高考浙江】已知 tan& = 2,则 cos2& = _______ , tan(6>-一) = ______ .3 1【答案】V 巧cos 2 0-sin 2 0 _ 1-tan 2 _ 1 -22cos 2 ^ + sin 2 0 1 + tan 2 0 1 + 223 1故答案为： 【点睛】本题考查二倍角余弦公式以及弦化切、两角差正切公式，考查基本分析求解能力，属基础题.13. [2020年高考江苏】将函数y = 3sin(2x +^)的图象向右平移夕个单位长度，则平移后的图象中与y 轴最 4 6近的对称轴的方程是▲ • 【答案】2-峯 24V/ 'j I r jl【解析】y — 3sin[2(x ---- ) —] = 3 sin(2x ------ ) 6 4 12小 TC TC , , x 7 TT k/C 7 x2x ------ — —F k 兀G Z)x — ----------- 1 ---- (k G Z) 12 2 24 2当k = -1时兀=——• 24故答案为：x =———24 【点睛】本题考查三角函数图象变换、正弦函数对称轴，考查基本分析求解能力，属基础题.14. [2020年新高考全国I 卷】某中学开展劳动实习，学生加工制作零件，零件的截面如图所示.O 为圆孔 及轮廓圆弧AB 所在圆的圆心，A 是圆弧AB 与直线AG 的切点，B 是圆弧与直线BC 的切点，四边 形 DEFG 为矩形，BC 丄DG,垂足为 C, tanZODC= - , BH//DG , EF=12 cm, DE=2 cm, A 到直线5DE 和EF 的距离均为7 cm,圆孔半径为1 cm,则图中阴影部分的面积为 ___________ cm 2.【解析】cos 20 = cos 2 0 - sin 2 0 = tan <9-1 l + tan& 2-11 + 2【答案】4 + »兀 2【解析】设05 = OA=r,由题意AM = AN = 1, EF = \2，所以NF = 5,因为 AP = 5,所以 ZAGP = 45\因为 BH//DG,所以 ZAH0 = 45°，因为AG 与圆弧4B 相切于A 点，所以Q4丄4G,即AOAH 为等腰直角三角形；在直角△0QD 中，0Q = 5_^r ，DQ = l-—r ，2 2因为 tanZ0DC = -^ = |，所以 21- —r = 25-^r ， DQ 5 22 解得 r = 2A /2 ；等腰直角MAH 的面积为恥》2屈2尽4；I 所以阴影部分的面积为S] + S?—㊁兀=4 +三-•故答案为：4 + T.扇形A0B 的面积S 2 = =3乃，【点睛】本题主要考查三角函数在实际中应用，把阴影部分合理分割是求解的关键，以劳动实习为背景，体现了五育并举的育人方针.15.【2020 年高考全国II 卷理数】/XABC 中，sin2A —sin2B—sin2C= sinBsinC.(1)求A；(2)若BC=3,求zMBC周长的最大值.【解析】(1)由正弦定理和已知条件得BC2-AC2-AB2^AC AB，①由余弦定理得BC2 = AC2 +AB2- 2AC AB cos A，②由①，②得cos A =—.22兀因为0<4<兀，所以A =—.3(2)由正弦定理及(1)得上匕=少-=-?£ = 2巧，sin B sin C sin A从而AC = 2A/3 sin B , AB = 2^3 sin(兀一A - B) = 3 cos B一A/3 sin B.故BC + 4C + AB = 3 + 7^sinB + 3cosB = 3 + 2V^sin(B + ¥).X0<B<-,所以当B =-时，AABC周长取得最大值3 + 2^3-3 616.[2020年高考江苏】在A ABC中，角A, B, C的对边分别为°, b, c,已知a = 3,c =迈,B = 45。
2020年高考数学试题解析分项版 专题5 三角函数 理
2020年高考试题解析数学（理科）分项版05 三角函数一、选择题:1. (2020年高考山东卷理科3)若点（a,9）在函数3xy =的图象上，则tan=6a π的值为 （A ）0 (B)33(C) 1 (D) 33.(2020年高考安徽卷理科9)已知函数()sin(2)f x x ϕ=+，其中ϕ为实数，若()()6f x f π≤对x R ∈恒成立，且()()2f f ππ>，则()f x 的单调递增区间是（A ）,()36k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦ （B ）,()2k k k Z πππ⎡⎤+∈⎢⎥⎣⎦（C ）2,()63k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦ （D ）,()2k k k Z πππ⎡⎤-∈⎢⎥⎣⎦【答案】C.【命题意图】本题考查正弦函数的有界性，考查正弦函数的单调性.属中等偏难题. 【解析】若()()6f x f π≤对x R ∈恒成立，则()sin()163f ππϕ=+=，所以,32k k Z ππϕπ+=+∈，,6k k Z πϕπ=+∈.由()()2f f ππ>，（k Z ∈），可知sin()sin(2)πϕπϕ+>+，即sin 0ϕ<，所以72,6k k Z πϕπ=+∈，代入()sin(2)f x x ϕ=+，得7()sin(2)6f x x π=+，由7222262k x k πππππ-++剟，得563k x k ππππ--剟，故选C.4.(2020年高考辽宁卷理科4)△ABC 的三个内角A 、B 、C 所对的边分别为a ，b ，c ，asin AsinB+bcos 2A=2a 则ba=（ ） (A) 23 (B) 22 (C) 3 (D)2 答案： D解析：由正弦定理得，sin 2AsinB+sinBcos 2A=2sinA ，即sinB （sin 2A+cos 2A ）=2sinA ，故sinB=2sinA ，所以2ba=； 5.(2020年高考辽宁卷理科7)设sin 1+=43πθ（），则sin 2θ=（ ） (A) 79- (B) 19- (C) 19 (D)79答案： A解析：217sin 2cos 22sin 121.2499ππθθθ⎛⎫⎛⎫=-+=+-=⨯-=- ⎪ ⎪⎝⎭⎝⎭6.(2020年高考浙江卷理科6)若02πα＜＜，02πβ-＜＜，1cos()43πα+=，3cos()42πβ-=cos()2βα+= （A 3（B ）3（C 53 （D ）6【答案】 C 【解析】：()()2442βππβαα+=+--Q cos()cos[()()]2442βππβαα∴+=+--cos()cos()442ππβα=+-sin()sin()442ππβα+++ 132263435333+=+== 故选C 7. (2020年高考全国新课标卷理科5)已知角θ的顶点与原点重合，始边与横轴的正半轴重合，终边在直线x y 2=上，则，=θ2cos （ ） A54-B 53-C 32D 43 9. (2020年高考天津卷理科6)如图，在△ABC 中，D 是边AC 上的点，且,23,2AB AD AB BD BC BD ===，则sin C 的值为（ ）A ．33 B ．36 C ．63 D ．66【答案】D【解析】设BD a =,则由题意可得:2,BC a = 32AB AD a ==,在ABD ∆中,由余弦定理得：222cos 2AB AD BD A AB AD +-==⋅22232432()a a a ⨯-⨯=13，所以sin A =21cos A -=223，在△ABC中，由正弦定理得，sin sin AB BCC A=，所以32sin 223aC a =，解得sin C =6，故选D. 10．(2020年高考湖北卷理科3)已知函数()3sin cos ,f x x x x R =-∈，若()1f x ≥，则x 的取值范围为A.{|,}3x k x k k z ππππ+≤≤+∈ B.{|22,}3x k k k z ππππ+≤+∈C.5{|,}66x k x k k z ππππ+≤≤+∈ D. 5{|22,}66x k x k k z ππππ+≤≤+∈ 答案：B解析：由3sin cos 1x x -≥，即1sin()62x π-≥，解得522,666πππππ+≤-≤+∈k x k k z ，即22,3k x k k z ππππ+≤≤+∈，所以选B.11．(2020年高考陕西卷理科6)函数()cos f x x x =-在[0,)+∞内（A ）没有零点 （B ）有且仅有一个零点 （C ）有且仅有两一个零点（D ）有无穷个零点 【答案】B 【解析】：令1y x =，2cos y x =，则它们的图像如图故选B12.(2020年高考重庆卷理科6)若ABC ∆的内角,,A B C 所对的边,,a b c 满足22()4a b c +-=，且060C =，则ab 的值为（A ）43(B) 843- (C)1 (D) 23解析：选A 。
2020年三角函数部分高考题(带答案)
作者：败转头作品编号44122544：GL568877444633106633215458 时间：2020.12.13三角函数部分高考题1.为得到函数πcos 23y x ⎛⎫=+ ⎪⎝⎭的图像，只需将函数sin 2y x =的图像（ A ） A ．向左平移5π12个长度单位B ．向右平移5π12个长度单位 C ．向左平移5π6个长度单位D ．向右平移5π6个长度单位2.若动直线x a =与函数()sin f x x =和()cos g x x =的图像分别交于M N ，两点，则MN 的最大值为（ B ）A ．1BCD ．23.()2tan cot cos x x x +=( D )（Ａ）tan x （Ｂ）sin x （Ｃ）cos x （Ｄ）cot x4.若02,sin απαα≤≤>，则α的取值范围是：( C )（Ａ）,32ππ⎛⎫⎪⎝⎭ （Ｂ）,3ππ⎛⎫ ⎪⎝⎭ （Ｃ）4,33ππ⎛⎫ ⎪⎝⎭ （Ｄ）3,32ππ⎛⎫⎪⎝⎭5.把函数sin y x =（x R ∈）的图象上所有点向左平行移动3π个单位长度，再把所得图象上所有点的横坐标缩短到原来的12倍（纵坐标不变），得到的图象所表示的函数是C （A ）sin(2)3y x π=-，x R ∈ （B ）sin()26x y π=+，x R ∈（C ）sin(2)3y x π=+，x R ∈ （D ）sin(2)32y x π=+，x R ∈ 6.设5sin 7a π=，2cos 7b π=，2tan 7c π=，则D（A ）c b a << （B ）a c b << （C ）a c b << （D ）b a c <<7.将函数sin(2)3y x π=+的图象按向量α平移后所得的图象关于点(,0)12π-中心对称，则向量α的坐标可能为（ C ）A ．(,0)12π-B ．(,0)6π-C ．(,0)12πD ．(,0)6π8.已知cos （α-6π）+sin α=的值是则)67sin(,354πα-（A ）-532 （B ）532 (C)-54 (D) 54 9.（湖北）将函数3sin()y x θ=-的图象F 按向量(,3)3π平移得到图象F ',若F '的一条对称轴是直线4x π=,则θ的一个可能取值是AA.π125 B. π125- C. π1211 D. 1112π- 10.函数2()sin 3sin cos f x x x x =+在区间,42ππ⎡⎤⎢⎥⎣⎦上的最大值是( C ) A.1 B.132+ C.32D.1+311.函数f(x)=sin 132cos 2sin x x x---(02x π≤≤) 的值域是B（A ）[-2,02] (B)[-1,0] （C ）[-2,0]（D ）[-3,0]12.函数f (x )=cos x (x )(x ∈R)的图象按向量(m,0) 平移后，得到函数y =-f ′(x )的图象，则m 的值可以为AA.2πB.πC.－πD.－2π 13.在同一平面直角坐标系中，函数])20[)(232cos(ππ，∈+=x x y 的图象和直线21=y 的交点个数是C（A ）0 （B ）1 （C ）2 （D ）4 14.若,5sin 2cos -=+a a 则a tan =B （A ）21 （B ）2 （C ）21- （D ）2- 15.已知函数y=2sin(ωx+φ)(ω>0)在区间[0，2π]的图像如下：那么ω=（ B ） A. 1 B. 2C. 1/2D. 1/316.0203sin 702cos 10--=（ C ）A.12B.2C. 2D.217.函数f (x )＝3sin x +sin(π2+x )的最大值是 218.已知a ，b ，c 为△ABC 的三个内角A ，B ，C 的对边，向量m ＝（1,3-），n ＝（cos A ,sin A ）.若m ⊥n ，且a cos B +b cos A =c sin C ，则角B ＝ 6π. 19.()cos 6f x x πω⎛⎫=-⎪⎝⎭的最小正周期为5π，其中0ω>，则ω= ．10 20.已知函数()(sin cos )sin f x x x x =-，x ∈R ，则()f x 的最小正周期是 ．π 21.已知()sin (0)363f x x f f ωωπππ⎛⎫⎛⎫⎛⎫=+>= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，，且()f x 在区间63ππ⎛⎫⎪⎝⎭，有最小值，无最大值，则ω＝__________．14322．设ABC △的内角A B C ，，所对的边长分别为a b c ，，，且3cos cos 5a Bb Ac -=． （Ⅰ）求tan cot A B 的值； （Ⅱ）求tan()A B -的最大值．解析：（Ⅰ）在ABC △中，由正弦定理及3cos cos 5a Bb Ac -= 可得3333sin cos sin cos sin sin()sin cos cos sin 5555A B B A C A B A B A B -==+=+ 即sin cos 4cos sin A B A B =，则tan cot 4A B =； （Ⅱ）由tan cot 4A B =得tan 4tan 0A B =>2tan tan 3tan 3tan()1tan tan 14tan cot 4tan A B B A B A B B B B --===+++≤34当且仅当14tan cot ,tan ,tan 22B B B A ===时，等号成立，故当1tan 2,tan 2A B ==时，tan()A B -的最大值为34.23.在ABC △中，5cos 13B =-，4cos 5C =．（Ⅰ）求sin A 的值；（Ⅱ）设ABC △的面积332ABC S =△，求BC 的长． 解：（Ⅰ）由5cos 13B =-，得12sin 13B =，由4cos 5C =，得3sin 5C =．所以33sin sin()sin cos cos sin 65A B C B C B C =+=+=． ··········· 5分 （Ⅱ）由332ABC S =△得133sin 22AB AC A ⨯⨯⨯=， 由（Ⅰ）知33sin 65A =，故65AB AC ⨯=， ···························· 8分又sin 20sin 13AB B AC AB C ⨯==，故2206513AB =，132AB =．所以sin 11sin 2AB A BC C ⨯==． ························10分24.已知函数2π()sin sin 2f x x x x ωωω⎛⎫=+ ⎪⎝⎭（0ω>）的最小正周期为π． （Ⅰ）求ω的值；（Ⅱ）求函数()f x 在区间2π03⎡⎤⎢⎥⎣⎦，上的取值范围．解：（Ⅰ）1cos 2()22x f x x ωω-=+112cos 222x x ωω=-+π1sin 262x ω⎛⎫=-+ ⎪⎝⎭．因为函数()f x 的最小正周期为π，且0ω>， 所以2ππ2ω=，解得1ω=．（Ⅱ）由（Ⅰ）得π1()sin 262f x x ⎛⎫=-+ ⎪⎝⎭． 因为2π03x ≤≤， 所以ππ7π2666x --≤≤，所以1πsin 2126x ⎛⎫-- ⎪⎝⎭≤≤， 因此π130sin 2622x ⎛⎫-+ ⎪⎝⎭≤≤，即()f x 的取值范围为302⎡⎤⎢⎥⎣⎦，． 25.求函数2474sin cos 4cos 4cos y x x x x =-+-的最大值与最小值。
2020全国卷高考专题：三角函数和解三角形
05三角函数和解三角形1.（2020•北京卷）2020年3月14日是全球首个国际圆周率日（π Day ）．历史上，求圆周率π的方法有多种，与中国传统数学中的“割圆术”相似．数学家阿尔·卡西的方法是：当正整数n 充分大时，计算单位圆的内接正6n 边形的周长和外切正6n 边形（各边均与圆相切的正6n 边形）的周长，将它们的算术平均数作为2π的近似值．按照阿尔·卡西的方法，π的近似值的表达式是（ ）．A . 30303sin tan n n n ︒︒⎛⎫+ ⎪⎝⎭ B . 30306sin tan n n n ︒︒⎛⎫+ ⎪⎝⎭ C . 60603sin tan n n n ︒︒⎛⎫+ ⎪⎝⎭D . 60606sin tan n n n ︒︒⎛⎫+ ⎪⎝⎭【答案】A【解析】计算出单位圆内接正6n 边形和外切正6n 边形的周长，利用它们的算术平均数作为2π的近似值可得出结果.【详解】单位圆内接正6n 边形的每条边所对应的圆周角为360606n n︒︒=⨯，每条边长为302sinn︒， 所以，单位圆的内接正6n 边形的周长为3012sin n n︒， 单位圆的外切正6n 边形的每条边长为302tann ︒，其周长为3012tan n n︒， 303012sin12tan 303026sin tan 2n n n n n n n π︒︒+︒︒⎛⎫∴==+ ⎪⎝⎭，则30303sintan n n n π︒︒⎛⎫=+ ⎪⎝⎭. 故选：A.【点睛】本题考查圆周率π的近似值的计算，根据题意计算出单位圆内接正6n 边形和外切正6n 边形的周长是解答的关键，考查计算能力，属于中等题.2.（2020•北京卷）若函数()sin()cos f x x x ϕ=++的最大值为2，则常数ϕ的一个取值为________．【答案】2π（2,2k k Z ππ+∈均可）【解析】根据两角和的正弦公式以及辅助角公式即可求得()()f x x θ=+2=，即可解出.【详解】因为()()()cos sin sin 1cos f x x x x ϕϕθ=++=+，2=，解得sin 1ϕ=，故可取2ϕπ=.故答案为：2π（2,2k k Z ππ+∈均可）.【点睛】本题主要考查两角和的正弦公式，辅助角公式的应用，以及平方关系的应用，考查学生的数学运算能力，属于基础题.3.（2020•北京卷）在ABC 中，11a b +=，再从条件①、条件②这两个条件中选择一个作为己知，求： （Ⅰ）a 的值：（Ⅱ）sin C 和ABC 的面积．条件①：17,cos 7c A ==-； 条件②：19cos ,cos 816A B ==．注：如果选择条件①和条件②分别解答，按第一个解答计分．【答案】选择条件①（Ⅰ）8（Ⅱ）sin 2C =, S =选择条件②（Ⅰ）6（Ⅱ）sin C =, 4S =. 【解析】选择条件①（Ⅰ）根据余弦定理直接求解，（Ⅱ）先根据三角函数同角关系求得sin A ,再根据正弦定理求sin C ,最后根据三角形面积公式求结果；选择条件②（Ⅰ）先根据三角函数同角关系求得sin ,sin A B ，再根据正弦定理求结果，（Ⅱ）根据两角和正弦公式求sin C ，再根据三角形面积公式求结果. 【详解】选择条件①（Ⅰ）17,cos 7c A ==-，11a b +=22222212cos (11)72(11)7()7a b c bc A a a a =+-∴=-+--⋅⋅-8a ∴=（Ⅱ）1cos (0,)sin 7A A A π=-∈∴==，由正弦定理得：7sin sin sin sin 7a c C A C C ==∴=11sin (118)822S ba C ==-⨯=选择条件②（Ⅰ）19cos ,cos ,(0,)816A B A B π==∈，sin A B ∴====由正弦定理得：6sin sin a b a A B === （Ⅱ）91sin sin()sin cos sin cos 8161684C A B A B B A =+=+=+=11sin (116)622S ba C ==-⨯=【点睛】本题考查正弦定理、余弦定理，三角形面积公式，考查基本分析求解能力，属中档题.4.（2020•全国1卷）设函数()cos π()6f x x ω=+在[π,π]-的图像大致如下图，则f (x )的最小正周期为（ ）A . 10π9 B .7π6 C . 4π3D . 3π2【答案】C【解析】由图可得：函数图象过点4,09π⎛⎫-⎪⎝⎭，即可得到4cos 096ππω⎛⎫-⋅+= ⎪⎝⎭，结合4,09π⎛⎫- ⎪⎝⎭是函数()f x 图象与x 轴负半轴的第一个交点即可得到4962πππω-⋅+=-，即可求得32ω=，再利用三角函数周期公式即可得解. 【详解】由图可得：函数图象过点4,09π⎛⎫-⎪⎝⎭，将它代入函数()f x 可得：4cos 096ππω⎛⎫-⋅+= ⎪⎝⎭又4,09π⎛⎫-⎪⎝⎭是函数()f x 图象与x 轴负半轴的第一个交点，所以4962πππω-⋅+=-，解得：32ω=所以函数()f x 的最小正周期为224332T πππω===故选：C 【点睛】本题主要考查了三角函数的性质及转化能力，还考查了三角函数周期公式，属于中档题.5.（2020•全国1卷）已知 π()0,α∈，且3cos28cos 5αα-=，则sin α=（ ） AB .23C .13D【答案】A 【解析】用二倍角余弦公式，将已知方程转化为关于cos α的一元二次方程，求解得出cos α，再用同角间的三角函数关系，即可得出结论.【详解】3cos28cos 5αα-=，得26cos 8cos 80αα--=， 即23cos 4cos 40αα--=，解得2cos 3α=-或cos 2α=（舍去），又(0,),sin απα∈∴==故选：A.【点睛】本题考查三角恒等变换和同角间的三角函数关系求值，熟记公式是解题的关键，考查计算求解能力，属于基础题.6.（2020•全国2卷）若α为第四象限角，则（ ） A. cos 2α＞0 B. cos 2α＜0C. sin 2α＞0D. sin 2α＜【答案】D【解析】由题意结合二倍角公式确定所给的选项是否正确即可. 【详解】方法一：由α为第四象限角，可得3222,2k k k Z ππαππ+<<+∈， 所以34244,k k k Z ππαππ+<<+∈此时2α的终边落在第三、四象限及y 轴的非正半轴上，所以sin 20α< 故选：D. 方法二：当6πα=-时，cos 2cos 03πα⎛⎫=-> ⎪⎝⎭，选项B 错误； 当3πα=-时，2cos 2cos 03πα⎛⎫=-< ⎪⎝⎭，选项A 错误； 由α在第四象限可得：sin 0,cos 0αα<>，则sin 22sin cos 0ααα=<，选项C 错误，选项D 正确； 故选：D.【点睛】本题主要考查三角函数的符号，二倍角公式，特殊角的三角函数值等知识，意在考查学生的转化能力和计算求解能力.7.（2020•全国2卷）ABC 中，sin 2A －sin 2B －sin 2C ＝sin B sinC. （1）求A ；（2）若BC ＝3，求ABC 周长的最大值.【答案】（1）23π；（2）3+ 【解析】（1）利用正弦定理角化边，配凑出cos A 的形式，进而求得A ；（2）利用余弦定理可得到()29AC AB AC AB +-⋅=，利用基本不等式可求得AC AB +的最大值，进而得到结果.【详解】（1）由正弦定理可得：222BC AC AB AC AB --=⋅，2221cos 22AC AB BC A AC AB +-∴==-⋅，()0,A π∈，23A π∴=（2）由余弦定理得：222222cos 9BC AC AB AC AB A AC AB AC AB =+-⋅=++⋅=，即()29AC AB AC AB +-⋅=.22AC AB AC AB +⎛⎫⋅≤ ⎪⎝⎭（当且仅当AC AB =时取等号），()()()22223924AC AB AC AB AC AB AC AB AC AB +⎛⎫∴=+-⋅≥+-=+ ⎪⎝⎭，解得：AC AB +≤（当且仅当AC AB =时取等号），ABC ∴周长3L AC AB BC =++≤+ABC ∴周长的最大值为3+【点睛】本题考查解三角形的相关知识，涉及到正弦定理角化边的应用、余弦定理的应用、三角形周长最大值的求解问题；求解周长最大值的关键是能够在余弦定理构造的等式中，结合基本不等式构造不等关系求得最值.8.（2020•全国3卷）在△ABC 中，cos C ＝23，AC ＝4，BC ＝3，则cos B ＝（ ） A.19B.13C.12D.23【答案】A【解析】根据已知条件结合余弦定理求得AB ，再根据222cos 2AB BC AC B AB BC+-=⋅，即可求得答案. 【详解】在ABC 中，2cos 3C =，4AC =，3BC = 根据余弦定理：2222cos AB AC BC AC BC C =+-⋅⋅,2224322433AB =+-⨯⨯⨯, 可得29AB = ，即3AB =,由22299161cos 22339AB BC AC B AB BC +-+-===⋅⨯⨯,故1cos 9B =.故选：A. .【点睛】本题主要考查了余弦定理解三角形，考查了分析能力和计算能力，属于基础题. 9.（2020•全国3卷）已知2tan θ–tan(θ＋π4)＝7，则tan θ＝（ ） A. –2 B. –1C. 1D. 2【答案】D【解析】利用两角和的正切公式，结合换元法，解一元二次方程，即可得出答案. 【详解】2tan tan 74πθθ⎛⎫-+= ⎪⎝⎭，tan 12tan 71tan θθθ+∴-=-，令tan ,1t t θ=≠，则1271tt t+-=-，整理得2440t t -+=，解得2t =，即tan 2θ=.故选：D.【点睛】本题主要考查了利用两角和的正切公式化简求值，属于中档题. 10.（2020•全国3卷）关于函数f （x ）＝1sin sin x x+有如下四个命题： ①f （x ）的图像关于y 轴对称． ②f （x ）的图像关于原点对称． ③f （x ）的图像关于直线x ＝2π对称． ④f （x ）的最小值为2．其中所有真命题的序号是__________． 【答案】②③【解析】利用特殊值法可判断命题①的正误；利用函数奇偶性的定义可判断命题②的正误；利用对称性的定义可判断命题③的正误；取0x π-<<可判断命题④的正误.综合可得出结论.【详解】对于命题①，152622f π⎛⎫=+=⎪⎝⎭，152622f π⎛⎫-=--=- ⎪⎝⎭，则66f f ππ⎛⎫⎛⎫-≠ ⎪ ⎪⎝⎭⎝⎭， 所以，函数()f x 的图象不关于y 轴对称，命题①错误；对于命题②，函数()f x 的定义域为{},x x k k Z π≠∈，定义域关于原点对称，()()()()111sin sin sin sin sin sin f x x x x f x x x x ⎛⎫-=-+=--=-+=- ⎪-⎝⎭，所以，函数()f x 的图象关于原点对称，命题②正确；对于命题③，11sin cos 22cos sin 2f x x x x x πππ⎛⎫⎛⎫-=-+=+⎪ ⎪⎛⎫⎝⎭⎝⎭- ⎪⎝⎭， 11sin cos 22cos sin 2f x x x x x πππ⎛⎫⎛⎫+=++=+⎪ ⎪⎛⎫⎝⎭⎝⎭+ ⎪⎝⎭，则22f x f x ππ⎛⎫⎛⎫-=+ ⎪ ⎪⎝⎭⎝⎭， 所以，函数()f x 的图象关于直线2x π=对称，命题③正确；对于命题④，当0x π-<<时，sin 0x <，则()1sin 02sin f x x x=+<<， 命题④错误.故答案为：②③.【点睛】本题考查正弦型函数的奇偶性、对称性以及最值的求解，考查推理能力与计算能力，属于中等题.11.（2020•江苏卷）已知2sin()4πα+ ＝23，则sin 2α的值是____. 【答案】13【解析】直接按照两角和正弦公式展开，再平方即得结果. 【详解】221sin ())(1sin 2)42παααα+=+=+121(1sin 2)sin 2233αα∴+=∴=,故答案为：13【点睛】本题考查两角和正弦公式、二倍角正弦公式，考查基本分析求解能力，属基础题.12.（2020•江苏卷）将函数y ＝πsin(2)43x ﹢的图象向右平移π6个单位长度，则平移后的图象中与y 轴最近的对称轴的方程是____. 【答案】524x π=-【解析】先根据图象变换得解析式，再求对称轴方程，最后确定结果. 【详解】3sin[2()]3sin(2)6412y x x πππ=-+=- 72()()122242k x k k Z x k Z πππππ-=+∈∴=+∈,当1k =-时524x π=-,故答案为：524x π=-【点睛】本题考查三角函数图象变换、正弦函数对称轴，考查基本分析求解能力，属基础题.13.（2020•江苏卷）在△ABC 中，角A ，B ，C 的对边分别为a ，b ，c，已知3,45a c B ==︒．（1）求sin C 的值；（2）在边BC 上取一点D ，使得4cos 5ADC ∠=-，求tan DAC ∠的值．【答案】（1）sin C =；（2）2tan 11DAC ∠=.【解析】（1）利用余弦定理求得b ，利用正弦定理求得sin C .（2）根据cos ADC ∠的值，求得sin ADC ∠的值，由（1）求得cos C 的值，从而求得sin ,cos DAC DAC ∠∠的值，进而求得tan DAC ∠的值.【详解】（1）由余弦定理得2222cos 92235b a c ac B =+-=+-⨯=，所以b =由正弦定理得sin sin sin sin c b c B C C B b =⇒==. （2）由于4cos 5ADC ∠=-，,2ADC ππ⎛⎫∠∈ ⎪⎝⎭，所以3sin 5ADC ∠==.由于,2ADC ππ⎛⎫∠∈⎪⎝⎭，所以0,2C π⎛⎫∈ ⎪⎝⎭，所以cos 5C == 所以()sin sin DAC DAC π∠=-∠()sin ADC C =∠+∠sin cos cos sin ADC C ADC C =∠⋅+∠⋅34555525⎛⎫=⨯+-⨯= ⎪⎝⎭. 由于0,2DAC π⎛⎫∠∈ ⎪⎝⎭，所以cos DAC ∠==.所以sin 2tan cos 11DAC DAC DAC ∠∠==∠.【点睛】本小题主要考查正弦定理、余弦定理解三角形，考查三角恒等变换，属于中档题. 14.（2020•新全国1山东）下图是函数y ＝ sin(ωx ＋φ)的部分图像，则sin(ωx ＋φ)＝ （ ）A. πsin(3x +）B. πsin(2)3x - C. πcos(26x +）D.5πcos(2)6x -【答案】BC【解析】首先利用周期确定ω的值，然后确定ϕ的值即可确定函数的解析式，最后利用诱导公式可得正确结果. 【详解】由函数图像可知：22362T πππ=-=，则222T ππωπ===，所以不选A , 当2536212x πππ+==时，1y =-∴()5322122k k Z ππϕπ⨯+=+∈， 解得：()223k k ϕππ=+∈Z ，即函数的解析式为：2sin 22sin 2cos 2sin 236263y x k x x x ππππππ⎛⎫⎛⎫⎛⎫⎛⎫=++=++=+=- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭.而5cos 2cos(2)66x x ππ⎛⎫+=-- ⎪⎝⎭,故选：B C. 【点睛】已知f (x )＝A sin(ωx ＋φ)(A ＞0，ω＞0)的部分图象求其解析式时，A 比较容易看图得出，困难的是求待定系数ω和φ，常用如下两种方法：(1)由ω＝2Tπ即可求出ω；确定φ时，若能求出离原点最近的右侧图象上升(或下降)的“零点”横坐标x 0，则令ωx 0＋φ＝0(或ωx 0＋φ＝π)，即可求出φ.(2)代入点的坐标，利用一些已知点(最高点、最低点或“零点”)坐标代入解析式，再结合图形解出ω和φ，若对A ，ω的符号或对φ的范围有要求，则可用诱导公式变换使其符合要求.15.（2020•新全国1山东）在①ac =②sin 3c A =，③=c 这三个条件中任选一个，补充在下面问题中，若问题中的三角形存在，求c 的值；若问题中的三角形不存在，说明理由．问题：是否存在ABC ，它的内角,,A B C 的对边分别为,,a b c ，且sin 3sin AB ，6C π=，________?注：如果选择多个条件分别解答，按第一个解答计分． 【答案】详见解析【解析】解法一：由题意结合所给的条件，利用正弦定理角化边，得到a ,b 的比例关系，根据比例关系，设出长度长度，由余弦定理得到c 的长度，根据选择的条件进行分析判断和求解.解法二：利用诱导公式和两角和的三角函数公式求得tanA 的值，得到角,,A B C 的值，然后根据选择的条件进行分析判断和求解.【详解】解法一：由sin 3sin AB 可得：ab=(),0a b m m ==>，则：2222222cos 322c a b ab C m m m m =+-=+-⨯⨯=，即c m =.选择条件①的解析：据此可得：2ac m =⨯==，1m ∴=，此时1c m ==.选择条件②的解析：据此可得：222222231cos 222b c a m m m A bc m +-+-===-，则：sin A ==，此时：sin 32c A m =⨯=，则：c m ==选择条件③的解析：可得1c mb m==，c b =，与条件=c 矛盾，则问题中的三角形不存在.解法二：∵(),,6sinA C B A C ππ===-+,∴()6sinA A C A π⎛⎫=+=+⎪⎝⎭,()1?2sinA A C =+= ，∴sinA =,∴tanA =23A π=,∴6B C π==,若选①，ac =,∵a ==2=c ＝1;若选②，3csinA =,3=,c =;若选③,与条件=c 矛盾. 【点睛】在处理三角形中的边角关系时，一般全部化为角的关系，或全部化为边的关系．题中若出现边的一次式一般采用到正弦定理，出现边的二次式一般采用到余弦定理．应用正、余弦定理时，注意公式变式的应用．解决三角形问题时，注意角的限制范围．16.（2020•天津卷）已知函数()sin 3f x x π⎛⎫=+ ⎪⎝⎭．给出下列结论： ①()f x 的最小正周期为2π； ②2f π⎛⎫⎪⎝⎭是()f x 的最大值； ③把函数sin y x =的图象上所有点向左平移3π个单位长度，可得到函数()y f x =的图象．其中所有正确结论的序号是 A . ① B . ①③C . ②③D . ①②③【答案】B【解析】对所给选项结合正弦型函数的性质逐一判断即可. 【详解】因为()sin()3f x x π=+，所以周期22T ππω==，故①正确；51()sin()sin 122362f ππππ=+==≠，故②不正确；将函数sin y x =的图象上所有点向左平移3π个单位长度，得到sin()3y x π=+的图象， 故③正确.故选：B.【点晴】本题主要考查正弦型函数的性质及图象的平移，考查学生的数学运算能力，逻辑分析那能力，是一道容易题.17.（2020•天津卷）在ABC 中，角,,A B C 所对的边分别为,,a b c．已知5,a b c ===．（Ⅰ）求角C 的大小； （Ⅱ）求sin A 的值； （Ⅲ）求sin 24A π⎛⎫+⎪⎝⎭的值． 【答案】（Ⅰ）4Cπ；（Ⅱ）sin A =；（Ⅲ）sin 2426A π⎛⎫+= ⎪⎝⎭.【解析】（Ⅰ）直接利用余弦定理运算即可； （Ⅰ）由（Ⅰ）及正弦定理即可得到答案；（Ⅰ）先计算出sin ,cos ,A A 进一步求出sin 2,cos 2A A ，再利用两角和的正弦公式计算即可.【详解】（Ⅰ）在ABC中，由5,a b c ===及余弦定理得222cos 22a b c C ab +-===，又因为(0,)C π∈，所以4C π；（Ⅰ）在ABC 中，由4Cπ，a c ==及正弦定理，可得sin sin a C A c=== （Ⅰ）由a c <知角A为锐角，由sin A =cos A= 进而2125sin 22sin cos ,cos22cos 11313A A A A A ===-=，所以125sin(2)sin 2coscos2sin444132132A A A πππ+=+=⨯+⨯=26.【点晴】本题主要考查正、余弦定理解三角形，以及三角恒等变换在解三角形中的应用，考查学生的数学运算能力，是一道容易题.17.（2020•浙江卷）.已知tan 2θ=，则cos2θ=________；πtan()4θ-=______． 【答案】 (1).35 (2). 13【解析】利用二倍角余弦公式以及弦化切得cos2θ，根据两角差正切公式得tan()4πθ-【详解】2222222222cos sin 1tan 123cos 2cos sin cos sin 1tan 125θθθθθθθθθ---=-====-+++， tan 1211tan()41tan 123πθθθ---===++，故答案为：31,53-【点睛】本题考查二倍角余弦公式以及弦化切、两角差正切公式，考查基本分析求解能力，属基础题.18.（2020•浙江卷）在锐角△ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，且2sin b A =．（I ）求角B ；（II ）求cos A ＋cos B ＋cos C 的取值范围．【答案】（I ）3B π=；（II ）32⎤⎥⎝⎦ 【解析】（I ）首先利用正弦定理边化角，然后结合特殊角的三角函数值即可确定∠B 的大小； （II ）结合(1)的结论将含有三个角的三角函数式化简为只含有∠A 的三角函数式，然后由三角形为锐角三角形确定∠A 的取值范围，最后结合三角函数的性质即可求得cos cos cos A B C ++的取值范围.【详解】（I ）由2sin b A =结合正弦定理可得：2sin sin ,sin 2B A A B =∴=△ABC 为锐角三角形，故3B π=.（II ）结合(1)的结论有：12cos cos cos cos cos 23A B C A A π⎛⎫++=++- ⎪⎝⎭11cos cos 22A A A =-+11cos 22A A =++1sin 62A π⎛⎫=++ ⎪⎝⎭.由203202A A πππ⎧<-<⎪⎪⎨⎪<<⎪⎩可得：62A ππ<<，2363A πππ<+<，则sin 32A π⎛⎤⎛⎫+∈ ⎥ ⎪ ⎝⎭⎝⎦，113sin ,2232A π⎛⎤⎛⎫++∈ ⎥ ⎪ ⎝⎭⎝⎦. 即cos cos cos A B C ++的取值范围是13,22⎛⎤⎥ ⎝⎦.【点睛】解三角形的基本策略：一是利用正弦定理实现“边化角”，二是利用余弦定理实现“角化边”；求最值也是一种常见类型，主要方法有两类，一是找到边之间的关系，利用基本不等式求最值，二是转化为关于某个角的函数，利用函数思想求最值.10.（2020•上海卷）已知()=sin (0)f x x ωω>. （1）若f (x )的周期是4π，求ω，并求此时1()2f x =的解集； （2）已知=1ω，2g()()()()2x f x x f x π=+--，0,4x π⎡⎤∈⎢⎥⎣⎦，求g (x )的值域. 【答案】（1）1=2ω，5|=44,33x x x k x k k Z ππππ⎧⎫∈+=+∈⎨⎬⎩⎭或;（2）1-,02⎡⎤⎢⎥⎣⎦。
2020高考精品系列之数学(理)专题05 三角函数(解析版)
专题05三角函数考纲解读三年高考分析1.任意角的概念、弧度制 (1)了解任意角的概念.(2)了解弧度制的概念,能进行弧度与角度的互化. 2.三角函数(1)理解任意角三角函数(正弦、余弦、正切)的定义.(2)能利用单位圆中的三角函数线推导出2πα+,π±α的正弦、余弦、正切的诱导公式,能画出y =sin x ,y =cos x ,y =tan x 的图像,了解三角函数的周期性. (3)理解正弦函数、余弦函数在区间[0,2π]上的性质(如单调性、最大值和最小值以及与x 轴的交点等),理解正切函数在区间(,)22ππ-内的单调性. (4)理解同角三角函数的基本关系式：sin 2x +cos 2x =1,sin cos xx=tan x. (5)了解函数y =A sin(ωx +ϕ)的物理意义；能画出y =A sin(ωx +ϕ)的图像,了解参数A ,ω,ϕ对函数图像变化的影响.(6)了解三角函数是描述周期变化现象的重要函数模型,会用三角函数解决一些简单实际问题.3.和与差的三角函数公式 (1)会用向量的数量积推导出两角差的余弦公式. (2)能利用两角差的余弦公式导出两角差的正弦、正切公式.(3)能利用两角差的余弦公式导出两角和的正弦、余弦、正切公式,导出二倍角的正弦、余弦、正切公式,了解它们的内在联系.4.简单的三角恒等变换能运用上述公式进行简单的恒等变换(包括导出积化和差、和差化积、半角公式,但对这三组公式不要求记忆). 三角函数的性质和诱导公式的应用是考查的重点，解题时常用到辅助角公式和两角和差正余弦公式，考查学生的数形结合思想和计算推理能力，题型以选择填空题为主，中等难度.1、以考查三角函数的图象和性质为主，题目涉及三角函数的图象及应用、图象的对称性、单调性、周期性、最值、零点．考查三角函数性质时，常与三角恒等变换结合，加强数形结合思想、函数与方程思想的应用意识．题型既有选择题和填空题，又有解答题，中档难度.2、以考查函数y ＝A sin(ωx ＋φ)的图象的五点法画图、图象之间的平移伸缩变换、由图象求函数解析式以及利用正弦型函数解决实际问题为主，常与三角函数的性质、三角恒等变换结合起来进行综合考查，加强数形结合思想的应用意识．题型为选择题和填空题，中档难度. 3、三角恒等变换是三角变换的工具，主要考查利用两角和与差的三角函数公式、二倍角公式进行三角函数的化简与求值，重在考查化简、求值，公式的正用、逆用以及变式运用，可单独考查，也可与三角函数的图象和性质、向量等知识综合考查，加强转化与化归思想的应用意识．选择、填空、解答题均有可能出现，中低档难度.1．【2019年天津理科07】已知函数f（x）＝A sin（ωx+φ）（A＞0，ω＞0，|φ|＜π）是奇函数，将y ＝f（x）的图象上所有点的横坐标伸长到原来的2倍（纵坐标不变），所得图象对应的函数为g（x）．若g（x）的最小正周期为2π，且g（），则f（）＝（）A．﹣2 B．C．D．2【解答】解：∵f（x）是奇函数，∴φ＝0，则f（x）＝A sin（ωx）将y＝f（x）的图象上所有点的横坐标伸长到原来的2倍（纵坐标不变），所得图象对应的函数为g （x）．即g（x）＝A sin（ωx）∵g（x）的最小正周期为2π，∴2π，得ω＝2，则g（x）＝A sin x，f（x）＝A sin2x，若g（），则g（）＝A sin A，即A＝2，则f（x）＝2sin2x，则f（）＝2sin（22sin2，故选：C．2．【2019年新课标3理科12】设函数f（x）＝sin（ωx）（ω＞0），已知f（x）在[0，2π]有且仅有5个零点．下述四个结论：①f（x）在（0，2π）有且仅有3个极大值点②f（x）在（0，2π）有且仅有2个极小值点③f（x）在（0，）单调递增④ω的取值范围是[，）其中所有正确结论的编号是（）A．①④B．②③C．①②③D．①③④【解答】解：当x∈[0，2π]时，∈[，]，∵f（x）在[0，2π]有且仅有5个零点，∴，∴，故④正确，因此由选项可知只需判断③是否正确即可得到答案，下面判断③是否正确，当x∈（0，）时，∈[，]，若f（x）在（0，）单调递增，则，即ω＜3，∵，故③正确．故选：D．3．【2019年全国新课标2理科09】下列函数中，以为周期且在区间（，）单调递增的是（）A．f（x）＝|cos2x| B．f（x）＝|sin2x| C．f（x）＝cos|x| D．f（x）＝sin|x|【解答】解：f（x）＝sin|x|不是周期函数，可排除D选项；f（x）＝cos|x|的周期为2π，可排除C选项；f（x）＝|sin2x|在处取得最大值，不可能在区间（，）单调递增，可排除B．故选：A．4．【2019年全国新课标2理科10】已知α∈（0，），2sin2α＝cos2α+1，则sinα＝（）A．B．C．D．【解答】解：∵2sin2α＝cos2α+1，∴可得：4sinαcosα＝2cos2α，∵α∈（0，），sinα＞0，cosα＞0，∴cosα＝2sinα，∵sin2α+cos2α＝sin2α+（2sinα）2＝5sin2α＝1，∴解得：sinα．故选：B．5．【2019年新课标1理科11】关于函数f（x）＝sin|x|+|sin x|有下述四个结论：①f（x）是偶函数②f（x）在区间（，π）单调递增③f（x）在[﹣π，π]有4个零点④f（x）的最大值为2其中所有正确结论的编号是（）A．①②④B．②④C．①④D．①③【解答】解：f（﹣x）＝sin|﹣x|+|sin（﹣x）|＝sin|x|+|sin x|＝f（x）则函数f（x）是偶函数，故①正确，当x∈（，π）时，sin|x|＝sin x，|sin x|＝sin x，则f（x）＝sin x+sin x＝2sin x为减函数，故②错误，当0≤x≤π时，f（x）＝sin|x|+|sin x|＝sin x+sin x＝2sin x，由f（x）＝0得2sin x＝0得x＝0或x＝π，由f（x）是偶函数，得在[﹣π，）上还有一个零点x＝﹣π，即函数f（x）在[﹣π，π]有3个零点，故③错误，当sin|x|＝1，|sin x|＝1时，f（x）取得最大值2，故④正确，故正确是①④，故选：C．6．【2018年新课标2理科10】若f（x）＝cos x﹣sin x在[﹣a，a]是减函数，则a的最大值是（）A．B．C．D．π【解答】解：f（x）＝cos x﹣sin x＝﹣（sin x﹣cos x），由，k∈Z，得，k∈Z，取k＝0，得f（x）的一个减区间为[，]，由f（x）在[﹣a，a]是减函数，得，∴．则a的最大值是．故选：A．7．【2018年新课标3理科04】若sinα，则cos2α＝（）A．B．C．D．【解答】解：∵sinα，∴cos2α＝1﹣2sin2α＝1﹣2．故选：B．8．【2018年北京理科07】在平面直角坐标系中，记d为点P（cosθ，sinθ）到直线x﹣my﹣2＝0的距离．当θ、m变化时，d的最大值为（）A．1 B．2 C．3 D．4【解答】解：由题意d，tanα，∴当sin（θ+α）＝﹣1时，d max＝13．∴d的最大值为3．故选：C．9．【2018年天津理科06】将函数y＝sin（2x）的图象向右平移个单位长度，所得图象对应的函数（）A．在区间[，]上单调递增B．在区间[，π]上单调递减C．在区间[，]上单调递增D．在区间[，2π]上单调递减【解答】解：将函数y＝sin（2x）的图象向右平移个单位长度，得到的函数为：y＝sin2x，增区间满足：2kπ≤2x，k∈Z，减区间满足：2x，k∈Z，∴增区间为[kπ，kπ]，k∈Z，减区间为[kπ，kπ]，k∈Z，∴将函数y＝sin（2x）的图象向右平移个单位长度，所得图象对应的函数在区间[，]上单调递增．故选：A．10．【2017年新课标1理科09】已知曲线C1：y＝cos x，C2：y＝sin（2x），则下面结论正确的是（）A．把C1上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向右平移个单位长度，得到曲线C2B．把C1上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向左平移个单位长度，得到曲线C2C．把C1上各点的横坐标缩短到原来的倍，纵坐标不变，再把得到的曲线向右平移个单位长度，得到曲线C2D．把C1上各点的横坐标缩短到原来的倍，纵坐标不变，再把得到的曲线向左平移个单位长度，得到曲线C2【解答】解：把C1上各点的横坐标缩短到原来的倍，纵坐标不变，得到函数y＝cos2x图象，再把得到的曲线向左平移个单位长度，得到函数y＝cos2（x）＝cos（2x）＝sin（2x）的图象，即曲线C2，故选：D．11．【2017年新课标3理科06】设函数f（x）＝cos（x），则下列结论错误的是（）A．f（x）的一个周期为﹣2πB．y＝f（x）的图象关于直线x对称C．f（x+π）的一个零点为xD．f（x）在（，π）单调递减【解答】解：A．函数的周期为2kπ，当k＝﹣1时，周期T＝﹣2π，故A正确，B．当x时，cos（x）＝cos（）＝cos cos3π＝﹣1为最小值，此时y＝f（x）的图象关于直线x对称，故B正确，C当x时，f（π）＝cos（π）＝cos0，则f（x+π）的一个零点为x，故C正确，D．当x＜π时，x，此时函数f（x）不是单调函数，故D错误，故选：D．12．【2017年天津理科07】设函数f（x）＝2sin（ωx+φ），x∈R，其中ω＞0，|φ|＜π．若f（）＝2，f（）＝0，且f（x）的最小正周期大于2π，则（）A．ω，φB．ω，φC．ω，φD．ω，φ【解答】解：由f（x）的最小正周期大于2π，得，又f（）＝2，f（）＝0，得，∴T＝3π，则，即．∴f（x）＝2sin（ωx+φ）＝2sin（x+φ），由f（），得sin（φ）＝1．∴φ，k∈Z．取k＝0，得φπ．∴，φ．故选：A．13．【2019年北京理科09】函数f（x）＝sin22x的最小正周期是．【解答】解：∵f（x）＝sin2（2x），∴f（x），∴f（x）的周期T，故答案为：．14．【2019年江苏13】已知，则sin（2α）的值是．【解答】解：由，得，∴，解得tanα＝2或tan．当tanα＝2时，sin2α，cos2α，∴sin（2α）；当tanα时，sin2α，cos2α，∴sin（2α）．综上，sin（2α）的值是．故答案为：．15．【2018年江苏07】已知函数y＝sin（2x+φ）（φ）的图象关于直线x对称，则φ的值为．【解答】解：∵y＝sin（2x+φ）（φ）的图象关于直线x对称，∴2φ＝kπ，k∈Z，即φ＝kπ，∵φ，∴当k＝0时，φ，故答案为：．16．【2018年新课标1理科16】已知函数f（x）＝2sin x+sin2x，则f（x）的最小值是．【解答】解：由题意可得T＝2π是f（x）＝2sin x+sin2x的一个周期，故只需考虑f（x）＝2sin x+sin2x在[0，2π）上的值域，先来求该函数在[0，2π）上的极值点，求导数可得f′（x）＝2cos x+2cos2x＝2cos x+2（2cos2x﹣1）＝2（2cos x﹣1）（cos x+1），令f′（x）＝0可解得cos x或cos x＝﹣1，可得此时x，π或；∴y＝2sin x+sin2x的最小值只能在点x，π或和边界点x＝0中取到，计算可得f（），f（π）＝0，f（），f（0）＝0，∴函数的最小值为，故答案为：．17．【2018年新课标2理科15】已知sinα+cosβ＝1，cosα+sinβ＝0，则sin（α+β）＝．【解答】解：sinα+cosβ＝1，两边平方可得：sin2α+2sinαcosβ+cos2β＝1，①，cosα+sinβ＝0，两边平方可得：cos2α+2cosαsinβ+sin2β＝0，②，由①+②得：2+2（sinαcosβ+cosαsinβ）＝1，即2+2sin（α+β）＝1，∴2sin（α+β）＝﹣1．∴sin（α+β）．故答案为：．18．【2018年新课标3理科15】函数f（x）＝cos（3x）在[0，π]的零点个数为．【解答】解：∵f（x）＝cos（3x）＝0，∴3x kπ，k∈Z，∴x kπ，k∈Z，当k＝0时，x，当k＝1时，xπ，当k＝2时，xπ，当k＝3时，xπ，∵x∈[0，π]，∴x，或xπ，或xπ，故零点的个数为3，故答案为：319．【2018年北京理科11】设函数f（x）＝cos（ωx）（ω＞0），若f（x）≤f（）对任意的实数x都成立，则ω的最小值为．【解答】解：函数f（x）＝cos（ωx）（ω＞0），若f（x）≤f（）对任意的实数x都成立，可得：，k∈Z，解得ω，k∈Z，ω＞0则ω的最小值为：．故答案为：．20．【2017年江苏05】若tan（α）．则tanα＝．【解答】解：∵tan（α）∴6tanα﹣6＝tanα+1，解得tanα，故答案为：．21．【2017年新课标2理科14】函数f（x）＝sin2x cos x（x∈[0，]）的最大值是．【解答】解：f（x）＝sin2x cos x1﹣cos2x cos x，令cos x＝t且t∈[0，1]，则y＝﹣t2t（t）2+1，当t时，f（t）max＝1，即f（x）的最大值为1，故答案为：122．【2017年北京理科12】在平面直角坐标系xOy中，角α与角β均以Ox为始边，它们的终边关于y轴对称，若sinα，则cos（α﹣β）＝．【解答】解：方法一：∵角α与角β均以Ox为始边，它们的终边关于y轴对称，∴sinα＝sinβ，cosα＝﹣cosβ，∴cos（α﹣β）＝cosαcosβ+sinαsinβ＝﹣cos2α+sin2α＝2sin2α﹣11方法二：∵sinα，当α在第一象限时，cosα，∵α，β角的终边关于y轴对称，∴β在第二象限时，sinβ＝sinα，cosβ＝﹣cosα，∴cos（α﹣β）＝cosαcosβ+sinαsinβ：∵sinα，当α在第二象限时，cosα，∵α，β角的终边关于y轴对称，∴β在第一象限时，sinβ＝sinα，cosβ＝﹣cosα，∴cos（α﹣β）＝cosαcosβ+sinαsinβ综上所述cos（α﹣β），故答案为：23．【2019年浙江18】设函数f（x）＝sin x，x∈R．（Ⅰ）已知θ∈[0，2π），函数f（x+θ）是偶函数，求θ的值；（Ⅱ）求函数y＝[f（x）]2+[f（x）]2的值域．【解答】解：（1）由f（x）＝sin x，得f（x）＝sin（x），∵f（x）为偶函数，∴（k∈Z），∵θ∈[0，2π），∴或，（2）y＝[f（x）]2+[f（x）]2＝sin2（x）+sin2（x）＝1，∵x∈R，∴，∴，∴函数y＝[f（x）]2+[f（x）]2的值域为：．24．【2018年江苏16】已知α，β为锐角，tanα，cos（α+β）．（1）求cos2α的值；（2）求tan（α﹣β）的值．【解答】解：（1）由，解得，∴cos2α；（2）由（1）得，sin2，则tan2α．∵α，β∈（0，），∴α+β∈（0，π），∴sin（α+β）．则tan（α+β）．∴tan（α﹣β）＝tan[2α﹣（α+β）]．25．【2018年浙江18】已知角α的顶点与原点O重合，始边与x轴的非负半轴重合，它的终边过点P（，）．（Ⅰ）求sin（α+π）的值；（Ⅱ）若角β满足sin（α+β），求cosβ的值．【解答】解：（Ⅰ）∵角α的顶点与原点O重合，始边与x轴非负半轴重合，终边过点P（，）．∴x，y，r＝|OP|，∴sin（α+π）＝﹣sinα；（Ⅱ）由x，y，r＝|OP|＝1，得，，又由sin（α+β），得，则cosβ＝cos[（α+β）﹣α]＝cos（α+β）cosα+sin（α+β）sinα，或cosβ＝cos[（α+β）﹣α]＝cos（α+β）cosα+sin（α+β）sinα．∴cosβ的值为或．26．【2018年上海18】设常数a∈R，函数f（x）＝a sin2x+2cos2x．（1）若f（x）为偶函数，求a的值；（2）若f（）1，求方程f（x）＝1在区间[﹣π，π]上的解．【解答】解：（1）∵f（x）＝a sin2x+2cos2x，∴f（﹣x）＝﹣a sin2x+2cos2x，∵f（x）为偶函数，∴f（﹣x）＝f（x），∴﹣a sin2x+2cos2x＝a sin2x+2cos2x，∴2a sin2x＝0，∴a＝0；（2）∵f（）1，∴a sin2cos2（）＝a+11，∴a，∴f（x）sin2x+2cos2x sin2x+cos2x+1＝2sin（2x）+1，∵f（x）＝1，∴2sin（2x）+1＝1，∴sin（2x），∴2x2kπ，或2xπ+2kπ，k∈Z，∴xπ+kπ，或xπ+kπ，k∈Z，∵x∈[﹣π，π]，∴x或x或x或x27．【2017年江苏16】已知向量（cos x，sin x），（3，），x∈[0，π]．（1）若，求x的值；（2）记f（x），求f（x）的最大值和最小值以及对应的x的值．【解答】解：（1）∵（cos x，sin x），（3，），∥，∴cos x＝3sin x，当cos x＝0时，sin x＝1，不合题意，当cos x≠0时，tan x，∵x∈[0，π]，∴x，（2）f（x）3cos x sin x＝2（cos x sin x）＝2cos（x），∵x∈[0，π]，∴x∈[，]，∴﹣1≤cos（x），当x＝0时，f（x）有最大值，最大值3，当x时，f（x）有最小值，最小值﹣2．28．【2017年浙江18】已知函数f（x）＝sin2x﹣cos2x﹣2sin x cos x（x∈R）．（Ⅰ）求f（）的值．（Ⅱ）求f（x）的最小正周期及单调递增区间．【解答】解：∵函数f（x）＝sin2x﹣cos2x﹣2sin x cos x sin2x﹣cos2x＝2sin（2x）（Ⅰ）f（）＝2sin（2）＝2sin2，（Ⅱ）∵ω＝2，故T＝π，即f（x）的最小正周期为π，由2x ∈[2k π，2k π]，k ∈Z 得：x ∈[k π，k π]，k ∈Z ，故f （x ）的单调递增区间为[k π，k π]或写成[k π，k π]，k ∈Z ．1．【北京市东城区2019届高三下学期综合练习（二模)】如图，在平面直角坐标系xOy 中，角α与角β均以Ox 为始边，终边分别是射线OA 和射线OB ．射线OA ，OC 与单位圆的交点分别为34,55A ⎛⎫⎪⎝⎭，(1,0)C -.若6BOC π∠=，则()cos βα-的值是A 343- B ．34310+ C 4-33D 433+ 【答案】C 【解析】依题意，有：3cos 5α=，4sin 5α=，cos 32β=-，1sin 2β=，()cos βα-＝3314433cos cos sin sin 252510βαβα-+=-+⨯=.故答案为：C.2．【安徽省江淮十校2019届高三年级5月考前最后一卷】已知函数()sin (0)4f x x πωω⎛⎫=+> ⎪⎝⎭的一个零点是4π，且在0,4π⎛⎫⎪⎝⎭内有且只有两个极值点，则（ ） A ．()sin 4f x x π⎛⎫=+⎪⎝⎭B ．()sin 34f x x π⎛⎫=+⎪⎝⎭C ．()sin 74f x x π⎛⎫=+ ⎪⎝⎭D ．()sin 114f x x π⎛⎫=+⎪⎝⎭【答案】C 【解析】A 选项，因为()sin 4f x x π⎛⎫=+ ⎪⎝⎭在0,4π⎛⎫⎪⎝⎭内为增函数，无极值点；不满足题意； B 选项，由232,242k x k k Z πππππ-+≤+≤+∈得22,43123k k x k Z ππππ-+≤≤+∈；由3232,242k x k k Z πππππ+≤+≤+∈得252,123123k k x k Z ππππ+≤≤+∈； 所以函数()sin 34f x x π⎛⎫=+⎪⎝⎭在0,12π⎛⎫ ⎪⎝⎭上单调递增，在,124ππ⎛⎫⎪⎝⎭上单调递减；故()sin 34f x x π⎛⎫=+ ⎪⎝⎭在04π⎛⎫⎪⎝⎭，内有一个极值点12π；不满足题意； C 选项，由272,242k x k k Z πππππ-+≤+≤+∈得322,287287k k x k Z ππππ-+≤≤+∈；由3272,242k x k k Z πππππ+≤+≤+∈得252,287287k k x k Z ππππ+≤≤+∈； 所以函数()sin 74f x x π⎛⎫=+ ⎪⎝⎭在0,28π⎛⎫⎪⎝⎭上单调递增，在5,2828ππ⎛⎫⎪⎝⎭上单调递减，在,284ππ⎛⎫⎪⎝⎭上单调递增；()sin 74f x x π⎛⎫=+ ⎪⎝⎭在04π⎛⎫ ⎪⎝⎭，内有极大值点28π，极小值点为528π，满足题意；D 选项，由2112,242k x k k Z πππππ-+≤+≤+∈得322,44114411k k x k Z ππππ-+≤≤+∈；由32112,242k x k k Z πππππ+≤+≤+∈得252,44114411k k x k Z ππππ+≤≤+∈；所以函数()sin 114f x x π⎛⎫=+⎪⎝⎭在0,44π⎛⎫⎪⎝⎭上单调递增；在5,4444ππ⎛⎫⎪⎝⎭上单调递减，在59,4444ππ⎛⎫⎪⎝⎭上单调递增，在9,444ππ⎛⎫⎪⎝⎭上单调递减， 所以()sin 114f x x π⎛⎫=+ ⎪⎝⎭在04π⎛⎫ ⎪⎝⎭，内有三个极值点44π，544π，944π，不满足题意. 故选C3．【广东省南海中学等七校联合体2019届高三下学期冲刺模拟】已知函数2()23sincos2cos 1(0)222xxxf x ωωωω=+->的周期为π，当0,2x π⎡⎤∈⎢⎥⎣⎦时，方程()f x m ＝恰有两个不同的实数解1x ，2x ，则()12f x x +=（ ） A ．2 B ．1C ．﹣1D ．﹣2【答案】B 【解析】2()23sincos2cos 1222xxxf x ωωω=+-3sin cos 2sin 6x x x πωωω⎛⎫=+=+ ⎪⎝⎭由2T ππω== ，得2ω=．()2sin 26f x x π⎛⎫∴=+ ⎪⎝⎭．作出函数()f x 在0,2x π⎡⎤∈⎢⎥⎣⎦上的图象如图：由图可知，123x x π+=，()1212sin 221362f x x ππ⎛⎫∴+=⨯+=⨯= ⎪⎝⎭． 故选B 项．4．【山东省淄博市部分学校2019届高三5月阶段性检测（三模)】已知函数()cos()(0f x A x A ωϕ=+>，>ω，||)2πϕ<的图象如图所示，若函数()()1h x f x=+的两个不同零点分别为1x，2x，则12||x x-的最小值为（）A．23πB．2πC．43πD．π【答案】A【解析】由图象可知，2A=，214362Tπππ=-=，2Tπ∴=，1ω=，()2cos()f x xϕ∴=+，()2cos()266fππϕ=+=Q，且1||2ϕπ<，6πϕ∴=-，()2cos()6f x xπ=-，令()()12cos()106h x f x xπ=+=-+=，可得1cos()62xπ-=-，解可得，2263x kπππ-=+，或4263x k k Zπππ-=+∈，，526x kππ=+，或322x k k Zππ=+∈，，则12||x x-的最小值为352263πππ-=，故选：A．5．【湖北省黄冈市2019届高三2月联考】已知函数()2sin cos22f x x xππ⎛⎫⎛⎫=--⎪ ⎪⎝⎭⎝⎭g的图象与直线()00ax y a-=>恰有三个公共点，这三个点的横坐标从小到大依次为123,,x x x，则()123123tan x x xx x x+-=+-（）A．-2 B．2 C．-1 D．1【答案】D【解析】由题意得，()sin 2f x x =-，则()2cos2f x x '=-，易知直线()00ax y a -=>过定点()0,0，如图，由对称性可知，直线与三角函数图象切于另外两个点，∴1320,0x x x +==，则切线方程过点()()()1133,sin 2,0,0,,sin 2x x x x --， ∴333sin 202cos 20x x x ---=-，即333sin 22cos 2x x x =，则33tan 22x x =，∴()()123133123133tan tan tan 212x x x x x x x x x x x x +---===+---.故选D.6．【山东省泰安市教科研中心2019届高三考前密卷】如图是函数()sin()0,0,||2f x A x A πωϕωϕ⎛⎫=+>>< ⎪⎝⎭的部分图象，将函数f （x ）的图象向右平移6π个单位长度得到g （x ）的图象，给出下列四个命题： ①函数f （x ）的表达式为2n 2)3(si f x x π⎛⎫=+ ⎪⎝⎭； ②g （x ）的一条对称轴的方程可以为4x π=-；③对于实数m ，恒有33f m f m ππ⎛⎫⎛⎫+=-⎪ ⎪⎝⎭⎝⎭； ④f （x ）+g （x ）的最大值为2．其中正确的个数有（ ）A ．1个B ．2个C ．3个D ．4个【答案】B 【解析】 由图象知，A ＝2，T 5746124πππ=-=，即T ＝π，则2πω＝π，得ω＝2，由五点对应法得522,63ππϕπϕ⨯+==，则f （x ）＝2sin （2x+3π），故①正确，当x ＝3π时，f （3π）＝2sinπ＝0，则函数关于x ＝3π不对称，故③错误， 将函数f （x ）的图象向右平移6π个单位长度得到g （x ）的图象，即g （x ）＝2sin[2（x ﹣6π）+3π]＝2sin2x ， 当4x π=-时，g （﹣4π）＝2sin （2π-）＝﹣2为最小值， 则4x π=-是函数g （x ）的一条对称轴，故②正确，f （x ）+g （x ）＝2sin （2x+3π）+2sin2x ＝2sinxcos 3π+2cos2xsin 3π+2sin2x ＝3＝3（2x+6π）， 则f （x ）+g （x ）的最大值为3 故正确的是①②， 故选：B ．7．【宁夏石嘴山市第三中学2019届高三四模考试】已知曲线sin(2)6y x π=+向左平移(0)ϕϕ>个单位，得到的曲线()y g x =经过点(,1)12π-，则（ ）A ．函数()y g x =的最小正周期2T π=B ．函数()y g x =在1117,1212ππ⎡⎤⎢⎥⎣⎦上单调递增 C ．曲线()y g x =关于点2,03π⎛⎫⎪⎝⎭对称 D ．曲线()y g x =关于直线6x π=对称【答案】C 【解析】由题意知：()()sin 2sin 2266g x x x ππϕϕ⎡⎤⎛⎫=++=++ ⎪⎢⎥⎣⎦⎝⎭ 则sin 2112g πϕ⎛⎫-== ⎪⎝⎭222k πϕπ∴=+，k Z ∈()cos 26g x x π⎛⎫∴=+ ⎪⎝⎭()g x 最小正周期22T ππ==，可知A 错误； 当1117,1212x ππ⎡⎤∈⎢⎥⎣⎦时，[]22,36x πππ+∈，此时()g x 单调递减，可知B 错误； 当23x π=时，3262x ππ+=且3cos 02π=，所以2,03π⎛⎫⎪⎝⎭为()g x 的对称中心，可知C 正确； 当6x π=时，()(2)(3)f f f π>->-且cos02π=，所以,02π⎛⎫⎪⎝⎭为()g x 的对称中心，可知D 错误.本题正确选项：C8．【甘肃省兰州市第一中学2019届高三6月高考冲刺模拟】将函数()πsin 23f x x ⎛⎫=+⎪⎝⎭的图象向右平移π2个单位长度得到()g x 图像，则下列判断错误的是（ ） A ．函数()g x 的最小正周期是π B ．()g x 图像关于直线7π12x =对称 C ．函数()g x 在区间ππ,63⎡⎤-⎢⎥⎣⎦上单调递减 D ．()g x 图像关于点π,03⎛⎫⎪⎝⎭对称 【答案】C 【解析】由题意，将函数()f x 的图象向右平移2π个单位长度， 可得2()sin[2()]sin(2)233g x x x πππ=-+=-，对于A ,函数的最小正周期为2=2ππ，所以该选项是正确的； 对于B ，令712x π=，则772()sin(2)sin 1121232g ππππ=⨯-==为最大值， ∴函数()g x 图象关于直线712x π=，对称是正确的；对于C 中，[,]63x ππ∈-，则22[3x ππ-∈-，0]， 则函数()g x 在区间[,]63ππ-上先减后增，∴不正确；对于D 中，令3x π=，则2()sin(2)sin 00333g πππ=⨯-==，()g x∴图象关于点(,0)3π对称是正确的，故选：C．9．【江西省名校（临川一中、南昌二中)2019届高三5月联合考】关于x的方程sin((0,1))kx x k=∈在(3,3)ππ-内有且仅有5个根，设最大的根是α，则α与tanα的大小关系是（）A．tanαα>B．tanαα<C．tanαα=D．以上都不对【答案】C【解析】由题意作出y kx=与siny x=在(3,3)ππ-的图象，如图所示：∵方程sin((0,1))kx x k=∈在(3,3)ππ-内有且仅有5个根，最大的根是α.∴α必是y kx=与siny x=在(2,3)ππ内相切时切点的横坐标设切点为()00,x y，052,2xππ⎛⎫∈ ⎪⎝⎭，则0xα=，斜率0cosk x=则00sincos cos tanyxxααααα=∴=⋅∴=故选：C.10．【天津市部分区2019届高三联考一模】函数()()()sin2f x xϕϕπ=+<的图象过点,06π⎛⎫⎪⎝⎭（如图所示），若将()f x的图象上所有点向右平移6π个单位长度，得到函数()g x的图象，则()g x图象的一条对称轴的方程为（）A ．512x π=B ．23x π=C ．4x π=D ．12x π=【答案】D 【解析】()sin 2y x ϕ=+Q 过,06π⎛⎫⎪⎝⎭，()3k πϕπϕπ∴+=<，k Z ∈,3ϕπ∴=-或23ϕπ=， 又()200,3f πϕ>∴=Q ， ∴()2sin 23f x x π⎛⎫=+⎪⎝⎭向右平移6π个单位， 得()2sin 263g x x ππ⎡⎤⎛⎫=-+⎪⎢⎥⎝⎭⎣⎦， 即()sin 23g x x π⎛⎫=+ ⎪⎝⎭，令232x k πππ+=+，212k x ππ=+，k Z ∈, 0k =时，12x π=为()y g x =的一条对称轴的方程，故选D.11．【四川省名校联盟2019届高考模拟信息卷（一)】将函数2()2sin 33f x x π⎛⎫=+⎪⎝⎭的图象向右平移12个周期后得到的函数为()g x ，则()g x 的图象的一条对称轴可以是（ ） A ．518x π=B ．56x π=C ．9x π=D ．3x π=【答案】A 【解析】解：2()2sin 33f x x π⎛⎫=+ ⎪⎝⎭的周期为23π，图象向右平移12个周期后得到的函数为()g x ，则()22sin 32sin 3333g x x x πππ⎡⎤⎛⎫⎛⎫=-+=- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦，由332x k πππ-=+，k Z ∈，得5318k x ππ=+，k Z ∈，取0k =，得518x π=为其中一条对称轴. 故选A.12．【天津市河北区2019届高三二模】已知函数()πππcos 22sin cos 344f x x x x ⎛⎫⎛⎫⎛⎫=--++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，x ∈R ，给出下列四个命题：①函数()f x 的最小正周期为2π； ②函数()f x 的最大值为1； ③函数()f x 在ππ,44⎡⎤-⎢⎥⎣⎦上单调递增； ④将函数()f x 的图象向左平移π12个单位长度，得到的函数解析式为()sin 2g x x =． 其中正确命题的个数是（ ） A ．1 B ．2C ．3D ．4【答案】B 【解析】()cos 2sin 2cos 2cos sin 2sin cos 23233f x x x x x x ππππ⎛⎫⎛⎫=--+=+- ⎪ ⎪⎝⎭⎝⎭312cos 2sin 2226x x x π⎛⎫=-=- ⎪⎝⎭ ()f x 最小正周期22T ππ==，可知①错误； []sin 21,16x π⎛⎫-∈- ⎪⎝⎭，即()f x 的最大值为1，可知②正确；当,44x ππ⎡⎤∈-⎢⎥⎣⎦时，22,633x πππ⎡⎤-∈-⎢⎥⎣⎦，此时()f x 不单调，可知③错误； ()f x 向左平移12π个单位，即()sin 2sin 212126g x f x x x πππ⎡⎤⎛⎫⎛⎫=+=+-= ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦，可知④正确. 故正确命题个数为2个本题正确选项：B13．【江西省上饶市横峰中学2019届高三考前模拟考试】在平面直角坐标系中，角α的顶点与原点重合，始边与x 的非负半轴重合，终边过点(1,2)P ，则sin(2)2πα+=______________。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
原创理科数学专题卷 专题 三角函数考点16：三角函数的有关概念、同角三角函数关系式及诱导公式（1-4题，13题，17题） 考点17：三角函数的图象及其变换（5,6题，18题）考点18：三角函数的性质及其应用（7-12题，14-16题，19-22题）考试时间：120分钟 满分：150分说明：请将选择题正确答案填写在答题卡上，主观题写在答题纸上第I 卷（选择题）一、选择题（本题共12小题，每小题5分，共60分。
在每小题给出的四个选项中，只有一项是最符合题目要求的。
） 1．【来源】2017届山西运城市高三上学期期中 考点16 易已知3cos()25πϕ+=，且||2πϕ<，则tan ϕ为（ ） A ．43- B ．43 C ．34- D ．342．【来源】2016-2017学年广东清远三中高二月考 考点16 易 设3tan =α，则=++--+-)2cos()2sin()cos()sin(απαπαππα（ ）.A ．3B ．2C ．1D ．﹣1 3．【来源】2017届山东临沂市高三理上学期期中 考点16 易 若点22sin,cos 33ππ⎛⎫ ⎪⎝⎭在角α的终边上，则sin α的值为 A. 12-B. 2-12D. 24．【来源】2017届山东德州市高三上学期期中 考点16 中难已知sin cos x x +=()0 x π∈，，则tan x =（ ）A.5．【来源】2017届湖南五市十校高三理12月联考 考点17 中难已知函数()()sin 0,2f x x πωϕωϕ⎛⎫=+>< ⎪⎝⎭的部分图象如图，则201616n n f π=⎛⎫= ⎪⎝⎭∑（ ）A ．-1B ．0C ．12D ．1 6．【2017课标1，理9】 考点17 中难 已知曲线C 1：y =cos x ，C 2：y =sin (2x +2π3)，则下面结论正确的是 A ．把C 1上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向右平移π6个单位长度，得到曲线C 2B ．把C 1上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向左平移π12个单位长度，得到曲线C 2C ．把C 1上各点的横坐标缩短到原来的12倍，纵坐标不变，再把得到的曲线向右平移π6个单位长度，得到曲线C 2D ．把C 1上各点的横坐标缩短到原来的12倍，纵坐标不变，再把得到的曲线向左平移π12个单位长度，得到曲线C 27.【2017课标3，理6】 考点18 易 设函数f (x )=cos (x +3π)，则下列结论错误的是 A ．f (x )的一个周期为−2πB ．y =f (x )的图像关于直线x =83π对称 C ．f (x +π)的一个零点为x =6π D ．f (x )在(2π,π)单调递减 8．【来源】2016-2017学年广东清远三中高二文上学期月考 考点18 中难定义行列式运算=a 1a 4﹣a 2a 3．将函数f （x ）=的图象向左平移n （n ＞0）个单位，所得图象对应的函数为偶函数，则n 的最小值为（）. A ．B ．C ．D ．9．【来源】2017届河南豫北名校联盟高三文上精英对抗赛 考点18 中难已知函数()sin f x x x =+，当[0,]x π∈时，()1f x ≥的概率为（ ） A.13 B.14 C.15 D.1210．【2017天津，理7】 考点18 中难设函数()2sin()f x x ωϕ=+，x ∈R ，其中0ω>，||ϕ<π.若5()28f π=，()08f 11π=，且()f x 的最小正周期大于2π，则（ ）A 23ω=，12ϕπ= B 23ω=，12ϕ11π=- C 13ω=，24ϕ11π=- D 13ω=，24ϕ7π= 11．【来源】2017届福建厦门一中高三理上期中 考点18 难若函数()1sin 2cos 2f x x a x =+在()0,π上单调递增，则a 的取值范围是（ ） A.(],1-∞- B.[)1,-+∞ C.(],1-∞ D.[)1,+∞12．【来源】2017届重庆市一中高三上学期期中 考点18 难 已知)2,0(π∈x ，则函数x x x x x f cot cos tan sin )(+=的值域为（ ）A ．)2,1[B ．),2[+∞C ．]2,1(D ．),1[+∞ 第Ⅱ卷（非选择题） 二.填空题（每题5分，共20分）13．【2017北京，理12】 考点16 中难在平面直角坐标系xOy 中，角α与角β均以Ox 为始边，它们的终边关于y 轴对称. 若1sin 3α=，cos()αβ-=___________. 14．【2017课标II ，理14】 考点18 易 函数()23sin 4f x x x =-（0,2x π⎡⎤∈⎢⎥⎣⎦）的最大值是 。
15.【来源】【百强校】2015-2016福建师大附中高一下期中考数学（实验班）试卷 考点18中难已知函数sin()4y x πω=+（0ω>）是区间3[,]4ππ上的增函数，则ω的取值范围是 . 16．【来源】2016届山西太原市高三第二次模拟考试 考点18 难已知关于x 的函数222sin()4()2cos tx x xf x x xπ+++=+的最大值为a ，最小值为b ，若2a b +=，则实数t 的值为_________.三.解答题（共70分） 17．（本题满分10分）【来源】2017届江苏南京市高三上学期学情调研 考点16易 如图，在平面直角坐标系xOy 中，以x 轴正半轴为始边的锐角α和钝角β的终边分别与单位圆交于点,A B ，若点A 的横坐标是31010，点B 的纵坐标是255.（1）求cos()αβ-的值；（2）求αβ+的值.18．（本题满分12分）【来源】2017届安徽六安一中高三上学期月考 考点17 易已知向量()1cos 3sin cos 22a x b x x x R ⎛⎫=-=∈ ⎪⎝⎭，，，，，设函数()f x a b =.（1）求()f x 的表达式并完成下面的表格和画出()f x 在[]0π，范围内的大致图象；0 2π π32πx0 π()f x（2）若方程()0f x m -=在[]0π，上有两个根α、β，求m 的取值范围及αβ+的值． 19.【2017山东，理16】考点18 易 设函数()sin()sin()62f x x x ππωω=-+-，其中03ω<<.已知()06f π=.（Ⅰ）求ω；（Ⅱ）将函数()y f x =的图象上各点的横坐标伸长为原来的2倍（纵坐标不变），再将得到的图象向左平移4π个单位，得到函数()y g x =的图象，求()g x 在3[,]44ππ-上的最小值.20.（本题满分12分）【来源】2017届江西省高三第一次联考考点18 中难 已知函数()21sin 2cos ,2f x m x x x R =--∈，若tan 3α=()326f α=-． （1）求实数m 的值及函数()f x 的最小正周期；（2）求()f x 在[]0,π上的递增区间．21．（本题满分12分）【来源】2017届湖北省百所重点校高三联合考试 考点18 中难 已知函数()233cos cos 2f x x x x =++． （1）当,63x ππ⎡⎤∈-⎢⎥⎣⎦时，求函数()y f x =的值域；（2）已知0ω>，函数()212x g x f ωπ⎛⎫=+⎪⎝⎭，若函数()g x 在区间2,36ππ⎡⎤-⎢⎥⎣⎦上是增函数，求ω的最大值．22．（本题满分12分）【来源】2017届湖北襄阳五中高三上学期开学考试 考点18 难 函数()sin()(0,||)2f x x πωϕωϕ=+><在它的某一个周期内的单调减区间是511[,]1212ππ． （1）求()f x 的解析式；（2）将()y f x =的图象先向右平移6π个单位，再将图象上所有点的横坐标变为原来的12倍（纵坐标不变），所得到的图象对应的函数记为()g x ，若对于任意的3[,]88x ππ∈，不等式|()|1g x m -<恒成立，求实数m 的取值范围.参考答案1．C【解析】333cos(),sin ,sin 2555πϕϕϕ+=∴-==-，又||2πϕ<，则43cos sin tan 54cos -==∴=ϕϕϕϕ 2．B 【解析】sin()cos()sin cos tan 1312cos sin 1tan 13sin()cos()22αππααααππααααα-+-------====----++3．A【解析】2132cos 32cos 32sin 32cossin 22-==+==ππππαry，故选A.4．D【解析】因为()0 x π∈，，且0sin cos 1x x <+=<，所以3 24x ππ⎛⎫∈ ⎪⎝⎭，，由sin cos x x +=2sin cos x x =，即42sin 22,33x x x ππ===，tan x = D.5．B【解析】由题意得25244126T πππωω==-⇒=，sin()1,326πππϕϕϕ+=<⇒=，因为sin 636n n f πππ⎛⎫⎛⎫=+ ⎪⎪⎝⎭⎝⎭，周期为6，一个周期的和为零，所以201616n n f π=⎛⎫=⎪⎝⎭∑0，选B.6.【答案】D【解析】)62cos()2322cos()322sin(:2ππππ+=-+=+=x x x y C ，则把1C 上各点的横坐标缩短到原来的21倍得到x y 2cos =，再将所得曲线向左平移12π个单位得到2C . 7.【答案】D 【解析】8．B【解析】由题意可知()3cos sin 2cos 6f x x x x π⎛⎫=-=+⎪⎝⎭，向左平移n 个单位后得2cos 6y x n π⎛⎫=++ ⎪⎝⎭为偶函数566n k n πππ∴+=∴=9．D【解析】由()sin 3cos 2sin()13f x x x x π=+=+≥及[0,]x π∈得[0,]2x π∈，所以所求概率为122P ππ==，故选D.15．【答案】A11．A【解析】∵()1sin 2cos 2f x x a x =+在区间()0,π上是增函数，∴()0sin 2cos >-='x a x x f ，∴0sin sin 212>--x a x ，即0122>+--at t ，(]1,0∈t ，∴tt a 12+-<，令()tt t g 12+-=，则()0122<--='tt g ，∴()t g 在(]1,0∈t 递减，∴()11-=<g a ，故答案为：1-<a .故选：A.12．B【解析】 x x x x x f cot cos tan sin )(+=x x x x x x x x x x x x x x x x x f cos sin ]cos sin 3)cos )[(sin cos (sin cos sin cos sin sin cos cos sin )(23322-++=+=+=∴设21cos sin )4sin(2cos sin 2-=⇒+=+=t x x x x x t π)2,0(π∈x ]2,1(]1,22()4sin()43,4(4∈⇒∈+⇒∈+∴t x x ππππ ]2,1(,1321)213()(23222∈--=--⨯-=∴t t t t t t t t t f 0)1(3)(224<---='∴t t t f )(t f ∴在区间]21，（上单调递减，21)2()2(23)2()(23min =--==f x f 13．【答案】79- 【解析】14．【答案】1 【解析】15.159(0,][,]434【解析】由题设因0>ω且ππ≤≤x 43,则44434πωππωωππ+≤+≤+x ,结合正弦函数的图象可知240ππωπ≤+<或⎪⎪⎩⎪⎪⎨⎧≤+≥+ππωππωππ25423434,解之得410≤<ω或4935≤≤ω.故应填159(0,][,]434. 16．1【解析】函数2222sin()4()2cos tx t x x f x x x π++=+xx x x x t tx cos 2cos 22sin 222222++⎪⎪⎭⎫ ⎝⎛++= ()()xx xx t t x x x x t x x t cos 2sin cos 2sin cos 2222+++=++++=令()xx xx t x g cos 2sin 2++=，则()xx xx t x g cos 2sin 2++-=-，设()x g 的最大值为M ，最小值为N ，则0=+N M ，即有a M t =+，b N t =+，222==++=+t N M t b a ，解得1=t ．故答案为：1． 17．（1）－210（2）34π【解析】因为锐角α的终边与单位圆交于A ，且点A 的横坐标是1010， 所以，由任意角的三角函数的定义可知，cos α＝310，从而sin＝． ………………………………(2分) 因为钝角β的终边与单位圆交于点B ，且点B的纵坐标是，所以sinβ＝5，从而cos5． ………………………………(4分)（1）cos(α－β)＝cos αcos β＋sin αsin β＝10×(－5)＋10×5＝－10． ………………………………(6分)（2）sin(α＋β)＝sin αcos β＋cos αsin β＝×(－)＋×＝2． ………………………………(8分)因为α为锐角，β为钝角，故α＋β∈(2π，32π)，所以α＋β＝34π． ………………………………(10分)18．（1）)62sin()(π-=x x f ，表格和图象见解析；（2）)1,21()21,1(-⋃--∈m ，=+βα32π或35π． 【解析】（1）()11cos 3sin cos 22cos 2sin 2226f x a b x x x x x x π⎛⎫==-=-=- ⎪⎝⎭，…………3分……………………………………(9分)（2）由图可知111122m ⎛⎫⎛⎫∈--- ⎪⎪⎝⎭⎝⎭，，， 4212αβπ+=或1012π，∴23αβπ+=或53π． ………………………………(12分)19.【答案】（Ⅰ）2ω=.（Ⅱ）得最小值32-. 【解析】（Ⅰ）因为()sin()sin()62f x x x ππωω=-+-， 所以31()cos cos 2f x x x x ωωω=-- 33cos 22x x ωω=- 133(sin cos )22x x ωω=-3(sin )3x πω=-………………………………(4分)由题设知()06f π=，所以63k ωπππ-=，k Z ∈.故62k ω=+，k Z ∈，又03ω<<， 所以2ω=.………………………………(5分)………………………………(12分) 20．（1） 3m =,T π=； （2） ()f x 在[]0,π上的递增区间是50,,,36πππ⎡⎤⎡⎤⎢⎥⎢⎥⎣⎦⎣⎦. 【解析】（1）()22212tan 11tan 4311sin 2cos 211121tan 21tan 26m f m m ααααααα--=--=--=-++，又∵()326fα=-，4311312626m --=-，即32m = ………………………………(4分) 故()312cos 21sin 2126f x x x x π⎛⎫=--=-- ⎪⎝⎭， ∴函数()f x 的最小正周期22T ππ== ………………………………(6分) （2） ()f x 的递增区间是222262k x k πππππ-≤-≤+，∴,63k x k k Zππππ-≤≤+∈，所以在[]0,π上的递增区间是50,,,36πππ⎡⎤⎡⎤⎢⎥⎢⎥⎣⎦⎣⎦ ………………………………(12分)21．（1）3,32⎡⎤⎢⎥⎣⎦；（2）1.【解析】（1）()31cos 23sin 2sin 222226x f x x x π+⎛⎫=++=++ ⎪⎝⎭．……………………(2分) ∵,63x ππ⎡⎤∈-⎢⎥⎣⎦，∴52,666x πππ⎡⎤+∈-⎢⎥⎣⎦，∴1sin 2126x π⎛⎫-≤+≤ ⎪⎝⎭，∴函数()y f x =的值域为3,32⎡⎤⎢⎥⎣⎦………………………………(4分)（2）()sin 22123x g x f x ωππω⎛⎫⎛⎫=+=++⎪ ⎪⎝⎭⎝⎭，当22,,3633363x x πππωππωππω⎡⎤⎡⎤∈-+∈-++⎢⎥⎢⎥⎣⎦⎣⎦，………………………………(6分) ∵()g x 在2,36ππ⎡⎤-⎢⎥⎣⎦上是增函数，且0ω>， ∴2,2,2,336322k k k Z ωππωππππππ⎡⎤⎡⎤-++⊆-++∈⎢⎥⎢⎥⎣⎦⎣⎦， 即223322632k k ωππππωππππ⎧-+≥-+⎪⎪⎨⎪+≤+⎪⎩，化简得534112k k ωω⎧≤-⎪⎨⎪≤+⎩，………………………………(10分) ∵0ω>，∴15,1212k k Z -<<∈，∴0k =，解得1ω≤，因此，ω的最大值为1 22．（1）()sin(2)3f x x π=-；（2）102m <<． 【解析】（1）由条件，115212122T πππ=-=，∴2ππω=，∴2ω=，又5sin(2)112πϕ⨯+=，∴3πϕ=-，∴()f x 的解析式为()sin(2)3f x x π=-．…………………………(4分)（2）将()y f x =的图象先向右平移6π个单位，得2sin(2)3y x π=-， ∴2()sin(4)3g x x π=-，………………………………(6分) 而3[,]88x ππ∈，∴254636x πππ-≤-≤，∴函数()g x 在3[,]88ππ上的最大值为1，此时2432x ππ-=，∴724x π=；最小值为12-，此时2436x ππ-=-，∴8x π=． 3[,]88x ππ∈时，不等式|()|1g x m -<恒成立，即1()1m g x m -<<+恒成立，即max min ()1()1g x m g x m <+⎧⎨>-⎩，∴11112m m <+⎧⎪⎨->-⎪⎩，∴102m <<．………………………………(12分)。