高二数学理科综合试题
高中数学人教A版选修212223综合测试含问题详解高二数学理科

实用文档高二下学期数学期末考试试卷(理)一、选择题:本大题共12小题,每题5分,共60分.在每题给出的四个选项中,只有一项为哪一项符合要求的.1.在某项测量中,测量结果X服从正态分布N(1,2)(0),假设X在(0,2)内取值的概率为,那么X在[0,)内取值的概率为A.B.C.D.曲线ysinx与x轴在区间[0,2]上所围成阴影局部的面积为A.4B.2C.2D.43 .假设复数z满足(1i)zi,那么z的虚部为i1C.i1 A.B.D.2 2224 .用反证法证明数学命题时首先应该做出与命题结论相矛盾的假设.否认“自然数a,b,c 中恰有一个偶数〞时正确的反设为A.自然数a,b,c都是奇数B.自然数a,b,cC.自然数a,b,c中至少有两个偶数D.自然数a,b,c都是偶数中至少有两个偶数或都是奇数5.在一次试验中,P(A),那么在4次独立重复试验中,事件A恰好在前两次发生的概率是A.B.C.D.6.某单位为了制定节能减排的目标,先调查了用电量y〔单位:度〕与气温x〔单位:c〕之间的关系,随机统计了某4天的用电量与当天气温,并制作了对照表:x(单位:c)1714101y(单位:度)24343864由表中数据得线性回归方程:y2x a.当气温为20c时,预测用电量约为A.20B.16C.10D.57.从1,2,3,4,5,6这六个数字中,任取三个组成无重复数字的三位数,但当三个数字中有2和3时,2必须排在3前面(不一定相邻),这样的三位数有A.108个B.102个C.98个D.96个在吸烟与患肺病这两个事件的统计计算中,以下说法正确的选项是A.假设2的观测值为 6.635,我们有99%的把握认为吸烟与患肺病有关系,那么在100个吸烟的人中必有99人患有肺病;B.从独立性检验可知有99%的把握认为吸烟与患肺病有关系时,我们说某人吸烟,那么他有99%的可能患有肺病;文案大全实用文档C.假设从统计量中求出有 95%的把握认为吸烟与患肺病有关系, 是指有5%的可能性使得推判出现错误;D.以上三种说法都不正确 .有6个座位连成一排,安排3个人就座,恰有两个空位相邻的不同坐法有A.36种B. 60种C.72种D.80种10.一个袋子里装有编号为 1,2,3, ,12的12个相同大小的小球, 其中1到6号球是红色球,其余为黑色球.假设从中任意摸出一个球,记录它的颜色和号码后再放回到袋子里,然 后再摸出一个球,记录它的颜色和号码,那么两次摸出的球都是红球,且至少有一个球的号码是偶数的概率是3B .173A .4 C .D .16x 3 2cx 216411.假设函数f(x)x 有极值点,那么实数 c 的范围为A .[3,)B .(3,)C .(,3] [3,)D .( ,3) (3,)222222以下给出的命题中:①如果三个向量a,b,c 不共面,那么对空间任一向量 p ,存在一个唯一的有序数组x,y,z 使pxa yb zc .②O(0,0,0),A(1,0,0),B(0,1,0),C(1,1,1).那么与向量AB 和OC 都垂直的单位向量只有n( 6 , 6 ,6).6 6 3③向量OA,OB,OC 可以构成空间向量的一个基底,那么向量OA 可以与向量OAOB 和向量OA OB 构成不共面的三个向量.④正四面体OABC ,M,N 分别是棱OA,BC 的中点,那么MN 与OB 所成的角为.4是真命题的序号为A .①②④B .②③④C .①②③D .①④二、填空题:本大题共 4小题,每题5分,共20分.把答案填在答题卡中相应题的横线上.13.函数f ( ) x 4 2 x 2 5在[ 1,2]上的最小值为_____________________. x14.等差数列{a n }的前n 项和为S n ,S 14 0,S 15 0,那么n _____时此数列的前n 项和取得最小值.15.长方体ABCDA 1B 1C 1D 1中,AB AA 11,AD 2,E 为侧面AB 1的中心,F文案大全实用文档为A1D1的中点,那么EFFC1.16.在数列{a n}中,a11,a2 2且a n2a n 1 (1)n(n N),那么S50.三、解答题:本大题共6小题,共70分.把解答写在答题卡中.解容许写出文字说明,证明过程或演算步骤.〔本小题总分值10分〕(2 x3x2)n的展开式中,第5项的二项式系数与第3项的二项式系数之比是7:2.11〔Ⅰ〕求展开式中含x2项的系数;〔Ⅱ〕求展开式中系数最大的项.〔本小题总分值12分〕为培养高中生综合实践能力和团队合作意识,某市教育部门主办了全市高中生综合实践知识与技能竞赛.该竞赛分为预赛和决赛两个阶段,参加决赛的团队按照抽签方式决定出场顺序.通过预赛,共选拔出甲、乙等六个优秀团队参加决赛.〔Ⅰ〕求决赛出场的顺序中,甲不在第一位、乙不在第六位的概率;〔Ⅱ〕假设决赛中甲队和乙队之间间隔的团队数记为X,求X的分布列和数学期望.19.〔本小题总分值12分〕观察以下等式112 3 493 4 5 6 7254 5 6 7 8 9 1049第一个式子第二个式子第三个式子第四个式子照此规律下去〔Ⅰ〕写出第6个等式;〔Ⅱ〕你能做出什么一般性的猜想?请用数学归纳法证明猜想.文案大全实用文档20. 点B〔2,0〕,OA(0,22),O为坐标原点,动点P满足OP OA OP OA 4 3.〔Ⅰ〕求点P的轨迹C的方程;〔Ⅱ〕当m为何值时,直线l:y3x m与轨迹C相交于不同的两点M、N,且满足BM BN?〔Ⅲ〕是否存在直线l:ykxm(k0)与轨迹C相交于不同的两点M、N,且满足BMBN?假设存在,求出m的取值范围;假设不存在,请说明理由.21.〔本小题总分值12分〕如图,直四棱柱ABCD A1B1C1D1的底面ABCD是平行四边形,DAB45,AA1AB2,AD22,点E是C1D1的中点,D1E C1点F在B1C1上且B1F2FC1.AB1F1〔Ⅰ〕证明:AC1平面EFC;〔Ⅱ〕求锐二面角A FC E平面角的余弦值.D CA B〔本小题总分值14分〕函数f(x)e x(x2ax a1),其中a是常数.(Ⅰ)当a1时,求曲线y f(x)在点(1,f(1))处的切线方程;〔Ⅱ〕假设f(x)在定义域内是单调递增函数,求a的取值范围;〔Ⅲ〕假设关于x的方程f(x)e x k在[0,)上有两个不相等的实数根,求k的取值范围.文案大全实用文档高二下学期数学期末考试试卷 (理)参考答案一.:每小 5分共60分ADBDA,AACCA,DD二.填空:13.6 14.715.167516.2三:17解:〔Ⅰ〕解由意知C n 4 7 ,整理得 42 (n 2)(n 3),解得n9⋯2 分C n 2 227 r27 r11,解得r∴通公式T r1C 9r 29rx64 分令 6.6211∴展开式中含x 2的系数C 96296 672 .⋯⋯⋯⋯⋯6分 〔Ⅱ〕第r1 的系数最大,有C 9r 29r C 9r1210r ⋯⋯⋯⋯⋯8分C 9r 29rC 9r128r10r3,rN 且0r9r3.⋯⋯⋯⋯⋯10分7r3∴展开式中系数最大的 T 4 C 93 26x 55376x 5 .⋯⋯⋯⋯⋯12分18〔本小分12分〕解:〔Ⅰ〕“甲不在第一位、乙不在第六位〞事件A ,1分P(A)A 66 2A 55 A 447⋯⋯⋯⋯3分A 6610所以甲不在第一位、乙不在第六位的概率7.⋯⋯⋯⋯4分X 的可能取0,1,2,3,410⋯⋯⋯⋯⋯⋯⋯5分〔Ⅱ〕随机量P(X0)A 22A 55 1P(X1)C 41A 22A 444A 66 ,A 66153P(XC 42A 22A 22A 331P(X 3) C 43A 22A 22A 3322) A 66,A 66155P(X4)A 22A 44 1(每个式子1分)⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯10分A 66,15文案大全实用文档随机量X 的分布列:X 01234P14 1 2 131551515因EX11 4 213 24 14,315515153所以随机量X 的数学期望4.⋯⋯⋯⋯⋯⋯⋯⋯12分3 11219.解:〔Ⅰ〕第6个等式6 7 816⋯⋯⋯⋯2分〔Ⅱ〕猜第n 个等式n(n 1) (n 2)(3n2)(2n1)2⋯⋯⋯⋯4分明:〔1〕当 n1然成立;〔2〕假n k(k 1,k N )也成立,即有k (k 1) (k 2) (3k2)(2k 1)2⋯⋯⋯⋯6分那么当n k 左(k 1) (k2)(3k2) (3k1) (3k)(3k1)1k (k 1) (k 2) (3k 2) (2k 1) 3k3k1(2k1)2 (2k1) (3k) (3k 1)4k 24k 1 8k (2k1)2[2(k1) 1]2而右[2(k1) 1]2就是n k 1等式也成立.⋯⋯⋯⋯10分根据〔1〕〔2〕知,等式任何n N 都成立.⋯⋯⋯⋯12分20解:〔Ⅰ〕点P(x,y) ,OP OA (x,y 2 2),OP OA(x,y22).由得x 2 (y 2 2)2x 2 (y 2 2)243.⋯⋯⋯〔3分〕即点P 到两定点〔0,22〕、〔0,-2 2〕的距离之和定 43,故迹C 是以〔0,22〕焦点,43的,其方程x 2 y 2 1.⋯⋯〔6分〕412(x 1 ,y 1)、N (x 2〔Ⅱ〕点 M,y 2),段MN 的中点M 0(x 0,y 0),由BMBN 得BM 0垂直平分MN .立y 3x m, 消去y 得6x 2 23mx m 2 120.3x 2 y 2 12.由(2 3)224( m 2 12) 0 得 26m 26.⋯⋯⋯〔10分〕m文案大全实用文档∴x 0x 1 x 2m3(m)mmm m22 ,y 02 3.即M 0( 2 3 ,).322m由BM 0⊥MN 得k BM 0kMN23 1.故m23所求.〔14分〕m 22 3〔Ⅲ〕假设存在直l 与C 相交于不同的两点M(x 1,y 1)、N (x 2 ,y 2),且足BMBN ,令段MN 的中点M 0(x 0,y 0),BM 0垂直平分MN .立3x 12 y 12 12,两式相减得3(x 1x 2)(x 1x 2)(y 1y 2)(y 1y 2).3x 22 y 2212.∴k MNy 1 y 23(x 1 x 2)3x 0k .x 1x 2 y 1 y 2y 0又由BM 0⊥MN 得k BM 0y 0 1 1,y 033 x 02.∴x 0 k .即M 0(1,).kk又点M 0在C 的内部,故3x 02y 02 12.即3 ( 1)2(3)212.3)在直l 上,∴3k解得k1.又点M 0(1, k m .kk∴mk 3 k3 23〔当且当k3取等号〕.kk故存在直l足条件,此m 的取范(, 2 3][23,〕.21〔本小分12分〕解:〔Ⅰ〕以A 坐原点,z D 1EC 1射AB x 的正半,建立如所示空直角坐F系Axyz .依意,可得以下各点的坐分A 1BA(0,0,0), C(4,2,0),C 1(4,2,2),E(3,2,2),y10 4 ⋯⋯⋯⋯⋯⋯3分DCF(,,2).3 3AxB(1,2,0),EC∴AC 1(4,2,2),EF (1,0, 2),3 3∴AC 1EF(4,2,2)(1, 2,0) 0.AC 1 EC(4,2,2) (1,0, 2) 03 3∴AC 1EF ,AC 1 EC .又EF,EC平面EFC∴AC 1平面EFC .⋯⋯⋯⋯⋯⋯6分文案大全实用文档〔Ⅱ〕向量n (x,y,z)是平面AFC 的法向量,n AC,n AF ,而AC(4,2,0),AF(10 , 4,2)∴4x2y 0, 10 x 4 y2z0,1) 3 33 3令 x1 得 (1,.⋯⋯⋯⋯⋯⋯9分n2,3又∵AC 1是平面EFC 的法向量,n AC 1 4 42∴cosn,AC 1369|n||AC 1|1.⋯11分16 441381 49所以二面角A FCE 平面角的余弦69.⋯⋯⋯⋯⋯⋯12分13822. 〔本小分14分〕解:(Ⅰ)由f ( x ) e x ( x 2axa 1)可得 f() e x [x 2(a 2)x 1].⋯2分x当a 1,f(1) 2e,f(1) 5e所以曲yf(x)在点(1,f(1))的切方程 y 2e 5e(x 1)即5exy 3e 0⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯4分〔Ⅱ〕由(Ⅰ)知f(x)e x [x 2(a 2)x1],假设f(x)是增函数,f(x)恒成立,⋯⋯⋯⋯⋯⋯⋯⋯5分即x 2(a 2)x 1 0恒成立,∴ (a 2)2 4 0,4a0,所以a 的取范[4,0].⋯⋯⋯⋯⋯⋯⋯⋯⋯7分〔Ⅲ〕令g(x)f(x) e x e x (x 2ax a),关于x 的方程g(x)k 在[0,)上有两个不相等的数根.令g(x)e x (x 2(2当 (a 2) 0,即a上的增函数.所以 方程g(x) k 在当 (a 2)0,即ax0 g(x) 0g(x)aa)x) 0,解得x(a2)或x 0 .⋯⋯⋯⋯⋯9分2,在区[0, )上,g(x) 0,所以g(x)是[0, )[0, )上不可能有两个不相等的数根 .⋯⋯⋯⋯10分2 ,g(x),g(x)随x 的化情况如下表(0, (a2)) (a 2) ((a2),)+↘a 4↗e a 2由上表可知函数g(x)在[0,)上的最小g((a2))a4a2.⋯⋯⋯⋯12分e因函数g(x)是(0,(a2))上的减函数,是((a2),)上的增函数,文案大全实用文档且当x,g(x)所以要使方程 g(x)k 即f(xe x k在[0,)上有两个不相等的数根,k 的取范)必是(a4,a].⋯⋯⋯⋯14分e a2文案大全。
学第一学期期末高二数学理科综合测试题三(附答案)

2015学年山东省文登第一中学第一学期期末高二数学理科综合测试题三1、双曲线2214x y -=的渐近线的方程为( ) A .2xy =±B .y x =±C .2y x =±D .4y x =± 2、已知a =(1,2,-y ),b =(x,1,2),且(a +2b )∥(2a -b ),则 ( ) A .x =13,y =1 B .x =12,y =-4 C .x =2,y =-14 D .x =1,y =-13、等差数列{}n a 的前n 项和是n S ,若12345,9a a a a +=+=,则10S 的值为( ) A .55 B .65 C .60 D .704、下列命题中,假命题是( )A .2,30x x R -∀∈>B .00,tan 2x R x ∃∈=C .020,log 2x R x ∃∈<D .2,(2)0x N x *∀∈->5、设n S 是公差为(0)d d ≠的无穷等差数列{}n a 的前n 项的和,则下列命题错误的是 ( )A.若0d <,则数列{}n a 有最大项B.若数列{}n a 有最大项,则0d <C.若数列{}n a 是递增数列,则对任意n N *∈,均有0n S >D.若对任意n N *∈,均有0n S >,则数列{}n a 是递增数列 6、设1a >,0b >,若2a b +=,则121a b+-的最小值为( )A .3+B .6C .D .7、 ∆ABC 中内角A 、B 、C 的对边分别是a 、b 、c .若22sin a c B C -==,,则A=( ) A .56π B .23π C .3π D .6π 8、一元二次方程2210(0)ax x a ++=≠有一个正跟和一个负根的充分不必要条件是( ) A .0a < B .0a > C .1a <- D .1a >9、已知F 1,F 2分别是双曲线)0,0(12222>>=-b a by a x 的左、右焦点,P 为双曲线右支上的任意一点.若a PF PF 8221=,则双曲线的离心率的取值范围是( )A .(1,2]B .[2,+∞)C .(1,3]D .[3,+∞)10.如图,正方体ABCD —A 1B 1C 1D 1中,O 为底面ABCD 的中心, M 为棱BB 1的中点,则下列结论中错误..的是( ) A.D 1O ∥平面A 1BC 1 B. 异面直线BC 1与AC 所成的角等于60° C. D 1O ⊥平面AMC D.二面角M -AC -B 等于45°第Ⅱ卷(非选择题 共90分)二、填空题:本大题共4小题,每小题4分,共16分,把答案填在答题卷的横线上。
高二理科数学综合测试题(含参考答案).doc
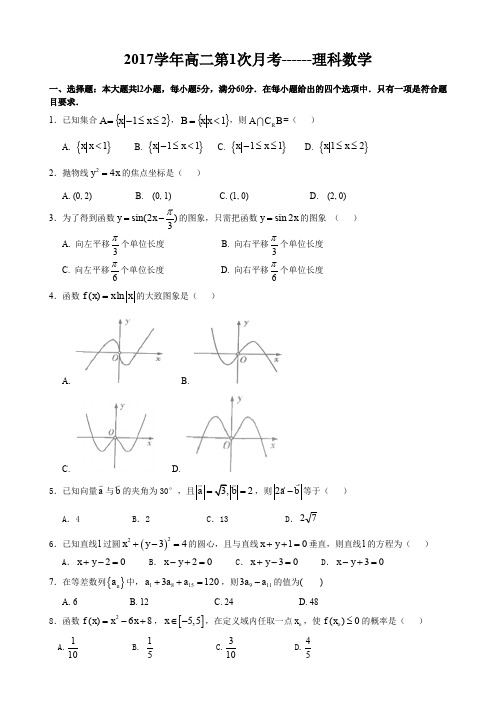
2017学年高二第1次月考------理科数学一、选择题:本大题共l2小题,每小题5分,满分60分.在每小题给出的四个选项中.只有一项是符合题目要求.1.已知集合{}21≤≤-=x x A ,{}1B <=x x ,则R AC B =( )A. {}1x x <B. {}11x x -≤<C. {}11x x -≤≤D. {}12x x ≤≤ 2.抛物线24y x =的焦点坐标是( )A. (0, 2)B. (0, 1)C. (1, 0)D. (2, 0) 3.为了得到函数sin(2)3y x π=-的图象,只需把函数sin 2y x =的图象 ( )A. 向左平移3π个单位长度 B. 向右平移3π个单位长度 C. 向左平移6π个单位长度 D. 向右平移6π个单位长度4.函数()ln f x x x =的大致图象是( )A. B.C. D.5.已知向量a 与b 的夹角为30°,且3,2a b ==,则b a-2等于( )A .4B .2C .13D .726.已知直线l 过圆()2234x y +-=的圆心,且与直线10x y ++=垂直,则直线l 的方程为( )A .20x y +-=B .20x y -+=C .30x y +-=D .30x y -+= 7.在等差数列{}n a 中,18153120a a a ++=,则9113a a -的值为( ) A. 6 B. 12 C. 24 D. 488.函数86)(2+-=x x x f ,[]5,5x ∈-,在定义域内任取一点o x ,使()0o f x ≤的概率是( )A.110 B. 51 C.310 D.459.直线1:(1)30l kx k y +--=和2:(1)(23)20l k x k y -++-=互相垂直,则k =( ) A. 1 B. -3 C. -3或1 D. 54-10.一个机器零件的三视图如图所示,其中侧视图是一个半圆与边长为2的正方形,俯视图是一个半圆内切于边长为2的正方形,则该机器零件的体积为( ) A. 83π+ B. 48π+C. 348π+D. 34π+11.若实数,x y 满足约束条件220,240,2,x y x y y --≤⎧⎪+-≥⎨⎪≤⎩则x y 的取值范围是( )A. 2,23⎡⎤⎢⎥⎣⎦B.13,22⎡⎤⎢⎥⎣⎦C.3,22⎡⎤⎢⎥⎣⎦ D.[]1,212.若实数x a x x x f cos 2sin 61)(-+=在[]44,-单调递增,则a 的取值范围是( ) A.⎥⎦⎤⎢⎣⎡-3232, B.⎥⎦⎤⎢⎣⎡-3131, C.⎥⎦⎤⎢⎣⎡-6161, D.[]22,-二、填空题:本大题共4小题,每小题5分,满分20分 13.定积分dx e x x⎰-1)2(的值为____________14.函数xxx f ln )(=的单调增区间 15.已知()1cos 3θ+π=-,则sin 22θπ⎛⎫+= ⎪⎝⎭ .16.设(),()f x g x 分别是R 上的奇函数和偶函数, 当0x <时,0)()()()(>'+'x g x f x g x f ,且0)3(=-g ,则不等式()()0f x g x <解集是CBAM三、解答题:本大题共6小题,满分70分.解答须写出文字说明、证明过程和演算步骤. 17.(本小题满分10分)求这个函数的极值。
高二数学理综合卷1(含答案)

高二数学(理)综合试卷1一、选择题(本题共12道小题,每小题5分,共60分)1.已知命题p :13x <<,q :31x>,则p 是q 的( ) A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件2.在三棱锥A -BCD 中,E 是CD 的中点,且2=,则=( )A .212121++ B .212121++- C. 313131++ D .313131++-3.设数列{a n }满足32111232n n a a a a n +++=-,则a n =( ) A. 112n -B. 312n -C. 12nD. 2n n4.在△ABC 中,已知a ,b ,c 分别是角A ,B ,C 的对边, cosA=54,c =2,△ABC 的面积S=6,则a 的值为( )A. 234B.45C. 62D. 725. 如果椭圆193622=+y x 的弦被点(4,2)平分,则这条弦所在的直线方程是 A .02=-y xB .042=-+y xC .01232=-+y xD .082=-+y x6.下列有关命题的叙述错误的是( )A 、对于命题P :R x ∈∃,使得x 2+x+1<0,则 ¬P 为:R x ∈∀,均有x 2+x+1≥0B 、命题“若x 2-3x+2=0,则x=1的逆否命题为“若x≠1,则x 2-3x+2≠0””C 、若p ∧q 为假命题,则p ,q 均为假命题D 、“x >2”是x 2-3x+2>0的充分不必要条件 7.若两个正实数x ,y 满足141x y +=,且不等式234yx m m +<-有解,则实数m 的取值范围是( ) A.(-1,4) B.(-∞,-1)∪(4,+∞) C. (-4,1) D. (-∞,0)∪(3,+∞)8.函数()cos f x x x =的导函数()f x '在区间[,]ππ-上的图像大致是( )A. B.C. D.9.在直角坐标系xOy中,F是椭圆C:22221x ya b+=(a>b>0)的左焦点,A,B 分别为左、右顶点,过点F作x轴的垂线交椭圆C于P,Q两点,连接PB交y轴于点E,连接AE交PQ于点M,若M是线段PF的中点,则椭圆C的离心率为A.2B.1 2C.1 3D.1 410.设x,y满足约束条件60330x yxx y-+⎧⎪⎨⎪+-⎩≥≤≥,则11x yzx++=+的取值范围是A.(-∞,-8]∪[1,+∞)B.(-∞,-10]∪[-1,+∞)C.[-8,1]D.[-10,-1]11.已知函数f(x)=f′()cosx+sinx,则f()=()A.B.C.1 D.012.设f(x)是定义在R上的奇函数,且f(2)=0,当x>0时,有xf′(x)﹣f(x)<0恒成立,则不等式x2f(x)>0的解集是()A.(﹣∞,﹣2)∪(0,2)B.(﹣2,0)∪(2,+∞)C.(﹣2,2)D.(﹣∞,﹣2)∪(2,+∞)二、填空题(本题共4道小题,每小题5分,共20分)13.数列{}n a 的通项公式为2141n a n =-,则其前n 项和为_______________.14.已知实数x >0,y >0,且满足24xy x y ++=,则x +2y 的最小值为________。
人教A版数学选修3第二学期高二理科综合测试题(一)

高中数学学习材料 (灿若寒星 精心整理制作)2014-2015学年度第二学期海南省洋浦中学高二理科综合测试题(一)一.选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的1.离心率为53,长轴长为10的椭圆的标准方程是( )A 、1162522=+y x B 、1162522=+y x 或1162522=+x y C 、16410022=+y x D 、16410022=+y x 或16410022=+x y 2.设F 1、F 2分别是椭圆x 24+y 2=1的左、右焦点,P 是第一象限内该椭圆上的一点,且PF 1⊥PF 2,则点P 的横坐标为( ).A .1 B.83 C .2 2 D.2633.经过点)62,62(-M 且与双曲线13422=-y x 有共同渐近线的双曲线方程为( )A 、18622=-y xB 、18622=-x y C 、16822=-y x D 、16822=-x y4.设双曲线)0,0(12222>>=-n m ny m x 的焦距为47,一条渐近线方程为x y 6=,则此双曲线的方程为( )A. 1622=-y x B. 124422=-y x C. 1622=-y x D. 132422=-y x 5.顶点在原点,坐标轴为对称轴的抛物线过点(-2,3),则它的方程是( )A .x 2=-92y ,或y 2=43x B .y 2=-92x ,或x 2=43yC .x 2=43yD .y 2=-92x6.过点M (3,2)作直线l 与抛物线y 2=8x 只有一个交点,这样的直线共有( ) A .0条 B .1条 C .2条 D .3条7.若函数f(x)=2x 2+1,图象上P(1,3)及邻近上点Q(1+Δx,3+Δy), 则xy∆∆=( ) A 4 B 4Δx C 4+2Δx D 2Δx8.函数()12ln 2+=x y 的导数是( ) A.1242+x x B. 1212+x C.()10ln 1242+x x D. ()e x x 22log 124+ 9.设y=x-lnx ,则此函数在区间(0,1)内为( )A .单调递增,B 、有增有减C 、单调递减,D 、不确定10.计算ʃ4016-x 2d x 等于 ( ) A .8π B .16π C .4πD .32π11. 已知椭圆的中心在原点,离心率12e =,且它的一个焦点与抛物线24y x =-的焦点重合,则此椭圆的方程为( )A 22143x y += B 22186x y += C 2212x y += D 2214x y += 12.若函数y =x 3-3bx +3b 在(0,1)内有极小值,则A.0<b <1B.b <1C.b >0D.b <21二、填空题(本大题共4小题,每小题5分,满分20分.把答案填写在题中的横线上)13.若动点P 在y =2x 2+1上移动,则点P 与点Q (0,-1)连线的中点的轨迹方程是________________.14.准线方程为2=x 的抛物线的标准方程是_____________. 15..设曲线y=a x-ln(x+1)在点(0,0)处的切线方程为y=2x ,则a = . 16.以下四个关于圆锥曲线的命题中:①设A 、B 为两个定点,k 为非零常数,||||PA PB k -=,则动点P 的轨迹为双曲线;②平面内到两定点距离之和等于常数的点的轨迹是椭圆③方程02522=+-x x 的两根可分别作为椭圆和双曲线的离心率;④双曲线13519252222=+=-y x y x 与椭圆有相同的焦点. 其中真命题的序号为 (写出所有真命题的序号)三.解答题(本大题共5小题,每题12分,共60分;解答应写出文字说明、证明过程或演算步骤)17.如图,设P 是圆x 2+y 2=25上的动点,点D 是P 在x 轴上的投影,M 为PD 上一点,且|MD |=45|PD |.(1)当P 在圆上运动时,求点M 的轨迹C 的方程;(2)求过点(3,0)且斜率为45的直线被C 所截线段的长度.18. 已知函数f (x )=ax 2+b ln x 在x =1处有极值12.(1)求a ,b 的值;(2)判断函数y =f (x )的单调性并求出单调区间.19.已知P 为半圆C :cos sin x y θθ=⎧⎨=⎩(θ为参数,0≤θ≤π)上的点,点A 的坐标为(1,0),O 为坐标原点,点M 在射线OP 上,线段OM 与C 的弧AP 的长度均为π3. (Ⅰ)以O 为极点,x 轴的正半轴为极轴建立极坐标系,求点M 的极坐标; (Ⅱ)求直线AM 的参数方程.20..已知椭圆G 的中心在坐标原点,长轴在x 轴上,离心率为23,两个焦点分别为1F 和2F ,椭 圆G 上一点到1F 和2F 的距离之和为12.圆k C :0214222=--++y kx y x )(R k ∈的圆心为点k A . (1)求椭圆G 的方程(2)求21F F A k ∆的面积 (3)问是否存在圆k C 包围椭圆G?请说明理由.21.已知f (x )=e x -ax -1. (1)求f (x )的单调增区间;(2)若f (x )在定义域R 内单调递增,求a 的取值范围.四、选做题(以下试题同学们只需从中任选一题即可,多做则按答题顺序的第一题记分,本题满分10分)22.已知点A 在圆C :31)2(22=-+y x 上运动,点B 在以)0,3(F 为右焦点的椭圆k ky x =+22上运动,求|AB|的最大值。
高二下学期数学综合测试题(带答案)

理科综合测试题(二)一、选择题:本大题共12小题,每小题4分,共48分.1.已知i 是虚数单位,复数22iz i=+,则z =( ) A. 2455i -+ B. 2455i + C. 2455i - D.2455i --2. 有一段“三段论”推理是这样的:对于可导函数()f x ,如果()0'0f x =,那么0x x =是函数()f x 的极值点。
因为函数()3f x x =在0x =处的导数值()'00f =,所以0x =是函数()3f x x =的极值点。
以上推理中( )A.小前提错误B.大前提错误C.推理形式错误D.结论正确3.下列四个函数,在0x =处取得极值的函数是( )①3y x=②2+1y x = ③y x = ④2xy =A. ① ②B. ② ③C. ③ ④D. ① ③4.某企业为研究企业员工工作积极性和对待企业改革态度的关系,随机抽取了72名员工进行调查,所得的数据如下表所示:与数据:21212211222112)(++++-=n n n n n n n n n χ.当23.841χ>时,有95%的把握说事件A 与B 有关;当2 6.635χ>时,有99%的把握说事件A 与B 有关; 当23.841χ<时认为事件A 与B 无关.)A.有99%的把握说事件A 与B 有关B.有95%的把握说事件A 与B 有关 C.有90%的把握说事件A 与B 有关 D.事件A 与B 无关5.已知,则的最大值是A .B .C .D. 6.1()n n N +≤+∈,某学生的证明过程如下: (1)当1n =时,11≤+,不等式成立.(2)假设()n k k N +=∈时,不等式成立,即1k <+,则1n k =+时,(1)1k =<==++∴当1n k =+时,不等式成立. 则上述证法A .过程全都正确B .1n =验证不正确C .归纳假设不正确D .从n k =到1n k =+的推理不正确7.设 2203n x dx =⎰,则12nx x ⎛⎫- ⎪⎝⎭的展开式中的常数项为( ) A.358- B. 358C. 70-D. 708.已知函数,是的导函数,则的图象大致是( )9.用数学归纳法证明不等式“11113(2)12224n n n n +++>≥++”的过程中,由n k =到1n k =+时,不等式的左边( )A .增加了一项12(1)k +B .增加了两项11212(1)k k +++ C .增加了两项11212(1)k k +++,又减少了一项11k +1220()(2)f a ax a x dx =⎰-()f a 23294349D .增加了一项12(1)k +,又减少了一项11k +10.用1,2,3这三个数字组成四位数,规定这三个数字必须都使用,但相同的数字不能相邻,以这样的方式组成的四位数共有________个A .9B .18C .12D .36 11. 已知e 为自然对数的底数,设函数()()()11kx f x e x =--,()1,2k =,则 ( ). A .当1k =时,()f x )在x =1处取到极小值 B .当1k =时,()f x 在1x =处取到极大值 C .当2k =时,()f x 在1x =处取到极小值 D .当2k =时,()f x 在1x =处取到极大值 12. 设是定义在R 上的函数,其导函数为,若,,则不等式(其中e 为自然对数的底数)的解集为( ) A . B . C . D .二、填空题:本大题共4题,每小题4分,共16分.13. 已知随机变量ξ服从正态分布()22,N δ,且()40.8P ξ<=,则()02P ξ<<=________14. 由曲线y x =,直线2y x =-及y 轴所围成的图形的面积为___________15.观察下列各式:211=,,,, ………………..第n 个式子是 .16.已知函数,若的单调减区间是 (0,4),则在曲线的切线中,斜率最小的切线方程是________________.三、解答题:本大题共5小题, 共56分.17.(本题满分10分)已知数列计算,由此推测计算的公式,并用数学归纳法证明。
高二年级理科数学综合试题

高二年级理科数学综合试题本试卷分选择题和非选择题两部分,共3页,满分150分.考试时间120分钟. 注意事项:1. 答第I 卷前,务必将自己的姓名、座位号、考试科目用铅笔涂写在答题卡上.2. 每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案,不能答在试题卷上.3. 考试结束后,监考人将答题卡收回,试卷考生自己保管.一、选择题:本大题共有8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的,请把它选出后在答题卡规定的位置上用铅笔涂黑. 1. “3x >”是“24x >”的( ).A .必要不充分条件B .充分不必要条件C .充分必要条件D .既不充分也不必要条件 2. 已知0a b >>,那么下列不等式成立的是( ).A a b ->- .B a c b c +<+ ()()22.C a b ->- 11.D a b> 3. 设n S 是等差数列{}n a 的前n 项和,若735S =,则4a =( ).A .8B .7C .6D .54. 已知命题p :所有有理数都是实数,命题q :正数的对数都是负数,则下列命题中为真命题的是 ( )A .q p ∨⌝)(B .q p ∧C .)()(q p ⌝∧⌝D .)()(q p ⌝∨⌝5. 小明在玩投石子游戏,第一次走1米放2颗石子,第二次走2米放4颗石子,…,第n 次走n 米放2n颗石子,当小明一共走了36米时,他投放石子的总数是( ) A .36 B .254 C .510 D .5126. 锐角ABC ∆中,角A 、B 、C 所对的边分别为a 、b 、c ,若2C A =,则ca 的取值范围是( )().1,2A (.B ).,2C .D7. 有甲、乙两个粮食经销商每次在同一粮食生产地以相同的价格购进粮食,他们共购进粮食两次,各次的粮食价格不同,甲每次购粮10000千克,乙每次购粮食10000元,在两次统计中,购粮的平均价格较低的是( )A.甲B.乙C.一样低D.不确定8. 设1F 、2F 分别为双曲线22221(0,0)x y a b a b-=>>的左、右焦点.若在双曲线右支上存在点P ,满足212PF F F =,且2F 到直线1PF 的距离等于双曲线的实轴长,则该双曲线的渐近线方程为 ( )A.340x y ±=B.350x y ±=C.430x y ±=D.540x y ±=二、填空题:本大题共有6个小题,每小题5分,共30分。
学第一学期期末高二数学理科综合测试题一(无答案)

2015学年山东省文登第一中学第一学期期末高二数学理科综合测试题一1.已知命题p :若y x >,则y x -<-;命题q :若y x <,则22y x >.在命题:①q p ∧;②q p ∨;③)(q p ⌝∧;④q p ∨⌝)(中,真命题是( )A .①③B .①④C .②③D .②④2.在正项等比数列{}n a 中,6lg lg lg 963=++a a a ,则111a a 的值是 ( )(A )10000 (B )1000 (C ) 100 (D )103.若双曲线0122=--y tx 的一条渐近线与直线012=++y x 垂直,则该双曲线的离心率为( )A .5B .25C .23D .34.在△ABC 中,角A 、B 、C 所对的边分别为a 、b 、c .若a cos A =b sin B ,则sin A cos A +cos 2B =( )A .-12 B.12 C .-1 D .15.空间四边形OABC 中,OB OC =,3AOB AOC π∠=∠=,则cos <,OA BC >的值是( )A .21B .22 C .-21 D .0 6.等差数列{}n a 的前n 项和为n S ,且1510S π=,则tan n a 的值是( )A B . C . D .- 7.“21≠≠b a 或”是“3≠+b a ”的( )A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件8.若△ABC 的内角A 、B 、C 所对的边a 、b 、c 满足(a +b )2-c 2=4,且C =60°,则ab 的值为( )A.43 B .8-4 3 C .1 D.239.已知A 、B 是抛物线px y 22=(p >0)上异于原点O 的两点,则“·=0”是“直线AB 恒过(0,2p )”的( ) A .充分非必要条件 B .充要条件 C .必要非充分条件D .非充分非必要条件 10.已知x >0,y >0,且2x +1y=1,若x +2y >m 2+2m 恒成立,则实数m 的取值范围是( ) A .m ≥4或m ≤-2 B .m ≥2或m ≤-4C .-2<m <4 D .-4<m <211.若不等式|2||3|x x a -++<的解集为∅,则a 的取值范围为 .12.若实数y x ,满足10,2,3,x y x y +-≥⎧⎪≤⎨⎪≤⎩,则z y x =-的最小值是 13.已知空间四边形OABC ,点,M N 分别为,OA BC 的中点,且c C O b B O a A O ===,,,用a ,b ,c 表示N M ,则N M =_______________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高二数学理科第I 卷(选择题,共60分)一、选择题:本大题共12小题,在每小题给出的四个选项中,只有一项符合题目要求。
1.复数ii -+1)1(4+2等于( ) A .2-2iB .-2iC .1-ID .2i2.若n n baR b a )(lim ,,∞→∈则存在的一个充分不必要条件是( ) A .b >a B .b <a C .b <a <0 D .0<b <a3.抽屈中有10只外观一样的手表,其中有3只是坏的,现从抽屈中随机地抽取4只,那么61等于( )A .恰有1只是坏的概率B .恰有2只是坏的概率C .恰有4只是好的概率D .至多2只是坏的概率4.将一个四棱锥的每一个顶点染上一种颜色,并使同一条棱上的两端点异色,如果只有4种颜色可供使用,则不同的染色的方法数为 ( ) A .24 B .60 C .48 D .72 5.设)(0,,0,2)(0x f im l x e x p x x f x x→⎩⎨⎧>≤-=若存在,则常数p 的值为 ( )A .-1B .0C .1D .e6.环卫工人准备在路的一侧依次载种7棵树,现只有梧桐树和柳树可供选择,则相邻两棵树不同为柳树的栽种方法有 ( ) A .21 B .34 C .33 D .147.已知(5x -3)n 的展开式中各项系数的和比n yy x 2)1(--的展开式中各项系数的和多1023, 则n 的值为 ( ) A .9B .10C .11D .128.设函数*)()(1,12)()(N n n f x x f tx x x f m ∈⎭⎬⎫⎩⎨⎧+='+=则数列的导数的前n 项和为( )A .nn 1-B .nn 1+ C .1+n n D .12++n n 9.设ξ是离散型随机变量,,,31)(,32)(2121x x x P x P <====且ξξ又已知 21,92,34x x D E +==则ξξ的值为( )A .35B .37C .3D .31110.已知关于x 的方程09)3(222=-+--b x a x ,其中a ,b 都可以从集合{1,2,3,4,5,6}中任意选取,则已知方程两根异号的概率为 ( )A .61B .21C .121 D .3111.设n 是奇数,12)(,,++∈n i x b a R x 分别表示的展开式中系数大于0与小于0的项的个数,那么( )A .a =b +2B .a =b +1C .a =bD .a =b -112.设函数b x a x g x f b a x g x f <<'<'则当且上均可导在),()(,],[)(),(时,有 ( ) A .)()(x g x f >B .)()(x g x f <C .)()()()(a f x g a g x f +<+D .)()()()(b f x g b g x f +<+第Ⅱ卷(非选择题,共90分)二、填空题:本大题共4小题,每小题4分,共16分。
把答案填空写在题中的横张上。
13.儿童救助协会由10位女性委员与5为男性委员组成,协会将选取6位委员组团出国考察,如以性别作分层,并在各层依比例选取,则此考察团共有 种组成方式。
14.某中学有六位同学参加英语口语演讲比赛的决赛,决出了第一至第六的名次。
评委告诉甲、乙两位同学:“你们两位都没有拿到冠军,但乙不是最差的。
”则六位同学的排名顺序有 种不同情况(要求用数字作答)。
15.若01111)(3=+-+-=x xx x f 在处连续,则f (0)=16.某射手射击1次,击中目标的概率是0.8,他连续射击4次,有各次射击是否击中目标相互之间没有影响。
有下列结论: (1)第二次击中目标的概率是0.8;(2)恰好击中目标三次的概率是0.83×0.2; (3)至少击中目标一次的概率是1-0.24;其中正确的结论的序号是 (写出所有正确结论的序号) 三、解答题:本大题共6小题,共74分。
解答应写出文字说明、证明过程或演算步骤。
17.(本题满分12分)为应对艾滋病对人类的威胁,现在甲、乙、丙三个研究所独立研制艾滋病疫苗,他们能够成功研制出疫苗的概率分别是41,31,21,求:(1)恰有一个研究所研制成功的概率;(2)若想在到研制成功(即至少有一个研究所研制成功)的概率不低于10099,至少需要多少个乙这样的研究所?(参考数据:lg2=0.3010, lg3=0.4771)18.(本题满分12分)在n xx )12(2+的展开式中,第三项的二项式系数比第二项的二项式系数大27,求展开式中的常数项及系数最大的项。
19.(本题满分12分)袋子中共有12个球,其中有5个黑球,4个白球,3个红球,从中任取2个球(假设取到每个球的可能性都相同)。
已知每取到一个黑球得0分,每取到一个白球得1分,每取到一个红球得2分。
用ξ表示任取2个球的得分的差的绝对值。
(1)求椭机变量ξ的分布列及ξ的数学期望E ξ;(2)记“不等式0212>+-x x ξξ的解集是实数集R ”为事件A ,求事件A 发生的概率P (A )。
20.(本题满分12分)已知函数)0()(2≠+=a ax axx f(1)当a =1时,求f (x )的极值;(2)若存在0)]([)(),1,0(2000=-'∈x f x f x 使成立,求实数a 的取值范围。
21.(本题满分12分)已知正数数列),1(21}{nn n n a a S n a +=项和的前 (1)求321,,a a a ;(2)猜想a n 的表达式,并用数学归纳法.....证明你的结论; 22.(本题满分14分)设函数22)1ln()1()(x x x f +-+=(1)求函数f (x )的单调区间;(2)若当]1,11[--∈e ex 时,不等式f (x )<m 恒成立,求实数m 的取值范围;(3)若关于x 的方程f (x )=x 2+x +a 在区间[0,2]上恰好有两个相异的实根,求实数a 的取值范围。
[参考答案]一、选择题:每小题5分,共计60分。
B C C D A B B C C B C C 二、填空题:每小题4分,共计16分。
13.2100 14.384 15.2316.①③三、解答题: 17.解:(1)记“恰有一个研究所研制成功”为事件A ,则2411413221433121433221)(=⨯⨯+⨯⨯+⨯⨯=A P故恰有一个研究所研制成功的概率为2411…………6分(2)设至少需要n 个乙这样的研究所,则有2)1001lg()32lg(,1001)32(,10099)32(1-=≤≤≥-n n n35.112lg 3lg 2≈-≥nn Z n ∴∈, 的最小值=12故至少需要乙这样的研究所12个。
…………12分18.解:由已知得:2712=-n nC C ,化简得:05432=--n n 解得:n =9,n =-6(舍) …………4分(1)r r r r r r r x C x x C T 399929912)2(----+== 令53762,3,0396394==∴==-C T r r 则故展开式的常数项为5376; …………8分(2)若设第r+1项的系数最大,则有:⎪⎩⎪⎨⎧≥≥--+-+---1919991919992222r r r r r r r r C C C C 解得:31037≤≤r ,5376,3,4=∴=∴∈∴T r Z r 为系数最大项(12分)19.解:(1)由已知可得ξ的取值为:0,1,2,)4(,6615)2(,6632)1(,6619)0(212131521213141415212232425分====+===++==C C C P C C C C C P C C C C P ξξξ∴ξ的概率分布列为: ξ 01 2 P6619 3316 225∴ξ的数学期望为E ξ=0×6619+1×3316+2×225=3331(2)显然ξ=0时不等式成立;若ξ≠0,则有:)12(665166326619)1()0()(,2020021402分=+==+==∴<≤∴<<⇒⎪⎩⎪⎨⎧<⨯-=∆>ξξξξξξξP P A P20.解:(1)当2,0)(,)2(2)(,2)(,12222±=='+-='+==x x f x x x f x x x f a 得令时(3分)x (-∞, -2)-2 (-2,2) 2 (2+∞)f ′(x ) - 0 + 0 -f (x ) 极小极大故函数的极大值、极小值分别为4242-和。
(6分) (2)0)2(2)]([)(,)2(2)(22020220200220200=+--=-'+-='x x a ax a x f x f x ax a x f.1,1120),1,0(),1,0()9.(12,01;2)1(,012)1(,0,022*******020220><+<∈∴∈+=≠+=+=+=+∴≠=--⇒a ax x ax a x a a x a a x a ax a 解得即分时当无解方程时当 因此,实数a 的取值范围是(1,+∞). (12分)21.解:(1)23;12;1321-=-==a a a (2)猜想1--=n n a n证明:①当11,11===a n 由时成立②假设,1,*)(--=∈=k k a N k k n k 即时结论成立 当)1(21)1(21,11111kk k k k k k a a a a S S a k n +-+=-=+=++++时 )9()1(21)11(21)1(21)7()111(21)1(211111111分分k a a a k k k k a a k k k k a a k k k k k k k -+=∴-++---+=--+---+=+++++++ 从而有k k k k a a a k a k k k k -+=++-=>=-++++12442,0,0121121解得又由这说明当n=k+1时结论成立。
由①②可知,1--=n n a n 对任意正整数n 都成立。
(12分)22.解:因为xx x f x x x f +-+='+-+=12)1(2)()1ln()1()(22所以 (1)令0120]11)1[(212)1(2)(2>++⇒>+-+=+-+='xxx x x x x x f12-<<-⇒x 或x >0,所以f (x )的单调增区间为(-2,-1)和(0,+∞); (3分)令0120]11)1[(212)1(2)(2<++⇒<+-+=+-+='xxx x x x x x f )(,201x f x x 所以或-<<<-⇒的单调减区间(-1,0)和(-∞,-2)。
