数字逻辑第4章
合集下载
第四章 数字逻辑基础(1)
锁存器和触发器工作波形示意图:
Set Reset R Q Set Reset Clock S C R Q Q S Q
Байду номын сангаас
Q
Q
4.3 锁存器 4.3.1 RS锁存器 (1) 电路结构及逻辑符号
SD
≥1
Q
≥1
S R
Q
或
S R
Q
RD
Q
Q
Q
SD :置位端(置1端); RD :复位端(置0端); 定义: Q=0,Q=1 为0状态; Q=1,Q=0 为1状态.
RD 0 0 0 1 0 1 0
1 0 0 0 × 1 1 0 1 1 0 × 0 0
4.3.2 门控RS锁存器 在RS锁存器的基础上, 加控制信号,使锁存器状态转换的时 间,受控制信号的控制.
R C
&
≥1 &
RD ≥1
Q
1S C1 Q
Q
1R
Q
S
SD
RD=R· C
SD=S· C
当C=1时:门控RS锁存器功能和RS锁存器完全相同; 当C=0时:RD=SD=0,锁存器状态保持不变.
(3) RS锁存器的功能描述 ① 特性表
② 特性方程
Qn+1=SD+RDQn SDRD=0
③ 状态图
SD=0 RD=×
0
SD=1 RD=0
1
SD=0 RD=1
SD=× RD=0
RS锁存器工作波形图（初态假设为0）
SD 0 Q Q
1 0 1 0 0 0 1 0 0 1 SD RD 0 0 0 0 0 1 0 1 1 0 1 0 1 1 1 1 Qn Qn+1 0 0 1 1 0 0 1 0 0 1 1 1 0 × 1 ×
第4章 时序逻辑电路设计
时序逻辑电路是具有记忆功能的逻辑电路，记忆元件 一般采用触发器。因此，时序逻辑电路由组合电路和 触发器组成，其等效模型如图4.5所示。
1模型
时序电路按其状态的改变方式不同，可分为同 步时序逻辑电路和异步时序逻辑电路两种，在 图4.5中，当CLK1与CLK2为相同信号时，该 电路为同步电路；当CLK1与CLK2为不同信号 时，该电路为异步电路。
output q;
reg
q;
always@(posedge clk or posedge rst)
begin
if(rst==1’b1)
q<=1’b0;
else if(en==1’b1)
q<=data;
else ;
end
endmodule
带同步复位、上升沿触发的触发器
module dff_synrst(data,rst,clk,q); input data,rst,clk; output q; reg q; always@(posedge clk) begin if(rst==1’b1) q<=1’b0; else q<=data; end
本设计要求用仿真和测试两种手段来验证 计数器的功能。实验时，可以通过修改十进 制计数器的设计得到六进制、100进制计数器。
三、设计要求
(1) 完成各模块的Verilog HDL设计编码； (2) 进行功能仿真； (3) 下载并验证计数器功能； (4) 如果60进制计数器要求用6进制和10进制
计数器搭建电路，请画出设计连接图，并 完成设计编码和验证。
else q<=data; end endmodule
带异步复位和置位、上升沿触发的触发器
module dff_asynrst(data,rst,set,clk,q);
1模型
时序电路按其状态的改变方式不同，可分为同 步时序逻辑电路和异步时序逻辑电路两种，在 图4.5中，当CLK1与CLK2为相同信号时，该 电路为同步电路；当CLK1与CLK2为不同信号 时，该电路为异步电路。
output q;
reg
q;
always@(posedge clk or posedge rst)
begin
if(rst==1’b1)
q<=1’b0;
else if(en==1’b1)
q<=data;
else ;
end
endmodule
带同步复位、上升沿触发的触发器
module dff_synrst(data,rst,clk,q); input data,rst,clk; output q; reg q; always@(posedge clk) begin if(rst==1’b1) q<=1’b0; else q<=data; end
本设计要求用仿真和测试两种手段来验证 计数器的功能。实验时，可以通过修改十进 制计数器的设计得到六进制、100进制计数器。
三、设计要求
(1) 完成各模块的Verilog HDL设计编码； (2) 进行功能仿真； (3) 下载并验证计数器功能； (4) 如果60进制计数器要求用6进制和10进制
计数器搭建电路，请画出设计连接图，并 完成设计编码和验证。
else q<=data; end endmodule
带异步复位和置位、上升沿触发的触发器
module dff_asynrst(data,rst,set,clk,q);
数字逻辑设计习题参考答案(第4章)
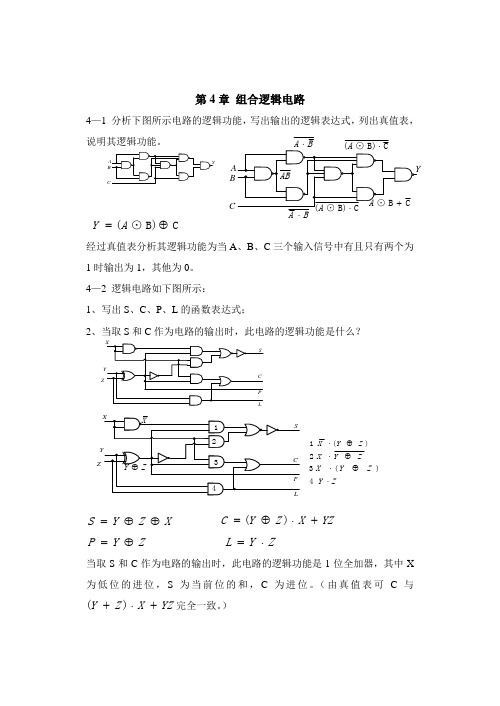
第4章 组合逻辑电路4—1 分析下图所示电路的逻辑功能，写出输出的逻辑表达式，列出真值表，说明其逻辑功能。
C B)⊙(⊕=A Y经过真值表分析其逻辑功能为当A 、B 、C 三个输入信号中有且只有两个为1时输出为1，其他为0。
4—2 逻辑电路如下图所示： 1、写出S 、C 、P 、L 的函数表达式；2、当取S 和C 作为电路的输出时，此电路的逻辑功能是什么？X Z Y S ⊕⊕= YZ X Z Y C +⋅⊕=)(Z Y P ⊕= Z Y L ⋅=当取S 和C 作为电路的输出时，此电路的逻辑功能是1位全加器，其中X 为低位的进位，S 为当前位的和，C 为进位。
（由真值表可C 与YZ X Z Y +⋅+)(完全一致。
）ZB CBA ⋅CB)⊙(⋅A Z)(Z Y X ⊕⋅ZY X ⊕⋅)(Z Y X ⊕⋅ZY ⋅12344—3 下图是由三个全加器构成的电路，试写出其输出1F ，2F ，3F ，4F 的表达式。
Z Y X F ⊕⊕=1 Z Y X F ⋅⊕=)(2Z XY Z XY F +⋅=3 XYZ F =44—4 下图是由3线/8线译码器74LS138和与非门构成的电路，试写出1P 和2P 的表达式，列出真值表，说明其逻辑功能。
ABC C B A m m m m Y Y P +⋅⋅=+=⋅=⋅=70707016543216543212m m m m m m Y Y Y Y Y Y P +++++=⋅⋅+⋅⋅=C B C A B A ++=P1的逻辑功能为当三个输入信号完全一致时输出为1。
P2的逻辑功能为当上输入信号不完全一致时输出为1。
4—5使用74LS138 译码器及少量门电路对三台设备状态进行监控，由不同指示灯进行指示。
当设备正常工作时，指示灯绿灯亮；当有一台设备出故障时，指示灯红灯亮；当有两台设备出故障时，指示灯黄灯亮；当有三台设备出故障时，指示灯红灯和黄灯都亮。
1234解：设输入变量A 、B 、C 分别对应三台设备的状态，0表示故障，1表示正常；输出变量X 、Y 、Z 表示绿、黄、红三个灯的亮灭，0表示灭，1表示亮，根据题意可得真值表如下：设ABC 分别连入74LS138的A 2A 1A 0 由真值表得 42104210Y Y Y Y m m m m Y ⋅⋅⋅=+++=6530Y Y Y Y Z ⋅⋅⋅=4—6 下图3.6是由八选一数据选择器构成的电路，试写出当1G 0G 为各种不同的取值时的输出Y 的表达式。
第4章(454)
执行【View】→【Toolbar】菜单命令，可以显示或隐 藏元件设计窗口的主工具栏。
执行【View】→【Status Bar】菜单命令，可以显示或 隐藏元件设计窗口的状态栏。
25
第4章 创建元件库、元件、中文标题栏和符号
2. 对象的选中与移动 在元件设计窗口中，引脚、线条、虚线矩形框、元件编 号首字母、〈Value〉、说明文字等都是对象。 在图4-8所示的元件设计窗口右边的创建元件工具栏上， 有一个选择按钮，如果按钮处于按下状态，鼠标就会是箭头 形状，这时可以用鼠标选择窗口中的对象；否则鼠标处于绘 制或放置对象状态。 单击选择按钮 ，然后单击某个对象，就会使其处于 选中状态。 结合Ctrl键，可以用鼠标选中多个对象。
29
第4章 创建元件库、元件、中文标题栏和符号
图4-9 【Preferences】对话框
30
第4章 创建元件库、元件、中文标题栏和符号
(2) 在该对话框中，切换到【Grid Display】标签页，然后 选中【Part and Symbol Grid】组合框中的“Dots”(点状)和 “Lines”(线状)两个选项中的一项，就可以改变元件设计窗口 中栅格的显示类型。
24
第4章 创建元件库、元件、中文标题栏和符号
在元件设计窗口的【View】菜单中有许多子菜单，这里 主要介绍以下4个子菜单的功能：
执行【View】→【Tool Palette】菜单命令，可以打开 或关闭元件设计窗口的创建元件工具栏。
执行【View】→【Grid】菜单命令，可以显示或隐藏 元件设计窗口的栅格。
【Grid Display】标签页右边的【Part and Symbol Grid】组 合框控制元件设计窗口，左边的【Schematic Page Grid】组合 框控制原理图设计窗口。
执行【View】→【Status Bar】菜单命令，可以显示或 隐藏元件设计窗口的状态栏。
25
第4章 创建元件库、元件、中文标题栏和符号
2. 对象的选中与移动 在元件设计窗口中，引脚、线条、虚线矩形框、元件编 号首字母、〈Value〉、说明文字等都是对象。 在图4-8所示的元件设计窗口右边的创建元件工具栏上， 有一个选择按钮，如果按钮处于按下状态，鼠标就会是箭头 形状，这时可以用鼠标选择窗口中的对象；否则鼠标处于绘 制或放置对象状态。 单击选择按钮 ，然后单击某个对象，就会使其处于 选中状态。 结合Ctrl键，可以用鼠标选中多个对象。
29
第4章 创建元件库、元件、中文标题栏和符号
图4-9 【Preferences】对话框
30
第4章 创建元件库、元件、中文标题栏和符号
(2) 在该对话框中，切换到【Grid Display】标签页，然后 选中【Part and Symbol Grid】组合框中的“Dots”(点状)和 “Lines”(线状)两个选项中的一项，就可以改变元件设计窗口 中栅格的显示类型。
24
第4章 创建元件库、元件、中文标题栏和符号
在元件设计窗口的【View】菜单中有许多子菜单，这里 主要介绍以下4个子菜单的功能：
执行【View】→【Tool Palette】菜单命令，可以打开 或关闭元件设计窗口的创建元件工具栏。
执行【View】→【Grid】菜单命令，可以显示或隐藏 元件设计窗口的栅格。
【Grid Display】标签页右边的【Part and Symbol Grid】组 合框控制元件设计窗口，左边的【Schematic Page Grid】组合 框控制原理图设计窗口。
数字逻辑-第四章习题-759
习题
4-1 试分析图题4-1中各电路的逻辑功能。
图题4 - 1
4-2 试分析图题4-2中各电路的逻辑功能。
图题4 - 2
4-3 分析图题4-3所示逻辑电路,写出其简化的逻辑表达 式,并用与非门改进设计。
图题4 - 3
4-4 分析图题4-4所示逻辑电路,写出其简化的逻辑表 达式。
图题4 - 4
4-5 分析图题4-5所示逻辑电路的逻辑功能,写出函数 的逻辑表达式,并用最简线路实现它。
4-16 举重比赛有3个裁判,一个是主裁判A,2个是辅 裁判B和C,杠铃完全举上的裁决由每个裁判按一下自己 面前的按钮来决定。只有2个基本点以上裁判(其中必须 有主裁判)判明成功时,表示成功的灯才亮。试设计此逻 辑电路。
4-17 试用与非门设计一个无反变量输入的最简三级 线路,以实现下列函数。
(1)F(A ,B,C)= Σ m(3,5,6) (2)F(A ,B,C,D)= Σm(1,4,5,8,12)+
Σd(3,6,9,15) (3)F(A ,B,C,D)= Σ m(0,6,10,11,14) (4)F(A ,B,C)= AB + AC + AB 4-18 试用8选1多路选择器组成64选1多路选择器。 4-19 试用中规模集成4位二进制比较器组成18位二 进制数字比较器。 4-20 试用中规模集成4位二进制比较器组成20位二 进制数字比较器。
4-10 设二进制补码[x]补= x0. x1 x2 x3 x4 ,分别写出下 列要求的判断条件:
(1)(1/2≤ x)或(x < - 1/2) (2)(1/4≤ x <1/2)或(- 1/2≤ x < - 1/4) (3)(1/8≤ x <1/4)或(- 1/4≤ x < - 1/8) (4)(0≤ x <1/8)或(- 1/8≤ x <0) 4-11 设输入ABCD是按余3码编码的二进制数码,其相 应的十进制数路如图题4-6 所示,其中A和B为输入变量 ,F为输出函数。试说明当S3 、S2 、S1 、S0 作为控制信 号时,F 与A、B 的逻辑关系。
4-1 试分析图题4-1中各电路的逻辑功能。
图题4 - 1
4-2 试分析图题4-2中各电路的逻辑功能。
图题4 - 2
4-3 分析图题4-3所示逻辑电路,写出其简化的逻辑表达 式,并用与非门改进设计。
图题4 - 3
4-4 分析图题4-4所示逻辑电路,写出其简化的逻辑表 达式。
图题4 - 4
4-5 分析图题4-5所示逻辑电路的逻辑功能,写出函数 的逻辑表达式,并用最简线路实现它。
4-16 举重比赛有3个裁判,一个是主裁判A,2个是辅 裁判B和C,杠铃完全举上的裁决由每个裁判按一下自己 面前的按钮来决定。只有2个基本点以上裁判(其中必须 有主裁判)判明成功时,表示成功的灯才亮。试设计此逻 辑电路。
4-17 试用与非门设计一个无反变量输入的最简三级 线路,以实现下列函数。
(1)F(A ,B,C)= Σ m(3,5,6) (2)F(A ,B,C,D)= Σm(1,4,5,8,12)+
Σd(3,6,9,15) (3)F(A ,B,C,D)= Σ m(0,6,10,11,14) (4)F(A ,B,C)= AB + AC + AB 4-18 试用8选1多路选择器组成64选1多路选择器。 4-19 试用中规模集成4位二进制比较器组成18位二 进制数字比较器。 4-20 试用中规模集成4位二进制比较器组成20位二 进制数字比较器。
4-10 设二进制补码[x]补= x0. x1 x2 x3 x4 ,分别写出下 列要求的判断条件:
(1)(1/2≤ x)或(x < - 1/2) (2)(1/4≤ x <1/2)或(- 1/2≤ x < - 1/4) (3)(1/8≤ x <1/4)或(- 1/4≤ x < - 1/8) (4)(0≤ x <1/8)或(- 1/8≤ x <0) 4-11 设输入ABCD是按余3码编码的二进制数码,其相 应的十进制数路如图题4-6 所示,其中A和B为输入变量 ,F为输出函数。试说明当S3 、S2 、S1 、S0 作为控制信 号时,F 与A、B 的逻辑关系。
数字逻辑电路与系统设计蒋立平主编习题解答
第4章习题及解答用门电路设计一个4线—2线二进制优先编码器。
编码器输入为3210A A A A ，3A 优先级最高，0A 优先级最低，输入信号低电平有效。
输出为10Y Y ，反码输出。
电路要求加一G 输出端，以指示最低优先级信号0A 输入有效。
题 解：根据题意，可列出真值表，求表达式，画出电路图。
其真值表、表达式和电路图如图题解所示。
由真值表可知3210G A A A A =。
(a)0 0 0 00 0 0 10 0 1 00 0 1 10 1 0 00 1 0 10 1 1 00 1 1 11 0 0 0 1 0 0 11 0 1 01 0 1 11 1 0 01 1 0 11 1 1 01 1 1 10000000000000000000000000010100011111010110000103A 2A 1A 0A 1Y 0Y G真值表≥1&1Y 3A 2A 1&&1A 0Y &1GA 00 01 11 100010001111000000001101113A 2A 1A 0A 03231Y A A A A =+00 01 11 1000000011110001000011103A 2A 1A 0A 132Y A A =(b) 求输出表达式(c) 编码器电路图图 题解4.1试用3线—8线译码器74138扩展为5线—32线译码器。
译码器74138逻辑符号如图（a ）所示。
题 解：5线—32线译码器电路如图题解所示。
&&&&11EN01234567BIN/OCTENY 0&G 1G 2AG 2B42101234567BIN/OCTEN&G 1G 2A G 2B42101234567BIN/OCT EN&G 1G 2A G 2B42101234567BIN/OCT EN&G 1G 2A G 2B421A 0A 1A 2A 3A 4Y 7Y 8Y 15Y 16Y 23Y 24Y 31图 题解4.3写出图所示电路输出1F 和2F 的最简逻辑表达式。
数字逻辑4-3-2组合电路中的险象判断
数字逻辑 第4章 组合逻辑电路
组合逻辑电路险象判断
卡诺图法
当描述电路的输出函数是“与-或”表达式时， 采用卡诺图判断比较方便。具体方法是先将函 数读入卡诺图中，并画出对应各个与项的卡诺 图圈。接着检查是否存在两个相邻的最小项没 有被任一个卡诺图圈圈在一起。若存在，则当 输入变量在这两个最小项对应的值之间变化时， 存在险象。若没有这种情况，则不存在险象。
数字逻辑
章晓卿
上海交通大学继续教育学院
第3章 集成门电路
4.1 组合电路的分析方法 4.2 组合电路的设计方法 4.3 组合电路中的险象问题
险象产生 险象判断 险象消除
数字逻辑 第4章 组合逻辑电路
组合逻辑电路险象判断
当某一个输入变量X同时以原变量X和反变 量X形式出现在函数表达式中，且在一定条件 下函数表达式可以转换为X+X或者XX的形式 时，则当输入X 变化时，由于竞争可能产生险 象。
数字逻辑
第4章 组合逻辑电路
组合逻辑电路险象判断
有两种方法判断组合电路是否存在险象： 代数法 根据描述电路的函数表达式来判断相应电 路是否具有产生险象的条件。具体步骤： 首先检查找出具备竞争条件的输入变量，该 变量X同时以原变量和反变量的形式出现在 表达式中。
数字逻辑 第4章 组合逻辑电路
组合逻辑电路险象判断
可见，输入C变化时不可能产生险象。
数字逻辑 第4章 组合逻辑电路
组合逻辑电路险象判断
例2 例如设描述电路的逻辑函数为：
F ( A B)( A C )( B C )
找出具有竞争条件的输入变量：A和B。分别对A、 B进行检查。
数字逻辑
第4章 组合逻辑电路
组合逻辑电路险象判断
（1）表达式中只保留A，BC分别以00、01、 10、11的逻辑值代入表达式，得到如下结果：
组合逻辑电路险象判断
卡诺图法
当描述电路的输出函数是“与-或”表达式时， 采用卡诺图判断比较方便。具体方法是先将函 数读入卡诺图中，并画出对应各个与项的卡诺 图圈。接着检查是否存在两个相邻的最小项没 有被任一个卡诺图圈圈在一起。若存在，则当 输入变量在这两个最小项对应的值之间变化时， 存在险象。若没有这种情况，则不存在险象。
数字逻辑
章晓卿
上海交通大学继续教育学院
第3章 集成门电路
4.1 组合电路的分析方法 4.2 组合电路的设计方法 4.3 组合电路中的险象问题
险象产生 险象判断 险象消除
数字逻辑 第4章 组合逻辑电路
组合逻辑电路险象判断
当某一个输入变量X同时以原变量X和反变 量X形式出现在函数表达式中，且在一定条件 下函数表达式可以转换为X+X或者XX的形式 时，则当输入X 变化时，由于竞争可能产生险 象。
数字逻辑
第4章 组合逻辑电路
组合逻辑电路险象判断
有两种方法判断组合电路是否存在险象： 代数法 根据描述电路的函数表达式来判断相应电 路是否具有产生险象的条件。具体步骤： 首先检查找出具备竞争条件的输入变量，该 变量X同时以原变量和反变量的形式出现在 表达式中。
数字逻辑 第4章 组合逻辑电路
组合逻辑电路险象判断
可见，输入C变化时不可能产生险象。
数字逻辑 第4章 组合逻辑电路
组合逻辑电路险象判断
例2 例如设描述电路的逻辑函数为：
F ( A B)( A C )( B C )
找出具有竞争条件的输入变量：A和B。分别对A、 B进行检查。
数字逻辑
第4章 组合逻辑电路
组合逻辑电路险象判断
（1）表达式中只保留A，BC分别以00、01、 10、11的逻辑值代入表达式，得到如下结果：
数字逻辑(欧阳星明)第四章
第四章
组合逻辑电路
设计的一般过程： 设计的一般过程： 1. 建立给定问题的逻辑描述 这一步的关键是正确理解设计要求， 这一步的关键是正确理解设计要求，弄清楚与给定问题相 关的变量及函数，即电路的输入和输出， 关的变量及函数，即电路的输入和输出，建立函数与变量之间 的逻辑关系，得到描述给定问题的逻辑表达式。 的逻辑关系，得到描述给定问题的逻辑表达式。求逻辑表达式 有两种常用方法， 真值表法和分析法。 有两种常用方法，即真值表法和分析法。 2. 求出逻辑函数的最简表达式 为了使逻辑电路中包含的逻辑门最少且连线最少， 为了使逻辑电路中包含的逻辑门最少且连线最少，要对逻 辑表达式进行化简，求出描述设计问题的最简表达式。 辑表达式进行化简，求出描述设计问题的最简表达式。 3. 选择逻辑门类型并将逻辑函数变换成相应形式 根据简化后的逻辑表达式及问题的具体要求， 根据简化后的逻辑表达式及问题的具体要求，选择合适的 逻辑门，并将逻辑表达式变换成与所选逻辑门对应的形式。 逻辑门，并将逻辑表达式变换成与所选逻辑门对应的形式。 4. 画出逻辑电路图 根据实际问题的难易程度和设计者熟练程度， 根据实际问题的难易程度和设计者熟练程度，有时可跳过 其中的某些步骤。设计过程可视具体情况灵活掌握。 其中的某些步骤。设计过程可视具体情况灵活掌握。
4
第四章
组合逻辑电路
4. 2 组合逻辑电路分析 所谓逻辑电路分析，是指对一个给定的逻辑电路， 所谓逻辑电路分析，是指对一个给定的逻辑电路，找出 其输出与输入之间的逻辑关系。 其输出与输入之间的逻辑关系。 分析是研究数字系统的一种基本技能。其目的是了解给 定逻辑电路的功能，评价设计方案的优劣，吸取优秀的设计 思想、改进和完善不合理方案等。 一. 分析的一般步骤
组合逻辑电路
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2）比较各个合并项， F=E1+E2……寻找合适 的替代因子，使尾部因 子种类最少。
Ei Hi
头部
Ti1Ti2...
尾部
4．5、无反变量输入的线路设计
例：
替代因子 Ei 原有尾因子 替代因子
B AC AC B
AC
B
ABC
AB
CB
ACB
怎样最简，用哪一个。
4．5、无反变量输入的线路设计
据以上原则，看下例： 用与非门实现
BC A 0 1
00
01 1
11 Φ Φ
10
F2=A+C
Φ
4
Φ
变换
F1 B C B C F2 A C A C
4．4、可利用任意项的线路设计
画电路： F2 F1
+
+
+
+
A
C
B
C
4．4、可利用任意项的线路设计
真值表
A 0 0 0 0 1 1 1 1 B 0 0 1 1 0 0 1 1 C 0 1 0 1 0 1 0 1 F4 0 0 0 0 1 Φ Φ Φ F3 0 0 0 1 0 Φ Φ Φ F2 0 0 1 0 0 Φ Φ Φ F1 0 1 0 0 0 Φ Φ Φ F0 1 0 0 0 0 Φ Φ Φ
F ABD ABC ABC
考虑任意项则
F BD BC A
化简原则：圈内必包 含至少一个函数项。 转换
F BD BC A BD BC A
4．4、可利用任意项的线路设计
画逻辑图： F
无任意项的逻辑函数 为完全定义函数。 包含任意项的逻辑函 数为不完全定义函数。
另一种方法：
F AB BC ABC
B AC AC( B C)
B AC ACBC
B ABC AC ABC
B A C
B ABC AC ABC
只需4个与非门
AB C
4．5、无反变量输入的线路设计
这种方法既实现了无反 变量输入，又节省了门 电路。 方法： 1）合并原变量相同，其 余为反变量的项。
kikj 0 i j
10,11,12,13,14,15 0
4．4、可利用任意项的线路设计
也就是有6个任意项：
A BC D 0 A BCD 0 ABC D 0 ABC D 0 ABC D 0 ABCD 0
4．4、可利用任意项的线路设计
真值表 二、利用任意项的设计举例 例1、用与非门设计一个判别 线路，判断8421码所表示 的十进制数之值是否大于 等于5。输入A B C D 表 示8421码，输出F：1表示 大于等于，0表示小于 约束方程
AB C D 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111
A B
C
D
ABC D ABCD
4.3、逻辑函数的变换
二、用与或非门实现 例
F AB BC C A
F F AB BC C A
A
B
B
+ +
F
C
C
A
4.3、逻辑函数的变换
方法二：
F AB BC C A
A B B C C A
ABC ABC
讨论如何由命题得到逻辑表达 式
一位全减器
D
Ci
A：被减数 B：减数 Ci-1：上一位的借位，D：差 Ci：本位借位 2、列真值表
A 0 0 0 0 1 1 1 1 B 0 0 1 1 0 0 1 1 Ci-1 0 1 0 1 0 1 0 1
D 0 1 1 0 1 0 0 1 Ci 0 1 1 1 0 0 0 1
供血者：A1—A,A2—B,A3—AB,A4—O 受血者：B1—A,B2—B,B3—AB,B4—O
A1 0 A2 0 A3 0 A4 1 B1 0 0 0 1 0 0 0 0 1 B2 0 0 1 0 0 0 1 0 0 B3 0 1 0 0 1 1 0 1 0 B4 1 0 0 0 0 0 0 0 0 F 1 1 1 1 1 1 1 1 1
F A, B, C, D 0,1,2,6,7,8,11,12,14
CD AB 00 01 11 10 12 8 11 0 1 7 2 6 14 00 01 11 10
F ABC AC D BCD ABC AC D ABCD
共11个与非门
4．5、无反变量输入的线路设计
' '
4.3、逻辑函数的变换
方法二：
BC A 0 0 1 1 1 00
F AB BC C A
01 11 10
1
1
1
0
1
最大项表达式： F A B C A B C
F A B C A B C
总结组合逻辑电路的设计步骤
k 0k1k 2...k 9 0 ..... k 0k1k 2...k 8k 9 0
这些逻辑值为0的最 小项为任意项 ，又称 为约束项。
4．4、可利用任意项的线路设计
约束方程为对输入条件 的的限制方程 2、七段译码器 A、B、C、D为8421码， 也就是只有0000….1001 这10种组合，其余六个 最小项逻辑值为0。
x1 1 1 0 x2 _ 1 1 y1 0 1 0 y2 _ 0 0 F 1 1 1
y1 x2 y2
F
F x1y1 x1x2 y1y2 x1x2 y1y2
第四章 组合线路的设计
例3、 客机安全起飞的条件，同时满足 1） 发动机启动开关接通 2） 飞行员入座，座位保险带扣上 3） 乘客入座，保险带扣上；或座位上无乘客 S=1, 发动机启动开关接通;A=1, 飞行员入座;B=1, 飞行员保险带扣上；Mi=1, 乘客入座；Ni=1, 乘客保险带扣上。 可直接列逻辑表达式
A 0 0 0 0 1 1 1 1
B 0 0 1 1 0 0 1 1
Ci-1 0 1 0 1 0 1 0 1
D 0 1 1 0 1 0 0 1
Ci 0 1 1 1 0 0 0 1
3、化简
BC A 0 1 4 00 01 1 7 11 10 2
D ABCi 1 ABCi 1 ABCi 1 ABCi 1
BC AC AB
BC AC AB
第四章 组合线路的设计
1、 5、画逻辑电路 B C A C
F
A B
确定输入、输出变量
总结组合逻辑电路的设计步骤
：
列真值表， 并写出逻辑 表达式
化简
按要求变换逻辑表达式
画逻辑电路
4.2逻辑问题的描述 例1、列出二进制一位全减器的输出逻辑表达式
A B Ci-1
F 0 0 0 0 0 1 1 1 1 1 Φ Φ Φ Φ Φ Φ
10,11,12,13,14,15 0
F 5,6,7,8,9 10,1112,13,14,15 ,
4．4、可利用任意项的线路设计
不加任意项则 化简
CD AB 00 01 11 10 Φ 8 5 Φ 9 7 Φ Φ 6 Φ Φ 00 01 11 10
4．5、无反变量输入的线路设计
要求逻辑电路只有原变形 式，无反变量形式。 采用增加非门的方法 例 ：用与非门实现下面 函数
BC A 0 1 5 00 01 11 3 10 2 6
F 2,3,5,6
AB BC ABC
4．5、无反变量输入的线路设计 F
需7个与非门
A
B
C
4．5、无反变量输入的线路设计 F
ABC
F1 1 5,6,7 BC
F 2 2 5,6,7 BC
F 3 3 5,6,7 BC
F 4 4 5,6,7 A
4．4、可利用任意项的线路设计
所以任意项的作用是可以得到一个更简 单的逻辑函数，从而化简了逻辑电路。
1 2，， ，47
Ci 1,2,3,7
BC A 0 1 00 01 1 11 3 7 10 2
＝AC AB BC
第四章 组合线路的设计
例2、 X=x1x2，Y=y1y2为两位二进制正整数，判是否X>Y。
x1
F=1,X>Y成立，F=0,X>Y不成立。 只列出使F=1的的部分真值表。
0 0 1
0 1 0
1 0 0
0 0 0
4.3、逻辑函数的变换
将最简式转换为要求的逻辑表达式形式。 一、用与非门实现
例1、 例2
F1 AB AB
F1 F1 AB AB
AB AB
F2 AB BC C D D A
F2 F2 AB BC C D D A
：
确定输入、输出变量
列真值表，并写出逻辑 表达式
化简
按要求变换逻辑表达式
画逻辑电路
4．4、可利用任意项的线路设计
abcde f g
一、任意项
A
七 段 译 码 器
B
C
D
按 键 输 入 译 码 器
k0
k9
5v 键盘显示线路
4．4、可利用任意项的线路设计
1、键盘译码器 k0…k9的取值为1024种， 但正常情况下每次只有 一个键按下，所以只有 10种有效组合，其余 1014种认为不可能出现， 也就是最小项的逻辑值 为0
F S A B MiNi M i