数字逻辑第四章答案
数字逻辑_习题四_答案

习题四部分习题参考答案4.1 将下列函数简化,并用与非门和或非门画出逻辑电路图。
& (3)C B C A D C A B A D C B A F +++=),,,( 解:化简得F=C B C A B A ++F 的与非式为:F=C B C A B A •• ,逻辑电路图如图1所示。
F 的或非式为:F=C B A C B A C B A ABC F +++++=+=,逻辑电路图如图2所示。
图1 图2 4.3分析图4.59所示的逻辑电路图,并说明其逻辑功能。
解:(1)由逻辑电路图写出逻辑表达式并化简可得:DC D B D C D B F D BC D C B D C A D BC D C B D C A F CDABD CD ABD F +=⋅=++=⋅⋅=+=⋅=012(2)根据逻辑表达式,其逻辑功能如表所示。
1 C1&1&&&& &&ABF≥1 0 ≥1≥1≥1ACB ≥1≥1F由真值表可知,DCBA 表示的二进制数,当该值小于等于5,F0=1,当当该值小于等于10,大于5,F1=1,当该值小于等于15,大于10,F2=1。
4.4 试分析图4.60 所示的码制转换电路的工作原理答:①写出逻辑表达式001G B B =⊕ 112G B B =⊕ 223G B B =⊕ 33G B =D C B A F2 F1 F0 输 入 输 出0 00 0 0 1 0 0 0 1 0 0 1 0 0 1 0 0 0 1 0 0 1 1 0 0 1 0 1 0 0 0 0 1 0 1 0 1 0 0 1 0 1 1 0 0 1 0 0 1 1 1 0 1 0 1 0 0 0 0 1 0 1 0 0 1 0 1 0 1 0 1 0 0 1 0 1 0 1 1 1 0 0 1 1 0 0 1 0 0 1 1 0 1 1 0 0 1 1 1 0 1 0 0 1 1 1 1 1 0 0③由真值表可以发现,任意相邻的两个代码之间只有一位不同,而其余各位均相同。
数字逻辑设计习题参考答案(第4章)
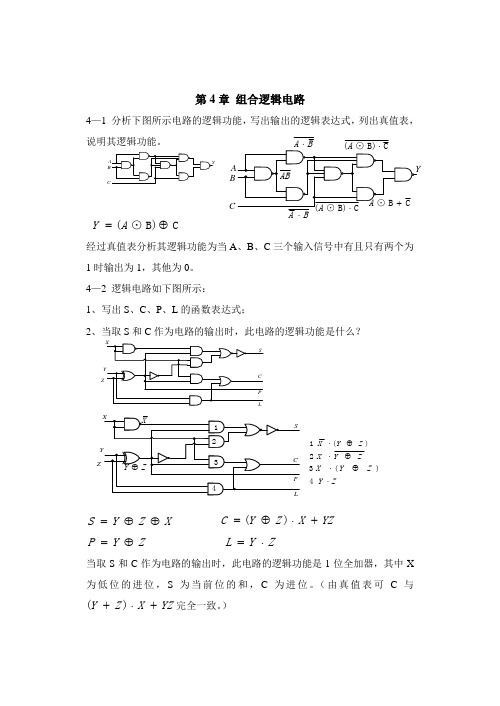
第4章 组合逻辑电路4—1 分析下图所示电路的逻辑功能,写出输出的逻辑表达式,列出真值表,说明其逻辑功能。
C B)⊙(⊕=A Y经过真值表分析其逻辑功能为当A 、B 、C 三个输入信号中有且只有两个为1时输出为1,其他为0。
4—2 逻辑电路如下图所示: 1、写出S 、C 、P 、L 的函数表达式;2、当取S 和C 作为电路的输出时,此电路的逻辑功能是什么?X Z Y S ⊕⊕= YZ X Z Y C +⋅⊕=)(Z Y P ⊕= Z Y L ⋅=当取S 和C 作为电路的输出时,此电路的逻辑功能是1位全加器,其中X 为低位的进位,S 为当前位的和,C 为进位。
(由真值表可C 与YZ X Z Y +⋅+)(完全一致。
)ZB CBA ⋅CB)⊙(⋅A Z)(Z Y X ⊕⋅ZY X ⊕⋅)(Z Y X ⊕⋅ZY ⋅12344—3 下图是由三个全加器构成的电路,试写出其输出1F ,2F ,3F ,4F 的表达式。
Z Y X F ⊕⊕=1 Z Y X F ⋅⊕=)(2Z XY Z XY F +⋅=3 XYZ F =44—4 下图是由3线/8线译码器74LS138和与非门构成的电路,试写出1P 和2P 的表达式,列出真值表,说明其逻辑功能。
ABC C B A m m m m Y Y P +⋅⋅=+=⋅=⋅=70707016543216543212m m m m m m Y Y Y Y Y Y P +++++=⋅⋅+⋅⋅=C B C A B A ++=P1的逻辑功能为当三个输入信号完全一致时输出为1。
P2的逻辑功能为当上输入信号不完全一致时输出为1。
4—5使用74LS138 译码器及少量门电路对三台设备状态进行监控,由不同指示灯进行指示。
当设备正常工作时,指示灯绿灯亮;当有一台设备出故障时,指示灯红灯亮;当有两台设备出故障时,指示灯黄灯亮;当有三台设备出故障时,指示灯红灯和黄灯都亮。
1234解:设输入变量A 、B 、C 分别对应三台设备的状态,0表示故障,1表示正常;输出变量X 、Y 、Z 表示绿、黄、红三个灯的亮灭,0表示灭,1表示亮,根据题意可得真值表如下:设ABC 分别连入74LS138的A 2A 1A 0 由真值表得 42104210Y Y Y Y m m m m Y ⋅⋅⋅=+++=6530Y Y Y Y Z ⋅⋅⋅=4—6 下图3.6是由八选一数据选择器构成的电路,试写出当1G 0G 为各种不同的取值时的输出Y 的表达式。
第四章1 《数字逻辑》(第二版)习题答案

第四章1.分析图1所示的组合逻辑电路,说明电路功能,并画出其简化逻辑电路图。
图1 组合逻辑电路解答○1根据给定逻辑电路图写出输出函数表达式CA B CBA B CAA B CF⋅+⋅+⋅=○2用代数法简化输出函数表达式CBA ABC CBA ABC C)B(A ABCCABCBABCAABCF+ =+ ++ =+ +=⋅+⋅+⋅=○3由简化后的输出函数表达式可知,当ABC取值相同时,即为000或111时,输出函数F的值为1,否则F的值为0。
故该电路为“一致性电路”。
○4实现该电路功能的简化电路如图2所示。
图24.设计一个组合电路,该电路输入端接收两个2位二进制数A=A2A1,B=B2B1。
当A>B时,输出Z=1,否则Z=0。
解答○1根据比较两数大小的法则,可写出输出函数表达式为○2根据所得输出函数表达式,可画出逻辑电路图如图6所示。
图66.假定X=AB代表一个2位二进制数,试设计满足如下要求 (2) Y=X3(Y也用二进制数表示。
)○1假定AB表示一个两位二进制数,设计一个两位二进制数立方器。
由题意可知,电路输入、输出均为二进制数,输出二进制数的值是输入二进制数AB的立方。
由于两位二进制数能表示的最大十进制数为3,3的立方等于27,表示十进制数27需要5位二进制数,所以该电路应有5个输出。
假定用TWXYZ表示输出的5位二进制数,根据电路输入、输出取值关系可列出真值表如表4所示。
由真值表可写出电路的输出函数表达式为T=AB,====BWAB,ZA,Y0,X根据所得输出函数表达式,可画出用与非门实现给定功能的逻辑电路图如图9所示。
图98.设计一个“四舍五入”电路。
该电路输入为1位十进制数的8421码,当其值大于或等于5时,输出F 的值为1,否则F 的值为0。
解答○1 根据题意,可列出真值表如表5所示。
表5○2 由真值表可写出输出函数表达式为 F(A,B,C,D)=∑m(5~9)+∑d(10~15)经化简变换后,可得到最简与非表达式为○3逻辑电路图如图11所示。
数字逻辑课后答案 第四章
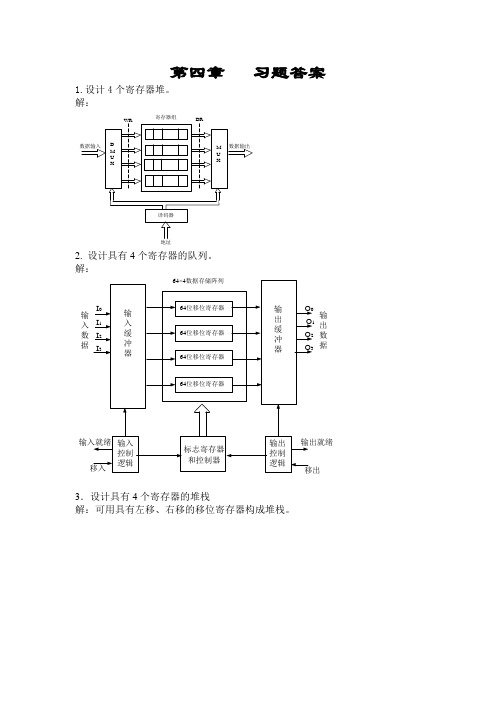
第四章 习题答案1.设计4个寄存器堆。
解:2. 设计具有4个寄存器的队列。
解:3.设计具有4个寄存器的堆栈解:可用具有左移、右移的移位寄存器构成堆栈。
寄存器组输入数据输出数据4.SRAM 、DRAM 的区别解:DRAM 表示动态随机存取存储器,其基本存储单元是一个晶体管和一个电容器,是一种以电荷形式进行存储的半导体存储器,充满电荷的电容器代表逻辑“1”,“空”的电容器代表逻辑“0”。
数据存储在电容器中,电容存储的电荷一般是会慢慢泄漏的,因此内存需要不时地刷新。
电容需要电流进行充电,而电流充电的过程也是需要一定时间的,一般是0.2-0.18微秒(由于内存工作环境所限制,不可能无限制的提高电流的强度),在这个充电的过程中内存是不能被访问的。
DRAM 拥有更高的密度,常常用于PC 中的主存储器。
SRAM 是静态的,存储单元由4个晶体管和两个电阻器构成,只要供电它就会保持一个值,没有刷新周期,因此SRAM 比DRAM 要快。
SRAM 常常用于高速缓冲存储器,因为它有更高的速率;5. 为什么DRAM 采用行选通和列选通解:DRAM 存储器读/写周期时,在行选通信号RAS 有效下输入行地址,在列选通信号CAS 有效下输入列地址。
如果是读周期,此位组内容被读出;如果是写周期,将总线上数据写入此位组。
由于DRAM 需要不断刷新,最常用的是“只有行地址有效”的方法,按照这种方法,刷新时,是在RAS 有效下输入刷新地址,存储体的列地址无效,一次选中存储体中的一行进行刷新。
每当一个行地址信号RAS 有效选中某一行时,该行的所有存储体单元进行刷新。
6. 用ROM 实现二进制码到余3码转换 解: 真值表如下:8421码 余三码B B BG G G栈顶SR 1SR 2SR 3输入数据输出数据压入弹出3232BG0 0 00 0 0 10 0 1 00 0 1 10 1 0 00 1 0 10 1 1 00 1 1 11 0 0 01 0 0 10 0 110 1 0 00 1 0 10 1 1 00 1 1 11 0 0 01 0 0 11 0 1 01 0 1 11 1 0 0最小项表达式为: G=G=G=G=阵列图为:7. 用ROM 实现8位二进制码到8421码转换10103∑)9,8,7,6,5(2∑)9,4,3,2,1(1∑)8,7,4,3,0(0∑)8,6,4,2,0(G 3G 2G 1G 0B 3B 2B 1B B 0解:输入为8位二进制数,输出为3位BCD码,12位二进制数,所以,所需8ROM的容量为:2*12=30728.ROM、EPROM和EEPROM的区别解:ROM 指的是“只读存储器”,即Read-Only Memory。
数字电子技术基础-课后习题答案第4章组合逻辑电路

第四章习题答案4-1(a)100A A F ⊕=,211A A F ⊕=,322A A F ⊕=,33A F =(b) 000B A C =,011111)()(C B A B A C ⊕+=,000B A S ⊕=,0111)(C B A S ⊕⊕= (c) B A AB F +=(同或)(d) B A AC F +=1,B A BC F +=2,C A BC F+=3, 4-2,F ,F ,F∑=)9,8,7,6,5(3m F ,∑=)9,4(2m F ,∑=)8,7,3,2(1m F ,∑=)8,6,3,1(0m F卡诺图化简D F =3,AD D C B F +=2,D A C B CD F ++=1,D B A D A F +=0,F ,F ,F∑=)9,8,7,6,5(3m Y ,∑=)9,4,3,2,1(2m Y , ∑=)8,7,4,3,0(1m Y ,∑=)8,6,4,2,0(0m Y用4-16线译码器实现987653F F F F F Y =,943212F F F F F Y =,874301F F F F F Y =,864200F F F F F Y =4-3将四片138译码器级联,ST 接高电平,ST 接低电平,ST 由译码控制3442A A ST =,3432A A ST =,3432A A ST =,3432A A ST =4-4113471347(1,3,4,7)F m m m m m F F F F ===∑ 2046046(0,4,6)F m m m m F F F ===∑4-51)一片8选1,输入A 、B 、C 分别接8选1的地址A 2,A 1,A 00,,1,17563420========D D D D D D D D D D2)两片8选1,输入A 、B 、C ,D 分别接4选1的地址012,,,A A A E1,01413121197651151084320================D D D D D D D D D D D D D D D D4-6A S SB A S S B A S S AB S S F 01010101)()(+⊕+++= A S S B A S S B A S S B S S A S S AB S S F 010*********+++++=将A S S ,,01分别接8选1的地址012,,A A A ,则输入端分别是0,1,,70635421========D D D D B D B D D D4-71) 输入A,B,C,D 分别接加法器的A 3,A 2,A 1,A 0, 加法器的B 3B 2B 1B 0=0011,CI=0 2) 输入A,B,C,D 分别接加法器的A 3,A 2,A 1,A 0, 加法器的B 3B 2B 1B 0=1101,CI=04-8假设四位被加数为ABCD ,加数为EFGH 输入A,B,C,D 分别接加法器的A 3,A 2,A 1,A 0, 加法器的B 3,B 2,B 1,B 0如下:M CI M H B M G B M F B M E B =⊕=⊕=⊕=⊕=,,,,01234-9真值表∑=)15,14,13,11,7(m F1)8选1数据选择器,将B A M ,,分别接8选1的地址012,,A A A ,则输入端分别是0,1,42107653========D D D D D C D D D2)用3-8译码器151413117151413117F F F F F m m m m m F ==4-10设三个开关分别为A,B,C ,开关的关闭为1,打开为0;灯的输出为F ,灯的亮为1,灭为0真值表C B A F =输入ABCD 分别接4-16译码器的地址段A 3,A 2,A 1,A 0 1) a 端:0158421=====D D D D D , 其余数据端接1 2) b 端:所有数据端均接1,1150=D D3) c 端:012109653======D D D D D D ,其余数据端接1 4) d 端:0158421=====D D D D D ,其余数据端接15) e 端:01514131187421=========D D D D D D D D D ,其余数据端接1 6) f 端:1150==D D ,其余数据端接07) g 端:08421====D D D D ,其余数据端接1设输出灯亮为1,灭为0真值表如下:1)4-16输入ABCD 分别接4-16译码器的地址段A 3,A 2,A 1,A 0(1) F 1端:143210=====D D D D D , 其余数据端接0 (2) F 2端:198765=====D D D D D , 其余数据端接0 (3) F3端:1151413121110======D D D D D D , 其余数据端接0 2)4位数据比较器实现用两片数据选择器,输入端ABCD 分别接两个比较器的A 3A 2A 1A 0,第一片比较器的B 3B 2B 1B 0=0101,第二片的B 3B 2B 1B 0=1001,两片的级联端0,1===<>=B A B A B A I I I ,则:B A I F <=11,B A I F >=23,212F F F =用4-16输入A 1A 0B 1B 0分别接4-16译码器的地址段A 3,A 2,A 1,A 0 (1) F 0端:1151375====D D D D , 其余数据端接0(2) F 1端:1141311976======D D D D D D , 其余数据端接0 (3) F 2端:1141110===D D D , 其余数据端接0 (4) F 3端:115=D , 其余数据端接04-141)只要把两片的B A I =直接相连就可以判断三个输入数据是否相等,假定输入为ABCD 四门课程,及格为1,不及格为0;输出F 为能否毕业,能够毕业为1,不能毕业为0。
数字电路逻辑设计课后习题答案第四章

Q4
4-10
解:由右图写出各触发器的特征方程,有:
Q1
n +1
= [ D ] ⋅ CP ↑= ⎡ Q1n + Q 2n ⎤ ⋅ CP ↑=⎡ Q1n Q 2n ⎤ ⋅ CP ↑ ⎣ ⎦ ⎣ ⎦
⎡ ⎤ Q 2 = [ D ] ⋅ CP ↓= ⎣ Q1n ⎦ ⋅ CP ↓
n +1
根据特征方程,可以画出在下列所示CP波形作用下 Q1和Q2的工作波形:
n +1
4-16(续) Q1 = ⎡ Q 2 ⎤ ⋅ A ↑ ⎢ ⎥ ⎣ ⎦
n +1 n
Q2
n +1
⎡Q n ⎤ ⋅ B ↑ = 1 ⎢ ⎥ ⎣ ⎦
Q1
Q2
4-17
解:由上图写出各触发器的特征方程,有:
⎧Qn+1 = ⎡JQn + KQn ⎤ ⋅ CP ↓⎫ 1⎥ ⎪ 1 ⎢ 1 ⎪ ⎣ ⎦ ⎪ ⎪ n n+1 ⎪ ⎪ ⎡(A⊕Qn )Qn + BQn ⎤ ⋅ CP ↓= ⎡ AQn + BQn ⎤ ⋅ CP ↓ ⎨J = A⊕Q ⎬ ⇒Q = ⎢ 1 1 1 1 1⎥ 1⎥ ⎢ 1 ⎣ ⎦ ⎣ ⎦ ⎪ ⎪ ⎪K = B ⎪ ⎪ ⎪ ⎩ ⎭
4-3 解: 边沿触发器在CP下跳时接收输入信号并可能 改变状态。 主从触发器CP下降沿从触发器接收主触发器 状态,并在CP=0期间保持不变,而主触发 器被封锁,状态保持不变。
4-4
解: 由两个或非门组成的基本触发器可以看出: 当RD=SD=0时,触发器状态保持不变,即Qn+1=Qn; 当RD=0、SD=1时,Qn+1=1,Q n+1 = 0 ,触发器置1; 当RD=1、SD=0时,Qn+1=0,Q n+1 = 1 ,触发器置0; 当RD=SD=1时,Qn+1=Qn=0,若同时跳变为0,则出现状态不定的 情况。 将以上分析结果用表格的形式列出,得到该基本触发器的状态转 移真值表如下 RD 0 0 1 1 SD 0 1 0 1 Qn+1 Qn 1 0 不允许
数字逻辑第四章答案

1 第4章 作业答案1、某工厂有三个车间,每个车间各需1kW 电力。
这三个车间有两台发电机组供电,一台是1kW ,另一台是2kW 。
三个车间经常不同时工作,有时共有1个车间工作,有时两个或三个车间同时工作。
为了节省能源又能保证电力供应,请设计一个逻辑电路,能自动完成供电分配任务。
(所需要的门电路输入引脚个数和类型无限制要求,但是尽量用与非门和异或门实现)。
解:设A 、B 、C 分别为三个车间工作时的电力需求情况,1为工作,需要用电,0为不工作不需要电力供应;输出为两个F 1、F 2,F 1=1表示需要1Kw 的发电机供电,F 2=1表示需要2Kw 的发电机供电,根据题意列阵真值根据真值表得F 1和F 2的逻辑函数为:电路图为:2、分析下面逻辑电路图的功能。
解:根据电路图写出布尔表达式为:BC A BC A F +=∙=根据真值表可知,当A 为1或B 、C 同时为1时,输出F=1;此电路可看作一个表决电路,A 为主裁判,B 、C 为副裁判,规则为:当主裁判通过或两个副裁判同时通过时,最终表决结果F 为通过。
3、使用74138和与非门(输入引脚数目无限制)实现函数BC A F +=解:将函数扩展成为最小项表达式:也可以如下操作:4、使用74151和逻辑门实现下列逻辑函数。
(1)∑=)7,3,1,0(),,(m C B A F解:7766554433221100D m D m D m D m D m D m D m D m Y +++++++=令输入D 0、D 1、D 3、D 7为1,D 2、D 4、D 5、D 6为0,可得:(2)∑=)14,11,9,5,4,3,1(),,,(m D C B A F (可参考课本P89 例解:ABC D A B B D F ++++++=设ABC 为输入地址,则有:D 2输入1,D 3、D 6输入0,D 0、D 1、D 4、D 5输入变量D ,D 7输入D。
数字逻辑第四章课后答案讲解

习题4解答4-1试用与非门设计实现函数F(A,B,C,D)=Σm(0,2,5,8,11,13,15)的组合逻辑电路。
解:首先用卡诺图对函数进行化简,然后变换成与非-与非表达式。
化简后的函数4-2试用逻辑门设计三变量的奇数判别电路。
若输入变量中1的个数为奇数时,输出为1,否则输出为0。
解:本题的函数不能化简,但可以变换成异或表达式,使电路实现最简。
真值表:逻辑函数表达式:CBACBACBACBAY⋅⋅+⋅⋅+⋅⋅+⋅⋅=CBA⊕⊕=)(BACDDCBDBADCBACDDCBDBADCBF⋅⋅⋅⋅⋅⋅⋅=++⋅⋅+⋅⋅=++⋅⋅+⋅⋅=逻辑图BACDF4-3用与非门设计四变量多数表决电路。
当输入变量A 、B 、C 、D 有三个或三个以上为1时输出为1,输入为其他状态时输出为0。
解:真值表: 先用卡诺图化简,然后变换成与非-与非表达式:逻辑函数表达式:4-4用门电路设计一个代码转换电路,输入为4位二进制代码,输出为4位循环码。
解:首先根据所给问题列出真值表,然后用卡诺图化简逻辑函数,按照化简后的逻辑函数画逻辑图。
ACDBCD ABC ABD ACD BCD ABC ABD ACD BCD ABC ABD Y ⋅⋅⋅=+++=+++=A逻辑图真值表: 卡诺图化简:化简后的逻辑函数:Y 1的卡诺图Y 2的卡诺图 Y 3的卡诺图 Y 4的卡诺图AY =1BA B A B A Y ⊕=+=2CB C B C B Y ⊕=+=3DC D C D C Y ⊕=+=4Y 逻辑图4-5图4.48所示是一个由两台水泵向水池供水的系统。
水池中安置了A 、B 、C 三个水位传感器。
当水池水位低于C 点时,两台水泵同时供水。
当水池水位低于B 点且高于C 点时,由水泵M1单独供水。
当水池水位低于A 点且高于B 点时,由水泵M2单独供水。
当水池水位高于A 点时,两台水泵都停止供水。
试设计一个水泵控制电路。
要求电路尽可能简单。
图4.48 习题4-5的示意图解:设水位低于传感器时,水位传感器的输出为1,水位高于传感器时,水位传感器的输出为0。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
图2
2. 分析图3 (1) 指出在哪些输入取值下,输出F的值为1 (2) 改用异或门实现该电路的逻辑功能。
解答
1 ○ 假定 AB
由题意可知,电路输入、输出均为二进制数,输出二进制数的值是输入二进 制数 AB 的平方。 由于两位二进制数能表示的最大十进制数为 3, 3 的平方等于 9, 表示十进制数 9 需要 4 位二进制数,所以该电路应有 4 个输出。假定用 WXYZ 表 示输出的 4 位二进制数, 根据电路输入、 输出取值关系可列出真值表如表 3 所示。 表3 W X Y Z 0 0 0 1 0 0 1 0 0 0 0 0 0 1 0 1
.
A
=1
.
B
=1
.
=1
C
D
图5
组合逻辑电路
解答
1 ○ 写出电路输出函数表达式如下:
W A, X A B, Y B C, Z CD
2 ○
列出真值表如表1所示。 表1 ABCD 1000 1001 1010 1011 1100 1101 1110 1111
ABCD 0000 0001 0010 0011 0100 0101 0110 0111 3 ○
逻辑电路图如图14所示。
图14 2 ○ 变换如下:
F A BC BCD ACD BCD (B D)AC BDC BDC BD AC BD BC BD CD BD AC BD BC BD CD
逻辑电路图如图15所示。
图15 12. 下列函数描述的电路是否可能发生竞争?竞争结果是否会产生险象?在什么情 况下产生险象? (1) (2) (3)
ABCD 0000 0001 0010 0011 0100 0101 0110 0111 2 ○
WXYZ 1011 1100 1101 1110 1111 dddd dddd dddd
由真值表可写出输出函数表达式为
W(A, B, C, D) m(8,9,10,11,12) d(0,1,2,13,14,15) X(A,B, C, D) m(7,9,10,11,12) d(0,1,2,13,14,15) Y(A, B, C, D) m(5,6,8,11,12) d(0,1,2,13,14,15) Z(A,B, C, D) m(4,6,8,10,12) d(0,1,2,13,14,15)
A 0 0 1 1 0 1 0 1
B
由真值表可写出电路的
T AB, W A, X 0, Y AB, Z B
根据所得输出函数表达式, 可画出用与非门实现给定功能的逻辑电路图如图 9所示。
图9 7.用与非门设计一个组合电路,该电路输入为1位十进制数的2421码,当输入的 数字为素数时,输出F为1,否则F为0。
3 ○ 根据逻辑表达式,可作出逻辑电路图如图13所示。
图 13 11 (1) (2)
F AB AC BC F ABC BC D AC D BCD
解答
1 ○ 变换如下:
F A B AC BC A B AC BC BC AC AB A(B C) (A B)C (A C)B A BC AB C AC B A ABC C ABC B ABC A ABC B ABC C ABC
解答
1 ○ 假定采用异或门实现给定功能,设输入的四位代码用 B4B3BB1 表示,输出
函数用 F
F B4 B3 B2 B1
2 ○ 逻辑电路图如图 12 所示。
图12 10.设计一个加/减法器,该电路在M控制下进行加、减运算。当M=0时,实现全 加器功能;当M=1时,实现全减器功能。
解答○ 1 设: A-----被加数/被减数
2 ○ 逻辑电路图如图 10
图10
8.设计一个“四舍五入”电路。该电路输入为1位十进制数的8421码,当其值大于 或等于5时,输出F的值为1,否则F的值为0。
解答
1 ○ 根据题意,可列出真值表如表5所示。 A 0 0 0 0 0 0 0 0 1 1 1 B C 0 0 0 0 0 1 0 1 1 0 1 0 1 1 1 1 0 0 0 0 0 1 ┇ 1 1 1 1 2 ○ 表5 D 0 1 0 1 0 1 0 1 0 1 0 F 0 0 0 0 0 1 1 1 1 1 d ┇ d
3 ○
因为逻辑表达式 F3 ( A B) ( A C ) 中有逻辑变量 A 以互补形式 出现,故会发生竞争。由于 BC=11 时,表达式会变成 A A 的形式, 所以 BC=11 时会产生险象。增加冗余项后的表达式为
F (A B)(A C)(B C)
解答
1 ○ 设 1 位十进制数的余 3 码为 ABCD, 相应 2421 码为 WXYZ, 根据余 3 码和 2421码的编码法则,可作出真值表如表2所示。 表 2 WXYZ ABCD dddd dddd dddd 0000 0001 0010 0011 0100 1000 1001 1010 1011 1100 1101 1110 1111
A 0 0 1 Biblioteka 0 1 0 1BW AB, X AB, Y 0, Z B
根据所得输出函数表达式, 可画出用与非门实现给定功能的逻辑电路图如图 8所示。
图8 1 ○ 假定 AB 表示一个两位二进制数,设计一个两位二进制
由题意可知,电路输入、输出均为二进制数,输出二进制数的值是输入二进 制数 AB 的立方。由于两位二进制数能表示的最大十进制数为 3,3 的立方等于 27, 表示十进制数 27 需要 5 位二进制数, 所以该电路应有 5 个输出。 假定用 TWXYZ 表示输出的 5 位二进制数,根据电路输入、输出取值关系可列出真值表如表 4 所示。 表4 T W X Y Z 0 0 0 1 0 0 1 1 0 0 0 0 0 0 0 1 0 1 0 1
解答
1 ○ 设一位十进制数的 2421 码用 ABCD 表示,由题意可知,当 ABCD 表示的十
进制数字为 2、3、5、7 时,输出 F 为 1,否则为 0。据此,可写出输出函数表达 F(A,B,C,D)=∑m(2,3,11,13)+∑d(5~10)
F(A,B,C,D) BC ACD BC ACD
B-----加数/减数 C-----来自低位的进位输入 /来自低位的借位输入 F-----本位“和”/本位“差” G-----向高位的“进位” /向高位的“进位” 根据题意,可列出真值表如表6所示。 M ABC F G M ABC F G 0 000 0 0 1 000 0 0 0 001 1 0 1 001 1 1 0 010 1 0 1 010 1 1 0 011 0 1 1 011 0 1 0 100 1 0 1 100 1 0 0 101 0 1 1 101 0 0 0 110 0 1 1 110 0 0 0 111 1 1 1 111 1 1
由真值表可写出输出函数表达式为 F(A,B,C,D)=∑m(5~9)+∑d(10~15)
F(A,B,C,D) A BC BD A BC BD
3 逻辑电路图如图 11 ○
图11
9.设计一个检测电路,检测4位二进制码中1的个数是否为偶数。若为偶数个1, 则输出为1,否则输出为0。
2 由真值表可写出输出函数表达式: ○ M=0: F( A,B,C) = ∑m(1,2,4,7) G ( A,B,C) = ∑m(3,5,6,7) M=1: F( A,B,C) = ∑m(1,2,4,7) G ( A,B,C) = ∑m(1,2,3,7)
经化简变换后,可得函数表达式如下:
M 0 : F A B C; G AB AC BC AB AC BC M 1 : F A B C; G AB AC BC AB AC BC
化简后可得:
WA X AB AC AD BCD A(B C D) BCD Y ACD ACD ACD ACD ACD ZD
3 ○ 逻辑电路图如图7所示。
图7 6.假定X=AB代表一个2位二进制数,试设计满 (1)
Y=X
2
(2)
Y=X
3
(Y也用二进制数表示。)
图3
组合逻辑电路
解答
分析给定逻辑电路,可求出输出函数最简表达式为
F ABC ABC
1 ○ 2 ○ 当ABC取值000、011、101、110时,输出函数F的值为1; 用异或门实现该电路功能的逻辑电路图如图4所示。
图4 3.析图5所示组合逻辑电路,列出真值表,并说明该电路的逻辑功能。
W X Y Z
第
四
章
1. 分析图1所示的组合逻辑电路,说明电路功能,并画出其简化逻辑电路图。
图1
组合逻辑电路
解答
1 根据给定逻辑电路图写出输出函数表达式 ○
F ABC A ABC B ABC C
2 用代数法简化输出函数表达式 ○
F ABC A ABC B ABC C ABC(A B C) ABC ABC ABC A BC
F1 AB AC CD
F2 AB ACD BC
F3 ( A B) ( A C )
解答
1 ○ 因为逻辑表达式 F1 AB AC CD 中没有以互补形式出现的逻辑 变量,故不会发生竞争。 2 ○ 因为逻辑表达式 F2 AB ACD BC 中有逻辑变量 A 以互补形式出 现, 故会发生竞争。 但由于不论 BCD 取何值, 表达式都不会变成 A A 或者 A A 的形式,所以不会产生险象。
