Zernike矩和最小二乘椭圆拟合的亚像素边缘提取

合集下载

Zernike矩和最小二乘椭圆拟合的亚像素边缘提取

Zernike矩和最小二乘椭圆拟合的亚像素边缘提取祝宏;曾祥进【期刊名称】《计算机工程与应用》【年(卷),期】2011(047)017【摘要】In order to improve the resolution and accuracy of micro-assembly systems,a novel sub-pixel edge detection and center localization algorithm for micro-parts is presented. Firstly,the invariant moments are employed to describe the feature of the micro parts.Then, the edge of micro parts at pixel level is extracted using Canny operator.Secondly,Zernike orthogonal moments are used to relocate the edge of microsize part at sub-pixel stly, least squares ellipse firing is applied to position the center. Experiment results show that the algorithm can achieve higher location accuracy and consume less time.%为了提高微操作系统的装配精度,提出了一种新型的亚像素边缘检测和中心定位算法.应用Canny算子提取了微零件在像素级的边缘.应用Zernike矩对微零件进行亚像素级的边缘定位.采用最小二乘椭圆拟合定位微零件的中心位置.实验结果表明,该算法能够实现更高的定位精度和消耗更少的时间.【总页数】3页(P148-150)【作者】祝宏;曾祥进【作者单位】华中科技大学文华学院信息科学与技术学部,武汉430074;华中科技大学控制科学与工程系,武汉430074【正文语种】中文【中图分类】TP24【相关文献】1.改进Zernike矩亚像素边缘检测算法研究 [J], 于微波;马艳辉;刘芳雪;刘克平2.基于Arimoto熵和Zernike矩的刀具图像亚像素边缘检测 [J], 吴一全;龙云淋;周杨3.基于改进的Sobel-Zernike矩法亚像素厚度测量 [J], 杨前华;姚励;赵力4.Zernike矩算法实现焊缝中心线亚像素检测 [J], 刘军;赵剑英;池云5.基于改进的Zernike矩亚像素边缘提取算法外螺纹非接触测量 [J], 蔡艳;叶连祥;孙大为;田华;朱俊杰;胡志云因版权原因，仅展示原文概要，查看原文内容请购买。

zernike矩特征提取 -回复

zernike矩特征提取-回复什么是Zernike矩特征提取？Zernike矩特征提取是一种用于描述图像的形状和纹理特征的方法。

它基于Zernike多项式的性质，将图像中的信息转化为一组具有判别能力的特征。

Zernike矩特征提取被广泛应用于图像分析、模式识别和计算机视觉等领域。

一、Zernike多项式的定义Zernike多项式是正交的极坐标函数，可以表示为：Z(n, m)(ρ, θ) = R(n, m)(ρ) ・Ξ(m)(θ)其中，n和m是整数，满足条件n≥m≥0，ρ是归一化的极坐标半径（0 ≤ρ≤1），θ是极坐标角度（0 ≤θ≤2π），R(n, m)(ρ)是Radial 多项式，Ξ(m)(θ)是Azimuthal多项式。

二、Zernike矩的计算Zernike矩是将图像在Zernike多项式下的正交分解系数。

根据Zernike多项式的正交性，可以将图像函数f(x, y)表示为一组系数的和：f(x, y) = ∑∑C(n, m) ・Z(n, m)(ρ, θ)其中，C(n, m)是系数。

通过对图像进行变换、归一化和积分等操作，可以计算得到Zernike矩的数值。

三、Zernike矩的性质和应用Zernike矩具有许多重要的性质，使其成为一种有效的特征描述方法。

1. 正交性：不同Zernike矩之间是正交的，能够提供良好的特征独立性。

2. 规范性：Zernike矩的值在一定范围内，并且与图像的平移、旋转、缩放等无关，具有尺度不变性。

3. 旋转不变性：Zernike矩可以描述图像的旋转性质，对于旋转不变的图像特征提取非常有效。

4. 形状描述：Zernike矩可以用来描述图像的形状信息，对于目标识别和边缘检测有广泛应用。

5. 纹理描述：Zernike矩还可以用来描述图像的纹理特征，对于纹理分析和纹理合成具有重要意义。

基于Zernike矩的特征提取方法可以应用于许多领域。

例如，在医学图像分析中，可以利用Zernike矩提取肿瘤的形状特征，用于肿瘤分类和定位；在工业质检中，可以使用Zernike矩提取产品表面的纹理特征，用于缺陷检测和品质评估；在模式识别中，可以利用Zernike矩提取目标图像的形状和纹理特征，用于目标识别和物体跟踪。

亚像素边缘提取算法

亚像素边缘提取算法随着计算机视觉技术的不断发展，边缘提取算法一直是计算机视觉领域中的一个重要问题。

在图像处理中，边缘是指图像中颜色、亮度、纹理等特征发生突变的区域。

边缘提取算法能够将图像中的边缘区域提取出来，是许多计算机视觉应用的基础。

在传统的边缘提取算法中，常用的方法是Sobel算子、Prewitt 算子、Canny算子等。

这些算法能够有效地提取图像中的边缘信息，但是它们存在一些问题。

例如，它们只能提取出粗略的边缘信息，无法提取出亚像素级别的边缘信息。

因此，在实际应用中，这些算法往往无法满足需求。

为了解决这个问题，研究人员提出了亚像素边缘提取算法。

亚像素边缘提取算法是一种能够提取出亚像素级别的边缘信息的算法。

它能够将图像中的边缘区域提取出来，并且能够提供更加精细的边缘信息，从而能够满足更多的应用需求。

亚像素边缘提取算法的基本思想是基于图像灰度值的变化率进行边缘提取。

它通过对图像中像素的灰度值进行差分计算，来得到图像中的边缘信息。

在差分计算的过程中，亚像素边缘提取算法采用了更加精细的计算方法，从而能够提取出亚像素级别的边缘信息。

亚像素边缘提取算法的具体实现方法有很多种，其中比较常用的方法是基于插值的方法。

在这种方法中，亚像素边缘提取算法会对图像中的像素进行插值处理，从而能够得到更加精确的灰度值。

这样，就能够提取出亚像素级别的边缘信息。

除了基于插值的方法外，亚像素边缘提取算法还有其他的实现方法。

例如，基于模板匹配的方法、基于概率模型的方法等。

不同的实现方法有着不同的优缺点，需要根据实际应用需求进行选择。

在实际应用中，亚像素边缘提取算法被广泛应用于计算机视觉领域中。

例如，在图像匹配中，亚像素边缘提取算法能够提供更加精确的匹配结果；在目标跟踪中，亚像素边缘提取算法能够提取出目标边缘信息，从而实现目标跟踪。

此外，亚像素边缘提取算法还可以应用于图像分割、三维重建、图像识别等领域。

总之，亚像素边缘提取算法是计算机视觉领域中的一个重要问题。

超大视场太阳敏感器图像质心提取算法

超大视场太阳敏感器图像质心提取算法詹银虎;郑勇;张超;马高峰;骆亚波【摘要】太阳图像质心提取是利用太阳敏感器进行天文导航的关键技术之一，直接决定了太阳敏感器的观测精度。

针对超大视场太阳敏感器非圆形太阳图像质心提取问题，首先提出像面椭圆拟合算法，较好地解决了椭圆及近似椭圆形太阳图像的质心提取问题，然后进一步提出了球面圆拟合算法。

该算法根据相机的投影和畸变模型，将太阳图像的边缘点映射到物方空间，对物方空间的边缘点进行球面圆拟合，从而确定太阳质心位置。

在估计球面圆拟合算法的精度时，需要将太阳质心位置映射回像面。

理论上，球面圆拟合算法不再需要顾及太阳图像的形状，算法更为严谨。

将椭圆拟合算法和球面圆拟合算法应用到实测的太阳图像质心提取中。

结果表明，椭圆拟合算法更适合处理半视场角70°～803．°的太阳图像，平均精度约为00．75 pi x el s；球面圆拟合算法更适合处理半视场角大于803．°的太阳图像，平均精度约为00．82 pi x el s。

%Sun image centroid algorithm is one of the key technologies of celestial navigation using sun sensors ,which directly determine the precision of the sensors .Due to the limitation of centroid algorithmfor non‐circular sun image of the sun sensor of large field of view,firstly ,the ellipse fitting algorithm is proposed for solving elliptical or sub‐elliptical sun images .Then t he spherical circle fitting algorithm is put forward .Based on the projection model and distortion model of the camera ,the spherical circle fitting algorithm is used to obtain the edge points of the sun in the object space ,and then the centroid of the sun can be determined by fitting the edge points as a spherical circle .In order to estimate the precision of spherical circle fitting algorithm ,the centroid ofthe sun should be projected back to the image space . Theoretically ,the spherical circle fitting algorithm is no longer need to take into account the shape of the sun image ,the algorithm is more precise .The results of practical sun images demonstrate that the ellipse fitting algorithm is more suitable for the sun image with 70°~80 .3° half angle o f view , and the mean precision is about 0 0.75 pixels;the spherical circle fitting algorithmis more suitable for the sun image with a half angle of view larger than 80 3.° ,and the mean precision is about 0 0.82 pixels .【期刊名称】《测绘学报》【年(卷),期】2015(000)010【总页数】7页(P1078-1084)【关键词】天文导航;太阳图像;质心提取算法;边缘检测;最小二乘拟合【作者】詹银虎;郑勇;张超;马高峰;骆亚波【作者单位】信息工程大学导航与空天目标工程学院，河南郑州450001;信息工程大学导航与空天目标工程学院，河南郑州450001;信息工程大学导航与空天目标工程学院，河南郑州450001;信息工程大学地理空间信息学院，河南郑州450001;郑州大学水利与环境学院，河南郑州450001【正文语种】中文【中图分类】P2281 引言太阳敏感器是一种通过观测太阳方向矢量确定载体姿态的传感器，在航空航天领域应用极其广泛。

基于zernike矩的亚像素边缘检测算法

基于zernike矩的亚像素边缘检测算法基于Zernike矩的亚像素边缘检测算法引言边缘检测是计算机视觉领域中的一项重要任务，它在图像处理和模式识别中起着至关重要的作用。

传统的边缘检测算法通常基于像素级别的操作，但在一些应用中，像素级别的边缘检测结果并不能满足需求。

因此，亚像素边缘检测算法应运而生。

本文将介绍一种基于Zernike矩的亚像素边缘检测算法。

Zernike矩Zernike矩是一种广泛应用于图像处理和模式识别中的特征提取方法。

它是由荷兰数学家Zernike于1934年提出的，用于描述图像中的形状和纹理信息。

Zernike矩具有旋转不变性和尺度不变性的特点，因此被广泛应用于边缘检测、目标识别等领域。

基于Zernike矩的亚像素边缘检测算法基于Zernike矩的亚像素边缘检测算法主要包括以下几个步骤：1. 图像预处理对输入图像进行预处理，包括灰度化、平滑化和边缘增强等操作。

这些操作可以提高图像质量，减少噪声对边缘检测结果的影响。

2. Zernike矩计算接下来，对预处理后的图像计算Zernike矩。

Zernike矩是一种二维矩阵，可以描述图像的形状和纹理信息。

计算Zernike矩需要使用到Zernike多项式，这些多项式是一组正交函数，用于描述图像的特征。

3. 边缘检测在计算Zernike矩之后，可以根据Zernike矩的值来进行边缘检测。

一般情况下，边缘在图像中表现为亮度和颜色的变化。

通过分析Zernike矩的变化情况，可以确定边缘的位置和形状。

4. 亚像素插值由于Zernike矩是基于像素级别的计算得到的，其结果精度有限。

为了提高边缘检测的精度，需要进行亚像素插值。

亚像素插值是一种通过对像素进行插值计算来确定边缘位置的方法，可以提高边缘检测的精度。

5. 结果评估对亚像素边缘检测结果进行评估。

评估指标可以包括检测准确率、召回率和F1值等。

通过评估结果，可以判断算法的性能和效果。

总结基于Zernike矩的亚像素边缘检测算法是一种有效的边缘检测方法，可以提高边缘检测的精度和准确性。

zernike矩特征提取

zernike矩特征提取什么是Zernike 矩特征提取？Zernike 矩是一种特征提取方法，主要用于对图像、图形或模式进行描述和分析。

它由荷兰数学家Frits Zernike在20世纪30年代提出，并广泛应用于光学和图像处理领域。

Zernike 矩可以捕捉到图像的形状、边缘和纹理等特征，具有良好的旋转和尺度不变性，适用于各种图像分析任务。

Zernike 矩的计算过程分为以下几个步骤：步骤一：对图像进行预处理在进行Zernike 矩计算之前，通常需要对图像进行预处理，以提高后续分析的效果。

预处理可以包括图像的去噪、平滑和增强等操作，具体方法根据任务的需要而定。

步骤二：将图像转换为二值图像为了计算Zernike 矩，需要将图像转换为二值图像。

二值图像中，像素只有两种取值，通常为0和255（或1），分别表示背景和目标。

可以采用阈值分割等方法将图像二值化。

步骤三：计算归一化的Zernike 矩一般来说，Zernike 矩是通过对二值图像的多项式函数进行积分计算得到的。

这些多项式函数是正交的，并且有一定的归一化约束。

计算每个Zernike 矩需要对二值图像中的像素进行加权求和，权重即为对应像素的数值。

步骤四：选择合适的矩阵来描述图像特征Zernike 矩具有一系列正交性质和归一化约束，根据应用需求，可以选择不同的矩阵来描述图像的特征。

常用的Zernike 矩包括Z0、Z1、Z2 等。

它们对应于图像的平均灰度、图像的对称性和图像的轮廓等特征。

步骤五：提取Zernike 矩特征通过计算得到的Zernike 矩，可以提取出图像的特征。

这些特征可以用于图像分类、目标识别、姿态估计等任务。

通常，可以通过对比不同图像的Zernike 矩特征来衡量它们之间的相似度。

步骤六：应用Zernike 矩特征Zernike 矩特征可以应用于多种图像处理和分析任务中。

例如，可以利用Zernike 矩特征进行人脸识别，通过比较不同人脸图像的Zernike 矩特征来判断它们是否属于同一个人。

基于Zernike正交矩的图像亚像素边缘检测算法改进

信电1&China Computer&Communication2021年第2期基于Zernike正交矩的图像亚像素边缘检测算法改进王肃国李龙华(山东服装职业学院，山东泰安271000)摘要：Zernike正交矩具有运算量大以及对噪声不敏感的缺点，不利于发挥其在亚像素边缘检测中的优势。

本文针对这种不足提出了改进方法，将数学形态学与Zernike正交矩相结合，发挥它们在图像处理中的优势，对含噪图像进行“预处理”,再提取Zernike正交矩的亚像素边缘信息.实验结果表明：这种算法在去除噪声的同时也提高了处理效率.关键词：Zernike正交矩；亚像素；数学形态学；预处理；处理效率中图分类号：TP391.41；TP183文献标识码：A文章编号：4003-9767(2021)02-071-04 Improvements Image Sub-pixel Edge Detection Algorithm Based on ZernikeOrthogonal MomentWANG Suguo,LI Longhua(Shandong Vocational Institute of Fashion Technology,Taian Shandong271000,China) Abstract:Zernike orthogonal moments have the disadvantages of large computational load and insensitive to noise,which is not conducive to exerting its advantages in sub-pixel edge detection.This paper proposes an improved method to solve this problem, combining mathematical morphology and Zernike orthogonal moments to give full play to their advantages in image processing,to "preprocess"noisy images,and then extract the sub-pixels of Zernike orthogonal moments.Edge information.Experimental results show that this algorithm improves processing efficiency while removing noise.Keywords:Zernike orthogonal moments;sub-pixels;mathematical morphology;preprocessing;processing efficiency0引言由于图像的边缘部分代表图像的重要信息，所以如何提取图像边缘一直是研究的热点。

三种基于矩的亚像素级边缘定位方法

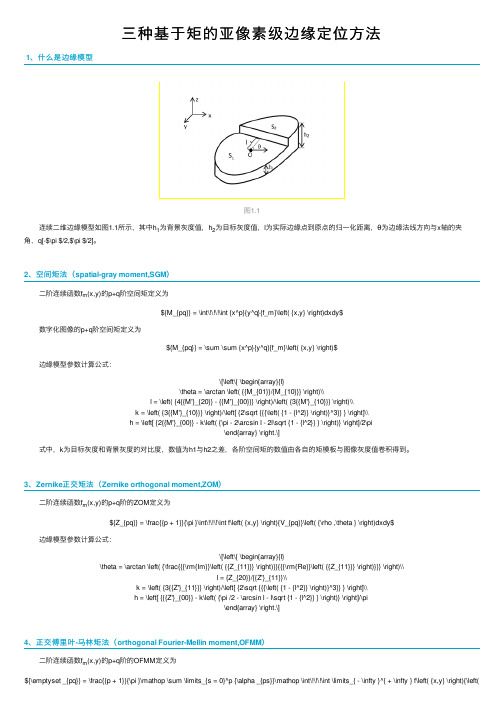
三种基于矩的亚像素级边缘定位⽅法1、什么是边缘模型图1.1连续⼆维边缘模型如图1.1所⽰，其中h1为背景灰度值，h2为⽬标灰度值，l为实际边缘点到原点的归⼀化距离，θ为边缘法线⽅向与x轴的夹⾓，q[-$\pi $/2,$\pi $/2]。

2、空间矩法（spatial-gray moment,SGM）⼆阶连续函数f m(x,y)的p+q阶空间矩定义为${M_{pq}} = \int\!\!\!\int {x^p}{y^q}{f_m}\left( {x,y} \right)dxdy$数字化图像的p+q阶空间矩定义为${M_{pq}} = \sum \sum {x^p}{y^q}{f_m}\left( {x,y} \right)$边缘模型参数计算公式：\[\left\{ \begin{array}{l}\theta = \arctan \left( {{M_{01}}/{M_{10}}} \right)\\l = \left( {4{{M'}_{20}} - {{M'}_{00}}} \right)/\left( {3{{M'}_{10}}} \right)\\k = \left( {3{{M'}_{10}}} \right)/\left[ {2\sqrt {{{\left( {1 - {l^2}} \right)}^3}} } \right]\\h = \left[ {2{{M'}_{00}} - k\left( {\pi - 2\arcsin l - 2l\sqrt {1 - {l^2}} } \right)} \right]/2\pi\end{array} \right.\]式中，k为⽬标灰度和背景灰度的对⽐度，数值为h1与h2之差，各阶空间矩的数值由各⾃的矩模板与图像灰度值卷积得到。

3、Zernike正交矩法（Zernike orthogonal moment,ZOM）⼆阶连续函数f m(x,y)的p+q阶的ZOM定义为${Z_{pq}} = \frac{{p + 1}}{\pi }\int\!\!\!\int f\left( {x,y} \right){V_{pq}}\left( {\rho ,\theta } \right)dxdy$边缘模型参数计算公式：\[\left\{ \begin{array}{l}\theta = \arctan \left( {\frac{{{\rm{Im}}\left( {{Z_{11}}} \right)}}{{{\rm{Re}}\left( {{Z_{11}}} \right)}}} \right)\\l = {Z_{20}}/{{Z'}_{11}}\\k = \left( {3{{Z'}_{11}}} \right)/\left[ {2\sqrt {{{\left( {1 - {l^2}} \right)}^3}} } \right]\\h = \left[ {{{Z'}_{00}} - k\left( {\pi /2 - \arcsin l - l\sqrt {1 - {l^2}} } \right)} \right]/\pi\end{array} \right.\]4、正交傅⾥叶-马林矩法（orthogonal Fourier-Mellin moment,OFMM）⼆阶连续函数f m(x,y)的p+q阶的OFMM定义为${\emptyset _{pq}} = \frac{{p + 1}}{\pi }\mathop \sum \limits_{s = 0}^p {\alpha _{ps}}\mathop \int\!\!\!\int \limits_{ - \infty }^{ + \infty } f\left( {x,y} \right){\left({x + jy} \right)^{\frac{{s - p}}{2}}}{(x - jy)^{\frac{{s + p}}{2}}}dxdy$边缘模型参数计算公式：\[\left\{ \begin{array}{l}\theta = \arctan \left[ { - \frac{{{\rm{Im}}\left( {2({\phi _{01}} + {\phi _{11}})} \right)}}{{{\rm{Re}}\left( {2({\phi _{01}} + {\phi _{11}})} \right)}}} \right]\\ l = \frac{3}{5}\left( {\frac{{4{\phi _{10}} + {\phi _{20}}}}{{2{{\phi '}_{01}} + {{\phi '}_{11}}}}} \right)\\k = \left( {2{{\phi '}_{01}} + {{\phi '}_{11}}} \right)/\left[ {2\sqrt {{{\left( {1 - {l^2}} \right)}^3}} } \right]\\h = \left[ {{{\phi '}_{00}} - k\left( {\arcsin \sqrt {1 - {l^2}} - l\sqrt {1 - {l^2}} } \right)} \right]/\pi\end{array} \right.\]由于OFMM和ZOM法所求的q和l相同，⽽最终亚像素级边缘定位结果仅仅与q和l有关，因此，OFMM和ZOM法的亚像素级边缘定位结果完全⼀致，另外三种⽅法获得的边缘⾓度q相同。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

摘
要：了高微操作系统的装配精度，出了一种新型的亚像素边缘检测和中心定位算法。应用Ｃｎｙ为提提ａｎ算子提取了微零件
在像素级的边缘。应用Ｚｍｉｅｅｋ矩对微零件进行亚像素级的边缘定位。采用最小二乘椭圆拟合定位微零件的中心位置。实验结
Ｃｏｕｅｎｉｅｒｎｎｐｉｔｎ，０１４（７：４ —５．ｍｐｔｒＥｇｎｅｉｇａｄＡｐｌａｏｓ２１，７１）１８１０ｃｉ
ＡｂｔａｔＩｒｅｏｉｒｖｈｅｏｕｉｎａｄａｃｒｃｆｍｉｏａｓｍｂｙｓｓｍｓａｎｖｌｓｂｐｘｌｅｇｅｃｏｎｓｃ：ｎｏｄｒｔｍｐｏｅｔｅｒｓｌｔｃｕａｙｏｃ－ｓｒｏｎｒｅｌｙｔ，ｏｅｕ－ｉｅｄｅｄｔｔｎａｄｅ－ｅｉ
ｏｅｍｉｒｐｒｓＴｅ，ｈｅｇｏｃｏａｔａｉｅｌｖｌｉｘｒｃｅｓｎｎｙｐｒｔｒｅｏｄｙ，ｍｉｅｏｔｏｏｆｔｃｏａｔ．ｈｎｔｅｄｅｆｍｉｒｐｒｓｔｐｘｌｅｅｅｔｔｄｕｉｇＣａｎｏｅａｏ．ｃｎｌＺｅｋｒｇ — ｈｓａＳｈｎｌａｍｏｎｓｒｓｄｔｅｏａｅｈｅｅｇｆｍｉｒｓｚａｔｔｓｂ．ｉｅｌｖ１ｓｌｌａｔｑａｅｅｌｓｆｔｇｓｐｌｄｍｅｔａｅｕｅｏｒｌｃｔｔｄｅｏｃｏｉｅｐｒａｕ・ｘｌｅｅ．ｔｐＬａｙ，ｅｓｓｕｒｓｌｐｅｉｉｉｉｔｎａｐｉｅｔｏｉｏｅｃｎｅ．ｐｒｎｅｕｔｈｗｈｈｌｏｔｍａｃｉｖｉｈｒｌｃｔｎａｃｒｃｎｏｓｍｅｌｓｍｅｏｐｓｔｎｔｅｔｒｉｈＥｘｅｍｅｒｓｌｓｏｔａｔｅａｇｒｈｃｎａｈｅｅｈｇｅｏａｉｃｕａｙａｄｃｎｕｅｓｔ．ｉｔｓｔｉｏｉＫｅｒｓｓｂｉｅｄｅｅｔａｔｎ；ｅｉｅｍｏｎｓｌａｔｓｕｅｌｐｅｆｔｎｃｎｅｏａｉｎ；ｃｏｎｉｕａｉｎｙｗｏｄ：ｕｐｘｌｅｇｘｒｃｉＺｍｋｏｍｅｔ；ｓｑａｓｅｌｓｉｇ；ｅｔｒｌｃｔｅｒｉｉｏｍｉｒｍａｐｌｔｏ
果表明，该算法能够实现更高的定位精度和消耗更少的时间。
关键词：亚像素边缘提取；ｅｋ￣；Ｚｍｉｅ最小二乘椭圆拟和；中心定位；微操作ＤＯ：０３７／ｉｓ，０－３１０１１．０文章编号：０２８３（０１１ —１８０文献标识码：中图分类￣：Ｐ４Ｉ１．７８．ｎ１２８３．１．７０ｊｓ．０２４１０－３１２１）７０４－３Ａ＇２Ｔ
Ｃｍｕｅｎ／ｅ／ｄｐ／ａ／ｎ计算机工程与应用ｏｐｔＥｇｎｒｇａＡｐ／ｔｓｒｅｎｎｃｏ
Ｚｒｉｅｅｎｋ矩和最小二乘椭圆拟合的亚像素边缘提取
祝宏曾祥进，
Ｚｏｇ，ＥＧａｇ￣ＨＵＨｎ。ＮＸｉｉＺｎ
ｃｎｅｌｃｌａｉｎｌｏｔｍｏｍｉｒ－ａｔｉｒｓｎｅ．ｉｓｙ，ｈｎａｉｎｍｏｎｓｒｍｐｏｅｏｅｃｂｔｅｆａｕｅｅｔｒｏａｉｔａｇｒｈｆｒｚｏｉｃｏｐｒｓｓｅｅｔｄＦｒｔｔｅｉｖｒｔｐｌａｍｅｔａｅｅｌｙｄｔｄｓｒｅｈｅｔｒｉ
ＺＨｏｇＺＮＸｉｎｊ．ｕ－ｉｅｄｅｄｔｃｉｎａｇｒｔｍｆＺｒｉｅｍｏｎｓａｄｌａｔｑａｅｌｐｅｆｔｇＨＵｎ，ＥＧａｇｉＳｂ．ｘｌｅｇｅｅｔｌｏｉｎｐｏｈｏｅｎｋｍｅｔｎｅｓ．ｕｒｓｅｌｓｔｎ．－ｓｉｉｉ
ｌ中科技大学文华学院信息科学与技术学部，华武汉４０７３０４
２华中科技大学控制科学与工程系，．武汉４０３０４
１￣．ｒｅｔｆＩｆｍｔｎＳｉｃｎｏａｉｃｎｅ＆Ｔｍｏｇ，ｕｚｏｇＵｉｅｉｆＳｉｃ＆ＴｃｎｌｙＷｅｈａＣｌｇ，ｈｎ４０７，ｈａｏｎｒｏｅ￣ｌｙＨａｎｎｒｔｏｃｎｏｈｖｓｙｅｅｅｈｏｇｎｕｏｌｅＷｕａ３０４Ｃｉｏｅｎ
２ＤｅａｔｎｆＣｏｔｏｃｅｃｎｇｎｅｉｇ，ａｈｎｉｅｓｔｆＳｉｎｅａｄＴｃｎｌｇＷｕａ３０４，ｉａ．ｐｒｍｅｔｏｎｒｌＳｉｎｅａｄＥｎｉｅｒｎＨｕｚｏｇＵｎｖｒｉｏｃｅｃｎｅｈｏｏｙ，ｈｎ４０７Ｃｈｎｙ