2012年上海市初中数学教学质量抽样分析试卷答案及评分标准

合集下载

上海市2012年中考数学抽样调查试卷(含参考答案)

上海市初中数学教学质量抽样分析试卷 (2012.5.18)一、选择题：（本大题共6题，每题4分，满分24分）【下列各题的四个选项中，有且只有一个选项是正确的，选择正确项的代号并填涂在答题纸的相应位置上】1．如果点P 与点Q （-2,3）关于x 轴对称，那么点P 的坐标是（）（A ）（2,3）；（B ）（-2,3）；（C ）（2,-3）；（D ）（-2,-3）． 2．在下列二次根式中，与a 同为同类二次根式的是（）（A ）a 2；（B ）23a ；（C ）3a ；（D ）4a ．3．如果从1、2、3这三个数字中任意选取两个数字，组成一个两位数，那么这个两位数是素数的概率等于（）（A ）21；（B ）31；（C ）41；（D ）61． 4．已知某班学生上学时乘车、步行、骑车的人数分布条形图和扇形图如图所示（两图都不完整），那么下列结论中错误的是（）（A ）该班总人数为40人；（B ）骑车人数占总人数的20%；（C ）步行人数为30人；（D ）乘车人数是骑车人数的2.5倍．5．如图，如果在高为2m ，坡度为1∶2的楼梯上铺地毯，那么地毯的长度至少应截取（）（A ）2m ；（B ）6m ；（C ）52m ；（D ）()526+m ．6．已知：⊙O 1、⊙O 2的半径分别是3和4，那么下列叙述中，一定正确的是（）（A ）当123O O =时，⊙O 1与⊙O 2相交；（B ）当121O O =时，⊙O 1与⊙O 2内含；（C ）当122O O <时，⊙O 1与⊙O 2没有公共点；（D ）当126O O >时，⊙O 1与⊙O 2有两个公共点．二、填空题：（本大题共12题，每题4分，满分48分）【请将结果直接填入答题纸的相应位置上】 7．计算：32a a ⋅= ．8．在实数范围内分解因式：822-x = ．9．不等式组12,2(2)32x x x ->-⎧⎨+>+⎩的解集是．10．如果x =6是方程12)(23=--t x x 的根，那么t = ． 11．已知函数12)(+=x x f ，那么=)2(f ． 12．已知一次函数y =kx +b （k ≠0）的图像经过点（0,1），且y 随x 的增大而增大，请你写出一个符合上述条件的一次函数解析式，这个解析式可以是．13．面积为300平方米的一块长方形绿地，长比宽多10米．如果设长方形绿地的宽为x 米，（第5题图）208骑车步行30% 乘车50%（第4题图）那么可列方程为．14．已知一组数据24、27、19、13、x 、12的中位数是21，那么x 的值等于． 15．正八边形的中心角等于度．16．如图，已知在△ABC 中，点D 在边BC 上，且BD ︰DC =1︰2．如果AB a =，AC b =，那么AD = （结果用含a 、b 的式子表示）．17．已知点E 在面积为4的平行四边形ABCD 的边上运动，那么使△ABE 的面积为1的点E 共有个．18．已知直线l 经过正方形ABCD 的顶点A ，过点B 和点D 分别作直线l 的垂线BM 和DN ，垂足分别为点M 、点N ，如果BM =5，DN =3，那么MN = ．三、解答题：（本大题共7题，满分78分） 19．（本题满分10分）计算：232)31(23)3(21+++----π．20．（本题满分10分）解方程：121442--=-x x ． 21．（本题满分10分，其中第（1）小题4分，第（2）小题6分）已知：如图，⊙O 的半径为5，弦AB 的长等于8，OD ⊥AB ，垂足为点D ，DO 的延长线与⊙O 相交于点C ，点E 在弦AB 的延长线上，CE 与⊙O 相交于点F ，54cos =C ．求：（1）CD 的长；（2）EF 的长．ABCD（第16题图）（第21题图）22．（本题满分10分，其中第（1）小题4分，第（2）小题6分）我们知道：任意一个有理数与无理数的和为无理数，任意一个不为零的有理数与一个无理数的积为无理数，而零与无理数的积为零．由此可得：如果ax +b =0，其中a 、b 为有理数，x 为无理数，那么a =0且b =0．运用上述知识，解决下列问题：（1）如果032)2(=++-b a ，其中a 、b 为有理数，那么a = ，b = ；（2）如果5)21()22(=--+b a ，其中a 、b 为有理数，求a +2b 的值． 23．（本题满分12分，其中第（1）小题4分，第（2）小题8分）已知：如图，在梯形ABCD 中，AD ∥BC ，点E 、F 分别是边BC 、CD 的中点，直线EF 交边AD 的延长线于点M ，交边AB 的延长线于点N ，联结BD ．（1）求证：四边形DBEM 是平行四边形；（2）联结CM ，当四边形ABCM 为平行四边形时，求证：MN =2DB ．24．（本题满分12分，其中第（1）小题5分，第（2）小题7分）已知在直角坐标系xOy 中，二次函数c bx x y ++-=2的图像经过点A （-2,3）和点B （0,-5）．（1）求这个二次函数的解析式；（2）将这个函数的图像向右平移，使它再次经过点B ，并记此时函数图像的顶点为M ．如果点P 在x 轴的正半轴上，且∠MPO =∠MBO ，求∠BPM 的正弦值．AB C D EFMN （第23题图）25．（本题满分14分，其中第（1）小题4分，第（2）小题6分，第（3）小题4分）已知：在Rt △ABC 中，∠C =90°，AC =4，∠A =60°，CD 是边AB 上的中线，直线BM ∥AC ，E 是边CA 延长线上一点，ED 交直线BM 于点F ，将△EDC 沿CD 翻折得△DC E '，射线E D '交直线BM 于点G ．（1）如图1，当CD ⊥EF 时，求BF 的值；（2）如图2，当点G 在点F 的右侧时；①求证：△BDF ∽△BGD ；②设AE =x ，△DFG 的面积为y ，求y 关于x 的函数解析式，并写出x 的取值范围；（3）如果△DFG 的面积为36，求AE 的长．（第25题图1）M（第25题图2）（第25题备用图）BDM上海市初中数学教学质量抽样分析试卷参考答案及评分说明一、选择题：1．D ； 2．C ； 3．A ； 4．C ； 5．B ； 6．A ．二、填空题：7．a 5； 8．2(x +2)(x -2)； 9．-1<x <2； 10．3； 11．5； 12．y =x +1等； 13．x (x +10)=300； 14．23；15．45；16．3132+； 17．2； 18．2或8．三、解答题：19．解：原式=）（3223231-++-+……………………………………………（各2分）=3．……………………………………………………………………………（2分）20．解：去分母，得4242+-+=x x ．…………………………………………………（3分）整理，得 022=--x x ．………………………………………………………（2分）解得 x 1=-1，x 2=2．………………………………………………………（4分）经检验：x 1=-1是原方程的根，x 2=2是增根．…………………………………（1分） ∴原方程的根为x =-1．21．解：（1）联结OA ．∵OD ⊥AB ，AB =8，∴AD =4．…………………………………………………（2分） ∵OA =5，∴OD =3．………………………………………………………………（1分） ∵OC =5，∴CD =8．………………………………………………………………（1分）（2）作OH ⊥CE ，垂足为点H ．∵OC =5，54cos =C ，∴CH =4．…………………………………………………（2分） ∵OH ⊥CE ，∴CF =2CH =8．……………………………………………………（1分）又∵CD =8，54cos =C ，∴CE =10．……………………………………………（2分） ∴EF =2．……………………………………………………………………………（1分）22．解：（1）2，-3；……………………………………………………………………（各2分）（2）整理，得0)52(2)(=--++b a b a ．……………………………………（2分）∵a 、b 为有理数，∴⎩⎨⎧=--=+.052,0b a b a …………………………………………（2分）解得⎪⎩⎪⎨⎧-==.35,35b a ……………………………………………………………………（1分）323．证明：（1）∵CE =BE ，CF =DF ，∴EF ∥BD ．………………………………………（2分）又∵AD ∥BC ，∴四边形DBEM 是平行四边形．……………………………（2分）（2）∵四边形ABCM 为平行四边形，∴AB =CM ，AB ∥CM ．………………（2分）∴CEBECM BN =．…………………………………………………………………（1分） ∵BE =CE ，∴BN =CM ．…………………………………………………………（1分） ∴AB =BN ．………………………………………………………………………（1分） ∵EF ∥BD ，∴ANABMN DB =．……………………………………………………（2分） ∴MN =2DB ．……………………………………………………………………（1分）24．解：（1）由题意，得⎩⎨⎧=-+--=.5,243c c b ………………………………………………（2分）解得⎩⎨⎧-=-=.5,6c b ……………………………………………………………………（2分）∴所求二次函数的解析式为562---=x x y ．………………………………（1分）（2）二次函数562---=x x y 图像的顶点坐标为（-3,4）．……………………（1分） ∴图像平移后顶点M 的坐标为（3,4）．………………………………………（1分）由题意∠MPO =∠MBO ，可得∠PMB =∠POB =90°．设点P 的坐标为（x ,0）． ∴2222225934)3(+=+++-x x ．…………………………………………（1分）解得x =15．………………………………………………………………………（1分） ∴点P 的坐标为（15,0）．………………………………………………………（1分） ∴103=BM ，105=PB ．………………………………………………（1分） ∴53sin =∠BPM ．………………………………………………………………（1分）另解：二次函数562---=x x y 图像的顶点坐标为（-3,4）．………………（1分） ∴图像平移后顶点M 的坐标为（3,4）．………………………………………（1分）由题意∠MPO =∠MBO ，可得∠PMB =∠POB =90°．过M 点作x 轴、y 轴的垂线，垂足分别为点H 、K ．在Rt △BKM 中，由题意，得tan ∠MBK =1∶3．在Rt △MPH 中，tan ∠MPH =tan ∠MBK =1∶3．………………………………（1分） ∴PH =12．∴OP =15．………………………………………………………………………（1分） ∴点P 的坐标为（15,0）．………………………………………………………（1分） ∴103=BM ，105=PB ．………………………………………………（1分）525．（1）解：∵∠ACB =90°，AD =BD ，∴CD =AD =BD ．………………………………（1分）∵∠BAC =60°，∴∠ADC =∠ACD =60°，∠ABC =30°，AD =BD =AC ． ∵AC =4，∴AD =BD =AC =4．……………………………………………………（1分） ∵BM ∥AC ，∴∠MBC =∠ACB =90°．又∵CD ⊥EF ，∴∠CDF =90°． ∴∠BDF =30°． ∴∠BFD =30°． ∴∠BDF =∠BFD ．∴BF =BD =4．……………………………………………………………………（2分）（2）①证明：由翻折，得CD E '∠=∠ACD =60°，∴∠ADC =CD E '∠．∴E C '∥AB ．∴D E C '∠=∠BDG ．……………………………………………………………（1分） ∵BM ∥AC ，∴∠CED =∠BFD ．又∵D E C '∠=∠CED ，∴∠BDG =∠BFD ．……………………………………（1分） ∵∠DBF =∠GBD ，∴△BDF ∽△BGD ．………………………………………（1分）②解：由△BDF ∽△BGD ，得BGBDBD BF =．由AE =x ，可得BF =x ．∴BGx 44=． ∴xBG 16=．……………………………………………………………………（1分）又∵点D 到直线BM 的距离为32， ∴32)16(21⋅-=x xy ，即x x y 3316-=．………………………………（1分）定义域为0<x <4．………………………………………………………………（1分）（3）解：（i ）当点G 在点F 的右侧时，由题意，得x x331636-=．整理，得01662=-+x x ．解得x 1=2，x 2=-8（不合题意，舍去）．………………………………………（2分）（ii ）当点G 在点F 的左侧时，由题意，得xx 316336-=．整理，得01662=--x x ．解得x 3=8，x 4=-2（不合题意，舍去）．………………………………………（2分）综上所述AE 的值为2或8．。

上海数学计算题评分标准

上海数学计算题评分标准
2012年上海市初中毕业统一学业考试数学卷答案要点于评分标准说明：
1、解答只列出试题的一种或几种解法，如果考生的解法与所列解法不同，可参照解答中评分标准相应评分；
2、第一、二大题若无特别说明，每题评分只有满分或零分；
3、第三大题中各题右端所注分数，表示考生正确做对这一步应得分数；
4、评阅试卷，要坚持每题评阅到底，不能因考生解答中出现错误而中断对本题的评阅，如果考生的解答在某一步出现错误，影响后继部分而未改变本题的内容和难度，视影响的程度决定后续部分的给分，但原则上不超过后继部分应得分数的一半；
5、评分时，给分或扣分均已1分为基本单位。

第1页共1页。

2012年上海市初中毕业统一学业考试数学考试试卷评析

（２）在第１８（１）、２１（２）、２４（３）、２５（３）题
中，至少有９处用到勾股定理，这在近年来的上海数学试卷中是少见的．
３一
数学教学
２０１３年第３期
（３）２０１２年上海数学试卷中，共有８个图形，其中有４个图形与直角三角形有关．３．图形运动要求较往年低．第２５题中的动点无实质性的意义．
学业考试数学考试试卷ｆ以下简称２０１２年上海数学试卷），有了一些想法，下面从七个方面对２０１２年上海数学试卷进行评析．试题的知识范围
一
图１
一
、
首先，对２０１２年上海数学试卷所涉及的知识内容进行分析，按大知识块分类，试卷中数与式占１７．３３％，一元一次方程与不等式
三角比占４．６７％，圆占７．３３％．可以看出，２０１２年上海数学试卷重视对教材内容的考查．重点知识重点考查，没有超过《考试手册》所规定的范围．这与近几年的上
Ｃ
图２
四边形ＢＣＥＤ的面积＞１２，不可能会有四边形ＢＣＥＤ的面积为５．
１．２０１２年上海数学试卷考查了３４个主要知识点ｆ《考试手册》中列出初中数学共有９９个主要知识点），覆盖面应该是基本合理的，这与近几年上海数学试卷的情况相同．２．试卷存在个别知识点反复考查的问题．

2012年上海市中考数学试题及答案(解析版)

ACDB EO2012年上学期第一次学力检测九年级数学试题卷温馨提示：请仔细审题，细心答题，相信你一定会有出色的表现！参考公式：二次函数y =ax 2+bx +c 图象的顶点坐标是)44,2(2ab ac a b --．一、选择题（本大题共10小题，每小题3分，共30分。

每小题都有四个备选答案，请把你认为正确的一个答案的代号填在答题纸的相应位置）． 1、13-的倒数是( )A ．3B ．-3C ．13D ．13-2、今年2月，随着第四条水泥熟料生产线的点火投产，浙江尖峰水泥熟料已达年产6000000吨，用科学记数法可记作（）A ．80.610⨯吨 B ． 70.610⨯吨 C ． 6610⨯吨 D ． 7610⨯吨 3、下面简单几何体的左视图是（）4、已知同一平面内的⊙O 1、⊙O 2的直径分别为6cm 、2cm ，且O 1O 2＝4cm ，则两圆的位置关系为（） A ．外切 B ．内切 C ．相交 D ．以上都不正确5、抛物线23(2)32y x =---的顶点坐标是( )A. (2, -3)B. (2，3 )C. (-2, 3 )D. (-2，-3 )6、一次函数5+-=x y 图象与反比例函数xy 6=图象的交点情况是( ) A. 只有一个交点，坐标是（2，3） B. 只有一个交点，坐标是（－1，6） C. 有两个交点，坐标是（2，3）、（3，2） D. 没有交点 7、如图，AB 是O ⊙的直径，弦CD AB ⊥于点E ，连结OC ，若5OC =，8CD =，则tan COE ∠=（） A ．35B ．45C ．43D ．34 8、将半径为30cm 的圆形铁皮，做成三个相同的圆锥容器的侧面（不浪费材料，不计接缝处的材料损耗），那么每个圆锥容器的底面半径为 ( )A ．10cmB ．20cmC ．30cmD ．60cm9、在物理实验课上，小明用弹簧秤将铁块A 悬于盛有水的水槽中（如图），然后匀速向上提起，直至铁块完全露出水面一定高度，则能反映弹簧秤的读数y （单位：N ）与铁块被提起的高度x （单位：cm ）之间的函数关系的图象大致是( )A ．B ．C ．D ．正面Ｏy x Ｏy x Ｏy xＯyx10．如图，在Rt △ABC 中，AB AC =，D 、E 是斜边BC 上两点，且∠DAE =45°，将△ADC 绕点A 顺时针旋转90︒后，得到△AFB ，连接EF ，下列结论：（） ①△AED ≌△AEF ； ②△ABE ∽△ACD ； ③BE DC DE +=； ④222BE DC DE += 其中正确的是 A ．②④； B ．①④；C ．②③；D ．①③．二、填空题（本大题共6题，每题4分，共24分．请把答案填在答题纸中相应的横线上） 11、分解因式：x 2－9＝．12、某校组织了一次数学竞赛活动，其中有4名学生的平均成绩为80分，另外有6名学生的平均成绩为90分，则这10名学生的平均成绩为 _________ 分．13、已知一次函数的图象经过点（0，1），且满足y 随x 的增大而增大，则该一次函数的解析式可以为 _________ ．14. 如图是圆锥的主视图(单位：cm)，则圆锥的表面积为________cm 2（结果保留π）. 15、如图所示，将边长为2的等边三角形沿x 轴正方向连续翻转2012次，依次得到点P 1，P 2，P 3…P 2012．则点P 2012的坐标是 _________ ．16、如图，矩形OABC 的两边OA ，OC 在坐标轴上，且OC =2OA ，M ，N 分别为OA ，OC 的中点，BM 与AN 交于点E ，且四边形EMON 的面积为2，（1）△ABE 的面积是．（2）经过点B 的双曲线的解析式为三、解答题（本题有8小题，第17~19题每题6分，第20、21题每题8分，第22、23题每题10分，第24题12分，共66分）（2）解方程： 12111xx x -=--17、（1）计算：18、如图，在ΔABC 和ΔDCB 中，AC 与BD 相交于点O ， AB = DC ，AC = BD. (1)求证: ΔABC ≌ΔDCB ；(2) Δ0BC 的形状是。

2012年上海市中考数学试卷分析

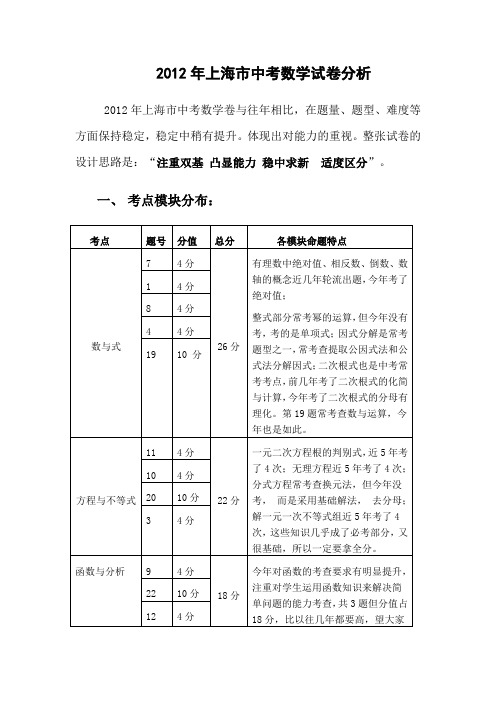
2012年上海市中考数学试卷分析2012年上海市中考数学卷与往年相比，在题量、题型、难度等方面保持稳定，稳定中稍有提升。

体现出对能力的重视。

整张试卷的设计思路是：“注重双基凸显能力稳中求新适度区分”。

一、考点模块分布：二、命题特点：第一、面向全体，加强对基础知识的考查通过前面考点模块分析，明显看出整份试卷在填空、选择、解答题中设置了大量的基础题,约占整卷的80%，主要考查数学概念、性质和解题方法，这既涵盖了义务教育阶段必须掌握的数学课程的核心知识点，又兼顾毕业和升学两方面功能的体现，必将对今后的教学起着良好的导向作用。

第二、稳中求变，注重对思维能力的考查。

试卷以基本题为载体，考查了不同层次学生的数学思维能力。

1．本卷与前几年相比，在试题结构设置中有明显调整，以往第22题是统计综合题，分3小题分布，现在设置成一次函数的应用题目，重在考查学生观察分析和逻辑思维的能力。

2.“信息题”出现，第17题是考查三角形重心的考题，但它是以给出新的定义来考查的信息题，这在近几年上海中考卷中是没有的，这反映出重视对学生接受新概念等信息能力的考查。

3. 压轴题（第25题）是最难的认识打破了，今年最后两题的难度设置不同与以往，如第25题反而略易于第24题，且没有考查分类讨论的思想。

这就要我们改变对最后两题的认识，其实这两题难度相当，迎考试复习时要平均用力，不可轻视第24题，同时也影射出上海市中考数学开始重视对函数知识的考查，这在难度上和分值上都有反映，这便于和高中数学接轨，有利于进一步的学习。

第三、合理铺设试卷难度。

试卷结构上，基础题、中档题、难题仍按8：1：1设置，这样配比既保证较高的及格率，又兼顾适度区分，既体现出对双基的重视，也体现出对思维过程中分析能力和计算能力的较高要求。

24．如图，在平面直角坐标系中，二次函数y=ax2+6x+c的图象经过点A（4，0）、B（-1，0），与y轴交于点C，点D在线段OC上，OD=t，点E在第二象限，∠ADE=90°，tan∠DAE= 1/2 ，EF⊥OD，垂足为F．（1）求这个二次函数的解析式；（2）求线段EF、OF的长（用含t的代数式表示）；（3）当∠ECA=∠OAC时，求t的值．考点：相似三角形的判定与性质；待定系数法求二次函数解析式；全等三角形的判定与性质；三角比；等量代换；勾股定理．分析：（1）已知点A 、B 坐标，用待定系数法求抛物线解析式即可；（2）关键是证明△EDF ∽△DAO ，然后利用相似三角形对应边的比例关系以及三角比的定义和等量代换求解；（3）如解答图，通过作辅助线构造一对全等三角形：△CAG ≌△OCA ，得到CG 、AG 的长度；然后利用勾股定理求得AE 、EG 的长度（用含t 的代数式表示）；最后在Rt △ECF 中，利用勾股定理，得到关于t 的无理方程，解方程求出t 的值．解答：（1）二次函数y=ax 2+6x+c 的图象经过点A （4，0）、B （-1，0），∴ 16a+6×4+c=0 a-6+c=0 ，解得 a=-2， c=8 ∴这个二次函数的解析式为：y=-2x 2+6x+8；（2）∵∠EFD=∠EDA=90°∴∠DEF+∠EDF=90°，∠EDF+∠ODA=90°，∴∠DEF=∠ODA ∴△EDF ∽△DAO ∴EF/ DO =ED /DA ． ∵ED /DA =tan ∠DAE=21， ∴EF/ DO =21， ∴EF/ t =21 ，∴EF=21t ．同理DF/ OA =ED/ DA ， ∴DF=2，∴OF=t-2．（3）∵抛物线的解析式为：y=-2x 2+6x+8；∴C （0，8），OC=8．如图，连接EC 、AC ，过A 作EC 的垂线交CE 于G 点． ∵∠ECA=∠OAC ，∴∠OAC=∠GCA （等角的余角相等）；在△CAG 与△OCA 中， ∠OAC=∠GCA AC=CA ∠ECA=∠OAC ，∴△CAG ≌△OCA ，∴CG=4，AG=OC=8．如图，过E 点作EM ⊥x 轴于点M ，则在Rt △AEM 中， ∴EM=OF=t-2，AM=OA+AM=OA+EF=4+21t ，由勾股定理得： ∵AE 2=AM 2+EM 2=(4+21t)2+(t-2)2；在Rt △AEG 中，由勾股定理得：∴EG= 22AG AE - = ()22282214--+⎪⎭⎫ ⎝⎛+t t =44452-t ∵在Rt △ECF 中，EF=21t ，CF=OC-OF=10-t ，CE=CG+EG= 44452-t +4 由勾股定理得：EF 2+CF 2=CE 2，即(21t)2+(10-t)2= （44452 t +4）2，解得t1=10（不合题意，舍去），t2=6， ∴t=6．点评：本题考查了相似三角形的判定与性质、锐角三角比、全等三角形的判定与性质、勾股定理和待定系数法求二次函数解析式等多个知识点，难度较大．第（3）问中，涉及到无理方程的求解，并且计算较为复杂，注意不要出错．通过试卷的分析对教师和学生有很好的借鉴作用。

答案

上海市初中数学教学质量抽样分析试卷参考答案及评分说明一、选择题：1．D ； 2．C ； 3．A ； 4．C ； 5．B ； 6．A ．二、填空题：7．a 5； 8．2(x +2)(x -2)； 9．-1<x <2； 10．3； 11．5； 12．y =x +1等；13．x (x +10)=300；14．23； 15．45； 16．b a 3132+； 17．2； 18．2或8．三、解答题：19．解：原式=）（3223231-++-+……………………………………………（各2分） =3．……………………………………………………………………………（2分）20．解：去分母，得4242+-+=x x ．…………………………………………………（3分）整理，得 022=--x x ．………………………………………………………（2分）解得 x 1=-1，x 2=2．………………………………………………………（4分）经检验：x 1=-1是原方程的根，x 2=2是增根．…………………………………（1分） ∴原方程的根为x =-1．21．解：（1）联结OA ．∵OD ⊥AB ，AB =8，∴AD =4．…………………………………………………（2分） ∵OA =5，∴OD =3．………………………………………………………………（1分） ∵OC =5，∴CD =8．………………………………………………………………（1分）（2）作OH ⊥CE ，垂足为点H ．∵OC =5，54cos =C ，∴CH =4．…………………………………………………（2分）∵OH ⊥CE ，∴CF =2CH =8．……………………………………………………（1分）又∵CD =8，54cos =C ，∴CE =10．……………………………………………（2分）∴EF =2．……………………………………………………………………………（1分）22．解：（1）2，-3；……………………………………………………………………（各2分）（2）整理，得0)52(2)(=--++b a b a ．……………………………………（2分）∵a 、b 为有理数，∴⎩⎨⎧=--=+.052,0b a b a …………………………………………（2分）解得⎪⎩⎪⎨⎧-==.35,35b a ……………………………………………………………………（1分） ∴352-=+b a ．…………………………………………………………………（1分）23．证明：（1）∵CE =BE ，CF =DF ，∴EF ∥BD ．………………………………………（2分）又∵AD ∥BC ，∴四边形DBEM 是平行四边形．……………………………（2分）（2）∵四边形ABCM 为平行四边形，∴AB =CM ，AB ∥CM ．………………（2分） ∴CE BECM BN=．…………………………………………………………………（1分）∵BE =CE ，∴BN =CM ．…………………………………………………………（1分） ∴AB =BN ．………………………………………………………………………（1分） ∵EF ∥BD ，∴AN ABMN DB=．……………………………………………………（2分）∴MN =2DB ．……………………………………………………………………（1分）24．解：（1）由题意，得⎩⎨⎧=-+--=.5,243c c b ………………………………………………（2分）解得⎩⎨⎧-=-=.5,6c b ……………………………………………………………………（2分）∴所求二次函数的解析式为562---=x x y ．………………………………（1分）（2）二次函数562---=x x y 图像的顶点坐标为（-3,4）．……………………（1分）∴图像平移后顶点M 的坐标为（3,4）．………………………………………（1分）由题意∠MPO =∠MBO ，可得∠PMB =∠POB =90°．设点P 的坐标为（x ,0）．∴2222225934)3(+=+++-x x ．…………………………………………（1分）解得x =15．………………………………………………………………………（1分） ∴点P 的坐标为（15,0）．………………………………………………………（1分） ∴103=BM ，105=PB ．………………………………………………（1分） ∴53sin =∠BPM ．………………………………………………………………（1分）另解：二次函数562---=x x y 图像的顶点坐标为（-3,4）．………………（1分） ∴图像平移后顶点M 的坐标为（3,4）．………………………………………（1分）由题意∠MPO =∠MBO ，可得∠PMB =∠POB =90°．过M 点作x 轴、y 轴的垂线，垂足分别为点H 、K ．在Rt △BKM 中，由题意，得tan ∠MBK =1∶3．在Rt △MPH 中，tan ∠MPH =tan ∠MBK =1∶3．………………………………（1分） ∴PH =12．∴OP =15．………………………………………………………………………（1分） ∴点P 的坐标为（15,0）．………………………………………………………（1分） ∴103=BM ，105=PB ．………………………………………………（1分）∴53sin =∠BPM ．………………………………………………………………（1分）25．（1）解：∵∠ACB =90°，AD =BD ，∴CD =AD =BD ．………………………………（1分）∵∠BAC =60°，∴∠ADC =∠ACD =60°，∠ABC =30°，AD =BD =AC ．∵AC =4，∴AD =BD =AC =4．……………………………………………………（1分） ∵BM ∥AC ，∴∠MBC =∠ACB =90°．又∵CD ⊥EF ，∴∠CDF =90°．∴∠BDF =30°．∴∠BFD =30°．∴∠BDF =∠BFD ．∴BF =BD =4．……………………………………………………………………（2分）（2）①证明：由翻折，得CD E '∠=∠ACD =60°，∴∠ADC =CD E '∠．∴E C '∥AB ．∴D E C '∠=∠BDG ．……………………………………………………………（1分） ∵BM ∥AC ，∴∠CED =∠BFD ．又∵D E C '∠=∠CED ，∴∠BDG =∠BFD ．……………………………………（1分） ∵∠DBF =∠GBD ，∴△BDF ∽△BGD ．………………………………………（1分） ②解：由△BDF ∽△BGD ，得BG BD BD BF =．由AE =x ，可得BF =x ． ∴BGx44=． ∴x BG 16=．……………………………………………………………………（1分）又∵点D 到直线BM 的距离为32， ∴32)16(21⋅-=x x y ，即x x y 3316-=．………………………………（1分）定义域为0<x <4．………………………………………………………………（1分）（3）解：（i ）当点G 在点F 的右侧时，由题意，得x x 331636-=．整理，得01662=-+x x ．解得x 1=2，x 2=-8（不合题意，舍去）．………………………………………（2分）（ii ）当点G 在点F 的左侧时，由题意，得x x 316336-=．整理，得01662=--x x ．解得x 3=8，x 4=-2（不合题意，舍去）．………………………………………（2分）综上所述AE 的值为2或8．。

2012中考数学上海市初中数学教学质量抽样分析试卷参考答案及评分说明

上海市初中数学教学质量抽样分析试卷参考答案及评分说明一、选择题：1．B ； 2．D ； 3．B ； 4．C ； 5．A ； 6．B ．二、填空题：7．21≥x ； 8．410616409.8⨯； 9．)2)(2(-+++y x y x ； 10．21≤<-x ； 11．m <1； 12．2； 13．y =2x -5； 14．a b 3232-； 15．332； 16．3或13； 17．52； 18．23．三、解答题：19．解：原式=1)12(223-++- ………（各2分）、=22+．……………（2分）20．解：去分母，得x x x 4532-=--．………………………………………………（3分）整理，得0232=+-x x ．………………………………………………………（2分）解得11=x ，22=x ．……………………………………………………………（4分）经检验：11=x ，22=x 都是原方程的根，……………………………………（1分） ∴原方程的根为11=x ，22=x ．21．解：（1）40；……………………………………………………………………………（2分）（2）略；……………………………………………………………………………（2分）（3）1~1.5，1~1.5；……………………………………………………………（各2分）（4）375．…………………………………………………………………………（2分）22．解：（1）点A '的坐标为（3,6），点B '的坐标为（6,6）；………………………（各2分）（2）由题意，得m +2=6．…………………………………………………………（2分） ∴m =4．……………………………………………………………………………（1分） ∴点C '的坐标为（4,6）．…………………………………………………………（1分）∴点C 的坐标为（34,2）．………………………………………………………（2分） 23．证明：（1）∵BE 、BF 分别是ABC ∠与它的邻补角ABD ∠的平分线， ∴ABC ABE ∠=∠21，ABD ABF ∠=∠21．……………………………………（1分）而∠ABC +∠ABD =180°，∴∠ABE +∠ABF =90°，即∠EBF =90°．……………（1分） ∵AE ⊥BE ，垂足为点E ，∴∠AEB =90°．………………………………………（1分）同理可得∠AFB =90°．……………………………………………………………（1分） ∴四边形AFBE 是矩形．…………………………………………………………（2分）（2）∵四边形AFBE 是矩形，∴AM =BM =EM ．……………………………（1分）∴∠MBE =∠MEB ．………………………………………………………………（1分） ∵∠MBE =∠EBC ，∴∠MEB =∠EBC ．…………………………………………（1分） ∴ME ∥BC ．………………………………………………………………………（1分）∴BC MN 21=．…………………………………………………………………（1分） 24．解：（1）根据题意，得点C 的坐标为（0,3）．………………………………………（1分）在Rt △AOC 中，∵tan ∠OAC =3，∴OA =1，即点A 的坐标为（1,0）．…………………………（1分） ∴⎩⎨⎧++=++=.34163,30b a b a ………………………………………………………………（1分）解得⎩⎨⎧-==.4,1b a ………………………………………………………………………（1分） ∴所求的函数解析式为342+-=x x y ．………………………………………（1分）顶点D 的坐标为（2,-1）．………………………………………………………（1分）（2）根据题意，得点E 的坐标为（-1,0）．……………………………………（1分）联结CE ． ∵10=CE ，10=DE ，52=CD ，∴222CD DE CE =+．……………（3分） ∴△CDE 是等腰直角三角形．…………………………………………………（1分） ∴∠CDE =45°．……………………………………………………………………（1分）25．解：（1）作BD ⊥AC ，垂足为点D ．∵⊙P 与边AC 相切，∴BD 就是⊙P 的半径．∵2cot =A ，∴55sin =A ．……………………………………………………（1分）又∵ABBD A =sin ，AB =15，∴53=BD ．……………………………………（2分）（2）作PH ⊥MN ，垂足为点H ．由垂径定理，得MN =2MH ．……………………………………………………（1分）而x PH 55=，53==BD PM ，……………………………………………（1分） ∴251452x y -=，即25112552x y -=．…………………………………（2分）定义域为1553<≤x ．…………………………………………………………（1分）（3）当AP =56时，∠CPN =∠A ．……………………………………………（1分）证明如下：当AP =56时，PH =6，MH =3，AH =12，∴AM =9．………………………（1分）∵AC =20，MN =6，∴CN =5．……………………………………………………（1分） ∵553539==MP AM ，553=CN PN ，∴CNPN MP AM =．………………………（1分）又∵PM =PN ，∴∠PMN =∠PNM ．∴∠AMP =∠PNC ．………………………………………………………………（1分）∴∠CPN=∠A．。

浦东新区2012学年度第一学期期末质量抽测初一数学参考答案及评分说明

浦东新区2012学年度第一学期期末质量抽测七年级数学试卷参考答案及评分说明一、选择题：（本大题共4题，每题2分，满分8分）1．D ； 2．A ； 3．B ； 4．C ．二、填空题：（本大题共16题，每题2分，满分32分）5．32-x ； 6．3-；7．7； 8．6102.7-⨯； 9．)5(+x xy ； 10．6x ； 11．12+m ；12．1-； 13．12223-+-xy y x x ； 14．4322-+x x ； 15．12+x ； 16．圆心； 17．HODE ； 18．90； 19．120； 20．3n ．三、简答题：21．解：（1）原式=962522+-+-x x x …………………………………………（2分、2分）=16622--x x ．…………………………………………………………（2分）（2）原式=xx x x x x 121)2(2+++-+-…………………………………………………（1分） =)2(222+++---x x x x x x …………………………………………………（2分） =)2(2++-x x x x ………………………………………………………………（1分） =)2()1(+--x x x x ………………………………………………………………（1分） =21+--x x ．………………………………………………………………（1分） 22．解：（1）原式=)132)(632(++-+m m ………………………………………………（3分）=)42)(32(+-m m ………………………………………………………（1分）=)2)(32(2+-m m ．……………………………………………………（2分）（2）原式=22)5(y x --……………………………………………………………（3分）=)5)(5(y x y x +--+． ………………………………………………（3分）23．解：原式=)9)(6343(2-+--+m m m m ………………………………………………（1分） =)9(6)3(4)3(2-++--m m m m …………………………………………（1分） =546124322-+---m m m m ……………………………………………（1分）=66772--m m ．…………………………………………………………（1分）当m =72时，原式=667277272-⨯-⎪⎭⎫ ⎝⎛⨯=6874-……………………………………………（1分） =7367-．……………………………………………………………………（1分）24．解：去分母，得2)5(43-=--x x ．…………………………………………………（2分）去括号，得22043-=+-x x ．…………………………………………………（1分）解得 22=x ．…………………………………………………………………（2分）经检验 22=x 是原方程的根．…………………………………………………（1分）所以原方程的根是22=x ．25．（1）画图正确．………………………………（3分）（2）画图正确．………………………………（3分）（3）绕点O 旋转180度，等．方案正确．…（2分）26．解：设小明步行的速度为每小时x 千米，……………………………………………（1分）则公交车的速度为每小时9x 千米．根据题意，得239362=+x x ．………………………………………………………（3分）解得x =4．…………………………………………………………………………（2分）经检验x =4是原方程的根，且符合题意．………………………………………（1分）答：小明步行的速度为每小时4千米．…………………………………………（1分）27．解：（1）取x =0，得5252-=-+bx ax ．…………………………………………………（1分）取x =1，得5252-=-+b a ．……………………………………………………（1分）所以b a 25-=． ……………………………………………………………（2分）（2）取x =0，得2=2b ．所以b =1．………………………………………………（1分）取x =1，得m +3=3(a +2) ．所以m =3a +3．………………………………（1分）取1-=x ，得a m -=-21．所以1-=a m ．……………………………（1分）所以133-=+a a ．解得2-=a ．所以3-=m ．………………………………………………………………（1分）。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

上海市初中数学教学质量抽样分析试卷
参考答案及评分说明
一、选择题：
1．D ； 2．C ； 3．A ； 4．C ； 5．B ； 6．A ．
二、填空题：
7．a 5； 8．2(x +2)(x -2)； 9．-1<x <2； 10．3； 11．5； 12．y =x +1等；
13．x (x +10)=300；
14．23； 15．45； 16．3132+； 17．2； 18．2或8．三、解答题：
19．解：原式=）
（3223231-++-+……………………………………………（各2分） =3．……………………………………………………………………………（2分）
20．解：去分母，得4242+-+=x x ．…………………………………………………（3分）
整理，得 022=--x x ．………………………………………………………（2分）解得 x 1=-1，x 2=2．………………………………………………………（4分）经检验：x 1=-1是原方程的根，x 2=2是增根．…………………………………（1分） ∴原方程的根为x =-1．
21．解：（1）联结OA ．
∵OD ⊥AB ，AB =8，∴AD =4．…………………………………………………（2分） ∵OA =5，∴OD =3．………………………………………………………………（1分） ∵OC =5，∴CD =8．………………………………………………………………（1分）
（2）作OH ⊥CE ，垂足为点H ．
∵OC =5，5
4cos =C ，∴CH =4．…………………………………………………（2分） ∵OH ⊥CE ，∴CF =2CH =8．……………………………………………………（1分）又∵CD =8，54cos =
C ，∴CE =10．……………………………………………（2分） ∴EF =2．……………………………………………………………………………（1分）
22．解：（1）2，-3；……………………………………………………………………（各2分）
（2）整理，得0)52(2)(=--++b a b a ．……………………………………（2分）
∵a 、b 为有理数，∴⎩
⎨⎧=--=+.052,0b a b a …………………………………………（2分）解得⎪⎩
⎪⎨⎧-==.35,35b a ……………………………………………………………………（1分） ∴3
5
2-=+b a ．…………………………………………………………………（1分）
23．证明：（1）∵CE =BE ，CF =DF ，∴EF ∥BD ．………………………………………（2分）
又∵AD ∥BC ，∴四边形DBEM 是平行四边形．……………………………（2分）
（2）∵四边形ABCM 为平行四边形，∴AB =CM ，AB ∥CM ．………………（2分） ∴CE
BE CM BN =．…………………………………………………………………（1分） ∵BE =CE ，∴BN =CM ．…………………………………………………………（1分） ∴AB =BN ．………………………………………………………………………（1分） ∵EF ∥BD ，∴AN
AB MN DB =．……………………………………………………（2分） ∴MN =2DB ．……………………………………………………………………（1分）
24．解：（1）由题意，得⎩
⎨⎧=-+--=.5,243c c b ………………………………………………（2分）解得⎩⎨⎧-=-=.
5,6c b ……………………………………………………………………（2分）
∴所求二次函数的解析式为562---=x x y ．………………………………（1分）
（2）二次函数562---=x x y 图像的顶点坐标为（-3,4）．……………………（1分） ∴图像平移后顶点M 的坐标为（3,4）．………………………………………（1分）由题意∠MPO =∠MBO ，可得∠PMB =∠POB =90°．
设点P 的坐标为（x ,0）．
∴2222225934)3(+=+++-x x ．…………………………………………（1分）解得x =15．………………………………………………………………………（1分） ∴点P 的坐标为（15,0）．………………………………………………………（1分） ∴103=BM ，105=PB ．………………………………………………（1分） ∴5
3sin =∠BPM ．………………………………………………………………（1分）另解：二次函数562---=x x y 图像的顶点坐标为（-3,4）．………………（1分） ∴图像平移后顶点M 的坐标为（3,4）．………………………………………（1分）由题意∠MPO =∠MBO ，可得∠PMB =∠POB =90°．
过M 点作x 轴、y 轴的垂线，垂足分别为点H 、K ．
在Rt △BKM 中，由题意，得tan ∠MBK =1∶3．
在Rt △MPH 中，tan ∠MPH =tan ∠MBK =1∶3．………………………………（1分） ∴PH =12．
∴OP =15．………………………………………………………………………（1分） ∴点P 的坐标为（15,0）．………………………………………………………（1分） ∴103=BM ，105=PB ．………………………………………………（1分）
∴5
3sin =∠BPM ．………………………………………………………………（1分） 25．（1）解：∵∠ACB =90°，AD =BD ，∴CD =AD =BD ．………………………………（1分）
∵∠BAC =60°，∴∠ADC =∠ACD =60°，∠ABC =30°，AD =BD =AC ．
∵AC =4，∴AD =BD =AC =4．……………………………………………………（1分） ∵BM ∥AC ，∴∠MBC =∠ACB =90°．
又∵CD ⊥EF ，∴∠CDF =90°．
∴∠BDF =30°．
∴∠BFD =30°．
∴∠BDF =∠BFD ．
∴BF =BD =4．……………………………………………………………………（2分）
（2）①证明：由翻折，得CD E '∠=∠ACD =60°，∴∠ADC =CD E '∠．
∴E C '∥AB ．
∴D E C '∠=∠BDG ．……………………………………………………………（1分） ∵BM ∥AC ，∴∠CED =∠BFD ．
又∵D E C '∠=∠CED ，∴∠BDG =∠BFD ．……………………………………（1分） ∵∠DBF =∠GBD ，∴△BDF ∽△BGD ．………………………………………（1分） ②解：由△BDF ∽△BGD ，得
BG
BD BD BF =．由AE =x ，可得BF =x ． ∴
BG
x 44=． ∴x BG 16=．……………………………………………………………………（1分）又∵点D 到直线BM 的距离为32， ∴32)16(21⋅-=x x
y ，即x x y 3316-=．………………………………（1分）定义域为0<x <4．………………………………………………………………（1分）
（3）解：（i ）当点G 在点F 的右侧时，由题意，得x x
331636-=．整理，得01662=-+x x ．
解得x 1=2，x 2=-8（不合题意，舍去）．………………………………………（2分）（ii ）当点G 在点F 的左侧时，由题意，得x
x 316336-=．整理，得01662=--x x ．
解得x 3=8，x 4=-2（不合题意，舍去）．………………………………………（2分）
综上所述AE的值为2或8．。