材料力学有用课件
合集下载
材料力学 ppt课件
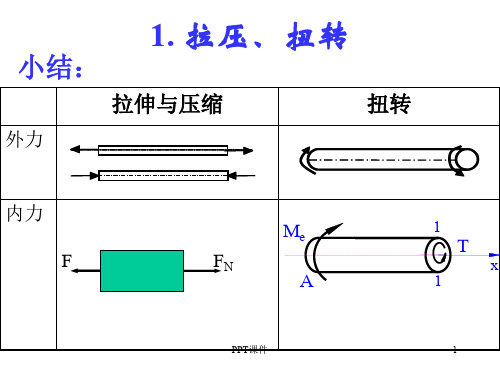
③应力分析:画危险面应力分布图,叠加;
④强度计算:建立危险点的强度条件,进行强度
计算。
PPT课件
20
2、两相互垂直平面内的弯曲
有棱角的截面
max
Mz Wz
My Wy
[ ]
圆截面
max
M
2 z
M
2 y
[ ]
W
3、拉伸(压缩)与弯曲
有棱角的截面
max
FN ,max A
(4)确定最大剪力和最大弯矩
3、弯曲应力与强度条件
(1)弯曲正应力
My
I PPT课件 z
12
M max Wz
yt,max yc,max
Oz y
PPT课件
t,max
Myt,max Iz
c,max
Myc,max Iz
13
(2)梁的正应力强度条件
M max
Wz
M
2 z
M
2 y
T
2
Mr4
M
2 z
M
2 y
0.75T
2
PPT课件
22
5、连接件的强度条件
剪切的强度条件
FS [ ]
AS
挤压强度条件
bs
Fbs Abs
[ bs ]
PPT课件
M z,max Wz
M y,max Wy
[ ]
圆截面
max
FN ,max A PPT课件
M max W
[ ]
21
4、弯曲与扭转
材料力学(全套)单辉祖ppt课件

(f)
.
例 试作图示杆的轴力图。
40kN
55kN 25kN
20kN
A
B
C
600 300 500
1800
D
E
400
解: 求支反力
FR 10kN
FR
1 F1=40kN 2F2=55kN3 F3=254kN F4= 20kN
A1
B 2 C 3D 4 E
.
FR
1 F1=40kN 2F2=55kN3 F3=254kN F4= 20kN
F
FF
F
2
2
影响区
影响区
FF
F2
2
F
.
}
例 试求此正方形砖柱由于荷载引起的横截面上的 最大工作应力。已知 F =50 kN。
F A FF B
3000
50kN
4000
C 370
150kN 240
解:Ⅰ段柱横截面上的正应力
FN1 50kN
1
FN1 A1
50 10 3 N
( 240 mm ) ( 240 mm )
变形x前
变x形后s
MN x
av
MNMN s
''
——MN段在X方向 上平均线应变
lxi m 0MN M N M N lxi m 0 xs ''
——M点沿X方 向的线应变
xyM lNi m 0(2L'M'N') (rad ) ——M点在XY平
面内的切应变
例2 求如图所示ab 的平均线应变和ab、 ad的夹角变化。
Ⅰ、拉(压)杆横截面上的应力
F
m
F
m
刘鸿文版材料力学课件(全套)

目录
§2.1
轴向拉伸与压缩的概念和实例
受力特点与变形特点:
作用在杆件上的外力合力的作用线与 杆件轴线重合,杆件变形是沿轴线方向的伸 长或缩短。
拉(压)杆的受力简图
拉伸
F F F
压缩
F
目录
§2.1
轴向拉伸与压缩的概念和实例
目录
§2.2 轴向拉伸或压缩时横截面上的内力和应力
m F m F FN FN F
类似地,可以定义 y , z
M点在xy平面内的切应变为: lim ( LM N ) MN 0 2 ML 0
, 均为无量纲的量。
目录
§1.5 变形与应变
例 1.2
已知:薄板的两条边 固定,变形后a'b, a'd 仍为直线。
250
c
200
b
0.025
求:ab 边的m 和 ab、ad 两边夹 角的变化。 解:
F
a b
a
c
c d
F
b
d
FN dA
A
dA A
A
FN A
目录
§2.2 轴向拉伸或压缩时横截面上的内力和应力
FN A
该式为横截面上的正应力σ计 算公式。正应力σ和轴力FN同号。 即拉应力为正,压应力为负。
圣 维 南 原 理
目录
§2.2 轴向拉伸或压缩时横截面上的内力和应力
剪切变形
目录
§1.6 杆件变形的基本形式
扭转变形
弯曲变形
目录
第二章
拉伸、压缩与剪切(1)
目录
第二章
§2.1 §2.2
拉伸、压缩与剪切
轴向拉伸与压缩的概念和实例 轴向拉伸或压缩时横截面上的内力和应力
材料力学:压杆稳定

坍塌后的奎拜克桥
材料力学教学课件
韩国汉城
1995年6月29日下午,韩国汉城三 丰百货大楼,由于盲目扩建、加层, 致使大楼四五层立柱不堪重负而产 生失稳破坏,大楼倒塌,死502人, 伤930人,失踪113人。
2020年2月3日星期一
10
第九章 压杆稳定
中国南京 2000年10月25日上午10时,南京电视台演播中 心演播大厅的屋顶的施工中,由于脚手架失稳, 造成屋顶模板倒塌,死6人,伤34人。
材料力学教学课件
2020年2月3日星期一
26
第九章 压杆稳定
1)、细长杆的临界应力
cr
2E 2
p
2E p
引入记号 1
2E p
欧拉公式的适用范围
l
i
1
2E p
2)、中长杆的临界应力(经验公式)
cr a b, 2 1
sin
kl
l
coskl
0
2020年2月3日星期一
19
第九章 压杆稳定
由于杆在微弯状态下保持平衡时,
Fy不可能等于零,故由上式得
1 sin kl l coskl 0 k 亦即 tan kl kl
满足此条件的最小非零解为kl=4.49,亦即 Fcr l 4.49 EI
从而得到此压杆求临界力的欧拉公式:
受均匀压力的球形薄壳或薄圆环,当压力超过一定数值时,圆环将 不能保持圆对称的平衡形式,而突然变为非圆对称的平衡形式。
材料力学教学课件
2020年2月3日星期一
9
第九章 压杆稳定
由于构件的失稳往往是突然发生的,因而其危害性也较大。 历史上曾多次发生因构件失稳而引起的重大事故。如1907年 加拿大劳伦斯河上,跨长为548米的奎拜克大桥,因压杆失 稳,导致整座大桥倒塌。近代这类事故仍时有发生。
材料力学第十三章压杆稳定ppt课件
2
11010 1 120 903 1012 12
1 32
该杆为中长杆。
σcr = 10.3MPa
79.9kN
Fcr = 111.5 kN
例2. 一压杆长l =2m,截面为10号工字钢,材料为Q 235钢, σs=235MPa,E =206GPa, σp =200MPa。压杆两端为柱 形铰,试求压杆的Fcr。
cos kl 0, kl n
2
, n 1,3,5...
Fcr
2EI
2l 2
Me x Fcr
l
w
x
2)、两端固定: M x Me Fcrw
EIw Me Fcr w
w kw k 2 M e Fcr
w Asin kx B cos kx M e Fcr
x 0, w 0, w 0; x l, w 0, w 0
cr a b, Fcr cr A
a、b为与材料有关的常数,单位:MPa。
适用范围: σP<σ cr <σ u
或 λP>λ >λ u
当λ≤λ u时,压杆为小柔度杆或短粗杆。短粗杆的破 坏是强度破坏。
显然, λ u是中柔度杆与短粗杆的分界值。
令σ cr = σ u得:
u
a
b
u
四、临界应力总图
(1) λ≥λP,大柔度杆,
Fcr
w Asin kx B cos kx F0 l x
Fcr
x
F0
Me
Fcr
x 0, w 0, w 0; x l, w 0;
A F0 , B F0l
kFcr
Fcr
w
F0 Fcr
1 k
sin kx l cos kx l
x
材料力学(扭转) PPT课件

y
3、斜截面上的 应力分析
x
n
x
z
t
Fn 0 dA zdAcos sin dAsin cos 0
Ft 0 dA dAcos cos dAsin sin 0
sin 2
讨论:
外力偶矩的计算、扭矩和扭矩图
功率、转速和外力偶矩之间的关系
ω = 2π n /60 ,1 kW = 1000 N•m/s
功率:P 角速度: 转速:n 外力偶矩:T 功率、转速和外力偶矩之间的关系:
T P P 2n
若功率P的单位为千瓦,转速n的单位为转/分:
T 9549 P ( N m) n
T
第三章 扭转
§3-2 外力偶矩、扭矩和扭矩图
例4-1 NA=19kW,NB=44kW,
TA
NC=25kW, n=150rpm
求:作图示传动轴的扭矩图
解:1. 求外力偶
TA
TA= 9549 19 =1210Nm
150
同样 TB=2800Nm, TC=1590Nm
TA
Mn
2.截面法求内力( 设正法)
Mn IPFra bibliotek变形
Mnl GI p
强度条件 max
Mn Wp
刚度条件 d Mn 180
dx G I p
第三章的基本要求
1.掌握根据轴的传递功率和转速计算外力偶矩;
2.掌握扭转时内力(即扭矩)的计算以及扭矩图的画 法;
3.掌握扭转切应力的计算方法;
45
第三章 扭转
《材料力学弯曲》课件

定义方式
弯曲应变通常用曲率半径的变化量与原始曲率半径的比值来表示,即 ΔR/R。其中 ΔR 是曲率半径的变化量,R 是原始曲率半径。
弯曲应变的计算
应变计法
通过在物体上粘贴应变片 ,并利用应变计测量应变 值,从而计算出弯曲应变 。
有限元分析法
利用有限元分析软件,建 立物体的有限元模型,通 过模拟受力情况下的变形 过程,计算出弯曲应变。
实验法
通过实验测试物体的弯曲 变形,利用相关公式计算 出弯曲应变。
弯曲应变的分布
应变分布图
通过绘制应变分布图,可以直观地了 解物体在弯曲变形过程中应变的大小 和分布情况。
应变集中
应变梯度
在弯曲变形过程中,物体不同部位上 的应变大小和方向可能不同,形成应 变梯度。
在物体受力点附近区域,应变会集中 增大,可能导致材料疲劳或断裂。
材料力学的重要性
总结词
材料力学在工程设计和实践中具有重要意义。
详细描述
在工程设计和实践中,材料力学是必不可少的学科之一。通过对材料力学的研究 ,工程师可以更好地理解材料的性能,预测其在各种工况下的行为,从而设计出 更加安全、可靠、经济的工程结构。
材料力学的基本假设
总结词
材料力学基于一系列基本假设,这些假设简 化了问题的复杂性,使得分析更为简便。
学习目标
01
02
03
04
掌握材料力学的基本概念、原 理和分析方法。
理解弯曲问题的特点和解决方 法。
能够运用所学知识解决简单的 弯曲问题。
培养分析问题和解决问题的能 力,提高力学素养。
02
材料力学基础
材料力学的定义
总结词
材料力学是一门研究材料在各种 力和力矩作用下的行为的学科。
弯曲应变通常用曲率半径的变化量与原始曲率半径的比值来表示,即 ΔR/R。其中 ΔR 是曲率半径的变化量,R 是原始曲率半径。
弯曲应变的计算
应变计法
通过在物体上粘贴应变片 ,并利用应变计测量应变 值,从而计算出弯曲应变 。
有限元分析法
利用有限元分析软件,建 立物体的有限元模型,通 过模拟受力情况下的变形 过程,计算出弯曲应变。
实验法
通过实验测试物体的弯曲 变形,利用相关公式计算 出弯曲应变。
弯曲应变的分布
应变分布图
通过绘制应变分布图,可以直观地了 解物体在弯曲变形过程中应变的大小 和分布情况。
应变集中
应变梯度
在弯曲变形过程中,物体不同部位上 的应变大小和方向可能不同,形成应 变梯度。
在物体受力点附近区域,应变会集中 增大,可能导致材料疲劳或断裂。
材料力学的重要性
总结词
材料力学在工程设计和实践中具有重要意义。
详细描述
在工程设计和实践中,材料力学是必不可少的学科之一。通过对材料力学的研究 ,工程师可以更好地理解材料的性能,预测其在各种工况下的行为,从而设计出 更加安全、可靠、经济的工程结构。
材料力学的基本假设
总结词
材料力学基于一系列基本假设,这些假设简 化了问题的复杂性,使得分析更为简便。
学习目标
01
02
03
04
掌握材料力学的基本概念、原 理和分析方法。
理解弯曲问题的特点和解决方 法。
能够运用所学知识解决简单的 弯曲问题。
培养分析问题和解决问题的能 力,提高力学素养。
02
材料力学基础
材料力学的定义
总结词
材料力学是一门研究材料在各种 力和力矩作用下的行为的学科。
材料力学课件哈工大第16章压杆稳定

或
π E
于是当 时p,欧拉公式成立。
p 满足 条p件的压杆,称为细长杆。
第16章 压杆稳 定 16-3 超过比例极限压杆的临界力计算
对于超过材料比例极限压杆的稳定性问题,曾进行过许多
理论和实验研究工作,得出了较多的分析结果。但目前工程中
普遍采用的是一些以实验为基础的经验公式。常用的经验公式
第一种情况表明压杆的直线平衡形态是稳定的;而第二种 情况表明压杆的直线平衡形态是不稳定的。
第16章 压 杆稳定
16-1 压杆稳定性概念
可见,压杆原来直线形态的平衡是否稳定,与所受的轴向压力 F 的大小有关;当轴向 压力 F 由小逐渐增加到某一个数值时,压杆的直线形态平衡由稳定过渡到不稳定 。
压杆的直线形态平衡由稳定过渡到不稳定所受的轴向压力的界限值,称 为压杆的临界力,用 Fcr 表示。
c rabu
u
s b
塑性材料 脆性材料
或
a u
b
令
sa bs (以塑性)材( 料 1 6为 7)
称为与材料屈服点相应的柔度值
于是,当 s p
时,直线公式成立。满足此
条件的压杆,成为中长杆。
p时,为细长杆
cr
π2E
2
综上所述,当 s p时,为中长杆crab
s时,为短粗杆强度问题
杆的临界力与两端铰支长为2l压杆的临界力相同,即
Fcr
π 2 EI (2l)2
用这种比较失稳后挠曲线形状的方法,同样会得
到其他约束情况下压杆的临界力公式,这些公式可统
一写成
Fcr(π2lE)2I
(16-2)
欧拉公式的一般形式
m 称为长度系数,可查手册; ml 称为压杆的相当长度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
F
a b
a
b
c
d
c d
F
横向线ab、cd 仍为直线,且 仍垂直于杆轴 线,只是分别 平行移至a’b’、 c’d’。
平面假设—变形前原为平面的横截面, 变形后仍保持为平面且仍垂直于轴线。
目录
§2.2 轴向拉伸或压缩时横截面上的内力和应力
从平面假设可以判断: (1)所有纵向纤维伸长相等
(2)因材料均匀,故各纤维受力相等 (3)内力均匀分布,各点正应力相等,为常量
— 正应力 — 切应力
1kPa=103N/m2 1MPa=106N/m2
C
F3
应力的国际单位为 Pa(帕斯卡) 1Pa= 1N/m2
1GPa=109N/m2
目录
§1.5 变形与应变
1.位移 2.变形 取一微正六面体
两种基本变形: 线变形 —— 线段长度的变化 L
MM'
M' M
刚性位移; 变形位移。
F1 F2
F5 F5
m
F4
(2)留下左半段或右半段
(3)将弃去部分对留下部
m
F3
F4
分的作用用内力代替
(4)对留下部分写平衡方
F1 F2
F3
程,求出内力的值。
目录
§1.4 内力、截面法和应力的概念
例如
F
a F M FS
a
FS=F
M Fa
目录
§1.4 内力、截面法和应力的概念
例 1.1 钻床 求:截面m-m上的内力。 解: 用截面m-m将钻床截为两部分,取上半 部分为研究对象, 受力如图:
改变。(宏观上看就是物体尺寸和形状的改变)
目录
§1.1 材料力学的任务
{
弹性变形 — 随外力解除而消失 塑性变形(残余变形)— 外力解除后不能消失
刚度:在载荷作用下,构件抵抗变形的能力。 3、内力:构件内由于 发生变形而产生的相 互作用力。(内力随 外力的增大而增大) 强度:在载荷作用下, 构件抵抗破坏的能力。
物体内任意两点的相对位置发生变化。
y
g
L'
x+s
角变形 M ——线段间夹角的变化 o
x
M' N
目录
N'
x
§1.5 变形与应变
3.应变 正应变(线应变)
y
g
L' L
x方向的平均应变:
x+s
xm
s x
o
M
x
M' N
N'
x
M点处沿x方向的应变:
切应变(角应变)
s x lim x 0 x
若:构件横截面尺寸不足或形状 不合理,或材料选用不当 ___ 不满足上述要求, 不能保证安全工作. 若:不恰当地加大横截面尺寸或 选用优质材料 ___ 增加成本,造成浪费
}
均 不 可 取
研究构件的强度、刚度和稳定性,还需要了解材料的力学性能。因此在 进行理论分析的基础上,实验研究是完成材料力学的任务所必需的途径和 手段。
目录
§1.1 材料力学的任务
四、材料力学的研究对象 构件的分类:杆件、板壳*、块体* 材料力学主要研究杆件
{ 曲杆—— 轴线为曲线的杆
直杆—— 轴线为直线的杆
{
等截面杆 ——横截面的大小 形状不变的杆 变截面杆 ——横截面的大小 或形状变化的杆 等截面直杆 ——等直杆
目录
§1.2 变形固体的基本假设
目录
§1.1 材料力学的任务
4、稳定性:
在载荷
作用下,构
件保持原有
平衡状态的 能力。 强度、刚度、稳定性是衡量构件承载能力 的三个方面,材料力学就是研究构件承载能力 的一门科学。
目录
§1.1 材料力学的任务
三、材料力学的任务 材料力学的任务就是在满足强度、刚度 和稳定性的要求下,为设计既经济又安全的构 件,提供必要的理论基础和计算方法。
FN1 FN2
F F
x
x
0
FN1 F1 10kN
BC段
0 FN 2 F2 F1
10 20 10 kN
F2
FN3
10
FN 2 F1 F2
F4
25 CD段
F
x
0
FN 3 F4 25kN
10
x
2、绘制轴力图。
目录
§2.2 轴向拉伸或压缩时横截面上的内力和应力
B
C
2
FN 1
FN 2 45°
y
B
F
FN 1 28.3 10 3 1 A1 20 2 10 6 4 90 10 6 Pa 90 MPa
FN 2 20 10 3 2 2 6 A2 15 10 89 10 6 Pa 89 MPa
目录
§2.1
轴向拉伸与压缩的概念和实例
受力特点与变形特点:
作用在杆件上的外力合力的作用线与 杆件轴线重合,杆件变形是沿轴线方向的伸 长或缩短。
拉(压)杆的受力简图
拉伸
F F F
压缩
F
目录
§2.1
轴向拉伸与压缩的概念和实例
目录
§2.2 轴向拉伸或压缩时横截面上的内力和应力
m F m F FN FN F
a d
a' b ab 0.025 125 10 6 m 200 ab
即为切应变g 。
g
a'
ab, ad 两边夹角的变化:
0.025 g tan g 100 10 6 (rad ) 250
目录
§1.6 杆件变形的基本形式
杆件的基本变形:拉伸(压缩)、剪切、扭转、弯曲
目录
§2.2 轴向拉伸或压缩时横截面上的内力和应力
例题2.2
A 1
45°
C
2
FN 1
FN 2 45°
y
B F
图示结构,试求杆件AB、CB的 应力。已知 F=20kN;斜杆AB为直 径20mm的圆截面杆,水平杆CB为 15×15的方截面杆。 解:1、计算各杆件的轴力。 B (设斜杆为1杆,水平杆为2杆) 用截面法取节点B为研究对象 F
目录
x
F
§2.2 轴向拉伸或压缩时横截面上的内力和应力
B d
C 1.9m
例题2.2 悬臂吊车的斜杆AB为直径 d=20mm的钢杆,载荷W=15kN。当W 移到A点时,求斜杆AB横截面上的 A 应力。
0.8m
解: 当载荷W移到A点时,斜杆AB
受到拉力最大,设其值为Fmax。
讨论横梁平衡
W
Fmax
Fmax
拉压变形
剪切变形
目录
§1.6 杆件变形的基本形式
扭转变形
弯曲变形
目录
第二章
拉伸、压缩与剪切(1)
目录
第二章
§2.1 §2.2
拉伸、压缩与剪切
轴向拉伸与压缩的概念和实例 轴向拉伸或压缩时横截面上的内力和应力
§2.3 §2.4 §2.5 §2.7 §2.8 §2.9 §2.10 §2.11 §2.12 §2.13
目录
FN
F
x
F
0
FN F 0 FN F
§2.2 轴向拉伸或压缩时横截面上的内力和应力
例题2.1
A
1 B 1 F2
2 C 2
3 D
已知F1=10kN;F2=20kN; F3=35kN;F4=25kN;试画 出图示杆件的轴力图。
F1 F1 F1
FN kN
F3
3
F4
解:1、计算各段的轴力。 AB段
目录
§1.3 外力及其分类
按外力与时间的关系分类 静载: 载荷缓慢地由零增加到某一定值后,就保持不变或变动很不显著, 称为静载。 载荷随时间而变化。 如交变载荷和冲击载荷
动载:
交变载荷 冲击载荷
目录
§1.4 内力、截面法和应力的概念
内力:外力作用引起构件内部的附加相互作用力。 求内力的方法 — 截面法 (1)假想沿m-m横截面将 杆切开
x
1、截面法求内力
F (1)假想沿m-m横截面将
杆切开 (2)留下左半段或右半段 (3)将弃去部分对留下部分 的作用用内力代替 (4)对留下部分写平衡方程 求出内力即轴力的值
F
0
FN F 0 FN F
目录
§2.2 轴向拉伸或压缩时横截面上的内力和应力
m F m F FN F
2、轴力:截面上的内力 由于外力的作用线 与杆件的轴线重合,内 力的作用线也与杆件的 轴线重合。所以称为轴 力。 3、轴力正负号: 拉为正、压为负 4、轴力图:轴力沿杆 件轴线的变化
在外力作用下,一切固体都将发生变形, 故称为变形固体。在材料力学中,对变形固体 作如下假设: 1、连续性假设: 认为整个物体体积内毫无空隙地充满物质 灰口铸铁的显微组织 球墨铸铁的显微组织
目录
§1.2 变形固体的基本假设
2、均匀性假设: 认为物体内的任何部分,其力学性能相同 普通钢材的显微组织 优质钢材的显微组织
目录
§1.2 变形固体的基本假设
3、各向同性假设: 认为在物体内各个不同方向的力学性能相同
(沿不同方向力学性能不同的材料称为各向异性 材料。如木材、胶合板、纤维增强材料等)
4、小变形与线弹性范围 认为构件的变形极其微小, 比构件本身尺寸要小得多。
如右图,δ远小于构件的最小尺寸, 所以通过节点平衡求各杆内力时,把支 架的变形略去不计。计算得到很大的简 化。
建于隋代(605年)的河北赵州桥桥 长64.4米,跨径37.02米,用石2800 吨
