2021年高考数学二轮复习专题四立体几何限时检测(文、理)

合集下载

2021届高考二轮复习数学专题训练：立体几何(2021-2021年全国卷高考题选)

2021-2021年高考全国卷数学之立体几何专题训练一．选择题（共13小题）A．2B．2C．3D．2 A．12B．18C．24D．54 A．64πB．48πC．36πD．32πA．B．C．D．A．E B．F C．G D．HA．6+4B．4+4C．6+2D．4+2 A．B．C．1D．A．8πB．4πC．2πD．πA．BM＝EN，且直线BM，EN是相交直线B．BM≠EN，且直线BM，EN是相交直线C．BM＝EN，且直线BM，EN是异面直线D．BM≠EN，且直线BM，EN是异面直线A．B．C．D．A．2x+y﹣z+2＝0B．2x+y+z﹣6＝0C．2x+y+z﹣4＝0D．2x+y﹣z﹣3＝0 A．B．C．D．A．B．C．D．二．填空题（共10小题）三．解答题（共17小题）（1）证明：平面ACD⊥平面ABC；（2）Q为线段AD上一点，P为线段BC上一点，且BP＝DQ＝DA，求三棱锥Q﹣ABP 的体积．（1）证明：P A⊥平面PBC；（2）求二面角B﹣PC﹣E的余弦值．（1）证明：平面P AB⊥平面P AC；（2）设DO＝，圆锥的侧面积为π，求三棱锥P﹣ABC的体积．（1）证明：AA1∥MN，且平面A1AMN⊥平面EB1C1F；（2）设O为△A1B1C1的中心．若AO∥平面EB1C1F，且AO＝AB，求直线B1E与平面A1AMN所成角的正弦值．（1）证明：点C1在平面AEF内；（2）若AB＝2，AD＝1，AA1＝3，求二面角A﹣EF﹣A1的正弦值．（1）当AB＝BC时，EF⊥AC；（2）点C1在平面AEF内．（1）证明：AA1∥MN，且平面A1AMN⊥平面EB1C1F；（2）设O为△A1B1C1的中心．若AO＝AB＝6，AO∥平面EB1C1F，且∠MPN＝，求四棱锥B﹣EB1C1F的体积．（1）证明：MN∥平面C1DE；（2）求点C到平面C1DE的距离．（1）证明：MN∥平面C1DE；（2）求二面角A﹣MA1﹣N的正弦值．（1）证明：BE⊥平面EB1C1；（2）若AE＝A1E，求二面角B﹣EC﹣C1的正弦值．（1）证明：BE⊥平面EB1C1；（2）若AE＝A1E，AB＝3，求四棱锥E﹣BB1C1C的体积．（1）证明：图2中的A，C，G，D四点共面，且平面ABC⊥平面BCGE；（2）求图2中的二面角B﹣CG﹣A的大小．（1）证明：图2中的A，C，G，D四点共面，且平面ABC⊥平面BCGE；（2）求图2中的四边形ACGD的面积．（1）证明：PO⊥平面ABC；（2）若点M在棱BC上，且MC＝2MB，求点C到平面POM的距离．（1）证明：平面AMD⊥平面BMC；（1）证明：平面PEF⊥平面ABFD；（2）求DP与平面ABFD所成角的正弦值．（1）证明：PO⊥平面ABC；（2）若点M在棱BC上，且二面角M﹣P A﹣C为30°，求PC与平面P AM所成角的正弦值．答案一．选择题（共13小题）1．【解答】解：由题意可知几何体是圆柱，底面周长16，高为：2，直观图以及侧面展开图如图：圆柱表面上的点N在左视图上的对应点为B，则在此圆柱侧面上，从M到N的路径中，最短路径的长度：＝2．故选：B．2．【解答】解：△ABC为等边三角形且面积为9，可得，解得AB＝6，球心为O，三角形ABC的外心为O′，显然D在O′O的延长线与球的交点如图：O′C＝＝，OO′＝＝2，则三棱锥D﹣ABC高的最大值为：6，则三棱锥D﹣ABC体积的最大值为：＝18．故选：B．3．【解答】解：由题意可知图形如图：⊙O1的面积为4π，可得O1A＝2，则AO1＝AB sin60°，，∴AB＝BC＝AC＝OO1＝2，外接球的半径为：R＝＝4，球O的表面积：4×π×42＝64π．故选：A．4．【解答】解：设正四棱锥的高为h，底面边长为a，侧面三角形底边上的高为h′，则依题意有：，因此有h′2﹣（）2＝ah′⇒4（）2﹣2（）﹣1＝0⇒＝（负值舍去）；故选：C．5．【解答】解：根据几何体的三视图转换为直观图：如图所示：根据三视图和几何体的的对应关系的应用，这个多面体某条棱的一个端点在正视图中对应的点为M，在俯视图中对应的点为N，所以在侧视图中与点E对应．故选：A．6．【解答】解：由三视图可知，几何体的直观图是正方体的一个角，如图：P A＝AB＝AC＝2，P A、AB、AC两两垂直，故PB＝BC＝PC＝2，几何体的表面积为：3×＝6+2，故选：C．7．【解答】解：由题意可知图形如图：△ABC是面积为的等边三角形，可得，∴AB＝BC＝AC＝3，可得：AO1＝＝，球O的表面积为16π，外接球的半径为：R；所以4πR2＝16π，解得R＝2，所以O到平面ABC的距离为：＝1．故选：C．8．【解答】解：如图，由P A＝PB＝PC，△ABC是边长为2的正三角形，可知三棱锥P﹣ABC为正三棱锥，则顶点P在底面的射影O1为底面三角形的中心，连接BO1并延长，交AC于G，则AC⊥BG，又PO1⊥AC，PO1∩BG＝O1，可得AC⊥平面PBG，则PB⊥AC，∵E，F分别是P A，AB的中点，∴EF∥PB，又∠CEF＝90°，即EF⊥CE，∴PB⊥CE，得PB⊥平面P AC，∴正三棱锥P﹣ABC的三条侧棱两两互相垂直，把三棱锥补形为正方体，则正方体外接球即为三棱锥的外接球，其直径为D＝＝＝＝．半径为，则球O的体积为．故选：D．9．【解答】解：∵点N为正方形ABCD的中心，△ECD为正三角形，平面ECD⊥平面ABCD，M是线段ED的中点，∴BM⊂平面BDE，EN⊂平面BDE，∵BM是△BDE中DE边上的中线，EN是△BDE中BD边上的中线，∴直线BM，EN是相交直线，设DE＝a，则BD＝，BE＝＝，∴BM＝a，EN＝＝a，∴BM≠EN，故选：B．10．【解答】解：∵正三棱锥P﹣ABC的侧面都是直角三角形，E，F分别是AB，BC的中点，∴以P为原点，P A为x轴，PB为y轴，PC为z轴，建立空间直角坐标系，设P A＝PB＝PC＝2，则A（2，0，0），B（0，2，0），C（0，0，2），E（1，1，0），F（0，1，1），＝（0，2，0），＝（1，1，0），＝（0，1，1），设平面PEF的法向量＝（x，y，z），则，取x＝1，得＝（1，﹣1，1），设PB与平面PEF所成角为θ，则sinθ＝＝＝．∴PB与平面PEF所成角的正弦值为．故选：C．11．【解答】解：设与平面2x+y﹣z+4＝0平行的平面方程为2x+y﹣z+k＝0，代入点（1，﹣1，3），得2×1﹣1﹣3+k＝0，解得k＝2，则所求的平面方程为2x+y﹣z+2＝0．故选：A．12．【解答】解以D为原点，DA为x轴，DC为y轴，DD1为z轴，建立空间直角坐标系，设正方体ABCD﹣A1B1C1D1棱长为2，则A（2，0，0），E（0，2，1），D（0，0，0），C（0，2，0），＝（﹣2，2，1），＝（0，﹣2，0），设异面直线AE与CD所成角为θ，则cosθ＝＝＝，sinθ＝＝，∴tanθ＝．∴异面直线AE与CD所成角的正切值为．故选：C．13．【解答】解：正方体的所有棱中，实际上是3组平行的棱，每条棱所在直线与平面α所成的角都相等，如图：所示的正六边形平行的平面，并且正六边形时，α截此正方体所得截面面积的最大，此时正六边形的边长，α截此正方体所得截面最大值为：6×＝．故选：A．二．填空题（共10小题）14．【解答】解：如图，∵A1、B1、C1分别为OA、OB、OC的中点，∴△A1B1C1∽△ABC，则，过O作OG⊥平面ABC，交平面A1B1C1于G1，则．∴＝＝．故答案为：．15．【解答】解：∵长方体ABCD﹣A1B1C1D1，AB＝AD＝4，AA1＝8，E、F、G为AB、A1B1、DD1的中点，H为A1D1上一点，则A1H＝1，∴以D为原点，DA为x轴，DC为y轴，DD1为z轴，建立空间直角坐标系，F（4，2，8），H（3，0，8），E（4，2，0），G（0，0，4），＝（﹣1，﹣2，0），＝（﹣4，﹣2，4），设异面直线FH与EG所成角为θ，则cosθ＝＝＝．故答案为：．16．【解答】解：由已知得BD＝AB＝，BC＝2，因为D、E、F三点重合，所以AE＝AD＝，BF＝BD＝AB＝，所以CE＝CF＝1，则在△BCF中，由余弦定理得cos∠FCB＝＝＝﹣，故答案为：﹣．17．【解答】解：向量＝（1，﹣1），＝（m+1，2m﹣4），若⊥，则m＝5，故答案为：5．18．【解答】解：因为圆锥内半径最大的球应该为该圆锥的内切球，如图，圆锥母线BS＝3，底面半径BC＝1，则其高SC＝＝2，不妨设该内切球与母线BS切于点D，令OD＝OC＝r，由△SOD∽△SBC，则＝，即＝，解得r＝，V＝πr3＝π，故答案为：π．19．【解答】解：∠ACB＝90°，P为平面ABC外一点，PC＝2，点P到∠ACB两边AC，BC的距离均为，过点P作PD⊥AC，交AC于D，作PE⊥BC，交BC于E，过P作PO⊥平面ABC，交平面ABC于O，连结OD，OC，则PD＝PE＝，∴由题意得CD＝CE＝OD＝OE＝＝1，∴PO＝＝＝．∴P到平面ABC的距离为．故答案为：．20．【解答】解：该半正多面体共有8+8+8+2＝26个面，设其棱长为x，则x+x+x＝1，解得x＝﹣1．故答案为：26，﹣1．21．【解答】解：该模型为长方体ABCD﹣A1B1C1D1，挖去四棱锥O﹣EFGH后所得的几何体，其中O为长方体的中心，E，F，G，H，分别为所在棱的中点，AB＝BC＝6cm，AA1＝4cm，∴该模型体积为：﹣V O﹣EFGH＝6×6×4﹣＝144﹣12＝132（cm3），∵3D打印所用原料密度为0.9g/cm3，不考虑打印损耗，∴制作该模型所需原料的质量为：132×0.9＝118.8（g）．故答案为：118.8．22．【解答】解：∵平面α截球O的球面所得圆的面积为π，则圆的半径为1，该平面与球心的距离d＝3，∴球半径R＝．∴球的表面积S＝4πR2＝40π．故答案为：40π．23．【解答】解：圆锥的顶点为S，母线SA，SB互相垂直，△SAB的面积为8，可得：，解得SA＝4，SA与圆锥底面所成角为30°．可得圆锥的底面半径为：2，圆锥的高为：2，则该圆锥的体积为：V＝＝8π．故答案为：8π．三．解答题（共17小题）24．【解答】解：（1）证明：∵在平行四边形ABCM中，∠ACM＝90°，∴AB⊥AC，又AB⊥DA．且AD∩AC＝A，∴AB⊥面ADC，∵AB⊂面ABC，∴平面ACD⊥平面ABC；（2）∵AB＝AC＝3，∠ACM＝90°，∴AD＝AM＝3，∴BP＝DQ＝DA＝2，由（1）得DC⊥AB，又DC⊥CA，∴DC⊥面ABC，∴三棱锥Q﹣ABP的体积V＝＝××＝＝1．25．【解答】解：（1）不妨设圆O的半径为1，OA＝OB＝OC＝1，AE＝AD＝2，，，，在△P AC中，P A2+PC2＝AC2，故P A⊥PC，同理可得P A⊥PB，又PB∩PC＝P，故P A⊥平面PBC；（2）建立如图所示的空间直角坐标系，则有，E（0，1，0），故，设平面PCE的法向量为，则由，得，取x＝1，则，z＝，所以平面PCE的法向量为，由（1）可知P A⊥平面PBC，不妨取平面PBC的法向量为，故，即二面角B﹣PC﹣E的余弦值为．26．【解答】解：（1）连接OA，OB，OC，△ABC是底面的内接正三角形，所以AB＝BC＝AC．O是圆锥底面的圆心，所以：OA＝OB＝OC，所以AP＝BP＝CP＝OA2+OP2＝OB2+OP2＝OC2+OP2，所以△APB≌△BPC≌△APC，由于∠APC＝90°，所以∠APB＝∠BPC＝90°，所以AP⊥BP，CP⊥BP，由于AP∩CP＝P，所以BP⊥平面APC，由于BP⊂平面P AB，所以：平面P AB⊥平面P AC．（2）设圆锥的底面半径为r，圆锥的母线长为l，所以．由于圆锥的侧面积为π，所以，整理得（r2+3）（r2﹣1）＝0，解得r＝1．所以AB＝＝．由于AP2+BP2＝AB2，解得则：＝．27．【解答】解：（1）证明：∵M，N分别为BC，B1C1的中点，底面为正三角形，∴B1N＝BM，四边形BB1NM为矩形，A1N⊥B1C1，∴BB1∥MN，∵AA1∥BB1，∴AA1∥MN，∵MN⊥B1C1，A1N⊥B1C1，MN∩A1N＝N，∴B1C1⊥平面A1AMN，∵B1C1⊂平面EB1C1F，∴平面A1AMN⊥平面EB1C1F，综上，AA1∥MN，且平面A1AMN⊥平面EB1C1F．（2）解：∵三棱柱上下底面平行，平面EB1C1F与上下底面分别交于B1C1，EF，∴EF∥B1C1∥BC，∵AO∥面EB1C1F，AO⊂面AMNA1，面AMNA1∩面EB1C1F＝PN，∴AO∥PN，四边形APNO为平行四边形，∵O是正三角形的中心，AO＝AB，∴A1N＝3ON，AM＝3AP，PN＝BC＝B1C1＝3EF，由（1）知直线B1E在平面A1AMN内的投影为PN，直线B1E与平面A1AMN所成角即为等腰梯形EFC1B1中B1E与PN所成角，在等腰梯形EFC1B1中，令EF＝1，过E作EH⊥B1C1于H，则PN＝B1C1＝EH＝3，B1H＝1，，sin∠B1EH＝＝，∴直线B1E与平面A1AMN所成角的正弦值为．28．【解答】（1）证明：在AA1上取点M，使得A1M＝2AM，连接EM，B1M，EC1，FC1，在长方体ABCD﹣A1B1C1D1中，有DD1∥AA1∥BB1，且DD1＝AA1＝BB1．又2DE＝ED1，A1M＝2AM，BF＝2FB1，∴DE＝AM＝FB1．∴四边形B1F AM和四边形EDAM都是平行四边形．∴AF∥MB1，且AF＝MB1，AD∥ME，且AD＝ME．又在长方体ABCD﹣A1B1C1D1中，有AD∥B1C1，且AD＝B1C1，∴B1C1∥ME且B1C1＝ME，则四边形B1C1EM为平行四边形，∴EC1∥MB1，且EC1＝MB1，又AF∥MB1，且AF＝MB1，∴AF∥EC1，且AF＝EC1，则四边形AFC1E为平行四边形，∴点C1在平面AEF内；（2）解：在长方体ABCD﹣A1B1C1D1中，以C1为坐标原点，分别以C1D1，C1B1，C1C所在直线为x，y，z轴建立空间直角坐标系．∵AB＝2，AD＝1，AA1＝3，2DE＝ED1，BF＝2FB1，∴A（2，1，3），E（2，0，2），F（0，1，1），A1（2，1，0），则，，．设平面AEF的一个法向量为．则，取x1＝1，得；设平面A1EF的一个法向量为．则，取x2＝1，得．∴cos＜＞＝＝．设二面角A﹣EF﹣A1为θ，则sinθ＝．∴二面角A﹣EF﹣A1的正弦值为．29．【解答】解：（1）因为ABCD﹣A1B1C1D1是长方体，所以BB1⊥平面ABCD，而AC⊂平面ABCD，所以AC⊥BB1，因为ABCD﹣A1B1C1D1是长方体，且AB＝BC，所以ABCD是正方形，所以AC⊥BD，又BD∩BB1＝B．所以AC⊥平面BB1D1D，又因为点E，F分别在棱DD1，BB1上，所以EF⊂平面BB1D1D，所以EF⊥AC．（2）取AA1上靠近A1的三等分点M，连接D1M，C1F，MF，C1E．因为点E在DD1，且2DE＝ED1，所以ED∥AM，且ED1＝AM，所以四边形AED1M为平行四边形，所以D1M∥AE，且D1M＝AE，又因为F在BB1上，且BF＝2FB1，所以A1M∥FB1，且A1M＝FB1，所以A1B1FM为平行四边形，所以FM∥A1B1，FM＝A1B1，即FM∥C1D1，FM＝C1D1，所以C1D1MF为平行四边形，所以D1M∥C1F，所以AE∥C1F，所以A，E，F，C1四点共面．所以点C1在平面AEF内．30．【解答】证明：（1）由题意知AA1∥BB1∥CC1，又∵侧面BB1C1C是矩形且M，N分别为BC，B1C1的中点，∴MN∥BB1，BB1⊥BC，∴MN∥AA1，MN⊥B1C1，又底面是正三角形，∴AM⊥BC，A1N⊥B1C1，又∵MN∩AM＝M，∴B1C1⊥平面A1AMN，∵B1C1⊂平面EB1C1F，∴平面A1AMN⊥平面EB1C1F；解：（2）∵AO∥平面EB1C1F，AO⊂平面A1AMN，平面A1AMN∩平面EB1C1F＝NP，∴AO∥NP，∵NO∥AP，∴AO＝NP＝6，∵O为△A1B1C1的中心，∴ON＝A1C1sin60°＝×6×＝，∴ON＝AP＝，∴AM＝3AP＝3，过M作MH⊥NP，垂足为H，∵平面A1AMN⊥平面EB1C1F，平面A1AMN∩平面EB1C1F＝NP，MH⊂平面A1AMN，∴MH⊥平面EB1C1F，∵在等边三角形中＝，即EF＝＝＝2，由（1）可知四边形EB1C1F为梯形，∵∠MPN＝，∴MH＝MP sin∠MPN＝＝3，31．【解答】解法一：证明：（1）连结B1C，ME，∵M，E分别是BB1，BC的中点，∴ME∥B1C，又N为A1D的中点，∴ND＝A1D，由题设知A1B1DC，∴B1C A1D，∴ME ND，∴四边形MNDE是平行四边形，MN∥ED，又MN⊄平面C1DE，∴MN∥平面C1DE．解：（2）过C作C1E的垂线，垂足为H，由已知可得DE⊥BC，DE⊥C1C，∴DE⊥平面C1CE，故DE⊥CH，∴CH⊥平面C1DE，故CH的长即为C到平面C1DE的距离，由已知可得CE＝1，CC1＝4，∴C1E＝，故CH＝，∴点C到平面C1DE的距离为．解法二：证明：（1）∵直四棱柱ABCD﹣A1B1C1D1的底面是菱形，AA1＝4，AB＝2，∠BAD＝60°，E，M，N分别是BC，BB1，A1D的中点．∴DD1⊥平面ABCD，DE⊥AD，以D为原点，DA为x轴，DE为y轴，DD1为z轴，建立空间直角坐标系，M（1，，2），N（1，0，2），D（0，0，0），E（0，，0），C1（﹣1，，4），＝（0，﹣，0），＝（﹣1，），＝（0，），设平面C1DE的法向量＝（x，y，z），则，取z＝1，得＝（4，0，1），∴MN∥平面C1DE．解：（2）C（﹣1，，0），＝（﹣1，，0），平面C1DE的法向量＝（4，0，1），∴点C到平面C1DE的距离：d＝＝＝．32．【解答】（1）证明：如图，过N作NH⊥AD，则NH∥AA1，且，又MB∥AA1，MB＝，∴四边形NMBH为平行四边形，则NM∥BH，由NH∥AA1，N为A1D中点，得H为AD中点，而E为BC中点，∴BE∥DH，BE＝DH，则四边形BEDH为平行四边形，则BH∥DE，∴NM∥DE，∵NM⊄平面C1DE，DE⊂平面C1DE，∴MN∥平面C1DE；（2）解：以D为坐标原点，以垂直于DC得直线为x轴，以DC所在直线为y轴，以DD1所在直线为z轴建立空间直角坐标系，则N（，，2），M（，1，2），A1（，﹣1，4），，，设平面A1MN的一个法向量为，由，取x＝，得，又平面MAA1的一个法向量为，∴cos＜＞＝＝＝．∴二面角A﹣MA1﹣N的正弦值为．33．【解答】证明：（1）长方体ABCD﹣A1B1C1D1中，B1C1⊥平面ABA1B1，∴B1C1⊥BE，∵BE⊥EC1，∵B1C1∩EC1＝C1，∴BE⊥平面EB1C1．解：（2）以C为坐标原点，建立如图所示的空间直角坐标系，设AE＝A1E＝1，则BE＝EB1，∵BE⊥平面EB1C1，∴BE⊥EB1，∴BE2+EB12＝2BE2＝＝4，∴BE2＝2，∵AE2+AB2＝1+AB2＝BE2＝2，∴AB＝1，则E（1，1，1），A（1，1，0），B1（0，1，2），C1（0，0，2），C（0，0，0），∵BC⊥EB1，∴EB1⊥面EBC，故取平面EBC的法向量为＝＝（﹣1，0，1），设平面ECC1的法向量＝（x，y，z），由，得，取x＝1，得＝（1，﹣1，0），∴cos＜＞＝＝﹣，∴二面角B﹣EC﹣C1的正弦值为．34．【解答】解：（1）证明：由长方体ABCD﹣A1B1C1D1，可知B1C1⊥平面ABB1A1，BE⊂平面ABB1A1，∴B1C1⊥BE，∵BE⊥EC1，B1C1∩EC1＝C1，∴BE⊥平面EB1C1；（2）由（1）知∠BEB1＝90°，由题设可知Rt△ABE≌Rt△A1B1E，∴∠AEB＝∠A1EB1＝45°，∴AE＝AB＝3，AA1＝2AE＝6，∵在长方体ABCD﹣A1B1C1D1中，AA1∥平面BB1C1C，E∈AA1，AB⊥平面BB1C1C，∴E到平面BB1C1C的距离d＝AB＝3，∴四棱锥E﹣BB1C1C的体积V＝×3×6×3＝18．35．【解答】证明：（1）由已知得AD∥BE，CG∥BE，∴AD∥CG，∴AD，CG确定一个平面，∴A，C，G，D四点共面，由已知得AB⊥BE，AB⊥BC，∴AB⊥面BCGE，∵AB⊂平面ABC，∴平面ABC⊥平面BCGE．解：（2）作EH⊥BC，垂足为H，∵EH⊂平面BCGE，平面BCGE⊥平面ABC，∴EH⊥平面ABC，由已知，菱形BCGE的边长为2，∠EBC＝60°，∴BH＝1，EH＝，以H为坐标原点，的方向为x轴正方向，建立如图所求的空间直角坐标系H﹣xyz，则A（﹣1，1，0），C（1，0，0），G（2，0，），＝（1，0，），＝（2，﹣1，0），设平面ACGD的法向量＝（x，y，z），则，取x＝3，得＝（3，6，﹣），又平面BCGE的法向量为＝（0，1，0），∴cos＜＞＝＝，∴二面角B﹣CG﹣A的大小为30°．36．【解答】解：（1）证明：由已知可得AD∥BE，CG∥BE，即有AD∥CG，则AD，CG确定一个平面，从而A，C，G，D四点共面；由四边形ABED为矩形，可得AB⊥BE，由△ABC为直角三角形，可得AB⊥BC，又BC∩BE＝B，可得AB⊥平面BCGE，AB⊂平面ABC，可得平面ABC⊥平面BCGE；（2）连接BG，AG，由AB⊥平面BCGE，可得AB⊥BG，在△BCG中，BC＝CG＝2，∠BCG＝120°，可得BG＝2BC sin60°＝2，可得AG＝＝，在△ACG中，AC＝，CG＝2，AG＝，可得cos∠ACG＝＝﹣，即有sin∠ACG＝，则平行四边形ACGD的面积为2××＝4．37．【解答】（1）证明：∵AB＝BC＝2，AC＝4，∴AB2+BC2＝AC2，即△ABC是直角三角形，又O为AC的中点，∴OA＝OB＝OC，∵P A＝PB＝PC，∴△POA≌△POB≌△POC，∴∠POA＝∠POB＝∠POC＝90°，∴PO⊥AC，PO⊥OB，OB∩AC＝O，∴PO⊥平面ABC；（2）解：由（1）得PO⊥平面ABC，PO＝，在△COM中，OM＝＝．＝××＝，S△COM＝＝．设点C到平面POM的距离为d．由V P﹣OMC＝V C﹣POM⇒，解得d＝，∴点C到平面POM的距离为．38．【解答】（1）证明：矩形ABCD所在平面与半圆弦所在平面垂直，所以AD⊥半圆弦所在平面，CM⊂半圆弦所在平面，∴CM⊥AD，M是上异于C，D的点．∴CM⊥DM，DM∩AD＝D，∴CM⊥平面AMD，CM⊂平面CMB，∴平面AMD⊥平面BMC；（2）解：存在P是AM的中点，理由：连接BD、AC交于O，取AM的中点P，连接OP，连接PD，PB，可得MC∥OP，MC⊄平面BDP，OP⊂平面BDP，所以MC∥平面PBD．39．【解答】（1）证明：由题意，点E、F分别是AD、BC的中点，则，，由于四边形ABCD为正方形，所以EF⊥BC．由于PF⊥BF，EF∩PF＝F，则BF⊥平面PEF．又因为BF⊂平面ABFD，所以：平面PEF⊥平面ABFD．（2）在平面PEF中，过P作PH⊥EF于点H，连接DH，由于EF为面ABCD和面PEF的交线，PH⊥EF，则PH⊥面ABFD，故PH⊥DH．在三棱锥P﹣DEF中，可以利用等体积法求PH，因为DE∥BF且PF⊥BF，所以PF⊥DE，又因为△PDF≌△CDF，所以∠FPD＝∠FCD＝90°，所以PF⊥PD，由于DE∩PD＝D，则PF⊥平面PDE，故V F﹣PDE＝，因为BF∥DA且BF⊥面PEF，所以DA⊥面PEF，所以DE⊥EP．设正方形边长为2a，则PD＝2a，DE＝a在△PDE中，，所以，故V F﹣PDE＝，又因为，所以PH＝＝，所以在△PHD中，sin∠PDH＝＝，即∠PDH为DP与平面ABFD所成角的正弦值为：．40．【解答】（1）证明：连接BO，∵AB＝BC＝2，O是AC的中点，∴BO⊥AC，且BO＝2，又P A＝PC＝PB＝AC＝4，∴PO⊥AC，PO＝2，则PB2＝PO2+BO2，则PO⊥OB，∵OB∩AC＝O，∴PO⊥平面ABC；（2）建立以O坐标原点，OB，OC，OP分别为x，y，z轴的空间直角坐标系如图：A（0，﹣2，0），P（0，0，2），C（0，2，0），B（2，0，0），＝（﹣2，2，0），设＝λ＝（﹣2λ，2λ，0），0＜λ＜1则＝﹣＝（﹣2λ，2λ，0）﹣（﹣2，﹣2，0）＝（2﹣2λ，2λ+2，0），则平面P AC的法向量为＝（1，0，0），设平面MP A的法向量为＝（x，y，z），则＝（0，﹣2，﹣2），令z＝1，则y＝﹣，x＝，即＝（，﹣，1），∵二面角M﹣P A﹣C为30°，∴cos30°＝||＝，即＝，解得λ＝或λ＝3（舍），则平面MP A的法向量＝（2，﹣，1），＝（0，2，﹣2），PC与平面P AM所成角的正弦值sinθ＝|cos＜，＞|＝||＝＝．。

2021-2022年高三数学专题复习专题4 立体几何检测题

2021年高三数学专题复习专题4 立体几何检测题一、重点知识梳理：1．一条主线“线线--线面--面面” 2．两个关系：平行与垂直3．三个平行：线线平行--线面平行--面面平行三个垂直：线线垂直--线面垂直--面面垂直2重要定理线面平行的判定定理：图形：数学符号语言：线面平行的性质定理：图形：数学符号语言：线面垂直的判定定理：图形：. 数学符号语言：线面垂直的性质定理：图形：数学符号语言：面面平行的判定定理：图形：数学符号语言：面面平行的性质定理：图形：数学符号语言：面面垂直的判定定理：图形：数学符号语言：面面垂直的性质定理：图形：数学符号语言：二：典型例题例1．设是两条不同的直线，、是两个不同的平面，则下列四个命题①若，则，②若，则,③若④若，则,其中正确的命题序号是．例2．如图，在四棱锥P－ABCD中，PD⊥底面ABCD，AD⊥AB，CD∥AB，，，直线PA与底面ABCD所成角为60°，点M、N分别是PA ，PB 的中点．（1）求证：MN ∥平面PCD ；（2）求证：四边形MNCD 是直角梯形；（3）求证：平面PCB ．例3．ABCD 为矩形，平面ABCD⊥平面BCE ，BE ⊥EC, （1）求证：平面AEC ⊥平面ABE ，（2）点F 在BE 上，若DE ∥平面ACF, 求的值三、巩固练习1．如图，在正三棱柱中，D 为棱的中点，若截面是面积为6的直角三角形，则此三棱柱的体积为。

2.将边长为2的正方形ABCD 沿对角线BD 折成直二面角A-BD-C ，若点A 、B 、C 、D 都在一个以O 为球心的球面上，则球O 的体积为。

3.已知直三棱柱ABC －A 1B 1C 1的侧棱长与底面三角形的各边长都等于a ，点D 为BC 的中点．求证：（1）平面AC 1D ⊥平面BCC 1B 1；（2）A 1B ∥平面AC 1D ．ABCA 1B 1C 1A1C 1B1BCAD 第（11）题4.如图，在四棱柱中，AB=BC=CA=，AD=CD=1,平面平面。

2021年高考数学二轮复习专项训练：立体几何

一、单选题1．用半径为，圆心角为的扇形纸片卷成一个圆锥筒，则这个圆锥筒的高为（）A．B．C．D．2．已知球的半径为4，球面被相互笔直的两个平面所截，得到的两个圆的公共弦长为，若球心到这两个平面的间隔持平，则这两个圆的半径之和为（）A．6B．8C．10D．123．若向量，，则（）A．B．C．3D．4．设、是两条不同的直线，、是两个不同的平面，给出下列四个出题：①若，，则；②若，，则；③若，，则；④若，，则.其间真出题的序号为（）A．①和②B．②和③C．③和④D．①和④5．已知三棱锥的侧棱长持平，底面正三角形的边长为，平面时，三棱锥外接球的外表积为（）A．B．C．D．6．在三棱锥中，，，则三棱锥外接球的体积是（）A．B．C．D．7．已知圆锥的底面半径为3，母线长为5.若球在圆锥内，则球的体积的最大值为（）A．B．C．D．8．四面体的四个极点坐标为，，，，则该四面体外接球的体积为（）A．B．C．D．9．若点为点在平面上的正投影，则记.如图，在棱长为的正方体中，记平面为，平面为，点是棱上一动点（与、不重合），.给出下列三个定论：①线段长度的取值规模是；②存在点使得平面；③存在点使得.其间，一切正确认论的序号是（）A．①②③B．②③C．①③D．①②10．如图，在正四棱台中，上底面边长为4，下底面边长为8，高为5，点别离在上，且.过点的平面与此四棱台的下底面会相交，则平面与四棱台的面的交线所围成图形的面积的最大值为A．B．C．D．二、填空题11．一个圆锥的旁边面打开图是半径为3，圆心角为的扇形，则该圆锥的体积为________.12．有一个别积为2的长方体，它的长、宽、高依次为a，b，1，现将它的长添加1，宽添加2，且体积不变，则所得长方体高的最大值为________；13．已知三棱锥P-ABC的四个极点在球O的球面上，，则球O的外表积为________.14．如图,已知正方体的棱长为4,点E、F别离是线段上的动点,点P是上底面内一动点,且满意点P到点F的间隔等于点P到平面的间隔,则当点P运动时,PE的最小值是__________.15．已知四边形为矩形, ,为的中点,将沿折起,得到四棱锥,设的中点为,在翻折过程中,得到如下有三个出题:①平面，且的长度为定值；②三棱锥的最大体积为；③在翻折过程中，存在某个方位，使得.其间正确出题的序号为__________．（写出一切正确认论的序号）三、解答题16．如图，已知正方形和矩形地点的平面相互笔直，交于点，为的中点，．（1）求证：平面；（2）求二面角的巨细．17．如图，在四棱锥中，底面是矩形，平面，，点、别离在线段、上，且，其间，衔接，延伸与的延伸线交于点，衔接．（Ⅰ）求证：平面；（Ⅱ）若时，求二面角的正弦值；（Ⅲ）若直线与平面所成角的正弦值为时，求值．参考答案1．B【解析】【剖析】设圆锥的底面半径为rcm,依据底面圆的周长即扇形的弧长求出半径r,使用勾股定理可得答案.【详解】设圆锥的底面半径为rcm，由题意底面圆的周长即扇形的弧长，可得2πr=即底面圆的半径为1，.所以圆锥的高,故选B【点睛】本题考察圆锥旁边面打开图的使用，圆锥旁边面打开图为扇形，扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长.2．A【解析】【剖析】设两圆的圆心为，，球心为，公共弦为，中点为，可知为正方形，依据和，代入长度求解即可.【详解】如图，设两圆的圆心为，，球心为，公共弦为，中点为，因为圆心到这两个平面的间隔持平，则为正方形.两圆半径持平，设两圆半径为，，，又，，，.这两个圆的半径之和为6.故选A【点睛】本题首要考察了球的几许运算，解题的要害是清楚球心和截面的方位联系，考察了空间幻想力，归于中档题.3．D【解析】【剖析】先求出的坐标，再求模长即可.【详解】则=故选D.【点睛】本题考察空间向量的坐标运算，模长公式，熟记加减运算性质，精确核算是要害，是根底题.4．A【解析】【剖析】逐个剖分出题①②③④的正误，可得出适宜的选项.【详解】关于出题①，若，过直线作平面，使得，则，，，，，出题①正确；关于出题②，关于出题②，若，，则，出题②正确；关于出题③，若，，则与相交、平行或异面，出题③过错；关于出题④，若，，则或，出题④过错.故选：A.【点睛】本题考察有关线面、面面方位联系的判别，考察推理才能，归于中等题.5．D【解析】【剖析】证明，得出，可得出的外接圆直径为，并核算出三棱锥的侧棱长，然后使用公式可得出外接球的半径，并使用球体外表积公式可得出外接球的外表积.【详解】如下图所示：由题意可知，，，则，.平面，平面，，，的外接圆直径为，易知三棱锥的旁边面都是等腰直角三角形，，设三棱锥的外接球半径为，则，得.因而，三棱锥的外接球的外表积为.故选：D.【点睛】本题考察三棱锥的外接球的外表积，剖分出几许体的结构，找出适宜的模型核算出外接球的半径是解题的要害，考察剖析问题和解决问题的才能，归于中等题.6．B【解析】【剖析】三棱锥是正三棱锥，取为外接圆的圆心，衔接，则平面，设为三棱锥外接球的球心，外接球的半径为，可求出，然后由可求出半径，然后求出外接球的体积.【详解】由题意，易知三棱锥是正三棱锥，取为外接圆的圆心，衔接，则平面，设为三棱锥外接球的球心.因为，所以.因为，所以.设三棱锥外接球的半径为，则，解得，故三棱锥外接球的体积是.故选B.【点睛】本题考察了三棱锥的外接球体积的求法，考察了学生的空间幻想才能与核算求解才能，归于中档题.7．A【解析】【剖析】设圆锥的轴截面为等腰△，则球的体积最大时，球的轴截面是△的内切圆，依据三角形面积公式和内切圆的性质求出半径，最终求出体积.【详解】设圆锥的轴截面为等腰△，则球的体积最大时，球的轴截面是△的内切圆，所以，解得：，所以球的体积的最大值为.故选：A【点睛】本题考察了求球体积最大问题，考察了球的几许性质，考察了数学运算才能.8．B【解析】【剖析】核算出线段长度，剖分出四面体的形状，然后可确认出外接球的球心，依据球心求解出球的半径即可求解出外接球的体积.【详解】由题意知，所以，所以，所以该四面体侧棱底面，且底面是边长为的正三角形，侧棱，所以底面正三角形的外接圆半径为，球心必在过中点且平行于底面的平面上，所以球半径，所以球的体积为.故选：B.【点睛】本题考察空间几许体的外接球体积核算，难度一般.求解空间几许体的外接球的问题，首先要确认出球心地点的方位，然后依据线段长度求解出外接球的半径，最终即可求解出球的体积或外表积.9．D【解析】【剖析】以点为坐标原点，、、地点直线别离为轴、轴、轴树立空间直角坐标系，设点的坐标为，求出点、的坐标，然后使用向量法来判别出出题①②③的正误.【详解】取的中点，过点在平面内作，再过点在平面内作，垂足为点.在正方体中，平面，平面，，又，，平面，即，，同理可证，，则，.以点为坐标原点，、、地点直线别离为轴、轴、轴树立空间直角坐标系，设，则，，，，.关于出题①，，，则，则，所以，，出题①正确；关于出题②，，则平面的一个法向量为，，令，解得，所以，存在点使得平面，出题②正确；关于出题③，，令，整理得，该方程无解，所以，不存在点使得，出题③过错.故选：D.【点睛】本题考察立体几许中线面联系、线线联系的判别，一起也触及了立体几许中的新界说，使用空间向量法来处理是解题的要害，考察推理才能，归于中等题.10．B【解析】【剖析】由题意可知，当平面α经过BCNM时获得的截面面积最大，此刻截面是等腰梯形；依据正四棱台的高及MN中点在底面的投影求得等腰梯形的高，然后求得等腰梯形的面积．【详解】当斜面α经过点时与四棱台的面的交线围成的图形的面积最大，此刻α为等腰梯形，上底为MN=4，下底为BC=8此刻作正四棱台俯视图如下：则MN中点在底面的投影到BC的间隔为8-2-1=5因为正四棱台的高为5，所以截面等腰梯形的高为所以截面面积的最大值为所以选B【点睛】本题考察了立体几许中过定点的截面面积问题，要害是剖分出截面的方位，再依据条件求得各数据，需求很好的空间幻想才能，归于难题．11．.【解析】【剖析】先求圆锥底面圆的半径，再由直角三角形求得圆锥的高，代入公式核算圆锥的体积即可。

高考数学二轮专题立体几何训练试题

卢氏一中2021届高考数学(sh ùxu é)二轮?立体几何?专题训练一、选择题(本大题一一共(y īg òng)10小题，每一小(y ī xi ǎo)题5分，一共(y īg òng)50分)1．(2021·全国卷)设f (x )是周期为2的奇函数，当0≤x ≤1时，f (x )＝2x (1－x )，那么f (－52)＝( )A ．－12B ．－14C.14D.12解析：依题意得f (－52)＝－f (52)＝－f (52－2)＝－f (12)＝－2×12×(1－12)＝－12.答案：A2．(2021·高考)曲线y ＝－x 3＋3x 2在点(1,2)处的切线方程为( ) A ．y ＝3x －1 B ．y ＝－3x ＋5 C ．y ＝3x ＋5D ．y ＝2x解析：依题意得，y ′＝－3x 2＋6x ，y ′|x ＝1＝－3×12＋6×1＝3，即所求切线的斜率等于3，故所求直线的方程是y －2＝3(x －1)，整理得y ＝3x －1.答案：A3．(2021·模拟)把函数y ＝sin(4x ＋π6)上的点的横坐标伸长到原来的2倍，然后再把所得到的图像向左平移π6个单位．所得函数图像的解析式为( )A ．y ＝sin(2x ＋π3)B ．y ＝sin(2x ＋5π12)C ．y ＝－cos2xD ．y ＝cos2x解析：依题意得所得函数图像的解析式为y ＝sin[2(x ＋π6)＋π6]＝sin(2x ＋π2)＝cos2x .答案：D4．(2021·模拟(m ón ǐ))一个四棱锥的三视图如下(r úxi à)图，其侧视图是等边三角形．该四棱锥的体积等于( )A. 3B ．2 3C ．3 3D ．6 3解析(ji ě x ī)：依题意得，该几何体是底面为一个直角(zh íji ǎo)梯形(该直角梯形的两底边长分别是1、2，高是2)、一个侧面为等边三角形，且该侧面垂直于底面的四棱锥．由于四棱锥的高为2sin60°＝3，因此该四棱锥的体积是13×[12(1＋2)×2]×3＝ 3.答案：A5．(2021·模拟)m 、n 、l 1、l 2表示直线，α、β表示平面．假设m ⊂α，n ⊂α，l 1⊂β，l 2⊂β，l 1∩l 2＝M ，那么α∥β的一个充分条件是( )A ．m ∥β且l 1∥αB ．m ∥β且n ∥βC ．m ∥β且n ∥l 2D ．m ∥l 1且n ∥l 2解析：由定理“假如一个平面内有两条相交直线分别与另一个平面平行，那么这两个平面平行〞与选项D 的条件可知，由选项D 可推知α∥β.答案：D6．(2021·东北师大模拟)a 、b 、c 、d 是空间四条直线，假如a ⊥c ，b ⊥c ，a ⊥d ，b ⊥d ，那么( )A ．a ∥b 且c ∥dB ．a 、b 、c 、d 中任意两条可能都不平行C ．a ∥b 或者c ∥dD ．a 、b 、c 、d 中至多有一对直线互相平行解析(jiěxī)：假设(jiǎshè)a与b相交，那么(nàme)存在平面β，使得(shǐde)a⊂β且b⊂β，由a⊥c，b⊥c，知c⊥β，同理d⊥β，所以c∥d.假设a∥b，那么c与d可能平行，也可能不平行．结合各选项知选C.答案：C7．(2021·高考)将长方体截去一个四棱锥，得到的几何体如下图，那么该几何体的侧(左)视图为()解析：如下图，点D1的投影为C1，点D的投影为C，点A的投影为B.答案：D8．假设{a n}是等差数列，公差为d.且a1，a2，a3，a4，a5，a6，a7的方差为4.那么d等于()A．±1 B．1C．2 D．±2解析：a1，a2，a3，a4，a5，a6，a7的平均值x＝a4.那么s2＝17[(a1－a4)2＋(a2－a4)2＋(a3－a4)2]×2＝4d2＝4.∴d＝±1.答案：A9．如图，在长方体ABCD－A1B1C1D1中，AB＝BC＝2，AA1＝1，那么BC1与平面BB1D1D所成角的正弦值为()A.63B.255C.155D.105解析(ji ě x ī)：建立(ji ànl ì)如下图坐标系，得 D (0,0,0)，B (2,2,0)，C 1(0,2,1)，B 1(2,2,1)，D 1(0,0,1)，那么(n à me)＝(2,2,0)，＝(0,0,1)，＝(－2,0,1)．设平面(p íngmi àn)BD 1的法向量n ＝(x ，y ，z )．∴⎩⎪⎨⎪⎧n ·DB ＝2x ＋2y ＝0，n ·1DD ＝z ＝0.∴取n ＝(1，－1,0)．设BC 1与平面BD 1所成的角为θ，那么sin θ＝|cos 〈n ，1BC 〉|＝|1BC ·n ||1BC ||n |＝25·2＝105.答案：D10.如图，在斜三棱柱ABC －A 1B 1C 1中，∠BAC ＝90°，BC 1⊥AC ，那么C 1在面ABC 上的射影H 必在( )A ．直线AB 上 B ．直线BC 上 C ．直线AC 上D ．△ABC 的内部解析：∵AC ⊥AB ，AC ⊥BC 1，AB ∩BC 1＝B ，∴AC ⊥平面ABC 1.又AC ⊂平面ABC . ∴平面ABC 1⊥平面ABC .∴C 1在面ABC 上的射影H 必在两平面交线AB 上，应选A. 答案：A二、填空题(本大题一一共有4小题，每一小题5分，一共20分)11．(2021·新课标全国卷)两个圆锥有公一共底面，且两圆锥的顶点和底面的圆周都在同一个球面上．假设圆锥底面面积是这个球面面积的316，那么这两个圆锥中，体积较小者的高与体积较大者的高的比值为________．解析(ji ě x ī)：设球心(qi úx īn)为O 1，半径(b ànj ìng)为r 1，圆锥(yu ánzhu ī)底面圆圆心为O 2，半径为r 2，那么有316×4πr 21＝πr 22，即r 2＝32r 1，所以O 1O 2＝r 21－r 22＝r 12. 设两个圆锥中，体积较小者的高与体积较大者的高分别为h 1、h 2，那么h 1h 2＝r 1－r 12r 1＋r 12＝13.答案：1312．(2021·全国高考)正方体ABCD －A 1B 1C 1D 1中，E 为C 1D 1的中点，那么异面直线AE 与BC 所成角的余弦值为________．解析：取A 1B 1的中点F ，连接EF ，F A ，那么有EF ∥B 1C 1∥BC ，∠AEF 即是直线AE 与BC 所成的角或者其补角．设正方体ABCD －A 1B 1C 1D 1的棱长为2a ，那么有EF ＝2a ，AF ＝(2a )2＋a 2＝5a ，AE ＝(2a )2＋(2a )2＋a 2＝3a .在△AEF 中，cos ∠AEF＝AE 2＋EF 2－AF 22AE ·EF＝9a 2＋4a 2－5a 22×3a ×2a ＝23.因此，异面直线AE 与BC 所成的角的余弦值是23.答案：2313．设m ，n 是异面直线，那么：①一定存在平面α，使m ⊂α且n ∥α；②一定存在平面α，使m ⊂α且n ⊥α；③一定存在平面γ，使m ，n 到γ的间隔相等；④一定存在无数对平面α和β，使m ⊂α，n ⊂β，且α⊥β.上述4个命题中正确命题的序号是________．解析：①正确，在直线m 上任取一点作n 的平行线n ′，那么直线m 和n ′相交，确定的平面为所求的α；②错误，当异面直线m 、n 不垂直的时候，就不存在平面α，使m ⊂α且n ⊥α；③正确，在异面直线m 、n 上各任意取一点A 、B ，过线段AB 的中点作一个平面γ，使平面γ与异面直线都平行，那么平面γ为所求；④正确，过直线m 任作一个平面α，那么过直线n 的平面β绕着直线n 旋转时，一定有一个位置，使得平面β与平面α垂直．答案(d á àn)：①③④14.如图，二面角α－l －β的大小(d àxi ǎo)是60°，线段(xi àndu àn)AB ⊂α，B ∈l ，AB 与l 所成的角为30°，那么(n à me)AB 与平面β所成的角的正弦值是________．解析：如图，过A 作AC ⊥平面β于C ，C 为垂足，连接CB ，过C 作CD ⊥l 于D ，连接AD ，那么AD ⊥l ，∴∠ADC 为二面角α－l －β的平面角．即∠ADC ＝60°. ∵AC ⊥β，∴∠ABC 为直线AB 与平面β所成角．设AB ＝1，那么AD ＝12，AC ＝12×32＝34，∴sin ∠ABC ＝AC AB ＝341＝34.答案：34三、解答题(本大题一一共有4小题，一共50分)15．(本小题满分是12分)(2021·高考)如图，正三棱柱ABC －A 1B 1C 1的各棱长都是4，E 是BC 的中点，动点F 在侧棱CC 1上，且不与点C 重合．(1)当CF ＝1时，求证：EF ⊥A 1C ；(2)设二面角C －AF －E 的大小为θ，求tan θ的最小值．解：(1)建立如下图的空间直角坐标系，连接EF ，AF ，那么由可得 A (0,0,0)，B (23，2,0)，C (0,4,0)，A 1(0,0,4)，E (3，3,0)，F (0,4,1)，于是＝(0，－4,4)，＝(－3，1,1)．那么(n à me)1CA ·EF ＝(0，－4,4)·(－3，1,1)＝0－4＋4＝0，故EF ⊥A 1C . (2)设CF ＝λ，(0＜λ≤4)，平面(p íngmi àn)AEF 的一个(y ī ɡè)法向量为m ＝(x ，y ，z )，那么(n à me)由(1)得F (0,4，λ)．＝(3，3,0)，AF ＝(0,4，λ)，于是由m ⊥，m ⊥AF 可得⎩⎪⎨⎪⎧m ·AE ＝0，m ·AF ＝0，即⎩⎪⎨⎪⎧3x ＋3y ＝0，4y ＋λz ＝0.取m ＝(3λ，－λ，4)．又由直三棱柱的性质可取侧面A 1C 的一个法向量为n ＝(1,0,0)，于是由θ为锐角可得cos θ＝|m ·n ||m |·|n |＝3λ2λ2＋4，sin θ＝λ2＋162λ2＋4，所以tan θ＝λ2＋163λ＝13＋163λ2. 由0＜λ≤4，得1λ≥14，即tan θ≥13＋13＝63. 故当λ＝4，即点F 与点C 1重合时，tan θ获得最小值63. 16．(本小题满分是12分)(2021·高考)如图，在△ABC 中，∠B ＝π2，AB ＝BC ＝2，P 为AB 边上一动点，PD ∥BC 交AC 于点D ，现将△PDA 沿PD 翻折至△PDA ′，使平面PDA ′⊥平面PBCD .(1)当棱锥A ′－PBCD 的体积最大时，求P A 的长； (2)假设点P 为AB 的中点，E 为A ′C 的中点，求证：A ′B ⊥DE .解：(1)令P A ＝x (0<x <2)，那么A ′P ＝PD ＝x ，BP ＝2－x ，因为A ′P ⊥PD 且平面A ′PD ⊥平面PBCD ，故A ′P ⊥平面PBCD ，所以V A ′－PBCD ＝13Sh ＝16(2－x )(2＋x )x ＝16(4x －x 3)，令f (x )＝16(4x －x 3)，由f ′(x )＝16(4－3x 2)＝0，得x ＝233，当x ∈(0，233)时，f ′(x )>0，f (x )单调(d āndi ào)递增，当x ∈(233，2)时，f ′(x )<0，f (x )单调(d āndi ào)递减，所以(su ǒy ǐ)，当x ＝233时，f (x )获得(hu òd é)最大值．即：当V A ′－PBCD 获得最大时，P A ＝233.(2)证明：设F 为A ′B 的中点，连接PF ，FE .那么有EF 綊12BC ，PD 綊12BC ，所以DE ∥PF ，又A ′P ＝PB . 所以PF ⊥A ′B ，故DE ⊥A ′B .17．(本小题满分是12分)(2021·海淀模拟)在如图的多面体中，EF ⊥平面AEB ，AE ⊥EB ，AD ∥EF ，EF ∥BC ，BC ＝2AD ＝4，EF ＝3，AE ＝BE ＝2，G 是BC 的中点．(1)求证：AB ∥平面DEG ； (2)求证：BD ⊥EG ；(3)求二面角C －DF －E 的余弦值．解：(1)证明：由AD ∥EF ∥BC ，易知AD ∥BG ，又BC ＝2AD ，AD ＝BG .∴四边形ABGD 为平行四边形，即AB ∥DG . 又AB ⊄面DEG ，∴AB ∥面DEG .(2)证明(zh èngm íng)：∵EF ⊥平面(p íngmi àn)AEB ，AE ⊂平面(p íngmi àn)AEB ，BE ⊂平面(p íngmi àn)AEB ，∴EF ⊥AE ，EF ⊥BE .又AE ⊥EB ，∴EB ，EF ，EA 两两垂直．以点E 为坐标原点，EB ，EF ，EA 分别为x ，y ，z 轴建立如下图的空间直角坐标系．由得，A (0,0,2)，B (2,0,0)，C (2,4,0)，F (0,3,0)，D (0,2,2)，G (2,2,0)． ∴＝(2,2,0)，＝(－2,2,2)．∴BD ·EG ＝－2×2＋2×2＝0. ∴BD ⊥EG . (3)由得＝(2,0,0)是平面EFDA 的一个法向量．设平面DCF 的法向量为n ＝(x ，y ，z )， ∵＝(0，－1,2)，＝(2,1,0)，∴⎩⎪⎨⎪⎧ FD ·n ＝0， FC ·n ＝0，即⎩⎪⎨⎪⎧－y ＋2z ＝0，2x ＋y ＝0.令z ＝1，得n ＝(－1,2,1)．设二面角C －DF －E 的大小为θ，那么cos θ＝cos 〈n ，EB 〉＝－226＝－66.∴二面角C －DF －E 的余弦值为－66. 18．(本小题满分是14分)如图，在长方体ABCD －A 1B 1C 1D 1中，E 、F 分别是棱BC ，CC 1上的点，CF ＝AB ＝2CE ，AB ∶AD ∶AA 1＝1∶2∶4.(1)求异面直线EF 与A 1D 所成角的余弦值；(2)证明(zh èngm íng)AF ⊥平面(p íngmi àn)A 1ED ；(3)求二面角A 1－ED －F 的正弦(zh èngxi án)值．解：如下图，建立空间(k ōngji ān)直角坐标系，点A 为坐标原点，设AB ＝1，依题意得D (0,2,0)，F (1,2,1)，A 1(0,0,4)，E (1，32，0)． (1)易得EF ＝(0，12，1)，＝(0,2，－4)．于是cos 〈EF ，1A D 〉＝EF ·1A D |EF ||1A D |＝－35. 所以异面直线EF 与A 1D 所成角的余弦值为35. (2)证明：连接ED ，易知AF ＝(1,2,1)，＝(－1，－32，4)，＝(－1，12，0)，于是AF ·1EA ＝0，AF ·ED ＝0.因此，AF ⊥EA 1，AF ⊥ED .又EA 1∩ED ＝E ，所以AF ⊥平面A 1ED .(3)设平面EFD 的一个法向量为u ＝(x ，y ，z )，那么⎩⎪⎨⎪⎧ u ·EF ＝0，u ·ED ＝0，即⎩⎨⎧ 12y ＋z ＝0，－x ＋12y ＝0. 不妨令x ＝1，可得u ＝(1,2，－1)．由(2)可知，AF 为平面A 1ED 的一个法向量．于是cos 〈u ，AF 〉＝u ·AF |u ||AF |＝23，从而sin 〈u ，AF 〉＝53.所以二面角A1－ED－F的正弦值为53.内容总结（1）卢氏一中2021届高考数学二轮。

2021年高中数学立体几何多选题专题复习附答案

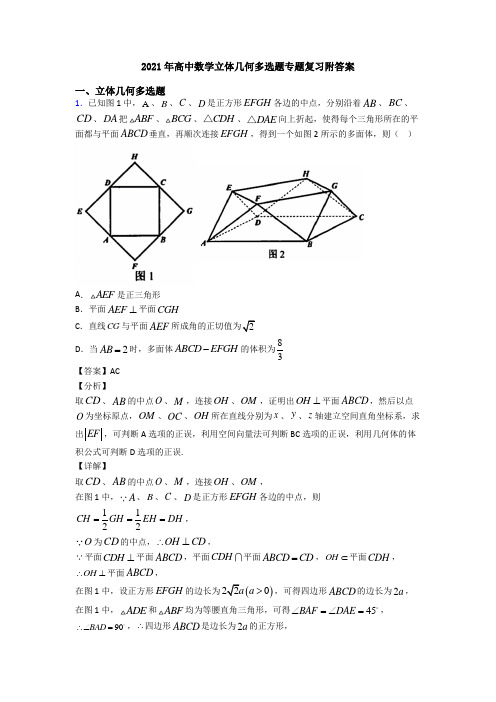
2021年高中数学立体几何多选题专题复习附答案一、立体几何多选题1．已知图1中，A 、B 、C 、D 是正方形EFGH 各边的中点，分别沿着AB 、BC 、CD 、DA 把ABF 、BCG 、CDH △、DAE △向上折起，使得每个三角形所在的平面都与平面ABCD 垂直，再顺次连接EFGH ，得到一个如图2所示的多面体，则（）A ．AEF 是正三角形B ．平面AEF ⊥平面CGHC ．直线CG 与平面AEF 2D ．当2AB =时，多面体ABCD EFGH -的体积为83【答案】AC 【分析】取CD 、AB 的中点O 、M ，连接OH 、OM ，证明出OH ⊥平面ABCD ，然后以点O 为坐标原点，OM 、OC 、OH 所在直线分别为x 、y 、z 轴建立空间直角坐标系，求出EF ，可判断A 选项的正误，利用空间向量法可判断BC 选项的正误，利用几何体的体积公式可判断D 选项的正误. 【详解】取CD 、AB 的中点O 、M ，连接OH 、OM ，在图1中，A 、B 、C 、D 是正方形EFGH 各边的中点，则1122CH GH EH DH ===，O 为CD 的中点，OH CD ∴⊥，平面CDH ⊥平面ABCD ，平面CDH 平面ABCD CD =，OH ⊂平面CDH ，OH ∴⊥平面ABCD ，在图1中，设正方形EFGH 的边长为()220a a >，可得四边形ABCD 的边长为2a ，在图1中，ADE 和ABF 均为等腰直角三角形，可得45BAF DAE ∠=∠=， 90BAD ∴∠=，∴四边形ABCD 是边长为2a 的正方形，O 、M 分别为CD 、AB 的中点，则//OC BM 且OC BM =，且90OCB ∠=，所以，四边形OCBM 为矩形，所以，OM CD ⊥，以点O 为坐标原点，OM 、OC 、OH 所在直线分别为x 、y 、z 轴建立空间直角坐标系，则()2,,0A a a -、()2,,0B a a 、()0,,0C a 、()0,,0D a -、(),,E a a a -、()2,0,F a a 、(),,G a a a 、()0,0,H a .对于A 选项，由空间中两点间的距离公式可得2AE AF EF a ===，所以，AEF 是正三角形，A 选项正确；对于B 选项，设平面AEF 的法向量为()111,,m x y z =，(),0,AE a a =-，()0,,AF a a =，由11110m AE ax az m AF ay az ⎧⋅=-+=⎪⎨⋅=+=⎪⎩，取11z =，则11x =，11y =-，则()1,1,1m =-，设平面CGH 的法向量为()222,,n x y z =，(),0,CG a a =，()0,,CH a a =-，由222200n CG ax az n CH ay az ⎧⋅=+=⎪⎨⋅=-+=⎪⎩，取21z =-，可得21x =，21y =-，则()1,1,1n =--，()22111110m n ⋅=+--⨯=≠，所以，平面AEF 与平面CGH 不垂直，B 选项错误；对于C 选项，6cos ,23CG m CG m a CG m⋅<>===⨯⋅，设直线CG 与平面AEF 所成角为θ，则sin 6θ=，23cos 1sin θθ=-=，所以，sin tan 2cos θθθ==，C 选项正确；对于D 选项，以ABCD 为底面，以OH 为高将几何体ABCD EFGH -补成长方体1111ABCD A B C D -，则E 、F 、G 、H 分别为11A D 、11A B 、11B C 、11C D 的中点，因为2AB =，即1a =，则1OH =，长方体1111ABCD A B C D -的体积为2214V =⨯=，11211111113326A A EF A EF V S AA -=⋅=⨯⨯⨯=△，因此，多面体ABCD EFGH -的体积为111044463ABCD EFGH A A EF V V V --=-=-⨯=， D 选项错误. 故选：AC. 【点睛】方法点睛：计算线面角，一般有如下几种方法：（1）利用面面垂直的性质定理，得到线面垂直，进而确定线面角的垂足，明确斜线在平面内的射影，即可确定线面角；（2）在构成线面角的直角三角形中，可利用等体积法求解垂线段的长度h ，从而不必作出线面角，则线面角θ满足sin hlθ=（l 为斜线段长），进而可求得线面角；（3）建立空间直角坐标系，利用向量法求解，设a 为直线l 的方向向量，n 为平面的法向量，则线面角θ的正弦值为sin cos ,a n θ=<>.2．已知球O 为正方体1111ABCD A B C D -的内切球，平面11A C B 截球O 的面积为24π，下列命题中正确的有（）A ．异面直线AC 与1BC 所成的角为60°B ．1BD ⊥平面11AC B C ．球O 的表面积为36πD ．三棱锥111B AC B -的体积为288 【答案】AD 【分析】连接11A C ，1A B ，通过平移将AC 与1BC 所成角转化为11A C 与1BC 所成角可判断A ；通过反证法证明B ；由已知平面11A C B 截球O 的面积为24π求出正方体棱长，进而求出内切球的表面积可判断C ；利用等体积法可求得三棱锥111B AC B -的体积可判断D. 【详解】对于A ，连接11A C ，1A B ，由正方体1111ABCD A B C D -，可知11//A C AC ，11AC B ∴∠为异面直线AC 与1BC 所成的角，设正方体边长为a ，则1111AC A B BC ==，由等边三角形知1160A C B ∠=，即异面直线AC 与1BC 所成的角为60，故A 正确；对于B ，假设1BD ⊥平面11A C B ，又1A B ⊂平面11A C B ，则11BD B A ⊥，设正方体边长为a ，则11A D a =，1A B =，1BD =，由勾股定理知111A D B A ⊥，与假设矛盾，假设不成立，故1BD 不垂直于平面11A C B ，故B 错误；对于C ，设正方体边长为a ，则112AC a =，内切球半径为2a，设内切球的球心O 在面11A C B 上的投影为O '，由等边三角形性质可知O '为等边11A C B △的重心，则111623332332O A AC a a =⨯'=⨯=，又132OA a =，∴球心O 到面11A C B 的距离为121222326336a a a OA O A ⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭=-='-，又球心与截面圆心的连线垂直于截面，∴截面圆的半径为2236626a a a ⎛⎫⎛⎫ ⎪ ⎪ ⎪⎝⎭⎝⎭-=，又截面圆的面积26246S a ππ⎛⎫= ⎪ ⎪⎝⎭=，解得12a =，则内切球半径为6，内切球表面积214644S ππ==⨯，故C 错误；对于D ，由等体积法知111111111111212122812383B A C B B A C B A C B V V S a --==⨯⨯=⨯⨯=，故D 正确；故选：AD【点睛】关键点点睛：本题考查了正方体和它的内切球的几何结构特征，关键是想象出截面图的形状，从而求出正方体的棱长，进而求出内切球的表面积及三棱锥的体积，考查了空间想象能力，数形结合的思想，属于较难题.3．在棱长为1的正方体1111ABCD A B C D -中，P 为底面ABCD 内（含边界）一点．（） A ．若13A P P 点有且只有一个 B ．若12A P ，则点P 的轨迹是一段圆弧 C ．若1//A P 平面11B D C ，则1A P 2D ．若12A P =且1//A P 平面11B DC ，则平面11A PC 截正方体外接球所得截面的面积为23π【答案】ABD 【分析】选项A ，B 可利用球的截面小圆的半径来判断；由平面1//A BD 平面11B D C ，知满足1//A P 平面11B D C 的点P 在BD 上，1A P 长的最大值为2；结合以上条件点P 与B 或D 重合，利用12sin 60A P r =︒，求出63r =，进而求出面积. 【详解】对A 选项，如下图：由13A P =，知点P 在以1A 为球心，半径为3的球上，又因为P 在底面ABCD 内（含边界），底面截球可得一个小圆，由1A A ⊥底面ABCD ，知点P 的轨迹是在底面上以A 为圆心的小圆圆弧，半径为22112r A P A A =-=，则只有唯一一点C满足，故A 正确；对B 选项，同理可得点P 在以A 为圆心，半径为22111r A P A A =-=的小圆圆弧上，在底面ABCD 内（含边界）中，可得点P 轨迹为四分之一圆弧BD .故B 正确；对C 选项，移动点P 可得两相交的动直线与平面11B D C 平行，则点P 必在过1A 且与平面11B D C 平行的平面内，由平面1//A BD 平面11B D C ，知满足1//A P 平面11B D C 的点P 在BD上，则1A P 长的最大值为12A B C 不正确；对选项D ，由以上推理可知，点P 既在以A 为圆心，半径为1的小圆圆弧上，又在线段BD 上，即与B 或D 重合，不妨取点B ，则平面11A PC 截正方体外接球所得截面为11A BC 的外接圆，利用2126622,,sin 603A B r r S r ππ==∴=∴==︒.故D 正确.故选：ABD 【点睛】（1）平面截球所得截面为圆面，且满足222=R r d +（其中R 为球半径，r 为小圆半径，d 为球心到小圆距离）；（2）过定点A 的动直线平行一平面α，则这些动直线都在过A 且与α平行的平面内.4．正方体1111ABCD A B C D -中，E 是棱1DD 的中点，F 在侧面11CDD C 上运动，且满足1//B F 平面1A BE .以下命题正确的有（）A ．侧面11CDD C 上存在点F ，使得11B F CD ⊥ B ．直线1B F 与直线BC 所成角可能为30︒C ．平面1A BE 与平面11CDD C 所成锐二面角的正切值为2D ．设正方体棱长为1，则过点E ，F ，A 5【答案】AC 【分析】取11C D 中点M ，1CC 中点N ，连接11,,B M B N MN ，易证得平面1//B MN 平面1A BE ，可得点F 的运动轨迹为线段MN ．取MN 的中点F ，根据等腰三角形的性质得1B F MN ⊥，即有11B F CD ⊥，A 正确；当点F 与点M 或点N 重合时，直线1B F 与直线BC 所成角最大，可判断B 错误；根据平面1//B MN 平面1A BE ，11B FC ∠即为平面1B MN 与平面11CDD C 所成的锐二面角，计算可知C 正确；取11C D 中点M ，1CC 中点N ，连接11,,B M B N MN ，则易证得11//B N A E ，1//MN A B ，从而平面1//B MN 平面1A BE ，所以点F 的运动轨迹为线段MN ．取MN 的中点F ，因为1B MN △是等腰三角形，所以1B F MN ⊥，又因为1//MN CD ，所以11B F CD ⊥，故A 正确；设正方体的棱长为a ，当点F 与点M 或点N 重合时，直线1B F 与直线BC 所成角最大，此时11tan C B F ∠=1tan 3023︒<=，所以B 错误；平面1//B MN 平面1A BE ，取F 为MN 的中点，则1MN C F ⊥，1MN B F ⊥，∴11B FC ∠即为平面1B MN 与平面11CDD C 所成的锐二面角，11111tan B C B FC C F∠==22，所以C 正确；因为当F 为1C E 与MN 的交点时，截面为菱形1AGC E （G 为1BB 的交点），面积为6，故D 错误. 故选：AC.【点睛】本题主要考查线面角，二面角，截面面积的求解，空间几何中的轨迹问题，意在考查学生的直观想象能力和数学运算能力，综合性较强，属于较难题．5．在长方体1111ABCD A B C D -中，23AB =12AD AA ==，,,P Q R 分别是11,,AB BB AC 上的动点，下列结论正确的是（） A ．对于任意给定的点P ，存在点Q 使得1D P CQ ⊥ B ．对于任意给定的点Q ，存在点R 使得1D R CQ ⊥ C ．当1AR A C ⊥时，1AR D R ⊥D ．当113AC A R =时，1//D R 平面1BDC 【答案】ABD如图所示建立空间直角坐标系，计算142D P CQ b ⋅=-，()12222D R CQ b λλ⋅=--，134AR D R ⋅=-，10D R n ⋅=，得到答案.【详解】如图所示，建立空间直角坐标系，设()2,,0P a，a ⎡∈⎣，()Q b ，[]0,2b ∈，设11A R AC λ=，得到()22,22R λλ--，[]0,1λ∈. ()12,,2P a D -=，()2,0,CQ b =，142D P CQ b ⋅=-，当2b =时，1D P CQ ⊥，A 正确；()122,2D R λλ=--，()12222D R CQ b λλ⋅=--，取22bλ=+时，1D R CQ ⊥，B 正确； 1AR A C ⊥，则()()12,222212440AR AC λλλλλ⋅=--⋅--=-+-+=， 14λ=，此时113313,,02222224AR D R ⎛⎫⎛⎫⋅=-⋅-=-≠ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭，C 错误； 113AC A R =，则4433R ⎛⎫ ⎪ ⎪⎝⎭，14233D R ⎛⎫=- ⎪ ⎪⎝⎭，设平面1BDC 的法向量为(),,n x y z =，则100n BD n DC ⎧⋅=⎪⎨⋅=⎪⎩，解得(3,n =-，故10D R n ⋅=，故1//D R 平面1BDC ，D 正确. 故选：ABD .【点睛】本题考查了空间中的线线垂直，线面平行，意在考查学生的计算能力和空间想象能力，推断能力.6．已知棱长为1的正方体1111ABCD A B C D -，过对角线1BD 作平面α交棱1AA 于点E ，交棱1CC 于点F ，以下结论正确的是（） A ．四边形1BFD E 不一定是平行四边形 B ．平面α分正方体所得两部分的体积相等 C ．平面α与平面1DBB 不可能垂直 D ．四边形1BFD E 面积的最大值为2 【答案】BD 【分析】由平行平面的性质可判断A 错误;利用正方体的对称性可判断B 正确;当E ､F 为棱中点时,通过线面垂直可得面面垂直,可判断C 错误;当E 与A 重合,F 与1C 重合时,四边形1BFD E 的面积最大,且最大值为2,可判断D 正确. 【详解】如图所示,对于选项A,因为平面1111//ABB A CC D D ,平面1BFD E 平面11ABB A BE =,平面1BFD E平面111CC D D D F =,所以1//BE D F ,同理可证1//D E BF ,所以四边形1BFD E 是平行四边形,故A 错误; 对于选项B,由正方体的对称性可知,平面α分正方体所得两部分的体积相等,故B 正确; 对于选项C,在正方体1111ABCD A B C D -中,有1,AC BD AC BB ⊥⊥, 又1BD BB B ⋂=,所以AC ⊥平面1BB D , 当E ､F 分别为棱11,AA CC 的中点时, 有//AC EF ,则EF ⊥平面1BB D , 又因为EF ⊂平面1BFD E ,所以平面1BFD E ⊥平面1BB D ,故C 错误;对于选项D,四边形1BFD E 在平面ABCD 内的投影是正方形ABCD , 当E 与A 重合,F 与1C 重合时,四边形1BFD E 的面积有最大值, 此时1212S D E BE =⋅=⋅=,故D 正确; 故选:BD. 【点睛】本题考查了正方体的几何性质与应用问题,也考查了点线面的位置关系应用问题,属于中档题.7．在正方体1111ABCD A B C D -中，如图，,M N 分别是正方形ABCD ，11BCC B 的中心.则下列结论正确的是（）A ．平面1D MN 与11BC 的交点是11B C 的中点 B ．平面1D MN 与BC 的交点是BC 的三点分点 C ．平面1D MN 与AD 的交点是AD 的三等分点 D ．平面1D MN 将正方体分成两部分的体积比为1∶1 【答案】BC 【分析】取BC 的中点E ，延长DE ，1D N ，并交于点F ，连FM 并延长分别交,BC AD 于,P Q ，连1,D Q PN 并延长交11B C 与H ，平面四边形1D HPQ 为所求的截面，进而求出,,P Q H 在各边的位置，利用割补法求出多面体11QPHD C CD 的体积，即可求出结论.【详解】如图，取BC 的中点E ，延长DE ，1D N ，并交于点F ，连接FM 并延长，设FM BC P ⋂=，FM AD Q ⋂=，连接PN 并延长交11B C 于点H .连接1D Q ，1D H ，则平面四边形1D HPQ 就是平面1D MN 与正方体的截面，如图所示.111111////,22NE CC DD NE CC DD ==，NE ∴为1DD F ∆的中位线，E ∴为DF 中点，连BF ， ,,90DCE FBE BF DC AB FBE DCE ∴∆≅∆==∠=∠=︒， ,,A B F ∴三点共线，取AB 中点S ，连MS ，则12//,,23BP FB MS BP MS BC MS FS =∴==， 22111,33236BP MS BC BC PE BC ∴==⨯=∴=， E 为DF 中点，11//,233PE DQ DQ PE BC AD ∴===N 分别是正方形11BCC B 的中心，11113C H BP C B ∴==所以点P 是线段BC 靠近点B 的三等分点，点Q 是线段AD 靠近点D 的三等分点，点H 是线段11B C 靠近点1C 的三等分点. 做出线段BC 的另一个三等分点P '，做出线段11A D 靠近1D 的三等分点G ，连接QP '，HP '，QG ，GH ，1H QPP Q GHD V V '--=，所以111113QPHD C CD QPHQ DCC D V V V -==多面体长方体正方体从而平面1D MN 将正方体分成两部分体积比为2∶1. 故选:BC.【点睛】本题考查直线与平面的交点及多面体的体积，确定出平面与正方体的交线是解题的关键，考查直观想象、逻辑推理能力，属于较难题.8．如果一个棱锥的底面是正方形，且顶点在底面内的射影是底面的中心，那么这样的棱锥叫正四棱锥．若一正四棱锥的体积为18，则该正四棱锥的侧面积最小时，以下结论正确的是（）．A ．棱的高与底边长的比为22B ．侧棱与底面所成的角为4π C ．棱锥的高与底面边长的比为2 D ．侧棱与底面所成的角为3π 【答案】AB 【分析】设四棱锥S ABCD -的高为h ，底面边长为a ，由21183V a h ==得254h a=，然后可得侧面积为242108a a+，运用导数可求出当32a =时侧面积取得最小值，此时3h =，然后求出棱锥的高与底面边长的比和SAO ∠即可选出答案. 【详解】设四棱锥S ABCD -的高为h ，底面边长为a 可得21183V a h ==，即254h a=所以其侧面积为2222244215410842244a a a h a a a a⋅⋅+=+=+ 令()242108f a a a =+，则()23321084f a a a⨯'=- 令()233210840f a a a⨯'=-=得32a = 当()0,32a ∈时()0f a '<，()f a 单调递减当()32,a ∈+∞时()0f a '>，()f a 单调递增所以当32a =时()f a 取得最小值，即四棱锥的侧面积最小此时3h =所以棱锥的高与底面边长的比为22，故A 正确，C 错误侧棱与底面所成的角为SAO ∠，由3h =，32a =可得3AO = 所以4SAO π∠=，故B 正确，D 错误故选：AB 【点睛】本题考查的知识点有空间几何体的体积和表面积、线面角及利用导数求最值，属于综合题.9．如图，正三棱柱11ABC A B C -中，11BC AB ⊥、点D 为AC 中点，点E 为四边形11BCC B 内（包含边界）的动点则以下结论正确的是（）A ．()1112DA A A B A BC =-+ B ．若//DE 平面11ABB A ，则动点E 2AC C ．异面直线AD 与1BC ，所成角的余弦值为66D ．若点E 到平面11ACC A 3EB ，则动点E 的轨迹为抛物线的一部分【答案】BCD 【分析】根据空间向量的加减法运算以及通过建立空间直角坐标系求解，逐项判断，进而可得到本题答案. 【详解】解析：对于选项A ，()1112AD A A B A BC =-+，选项A 错误；对于选项B ，过点D 作1AA 的平行线交11A C 于点1D ．以D 为坐标原点，1DA DB DD ,,分别为,,x y z 轴的正方向建立空间直角坐标系Oxyz ．设棱柱底面边长为a ，侧棱长为b ，则002a A ⎛⎫⎪⎝⎭,,，00B ⎛⎫ ⎪ ⎪⎝⎭,，10B b ⎛⎫ ⎪ ⎪⎝⎭,，102a C b ⎛⎫- ⎪⎝⎭,,，所以122a BC a b ⎛⎫=-- ⎪ ⎪⎝⎭,,，122a AB a b ⎛⎫=- ⎪ ⎪⎝⎭,,． ∵11BC AB ⊥，∴110BC AB ⋅=，即222022a a b ⎛⎫⎛⎫--+= ⎪ ⎪ ⎪⎝⎭⎝⎭，解得2b a =．因为//DE 平面11ABB A ，则动点E的轨迹的长度等于1BB =．选项B 正确．对于选项C ，在选项A 的基础上，002a A ⎛⎫⎪⎝⎭,,，00B ⎛⎫ ⎪ ⎪⎝⎭,，()0,0,0D ，1022a C a ⎛⎫- ⎪ ⎪⎝⎭,,，所以002a DA ⎛⎫= ⎪⎝⎭,,，1222a BC a ⎛⎫=- ⎪ ⎪⎝⎭,-,，因为2111cos ,||||aBC DA BC DA BC DA a ⎛⎫- ⎪⋅<>===1,BC DA 所成角C 正确．对于选项D，设点E 在底面ABC 的射影为1E ，作1E F 垂直于AC ，垂足为F ，若点E 到平面11ACC A 的距离等于2EB ，即有12E F EB =，又因为在1CE F ∆中，11E F C =，得1EB E C =，其中1E C 等于点E 到直线1CC 的距离，故点E 满足抛物线的定义，另外点E 为四边形11BCC B 内（包含边界）的动点，所以动点E 的轨迹为抛物线的一部分,故D 正确.故选：BCD 【点睛】本题主要考查立体几何与空间向量的综合应用问题，其中涉及到抛物线定义的应用.10．如图，1111ABCD A B C D -为正方体，下列结论中正确的是（）A ．11A C ⊥平面11BB D D B ．1BD ⊥平面1ACBC ．1BD 与底面11BCC B 2 D ．过点1A 与异面直线AD 与1CB 成60角的直线有2条【答案】ABD 【分析】由直线与平面垂直的判定判断A 与B ；求解1BD 与底面11BCC B 所成角的正切值判断C ；利用空间向量法可判断D ．【详解】对于A 选项，如图，在正方体1111ABCD A B C D -中，1BB ⊥平面1111D C B A ，11A C ⊂平面1111D C B A ，则111BB A C ⊥，由于四边形1111D C B A 为正方形，则1111AC B D ⊥， 1111BB B D B =，因此，11A C ⊥平面11BB D D ，故A 正确；对于B 选项，在正方体1111ABCD A B C D -中，1DD ⊥平面ABCD ，AC ⊂平面ABCD ，1AC DD ∴⊥，因为四边形ABCD 为正方形，所以，AC BD ⊥，1D DD BD =，AC ∴⊥平面11BB D D ， 1BD ⊂平面11BB D D ，1AC BD ∴⊥，同理可得11BD B C ⊥，1ACB C C =，1BD ∴⊥平面1ACB ，故B 正确；对于C 选项，由11C D ⊥平面11BCC B ，得11C BD ∠为1BD 与平面11BCC B 所成角，且111112tan 2C D C BD BC ∠==，故C 错误；对于D 选项，以点D 为坐标原点，DA 、DC 、1DD 所在直线分别为x 、y 、z 轴建立如下图所示的空间直角坐标系，设正方体的棱长为1，则()1,0,0A 、()0,0,0D 、()0,1,0C 、()11,1,1B ，()1,0,0DA =，()11,0,1CB =，设过点1A 且与直线DA 、1CB 所成角的直线的方向向量为()1,,m y z =，则221cos ,21DA m DA m DA my z ⋅<>===⋅++， 1122111cos ,221CB m zCB m CB my z ⋅+<>===⋅⋅++，整理可得2222341y z y z z ⎧+=⎨=++⎩，消去y 并整理得2210z z +-=，解得12z =-12z =-由已知可得3z ≤，所以，12z =-+22y =± 因此，过点1A 与异面直线AD 与1CB 成60角的直线有2条，D 选项正确. 故选：ABD. 【点睛】方法点睛：证明线面垂直的方法：一是线面垂直的判定定理；二是利用面面垂直的性质定理；三是平行线法（若两条平行线中一条垂直于这个平面，则另一条也垂直于这个平面），解题时，注意线线、线面与面面关系的相互转化；另外，在证明线线垂直时，要注意题中隐含的垂直关系，如等腰三角形的底边上的高、中线和顶角的角平分线三线合一、矩形的内角、直径所对的圆周角、菱形的对角线互相垂直、直角三角形（或给出线段长度，经计算满足勾股定理）、直角梯形等等．。

欣宜市实验学校二零二一学年度高中数学高考二轮复习跟踪测试：立体几何国通用试题

黔西北州欣宜市实验学校二零二一学年度2021届高考二轮复习跟踪测试(立体几何)数学试卷本卷须知：1.本卷一共150分，考试时间是是100分 2.题型难度:中等难度 3.考察范围：立体几何4.试题类型：选择题12道，填空题4道，简答题6道。

6.试卷类型：高考二轮复习专题训练一、选择题1.有一个几何体的三视图及其尺寸如下〔单位：cm 〕，那么该几何体的外表积和体积为()A.3212,24cm cm ππB.3212,15cm cm ππ C.3236,24cm cm ππ2.地球半径为R ，在北纬︒30的纬线上有两点A 、B ，A 点在东经︒120上，B 点在西经︒60，那么A 、B 两点的球面间隔〔〕A ．R π31B ．R π21C ．R π23D ．R π32侧视63.正六棱锥的斜高为3，侧面与底面所成的角为︒30，那么它的体积〔〕A ．432B ．49C ．429D ．833 4.长方体的一个顶点上三条棱长是3、4、5，且它的八个顶点都在同一球面上，这个球的体积是〔〕A ．π125B ．π2125C ．π50D ．π321255.直线b a //，α⊂b ，那么直线a 与平面α的位置关系〔〕A ．平行B ．在平面内C ．平行或者在平面内D ．相交或者平行 6.以下命题正确的选项是〔〕 A ．两个平面可以只有一个交点B ．一条直线与一个平面最多有一个公一共点C ．两个平面有一个公一共点，它们必有一条交线D ．两个平面有三个公一共点，它们一定重合7.平面α//平面β的一个充分条件是8.空间四边形ABCD ，假设AB 、AC 、AD 与平面BCD 所成角相等，那么A 点在平面BCD 的射影为BCD ∆的〔〕 A ．外心B ．内心C ．重心D ．垂心9.将正方形ABCD 沿对角线BD 折起，使平面ABD ⊥平面CBD ，E 是CD 的中点，那么异面直线AE 、BC 所成角的正切值为〔〕A ．2B ．22 C ．2 D ．21 10.长方体''''D C B A ABCD -'AB 与CD 的间隔〔〕A ．3B ．2C ．32D ．1311.在正四棱柱1111ABCD A B C D -中，顶点1B 到对角线1BD 和到平面11A BCD 的间隔分别为h 和d ，那么以下命题中正确的选项是〔〕A ．假设侧棱的长小于底面的变长，那么h d的取值范围为(0,1)B ．假设侧棱的长小于底面的变长，那么h d 的取值范围为C ．假设侧棱的长大于底面的变长，那么h d 的取值范围为D ．假设侧棱的长大于底面的变长，那么h d的取值范围为)+∞ 12.正三棱锥ABC S —的侧棱长和底面边长相等，假设E 、F 分别为SC ，AB 的中点，那么异面直线EF 与SA 所成角为〔〕 A ．090B ．060C ．045D ．030 二、填空题13.ABC ∆的三个项点在同一球面上，.2,90==︒=∠AC AB BAC 假设球心O 到平面ABC 的间隔为1，那么该球的半径为。

2021高考数学复习单元测试(理)：立体几何(含答案)

高考数学复习单元测试（理）：立体几何（含答案）单元质量测试(六)时间：120分钟满分：150分第Ⅰ卷(选择题，共60分)一、选择题(本大题共12小题，每小题5分，共60分)1．某空间几何体的三视图中，有一个是正方形，则该空间几何体不可能是( ) A．圆柱 B．圆锥 C．棱锥 D．棱柱答案 B解析易知仅圆锥的三视图中一定不会出现正方形，故选B．2．(2018·郑州检测)已知一三棱锥的俯视图与侧视图如图所示，俯视图是边长为2的正三角形，侧视图是有一条直角边为2的直角三角形，则该三棱锥的正视图可能为( )答案 C解析由已知条件得直观图如图所示，正视图是直角三角形，中间的线是看不见的线PA形成的投影，应为虚线．故选C．3．已知各顶点都在一个球面上的正四棱柱的高为2，这个球的表面积为6π，则这个正四棱柱的体积为( )A．1 B．2 C．3 D．4答案 B解析 S 表＝4πR 2＝6π，∴R ＝62，设正四棱柱底面边长为x ，则x 2＋x 2＋22＝(2R )2，∴x ＝1．∴V 正四棱柱＝2．故选B ．4．(2018·贵阳模拟)设m ，n 为两条不同的直线，α，β为两个不同的平面，给出下列命题：①若m ⊥α，m ⊥β，则α∥β； ②若m ∥α，m ∥β，则α∥β； ③若m ∥α，n ∥α，则m ∥n ； ④若m ⊥α，n ⊥α，则m ∥n ．上述命题中，所有真命题的序号是( ) A ．①④ B ．②③ C ．①③ D ．②④ 答案 A解析对于①，垂直于同一条直线的两个平面互相平行，所以①正确；对于②，平行于同一条直线的两个平面的位置关系不确定，所以②错误；对于③，平行于同一个平面的两条直线的位置关系不确定，所以③错误；对于④，垂直于同一个平面的两条直线互相平行，所以④正确．故选A ．5．(2018·太原三模)如图是某几何体的三视图，则这个几何体的体积是( )A ．2＋π2B ．2＋π3C ．4＋π3D ．4＋π2答案 A解析由三视图可知，该几何体由一个半圆柱与三棱柱组成，这个几何体的体积V ＝12×π×12×1＋12×(2)2×2＝2＋π2．故选A ．6．(2018·江西赣州二模)某几何体的主视图和左视图如图1，它的俯视图的直观图是矩形O1A1B1C1，如图2，其中O1A1＝6，O1C1＝2，则该几何体的侧面积为( )A．48 B．64 C．96 D．128答案 C解析由题图2及斜二测画法可知原俯视图为如图所示的平行四边形OABC，设CB与y 轴的交点为D，则易知CD＝2，OD＝2×22＝42，∴CO＝CD2＋OD2＝6＝OA，∴俯视图是以6为边长的菱形，由三视图知几何体为一个直四棱柱，其高为4，所以该几何体的侧面积为4×6×4＝96．故选C．7．(2018·郑州质检三)已知A，B，C，D四点在半径为5的球面上，且AC＝BD＝4，AD ＝BC＝11，AB＝CD，则三棱锥D－ABC的体积是( )A．67 B．47 C．27 D．7答案 C解析如图所示，将三棱锥D－ABC放在长、宽、高分别为a，b，c的长方体中，则依题意有⎩⎪⎨⎪⎧a 2＋c 2＝AC 2＝16，a 2＋b 2＝BC 2＝11，a 2＋b 2＋c 2＝(2R )2＝20，解得⎩⎨⎧a ＝7，b ＝2，c ＝3，则三棱锥D －ABC 的体积为abc －413·12abc ＝27．选C ．8．(2018·山西四校联考)如图所示，P 为矩形ABCD 所在平面外一点，矩形对角线交点为O ，M 为PB 的中点，给出下列五个结论：①PD ∥平面AMC ；②OM ∥平面PCD ；③OM ∥平面PDA ；④OM ∥平面PBA ；⑤OM ∥平面PBC ．其中正确的个数是( ) A ．1 B ．2 C ．3 D ．4 答案 C解析矩形ABCD 的对角线AC 与BD 交于点O ，所以O 为BD 的中点．在△PBD 中，M 是PB 的中点，所以OM 是△PBD 的中位线，OM ∥PD ，则PD ∥平面AMC ，OM ∥平面PCD ，且OM ∥平面PDA ．因为M ∈PB ，所以OM 与平面PBA 、平面PBC 相交．故选C ．9．(2018·大庆质检一)已知一个圆柱的轴截面是边长为a 的正方形．在圆柱内有一个球O ，该球与圆柱的上、下底面及母线均相切，则圆柱内除了球之外的几何体的体积为( )A ．πa 34 B ．πa 36 C ．πa 38 D ．πa312答案 D解析由题意可知，该圆柱底面直径和高都是a ，故其体积为V 1＝πR 2h ＝π×a 22×a ＝πa 34．而圆柱体的内切球的直径也为a ，故其体积为V 2＝4π3R 3＝4π3×a 23＝πa36，所以圆柱体内除球体以外部分的体积为V ＝V 1－V 2＝πa 312．故选D ．10．(2018·湖南长沙四校联考)祖暅是南北朝时代的伟大数学家，5世纪末提出体积计算原理，即祖暅原理：“幂势既同，则积不容异”．意思是：夹在两个平行平面之间的两个几何体，被平行于这两个平面的任何一个平面所截，如果截面面积都相等，那么这两个几何体的体积一定相等．现有以下四个几何体：图①是从圆柱中挖去一个圆锥所得的几何体，图②、图③、图④分别是圆锥、圆台和半球，则满足祖暅原理的两个几何体为( )A ．①② B．①③ C．②④ D．①④ 答案 D解析设截面与底面的距离为h ，则①中截面内圆的半径为h ，则截面圆环的面积为π(R 2－h 2)；②中截面圆的半径为R －h ，则截面圆的面积为π(R －h )2；③中截面圆的半径为R －h2，则截面圆的面积为πR －h 22；④中截面圆的半径为R 2－h 2，则截面圆的面积为π(R2－h 2)．所以①④中截面的面积相等，故其体积相等，故选D ．11．(2018·浙江高考)已知四棱锥S －ABCD 的底面是正方形，侧棱长均相等，E 是线段AB 上的点(不含端点)．设SE 与BC 所成的角为θ1，SE 与平面ABCD 所成的角为θ2，二面角S －AB －C 的平面角为θ3，则( )A ．θ1≤θ2≤θ3B ．θ3≤θ2≤θ1C ．θ1≤θ3≤θ2D ．θ2≤θ3≤θ1 答案 D解析由题意知该四棱锥为正四棱锥，设AB ，AD ，BC 的中点分别为P ，M ，N 连接MN ，过点E 作直线MN 的垂线交MN 于点Q ．设O 为S 在底面ABCD 内的射影，连接SO ，OP ，OE ，SP ，SQ ，则∠SEQ ＝θ1，∠SEO ＝θ2，∠SPO ＝θ3，∴tan θ2＝OS OE ，tan θ3＝OSOP，∵OP ≤OE ，∴tan θ3≥tan θ2．又EQ ⊥MN ，EQ ⊥SO ，MN ∩SO ＝O ，MN ，SO ⊂平面SOQ ，∴EQ ⊥平面SOQ ，又SQ ⊂平面SOQ ，∴EQ ⊥SQ ．∴tan θ1＝SQEQ，∵SQ ≥SO ，EQ ＝OP ，∴tan θ1≥tan θ3．故有tan θ1≥tan θ3≥tan θ2．由图可知θ1，θ2，θ3∈0，π2．∴θ1≥θ3≥θ2，故选D ．12．(2018·全国卷Ⅰ)已知正方体的棱长为1，每条棱所在直线与平面α所成的角相等，则α截此正方体所得截面面积的最大值为( )A ．334B ．233C ．324D ．32答案 A解析根据相互平行的直线与平面所成的角是相等的，所以在正方体ABCD －A 1B 1C 1D 1中，平面AB 1D 1与线AA 1，A 1B 1，A 1D 1所成的角是相等的，所以平面AB 1D 1与正方体的每条棱所在的直线所成角都是相等的，同理平面C 1BD 也满足与正方体的每条棱所在的直线所成的角都是相等的，要求截面面积最大，则截面的位置为夹在两个面AB 1D 1与C 1BD 中间的，且过棱的中点的正六边形，边长为22，所以其面积为S ＝6×34×⎝ ⎛⎭⎪⎫222＝334，故选A ．第Ⅱ卷 (非选择题，共90分)二、填空题(本大题共4小题，每小题5分，共20分)13．如图，一个底面半径为R 的圆柱形量杯中装有适量的水．若放入一个半径为r 的实心铁球，水面高度恰好升高r ，则R r＝________．答案233解析由水面高度升高r ，得圆柱体积增加πR 2r ，恰好是半径为r 的实心铁球的体积，因此有43πr 3＝πR 2r ．故R r ＝233．14．直三棱柱ABC －A 1B 1C 1的六个顶点都在球O 的球面上．若AB ＝BC ＝2，∠ABC ＝90°，AA 1＝22，则球O 的表面积为________．答案16π解析由题设可知，直三棱柱可以补成一个球的内接长方体，所以球的直径为长方体的体对角线长，即22＋22＋(22)2＝4，故球O的表面积S＝4πR2＝16π．15．已知某几何体的三视图如图所示，则其体积为________．答案8π解析由三视图可知该几何体为一个底面半径为1，高为5的圆柱与一个底面半径为1，高为3的圆柱的组合体，其体积为V＝π×12×(5＋3)＝8π．16．(2018·唐山模拟)已知一个几何体由八个面围成，每个面都是正三角形，有四个顶点在同一平面内且为正方形，若该八面体的棱长为2，所有顶点都在球O上，则球O的表面积为________．答案8π解析依题意，该八面体的各个顶点都在同一球面上，则其中四点所组成的截面在球的大圆面上，因为该八面体的棱长为2，所以这四点组成的正方形的对角线的长为22，故球的半径为2，该球的表面积为4π(2)2＝8π．三、解答题(本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤)17．(2018·珠海摸底)(本小题满分10分)中秋节即将到来，为了做好中秋节商场促销活动，某商场打算将进行促销活动的礼品盒重新设计．方案如下：将一块边长为10的正方形纸片ABCD剪去四个全等的等腰三角形(△SEE′，△SFF′，△SGG′，△SHH′)，再将剩下的阴影部分折成一个四棱锥形状的包装盒S－EFGH，其中A，B，C，D重合于点O，E与E′重合，F 与F ′重合，G 与G ′重合，H 与H ′重合(如图所示)．(1)求证：平面SEG ⊥平面SFH ；(2)已知AE ＝52，过O 作OM ⊥SH 于点M ，求cos ∠EMO 的值．解 (1)证明：因为折叠后A ，B ，C ，D 重合于一点O ，所以拼接成底面EFGH 的四个直角三角形必为全等的等腰直角三角形，所以底面EFGH 是正方形，故EG ⊥FH ．因为在原平面图形中，△SEE ′≌△SGG ′，所以SE ＝SG ，所以EG ⊥SO ．又FH ∩SO ＝O ，FH ⊂平面SFH ，SO ⊂平面SFH ，故EG ⊥平面SFH ．又因为EG ⊂平面SEG ，所以平面SEG ⊥平面SFH ． (2)依题意，当AE ＝52时，即OE ＝52．Rt △SHO 中，OH ＝52，SH ＝552，故SO ＝5，所以OM ＝SO ·OHSH＝5．由(1)知EG ⊥平面SFH ，且OM ⊂平面SFH ，故EG ⊥OM ，从而EO ⊥OM ，故Rt △EMO 中，EM ＝EO 2＋OM 2＝352，所以cos ∠EMO ＝OM EM ＝23．18．(2018·安徽江淮十校联考)(本小题满分12分)四棱锥A －BCDE 中，EB ∥DC ，且EB ⊥平面ABC ，EB ＝1，DC ＝BC ＝AB ＝AC ＝2，F 是棱AD 的中点．(1)证明：EF ⊥平面ACD ； (2)求二面角B －AE －D 的余弦值．解 (1)证明：取AC 中点M ，连接FM ，BM ， ∵F 是AD 中点，∴FM ∥DC ，且FM ＝12DC ＝1．又∵EB ∥DC ，EB ＝1， ∴FM 綊EB ，∴四边形FMBE 是平行四边形． ∴EF ∥BM ，又BC ＝AB ＝AC ， ∴△ABC 是等边三角形，∴BM ⊥AC ， ∵EB ⊥平面ABC ，EB ∥DC ， ∴CD ⊥平面ABC ，∴CD ⊥BM ．又CD ∩AC ＝C ，∴BM ⊥平面ACD ，∴EF ⊥平面ACD ．(2)取BC 中点N ，连接AN ，则AN ⊥BC ⇒AN ⊥平面BCD ．以N 为原点建立如图所示的空间直角坐标系．则各点坐标为A (0，0，3)，B (0，－1，0)，C (0，1，0)，D (2，1，0)，E (1，－1，0)．可得BA →＝(0，1，3)，BE →＝(1，0，0)，EA →＝(－1，1，3)，ED →＝(1，2，0)，设平面ABE 的法向量为n 1＝(x 1，y 1，z 1)，则⎩⎪⎨⎪⎧ n 1·BA →＝0，n 1·BE →＝0，得⎩⎨⎧y 1＋3z 1＝0，x 1＝0，可取n 1＝(0，－3，1)，设平面ADE 的法向量为n 2＝(x 2，y 2，z 2)，则⎩⎪⎨⎪⎧n 2·EA →＝0，n 2·ED →＝0，得⎩⎨⎧－x 2＋y 2＋3z 2＝0，x 2＋2y 2＝0，可取n 2＝(－2，1，－3)，于是cos 〈n 1，n 2〉＝－3－32×8＝－64，注意到二面角B －AE －D 是钝二面角，因此，所求二面角的余弦值就是－64． 19．(2018·湖北重点中学联考二)(本小题满分12分)如图1，等腰直角三角形ABC 的底边AB ＝2，点D 在线段AC 上，DE ⊥AB 于点E ，现将△ADE 沿DE 折起到△PDE 的位置(如图2)．(1)求证：PB ⊥DE ；(2)若PE ⊥BE ，直线PD 与平面PBC 所成的角为30°，求平面PDE 与平面PBC 所成的锐二面角的正弦值．解 (1)证明：由图1，图2可知，DE ⊥PE ，DE ⊥BE ，PE ∩BE ＝E ， ∴DE ⊥平面PBE ，又PB ⊂平面PBE ，∴PB ⊥DE ．(2)由(1)及PE ⊥BE 可知，DE ，BE ，PE 两两互相垂直．分别以ED →，EB →，EP →的方向为x 轴、y 轴、z 轴的正方向建立空间直角坐标系Exyz ．设|PE |＝a (0<a <1)，则B (0，2－a ，0)，D (a ，0，0)，C (1，1－a ，0)，P (0，0，a )， ∴PB →＝(0，2－a ，－a )，BC →＝(1，－1，0)．设平面PBC 的法向量为n ＝(x ，y ，z )，则⎩⎪⎨⎪⎧PB →·n ＝0，BC →·n ＝0，∴⎩⎪⎨⎪⎧(2－a )y －az ＝0，x －y ＝0，∴平面PBC 的一个法向量为n ＝(a ，a ，2－a )， ∵直线PD 与平面PBC 所成的角为30°，且PD →＝(a ，0，－a )， ∴sin30°＝|a 2－a (2－a )|2a 2·a 2＋a 2＋(2－a )2，∴a ＝2(舍去)或a ＝25．∴平面PBC 的一个法向量为n ＝25，25，85．易知平面PDE 的一个法向量为m ＝(0，1，0)，设所求的锐二面角为θ，则cos θ＝m ·n |m ||n |＝26，所以sin θ＝346，即平面PDE 与平面PBC 所成的锐二面角的正弦值为346．20．(2018·山东青岛统一质检)(本小题满分12分)如图，圆柱H 横放在底面边长为1的正六棱锥P －ABCDEF 的顶点P 上，O 1和O 2分别是圆柱左和右两个底面的圆心，正六棱锥P－ABCDEF 的底面中心为O ，PO ＝1，M ，N 分别是圆柱H 的底面圆O 1的最高点和最低点，G 是圆柱H 的底面圆O 2的最低点，P 为NG 的中点，点M ，O 1，N ，A ，O ，D ，G ，P 共面，O 1，P ，D 共线，四边形ADGN 为矩形．(1)证明：MG ∥平面PCD ； (2)求二面角M －CD －A 的大小．注：正棱锥就是底面是一个正多边形，顶点在底面上的正投影为底面的中心的棱锥．解 (1)证明：连接PO 1(图略)，∵P 为NG 的中点，O 1为MN 的中点，∴PO 1∥MG ，又点O 1，P ，D 共线，∴PD ∥MG ， ∵PD ⊂平面PCD ，MG ⊄平面PCD ， ∴MG ∥平面PCD ．(2)∵O 为正六棱锥P －ABCDEF 的底面中心， ∴PO ⊥底面ABCDEF ，取BC 的中点W (图略)，连接OW ，AD ，则点O 在AD 上，OW ⊥AD ．分别以OA ，OW ，OP 为x 轴、y 轴、z 轴建立空间直角坐标系Oxyz ． ∵P 为NG 的中点，四边形ADGN 为矩形，O 为AD 的中点，PO ＝1， ∴NA ∥PO ，NA ＝PO ＝1，从而NA ⊥底面ABCDEF ， ∵M ，N 分别是圆柱H 的底面圆O 1的最高点和最低点， ∴O 1N ⊥底面ABCDEF ，从而M ，O 1，N ，A 四点共线， ∵正六棱锥P －ABCDEF 的底面边长为1，∴AD ＝2， ∵四边形ADGN 为矩形，NG ∥AD ，且NG ＝AD ＝2，又P 为NG 的中点，NP ∥AD ，且NP ＝12AD ＝1，∴在△O 1AD 中，NP 为△O 1AD 的中位线，从而N 为O 1A 的中点，∴O 1N ＝AN ＝1，故M (1，0，3)，C －12，32，0，D (－1，0，0)，DC →＝12，32，0，DM →＝(2，0，3)．设平面MCD 的法向量为m ＝(x ，y ，z )，由⎩⎪⎨⎪⎧m ·DC →＝0，m ·DM →＝0⇒⎩⎪⎨⎪⎧x 2＋3y 2＝0，2x ＋3z ＝0.令x ＝1，则y ＝－33，z ＝－23， ∴m ＝1，－33，－23．取平面ABCDEF 的一个法向量为n ＝OP →＝(0，0，1)．设二面角M －CD －A 的大小为锐角θ，则cos θ＝|m ·n ||m ||n |＝12，因此θ＝π3，即二面角M －CD －A 的大小为π3．21．(2018·河北衡水中学九模)(本小题满分12分)已知正三棱柱ABC －A 1B 1C 1中，E ，F 分别为BB 1，AB 的中点，设AA 1AB＝λ．(1)求证：平面A 1CF ⊥平面A 1EF ；(2)若二面角F －EA 1－C 的平面角为π3，求实数λ的值，并判断此时二面角E －CF －A 1是否为直二面角，请说明理由．解 (1)证明：因为三棱柱ABC －A 1B 1C 1是正三棱柱，所以AA 1⊥平面ABC ，所以AA 1⊥CF ．又△ABC 是正三角形，F 为AB 的中点，所以CF ⊥AB ，又AB ∩AA 1＝A ，故CF ⊥平面A 1EF ，又CF ⊂平面A 1CF ，所以平面A 1CF ⊥平面A 1EF ．(2)如图，以F 为坐标原点，FB →，FC →方向分别为x 轴、y 轴的正方向建立如图所示的空间直角坐标系，不妨设底边长AB ＝2，由题意AA 1＝2λ，则F (0，0，0)，A 1(－1，0，2λ)，E (1，0，λ)，C (0，3，0)． EC →＝(－1，3，－λ)，FC →＝(0，3，0)，A 1E →＝(2，0，－λ)，设平面EA 1C 的法向量为n ＝(x ，y ，z )，则⎩⎪⎨⎪⎧n ·EC →＝－x ＋3y －λz ＝0，n ·A 1E →＝2x －λz ＝0，令z ＝2，则平面EA 1C 的一个法向量为n ＝(λ，3λ，2)，由(1)可知FC →＝(0，3，0)为平面A 1EF 的一个法向量，故cos π3＝FC →·n |FC →||n |＝3λ4λ2＋4×3，解得λ＝22，由(1)可知EF ⊥CF ，A 1F ⊥CF ，由定义可知∠EFA 1为二面角E －CF －A 1的平面角．EF ＝12＋222＝62，A 1F ＝12＋(2)2＝3， A 1E ＝22＋222＝322，满足EF 2＋A 1F 2＝A 1E 2，则∠EFA 1＝π2，此时二面角E －CF －A 1为直二面角．22．(2018·江西南昌二模)(本小题满分12分)如图，四棱锥P －ABCD 中，底面ABCD 是直角梯形，AB ∥CD ，AB ⊥AD ，AB ＝2CD ＝2AD ＝4，侧面PAB 是等腰直角三角形，PA ＝PB ，平面PAB ⊥平面ABCD ，点E ，F 分别是棱AB ，PB 上的点，平面CEF ∥平面PAD ．(1)确定点E ，F 的位置，并说明理由； (2)求二面角D －EF －C 的余弦值．解 (1)因为平面CEF ∥平面PAD ，平面CEF ∩平面ABCD ＝CE ，平面PAD ∩平面ABCD ＝AD ，所以CE ∥AD ，又因为AB ∥DC ，所以四边形AECD 是平行四边形，所以DC ＝AE ＝12AB ，即点E 是AB 的中点．因为平面CEF ∥平面PAD ，平面CEF ∩平面PAB ＝EF ，平面PAD ∩平面PAB ＝PA ，所以EF ∥PA ，因为点E 是AB 的中点，所以点F 是PB 的中点，综上，E ，F 分别是AB ，PB 的中点． (2)连接PE ，因为PA ＝PB ，AE ＝EB ，所以PE ⊥AB ，又因为平面PAB ⊥平面ABCD ，平面PAB ∩平面ABCD ＝AB ，所以PE ⊥平面ABCD ，又因为AB ⊥AD ，所以CE ⊥AB ．如图，以点E 为坐标原点，EC ，EB ，EP 所在直线分别为x 轴、y 轴、z 轴建立空间直角坐标系，则B (0，2，0)，C (2，0，0)，D (2，－2，0)，E (0，0，0)，P (0，0，2)，由中点公式得到F (0，1，1)，则EC →＝(2，0，0)，EF →＝(0，1，1)，ED →＝(2，－2，0)，设平面CEF 、平面DEF 的法向量分别为m ＝(x 1，y 1，z 1)，n ＝(x 2，y 2，z 2)，由m ⊥EC →，m ⊥EF →，得⎩⎪⎨⎪⎧2x 1＋0·y 1＋0·z 1＝0，0·x 1＋y 1＋z 1＝0，令y 1＝1，得m ＝(0，1，－1)，由n ⊥ED →，n ⊥EF →，得⎩⎪⎨⎪⎧2x 2－2y 2＋0·z 2＝0，0·x 2＋y 2＋z 2＝0，令y 2＝1，得n ＝(1，1，－1)，所以cos 〈m ·n 〉＝m ·n |m ||n |＝22×3＝63，因为二面角D －EF －C 是锐角，所以二面角D －EF －C 的余弦值是63．。

2021届高考数学二轮复习常考题型大通关(新高考)选择题：立体几何

2021届高考数学二轮复习常考题型大通关（新高考）选择题：立体几何1.已知圆锥的底面半径为2，高为42，则该圆锥内切球的表面积为( ) A.4πB.42πC.82πD.8π2.某同学在参加《通用技术》实践课时，制作了一个工艺品，如图所示，该工艺品可以看成是一个球被一个棱长为43的正方体的六个面所截后剩余的部分(球心与正方体的中心重合)，若其中一个截面圆的周长为4π，则该球的半径是( )A.2B.4C.26D.463.《九章算术》是我国古代的数学名著，书中提到了一种名为“刍甍”的五面体(如图)：底面ABCD 为矩形，棱EFAB .若此几何体中，4,2,AB EF ADE ==和BCF 都是边长为2的等边三角形，则此几何体的表面积为( )A.83B.883+C.6223D.86223+4.已知ABC 93O 的球面上.若球O 的表面积为16π，则O 到平面ABC 的距离为( ) 3 B.32C.1 3 5.已知,a b 是两条异面直线，α是一个平面，直线c 与,a b 都垂直，则下列说法正确的是( )A.若c α⊂，则a α⊥B.若c α⊥，则,ab ααC.存在α，使得,,c a b ααα⊥⊂D.存在α，使得,,c a b ααα⊥⊥6.在三棱柱111ABC A B C -中，1AA ⊥平面1,,2ABC AB BC AA BC AB ⊥==，则异面直线1A B 与1B C 所成角的余弦值为( )A.25B.5 C.15 D.10 7.在四面体P ABC -中，,,PA PB PC 两两垂直，设PA PB PC a ===，则点P 到平面ABC 的距离为( ) A.6a B.3a C.3a D.6a8.已知,m n 表示两条不同的直线，α表示平面，下列说法正确的是( ) A.若,m n αα，则m nB.若,m n αα⊥⊥，则m nC.若,m m n α⊥⊥，则nα D.若,mm n α⊥，则n α⊥9.在长方体1111ABCD A B C D -中，1AB BC ==，异面直线1AD 与BD 所成角的余弦值为10，则1AA =( ) A.1B.2C.19D.2210.已知四棱锥P ABCD -的体积是363，底面ABCD 是正方形，PAB 是等边三角形，平面PAB ⊥平面ABCD ，则四棱锥P ABCD -的外接球的体积为( ) A.2821πB.9911π C.637π D.1083π11.如图，点E 是正方体1111ABCD A B C D -的棱1DD 的中点，点,F M 分别在线段1,AC BD (不包含端点)上运动，则( )A.在点F 的运动过程中，存在1EFBCB.在点M 的运动过程中，不存在1B M AE ⊥C.四面体EMAC 的体积为定值D.四面体11FAC B 的体积不为定值12.已知,,,A B C D 四点均在球O 的球面上，ABC 是边长为6的等边三角形，点D 在平面ABC 上的射影为ABC 的中心，E 为线段AD 的中点，若BD CE ⊥，则球O 的表面积为( ) A.36πB.42πC.54πD.246π13.如图，在正方体1111ABCD A B C D -中，F 是棱11A D 上的动点.下列说法正确的是( )A.对任意动点F ，在平面11ADD A 内不存在与平面CBF 平行的直线B.对任意动点F ，在平面ABCD 内存在与平面CBF 垂直的直线C.点F 从1A 运动到1D 的过程中，FC 与平面ABCD 所成的角逐渐变大D.点F 从1A 运动到1D 的过程中，点D 到平面CBF 的距离逐渐变小14.如图，点,M N 分别是棱长为2的正方体1111ABCD A B C D -中棱1,BC CC 的中点，动点P 在正方形11BCC B (包括边界)内运动，若1A P平面AMN ，则1A P 的取值范围是( )A.[2,5]B.325⎡⎤⎢⎥⎣C.32⎤⎥⎣⎦D.[2,22]15.将边长为1的正方形ABCD沿BD翻折，使得二面角A BD C--的平面角的大小为π3，若点,E F分别是线段AC和BD上的动点，则BE CF⋅的取值范围为( )A.[1,0]- B.11,4⎡⎤-⎢⎥⎣⎦C.1,02⎡⎤-⎢⎥⎣⎦D.11,24⎡⎤-⎢⎥⎣⎦答案以及解析1.答案：D解析：设该圆锥的内切球的半径为r ，依题意可得圆锥的母线长为22(42)26+=，由过球心的截面三角形的面积11(664)44222S r r r =⨯++=⨯⨯，解得2r =，所以圆锥的内切球的表面积为224π4π(2)8πr ==，选D. 2.答案：B解析：设截面圆半径为r ，则有2π4πr =，所以2r =.由题意知，球的球心为正方体的中心，设球的半径为R ，则222(23)216R =+=，所以4R =，故选B. 3.答案：B解析：过F 作FO ⊥平面ABCD ，垂足为O ，取BC 的中点P ，连接,PF PO ，过F 作FQ AB ⊥，垂足为Q ，连接OQ .ADE 和BCF 都是边长为2的等边三角形，114,2,()1,3,122AB EF OP AB EF PF OQ BC ==∴=-====.22222,3OF PF OP FQ OF OQ ∴=-==+=，1(24)3332ABFE CDEF S S ∴==⨯+⨯=梯形梯形，又343,428,BCFADE ABCD SS S ∆==⨯==⨯=∴梯形所求几何体的表面积332328883S =⨯+⨯+=+.4.答案：C解析：由等边三角形ABC 932393AB =3AB =，则ABC 的外接圆半径23333r AB AB ==设球的半径为R ，则由球的表面积为16π，得24π16πR =，得2R =，则球心O 到平面ABC 的距离221d R r =-=，故选C.5.答案：C解析：由,a b 是两条异面直线，直线c 与,a b 都垂直，知：在A 中，若c α⊂，则a 与平面 α相交、平行或a α⊂，故A 错误；在B 中，若c α⊥，则,a b 与平面 α平行或a α⊂或b α⊂，故B 错误；在C 中，易得存在α，使得,,c a b ααα⊥⊂，故C 正确；在D 中，若存在α，使得,,c a b ααα⊥⊥，则a b ，与已知,a b 是两条异面直线矛盾，故D 错误.故选C. 6.答案：D 解析：1AA ⊥平面1,ABC AA AB ∴⊥，又111,BB AA BB AB ∴⊥，又1,,AB BC BB BC B AB ⊥⋂=∴⊥平面11,BB C C ∴该三棱柱可以补形成长方体111ABCD A B C D -，连接111,CD B D ，则1111,A B CD B CD ∴∠是1A B 与1B C 所成的角或其补角.令1AB =，则12A A BC ==，在11B CD 中，11115,22B D CD B C ===，由余弦定理得1110cos B CD ∠=，故选D. 7.答案：B解析：根据题意，可建立如图所示的空间直角坐标系P xyz -，则(0,0,0),(,0,0),(0,,0),(0,0,)P A a B a C a .过点P 作PH ⊥平面ABC ，交平面ABC 于点H ，则PH 的长即为点P 到平面ABC 的距离.,PA PB PC a H ===∴为ABC 的外心.易知ABC 为正三角形，H ∴为ABC 的重心，可得点H 的坐标为,,333a a a ⎛⎫⎪⎝⎭.2223||000333a a a PH a ⎛⎫⎛⎫⎛⎫∴=-+-+-= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.∴点P 到平面ABC 的距离为3a . 8.答案：B解析：若,m n αα，则,m n 相交或平行或异面，故A 错；若,m n αα⊥⊥，由线面垂直的性质定理可知m n ，故B 正确；若,m m n α⊥⊥，则nα或n α⊂，故C 错；若,mm n α⊥，则n α或n α⊂或 n 与 α相交，故D 错.选B.9.答案：B解析：如图，以D 为原点，1,,DA DC DD 所在直线分别为,,x y z 轴，建立空间直角坐标系O xyz -，设1AA 的长为(0)t t >，易知1(1,0,0),(0,0,),(1,1,0),(0,0,0)A D t B D ，则1(1,0,),(1,1,0)AD t BD =-=--.异面直线1AD 与BD 所成角的余弦值为1211010,12AD BD t AD BD⋅∴==+⋅⋅，又0,2t t >∴=.故选B.10.答案：A解析：由已知可得133633AB AB AB =⨯⨯，则6AB =，设球心为,O O 到平面ABCD 的距离为x ，球O 的半径为R ，则由OP OA =，得22222333(33)x x ++=+，解得3x =所以2233321R ++34π2821π3V R ==球，选A.11.答案：C解析：取AD 的中点G ，连接1,EG AD ，则1EG AD ，又11AD BC ，所以1EG BC ，又EG 与AC 是异面直线，故不存在1EFBC ，A 选项不正确；连接BD 交AC 于点O ，连接EO ，则1BD EO ，连接11B D ，易得AC ⊥平面11DBB D ，所以1AC B M ⊥，当11BD B M ⊥时，1B M EO ⊥，又EO AC O ⋂=，所以1B M ⊥平面AEO ，所以1B M AE ⊥，故B 选项不正确；因为1BD 平面AEC ，所以点M 到平面AEC 的距离为定值，所以四面体EMAC 的体积为定值，故C 选项正确；同理可得，四面体11FAC B 的体积为定值，故D 选项不正确.故选C. 12.答案：C解析：如图，设ABC 的中心为G ，连接BG 并延长，交AC 于F ，则F 为AC 的中点，连接,DF DG .由题知DG ⊥平面,ABC AC GB ⊥，得AC BD ⊥.又BD CE ⊥，故BD ⊥平面ACD ，又D ABC -为正三棱锥，故,,DA DB DC 两两垂直，故三棱锥D ABC -可看作以,,DA DB DC 为棱的正方体的一部分，两者有共同的外接球，正方体外接球的直径为32336⨯=，所以球O 的表面积为54π，故选C.13.答案：C解析：因为AD 在平面11ADD A 内，且平行平面CBF ，故A 错误；连接11,A B D C ，平面CBF 即平面11A D CB ，又平面11A D CB 与平面ABCD 相交(不垂直)，所以在平面ABCD 内不存在与平面CBF 垂直的直线，故B 错误；点F 到平面ABCD 的距离不变，点F 从1A 运动到1D 的过程中，FC 逐渐变小，故FC 与平面ABCD 所成的角逐渐变大，故C 正确；平面CBF 即平面11A D CB ，点D 到平面11A D CB 的距离为定值，故D 错误.故选C. 14.答案：B解析：如图所示，分别取111,BB B C 的中点,E F ，连接111,,,EF A F A E BC ，因为,,,M N E F 为所在棱的中点，所以11,,MN BC EFBC MNEF ，又EF ⊄平面,AMN MN ⊂平面AMN ，所以EF平面AMN ，易知1A F AM ，又1A F ⊄平面,AMN MN ⊂平面AMN ，所以1A F平面AMN ，又1A F EF F ⋂=，所以平面1A EF 平面AMN ，因为 P 是侧面11BCC B 内一点，且1A P平面AMN ，则 P 必在线段EF 上.在11Rt A B E 中，1415A E =+=，同理，在11Rt A B F 中，1415A F =+=，所以1A EF 为等腰三角形，当P 在EF 中点O 处时，1A P EF ⊥，此时1A P 最短， P 位于,E F 处时1A P 最长，22111232(5),52A O A E A F ⎛⎫=-=== ⎪ ⎪⎝⎭，所以线段1A P 的取值范围为32,5⎡⎤⎢⎥⎣，故选B.15.答案：B解析：连接,AC BD ，设,AC BD 交于点O ，由题意知,AO BD CO BD ⊥⊥，所以π3AOC ∠=，作AP OC ⊥，则P 为OC 的中点，作EQAP ，则EQ ⊥平面BCD ，所以()BE CF BQ QE CF BQ CF ⋅=+⋅=⋅.如图，建立平面直角坐标系，则(1,0),(1,1)B C ，设3(,)1,(,1)(01)4Q m m m F n n n ⎛⎫≤≤-≤≤ ⎪⎝⎭，则1BE CF m n ⋅=--+，因为324m n ≤+≤，所以11,4BE CF ⎡⎤⋅∈-⎢⎥⎣⎦，故选B.版权所有©正确教育侵权必纠！。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

年高考数学二轮复习专题四立体几何限时检测（文、理）一、选择题(本大题共8小题，每小题6分，共48分；在每小题给出四个选项中，只有一项是符合题目要求的)1．(xx·福建省质检)如图，AB是⊙O的直径，VA垂直⊙O所在的平面，C是圆周上不同于A、B的任意一点，M、N分别为VA、VC的中点，则下列结论正确的是( )A．MN∥ABB．MN与BC所成的角为45°C．OC⊥平面VACD．平面VAC⊥平面VBC[答案] D[解析] 依题意，MN∥AC，又直线AC与AB相交，因此MN与AB不平行；注意到AC ⊥BC，因此MN与BC所成的角是90°；注意到直线OC与AC不垂直，因此OC与平面VAC 不垂直；由于BC⊥AC，BC⊥VA，因此BC⊥平面VAC.又BC⊂平面VBC，所以平面VBC⊥平面VAC.综上所述可知选D.2．(xx·菱湖月考)若某多面体的三视图(单位：cm)如图所示，则此多面体的体积是( )A.12cm 3 B.23cm 3 C.56cm 3 D.78cm 3 [答案] C[解析] 由三视图知，该几何体是由一个正方体割去一个角所得到的多面体，如图，其正方体的棱长为1，则该多面体的体积为13－13×12×13＝56cm 3.3．(文)已知某个几何体的三视图如下，根据图中标出的尺寸(单位：cm)，可得这个几何体的体积是( )A.13cm 3 B.23cm 3 C.43cm 3 D.83cm 3 [答案] C[解析] 由三视图知几何体为三棱锥，底面等腰三角形底边长2，高为2，棱锥高为2，V ＝13×(12×2×2)×2＝43cm 3.(理)正方体ABCD －A 1B 1C 1D 1中，E 是棱AB 上的动点，则直线A 1D 与直线C 1E 所成的角等于( )A ．60°B ．90°C ．30°D ．随点E 的位置而变化[答案] B[解析] ∵A 1D ⊥AB ，A 1D ⊥AD 1， ∴A 1D ⊥平面AD 1C 1B ，∴A 1D ⊥C 1E .4．(文)(xx·河北名校名师俱乐部模拟)一简单组合体的三视图及尺寸如图所示(单位：cm)，该组合体的体积为( )A ．42cm 3B ．48cm 3C ．56cm 3D ．44cm 3[答案] D[解析] 由三视图可知该几何体是一个长、宽、高分别为6、4、1的长方体和一个直三棱柱组合而成，直三棱柱的底面是等腰三角形，三角形的底边长为4，高为5，棱柱的高为2，其体积V ＝1×4×6＋12×4×5×2＝44(cm 3)．(理)(xx·郑州市质检)如图，四边形ABCD 中，AB ＝AD ＝CD ＝1，BD ＝2，BD ⊥CD .将四边形ABCD 沿对角线BD 折成四面体A ′－BCD ，使平面A ′BD ⊥平面BCD ，则下列结论正确的是( )A ．A ′C ⊥BDB ．∠BA ′C ＝90°C ．CA ′与平面A ′BD 所成的角为30° D ．四面体A ′－BCD 的体积为13[答案] B[解析] 取BD 的中点O ，∵A ′B ＝A ′D ，∴A ′O ⊥BD ，又平面A ′BD ⊥平面BCD ，平面A ′BD ∩平面BCD ＝BD ，∴A ′O ⊥平面BCD ，∵CD ⊥BD ，∴OC 不垂直于BD .假设A ′C ⊥BD ，∵OC 为A ′C 在平面BCD 内的射影，∴OC ⊥BD ，矛盾，∴A ′C 不垂直于BD ，A 错误；∵CD ⊥BD ，平面A ′BD ⊥平面BCD ，∴CD ⊥平面A ′BD ，A ′C 在平面A ′BD 内的射影为A ′D ，∵A ′B ＝A ′D ＝1，BD ＝2，∴A ′B ⊥A ′D ，A ′B ⊥A ′C ，B 正确；∠CA ′D 为直线CA ′与平面A ′BD 所成的角，∠CA ′D ＝45°，C 错误；V A ′－BCD ＝13S △A ′BD ·CD ＝16，D 错误，故选B.5．(文)(xx·济南四校联考)已知m 、n 是两条不同直线，α、β为两个不同平面，那么使m ∥α成立的一个充分条件是( )A ．m ∥β，α∥βB ．m ⊥β，α⊥βC ．m ⊥n ，n ⊥α，m ⊄αD ．m 上有不同的两个点到α的距离相等 [答案] C[解析] 对于A ，直线m 可能位于平面α内；对于B ，直线m 可能位于平面α内；对于D ，当直线m 与平面α相交时，显然在该直线上也能找到两个不同的点到平面α的距离相等．故选C.(理)过正方形ABCD 的顶点A ，引PA ⊥平面ABCD .若PA ＝BA ，则平面ABP 和平面CDP 所成的二面角的大小是( )A ．30°B ．45°C ．60°D ．90°[答案] B[解析] 建立如图所示的空间直角坐标系，不难求出平面APB 与平面PCD 的法向量分别为n 1＝(0,1,0)，n 2＝(0,1,1)，故平面ABP 与平面CDP 所成二面角(锐角)的余弦值为|n 1·n 2||n 1||n 2|＝22，故所求的二面角的大小是45°.6．如图，在正四面体P －ABC 中，D 、E 、F 分别是AB 、BC 、CA 的中点，下列四个结论不成立的是( )A ．BC ∥平面PDFB ．DF ⊥平面PAEC ．平面PDF ⊥平面PAED ．平面PDE ⊥平面ABC [答案] D[解析] ∵D 、F 分别为AB 、AC 的中点，∴BC ∥DF ，∵BC ⊄平面PDF ，∴BC ∥平面PDF ，故A 正确；在正四面体中，∵E 为BC 中点，易知BC ⊥PE ，BC ⊥AE ，∴BC ⊥平面PAE ，∵DF ∥BC ，∴DF ⊥平面PAE ，故B 正确；∵DF ⊥平面PAE ，DF ⊂平面PDF ，∴平面PDF ⊥平面PAE ，∴C 正确，故选D.7．(文)如图，在棱长为5的正方体ABCD －A 1B 1C 1D 1中，EF 是棱AB 上的一条线段，且EF ＝2，Q 是A 1D 1的中点，点P 是棱C 1D 1上的动点，则四面体P －QEF 的体积( )A ．是变量且有最大值B ．是变量且有最小值C ．是变量且有最大值和最小值D ．是常量 [答案] D[解析] 因为EF ＝2，点Q 到AB 的距离为定值，所以△QEF 的面积为定值，设为S ，又因为D 1C 1∥AB ，所以D 1C 1∥平面QEF ；点P 到平面QEF 的距离也为定值，设为d ，从而四面体P －QEF 的体积为定值13Sd .(理)一个四面体的四个顶点在空间直角坐标系O －xyz 中的坐标分别是(0,0,0)、(1,2,0)、(0,2,2)、(3,0,1)，则该四面体中以yOz 平面为投影面的正视图的面积为( )A ．3B.52C ．2 D.72[答案] A[解析] 四个点在yOz 平面上的正投影依次为(0,0,0)，(0,2,0)，(0,2,2)，(0,0,1)，故其面积S ＝12×(1＋2)×2＝3.8．(文)已知α、β、γ是三个不同的平面，命题“α∥β，且α⊥γ⇒β⊥γ”是真命题，如果把α、β、γ中的任意两个换成直线，另一个保持不变，在所得的所有新命题中，真命题有( )A ．0个B ．1个C ．2个D ．3个[答案] C[解析] 若α、β换成直线a 、b ，则命题化为“a ∥b ，且a ⊥γ⇒b ⊥γ”，此命题为真命题；若α、γ换为直线a 、b ，则命题化为“a ∥β，且a ⊥b ⇒b ⊥β”，此命题为假命题；若β、γ换为直线a 、b ，则命题化为“a ∥α，且b ⊥α⇒a ⊥b ”，此命题为真命题，故选C.(理)如图，在△ABC 中，AB ⊥AC ，若AD ⊥BC ，则AB 2＝BD ·BC ；类似地有命题：在三棱锥A －BCD 中，AD ⊥平面ABC ，若A 点在平面BCD 内的射影为M ，则有S 2△ABC ＝S △BCM ·S △BCD .上述命题是( )A ．真命题B ．增加条件“AB ⊥AC ”才是真命题C ．增加条件“M 为△BCD 的垂心”才是真命题 D ．增加条件“三棱锥A －BCD 是正三棱锥”才是真命题 [答案] A[解析] 因为AD ⊥平面ABC ，所以AD ⊥AE ，AD ⊥BC ，在△ADE 中，AE 2＝ME ·DE ，又A 点在平面BCD 内的射影为M ，所以AM ⊥平面BCD ，AM ⊥BC ，所以BC ⊥平面ADE ，所以BC ⊥DE ，将S △ABC 、S △BCM 、S △BCD 分别表示出来，可得S 2△ABC ＝S △BCM ·S △BCD ，故选A.二、填空题(本大题共2小题，每小题6分，共12分，将答案填写在题中横线上．) 9．(文)已知四棱锥P －ABCD 的底面ABCD 是矩形，PA ⊥底面ABCD ，点E 、F 分别是棱PC 、PD 的中点，则①棱AB 与PD 所在直线垂直； ②平面PBC 与平面ABCD 垂直； ③△PCD 的面积大于△PAB 的面积； ④直线AE 与平面BF 是异面直线．以上结论正确的是________．(写出所有正确结论的编号) [答案] ①③[解析] 由条件可得AB ⊥平面PAD ，∴AB ⊥PD ，故①正确；若平面PBC ⊥平面ABCD ，由PB ⊥BC ，得PB ⊥平面ABCD ，从而PA ∥PB ，这是不可能的，故②错；S △PCD ＝12CD ·PD ，S △PAB ＝12AB ·PA ，由AB ＝CD ，PD >PA 知③正确；由E 、F 分别是棱PC 、PD 的中点，可得EF ∥CD ，又AB ∥CD ，∴EF ∥AB ，故AE 与BF 共面，④错，故填①③.(理)如图，正方形BCDE 的边长为a ，已知AB ＝3BC ，将直角△ABE 沿BE 边折起，A 点在面BCDE 上的射影为D 点，则翻折后的几何体中有如下描述：①AB 与DE 所成角的正切值是2； ②V B －ACE 的体积是16a 3；③AB ∥CD ；④平面EAB ⊥平面ADE ；⑤直线BA 与平面ADE 所成角的正弦值为33. 其中正确的叙述有________(写出所有正确结论的编号)． [答案] ①②④⑤[解析] 由题意可得如图所示的几何体，对于①，AB 与DE 所成角为∠ABC ，在△ABC 中，∠ACB ＝90°，AC ＝2a ，BC ＝a ，所以tan ∠ABC ＝2，故①正确；对于②，V B －ACE ＝V A －ECB ＝13×a ×12×a ×a ＝16a 3，故②正确；③明显错误；对于④，因为AD ⊥平面BCDE ，所以AD ⊥BE ，又因为DE ⊥BE ，所以BE ⊥平面ADE ，可得平面EAB ⊥平面ADE ，故④正确；对于⑤，由④可知，∠BAE 即为直线BA 与平面ADE 所成的角，在△ABE 中，∠AEB ＝90°，AB ＝3a ，BE ＝a ，所以sin ∠BAE ＝33，故⑤正确． 10．(xx·邯郸一模)已知直角梯形ABCD ，AB ⊥AD ，CD ⊥AD ，AB ＝2AD ＝2CD ＝2沿AC 折成三棱锥，当三棱锥体积最大时，求此时三棱锥外接球的体积________．[答案] 43π[解析] 在直角梯形ABCD 中，AB ⊥AD ，CD ⊥AD ，AB ＝2AD ＝2CD ＝2，∴AB ＝2，AD ＝1，CD ＝1，∴AC ＝2，BC ＝2，∴BC ⊥AC ，取AC 的中点E ，AB 中点O ，当三棱锥体积最大时，平面DCA ⊥平面ACB ，∴OA ＝OB ＝OC ＝OD ，∴OB ＝1，∴V ＝43πR 3＝43π.三、解答题(本大题共3小题，共40分，解答应写出文字说明、证明过程或演算步骤) 11．(本小题满分13分)(文)如图，已知矩形ABCD 中，AB ＝10，BC ＝6，沿对角线BD 把△ABD 折起，使A 点移到A 1点，且A 1在平面BCD 上的射影O 恰好在CD 上．(1)求证：BC ⊥A 1D ；(2)求证：平面A 1BC ⊥平面A 1BD ； (3)求三棱锥A 1－BCD 的体积．[解析] (1)∵A 1在平面BCD 上的射影O 在CD 上， ∴A 1O ⊥平面BCD ，又BC ⊂平面BCD ，∴BC ⊥A 1O .又BC ⊥CO ，CO ∩A 1O ＝O ，CO ⊂平面A 1CD ，A 1O ⊂平面A 1CD ， ∴BC ⊥平面A 1CD ，又A 1D ⊂平面A 1CD ，∴BC ⊥A 1D . (2)∵四边形ABCD 为矩形， ∴A 1D ⊥A 1B ，由(1)知BC ⊥A 1D .又BC ∩A 1B ＝B ，BC ⊂平面A 1BC ，A 1B ⊂平面A 1BC ， ∴A 1D ⊥平面A 1BC ，又A 1D ⊂平面A 1BD ， ∴平面A 1BC ⊥平面A 1BD .(3)∵A 1D ⊥平面A 1BC ，∴A 1D ⊥A 1C . ∵CD ＝10，A 1D ＝6，∴A 1C ＝8，∴VA 1－BCD ＝VD －A 1BC ＝13×12×6×8×6＝48.(理)(xx·大兴区模拟)如图，直三棱柱ABC －A 1B 1C 1中，△ABC 是等边三角形，D 是BC的中点．(1)求证：直线A1D⊥B1C1；(2)判断A1B与平面ADC1的位置关系，并证明你的结论．[解析] (1)在直三棱柱ABC－A1B1C1中，AA1⊥平面ABC，所以AA1⊥BC，在等边△ABC中，D是BC中点，所以AD⊥BC，因为在平面A1AD中，A1A∩AD＝A，所以BC⊥平面A1AD，又因为A1D⊂平面A1AD，所以A1D⊥BC，在直三棱柱ABC－A1B1C1中，四边形BCC1B1是平行四边形，所以B1C1∥BC，所以，A1D⊥B1C1.(2)在直三棱柱ABC－A1B1C1中，四边形ACC1A1是平行四边形，在平行四边形ACC1A1中连接A1C，交AC1于点O，连接DO.故O为A1C的中点．在三角形A1CB中，D为BC中点，O为A1C中点，故DO∥A1B.因为DO⊂平面ADC1，A1B⊄平面ADC1，所以，A1B∥平面ADC1，故A1B与平面ADC1平行．12．(本小题满分13分)(文)如图，直四棱柱ABCD－A1B1C1D1中，底面ABCD是直角梯形，∠BAD＝∠ADC＝90°，AB＝2AD＝2CD＝2.(1)求证：AC ⊥平面BB 1C 1C ；(2)在A 1B 1上是否存在一点P ，使得DP 和平面BCB 1、平面ACB 1都平行？证明你的结论． [解析] (1)直四棱柱ABCD －A 1B 1C 1D 1中，BB 1⊥平面ABCD ，AC ⊂平面ABCD ，∴BB 1⊥AC . 又∵∠BAD ＝∠ADC ＝90°，AB ＝2AD ＝2CD ＝2， ∴AC ＝2，∠CAB ＝45°，∴BC ＝2，∴BC ⊥AC ，又BB 1∩BC ＝B ，BB 1、BC ⊂平面BB 1C 1C ， ∴AC ⊥平面BB 1C 1C ；(2)存在符合条件的点P ，且P 为A 1B 1的中点．证明：∵P 为A 1B 1的中点，所以PB 1∥AB ，且PB 1＝12AB ，又DC ∥AB ，DC ＝12AB ，∴DC ∥PB 1，且DC ＝PB 1.∴四边形CDPB 1为平行四边形，从而CB 1∥DP . 又CB 1⊂平面ACB 1，DP ⊄平面ACB 1. ∴DP ∥平面ACB 1，同理DP ∥平面BCB 1.[点评] (2)问中假如存在点P ，使得DP ∥平面BCB 1，DP ∥平面ACB 1，又∵平面BCB 1∩平面ACB 1＝CB 1，∴DP ∥CB 1，又CD ∥PB 1，故四边形CDPB 1为平行四边形，∵A 1B 1＝2CD ，故只须P 为A 1B 1的中点，即有PB 1綊DC ，而获解．对于存在性命题，常常是先假设存在，把其作为一个条件与其他已知条件结合加以分析，探寻解题的思路．(理)(xx·哈三中一模)如图，在四棱锥P －ABCD 中，底面ABCD 为菱形，∠BAD ＝60°，Q 为AD 的中点．(1)若PA ＝PD ，求证：平面PQB ⊥平面PAD ；(2)若平面PAD ⊥平面ABCD ，且PA ＝PD ＝AD ＝2，点M 在线段PC 上，试确定点M 的位置，使二面角M －BQ －C 大小为60°，并求出PMPC的值．[解析] (1)∵PA ＝PD ，Q 为AD 的中点，∴PQ ⊥AD ，又∵底面ABCD 为菱形，∠BAD ＝60°，∴BQ ⊥AD ，又PQ ∩BQ ＝Q ，∴AD ⊥平面PQB ，又∵AD ⊂平面PAD ，∴平面PQB ⊥平面PAD ；(2)∵平面PAD ⊥平面ABCD ，平面PAD ∩平面ABCD ＝AD ，PQ ⊥AD,∴PQ ⊥平面ABCD .∴以Q 为坐标原点，分别以QA 、QB 、QP 为x 轴、y 轴、z 轴建立空间直角坐标系如图．则Q (0,0,0)，P (0,0，3)，B (0，3，0)，C (－2，3，0)，设PM →＝λPC →(0<λ<1)，所以M (－2λ，3λ，3(1－λ))，平面CBQ 的一个法向量是n 1＝(0,0,1)，设平面MQB 的一个法向量为n 2＝(x ，y ，z )，所以⎩⎪⎨⎪⎧QM →·n 2＝0，QB →·n 2＝0，∴⎩⎨⎧－2λx ＋3λy ＋3z 1－λ＝0，3y ＝0，∴⎩⎪⎨⎪⎧y ＝0，x ＝31－λz 2λ.取n 2＝(3－3λ2λ，0，3)，由二面角M －BQ －C 大小为60°，可得： 12＝|n 1·n 2||n 1|·|n 2|，解得λ＝13，此时PM PC ＝13. 13．(本小题满分14分)(文)(xx·福建文，18)如图，在四棱锥P －ABCD 中，PD ⊥平面ABCD ，AB ∥DC ，AB ⊥AD ，BC ＝5，DC ＝3，AD ＝4，∠PAD ＝60°.(1)当正视方向与向量AD →的方向相同时，画出四棱锥P －ABCD 的正视图(要求标出尺寸，并写出演算过程)；(2)若M 为PA 的中点，求证：DM ∥平面PBC ； (3)求三棱锥D －PBC 的体积．[解析] (1)在梯形ABCD 中，过点C 作CE ⊥AB ，垂足为E .由已知得，四边形ADCE 为矩形，AE ＝CD ＝3，在Rt △BEC 中，由BC ＝5，CE ＝4，依勾股定理知BE ＝3，从而AB ＝6.又由PD ⊥平面ABCD 得PD ⊥AD ，从而在Rt △PDA 中，由AD ＝4，∠PAD ＝60°，得PD ＝4 3. 正视图如图所示：(2)取PB 中点为N ，连接MN 、CN .在△PAB 中，∵M 是PA 中点，∴MN ∥AB ，MN ＝12AB ＝3，又CD ∥AB ，CD ＝3，∴MN ∥CD ，MN ＝CD ，∴四边形MNCD 为平行四边形，∴DM ∥CN . 又DM ⊄平面PBC ，CN ⊂平面PBC ， ∴DM ∥平面PBC .(3)V D －PBC ＝V P －DBC ＝13S △DBC ·PD ，又S △DBC ＝6，PD ＝43，所以V D －PBC ＝8 3.(理)(xx·陕西理，18)如图，四棱柱ABCD －A 1B 1C 1D 1的底面ABCD 是正方形，O 为底面中心，A 1O ⊥平面ABCD ，AB ＝AA 1＝ 2.(1)证明：A 1C ⊥平面BB 1D 1D(2)求平面OCB 1与平面BB 1D 1D 的夹角θ的大小． [解析] 如图建立空间直角坐标系，由AB ＝AA 1＝2可知O (0,0,0)，A (1,0,0)，B (0,1,0)，B 1(－1,1,1)，C (－1,0,0)，A 1(0,0,1)，D 1(－1，－1,1)，D (0，－1,0)．(1)∵A 1C →＝(－1,0，－1)，DB →＝(0,2,0)，BB 1→＝(－1，0,1) ∴A 1C →·DB →＝0，A 1C →·BB 1→＝0，即A 1C ⊥DB ，A 1C ⊥BB 1且DB ∩BB 1＝B ， ∴A 1C ⊥平面BB 1D 1D(2)易求得平面OCB 1的一个法向量n ＝(0,1，－1)，平面BB 1D 1D 的一个法向量为m ＝(1,0,1)，所求夹角余弦值为cos θ＝|m ·n ||m ||n |＝12，所求夹角的大小为60°.一、选择题1．(xx·郑州质检)一个几何体的三视图如图所示，则这个几何体的表面积为( )A ．6＋ 5B ．6＋2 5C ．8＋ 5D ．8＋2 5[答案] D[解析] 由三视图可知该几何体为一横放的直三棱柱，其中底面正对观察者，为一直角三角形，两直角边长分别为1,2，棱柱的高为2，故其表面积S ＝(2＋1＋5)×2＋2×1＝8＋2 5.2．(xx·福州质检)如图是一个空间几何体的三视图，这个几何体的体积是( )A ．2πB ．4πC ．6πD ．8π[答案] D[解析] 由图可知该几何体是一个圆柱内挖去一个圆锥所得的几何体，V ＝V 圆柱－V圆锥＝π×22×3－13π×22×3＝8π，故选D.3．(文)在正四面体(棱长都相等的四面体)A －BCD 中，棱长为4，M 是BC 的中点，点P 在线段AM 上运动(P 不与A 、M 重合)，过点P 作直线l ⊥平面ABC ，l 与平面BCD 交于点Q ，给出下列命题：①BC ⊥平面AMD ； ②Q 点一定在直线DM 上； ③V C －AMD ＝4 2. 其中正确的是( )A ．①②B ．①③C ．②③D ．①②③[答案] A[解析] 由BC ⊥AM ，BC ⊥MD ，可得BC ⊥平面AMD ，即①正确；由BC ⊥平面AMD 可得平面AMD ⊥平面ABC ，则若过P 作直线l ⊥平面ABC ，l 与平面BCD 交于点Q ，Q 点一定在直线DM 上，即②正确；由V C －AMD ＝12V C －ABD ＝12×212×43＝823，即③不正确，综上可得正确的命题序号为①②，故应选A.(理)(xx·唐山市二模)直三棱柱ABC －A 1B 1C 1的所有顶点都在半径为2的球面上，AB ＝AC ＝3，AA 1＝2，则二面角B －AA 1－C 的余弦值为( )A ．－13B ．－12C.13D.12[答案] D[解析] 如图，设球心为O ，底面△ABC 外接圆的圆心为O ′，则OA ＝OB ＝OC ＝2，OO ′＝1，∴O ′A ＝O ′B ＝O ′C ＝1，∴BC ＝3，∴△ABC 为正三角形，∴二面角B －AA 1－C 的平面角BAC ＝60°，∴二面角B －AA 1－C 的余弦值为12.4．(文)设m 、n 是两条不同的直线，α、β是两个不同的平面，则下列命题不正确的是( )A ．若m ⊥n ，m ⊥α，n ⊄α，则n ∥αB ．若m ⊥β，α⊥β，则m ∥α或m ⊂αC ．若m ⊥n ，m ⊥α，n ⊥β，则α⊥βD ．若m ∥α，α⊥β，则m ⊥β [答案] D[解析] 对于选项D ，当直线m 位于平面β内且与平面α，β的交线平行时，直线m ∥α，显然m 与平面β不垂直，因此选项D 不正确．(理)(xx·嘉兴二测)已知α、β、γ是三个不重合的平面，m 、n 是不重合的直线，下列判断正确的是( )A ．若α⊥β，β⊥γ，则α∥γB ．若α⊥β，l ∥β，则l ∥αC ．若m ∥α，n ∥α，则m ∥nD ．若m ⊥α，n ⊥α，则m ∥n [答案] D[解析] A 错，两平面还可垂直；B 错，还可能有l ∥α；C 错，两直线m ，n 的位置关系不确定；D 正确，垂直于同一平面的两直线互相平行．5.如图，正△ABC 的中线AF 与中位线DE 相交于G ，已知△A ′ED 是△AED 绕DE 旋转过程中的一个图形，下列命题中，错误的是( )A ．动点A ′在平面ABC 上的投影在线段AF 上B ．恒有平面A ′GF ⊥平面BCEDC ．三棱锥A ′－FED 的体积有最大值 D ．异面直线A ′E 与BD 不可能垂直 [答案] D[解析] 由题意，DE ⊥平面AGA ′， ∴A 、B 、C 正确，故选D.6．(文)(xx·山西太原月考)如图所示，正方体ABCD －A ′B ′C ′D ′的棱长为1, E 、F 分别是棱AA ′、CC ′的中点，过直线EF 的平面分别与棱BB ′、DD ′交于M 、N ，设BM ＝x ，x ∈[0,1]，给出以下四个命题：①平面MENF ⊥平面BDD ′B ′；②当且仅当x ＝12时，四边形MENF 的面积最小；③四边形MENF 周长L ＝f (x )，x ∈[0,1]是单调函数； ④四棱锥C ′－MENF 的体积V ＝h (x )为常函数；以上命题中假命题的序号为( )A ．①④B ．②C ．③D ．③④[答案] C[解析] AC ⊥平面BDD ′B ′，EF ∥AC ，∴EF ⊥平面BDD ′B ′，∴①正确；∵EF 为所在棱的中点，由对称性及条件知四边形EMFN 为菱形，其面积随着对角线MN 的增大而增大，当x ＝12时，M 为BB ′的中点，此时MN 取最小值，∴②正确，③错误；V 四棱锥C ′－MENF ＝2V C ′－MEF ＝2V E －MFC ′为常数，∴V ＝h (x )为常函数．(理)(xx·杭州质检)如图，设平面α∩β＝EF ，AB ⊥α，CD ⊥α，垂足分别是B 、D ，如果增加一个条件，就能推出BD ⊥EF ，这个条件不可能是下面四个选项中的( )A ．AC ⊥βB ．AC ⊥EFC ．AC 与BD 在β内的射影在同一条直线上 D ．AC 与α、β所成的角相等 [答案] D[解析] 因为BD 是AC 在平面α内的射影，所以只需得到AC ⊥EF ，那么由三垂线定理的逆定理可得BD ⊥EF .对于选项A ，因为AC ⊥β，EF ⊂β⇒AC ⊥EF ⇒BD ⊥EF .选项B ，因为AC ⊥EF ，所以BD ⊥EF .对于选项C ，可得平面ABDC ⊥β，所以BD ⊥EF .对于选项D ，AC 与α、β所成的角相等，无法保证AC ⊥EF .综上知选D.7．(文)已知某个几何体的三视图如图所示，根据图中标出的尺寸，可知这个几何体的侧面积是( )A.3πB.π3C.2π3D.5π[答案] D[解析] 由三视图知，该几何体是一个圆锥，底半径为1，高为2，母线长l ＝22＋12＝5，∴侧面积S ＝5π.(理)已知正四面体A －BCD ，设异面直线AB 与CD 所成的角为α，侧棱AB 与底面BCD 所成的角为β，侧面ABC 与底面BCD 所成的角为γ，则( )A ．α>β>γB ．α>γ>βC ．β>α>γD ．γ>β>α[答案] B[解析] 如图，设底面BCD 的中心为点O ，连接AO ，BO ，易知∠ABO ＝β，取BC 的中点E ，连接AE 、OE ，易知∠AEO ＝γ，在正三角形BCD 中，OB >OE ，因此0<β<γ<π2，延长BO 交CD 于F ，则BF ⊥CD ，又AO ⊥CD ，∴CD ⊥平面ABF .∴CD ⊥AB ，即α＝π2.∴α>γ>β.8．(文)在棱长为a 的正方体ABCD －A 1B 1C 1D 1中，M 为AB 的中点，则点C 到平面A 1DM 的距离为( )A.63aB.66a C.22a D.12a [答案] A[解析] 设点C 到平面A 1DM 的距离为h ，则由已知得DM ＝A 1M ＝a 2＋a22＝52a ，A 1D ＝2a ，S △A 1DM ＝12×2a ×52a 2－22a 2＝64a 2，连接CM ，S △CDM ＝12a 2，由VC －A 1DM ＝VA 1－CDM ，得13S △A 1DM ·h ＝13S △CDM ·a ，即64a 2·h ＝12a 2·a ，得h ＝63a ，所以点C到平面A 1DM 的距离为63a ，选A. (理)已知正方形ABCD 的边长为22，将△ABC 沿对角线AC 折起，使平面ABC ⊥平面ACD ，得到如右图所示的三棱锥B －ACD .若O 为AC 边的中点，M 、N 分别为线段DC 、BO 上的动点(不包括端点)，且BN ＝CM .设BN ＝x ，则三棱锥N －AMC 的体积y ＝f (x )的函数图象大致是( )[答案] B[解析] 由条件知，AC ＝4，BO ＝2，S △AMC ＝12CM ·AD ＝2x ，NO ＝2－x ，∴V N －AMC ＝13S △AMC ·NO＝23x (2－x )，即f (x )＝23x (2－x )，故选B. 二、填空题9．如图，在正方体ABCD －A 1B 1C 1D 1中，点P 是上底面A 1B 1C 1D 1内一动点，则三棱锥P －ABC 的正(主)视图与侧(左)视图的面积的比值为________．[答案] 1[解析] 依题意得三棱锥P －ABC 的主视图与左视图均为三角形，且这两个三角形的底边长都等于正方体的棱长，底边上的高也都相等，因此三棱锥P －ABC 的主视图与左视图的面积之比等于1.10．(文)一个几何体的三视图如图所示(单位：m)，则该几何体的体积为________m 3.[答案] 30[解析] 本题考查三视图及柱体体积公式．由三视图知该几何体由一个棱长为3,4,2的长方体和一个底面是直角梯形高为4的直棱柱组成，则体积V ＝3×4×2＋2＋12×1×4＝30.[点评] 解决三视图问题应弄清图中各量与原几何体的量的关系．(理)设C 是∠AOB 所在平面外的一点，若∠AOB ＝∠BOC ＝∠AOC ＝θ，其中θ是锐角，而OC 和平面AOB 所成角的余弦值等于33，则θ的值为________． [答案] 60°[解析] 作CC 1⊥平面AOB 于点C 1，C 1A 1⊥OA 于点A 1，C 1B 1⊥OB 于点B 1，连接OC 1，则∠COC 1为直线OC 与平面AOB 所成的角，且OC 1是∠AOB 的平分线，设OA 1＝x ，则OC ＝xcos θ，OC 1＝x cosθ2，易求得cos ∠COC 1＝cos θcos θ2＝2cos 2θ2－1cosθ2＝33，即2cos2θ2－33cos θ2－1＝0，解之得 cos θ2＝32或cos θ2＝－33(舍去)，故θ2＝30°，所以θ＝60°. 三、解答题11．(文)(xx·威海两校质检)如图，四棱锥P －ABCD 的底面是边长为1的正方形，侧棱PA ⊥底面ABCD ，且PA ＝2，E 是侧棱PC 上的动点．(1)求四棱锥P －ABCD 的体积；(2)如果E 是PA 的中点，求证PC ∥平面BDE ；(3)是否不论点E 在侧棱PA 的任何位置，都有BD ⊥CE ？证明你的结论． [解析] (1)∵PA ⊥平面ABCD ， ∴V P －ABCD ＝13S 正方形ABCD ·PA ＝13×12×2＝23.即四棱锥P －ABCD 的体积为23.(2)连接AC 交BD 于O ，连接OE .∵四边形ABCD 是正方形，∴O 是AC 的中点．又∵E 是PA 的中点，∴PC ∥OE .∵PC ⊄平面BDE ，OE ⊂平面BDE ，∴PC ∥平面BDE . (3)不论点E 在何位置，都有BD ⊥CE .证明如下：∵四边形ABCD 是正方形，∴BD ⊥AC . ∵PA ⊥底面ABCD ，且BD ⊂平面ABCD ，∴BD ⊥PA . 又∵AC ∩PA ＝A ，∴BD ⊥平面PAC . ∵不论点E 在何位置，都有CE ⊂平面PAC . ∴不论点E 在何位置，都有BD ⊥CE .(理)(xx·成都一诊)如图，PO ⊥平面ABCD ，点O 在AB 上，EA ∥PO ，四边形ABCD 为直角梯形，BC ⊥AB ，BC ＝CD ＝BO ＝PO ，EA ＝AO ＝12CD .(1)求证：PE ⊥平面PBC ；(2)直线PE 上是否存在点M ，使DM ∥平面PBC ，若存在，求出点M ；若不存在，说明理由．(3)求二面角E －BD －A 的余弦值．[解析] (1)证明：∵EA ∥OP ，AO ⊂平面ABP ， ∴点A ，B ，P ，E 共面．∵PO ⊥平面ABCD ，PO ⊂平面PEAB . ∴平面PEAB ⊥平面ABCD ， ∵BC ⊂平面ABCD ，BC ⊥AB ，平面PEAB ∩平面ABCD ＝AB ， ∴BC ⊥平面PEAB ，∴PE ⊥BC .由平面几何知识知PE ⊥PB ，又BC ∩PB ＝B ， ∴PE ⊥平面PBC .(2)点E 即为所求的点，即点M 与点E 重合．取PB 的中点F ，连接EF 、CF 、DE ，延长PE 交BA 的延长线于H ，则E 为PH 的中点，O 为BH 的中点，∴EF 綊OB ，又OB 綊CD ，∴EF ∥CD ，且EF ＝DC ，∴四边形DCFE 为平行四边形，所以DE ∥CF . ∵CF 在平面PBC 内，DE 不在平面PBC 内， ∴DE ∥平面PBC .(3)由已知可知四边形BCDO 是正方形，显然OD 、OB 、OP 两两垂直，如图建立空间直角坐标系，设DC ＝1，则B (0,1,0)，D (1,0,0)，E (0，－12，12)，设平面BDE 的一个法向量为n 1＝(x ，y ，z )， BD →＝(1，－1,0)，BE →＝(0，－32，12)，⎩⎪⎨⎪⎧n 1·BD →＝0，n 1·BE →＝0，即⎩⎪⎨⎪⎧x －y ＝0，－32y ＋12z ＝0.取y ＝1，则x ＝1，z ＝3，从而n 1＝(1,1,3)．取平面ABD 的一个法向量为n 2＝(0,0,1)．cos 〈n 1，n 2〉＝n 1·n 2|n 1|·|n 2|＝311·1＝31111，故二面角E －BD －A 的余弦值为31111.12．(文)已知四棱锥P －ABCD 的直观图和三视图如图所示，E 是PB 的中点．(1)求三棱锥C －PBD 的体积；(2)若F 是BC 上任一点，求证：AE ⊥PF ；(3)边PC 上是否存在一点M ，使DM ∥平面EAC ，并说明理由．[解析] (1)由该四棱锥的三视图可知，四棱锥P －ABCD 的底面是边长为2和1的矩形，侧棱PA ⊥平面ABCD ，且PA ＝2，∴V C －PBD ＝V P －BCD ＝13×12×1×2×2＝23.(2)证明：∵BC ⊥AB ，BC ⊥PA ，AB ∩PA ＝A . ∴BC ⊥平面PAB ，∴BC ⊥AE ，又在△PAB 中，∵PA ＝AB ，E 是PB 的中点， ∴AE ⊥PB .又∵BC ∩PB ＝B ，∴AE ⊥平面PBC ，且PF ⊂平面PBC ，∴AE ⊥PF . (3)存在点M ，可以使DM ∥平面EAC .连接BD ，设AC ∩BD ＝O ，连接EO . 在△PBD 中，EO 是中位线． ∴PD ∥EO ，又∵EO ⊂平面EAC ，PD ⊄平面EAC ， ∴PD ∥平面EAC ，∴当点M 与点P 重合时，可以使DM ∥平面EAC .(理)如图①，边长为1的正方形ABCD 中，点E 、F 分别为AB 、BC 的中点，将△BEF 剪去，将△AED 、△DCF 分别沿DE 、DF 折起，使A 、C 两点重合于点P ，得一三棱锥如图②所示．(1)求证：PD ⊥EF ；(2)求三棱锥P －DEF 的体积； (3)求DE 与平面PDF 所成角的正弦值．[解析] (1)依题意知图①折前AD ⊥AE ，CD ⊥CF ， ∴折起后PD ⊥PE ，PF ⊥PD ， ∵PE ∩PF ＝P ，∴PD ⊥平面PEF . 又∵EF ⊂平面PEF ，∴PD ⊥EF .(2)依题意知图①中AE ＝CF ＝12，∴PE ＝PF ＝12，在△BEF 中EF ＝2BE ＝22，在△PEF 中，PE 2＋PF 2＝EF 2，∴PE ⊥PF ， ∴S △PEF ＝12·PE ·PF ＝12·12·12＝18，∴V P －DEF ＝V D －PEF ＝13S △PEF ·PD ＝13×18×1＝124.(3)由(2)知PE ⊥PF ，又PE ⊥PD ，∴PE ⊥平面PDF ， ∴∠PDE 为DE 与平面PDF 所成的角．在Rt △PDE 中， ∵DE ＝PD 2＋PE 2＝1＋14＝52，PE ＝12，∴sin ∠PDE ＝PE DE＝1252＝55. 13．(文)如图所示，在直三棱柱ABC －A 1B 1C 1中，AB ＝BB 1＝BC ，AC 1⊥平面A 1BD ，D 为AC 的中点．(1)求证：B 1C ∥平面A 1BD ； (2)求证：B 1C 1⊥平面ABB 1A 1；(3)在CC 1上是否存在一点E ，使得∠BA 1E ＝45°，若存在，试确定E 的位置，并判断平面A 1BD 与平面BDE 是否垂直？若不存在，请说明理由．[分析] (1)连接AB 1，交A 1B 于M ，则MD 就是平面A 1BD 内与B 1C 平行的直线；(2)需在平面ABB 1A 1中找两条相交直线都与B 1C 1垂直，由直三棱柱的概念，知BB 1⊥B 1C 1，另一条的寻找，从AC 1⊥平面A 1BD ，以平行四边形ABB 1A 1为正方形入手，证明A 1B ⊥平面AB 1C 1从而得出A 1B ⊥B 1C 1.(3)用余弦定理解△A 1BE .[解析] (1)连接AB 1与A 1B 相交于M ，则M 为A 1B 的中点．连接MD ，又D 为AC 的中点，∴B 1C ∥MD ，又B 1C ⊄平面A 1BD ，MD ⊂平面A 1BD ，∴B 1C ∥平面A 1BD . (2)∵AB ＝B 1B ，∴平行四边形ABB 1A 1为正方形， ∴A 1B ⊥AB 1.又∵AC 1⊥平面A 1BD ，∴AC 1⊥A 1B ，∴A 1B ⊥平面AB 1C 1，∴A 1B ⊥B 1C 1. 又在直三棱柱ABC －A 1B 1C 1中，BB 1⊥B 1C 1， ∴B 1C 1⊥平面ABB 1A 1.(3)设AB ＝a ，CE ＝x ，∵B 1C 1⊥A 1B 1，在Rt △A 1B 1C 1中有A 1C 1＝2a ，同理A 1B 1＝2a ，∴C 1E ＝a －x ，∴A 1E ＝2a 2＋a －x2＝x 2＋3a 2－2ax ，BE ＝a 2＋x 2，∴在△A 1BE 中，由余弦定理得BE 2＝A 1B 2＋A 1E 2－2A 1B ·A 1E ·cos45°，即 a 2＋x 2＝2a 2＋x 2＋3a 2－2ax －22a 3a 2＋x 2－2ax ·22， ∴3a 2＋x 2－2ax ＝2a －x ， ∴x ＝12a ，即E 是C 1C 的中点，∵D 、E 分别为AC 、C 1C 的中点，∴DE ⊥AC 1. ∵AC 1⊥平面A 1BD ，∴DE ⊥平面A 1BD . 又DE ⊂平面BDE ，∴平面A 1BD ⊥平面BDE .[点评] 空间中直线与直线垂直、直线与平面垂直、平面与平面垂直三者之间可以相互转化，每一种垂直的判定都是从某种垂直开始转向另一种垂直，最终达到目的，其转化关系为线线垂直判定定理性质定理线面垂直判定定理性质定理面面垂直．(理)(xx·齐鲁名校联考)如图，在直三棱柱ABC －A 1B 1C 1中，AB ＝BC ＝2AA 1，∠ABC ＝90°，D 是BC 的中点．(1)求证：A 1B ∥平面ADC 1； (2)求二面角C 1－AD －C 的余弦值；(3)试问线段A 1B 1上是否存在点E ，使得AE 与DC 1成60°角？若存在，确定E 点位置；若不存在，说明理由．[解析] (1)证明：连接A 1C ，交AC 1于点O ，连接OD .由ABC －A 1B 1C 1是直三棱柱得四边形ACC 1A 1为矩形，O 为A 1C 的中点．又D 为BC 中点，所以OD 为△A 1BC 中位线，所以A 1B ∥OD ，所以OD ⊂平面ADC 1，A 1B ⊄平面ADC 1，所以A 1B ∥平面ADC 1.(2)由ABC －A 1B 1C 1是直三棱柱，且∠ABC ＝90°，故BA 、BC 、BB 1两两垂直．如图建立空间直角坐标系B －xyz .设BA ＝2，则B (0,0,0)，C (2,0,0)，A (0,2,0)，C 1(2,0,1)，D (1,0,0)．所以AD →＝(1，－2,0)，AC 1→＝(2，－2,1)．设平面ADC 1的法向量为n ＝(x ，y ，z )，则有 ⎩⎪⎨⎪⎧n ·AD →＝0，n ·AC 1→＝0.所以⎩⎪⎨⎪⎧x －2y ＝0，2x －2y ＋z ＝0.取y ＝1，得n ＝(2,1，－2)．易知平面ADC 的法向量为v ＝(0,0,1)．由二面角C 1－AD －C 的平面角是锐角，得 cos 〈n ，v 〉＝|n ·v ||n ||v |＝23.所以二面角C 1－AD －C 的余弦值为23.(3)假设存在满足条件的点E .因为E 在线段A 1B 1上，A 1(0,2,1)，B 1(0,0,1)，故可设E (0，λ，1)，其中0≤λ≤2. 所以AE →＝(0，λ－2,1)，DC 1→＝(1,0,1)．因为AE 与DC 1成60°角，所以⎪⎪⎪⎪⎪⎪⎪⎪AE →·DC 1→|AE →||DC 1→|＝12. 即⎪⎪⎪⎪⎪⎪1λ－22＋1·2＝12，解得λ＝1，舍去λ＝3.所以当点E 为线段A 1B 1中点时，AE 与DC 1成60°角．。