三坐标机测量齿轮齿廓的不确定度评价
基于GPS的三坐标测量机不确定度评定

基于 G P S的 三 坐 标 测 量 机 不 确 定 度 评 定
杨 桥 徐 磊 姜 瑞
( 合肥工业大学仪器科学与光电工程 学院 , 安徽 合肥 2 3 0 0 0 9 )
摘
要: 三坐标测 机足一个广 ‘ 泛应 用的儿何量测量仪器 , 准确评价其测量结果的不确定皮 , 对 于提升测量结果的可用性具 有重要意 义。本文基于产 品几
操作 规 范 的前 提下 , 由各 测量者 自行拟 定测 量策 略 , 不 同 测 量者 的测量 是相互 独立 的。 即每 个测 量者 均 须根 据 自
C MM) , 作 为一 种通用 的精 密 测量 仪 器 , 广 泛 地 应 用 于机 床、 模具 、 汽车、 航 空航 天 等众 多加工 制造 领域 , 是现代 产 品几 何量 检 测 中最重要 的手段 之一 。然 而 目前 的商 用三 坐标 测量 机 在应 用 时 , 通 常 只给 出、 狈 4 量结 果 的估 计值 , 而 无法 获得 测 量结 果 的不确 定度 。测 量不确 定度 反应 了测 量结 果 的可 信程 度 , 是 测量 结果 中必 须包 含 的部 分 , 缺少
*基 金 项 目 : 国 家 自然 科 学 基 金 资 助 项 目 ( N o . 5 1 2 7 5 1 4 8 ) 收 稿 日期 : 2 0 1 4—0 4—0 8
《 钟 童与潮试 技术》 2 。 ’ 4羊 第4 /卷 第 9期
Th r e e Co o r d i na t e Me a s u r i n g Ma c h i n e Ba s e d o n GPS Ev a l u a t i o n o f Un c e r t a i n t y
三坐标测量机示值误差测量结果的不确定度评定

通过计算结果估 计 :
k=2 参 考 文 献 【 ] ] J J F 1 0 6 4 — 2 0 1 0 , 坐标 测 量 机校 准规 范. [ 2 ] J J F 1 0 5 9 . 1 — 2 0 1 2 , 测量不确定度评定 与表示 U一( 0 . 1 3 + 4 / 5 L ) m
— — — — — 一
u ( e r ) = 、 Y / 去 J J ∑( iR / 1 . 6 9 ) = 0 . 0 2 X I m
=
1
4不 确 定 度 一 览 表 ( 表 4)
( E ) =√ ( P f ) +U 2 ( P 口 ) +R 2 ( P f ) - t - U 2 ( ) +U 2 ( P w ) +U 2 ( P , )
1 概 述
测量依据 J J F 1 0 6 4 — 2 0 1 0 ( ( 坐标测量机校准规范》 , 采用三等 大十 块量 块, 校准 三坐标测 量机 的示值 误差 时 , 通过 比较 5个不 同长度 尺寸 实物标准 器在测量空 间的 7个不 同的方 向或 位置 的校 准值 和 指示值 , 评价坐标测量机是 否符合规定 的最大允许示值误 差 MP E 。 每个 长度各测量 3次 。对测 量值与尺 寸实物标准 器 的约定 真值之 差, 计算 每一尺寸测量的示值误差 E 。
8 2 ( 口 ) = I △ 一( 1 A 1 l +l A 2 1 ) l= o . 0 7 x I m
3 . 6测量 重复性引入的标准不确定度 u( 已 r ) 重复 性的评价 按 3 5组 ( m = 3 5 ) 3次( n = 3 ) 重复 测量确定 合并样 本标准差 。设 3 5组测 量中 , 每 3组测量 的极差为 R i , 则 由重复性引 入的不确定度分量 为 :
三坐标测量不确定度评定

三坐标测量不确定度评定作者:陈相国刘赞来源:《中小企业管理与科技·下旬刊》2016年第06期摘要:本文对三坐标测量以ϕ40mm3等标准环规进行了实例评定,对三坐标尺寸检测方法的改进有一定意义。
关键词:三坐标;不确定度中图分类号: U467 文献标识码: A 文章编号: 1673-1069(2016)18-190-21 试验部分1.1 试验任务测量ϕ40mm3等标准环规刻度线处的直径D。
1.2 试验原理、方法和条件1.2.1 试验原理接触式,直接法,绝对测量。
1.2.2 试验方法在三坐标测量机PRISMO上测量,测量前将标准环规固定于三坐标测量工作平台上,将仪器调整满足测量需要的状态。
测量时,首先在环规刻度线处取对称两点x1、x2,构成环规的一条弦x1x2,并确定弦的中心O(以O点为坐标原点),在环规刻度线处取一点A0,连接OA0交环规另一边A(以AA0为坐标X轴),则A、A0在坐标X轴上读数差即是环规刻度线处的直径值D。
1.2.3 试验条件试验环境温度为(20±1)C,温度变化每小时不应超过0.5℃/h,环境相对湿度为≤65%;三坐标测量机常年固定安装在实验室内,受测标准环规置于实验室内的平衡时间24小时以上。
2 数学模型由试验原理和方法,得到数学模型:4 测量不确定度来源及说明测量不确定度来源及说明见表1:5 标准不确定度评定5.1 由三坐标测量机的示值误差引入的标准不确定度分量u1根据设备出厂证书三坐标测量机最大允许误差MPE为±(1.4+L/333mm)m,符合均匀分布,k=,受测标准环规的直径按40mm计算,则:u1=(1.4+40/333)/=0.8777μm5.2 由测量重复性引入的标准不确定度分量u2在各种条件均不改变的情况下,在短时间内重复性测量20次(即n=20)。
实验数据见表2。
5.3 由测量环境温度变化引入的标准不确定度分量u3由于测量设备及环规置于实验室恒温恒湿的环境中足够时间,且测量过程中启用测量设备温度补偿功能,避免温度变化引起设备与环规的热膨胀,因此此项因素引起的测量不确定度分量可忽略不计,则u3=0。
浅析测量不确定度评定及在三坐标测量机的应用

10.16638/ki.1671-7988.2019.21.024浅析测量不确定度评定及在三坐标测量机的应用谢周武(广州汽车集团股份有限公司汽车工程研究院,广东广州511434)摘要:随着科学的进步及对精工极致的追求,测量不确定度评定越来越多的应用于检测实验室,用测量结果及测量结果的不确定度判断零部件某一属性的质量情况。
文章以JJF1059.1-2012《测量不确定度评定与指南》为基础,浅析测量不确定度的定义及评定的一般流程,并以三坐标测量机检测二等标准量块的不确定度评定为例加以描述。
关键词:测量结果;测量不确定度;三坐标测量机中图分类号:U467 文献标识码:B 文章编号:1671-7988(2019)21-70-03The evaluation of measurement uncertainty and its application in CMM are analyzedXie Zhouwu(Guangzhou automotive engineering research institute, Guangdong Guangzhou 511434)Abstract: With the progress of science and the pursuit of the perfection of seiko, the evaluation of measurement uncertainty is more and more applied in testing laboratories. The quality of a component can be judged by the measurement results and the uncertainty of the measurement results. Based on JJF1059.1-2012 measurement uncertainty evaluation and guidelines, this paper analyzes the definition of measurement uncertainty and the general process of evaluation, and describes the uncertainty evaluation of second-class standard gauge block detected by CMM as an example.Keywords: Measurement results; Measurement uncertainty; Coordinate measuring machineCLC NO.: U467 Document Code: B Article ID: 1671-7988(2019)21-70-03前言随着精密测量设备的发展,测量已成为汽车行业发展的重要基础,想要提高产品的的竞争力,就必须改善产品的质量,而改善产品的质量需要通过测量发现产品零部件存在的缺陷和改善的空间。
三坐标机测量齿轮齿廓的不确定度评价

三坐 标 机 测 量 齿 轮 齿 廓 的不 确 定 度 评 价
石照耀 , 宇 , 白 张 张
( 北京工业大学 机械与应用 电子技术学院, 北京 10 2 ) 0 14
摘 要 : 绍 了坐 标 测 量 中几 种 常用 的 不 确 定 度 评 价 方 法 。指 出 传 统 的 三 坐 标 测 量 机 的测 量 不 确 定 度 评 价 方 法 大 都 不 适 介 用 于 评 价 坐 标 测 量 中 面 向对 象 的 测 量 不 确 定 度 , 对 使 用 蒙 特 卡 洛 方 法 评 价 测 量 不 确 定 度 进行 了 研 究 。首 先 , 据 三 坐 并 根 标 测 量 机 详 细 标 定 文 件 及 补 偿 策 略 说 明建 立 测 量模 型 。然 后 , 测 量 中 的 采 样 点 通 过 测 量 模 型 生 成 大 量 测 量 结 果 , 以 将 并 此 评 价 测 量 不 确 定 度 。在 齿 廓 评 价 实 验 中 , 定 齿 廓 误 差 的测 量 不 确 定 度 为 0 9 m 时 , 次 评 价 结 果 之 间 的 最 大 差 值 评 . 6t * 多 不 超 过 00 m, 有 可 靠 的 理 论 依 据 和 较 稳 定 的评 定 结 果 。 文 章 指 出 , .3 具 目前 商 用 三 坐 标 测 量 机 大 都 不 能 为 特 定 的 测 量 对象提供 测量不确定度报告 , 用蒙特卡洛方法有希 望改变此现状 。 使
nu b r o a pl o nt . U s n h s i ul t d r s t m e fs m e p i s i g t e e sm a e e uls,t e u e t i i sc n b v l a e o e C I— h nc r ante a e e a u t d m r Ol
三坐标机测量齿轮齿廓的不确定度评价

三坐标机测量齿轮齿廓的不确定度评价石照耀;张宇;张白【摘要】Several kinds of evaluation methods for the uncertainty in coordinate measurement are introduced and it points out that most of these methods are failed to the uncertainty evaluation for special objectives because of lack of theory support or practicability. Therefore, this paper investigates the uncertainty evaluation of gear measurement with Coordinate Measurement Machines (CMMs) by the Monte Carlo method. Firstly, a measuring model is established based on the files for the calibration and compensation of the specific CMM, then the mode is used to obtain measuring results with a large number of sample points. Using these simulated results, the uncertainties can be evaluated more conveniently. Finally,the Monte Carlo method is successfully used in evaluating measurement uncertainty of gear profiles and obtained stable results show that the maximal difference among the results is less than 0. 03μm when the typical uncertainty is 0. 96μm. The paper suggests that Monte Carlo method can support specific uncertainty measurement and can change the situation that common evaluation method can not be suitable for the commercial CMMs.%介绍了坐标测量中几种常用的不确定度评价方法.指出传统的三坐标测量机的测量不确定度评价方法大都不适用于评价坐标测量中面向对象的测量不确定度,并对使用蒙特卡洛方法评价测量不确定度进行了研究.首先,根据三坐标测量机详细标定文件及补偿策略说明建立测量模型.然后,将测量中的采样点通过测量模型生成大量测量结果,并以此评价测量不确定度.在齿廓评价实验中,评定齿廓误差的测量不确定度为0.96 μm时,多次评价结果之间的最大差值不超过0.03 μm,具有可靠的理论依据和较稳定的评定结果.文章指出,目前商用三坐标测量机大都不能为特定的测量对象提供测量不确定度报告,使用蒙特卡洛方法有希望改变此现状.【期刊名称】《光学精密工程》【年(卷),期】2012(020)004【总页数】6页(P766-771)【关键词】坐标测量机;齿轮齿廓;蒙特卡洛方法;不确定度【作者】石照耀;张宇;张白【作者单位】北京工业大学机械与应用电子技术学院,北京100124;北京工业大学机械与应用电子技术学院,北京100124;北京工业大学机械与应用电子技术学院,北京100124【正文语种】中文【中图分类】TH721;TG861 引言国际标准化组织(ISO)和国际电工委员会(IEC)发布的《测量不确定度的表示方法指南》(GUM)指出,“一项完整的测量结果表述应当包含测量不确定度”[1]。
三坐标测量机不确定度

三坐标测量机示值校准结果不确定度的评定1. 测量方法(依据JJF1064-2004《坐标测量机校准规范》)尺寸测量校准方法的原理,是通过比较5个不同长度的尺寸实物标准器的校准值和指示值,评价测量尺寸的坐标测量机是否符合规定的最大允许示值误差MPE E 。
5个尺寸实物标准器放在测量空间的7个不同的方向或位置,各测量3次,共进行105次测量。
大值与最小值的。
2. 数学模型对标准器进行测量,得到的测量长度值为E L L L t L L L S S S +∆-∆-∆-∆+=321α其中S L 标准器的校准长度,1L ∆为标准器形状误差等因素引起的误差,2L ∆为长度稳定性引起的误差,3L ∆为测量重复性引起的误差,S α为标准器的热膨胀系数,t ∆为标准器温度对20℃的偏差,E 为坐标测量机的示值L 的误差。
3. 灵敏度系数11/1≈∆+=∂∂=t L L c S S α t L L L c S S ∆=∂∂=/2S S L t L c α=∆∂∂=)(/3 1)(/14-=∆∂∂=L L c1)(/25-=∆∂∂=L L c 1)(/36-=∆∂∂=L L c1/7=∂∂=E L c4. 标准不确定度1u 为标准器校准值S L 的标准不确定度,2u 为标准器热膨胀系数s α的标准不确定度,根据标准器的校准证书确定标准不确定度值。
3u 为标准器温度测量的标准不确定度,由于标准器的温度测量是坐标测量机上的功能,测量误差是坐标测量机示值误差的一部分,与校准方法无关,不予单独考虑。
4u 为标准器的长度变动量引入的标准不确定度。
5u 为标准器的长度稳定度引入的标准不确定度。
6u 为测量重复性引入的标准不确定度。
7u 为坐标测量机示值误差的标准不确定度,也是坐标测量机的测量示值误差的组成部分,与校准方法无关,不予单独考虑。
5. 合成标准不确定度[]2/12625242221)(u u u tu L u u S c +++∆+=。
三座标测量结果不确定度评定-2014-4-10
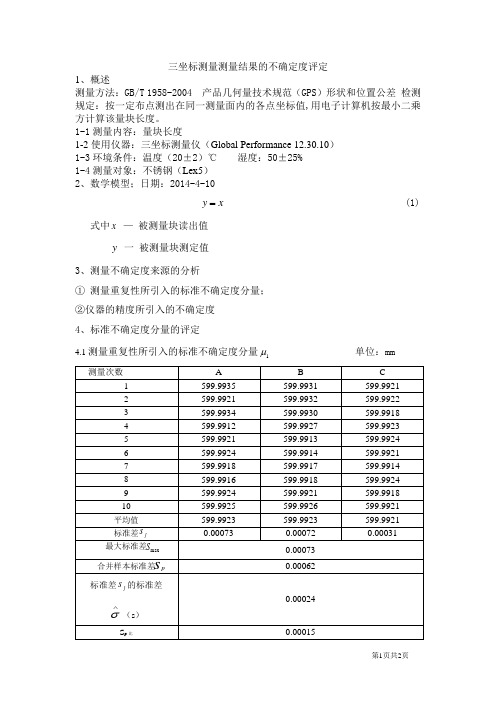
三坐标测量测量结果的不确定度评定1、概述测量方法:GB/T 1958-2004 产品几何量技术规范(GPS)形状和位置公差检测规定:按一定布点测出在同一测量面内的各点坐标值,用电子计算机按最小二乘方计算该量块长度。
1-1测量内容:量块长度1-2使用仪器:三坐标测量仪(Global Performance 12.30.10)1-3环境条件:温度(20±2)℃湿度:50±25%1-4测量对象:不锈钢(Lex5)2、数学模型;日期:2014-4-10y= (1)x式中x—被测量块读出值y一被测量块测定值3、测量不确定度来源的分析①测量重复性所引入的标准不确定度分量;②仪器的精度所引入的不确定度4、标准不确定度分量的评定μ单位:mm4.1测量重复性所引入的标准不确定度分量1合并样本标准差为:∑==mj p s s j m 121 =0.62μm (其中m=3)标准差j s 的标准差:1)(12)(-=∑-=∧m j s m j s s σ=0.24μm)1(2-=n S spP 比=0.15μm (其中n=10)如≤∧)(s σ S p 比,则可采用合并样本标准差Sp 来评定标准不确定度分量,反之,若子 )(s ∧σ>S p 比,则应采用Sj 中的最大值S max 来评定标准不确定度分量。
所以,1u =10/73.0=0.23μm自由度:)1(-=n m pν=)110(*3-=274.2仪器的精度所引入的不确定度2u仪器的示值误差为±2.8+3L/1000m μ按均匀分布 k=3 a=2.8+3*600/1000m μ(L 取值600mm)2u =66.23/≈a m μ2221μμ+=U =2266.223.0+=2.75m μ5.扩展不确定度取置信概率P=95%,, k 95=2 扩展不确定度U 95为U 95=k 95)(e U c ⨯=2⨯2.75≈5.51m μ 6.测量结果不确定度报告与表示三坐标测量该量块的长度为599.9922±0.00551mm报告审核: 报告编制:邓过房。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
交线。
烄x=rb[cos(ξ+Λ+θ)+ξsin(ξ+Λ+θ)] y=rb[sin(ξ+Λ+θ)-cos(ξ+Λ+θ)]
计算机仿真法的主要思想是根据特定坐标测 量机中各误差源 向 最 终 被 测 量 的 传 播 关 系,建 立 测量系统模型;然 后 用 数 学 的 方 法 重 现 测 量 过 程 中误差 的 大 小 和 分 布 特 征。 将 各 误 差 源 输 入 模 型 ,可 得 到 测 量 结 果 并 计 算 出 不 确 定 度 。
2 不确定度评定中的蒙特卡洛方法
蒙特卡洛方 法 是 一 种 针 对 待 求 问 题,根 据 对 象本身的统计规律或人为构造其合适的依赖随机 变量的概率模型,使 某 些 随 机 变 量 的 统 计 量 为 待 求问题的解,进行 大 统 计 量 (N → ∞ )的 计 算 机 随 机模拟方法 。 [8] 应用在虚拟仿真测量时,首 先,要 构造测量中各误 差 源 的 概 率 模 型,并 使 测 量 结 果 成 为 待 求 的 解 ,然 后 ,通 过 多 次 仿 真 测 量 得 到 大 量 的 测 量 结 果 ,根 据 这 些 结 果 评 价 测 量 不 确 定 度 。
烅z=
-rb·θ tanβ
. (1)
烆A·x+B·y+C·z=a
如上式所示,前3个式子组成了斜齿轮单侧渐
开线螺旋 面 的 方 程,第 4 个 式来自子 是 测 量 平 面 的 方
程。方程组确定的是测量平面倾斜时的采样路径。
3 获取齿轮测量采样点
4 CMM 的仿真模型
仿真测量时,由 于 不 同 位 置 引 入 的 误 差 大 小 不同,需要已知被测点在 CMM 坐标系中的位置。 当实际测量采样 点 可 用 时,可 用 实 际 测 量 点 作 为 仿 真 的 采 样 点 ;当 缺 乏 实 际 测 量 数 据 时 ,可 以 使 用 理论坐标点。这里给出了利用几何模型计算采样 点的方法。
解析法要求求解出原始误差源传播到最终 测量结果的灵敏 系 数,将 各 误 差 源 对 测 量 不 确 定 的影响合成。这就要求测量模型具有较好的线性 以及可 解 析 性。CMM 的 测 量 不 确 定 度 来 源 多, 传 播 关 系 复 杂 ,使 得 解 析 法 很 难 有 效 的 实 施 。
统计方法虽然能提供比较可靠的评价结果, 但需要对被测量 进 行 大 量 的 反 复 测 量,用 大 量 测 量数据的离散程度来反映测量不确定度。这种方 法 需 要 耗 费 大 量 的 时 间 ,对 于 工 业 生 产 并 不 实 用 。
用蒙特卡洛方法评定 CMM 的测量不确定度 时的主要实施过程如图1所示。
图 1 蒙 特 卡 洛 仿 真 方 法 的 实 施 Fig.1 Process of Monte Carlo simulation
首 先 ,对 系 统 的 所 有 输 入 误 差 源 ,按 照 其 概 律 分布及其所在的采样点信息进行大量随机抽样。 假设系统输 入 误 差 源 数 量 为 n,每 个 误 差 源 按 其
计量检测:www.cqstyq.com
计量检测:www.cqstyq.com
概率分布随机抽取 的 样 本 的 容 量 为 m,则 可 得 到 m 个输出测 量 结 果yi~ym 。 仿 真 测 量 结 果 的 分 布较真实地反映 了 实 际 测 量 结 果 的 分 布 规 律,对 此统计分析,即可评价出测量不确定度 。 [9]
计量检测:www.cqstyq.com
三坐标机测量齿轮齿廓的不确定度评价
石照耀,张 宇* ,张 白
(北京工业大学 机械与应用电子技术学院,北京100124)
摘要:介绍了坐标测量中几种常用的不确定度评价方法。指出 传 统 的 三 坐 标 测 量 机 的 测 量 不 确 定 度 评 价 方 法 大 都 不 适 用于评价坐标测量中面向对象的测量不确定度,并对使用蒙特卡洛方法评价测量不确定度进行了研究。 首 先,根 据 三 坐 标测量机详细标定文件及补偿策略说明建立测量模型。然后,将测量中的采样点通过测量模型生成大量 测 量 结 果,并 以 此评价测量不确定度。在齿廓评价实验中,评定齿廓误差的测量不确定度为0.96μm 时,多次评价结果之间的最大差值 不超过0.03μm,具有可靠的理论依据和较稳定的评定结果。文章指出,目前商用三坐标测量 机 大 都 不 能 为 特 定 的 测 量 对 象 提 供 测 量 不 确 定 度 报 告 ,使 用 蒙 特 卡 洛 方 法 有 希 望 改 变 此 现 状 。 关 键 词 :坐 标 测 量 机 ;齿 轮 齿 廓 ;蒙 特 卡 洛 方 法 ;不 确 定 度 中 图 分 类 号 :TH721;TG86 文 献 标 识 码 :A doi:10.3788/OPE.20122004.0766
1 引 言
国 际 标 准 化 组 织 (ISO)和 国 际 电 工 委 员 会 (IEC)发 布 的 《测 量 不 确 定 度 的 表 示 方 法 指 南 》 (GUM)指出,“一 项 完 整 的 测 量 结 果 表 述 应 当 包 含测量不确 定 度”[1]。ISO 17025 特 别 强 调,测 量 量值的可追溯性 要 靠 不 间 断 的 标 定 链 传 递;在 保 证可追溯性的标 定 链 中,每 层 都 要 给 出 标 定 中 的 测量值,以及测量结果的不确定度 。 [2] 同样,坐 标 测量机 (CMM)的 测 量 表 述 也 应 满 足 以 上 要 求。 CMM 广泛应 用 于 多 种 工 件 的 测 量 中,适 用 范 围 广泛,但存在 测 量 不 确 定 度 难 以 评 价 的 问 题。 目 前,CMM 测量 不 确 定 度 的 评 价 方 法 主 要 有 统 计 学 方 法 、灵 敏 系 数 解 析 法 、专 家 判 断 法 和 计 算 机 仿 真法等 。 [3]
*Corresponding author,E-mail:beammild@gmail.com
Abstract:Several kinds of evaluation methods for the uncertainty in coordinate measurement are intro- duced and it points out that most of these methods are failed to the uncertainty evaluation for special objectives because of lack of theory support or practicability.Therefore,this paper investigates the uncertainty evaluation of gear measurement with Coordinate Measurement Machines (CMMs)by the Monte Carlo method.Firstly,a measuring model is established based on the files for the calibration and compensation of the specific CMM,then the mode is used to obtain measuring results with a large number of sample points.Using these simulated results,the uncertainties can be evaluated more con- veniently.Finally,the Monte Carlo method is successfully used in evaluating measurement uncertainty of gear profiles and obtained stable results show that the maximal difference among the results is less than 0.03μm when the typical uncertainty is 0.96μm.The paper suggests that Monte Carlo method can support specific uncertainty measurement and can change the situation that common evaluation method can not be suitable for the commercial CMMs. Key words:Coordinate Measurement Machine(CMM);gear profile;Monte Carlo method;uncertainty evaluation
基于计算机仿 真 方 法,很 多 研 究 者 提 出 了 不 同 的 虚 拟 测 量 解 决 方 案 。 德 国 国 家 计 量 院 (PTB) 率先提出了虚拟坐标机(VCMM)的 概 念,并 应 用 于齿 轮 测 量 的 不 确 定 度 评 价 中 。 [4] 荷 兰 Eind- hoven大学用替代信号 模 拟 CMM 的 机 构 误 差 得 到测量结果 。 [5] 不 仅 在 坐 标 测 量 领 域,计 算 机 仿 真法在其它量仪的测量不确定度评价中也得到了 广泛应用。英国 Bath 大 学 用 虚 拟 测 量 的 理 念 建
Uncertainty evaluation of CMM measurement for gear profile
SHI Zhao-yao,ZHANG Yu* ,ZHANG Bai
(College of Mechanical Engineering and Applied Electronics Technology,Beijing University of Technology,Beijing100124,China)
