三坐标角度示值的不确定度评定报告(47BQD-01-2017)
三坐标测量机示值误差测量结果的不确定度评定

通过计算结果估 计 :
k=2 参 考 文 献 【 ] ] J J F 1 0 6 4 — 2 0 1 0 , 坐标 测 量 机校 准规 范. [ 2 ] J J F 1 0 5 9 . 1 — 2 0 1 2 , 测量不确定度评定 与表示 U一( 0 . 1 3 + 4 / 5 L ) m
— — — — — 一
u ( e r ) = 、 Y / 去 J J ∑( iR / 1 . 6 9 ) = 0 . 0 2 X I m
=
1
4不 确 定 度 一 览 表 ( 表 4)
( E ) =√ ( P f ) +U 2 ( P 口 ) +R 2 ( P f ) - t - U 2 ( ) +U 2 ( P w ) +U 2 ( P , )
1 概 述
测量依据 J J F 1 0 6 4 — 2 0 1 0 ( ( 坐标测量机校准规范》 , 采用三等 大十 块量 块, 校准 三坐标测 量机 的示值 误差 时 , 通过 比较 5个不 同长度 尺寸 实物标准 器在测量空 间的 7个不 同的方 向或 位置 的校 准值 和 指示值 , 评价坐标测量机是 否符合规定 的最大允许示值误 差 MP E 。 每个 长度各测量 3次 。对测 量值与尺 寸实物标准 器 的约定 真值之 差, 计算 每一尺寸测量的示值误差 E 。
8 2 ( 口 ) = I △ 一( 1 A 1 l +l A 2 1 ) l= o . 0 7 x I m
3 . 6测量 重复性引入的标准不确定度 u( 已 r ) 重复 性的评价 按 3 5组 ( m = 3 5 ) 3次( n = 3 ) 重复 测量确定 合并样 本标准差 。设 3 5组测 量中 , 每 3组测量 的极差为 R i , 则 由重复性引 入的不确定度分量 为 :
三坐标测量不确定度评定

三坐标测量不确定度评定作者:陈相国刘赞来源:《中小企业管理与科技·下旬刊》2016年第06期摘要:本文对三坐标测量以ϕ40mm3等标准环规进行了实例评定,对三坐标尺寸检测方法的改进有一定意义。
关键词:三坐标;不确定度中图分类号: U467 文献标识码: A 文章编号: 1673-1069(2016)18-190-21 试验部分1.1 试验任务测量ϕ40mm3等标准环规刻度线处的直径D。
1.2 试验原理、方法和条件1.2.1 试验原理接触式,直接法,绝对测量。
1.2.2 试验方法在三坐标测量机PRISMO上测量,测量前将标准环规固定于三坐标测量工作平台上,将仪器调整满足测量需要的状态。
测量时,首先在环规刻度线处取对称两点x1、x2,构成环规的一条弦x1x2,并确定弦的中心O(以O点为坐标原点),在环规刻度线处取一点A0,连接OA0交环规另一边A(以AA0为坐标X轴),则A、A0在坐标X轴上读数差即是环规刻度线处的直径值D。
1.2.3 试验条件试验环境温度为(20±1)C,温度变化每小时不应超过0.5℃/h,环境相对湿度为≤65%;三坐标测量机常年固定安装在实验室内,受测标准环规置于实验室内的平衡时间24小时以上。
2 数学模型由试验原理和方法,得到数学模型:4 测量不确定度来源及说明测量不确定度来源及说明见表1:5 标准不确定度评定5.1 由三坐标测量机的示值误差引入的标准不确定度分量u1根据设备出厂证书三坐标测量机最大允许误差MPE为±(1.4+L/333mm)m,符合均匀分布,k=,受测标准环规的直径按40mm计算,则:u1=(1.4+40/333)/=0.8777μm5.2 由测量重复性引入的标准不确定度分量u2在各种条件均不改变的情况下,在短时间内重复性测量20次(即n=20)。
实验数据见表2。
5.3 由测量环境温度变化引入的标准不确定度分量u3由于测量设备及环规置于实验室恒温恒湿的环境中足够时间,且测量过程中启用测量设备温度补偿功能,避免温度变化引起设备与环规的热膨胀,因此此项因素引起的测量不确定度分量可忽略不计,则u3=0。
三坐标角度示值的不确定度评定报告(47BQD-01-2017)

测 量 不 确 定 度 报 告47BQD-01-20171目的为了验证产品角度尺寸与设计值的符合性,需要对产品的角度尺寸进行测量,三坐标测量机测量分辨率高是一种有效的测量设备。
根据JJF1059.1-2012《测量不确定度评定与表示》对三坐标测量机的角度测量进行测量不确定度评定。
2依据GB/T3177-2009 产品几何技术规范(GPS)光滑工件尺寸的检验 3适用范围用单一材料或层积材料制成的有一定刚性的产品,产品尺寸在设备测量范围以内。
4方法概要采用三坐标测量机对任意工件(本例中采用二级角度40°量块)在标准环境(温度20±2℃,湿度<65%)中,进行测量,在直角坐标系空间的有效量程上,记录三坐标测量机示值,各机器平面测量三次,得到9组读数,将读数作为测量结果。
5数学模型由测量的方式,建立数学模型如下:(采用40°的量块)i i T M = (i =1,2…9)式中:i M ——测量结果,i T ——三坐标测量机的读数 6使用的计量器具、标准物质和仪器设备① 三坐标测量机,该设备的分辨率为0.5μm ,假定三角分布,k =61/2 ② 三坐标测量机,该设备的校准证书指出最大允许示值误差(MPE E )为 8.0+7.5L/1000 (μm ) ,在本例中L ≤70mm ,得MPE E =8.525μm ,假定均匀分布,k =31/2;③ 三坐标测量机,该设备的校准证书指出最大允许探测误差(MPE P )为8.0μm,假定均匀分布,k=31/2。
④三坐标测量机,该设备说明中设备轴间垂直度允差为0.0005°,假定为均匀分布,k=31/2。
7测量结果M及典型值用40°角度量块进行9次测量结果如下:XY面YZ面ZX面读数1 读数2 读数3 读数4 读数5 读数6 读数7 读数8 读数9 40.0014 39.9987 40.0025 39.9995 40.0009 39.9971 39.9988 39.9980 39.9991 平均值: 39.9996°8不确定度分量的识别、分析和量化按照数学模型及方法概要,其不确定度来源有5方面:① M的测量重复性u1 (M)(8.1)②三坐标测量机的分辨率引入的标准不确定度u2 (M)(8.2)③三坐标测量机的最大允许示值误差引入的标准不确定度u3 (M)(8.3)④三坐标测量机的最大允许探测误差引入的标准不确定度u4(M)(8.4)⑤三坐标测量机的轴间垂直度允差引入的标准不确定度u(M) (8.5)58.1 测量重复性u1(M)用40°角度量块进行9次测量重复性,贝塞尔公式计算单次测量标准差s(M)=[∑M i2/(n-1)]1/2= 0.001726°u1(M)=s(M)/ 91/2= 0.0005754°8.2 设备的分辨率引入的标准不确定度u2(M)考虑设备在根据测点构造矢量时,因设备的示值误差±0.5μm会发生角度偏差,在L=70的长度内,设测点间距为60mm,角误差即为±0.0009549°,双矢量则为:±0.001910°,假定为三角分布,k=61/2,u2(M)=0.001910°/61/2=0.0007797°8.3 设备的最大允许示值误差引入的标准不确定度u3(M)设备的最大允许示值误差是MPE E=8.525μm, 同样在L=70的长度内,设测点间距为60mm,角误差即为:0.01628°,双矢量则为:0.03256°,假定均匀分布,k=31/2u3(M)=0.03256°/31/2=0.01880°8.4设备的最大允许探测误差引入的标准不确定度u4(M)设备的最大允许探测误差是MPE P =8μm, 同样在L=70的长度内,设测点间距为60mm,角误差即为:0.01528°,双矢量则为:0.03056°,假定均匀分布,k=31/2U4(M)=0.03056°/31/2=0.01764°8.5设备的轴间垂直度允差为0.0005°,考虑到有三轴存在,彼此无明显相关性,则合成允差为:(0.00052+0.00052+0.00052)1/2=0.0008660°假定为均匀分布,k=31/2U5(M)=0.0008660°/31/2=0.0005°9计算相对合成标准不确定度u cr(M)符号来源类别量值量序U1(M) 测量重复性A类0.0005754° 1U2(M)设备分辨率B类0.0007797° 2U3(M) 设备示值误差B类0.01880° 3U4(M) 设备探测误差B类0.01764° 4U5(M)垂直度允差B类0.0005° 5u c(M)=[∑u i2(M)]1/2=(0.0005752+0.00077972+0.018802+0.017642+0.00052)1/2=0.02581°10计算扩展不确定U(M)取k=2,U(M)=2×u c(M)=2×0.02581°=0.05162°11结果完整表达该量块的测量结果M=39.9996°U(M)=0.05162°, k=2编制人审核人批准人日期日期日期。
三坐标测量不确定度评估

测量不确定度评估示例C.1 尺寸测量示值误差E测量结果的不确定度计算C.1.1 测量模型对标准器进行测量,得到的测量尺寸示值E的标准不确定度为:u2 (E)= u2 (εcal)+u2(εα)+ u2(εt)+ u2(εalign) +u2(εfixt) +u2(εR)其中:εcal——标准器的校准误差;εα——标准器的热膨胀系数引起的E误差;εt——输入的标准器温度引起的E误差;εalign——标准器定向引起的E误差;εfixt ——标准器装卡稳定性引起的E误差;εR——测量重复性引起的E误差。
C.1.2 不确定度因素分析C.1.2.1 u(εcal)为标准器校准值Ls的标准不确定度。
u(εcal)=U cal/k其中:U cal——标准器校准证书上注明的扩展不确定度;k——标准器校准证书上注明扩展不确定度的扩展因子。
C1.2.2 u(εα)为标准器热膨胀系数αs引起E的标准不确定度,根据标准器的校准证书确定标准不确定度值。
本参数只有当被校坐标测量机要求输入热膨胀系数时才需要考虑。
对于没有温度修正功能的坐标测量机,此项不需要考虑,即认为u(εα)=0。
u(εα)=L×(|t-20℃|)×u(α)其中:L——标准器长度;t——测量时标准器的温度;u(α)——标准器热膨胀系数引起的E标准不确定度。
式中t应在每个测量位置分别确定。
C.1.2.3 u(εt)为标准器温度测量引起E的标准不确定度。
由于标准器的温度测量是坐标测量机上的功能,测量误差是坐标测量机示值误差的一部分,与校准方法无关,不予单独考虑。
当被校坐标测量机有温度补偿功能,此项不确定度不予考虑。
只有当被校坐标测量机具有温度补偿功能,但标准器的温度值是有校准方的温度测量系统获得的,此时:u(εt)=L·α·u(t)其中:L——标准器长度;α——标准器的热膨胀系数;u(t)——标准器温度值的标准不确定度。
三坐标测量机不确定度

三坐标测量机示值校准结果不确定度的评定1. 测量方法(依据JJF1064-2004《坐标测量机校准规范》)尺寸测量校准方法的原理,是通过比较5个不同长度的尺寸实物标准器的校准值和指示值,评价测量尺寸的坐标测量机是否符合规定的最大允许示值误差MPE E 。
5个尺寸实物标准器放在测量空间的7个不同的方向或位置,各测量3次,共进行105次测量。
大值与最小值的。
2. 数学模型对标准器进行测量,得到的测量长度值为E L L L t L L L S S S +∆-∆-∆-∆+=321α其中S L 标准器的校准长度,1L ∆为标准器形状误差等因素引起的误差,2L ∆为长度稳定性引起的误差,3L ∆为测量重复性引起的误差,S α为标准器的热膨胀系数,t ∆为标准器温度对20℃的偏差,E 为坐标测量机的示值L 的误差。
3. 灵敏度系数11/1≈∆+=∂∂=t L L c S S α t L L L c S S ∆=∂∂=/2S S L t L c α=∆∂∂=)(/3 1)(/14-=∆∂∂=L L c1)(/25-=∆∂∂=L L c 1)(/36-=∆∂∂=L L c1/7=∂∂=E L c4. 标准不确定度1u 为标准器校准值S L 的标准不确定度,2u 为标准器热膨胀系数s α的标准不确定度,根据标准器的校准证书确定标准不确定度值。
3u 为标准器温度测量的标准不确定度,由于标准器的温度测量是坐标测量机上的功能,测量误差是坐标测量机示值误差的一部分,与校准方法无关,不予单独考虑。
4u 为标准器的长度变动量引入的标准不确定度。
5u 为标准器的长度稳定度引入的标准不确定度。
6u 为测量重复性引入的标准不确定度。
7u 为坐标测量机示值误差的标准不确定度,也是坐标测量机的测量示值误差的组成部分,与校准方法无关,不予单独考虑。
5. 合成标准不确定度[]2/12625242221)(u u u tu L u u S c +++∆+=。
三座标测量结果不确定度评定-2014-4-10
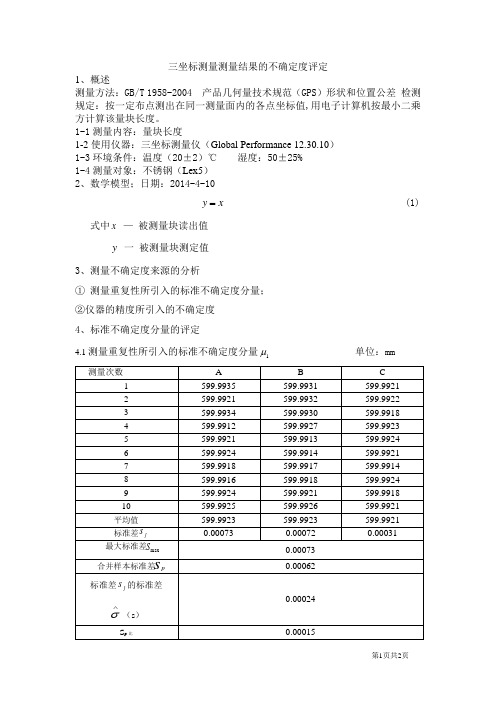
三坐标测量测量结果的不确定度评定1、概述测量方法:GB/T 1958-2004 产品几何量技术规范(GPS)形状和位置公差检测规定:按一定布点测出在同一测量面内的各点坐标值,用电子计算机按最小二乘方计算该量块长度。
1-1测量内容:量块长度1-2使用仪器:三坐标测量仪(Global Performance 12.30.10)1-3环境条件:温度(20±2)℃湿度:50±25%1-4测量对象:不锈钢(Lex5)2、数学模型;日期:2014-4-10y= (1)x式中x—被测量块读出值y一被测量块测定值3、测量不确定度来源的分析①测量重复性所引入的标准不确定度分量;②仪器的精度所引入的不确定度4、标准不确定度分量的评定μ单位:mm4.1测量重复性所引入的标准不确定度分量1合并样本标准差为:∑==mj p s s j m 121 =0.62μm (其中m=3)标准差j s 的标准差:1)(12)(-=∑-=∧m j s m j s s σ=0.24μm)1(2-=n S spP 比=0.15μm (其中n=10)如≤∧)(s σ S p 比,则可采用合并样本标准差Sp 来评定标准不确定度分量,反之,若子 )(s ∧σ>S p 比,则应采用Sj 中的最大值S max 来评定标准不确定度分量。
所以,1u =10/73.0=0.23μm自由度:)1(-=n m pν=)110(*3-=274.2仪器的精度所引入的不确定度2u仪器的示值误差为±2.8+3L/1000m μ按均匀分布 k=3 a=2.8+3*600/1000m μ(L 取值600mm)2u =66.23/≈a m μ2221μμ+=U =2266.223.0+=2.75m μ5.扩展不确定度取置信概率P=95%,, k 95=2 扩展不确定度U 95为U 95=k 95)(e U c ⨯=2⨯2.75≈5.51m μ 6.测量结果不确定度报告与表示三坐标测量该量块的长度为599.9922±0.00551mm报告审核: 报告编制:邓过房。
三坐标测量机长度测量不确定度评定

加以分析 ,推导不确定度计算 的传递链 函数 ,并且与蒙 特卡 罗模拟 方法 的不确定度 评定 结果相 比较 ,验证 了此
模型 的准确性 。此模型可推广应 用于三坐标测量机各种 测量任 务 的不确定度 评定 中 ,从 而实 现三 坐标测量 机测 量值和不确定度评定 的完整 报告 ,提高三坐标测量机测量结果 的准确度 和可信 度 。
是测 量结 果含 有 的 一个 参 数 ” 。没 有 不 确定 度 的测
0 引 言
测量 不确 定 度 是 评 价 测 量 结 果 质 量 的重 要 指
量结 果 是不 完整 的 、没 有 意义 的 、不 具有 实用 价值 的 。现 有 的三坐 标测 量机 在应用 时 ,通 常得 到 的只 是被 测参 数 的估计 值 ,而 没有 给 出相应 的测量 不确
定度 Ⅲ 。
标 。 由 IO 等 7个 国 际 组 织 制 订 并 颁 布 实 施 的 S 《 测量 不确 定 度 表示 指 南 》 ( 简称 为 GUM)定 义 : “ 量不 确定 度表 征合 理地 赋予 被测 量值 的分散性 , 测
三 坐标测 量 机在应 用 中引起 被测 参数 不确 定度 的来 源非 常 复 杂 ,它 不 仅 与 测 量 机 本 身 的精 度 有
A s a t MM p l ai sal js gv h si tdv leo h aa tr n a o iet e b t c :C r i a pi t n u u l t iet eet e au f ep rmees dcnn t v h n c o yu ma t a g
CAO em e , CH EN a — u i L o g l Xu — i Xio h a , IH n —i
三维坐标测量不确定度分析

三维坐标测量不确定度分析摘要:文章联系实际,从三维坐标测量不确定度的目的、范围等方面对其进行分类分析。
关键词:三维坐标;测量;不确定度1目的提供完整的信息对三维坐标测量不确定度进行评定与表示,评价测量结果是否有效、是否可信,判定测量结果的质量。
2适用范围方法适用于Vento-R601620/2双悬臂地轨测量机的不确定度分析。
3三维坐标测量不确定度分析3.1A类标准不确定度分量表1是针对被测件长度(800mm)进行的10次等精度测量数据及计算平均值、残差、残差平方。
被测件长度10次测量的平均值x=799.99225 mm残差平方和=0.000178625mm2自由度n=n-1=9,n为测量次数。
据此可求出对应的估计的标准偏差:对于测量结果来说,我们通常把算术平均值的标准偏差称为A类标准不确定度。
而且由于被测量的A类标准不确定度uA按照正态分布,因此:3.2B类标准不确定度分量3.2.1测量仪器的不确定度UB1由于Vento-R601620/2三坐标测量机双臂测量的精度为:50+28L/1000≤108(μm),由此得出长度L≤2071.428571 mm。
当被测件的长度为800 mm时,由于其测量的半宽度U′遵循线性分布,因此U′可以由以下比例关系得出:其标准不确定度UB1为:UB1=U′/K=0.0417/1.7321=0.0241 mm 。
3.2.2由温度引起的测量不确定度UB2经反复测量比较,在环境温度为20℃附近,温度每增加或减少1度,测量结果就相应增加或减少0.01 mm,在20°±2℃相对恒温的正常测量条件下,由温度引起的测量半宽度为0.04 mm。
0.0231mm。
3.3 合成标准不确定度我们可以视合成标准不确定度分布为正态分布,将上述不确定度分量合成,得出合成标准不确定度Uc为:Uc=(UA2+UB12+UB22)1/2=0.03368mm3.4扩展不确定度我们也可以视扩展不确定度分布为正态分布,包含因子K=2.58,置信概率为99%,则扩展不确定度为:U=kUc=0.08689 mm被测件长度最终测量结果可表示为:L=799.99225±0.08689 mm4结语报告的长度是针对被测件长度做10次重复测量的平均值,且充分考虑了三坐标测量机双臂测量的精度对测量结果的影响,估计了由环境温度变化而引起的测量结果的差异,并在此基础上对测量结果作了相应的修正。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
测 量 不 确 定 度 报 告
47BQD-01-2017
1目的
为了验证产品角度尺寸与设计值的符合性,需要对产品的角度尺寸进行测量,三坐标测量机测量分辨率高是一种有效的测量设备。
根据JJF1059.1-2012《测量不确定度评定与表示》对三坐标测量机的角度测量进行测量不确定度评定。
2依据
GB/T3177-2009 产品几何技术规范(GPS)光滑工件尺寸的检验 3适用范围
用单一材料或层积材料制成的有一定刚性的产品,产品尺寸在设备测量范围以内。
4方法概要
采用三坐标测量机对任意工件(本例中采用二级角度40°量块)在标准环境(温度20±2℃,湿度<65%)中,进行测量,在直角坐标系空间的有效量程上,记录三坐标测量机示值,各机器平面测量三次,得到9组读数,将读数作为测量结果。
5数学模型
由测量的方式,建立数学模型如下:(采用40°的量块)
i i T M = (i =1,2…9)
式中:i M ——测量结果,i T ——三坐标测量机的读数 6使用的计量器具、标准物质和仪器设备
① 三坐标测量机,该设备的分辨率为0.5μm ,假定三角分布,k =61/2 ② 三坐标测量机,该设备的校准证书指出最大允许示值误差(MPE E )为 8.0+7.5L/1000 (μm ) ,在本例中L ≤70mm ,得MPE E =8.525μm ,假定均匀分布,k =31/2;
③ 三坐标测量机,该设备的校准证书指出最大允许探测误差(MPE P )为
8.0μm,假定均匀分布,k=31/2。
④三坐标测量机,该设备说明中设备轴间垂直度允差为0.0005°,假定
为均匀分布,k=31/2。
7测量结果M及典型值
用40°角度量块进行9次测量结果如下:
XY面YZ面ZX面
读数1 读数2 读数3 读数4 读数5 读数6 读数7 读数8 读数9 40.0014 39.9987 40.0025 39.9995 40.0009 39.9971 39.9988 39.9980 39.9991 平均值: 39.9996°
8不确定度分量的识别、分析和量化
按照数学模型及方法概要,其不确定度来源有5方面:
① M的测量重复性u1 (M)(8.1)
②三坐标测量机的分辨率引入的标准不确定度u2 (M)(8.2)
③三坐标测量机的最大允许示值误差引入的标准不确定度u3 (M)(8.3)
④三坐标测量机的最大允许探测误差引入的标准不确定度u4(M)(8.4)
⑤三坐标测量机的轴间垂直度允差引入的标准不确定度u
(M) (8.5)
5
8.1 测量重复性u1(M)
用40°角度量块进行9次测量重复性,贝塞尔公式计算单次测量标准差
s(M)=[∑M i2/(n-1)]1/2= 0.001726°
u1(M)=s(M)/ 91/2= 0.0005754°
8.2 设备的分辨率引入的标准不确定度u2(M)
考虑设备在根据测点构造矢量时,因设备的示值误差±0.5μm会发生角度偏差,在L=70的长度内,设测点间距为60mm,角误差即为±0.0009549°,双矢量则为:±0.001910°,假定为三角分布,k=61/2,
u2(M)=0.001910°/61/2=0.0007797°
8.3 设备的最大允许示值误差引入的标准不确定度u3(M)
设备的最大允许示值误差是MPE E=8.525μm, 同样在L=70的长度内,设测点间距为60mm,角误差即为:0.01628°,双矢量则为:0.03256°,
假定均匀分布,k=31/2
u3(M)=0.03256°/31/2=0.01880°
8.4设备的最大允许探测误差引入的标准不确定度u4(M)
设备的最大允许探测误差是MPE P =8μm, 同样在L=70的长度内,设测点间距为60mm,角误差即为:0.01528°,双矢量则为:0.03056°,假定均匀分布,k=31/2
U4(M)=0.03056°/31/2=0.01764°
8.5设备的轴间垂直度允差为0.0005°,考虑到有三轴存在,彼此无明显相关性,则合成允差为:(0.00052+0.00052+0.00052)1/2=0.0008660°假定为均匀分布,k=31/2
U5(M)=0.0008660°/31/2=0.0005°
9计算相对合成标准不确定度u cr(M)
符号来源类别量值量序
U1(M) 测量重复性A类0.0005754° 1
U2(M)设备分辨率B类0.0007797° 2
U3(M) 设备示值误差B类0.01880° 3
U4(M) 设备探测误差B类0.01764° 4
U5(M)垂直度允差B类0.0005° 5
u c(M)=[∑u i2(M)]1/2
=(0.0005752+0.00077972+0.018802+0.017642+0.00052)1/2=0.02581°
10计算扩展不确定U(M)
取k=2,U(M)=2×u c(M)=2×0.02581°=0.05162°
11结果完整表达
该量块的测量结果M=39.9996°
U(M)=0.05162°, k=2
编制人审核人批准人
日期日期日期。
