四年级数学下册课件_三角形内角和
青岛版四年级数学下册4.3三角形三边关系和内角和PPT课件

不能
能
能
依据三角形任意两边长度的和大于第三边,解决此类问题。
探索新知
一个三角形的一个 内角是30°,一个 内角是65° 求另一个内角是多 少度?
30° 65°
要求另一个角是多少 度,需要知道三角形3 个内角的和是多少度。
三角形3个内角的和是多少度? 三角形“内角和”的含义:
三角形的内角和 =∠1+∠2+∠3
探索新知
任意的三根小棒,能围成一个三角形吗?
探索活动要求:
1.从4根小棒(6cm、5cm、3cm、2cm)中,任意选取3根,试着围成 三角形。
2.将探究的结果记录在下表中。 能否围成 三条边的长度 三角形 (厘米)
围成 围 不成
以小组为单位,根据前面围三角形的情况讨论交流,找 出三角形三条边之间的关系。 1、有哪几种取法? 2、是不是任意三根都能摆出三角形?若不是,哪些可以? 哪些不可以? 3、用三根什么样的小棒才能拼成三角形呢?你从中发现了 什么? 1、(1)6cm、5cm、2cm(2)6cm、5cm、3cm (3)2cm、3cm、5cm(4)2cm、3cm、6cm 2、经过实践可知: (1)、(2)可以摆出三角形 (3)、(4)不可以摆出三角形
5, 3 ,7 5, 3 ,6
5dm 3dm
5, 3 ,5
5, 3 ,4 5, 3 ,3
3.埃及金字塔的四个侧面的形状都是等腰三角形,每个等腰 三角形的顶角约是52°。金字塔每个侧面的底角大约是多少 度?
(180-52°)÷2 = 64°
答:金字塔每个侧面的底 角大约是64°。
52 °
?
?
2 3
我的两个锐角 之和大于90°
我的两个锐角 之和等于90°
冀教版四年级数学下册4.1.3三角形的内角和课件
第二种情况:当这个角是顶角时:
拓
展
(180°- 70°)÷ 2 = 55°
训
练
答:另外两个角的度数是70°,40°或者55°,55°。
8. 成成不小心把一块三角形玻璃打碎了,他要去玻璃店配一 块形状完全一样的玻璃,他应该带哪一块?为什么?
应该带第③块
第③块知道三角形2个角的度数和
拓
一条边的长,知道2个角的度数,
形的内角和。 3. 三角形内角和与三角形的大小形状无关,任意一个
三角形的内角和都是180°。
课后作业
根据三角形内角和是180度,你能求出其他多边 形的内角和吗?
课后作业
完成练习册中本课时 的相应作业.
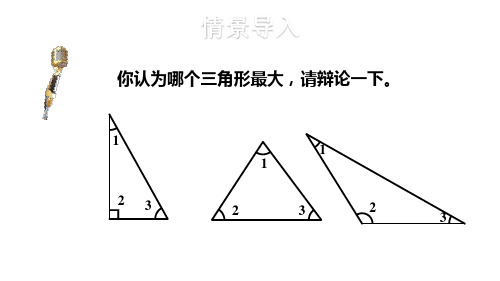
情景导入
你认为哪个三角形最大,请辩论一下。
1 23
1 1
2
3
2
3
三角形的内角和
冀教版·四年级下册
新课导入
(说1)一观说察,下这面两两个个三特角殊形的是三什角么形三,角猜形测?一有下什:么它特们点的?角有什么特点?
⑤
⑥
(2)折一折,用量角器分别测量等腰三角形和等边三 角形的三个角,看一看你的猜测是否正确。
三角形的内角和
小组合作
1. 以小组为单位,分别画出一个锐角、直角、钝角三 角形。
2. 测量并标出每个角的度数,三个角的度数都量好后, 再汇报给小组长记录。
3. 组内讨论,通过测量和计算,谈谈你们有什么发现。
学生姓名
小组活动记录表
三角形的形状 每个内角的度数
第
组
三个内角的和
我们的发现: 任意三角形的内角和是180 ° 。
【单击三角形,三角形可连续单击】
一个三角形,要知道三个内角各是多少度,最多量几次? 最少呢?
人教版数学四年级下册三角形的分类PPT课件

人教版数学四年级下册三角形的分类PPT课件•三角形基本概念与性质•三角形分类方法及特点•三角形面积计算公式与应用•相似与全等三角形判定定理•直角三角形及其性质•三角形在生活中的应用举例三角形基本概念与性质由不在同一直线上的三条线段首尾顺次连接所组成的图形。
三角形的定义三角形的元素特殊三角形三角形的边、角、顶点、高、中线、角平分线等。
等腰三角形、等边三角形、直角三角形等。
030201三角形定义及元素三角形的三个内角之和等于180°。
三角形内角和定理通过测量或撕拼的方式验证三角形内角和定理。
验证方法利用三角形内角和定理求角度、判断三角形形状等。
应用举例三角形内角和定理三角形外角性质三角形外角性质三角形的一个外角等于与它不相邻的两个内角之和。
验证方法通过测量或推理的方式验证三角形外角性质。
应用举例利用三角形外角性质求角度、判断三角形形状等。
稳定性与不稳定性三角形的稳定性当三角形的三条边长确定时,三角形的形状和大小也就唯一确定了,这种性质叫做三角形的稳定性。
例如,在建筑、桥梁等工程中,经常利用三角形的稳定性来增强结构的稳固性。
三角形的不稳定性当三角形的边长或角度发生变化时,三角形的形状和大小也会随之改变,这种性质叫做三角形的不稳定性。
例如,在地震等自然灾害中,建筑物或桥梁等结构可能会因为受到外力作用而发生变形或破坏,其中就涉及到三角形的不稳定性。
三角形分类方法及特点03钝角三角形有一个角是钝角的三角形。
01锐角三角形三个角都是锐角的三角形。
02直角三角形有一个角是直角的三角形。
按角分类按边分类不等边三角形三边长度都不相等的三角形。
等腰三角形有两边长度相等的三角形。
等边三角形三边长度都相等的三角形。
特殊三角形介绍直角三角形中的等腰直角三角形既是直角三角形又是等腰三角形的特殊三角形。
等边三角形中的正三角形三边长度相等且三个角都是60度的特殊等边三角形。
等边三角形性质三边相等,三个内角都是60度,有三条对称轴。
三角形内角和 课件

三角形的内角和
数学文化
法国著名的数学家帕斯卡在12岁 的某一天正在拿着粉笔在地上画各 种图形,画着画着,他突然发现了 一个惊人的秘密,从此,图形的世界 更加流光溢彩,我们的探究之旅也 由此展开……
帕斯卡的验证过程
直角三角形内角和
360°÷ 2 = 180°
直角三角形内角和
量
600
锐角三角形
480
720
600+480+720=1800
量
380
钝角三角形
260
1160
1160+260+380=1800
撕
3
1
2
3
21
平角:180°
折
1
22 3 3
平角:180°
1
算
180° 180°
180°×2-90°-90°=180°
算
180° 180°
180°×2-90°-90°=180°
45°
60°
45°
30°
∟
∟
所有直角三角形的内角和是180°
小组合作要求
1.请把三角形的三个角涂成不同的颜色,并 标出∠1 ∠2 ∠3。
2.想办法验证手中不同的三角形的内角和是多少。
小组汇报要求
1.汇报流程:
选了什么三角形 用什么方法验证 结论是什么
2.其他小组汇报后,如果同意请送出掌声; 如果不同意请举手发言。
结论:
所有三角形的内角和都是180 °
1.算出笑脸所遮盖角的度数。
70° 80° 30°
∟
பைடு நூலகம்65°
25°
180 °— 80 °— 30 °=70 ° 180 °— 90 °— 25 °=65 °
《三角形的内角和 》PPT课件(共24张PPT)

我有一个钝角,比你三个角都大,所以我的内角和才是最大的。
900 算一算,三角形的内角和是多少度呢?
一个三角形的三个内角度数分别是65°,35°,80°. 三角形内角和等于1800。
540
(1) 这个三角形的内角和是多少度?
抢答游戏:
(3)把这个小三角形再分成一 大一小两个三角形,这两个三角 形的内角和分别是多少度?
抢答游戏:
(4)把两个小三角形拼成一个 大三角形,这个大三角形的内角 和是多少度?
抢答游戏:
(5) 3个小三角形拼成一个更 大的三角形,它的内角和是多少 度?
判断(用手语表示)
√ 1.一个三角形的三个内角度数分别是65°,35°,80°.( )
2.三角形的内角和与三角形的大小无关。( ) √
× 3.一个直角三角形,一个内角是37°,另一个内角是48°。( )
4、一个三角形中不可能有2个直角。 ( )
√
∠1=40º
2
∠ 2=48º
3
∠ 3=92º
1
猜猜∠3有多少度?
你能求出等边三角形每个角的度数吗?
等边三角形
400 1800-700 -700
520
300
800
东东把一块三角形的玻璃打碎成三 片,现在他要到玻璃店去配一块形状完 全一样的玻璃,那么最省事的办法是带 ( )去。 为什么?
帕斯卡:法国的数学家、物理 学家,为人类创造了无数的奇
迹,早在300年前这位法国著名
的科学家就已经发现了:
任何三角形的内角和 都是180°
当时才12岁
460 拿出准备好的三角形,小组合作,动手验证:三角形的内角和是不是180度?
人教版四年级数学下册第五单元《内角和》复习课件

知识点 1 探究四边形的内角和
1.填一填。 (1)长方形和正方形的四个角都是( 直 )角,所以长方形
和正方形的内角和都是( 360 )°。 (2)将任意一个四边形的四个角剪下来,可以拼成一个
BD EF
A
CA
CA
CA
C
图一
图二
图三
图四
答:这些图形中三角形的个数分别为1、3、6、10……
其中的规律:相邻两个图形中,三角形个数的差依次为2、3、
4……
帮角找朋友(每组卡片中,哪三个角可以组成 三角形?)
600 900
450 300
540 460
520
800
6√00
√900
450 300 √
角是多少度?
根据三角形的内角 和以及等腰三角形 的定义进行求解。
180°-50°×2 = 180°-100° = 80° 答:它的顶角是80°。
一个直角三角形,其中一个锐角是36°,另一个 锐角是多少度?
180°-90°-36° = 90°-36° = 54° 答:另一个锐角是54°。
如下图,∠1是多少度?
三角形内角和及边的关系的应用
经典例题
一个等腰三角形的周长是28厘米,它的底边比一条腰长 的2倍少4厘米,这个三角形的底边长是多少厘米?
规范解答: (28+4)÷(1+1+2)
=32÷4 =8(厘米)
8×2-4=12(厘米) 答:这个三角形的底边长是12厘米。
类 型 1 三角形内角和的应用
1.如图,在三角形ABC中,∠A=60°,∠A比∠B多 15°,求∠C的度数。
《三角形的内角和》标准课件(人教版)1

四年级的学生已经初步具备了动手操作的意识和能力,并形成了一定的空间观念,能够在探究问题的过程中,运用已有知识和经验,
通过交流、比较、评价寻找解决问题的途径和策略。
学法:合作交流法、动手实践法、自主探究法
这节课我设计了以“猜想一验证一归纳一运用”为主线,让学生在自主学习中“不知不觉”学习到新的知识。
在学生猜测三角形内角和是多少度的基础上,引导学生通过探究活动来验证自己的观点是否正确,激发求知的渴望和学习的热情,最 后达成共识。 43 ° 小学数学人教版四年级下册第五单元 直角三角形的内角和是180° 。 =40°-25° 结论不重要,重要的是让学生体会得到结论的过程,学会用转化的思想来解决生活中的问题。 3、在探索发现的过程中,培养学生大胆猜想,细心验证的数学思维。 直角三角形的内角和是180° 。 结论 三角形的内角和是180度 三角形的内角和都是180°
(一)复习引入,引发猜想 三角形的内角和都是180°
三角形的内角和都是180°
(一)复习引入,引发猜想 39°
通过复习上节课三角形按角分可
以分为哪几类,从而引入学习新课 三角形的内角和都是180°
在学生猜测三角形内角和是多少度的基础上,引导学生通过探究活动来验证自己的观点是否正确,激发求知的渴望和学习的热情,最
直角三角形的内角和是180° 。
两个大小一样的直角三角形
在学生猜测三角形内角和是多少度的基础上,引导学生通过探究活动来验证自己的观点是否正确,激发求知的渴望和学习的热情,最
后达成共识。
数学讲究严谨性,为了得到准确的值,学生用拼、折等多种方法得出三角形内角和是180度,验证了自己的猜想
三角形的内角和与外角和课件

三角形的内角和与外角和课件一、教学内容本节课的教学内容来自于人教版小学数学四年级下册第107页至108页,主要讲述三角形的内角和与外角和。
学生将通过学习,了解三角形的内角和总是180度,以及外角与相邻内角的关系。
二、教学目标1. 学生能够通过实际操作,探究并证明三角形的内角和总是180度。
2. 学生能够理解三角形外角与相邻内角的关系,并能运用这一关系解决实际问题。
3. 培养学生的观察能力、操作能力和逻辑思维能力。
三、教学难点与重点重点:三角形内角和总是180度,外角与相邻内角的关系。
难点:如何引导学生通过实际操作发现并证明三角形的内角和,以及如何理解外角与相邻内角的关系。
四、教具与学具准备教具:三角板、量角器、直尺。
学具:每个学生准备一个三角形模型,以及用于画图的铅笔和橡皮。
五、教学过程1. 实践情景引入:让学生拿出自己的三角形模型,观察并描述三角形的特征。
3. 理解外角和:让学生用自己的三角形模型,尝试测量每个三角形的外角,并记录下来。
然后,引导学生发现并理解外角与相邻内角的关系。
4. 例题讲解:出示一些有关三角形内角和与外角的例题,让学生们运用所学知识解决问题。
5. 随堂练习:让学生独立完成一些有关三角形内角和与外角的练习题,巩固所学知识。
六、板书设计三角形的内角和:总是180度外角与相邻内角的关系:外角等于不相邻的两个内角之和七、作业设计1. 请用你所学的知识,画出一个任意的三角形,并测量其内角和。
答案:三角形的内角和总是180度。
2. 请用你所学的知识,解释下面这个问题:一个三角形的两个内角分别是60度和70度,求第三个内角的度数。
答案:第三个内角的度数是50度。
八、课后反思及拓展延伸本节课通过实际操作,让学生们发现了三角形的内角和总是180度,以及外角与相邻内角的关系。
在教学过程中,学生们积极参与,课堂氛围良好。
但在今后的教学中,还需要注意引导学生更好地理解外角与相邻内角的关系,并能够灵活运用这一关系解决实际问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
下面的三角形中,∠1的度数是∠2的2倍, ∠3的度数是∠2的3倍,∠1、∠2、∠3 分别是多少度?
1 3 2 2 1 3
三角形中,∠1=30 ,∠2=∠3,求∠3
0
1
2
3
一块三角尺的内角和是180度,用两块完全 一样的三角尺拼成一个三角形,这个三角形 的内角和是360度?
?
一块三角尺的内角和是180度,用两块完全 一样的三角尺拼成一个三角形,这个三角形 的内角和( )。
正方形 内角和( )度
( )形 内角和( )度
( )形 内角和( )度
一个直角三角形中最多有( 为什么? 一个钝角三角形中最多有( 为什么?
)个直角,
)个钝角,
人教版四年级数学下册
三角形内角和
本节课我们主要来学习三角形的内 角和,同学们要理解并掌握三角形 的内角和,知道三角形的内角和是 180°,能够解决相关的实际问题。
90 +60 +30 =180
0
0
0
0
90 +45 +45 =180
0
0
0
0
所有三角形的内角和都是1ቤተ መጻሕፍቲ ባይዱ0度吗?
所有三角形的内角和都是180度!
?
2 1 3
三角形中,∠1=75 ,∠2=39 , 0 ∠3=( )
1 2 3
0 0 0
0
0
∠3=180 —75 —39 0 0 =105 —39 0 =66
∠3=180 —(75 +39 ) 0 0 =180 —114 0 =66
0
0
0
想一想:在一个直角三角形中, 已知一个锐角是52度,能求出 另一个锐角是多少度吗?
