The Beta-Function of the Chiral Gross Neveu Model at O(1N^2)
7097044-Fractional-Calculus

1.2 Historical Survey Most authors on this topic will cite a particular date as the birthday of so called 'Fractional Calculus'. In a letter dated September 30th, 1695 L’Hospital wrote to Leibniz asking him about a particular notation he had used in his publications for the nth-derivative of the Dn x linear function f(x) = x, . L’Hospital posed the question to Leibniz, Dx n what would the result be if n = 1/ 2. Leibniz's response: "An apparent paradox, from which one day useful consequences will be drawn." In these words fractional calculus was born. [7]
Chapter 1
Definition and Applications
3
Fractional Calculus History
value x, verifiable by infinite series expansion, or more practically, by calculator. Now, in the same way consider the integral and derivative. Although they are indeed concepts of a higher complexity by nature, it is still fairly easy to physically represent their meaning. Once mastered, the idea of completing numerous of these operations, integrations or differentiations follows naturally. Given the satisfaction of a very few restrictions (e.g. function continuity) completing n integrations can become as methodical as multiplication. [7] But the curious mind can not be restrained from asking the question what if n were not restricted to an integer value? Again, at first glance, the physical meaning can become convoluted (pun intended), but as this report will show, fractional calculus flows quite naturally from our traditional definitions. And just as fractional exponents such as the square root may find their way into innumerable equations and applications, it will become apparent that integrations of order 1/ 2 and beyond can find practical use in many modern problems. [7]
steam Chap 05

Chapter 5Boiling Heat Transfer, Two-Phase Flow and CirculationA case of heat transfer and flow of particular inter-est in steam generation is the process of boiling and steam-water flow. The boiling or evaporation of wa-ter is a familiar phenomenon. In general terms, boil-ing is the heat transfer process where heat addition to a liquid no longer raises its temperature under con-stant pressure conditions; the heat is absorbed as the liquid becomes a gas. The heat transfer rates are high, making this an ideal cooling method for surfaces ex-posed to the high heat input rates found in fossil fuel boilers, concentrated solar energy collectors and the nuclear reactor fuel bundles. However, the boiling phenomenon poses special challenges such as: 1) the sudden breakdown of the boiling behavior at very high heat input rates, 2) the potential flow rate fluctuations which may occur in steam-water flows, and 3) the ef-ficient separation of steam from water. An additional feature of boiling and two-phase flow is the creation of significant density differences between heated and unheated tubes. These density differences result in water flowing to the heated tubes in a well designed boiler natural circulation loop.Most fossil fuel steam generators and all commer-cial nuclear steam supply systems operate in the pres-sure range where boiling is a key element of the heat transfer process. Therefore, a comprehensive under-standing of boiling and its various related phenom-ena is essential in the design of these units. Even at operating conditions above the critical pressure, where water no longer boils but experiences a continuous transition from a liquid-like to a gas-like fluid, boil-ing type behavior and special heat transfer charac-teristics occur.Boiling process and fundamentalsBoiling point and thermophysical properties The boiling point, or saturation temperature, of a liquid can be defined as the temperature at which its vapor pressure is equal to the total local pressure. The saturation temperature for water at atmospheric pres-sure is 212F (100C). This is the point at which net vapor generation occurs and free steam bubbles are formed from a liquid undergoing continuous heating. As discussed in Chapter 2, this saturation tempera-ture (T sat) is a unique function of pressure. The Ameri-can Society of Mechanical Engineers (ASME) and the International Association for the Properties of Steam (IAPS) have compiled extensive correlations of thermo-physical characteristics of water. These characteristics include the enthalpy (or heat content) of water, the enthalpy of evaporation (also referred to as the latent heat of vaporization), and the enthalpy of steam. As the pressure is increased to the critical pressure [3200 psi (22.1 MPa)], the latent heat of vaporization declines to zero and the bubble formation associated with boil-ing no longer occurs. Instead, a smooth transition from liquid to gaseous behavior occurs with a continuous in-crease in temperature as energy is applied.Two other definitions are also helpful in discussing boiling heat transfer:1.Subcooling For water below the local saturationtemperature, this is the difference between the saturation temperature and the local water tem-perature (T sat – T).2.Quality This is the flowing mass fraction of steam(frequently stated as percent steam by weight or %SBW after multiplying by 100%):xmm m=+steamwater steam(1) wheremsteam=steam flow rate, lb/h (kg/s)mwater=water flow rate, lb/h (kg/s) Thermodynamically, this can also be defined as:xH HHorH HH Hffgfg f=−−−(2) whereH=local average fluid enthalpy, Btu/lb (J/kg) H f=enthalpy of water at saturation, Btu/lb (J/kg) H g=enthalpy of steam at saturation, Btu/lb (J/kg) H fg=latent heat of vaporization, Btu/lb (J/kg) When boiling is occurring at saturated, thermal equilibrium conditions, Equation 2 provides the frac-tional steam flow rate by mass. For subcooled condi-tions where H < H f , quality (x ) can be negative and is an indication of liquid subcooling. For conditions where H > H g , this value can be greater than 100% and repre-sents the amount of average superheat of the steam.Boiling curveFig. 1 illustrates a boiling curve which summarizes the results of many investigators. This curve provides the results of a heated wire in a pool, although the characteristics are similar for most situations. The heat transfer rate per unit area, or heat flux , is plotted versus the temperature differential between the metal surface and the bulk fluid. From points A to B, con-vection heat transfer cools the wire and boiling on the surface is suppressed. Moving beyond point B, which is also referred to as the incipient boiling point , the temperature of the fluid immediately adjacent to the heated surface slightly exceeds the local saturation temperature of the fluid while the bulk fluid remains subcooled. Bubbles, initially very small, begin to form adjacent to the wire. The bubbles then periodically collapse as they come into contact with the cooler bulk fluid. This phenomenon, referred to as subcooled boil-ing , occurs between points B and S on the curve. The heat transfer rate is quite high, but no net steam gen-eration occurs. From points S to C, the temperature of the bulk fluid has reached the local saturation tem-perature. Bubbles are no longer confined to the area immediately adjacent to the surface, but move into the bulk fluid. This region is usually referred to as the nucleate boiling region, and as with subcooled boil-ing, the heat transfer rates are quite high and the metal surface is only slightly above the saturation temperature.As point C is approached, increasingly large sur-face evaporation rates occur. Eventually, the vapor generation rate becomes so large that it restricts the liquid return flow to the surface. The surface eventu-ally becomes covered (blanketed) with an insulating layer of steam and the ability of the surface to trans-fer heat drops. This transition is referred to as thecritical heat flux (CHF), departure from nucleate boil-ing (DNB), burnout , dryout , peak heat flux , or boil-ing crisis . The temperature response of the surface un-der this condition depends upon how the surface is being heated. In fossil fuel boiler furnaces and nuclear reactor cores, the heat input is effectively independent of surface temperature. Therefore, a reduction in the heat transfer rate results in a corresponding increase in surface temperature from point D to D ′ in Fig. 1.In some cases, the elevated surface temperature is so high that the metal surface may melt. If, on the other hand, the heat input or heat transfer rate is depen-dent upon the surface temperature, typical of a nuclear steam generator, the average local tempera-ture of the surface increases as the local heat trans-fer rate declines. This region, illustrated in Fig. 1 from points D to E, is typically referred to as unstable film boiling or transition boiling . Because a large surface temperature increase does not occur, the main conse-quences are a decline in heat transfer performance per unit surface area and less overall energy transfer. The actual local phenomenon in this region is quite com-plex and unstable as discrete areas of surface fluctu-ate between a wetted boiling condition and a steam blanketed, or dry patch, condition. From position E through D ′ to F, the surface is effectively blanketed by an insulating layer of steam or vapor. Energy is transferred from the solid surface through this layer by radiation, conduction and microconvection to the liquid-vapor interface. From this interface, evapora-tion occurs and bubbles depart. This heat transfer region is frequently referred to as stable film boiling .In designing steam generating systems, care must be exercised to control which of these phenomena oc-cur. In high heat input locations, such as the furnace area of fossil fuel boilers or nuclear reactor cores, it is important to maintain nucleate or subcooled boiling to adequately cool the surface and prevent material failures. However, in low heat flux areas or in areas where the heat transfer rate is controlled by the boil-ing side heat transfer coefficient, stable or unstable film boiling may be acceptable. In these areas, the resultant heat transfer rate must be evaluated, any temperature limitations maintained and only allow-able temperature fluctuations accepted.Flow boilingFlow or forced convective boiling , which is found in virtually all steam generating systems, is a more com-plex phenomenon involving the intimate interaction of two-phase fluid flow, gravity, material phenomena and boiling heat transfer mechanisms. Fig. 2 is a clas-sic picture of boiling water in a long, uniformly heated,circular tube. The water enters the tube as a subcooled liquid and convection heat transfer cools the tube. The point of incipient boiling is reached (point 1 in Fig. 2).This results in the beginning of subcooled boiling and bubbly flow. The fluid temperature continues to rise until the entire bulk fluid reaches the saturation tem-perature and nucleate boiling occurs, point 2. At this location, flow boiling departs somewhat from the simple pool boiling model previously discussed. The steam-water mixture progresses through a series ofFig. 1Boiling curve – heat flux versus applied temperature difference.flow structures or patterns: bubbly, intermediate and annular. This is a result of the complex interaction of surface tension forces, interfacial phenomena, pres-sure drop, steam-water densities and momentum ef-fects coupled with the surface boiling behavior. While boiling heat transfer continues throughout, a point is reached in the annular flow regime where the liquid film on the wall becomes so thin that nucleation in the film is suppressed, point 3. Heat transfer then occurs through conduction and convection across the thin annular film with surface evaporation at the steam-water interface. This heat transfer mechanism, called convective boiling , also results in high heat transfer rates. It should also be noted that not all of the liquid is on the tube wall. A portion is entrained in the steam core as dispersed droplets.Eventually, an axial location, point 4, is reached where the tube surface is no longer wetted and CHF or dryout occurs. This is typically associated with a temperature rise. The exact tube location and magni-tude of this temperature, however, depend upon a variety of parameters, such as the heat flux, mass flux, geometry and steam quality. Fig. 3 illustrates the effect of heat input rate, or heat flux, on CHF loca-tion and the associated temperature increase. From points 4 to 5 in Fig. 2, post-CHF heat transfer, which is quite complex, occurs. Beyond point 5, all of the liq-uid is evaporated and simple convection to steam occurs.Boiling heat transfer evaluationEngineering design of steam generators requires the evaluation of water and steam heat transfer rates un-der boiling and nonboiling conditions. In addition, theidentification of the location of critical heat flux (CHF)is important where a dramatic reduction in the heat transfer rate could lead to: 1) excessive metal tempera-tures potentially resulting in tube failures, 2) an un-acceptable loss of thermal performance, or 3) unaccept-able temperature fluctuations leading to thermal fa-Fig. 3Tube wall temperatures under different heat input conditions.Fig. 2 Simplified flow boiling in a vertical tube (adapted from Collier 1).tigue failures. Data must also be available to predict the rate of heat transfer downstream of the dryout point.CHF phenomena are less important than the heat transfer rates for performance evaluation, but are more important in defining acceptable operating conditions.As discussed in Chapter 4, the heat transfer rate per unit area or heat flux is equal to the product of tem-perature difference and a heat transfer coefficient.Heat transfer coefficientsHeat transfer correlations are application (surface and geometry) specific and The Babcock & Wilcox Company (B&W) has developed extensive data for its applications through experimental testing and field experience. These detailed correlations remain propri-etary to B&W. However, the following generally avail-able correlations are provided here as representative of the heat transfer relationships.Single-phase convection Several correlations for forced convection heat transfer are presented in Chap-ter 4. Forced convection is assumed to occur as long as the calculated forced convection heat flux is greater than the calculated boiling heat flux (point 1 in Fig. 2):′′>′′q q Forced Convection Boiling(3)While not critical in most steam generator applica-tions, correlations are available which explicitly de-fine this onset of subcooled boiling and more accuratelydefine the transition region.1Subcooled boiling In areas where subcooled boil-ing occurs, several correlations are available to char-acterize the heat transfer process. Typical of these is the Jens and Lottes 2 correlation for water. For inputs with English units:∆T q e sat P =′′()−6010614900///(4a)and for inputs with SI units:∆T q e sat P =′′()−251462//.(4b)where ∆T sat =T w – T sat , F (C)T w =wall temperature, F (C)T sat =saturated water temperature, F (C)′′q =heat flux, Btu/h ft 2 (MW t /m 2)P=pressure, psi (MPa)Another relationship frequently used is that developed by Thom.3Nucleate and convective boiling Heat transfer in the saturated boiling region occurs by a complex combi-nation of bubble nucleation at the tube surface (nucle-ate boiling) and direct evaporation at the steam-wa-ter interface in annular flow (convective boiling). At low steam qualities, nucleate boiling dominates while at higher qualities convective boiling dominates. While separate correlations are available for each range, the most useful relationships cover the entire saturated boiling regime. They typically involve the summation of appropriately weighted nucleate and convectiveboiling components as exemplified by the correlation developed by J.C. Chen and his colleagues.4 While such correlations are frequently recommended for use in saturated boiling systems, their additional precision is not usually required in many boiler or reactor ap-plications. For general evaluation purposes, the subcooled boiling relationship provided in Equation 4 is usually sufficient.Post-CHF heat transfer As shown in Fig. 3, substan-tial increases in tube wall metal temperatures are possible if boiling is interrupted by the CHF phenom-enon. The maximum temperature rise is of particular importance in establishing whether tube wall over-heating may occur. In addition, the reliable estima-tion of the heat transfer rate may be important for an accurate assessment of thermal performance. Once the metal surface is no longer wetted and water droplets are carried along in the steam flow, the heat transfer process becomes more complex and includes: 1) con-vective heat transfer to the steam which becomes su-perheated, 2) heat transfer to droplets impinging on the surface from the core of the flow, 3) radiation di-rectly from the surface to the droplets in the core flow,and 4) heat transfer from the steam to the droplets.This process results in a nonequilibrium flow featur-ing superheated steam mixed with water droplets.Current correlations do not provide a good estimate of the heat transfer in this region, but computer models show promise. Accurate prediction requires the use of experimental data for similar flow conditions.Reflooding A key concept in evaluating emergency core coolant systems for nuclear power applications is reflooding . In a loss of coolant event, the reactor core can pass through critical heat flux conditions and can become completely dry. Reflooding is the term for the complex thermal-hydraulic phenomena involved in rewetting the fuel bundle surfaces as flow is returned to the reactor core. The fuel elements may be at very elevated temperatures so that the post-CHF, or steam blanketed, condition may continue even in the presence of returned water flow. Eventually, the surface tem-perature drops enough to permit a rewetting front to wash over the fuel element surface. Analysis includes transient conduction of the fuel elements and the in-teraction with the steam-water heat transfer processes.Critical heat flux phenomenaCritical heat flux is one of the most important pa-rameters in steam generator design. CHF denotes the set of operating conditions (mass flux, pressure, heat flux and steam quality) covering the transition from the relatively high heat transfer rates associated with nucleate or forced convective boiling to the lower rates resulting from transition or film boiling (Figs. 1 and 2). These operating conditions have been found to be geometry specific. CHF encompasses the phenomena of departure from nucleate boiling (DNB), burnout,dryout and boiling crisis. One objective in recirculat-ing boiler and nuclear reactor designs is to avoid CHF conditions. In once-through steam generators, the objective is to design to accommodate the temperature increase at the CHF locations. In this process, the heat flux profile, flow passage geometry, operating pressureand inlet enthalpy are usually fixed, leaving mass flux, local quality, diameter and some surface effects as the more easily adjusted variables.Factors affecting CHF Critical heat flux phenomena under flowing conditions found in fossil fuel and nuclear steam generators are affected by a variety of parameters.5 The primary parameters are the operat-ing conditions and the design geometries. The oper-ating conditions affecting CHF are pressure, mass flux and steam quality. Numerous design geometry factors include flow passage dimensions and shape, flow path obstructions, heat flux profile, inclination and wall surface configuration. Several of these effects are il-lustrated in Figs. 3 through 7.Fig. 3 illustrates the effect of increasing the heat input on the location of the temperature excursion in a uniformly heated vertical tube cooled by upward flow-ing water. At low heat fluxes, the water flow can be al-most completely evaporated to steam before any tem-perature rise is observed. At moderate and high heat fluxes, the CHF location moves progressively towards the tube inlet and the maximum temperature excur-sion increases. At very high heat fluxes, CHF occurs at a low steam quality and the metal temperature excur-sion can be high enough to melt the tube. At extremely high heat input rates, CHF can occur in subcooled water. Avoiding this type of CHF is an important de-sign criterion for pressurized water nuclear reactors. Many large fossil fuel boilers are designed to oper-ate between 2000 and 3000 psi (13.8 and 20.7 MPa). In this range, pressure has a very important effect, shown in Fig. 4, with the steam quality limit for CHF falling rapidly near the critical pressure; i.e., at con-stant heat flux, CHF occurs at lower steam qualities as pressure rises.Many CHF correlations have been proposed and are satisfactory within certain limits of pressure, mass velocity and heat flux. Fig. 5 is an example of a corre-lation which is useful in the design of fossil fuel natu-ral circulation boilers. This correlation defines safe and unsafe regimes for two heat flux levels at a given pres-sure in terms of steam quality and mass velocity. Ad-ditional factors must be introduced when tubes are used in membrane or tangent wall construction, are inclined from the vertical, or have different inside di-ameter or surface configuration. The inclination of the flow passage can have a particularly dramatic effect on the CHF conditions as illustrated in Fig. 6.6 Ribbed tubes Since the 1930s, B&W has investi-gated a large number of devices, including internal twisters, springs and grooved, ribbed and corrugated tubes to delay the onset of CHF. The most satisfactory overall performance was obtained with tubes having helical ribs on the inside surface.Two general types of rib configurations have been developed:1.single-lead ribbed (SLR) tubes (Fig. 8a) for smallinternal diameters used in once-through subcriti-cal pressure boilers, and2.multi-lead ribbed (MLR) tubes (Fig. 8b) for larger in-ternal diameters used in natural circulation boilers. Both of these ribbed tubes have shown a remark-able ability to delay the breakdown of boiling. Fig. 7Fig. 5Steam quality limit for CHF as a function of mass flux.compares the effectiveness of a ribbed tube to that of a smooth tube in a membrane wall configuration. This plot is different from Fig. 5 in that heat flux is given as an average over the flat projected surface. This is more meaningful in discussing membrane wall heat absorption.The ribbed bore tubes provide a balance of improved CHF performance at an acceptable increase in pres-sure drop without other detrimental effects. The ribs generate a swirl flow resulting in a centrifugal action which forces the water to the tube wall and retards entrainment of the liquid. The steam blanketing and film dryout are therefore prevented until substantially higher steam qualities or heat fluxes are reached.Because the ribbed bore tube is more expensive than a smooth bore tube, its use involves an economic bal-ance of several design factors. In most instances, there is less incentive to use ribbed tubes below 2200 psi (15.2 MPa).Evaluation CHF is a complex combination of ther-mal-hydraulic phenomena for which a comprehensive theoretical basis is not yet available. As a result, ex-perimental data are likely to continue to be the basis for CHF evaluations. Many data and correlations de-fine CHF well over limited ranges of conditions and geometries. However, progress is being made in de-veloping more general evaluation procedures for at least the most studied case – a uniformly heated smooth bore tube with upward flowing water.To address this complex but critical phenomenon in the design of reliable steam generating equipment, B&W has developed an extensive proprietary data-base and associated correlations. A graphical example is shown in Fig. 5 for a fossil fuel boiler tube. A B&W correlation7 for nuclear reactor fuel rod bundle subchannel analysis is shown in Table 1.CHF criteria A number of criteria are used to assess the CHF margins in a particular tube or tube bundle geometry.8 These include the CHF ratio, flow ratio and quality margin, defined as follows:1.CHF ratio minimum value ofCHF heat fluxupset heat flux=2.flow ratio minimum value ofmin. design mass fluxmass flux=at CHF3.quality margin CHF quality max. design quality=−The CHF ratios for a sample fossil fuel boiler are illustrated in Fig. 9 for a smooth bore tube ′′′′()q qB A/ and a ribbed bore tube ′′′′()q qC A/. The graph indicates the relative increase in local heat input which can be tol-erated before the onset of CHF conditions. A similar relationship for a nuclear reactor fuel rod applicationis shown in Fig. 10. Fig. 8aSingle-lead ribbed tube. Fig. 8b Multi-lead ribbed tube.Supercritical heat transferUnlike subcritical pressure conditions, fluids at su-percritical pressures experience a continuous transi-tion from water-like to steam-like characteristics. As a result, CHF conditions and boiling behavior would not be expected. However, at supercritical pressures, especially in the range of 1 < P/P c < 1.15 where P c is the critical pressure, two types of boiling-like behav-ior have been observed: pseudo-boiling and pseudo-film boiling. Pseudo-boiling is an increase in heat transfer coefficient not accounted for by traditional convection relationships. In pseudo-film boiling, a dramatic reduction in the heat transfer coefficient is observed at high heat fluxes. This is similar to the critical heat flux condition at subcritical pressures. These behaviors have been attributed to the sharp changes in fluid properties as the transition from water-like to steam-like behavior occurs.Fluid properties In the supercritical region, the ther-mophysical properties important to the heat transfer process, i.e., conductivity, viscosity, density and spe-cific heat, experience radical changes as a certain pres-sure-dependent temperature is approached and ex-ceeded. This is illustrated in Fig. 11. The transition temperature, referred to as the pseudo-critical tem-perature, is defined as the temperature where the specific heat, c p, reaches its maximum. As the operat-ing pressure is increased, the pseudo-critical tempera-ture increases and the dramatic change in the ther-mophysical properties declines as this temperature is approached and exceeded.Heat transfer rates Because of the significant changes in thermophysical properties (especially in specific heat) near the pseudo-critical temperature, a modified approach to evaluating convective heat transfer is needed. A number of correlations have been developed and a representative relationship for smooth bore tubes is:9hDkD GH HT T kiwiww bw bww=×−−0004590923..µµ06130231..υυbw(5)Table 1B&W2 Reactor Rod Bundle Critical HeatFlux (CHF) Correlation7(a − bDi) A1 (A2G)A3+A4(P−2000)−A9Gx CHF H fg q"CHF=A5(A6G)A7+A8(P−2000)wherea = 1.15509 A =area,in.2b = 0.40703 D i= equivalent diameter = 4A/Per A1= 0.37020 x 108G= mass flux, lb/h ft2A2= 0.59137 x 10−6Hfg= latent heat of vaporization,A3 = 0.83040 Btu/lbA4= 0.68479 x 10−3P =pressure,psiA5 = 12.710 Per= wetted perimeter, in.A6= 0.30545 x 10−5xCHF= steam quality at CHF condi-A7 = 0.71186 tions, fraction steam by weight A8= 0.20729 x 10−3q"CHF= heat flux at CHF conditions, A9 = 0.15208 Btu/h ft2whereh=heat transfer coefficient, Btu/h ft2 F (W/m2 K) k=thermal conductivity, Btu/h ft F (W/m K)D i=inside tube diameter, ft (m)G=mass flux, lb/h ft2 (kg/m2 s)µ=viscosity, lb/ft h (kg/m s)H=enthalpy, Btu/lb (J/kg)T=temperature, F (C)υ=specific volume, ft3/lb (m3/kg)The subscripts b and w refer to properties evaluated at the bulk fluid and wall temperatures respectively. This correlation has demonstrated reasonable agreement with experimental data from tubes of 0.37 to 1.5 in. (9.4 to 38.1 mm) inside diameter and at low heat fluxes.Pseudo-boiling For low heat fluxes and bulk fluid temperatures approaching the pseudo-critical tem-perature, an improvement in the heat transfer rate takes place. The enhanced heat transfer rate observed is sometimes referred to as pseudo-boiling. It has been attributed to the increased turbulence resulting from the interaction of the water-like and steam-like fluids near the tube wall.Pseudo-film boiling Potentially damaging tem-perature excursions associated with a sharp reduction in heat transfer can be observed at high heat fluxes. This temperature behavior is similar to the CHF phe-nomenon observed at subcritical conditions and is re-ferred to as pseudo-film boiling. This phenomenon has been attributed to a limited ability of the available turbulence to move the higher temperature steam-like fluid away from the tube wall into the colder, higher density (water-like) fluid in the bulk stream. A phe-nomenon similar to steam blanketing occurs and the wall temperature increases in response to the rela-tively constant applied heat flux.Single-lead ribbed (SLR) bore tubes are very effec-tive in suppressing the temperature peaks encoun-tered in smooth bore tubes.10Two-phase flowFlow patternsAs illustrated in Fig. 2, two-phase steam-water flow may occur in many regimes or structures. The transi-tion from one structure to another is continuous rather than abrupt, especially under heated conditions, and is strongly influenced by gravity, i.e., flow orientation. Because of the qualitative nature of flow pattern iden-tification, there are probably as many flow pattern descriptions as there are observers. However, for ver-tical, heated, upward, co-current steam-water flow in a tube, four general flow patterns are generally recognized (see Fig. 12):1.Bubbly flow Relatively discrete steam bubbles aredispersed in a continuous liquid water phase.Bubble size, shape and distribution are dependent upon the flow rate, local enthalpy, heat input rate and pressure.2.Intermediate flow This is a range of patterns be-tween bubbly and annular flows; the patterns are also referred to as slug or churn flow. They range from: a) large bubbles, approaching the tube size in diameter, separated from the tube wall by thin annular films and separated from each other by slugs of liquid which may also contain smaller bubbles, to b) chaotic mixtures of large nonsym-metric bubbles and small bubbles.3.Annular flow A liquid layer is formed on the tubewall with a continuous steam core; most of the liq-。
英汉对照计量经济学术语

计量经济学术语A校正R2(Adjusted R-Squared):多元回归分析中拟合优度的量度,在估计误差的方差时对添加的解释变量用一个自由度来调整。
对立假设(Alternative Hypothesis):检验虚拟假设时的相对假设。
AR(1)序列相关(AR(1) Serial Correlation):时间序列回归模型中的误差遵循AR(1)模型。
渐近置信区间(Asymptotic Confidence Interval):大样本容量下近似成立的置信区间。
渐近正态性(Asymptotic Normality):适当正态化后样本分布收敛到标准正态分布的估计量。
渐近性质(Asymptotic Properties):当样本容量无限增长时适用的估计量和检验统计量性质。
渐近标准误(Asymptotic Standard Error):大样本下生效的标准误。
渐近t 统计量(Asymptotic t Statistic):大样本下近似服从标准正态分布的t 统计量。
渐近方差(Asymptotic Variance):为了获得渐近标准正态分布,我们必须用以除估计量的平方值。
渐近有效(Asymptotically Efficient):对于服从渐近正态分布的一致性估计量,有最小渐近方差的估计量。
渐近不相关(Asymptotically Uncorrelated):时间序列过程中,随着两个时点上的随机变量的时间间隔增加,它们之间的相关趋于零。
衰减偏误(Attenuation Bias):总是朝向零的估计量偏误,因而有衰减偏误的估计量的期望值小于参数的绝对值。
自回归条件异方差性(Autoregressive Conditional Heteroskedasticity, ARCH):动态异方差性模型,即给定过去信息,误差项的方差线性依赖于过去的误差的平方。
一阶自回归过程[AR(1)](Autoregressive Process of Order One [AR(1)]):一个时间序列模型,其当前值线性依赖于最近的值加上一个无法预测的扰动。
某些极大交换子在非倍测度Hardy型空间上的有界性

1
!
1 Introduction
2
We will work on the d-dimensional Euclidean space R d with a non-negative Radon measure µ which only satisfies the following growth condition that there exists a constant C 0 > 0 such that µ(B (x, r )) ≤ C0 r n (1.1) for all x ∈ Rd and r > 0, where B (x, r ) = {y ∈ Rd : |y − x| < r }, n is a fixed number and 0 < n ≤ d. The measure µ is not necessary to satisfy the doubling condition. The doubling condition, namely, there exists a constant C > 0 such that µ(B (x, 2r )) ≤ Cµ(B (x, r )) for all x ∈ supp (µ) and r > 0, is a key assumption in the analysis on spaces of homogeneous type. However, during the last several years, considerable attention has been paid to the study of function spaces and the boundedness of Calder´ on-Zygmund operators with non-doubling measures and many classical results have been proved still valid if the underlying measure µ is substituted by a non-doubling Radon measure as in (1.1); see [6, 13, 14, 15, 8, 9, 10] and their references. The analysis with non-doubling measures played an essential role in solving the long open Painlev´ e’s problem by Tolsa in [16]; see also [18] for more background. The main purpose of this paper is to establish the boundedness of a class of maximal Calder´ on-Zygmund operators and maximal commutators which are the variant of the maximal commutators generated by Calder´ on-Zygmund operators and RBMO(µ) functions in some Hardy-type spaces. Before stating our results, we first recall some necessary notation and definitions. Let K be a function on Rd × Rd \ {(x, y ) : x = y } satisfying that for x = y , |K (x, y )| ≤ C |x − y |−n , and |K (x, y ) − K (x, y )| + |K (y, x) − K (y , x)| dµ(x) ≤ C,
β表示流体的体膨胀系数

β表示流体的体膨胀系数英文回答:The coefficient of volume expansion, denoted as β, is a property of a fluid that describes how much the fluid expands when its temperature increases. It is defined as the fractional change in volume per unit change in temperature, typically expressed i n units of 1/°C or 1/K.To understand the concept of β, let's consider an example. Imagine you have a container filled with a liquid, such as water. When you heat up the liquid, its temperature rises, causing the molecules to move faster and occupy more space. As a result, the volume of the liquid increases. The coefficient of volume expansion, β, quantifies this change in volume relative to the change in temperature.For instance, if the coefficient of volume expansion of water is β = 0.00021/°C,it means that for every 1°C increase in temperature, the volume of water increases by0.00021 times its original volume. So, if you heat up 1 liter of water from 20°C to 21°C, the volume of water would increase by approximately 0.00021 liters.The coefficient of volume expansion is not only applicable to liquids but also to gases. Gases generally have higher coefficients of expansion compared to liquids. For example, air has a coefficient of volume expansion of approximately β = 0.003/°C. This means t hat for every 1°C increase in temperature, the volume of air expands by 0.003 times its original volume.Understanding the coefficient of volume expansion is important in various practical applications. For example, it is crucial in the design and operation of thermal systems, such as heat exchangers and boilers. By knowing the coefficient of volume expansion of a fluid, engineers can accurately predict and account for the changes in volume that occur with temperature variations.中文回答:体膨胀系数β是描述流体在温度升高时膨胀程度的一个属性。
开放经济下的结构转型_一个三部门一般均衡模型
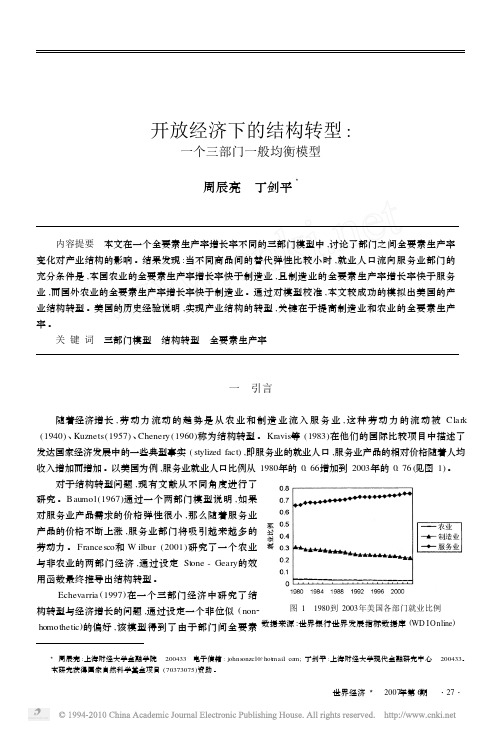
根据 (2)至 (4)式 ,我们可以将制造业产品衡量的总产出表示为 :
3
∑ Yt =
α
Pi, t Yi, t = A2, t kt L = w tL t + it Kt
(5)
i =1
为了将模型封闭起来 ,我们需要设定需求方 。
典型代理人最大化一生的效用 :
∑∞ βt
t =0
C1t -γ 1-
-1 γ
i =1
这里 , C1, t表示农产品的消费量 , C2, t表示制造业产品的消费量 , 其中即包括对本国制造业产品的消
费 ,也包括对国外制造业产品的消费 , C3, t表示服务的消费量 , C4, t表示国内消费的国外农产品的消费量 。
4
4
ε > 0为各产品的替代弹性
,
∑<
i=1
i
=
1
。当
γ= 1时
其中 C43, t表示国外消费的本国农产品 。
均衡消费要求消费者在等式 (8)的约束下最大化等式 (7) ,求解消费者的问题 ,得到各商品的需求函
数: 我们将物价指数定义为 :
Ci, t
∑< < =
P ε -ε
i i, t
P 4 ε -ε
j = 1 j j, t
(w tL + it Kt -
( 15 )
L3, t L
∑ =
< 3 < < i =1
ε 3
(A3, A2,
t t
)ε-
1
ε i
( A i, A2,
t t
)ε-
1
+
ε 4
(
A13, A23,
Some computation on g Function and Disc Partition Function and Boundary String Field Theory

Let us calculate the partition function in the Lagrange formalism. We expand the =
Am,µj eimt/r sin µj(x − l), Am,µj = A−m,µj .
(6)
m∈Z j
of Sen’s tachyon condensation[2] both in bosonic and supersymmetric string theory. In the
bosonic BSFT the spacetime string action S is conjectured to satisfy [3]-[7]
arXiv:hep-th/0105247v2 30 May 2001
May, 2001 OU-HET 387,
YITP-01-46, hep-th/0105247
Some Computation on g Function and Disc Partition Function and Boundary String Field Theory
Because we assume the periodic boundary condition in t-direction, m runs over integers. In x-
direction, we impose the mixed boundary condition (5), which gives the equation determining
ground state degeneracy (g-function)[8] in statistical models. In fact the studies based on
低能跑动耦合常数形式对低能常数的影响

低能跑动耦合常数形式对低能常数的影响陈清森;蒋绍周【摘要】[目的]探寻一种理论值与实验值接近的低能跑动耦合常数的形式,比较几种低能跑动耦合常数形式对低能常数的影响.[方法]选取3种低能跑动耦合常数的形式及其变形,利用已有的耦合常数和低能常数的关系,数值计算出低能常数并与实验值作比较.[结果]发现1种与实验符合的低能跑动耦合常数的可能形式,并给出低能常数新的理论预言值.[结论]对于跑动耦合常数低能部分是一个平台的情况,无论其二阶导数是否连续,数值结果对低能常数的影响均较小,并且绝对值都系统地偏大;对于给出的低能耦合常数不是平台的形式,可以通过对参数的调节使得计算的低能常数与实验结果相符.【期刊名称】《广西科学》【年(卷),期】2015(022)001【总页数】4页(P109-112)【关键词】跑动耦合常数;低能常数;夸克自能【作者】陈清森;蒋绍周【作者单位】广西大学物理学院,广西大学-国家天文台天体物理和空间科学研究中心,广西南宁530004;广西大学物理学院,广西大学-国家天文台天体物理和空间科学研究中心,广西南宁530004【正文语种】中文【中图分类】O412.3【研究意义】自然界存在四种相互作用,作用的强弱用耦合常数来描述。
耦合常数会随着动量标度的改变而改变,又称为跑动耦合常数。
对于强相互作用,跑动耦合常数随着动量标度的增加而减小,称为强相互作用的渐进自由效应[1,2]。
对于高能端,理论上已经给出跑动耦合常数到四圈图的结果[3,4]。
然而由于强相互作用在低能端耦合常数比较大,不能使用传统的微扰理论计算,需要采用其他方法近似计算。
赝标介子的手征微扰理论就是其中的一种[5~7],用于描述低能赝标介子的强相互作用。
但是理论本身并不能给出赝标介子手征有效拉氏量的系数(称为低能常数)。
从量子色动力学的第一原理出发,可以得到夸克自能和低能常数的关系,而夸克自能可以由耦合常数通过Schwinger-Dyson方程给出[8,9]。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
arXiv:hep-th/9406162v1 24 Jun 1994
The β -function of the chiral Gross Neveu model at O(1/N 2 ).
J.A. Gracey, Department of Applied Mathematics and Theoretical Physics, University of Liverpool, P.O. Box 147, Liverpool, L69 3BX, United Kingdom.
1
ห้องสมุดไป่ตู้
1
Introduction.
The large N expansion has proved to be a useful technique in providing an alternative method of analysing renormalizable quantum field theories which possess N fundamental fields. For example, it was demonstrated in [1] that the (perturbatively massless) two dimensional Gross Neveu models with discrete and continuous chiral symmetry exhibit dynamical mass generation as well as being asymptotically free field theories with this technique. This former property cannot be accessed in conventional perturbation theory and such toy models have proved to be important as a step to understanding similar phenomena in complicated four dimensional gauge theories such as quantum chromodynamics. One of the limitations, however, of a conventional large N analysis is that one cannot proceed much beyond the leading order due in part to the appearance of intractable integrals whose treatment is hindered primarily by the presence of the dynamically generated mass. Methods to overcome this problem have been developed in [2, 3] and applied initially to the O(N ) bosonic σ model to solve that theory to O(1/N 2 ). The technique exploits the properties of the field theory at its d-dimensional critical point which is defined to be the non-trivial zero of the β -function. The simplifying feature of studying a model there is the additional symmetry present. As the β -function vanishes the Green’s function of the fields are conformally invariant and obey simple power law behaviour which, of course, has a massless form. In essence one is using the conformal bootstrap approach to solve the field theory, [4]. As a consequence, one avoids one of the difficulties of the conventional large N approach in that the previously intractable integrals become calculable using techniques developed to compute massless Feynman diagrams, [5]. This technique, known as uniqueness, is in effect a method of conformal integration in d-dimensions. Essentially when the sum of the exponents of bosonic propagators at a 3-vertex in coordinate space sum to the dimension of space time, the vertex is replaced by a triangle of propagators whose exponents are related to the original vertex. This represents an integration within the overall Feynman diagram. In essence it is the Yang Baxter star triangle relation, but is more general since it is valid in arbitrary (fixed) space time dimension. Moreover, as one is now dealing with a scale invariant situation the problem of solving the model becomes one of computing the critical indices or exponents of the fields which will have an anomalous portion in addition to the canonical dimension. The anomalous piece is the part which carries the quantum properties of the model and from the universality criterion of statistical mechanics (see, for 2
example, [6]), it will be a function of the spacetime dimension and the basic parameters of the model, such as N in the case of a large N expandable theory, and can be calculated order by order in 1/N . The equations which one uses to do this are deduced by representing the Dyson equations of the Green’s functions in the critical region of the theory from which one can deduce self consistent equations whose solution yields the exponents, [2]. The analytic expressions which result for the anomalous dimensions can be related to the respective renormalization group functions precisely at the critical point, [2, 6]. One important function which characterizes a field theory is the β -function which governs how the coupling constant behaves with the renormalization scale. Ordinarily one calculates it order by order in powers of the perturbative coupling constant, which is assumed to be small. In the large N critical point approach which we concentrate on here it can, however, be determined by computing the critical exponent 2λ = − β ′ (gc ) where gc is the critical point. Whilst this may seem to be an indirect way to proceed it is important to note that the O(1/N 2 ) corrections to the β -function of the O(N ) bosonic σ model could only be deduced in this way, [3]. Following the pioneering work of [2, 3] the method has been extended to analyse models with fermions, [7-11]. In particular the O(N ) Gross Neveu model has been solved at O(1/N 2 ) with the fermion and auxiliary field anomalous dimensions, [7, 8], and the β -function exponent λ, [9, 10], all having been computed in arbitrary dimensions. Now that matter fields have been successfully incorporated within the critical point approach it is possible to examine other models to the same precision. One such model which is currently relevant and related to the O(N ) Gross Neveu model is the chiral Gross Neveu model, [1, 12], which possesses a continuous chiral symmetry. This was first discussed in [12] by Nambu and Jona-Lasinio in four dimensions and later in [13] where the connection with hadronic physics was first introduced. Moreover, four fermi interactions have recently been a subject of intense study as it provides a possible alternative to the Higgs mechanism in the standard model. There a fermion fermion bound state plays the role of the Higgs boson, [14, 15] and so it is important to have as complete a picture as possible of the quantum structure of the model. Therefore, the aim of this paper is to compute the exponent λ of the chiral Gross Neveu or Nambu–Jona-Lasinio model at O(1/N 2 ) which relates to the β -function. This is one order beyond what has been computed before in this model. One property that the chiral Gross Neveu model shares with other models in two dimensions is that it possesses an exact S -matrix, [16], from which 3
