13 矩阵位移法
矩阵位移法和有限元法的异同
矩阵位移法和有限元法的异同矩阵位移法和有限元法是数值计算领域中常用的两种方法，它们都具有非常优秀的数值精度和高度的计算效率。
在工程领域中，它们常常用于解决结构振动、热传导、电场、磁场等问题，因此其应用非常广泛。
本文将从多个角度比较两种方法的异同。
一、基本原理矩阵位移法是基于结构受力平衡公式推导而来，通过建立刚度矩阵，利用矩阵乘法计算结构中各点受力情况，从而得到结构变形情况。
有限元法则是将结构分割成很多有限元，建立每个有限元内部的受力方程，通过组合各个有限元的受力方程形成整个结构的受力方程，从而得到变形情况。
二、精度和适用范围矩阵位移法是一种较为精确的计算方法，适用于较小结构和较短时间内的计算。
而有限元法精度相对较差，但它适用于更为复杂的结构和更长时间内的计算，且可以模拟非线性问题。
三、模型建立和求解在矩阵位移法中，需要先根据实际结构建立刚度矩阵，然后将载荷矩阵和位移矩阵代入方程中求解。
而在有限元法中，需要将结构分割成有限元，并建立每个有限元的受力方程，然后进行求解。
有限元法需要进行剖分后求解，模型的建模过程相对较为复杂，计算量较大。
四、应用领域和优缺点矩阵位移法适用于解决结构较小、较简单的问题，在建模和求解过程中较为简单，计算速度快。
但它的缺点是在处理较复杂的问题时很难得到精确解。
有限元法适用于处理复杂问题，精度相对更高。
但在建模和求解过程中计算量比较大，时间较长，适用于需要高精度计算的问题。
综上所述，矩阵位移法和有限元法都是重要的数值计算方法，适用于不同的领域。
在遇到具体问题时，需要根据问题的特点选择合适的数值计算方法，从而得到更好的计算效果。
矩阵位移法中,结构的原始刚度方程
矩阵位移法是结构分析中常用的一种方法，它通过将结构刚度矩阵和位移向量进行相乘，来求解结构的位移。
在矩阵位移法中，结构的原始刚度方程是一个关键的内容，它描述了结构在外部荷载作用下的位移响应。
一、什么是矩阵位移法矩阵位移法是一种基于矩阵运算的结构分析方法。
它通过建立结构的刚度矩阵和荷载矩阵，将结构的位移表示为荷载、边界条件和材料性质的函数，然后利用矩阵运算的方法求解结构的位移响应。
矩阵位移法的优点是可以较为准确地分析复杂结构的位移响应，适用范围广泛。
二、结构的原始刚度方程在矩阵位移法中，结构的原始刚度方程是描述结构在受到外部荷载作用下的位移响应的重要方程。
它通常表示为Ku=f，其中K是结构的刚度矩阵，u是结构的位移向量，f是结构受到的外部荷载。
结构的刚度矩阵K可以根据结构的几何形状、材料性质和边界条件进行求解。
它包含了结构的刚度信息，可以反映出结构在受到荷载作用时的变形特性。
结构的位移向量u是结构的位移表示，它包含了结构在各个节点的位移信息。
结构受到的外部荷载f可以根据结构所受到的力的大小和作用位置进行求解。
三、矩阵位移法的求解步骤在使用矩阵位移法求解结构的位移响应时，一般可以按照以下步骤进行：1.建立结构的刚度矩阵和荷载矩阵需要根据结构的几何形状、材料性质和边界条件建立结构的刚度矩阵K和荷载矩阵f。
在建立刚度矩阵和荷载矩阵时，需要考虑结构的整体刚度特性和外部荷载的作用情况，确保建立的矩阵能够准确地描述结构的位移响应。
2.确定结构的边界条件和荷载接下来，需要确定结构的边界条件和受到的外部荷载。
结构的边界条件包括固定节点的位移约束和受固定支撑等信息，外部荷载包括施加在结构上的力和力矩等。
3.求解结构的位移响应利用已建立的刚度矩阵和荷载矩阵，结合结构的边界条件和受到的外部荷载，可以通过矩阵运算的方法求解结构的位移响应。
具体的求解方法包括直接求解、迭代法和分解法等，根据实际情况选择合适的方法进行求解。
4.分析结构的位移响应根据求解得到的结构位移向量u，可以分析结构在受到外部荷载作用时的位移响应情况。
矩阵位移法小结
式中K为总刚度矩阵，为结构的结点位移列向量，P
为结点力列向量。
总刚度矩阵K反应了整个结构的刚度，是描述结点 力与结点位移之间关系的系数矩阵。其矩阵的性质与 特点：
总结
( 1 )元素kij的物理意义为：当△j=1而其他位移分量为零 时产生在△i方向的杆端力。
（2）主子块Kii是由结点i的相关单元中与结点i相应的主 子块叠加而得。
3. 弹性支座的处理 通常用主对角元素叠加法处理弹性支座。如果结构的 第j个自由度是弹性约束，那么，把弹性支座的刚度系数 叠加到原始刚度矩阵主对角线的第j个元素上即可得到经 约束处理后的总刚度方程。
总结
4. 总刚度方程和总刚度矩阵的性质与特点 总刚度方程为整体结构的结点荷载与结点位移之间的 关系式，是结构应满足的平衡条件。无论何种结构，其总 刚度方程都具有统一的形式:
总结
对于每个结点位移分量数相同的结构，原始刚度矩阵 的阶数为结构的总结点数乘以结点位移分量的数目，例 如，每个结点位移分量数为3的平面刚架，结构原始刚 度矩阵的阶数为3n×3n 。
总结
（2）边界条件处理
对于刚性支座，用划行划列法处理刚性支座，即直接 划去原始刚度方程中与零位移对应的行和列。这样做有 时要改变原方程的排列顺序,会给编程带来麻烦。为了不 改变原方程的排列顺序，同时又要引入边界条件,采用 “主一副零”法。
的单元刚度方程中求杆端内
力
总结
一、基本概念
结构矩阵分析是采用矩阵方法分析结构力学问题的一种 方法。与传统的力法、位移法相对应，在结构矩阵分析中 也有矩阵力法和矩阵位移法，或柔度法与刚度法。矩阵位 移法易于实现计算过程程序化而被广泛应用。
矩阵位移法是结构力学中的位移法加上矩阵方法。矩阵 位移法的基本未知量也是结点位移——独立的线位移和转 角。但由于有时考虑杆件的轴向变形，且把杆件铰结端的 转角也作为基本未知量，因此，基本未知量数目比传统位 移法的基本未知量多一些。
第十三章 矩阵位移法
0 sin 0 0
0 0 0 0 0 1
坐标转换矩阵（正交矩阵）
T
1
T
T
13-2 整体坐标系下的单元刚度矩阵
同理：
e
T
e
其中:
1 2 3 4 5 6
13-1 概述
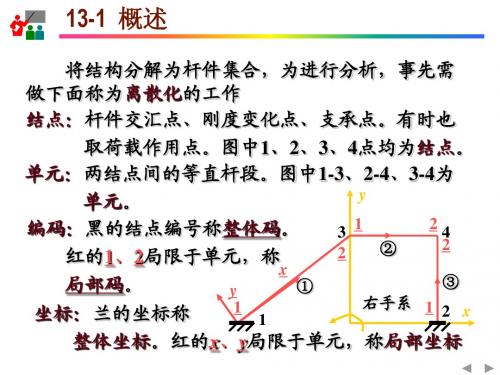
将结构分解为杆件集合，为进行分析，事先需 做下面称为离散化的工作 结点：杆件交汇点、刚度变化点、支承点。有时也 取荷载作用点。图中1、2、3、4点均为结点。 单元：两结点间的等直杆段。图中1-3、2-4、3-4为 y 单元。 24 编码：黑的结点编号称整体码。 3 1 2 ② 2 红的1、2局限于单元，称 x ③ 局部码。 ① y 右手系 1 2 x 1 坐标：兰的坐标称 1 整体坐标。红的x、y局限于单元，称局部坐标
13-2局部坐标系下的单元刚度矩阵
EA EA F1 1 0 0 4 l l 12 EI 6 EI F 2 0 3 2 2 3 0 l l 6 EI 4 EI F 3 0 2 3 0 2 l l EA EA F 4 1 0 0 4 l l 12 EI 6 EI F 5 0 3 2 2 3 0 l l 6 EI 2 EI F 6 0 2 2 3 0 l l
局部坐标下自由单元的单元刚度矩阵
13-2局部坐标系下的单元刚度矩阵
2 单元刚度矩阵的性质
（1）单元刚度系数的意义
（2）单元刚度矩阵是对称矩阵 （3）自由单元刚度矩阵是奇异矩阵 矩阵行列式等于零，逆阵不存在。
单位杆端位移引起的杆端力
反力互等定理
F
e
结构力学十三讲矩阵位移法
-6EI l2
4EI l
4
§13-3 单元刚度矩阵(整体座标系)
一、单元座标转换矩阵 Y1
X1
X1
Y1
MM21
e
x
M2 X2
正交矩阵 [T]-1 =[T]T
e e
e T T e
v1
y e
X 2
Y2
Fⓔ T T F ⓔ
ee
F T F ee
座标转换矩阵
5
二、整体座标系中旳单元刚度矩阵
[k] e = [T]T k e [T]
(4)
(6)
00
(5)
y
单元 局部码总码
单元 局部码总码
（1） 1 （2） 2 （3） 3 （4） 0 （5） 0 （6） 4
1
2
3 0
0
4
（1） 1
1
（2） 2
2
（3） 3 （4） 0
3 0
（5） 0
0
（6） 0
0
18
1 2
[k] 1 = 3
0 0 4
1 2
[k] 2= 3
0 0 0
123004 101 102 103 104 105 106 201 202 203 204 205 206 301 302 303 304 305 306 401 402 403 404 405 406 501 502 503 504 505 506 601 602 603 604 605 606 123000 11 12 13 14 15 16 21 22 23 24 25 26 31 32 33 34 35 36 41 42 43 44 45 46 51 52 53 54 55 56 61 62 63 64 65 66
矩阵位移法——精选推荐
第十二章矩阵位移法12-1 概述用经典的力法和位移法求解超静定结构，随着基本未知量数目的增多，相应需要建立和求解的多元代数方程的个数也增多，计算工作极为冗繁和困难。
由于计算技术的飞速发展，电子计算机广泛应用于结构分析，使力学学科在计算技术上实现了现代化，大大推动了工程设计技术上的改进和结构理论的发展。
基于上述情况，结构矩阵分析方法已从本世纪六十年代迅速发展起来。
在结构矩阵分析中，运用矩阵进行计算，不仅能使公式非常紧凑，而且在形式上规格统一，便于使计算过程程序化，因而适用于电子计算机进行自动化的数学计算。
结构矩阵分析的两种基本方法是矩阵位移法(刚度法)和矩阵力法(柔度法)，前者在计算中采用结点位移作为基本未知量，后者则采用多余力作为基本未知量。
对于杆件结构，矩阵位移法比矩阵力法便于编制通用的程序，因而在工程界应用较为广泛。
矩阵位移法与位移法在本质上并无区别，两者的差异仅在于矩阵位移法是从电算这一角度出发，它在解题步骤上以矩阵作为组织运算的数学工具。
在杆件结构的矩阵位移法中，把复杂的结构视为有限个单元(杆件)的集合，各单元彼此在结点处连接而组成整体。
因而先把结构分解成有限个单元和结点，即对结构进行离散化。
继而对单元进行分析，建立单元杆端力与杆端位移之间的关系。
再根据变形谐调条件、静力平衡条件使离散化的结构恢复为原结构，从而形成结构刚度方程，据此不难求解结构的结点位移和单元杆端力。
矩阵位移法的基本思路是“先分后合”，即先将结构离散然后集合，这样一分一合的过程，就把复杂结构的计算问题转化为简单杆件的分析与综合问题了。
因此，它的解题方法可分为两大步骤:(1)单元分析。
研究单元的力学特性。
(2)整体分析。
考虑单元的集合，研究整体方程的组成原理和求解方法。
12一2 单元刚度矩阵一、单元的划分在杆件结构中，一般是把每个杆件作为一个单元。
为了计算方便起见，只采用等截面直杆这种形式的单元，并且还规定荷载只作用于结点处。
《结构力学》第十章矩阵位移法
《结构力学》第十章矩阵位移法矩阵位移法是结构力学中的一种重要分析方法，通过将结构的受力分析转化为矩阵运算，可以有效地求解复杂结构的位移和应力分布。
本文将分为四个部分来介绍矩阵位移法的基本原理和应用。
第一部分将介绍矩阵位移法的基本原理。
矩阵位移法基于结构的受力平衡方程和变形条件，建立了适用于不同类型结构的一般形式的位移函数。
通过对这些位移函数进行适当组合，可以得到一个较为简化的位移矩阵方程。
这个方程可以通过矩阵运算求解，从而得到结构的位移和应力分布。
第二部分将介绍矩阵位移法的应用。
矩阵位移法可以用于求解各种类型的结构，包括梁、柱、框架等。
具体应用时，首先需要确定结构的边界条件和受力情况，然后根据结构的几何形状和材料性质，建立相应的位移函数。
之后，将位移函数按照一定的规则组合起来，建立一个位移矩阵方程。
通过解这个方程，可以得到结构的位移和应力分布。
第三部分将介绍矩阵位移法的优点。
相比于传统的力方法，矩阵位移法具有计算简单、准确性高、适用范围广等优点。
这是因为矩阵位移法可以通过矩阵运算将结构的受力分析转化为代数运算，减少了繁琐的计算过程，并且可以应用于各种不规则结构。
第四部分将介绍矩阵位移法的局限性。
矩阵位移法虽然具有很多优点，但也有一些限制。
首先，矩阵位移法对结构的刚度矩阵的求取较为复杂，需要通过精确和谐振数法等途径进行求解。
其次，矩阵位移法不能用于解决非线性和动力问题。
总结起来，矩阵位移法是一种重要的结构力学分析方法，通过将结构的受力分析转化为矩阵运算，可以有效地求解复杂结构的位移和应力分布。
它具有计算简单、准确性高、适用范围广等优点，但也有一些局限性。
因此，在实际应用中需要根据具体情况选择合适的方法。
同时，矩阵位移法的进一步研究和发展也是一个非常重要的方向。
矩阵位移法基本原理
1 ④
①
2 ⑤
②
⑥ 6
3 ⑧ 7 11 P2
P1
⑦
⑨ y
5
⑩
x
其形成已随结点号和单元号的形成而产生。但还要指定
始结点和终结点（随意指定），这很重要。
1 ③ 4 ⑨ ④
①
2 ⑤
②
⑥ 6
3 ⑧ 7 11 P2
P1
⑦
5
⑩
图示结构的关联节点表可如下：
单元 ① ② ③ ④ ⑤ ⑥ ⑦ ⑧ ⑨ ⑩ 11
0 y 4
1
2
3
P1
6 7 5 P2 x
任意选定坐标系，依结点号顺序给出结点坐标。
目的是计算杆长，杆的方向，以计算坐标转换矩阵。
此信息可存放在二维数组中
3．单元编号
不受结点号的影响， 任意编号。目的是 给出计算机计算顺序。 4．单元关联节点表 它是计算的重要信息表， 0 是获得坐标转换矩阵、 组装总刚度矩阵的依据
e ij e jj
e
同样，把
F e ，D
Yi
vi
T
e
也相应分块，写为：
eT
F X i
e
Xj
uj
Y j Fi
eT
e
D
e
e
i u
v j Di
j
e
F D
j
e T j
e T
Fi X i
e e
Yi ,
e
F X
0 0 0 0
T
K
e
EA L 0 EA L 0
e i
EA L 0 EA L 0
《矩阵位移法》课件
实际工程案例分析
总结词
为了验证矩阵位移法的有效性，可以通过实际工程案例 进行分析。通过与实验结果的对比，可以评估方法的精 度和可靠性。
详细描述
选取具有代表性的实际工程案例，如高层建筑、大跨度 桥梁等，利用矩阵位移法进行计算，并将结果与实验数 据进行对比。通过对比分析，可以评估矩阵位移法的精 度和可靠性，为该方法在实际工程中的应用提供依据。 同时，也可以针对不同工程案例的特点，对矩阵位移法 进行优化和改进，提高其适用性和计算效率。
05
矩阵位移法的优缺点
优点
精确度高
矩阵位移法基于严格的数学推导，能 够精确地计算出结构的位移和内力， 尤其适用于复杂结构的分析。
适用性强
矩阵位移法可以处理多种类型的载荷 ，包括静载、动载以及温度载荷等， 适用范围广泛。
便于计算机化
矩阵位移法的计算过程可以通过计算 机程序实现，便于进行大规模的结构 分析。
多尺度方法
将矩阵位移法应用于多尺度问题 ，考虑不同尺度之间的相互作用 和影响，为复杂系统提供更准确 的模拟结果。
THANKS
感谢观看ts
目录
• 引言 • 矩阵位移法的基本概念 • 矩阵位移法的实施步骤 • 矩阵位移法的应用实例 • 矩阵位移法的优缺点 • 未来展望与研究方向
01
引言
什么是矩阵位移法
矩阵位移法是一种数值分析方法，用 于求解线性方程组和解决各种数值计 算问题。
它通过将原问题转化为矩阵形式，利 用矩阵运算来求解未知数，具有高效 、精确和灵活的特点。
并行计算
利用并行计算技术，将计算任务分解为多个子任务，同时运行在多 个处理器上，加快计算速度。
智能优化
结合人工智能和机器学习技术，自动调整算法参数，实现自适应优 化，提高算法的效率和稳定性。
矩阵位移法
k22坐k11标局k01成部1k029坐200标时kk20与32，3 整局k0体12部45 单k0k20514
0 k26 k26
To 47
k e ke
刚和有何整k关体3k3系单33 ？刚k0k间454535
k35 00
k3k6 36
0 k56
对称对称
kk5544
kk65k66 66
F e FEe k e e
单元杆端位移矩阵
e 1
2
3
4
T e
单元刚度矩阵(应熟记)
12 6l 12 6l
k
e
EI l3
6l
12
4l 2 6l
6l 12
2l
2
6l
6l 2l 2 6l 4l 2
是转角位移方程的矩阵表示
单元等效结点荷载矩阵
根据单跨梁的载常数，可得
向上满跨均布荷载 q 作用
(F FE )e k e e F e FEe k e e
连续梁单元需要 进行坐标转换吗？
连续梁的局部坐标与整 体坐标一致，所以不需 要转换。
第一种做法
桁架单元如何
进行坐标转换？ T
力的转换
T
F1
F2
F3
F4
T
cos
0
位移的转换
sin
0
0
cos
0 T F1
sin F2
1 2
3. 坐标转换问题
在搞清单元特性后，像位移法一样，需将单 元拼装回去。在结点处位移自动满足协调条件 的基础上，令全部结点平衡，即可建立求解位 移的方程，这是下一节将讨论的内容。
除连续梁外，一般结构单元不全同方位， 为保证协调和平衡，应将杆端位移和杆端力 都转换成统一的，对整体坐标的量，因此要 先解决坐标转换问题。下面先讨论自由式梁 单元的转换问题。
矩阵位移法基本流程
矩阵位移法基本流程下载温馨提示:该文档是我店铺精心编制而成，希望大家下载以后，能够帮助大家解决实际的问题。
文档下载后可定制随意修改，请根据实际需要进行相应的调整和使用，谢谢!并且，本店铺为大家提供各种各样类型的实用资料，如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等，如想了解不同资料格式和写法，敬请关注!Download tips: This document is carefully compiled by theeditor. I hope that after you download them,they can help yousolve practical problems. The document can be customized andmodified after downloading,please adjust and use it according toactual needs, thank you!In addition, our shop provides you with various types ofpractical materials,such as educational essays, diaryappreciation,sentence excerpts,ancient poems,classic articles,topic composition,work summary,word parsing,copy excerpts,other materials and so on,want to know different data formats andwriting methods,please pay attention!矩阵位移法基本流程一、结构离散化阶段。
在运用矩阵位移法进行分析之前，首先要对结构进行离散化处理。
矩阵位移法程序化解题方法
矩阵位移法解法步骤解：1）、单元及结点位移分量统一编码单元及结点位移分量编码、整体坐标系如图所示，局部坐标系横轴正向在各单元上标出。
注：编结点位移分量总码时，后处理法和先处理法有区别：采用后处理法编码时暂不考虑边界条件对支座处位移分量的限制，皆视为一般情形处理；采用先处理法时，对已知为零的位移分量总是以零编码。
对于连接于铰结点的杆端编码时，线位移采用同码，而角位移异码。
2）、形成局部坐标中单元刚度矩阵 k e：首先，计算各单元杆件的几何特征：⋯ ⋯各单元的单元刚度矩阵如下：单元①： ⋯ ⋯3）、形成整体坐标中单元刚度矩阵：（计算公式： k e = T T ke T ） 整体坐标系中的各单元刚度矩阵转换如下：单元①： ⋯ ⋯4）、集成整体刚度矩阵 K （单元集成法或直接刚度法）：首先，由各单元的局部码与总码的对应关系写出各单元的定位向量如下：λ e = ⋯ ⋯ T其次，将各单元刚度矩阵 k e 按其定位向量 λ e 在整体刚度矩阵 K 中定位并累加 得整体刚度矩阵如下：K =(⋯ ⋯)5）、计算综合等效结点荷载向量 F P ：①、计算局部坐标系中各杆件单元的固端力向量：F P e =(F N1F ，F Q1F ，M 1F ，F N2F ，F Q2F ，M 2F )T ②、转换整体坐标系中各杆件单元的固端力向量：{F P }e =(F x1F ，F y1F ，M 1F ，F x2F ，F y2F ，M 2F )T ③、将各杆件单元的固端力反其指向，并按其定位向量 λ e 在综合等效结点荷载向量 F P 定位并累加，得综合等效结点荷载向量如下：F P = ⋯ ⋯ T6）、计入边界条件条件，写出刚度方程并解之：刚度方程： K Δ = F P采用后处理法时，对已知为零的结点位移，在整体刚度矩阵 K 中将其所对应行列的主元素记为1，其余都变为零，然后写出刚度方程，解之。
采用先处理法时，由于在进行位移分量编码时已考虑边界条件，因而无须再计入，只写出刚度方程求解即可。
矩阵位移法
TT T T T T I
Fx1 F y1 M1 单元坐标 转换矩阵 F x2 Fy 2 M 2
e
Hale Waihona Puke eF e TF e
T 1 T T
单元坐标转换矩阵T是一正交矩阵。
EI 25 104 kN m l
0 300 0
5m
0 为了简洁，下面将矩阵 中各元素的单位略去。 12 30 0 12 30 30 100 0 30 50 4 EA 10 0 0 l 0 0 300 0 0 12 30 0 12 30 12 EI 6 EI [k11 ] 0 3 2 30 50 0 30 100 l l 6 EI 4 EI 第一列元素变符号即第四列，第二列元素变符号即第五列 0 ①： 2 ②求整体坐标系中的单刚， k l l 第一行元素变符号即第四行，第二行元素变符号即第五行
3、有限单元法的三个基本环节： ①单元划分：一根等截面直杆作为一个单元，单元间由结点相联。 ②单元分析：建立单元刚度方程，形成单元刚度矩阵(物理关系)。 ③整体分析：由单元刚度矩阵形成整体刚度矩阵，建立结构的 位移法基本方程(几何关系、平衡条件)。
§9-2 单元刚度矩阵(element stiffnessmatrix)（局部坐标系）
T11 T12 T T T 21 22
因此，(a)式的逆转换式为： 同理
F e T TF e
e T e
(b)
e T T e
整体坐标系中的单元刚度矩阵
F e TF e
(a)
e T e
(b)
单元刚度矩阵的性质 设局部坐标系中、整体坐标系中的单元刚度方程分别为： ①单元刚度矩阵是杆端力用杆端位移来表达的联系矩阵。 e e e F k Δ (c) ②其中每个元素称为单元刚度系数，表示由于单位杆端位移引起的杆端力。 ③单元刚度矩阵是对称矩阵。 F e k eΔe (d ) ④第k列元素分别表示当第k个杆端位移=1时引起的六个杆端力分量。 e e e e ⑤一般单元刚度矩阵是奇异矩阵。不存在逆矩阵。因此， 将式(a)、(b)代入式(c) k eT IF T T TTF ke T T 可由单元刚度方程，由杆端位移唯一确定杆端力；但由杆端力反推杆端位移时， 可能无解、可能解不唯一。 k e T T k eT
矩阵位移法
D1 = D2 = 0
； D5 = D6 = 0
则有修正后的总刚度矩阵：
-100 2 [K ] = 100 600
[k11 ] [k12 ] {F1} = {F2 } [k 21 ] [k 22 ]
{D1} {D 2 }
@
单元刚度矩阵的性质：①对称性；②奇异性； ③主对角元恒为正值
3、整体刚度矩阵
K ij ：单元仅发生第j个杆端单位位移时，在第
Y2 = QBA
写成矩阵表达式为：
4 EI 2 EI 6 EI q + q + -v ) ( v l 1 l 2 l2 1 2 2 EI 4 EI 6 EI q + q + -v ) ( M2 = v l 1 l 2 l2 1 2 6 EI 12 EI (v1 - v2 ) Y1 = (q1 +q 2 ) + l2 l2 6 EI 12 EI = q + q (v1 - v2 ) Y2 ( 1 2) l2 l2 M1 =
2
3
1 2
Hale Waihona Puke 3-1 50 1 50 50 300 -50 150 -1 -50 2 -100 -1 -50 = 50 150 -100 600 50 150 -1 50 1 50 -50 150 50 300
计入边界条件：因边界结点1和3 为固定端，故有：
0 12EI l3 6 EI - 2 l 0 12EI l3 6 EI - 2 l
@
0 6 EI l2 2 EI l 0 6 EI - 2 l 4 EI l
EA l 0 0
01_结构力学——矩阵位移法1
kij 表示 u j 1 引起的杆端力Fi 的大小。
15 / 48
第十三章 矩阵位移法 第二节 单元分析（局部坐标系下的单元分析 ）
3、局部坐标系中的单元刚度矩阵性质
EA 1 1 k11 k12 k l 1 1 k21 k22
1、矩阵位移法的基本思路 b、基本假设和基本原理
线弹性、小变形。满足叠加原理、功能原理
c、正负号规定（采用右手法则）
杆端内力规定当与坐标轴正方向一致时为正；
杆端位移和结点位移规定当与坐标轴正方向一致时为正。
结点外力规定当与坐标轴正方向一致时为正；
8 / 48
第十三章 矩阵位移法 第一节 矩阵位移法概述
杆端内力：
u1 , u2
F1 , F2
13 / 48
第十三章 矩阵位移法 第二节 单元分析（局部坐标系下的单元分析 ）
2、局部坐标系中的单元刚度矩阵
EA u1 l EA u2 l
F1e
u1
1 1
EA EA
e
e
2 2
u2
EA u1 l EA u2 l
局部坐标 系下的单 刚方程
e
EA e EA e u1 u2 l l
法
杆件端点位移 结构结点位移
位移法
法 需要选择基本体系和多余约束。所以较多地依赖于结构的具 体情况，不宜实现计算机计算的自动化，但其优点是计算出 的结果就是力。 位移法 是先求结点位移，再换算成力，该法的计算自动化和通用性强， 目前广为采用。 7 / 48 力
第十三章 矩阵位移法 第一节 矩阵位移法概述
x
第十三章 矩阵位移法 第六节 连续梁受力分析
第六节
M1
连续梁受力分析
M2
iபைடு நூலகம் l
P K 目标：建立整体刚度方程
1 i1 l 2
3 M3
按自然位置选每跨为一个单元。分别给单元和结点编号。 选基本未知量为支座转角位 结点力： 结点位移： 移 ，它们可以用基本结构 1 M 1 中的附加约束加以指定，组 成整体结点位移向量{}， Δ 2 P M 2 附加约束力向量{P}。
1
2
1 2 4 i 2 i 2 2
2 21
2 2 2 2 i 4 i 21 2 2
牛顿第三定律 M1
1 1 4 i 2 i 11 1 2
M2
1 1 2
2 21
1 1
2 i 4 i 2 2
1 11
4 i 2 i
2 221 2 2
2 i 4 i
K K P F F F F R R F 该方法改变了刚度方程的排列顺序，破 0 坏了刚度矩阵的带形特征，仅适合于手 R 1 K P 算。电算应避免改变原行列位置。 F FF F 从而可求出{F}和{PR} K P R F F R
2 2 2 F k
84 1 / 6 1 / 2 4 8 11 / 24 3
1/2 M 6 19/4 3
7/4
Q
14
第六节
P1 1
1 P2 2
连续梁受力分析
Pnn
多跨连续梁的总刚方程
连续梁受力分析
对于复杂结构，传统位移法将非常繁琐且不宜模式化， 为使计算过程纳入一种统一的模式，一般均采用单元集 成法，或称直接刚度法。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
0 12 EI l 6 EI l
2 3
-
6 EI l 2 EI l
一个具有相同的行数和列数的矩阵，即m=n 时，称为 n 阶方阵。
3、行矩阵和列矩阵
一个单独的行组成的矩阵称为行矩阵，如：
a12 a13 · · · a1n
a11 ê a ê 21 A= ê ê┇ ê ê m1 a
A= a11
[
]
由单列组成的矩阵称为列矩阵，如：
2013-4-20
第十三章
§13-1 概
矩 阵 位 移 法
述
进入 进入
§13-2 单元刚度矩阵(局部座标) §13-3 单元刚度矩阵(整体座标 系) §13-4 连续梁的整体刚度矩阵 §13-5 刚架的整体刚度矩阵 §13-6 等效结点荷载 §13-7计算步骤和算例
进入 进入
进入
进入 进入
§13-8忽略轴向变形时矩形刚架的整体分析
(e)
Y2
X1 Y1 M1 = X2 Y 2 M 2
(e)
(e)
F
(e)
凡是符号上面带了一横杠的就表示是基于局部座标系而言的。
2013-4-20 9
§13-2
单元刚度矩阵(局部座标系)
进行单元分析，推导单元刚度方程和单元刚度矩阵。 现在讨论单元刚度方程。单元刚度方程是指由单元杆端位移求单元杆 端力时的一组方程，可以用“ F ”表示，由位移求力称为正问题。
0 1 0 0
0 0 O 0
0 0 0 1
任意矩阵与单位矩阵相乘仍等于原矩阵，即 AI =A
2013-4-20
IA =A
5
10、逆矩阵 在矩阵运算中，没有矩阵的直接除法， 除法运算由矩阵求逆来完成。例如，若 此处 A-1 则 AB =C 称为矩阵 A 的逆矩阵。
B=A 1 C
从力学上的理解是，根据单元刚度方程
F
e
= k
e
e
F
e e
F
e
有一组力的解答(唯一的)，即正问题。 如果 F
由
2013-4-20
e
e
不是一组平衡力系则无解；若是一
14
组平衡力系，则解答不是唯一的，即反问题。
三、特殊单元
以连续 梁为例：
若单元六个杆端位移中有某一个或几个已知为零，则该
一、一般单元
在单元两端加上人为控制的附加约束，使基本杆单元的两端产生任意指
定的六个位移，然后根据这六个杆端位移来推导相应的六个杆端力。 1
v1
X1
e
M1
2
e
2
e
u1
1
e M
2
v2
X
Y1
e
e
2
u2
我们忽略轴向受力状态和弯曲受力状态之间的相互影响，分别推导轴向
2013-4-20 变形和弯曲变形的刚度方程。 10
用矩阵形式表示位 移法基本方程
7
二、杆端位移、杆端力的正负号规定
一般单元： 指杆件除有弯曲变形外，还有轴向变形和剪切变形的单元， 杆件两端各有三个位移分量，
这是平面结构杆件单元的一般情况。
符号规则：图(a)表示单元编号、杆端编号和局部座标，局部座标的 x 座标与杆轴重合；图(b)表示的杆端位移均为正方向。 1 (a)
其转置矩阵为
a11 a21 a31 A = a12 a22 a32
T
当连乘矩阵的乘积被转置时，等于倒转了顺序的各矩阵的转置 矩阵之乘积。若
A=B C D
则
7、零矩阵
AT =DT CT BT
元素全部为零的矩阵称为零矩阵，用0表示。 若 AB=0， 但不一定 A=0 或 B=0。
2013-4-20
e
v2 = 0
0 6 EI l 4 EI l 0 EA l
2
e
6 EI 2 l 2 EI l 0 6 EI 2 l 4 EI l 0
0 12 EI l 6 EI l
2 3
-
EA l 0 0 -
0 12 EI l 6 EI l 0 12 EI l 6 EI l
Y2
e
分别推导轴向变形和弯曲变形的刚度方程。
X1
e
u1
M1
e
e
M2
e
X
e Y
1
e
2
u2
Y2
e
首先，由两个杆端轴向位移 u 1 和 u 2 可推算出相应的杆端轴向力 X 1e和 X 2 e e 1 2
X1
e
u1
X
1
u2
= EA l = -
X
M
e
2
u 1
- u2
X
EA l
2
u 1
- u 2
进入
§13-8桁架及组合结构的整体分析
进入
2013-4-20
1
矩阵代数复习
1、矩阵定义 一组元素按行、列次序排列成的矩形阵列称为矩阵。若矩阵 的元素排列为m 行和n列，称为mn 阶矩阵。
a11 a12 a21 a22 A= M am1 am2
2、方阵
L a1n a2 n L O M L amn
单元称为特殊单元，其刚度方程是一般单元刚度方程的特例。
e
1
u1 = 0
1
v1 = 0
e
2
2
u2 = 0
X1 EA l Y1 0 0 M1 = EA X 2 l 0 Y2 0 2013-4-20 M 2
u1 v1 1 u 2 v2 2
e
12
上面的式子可以用矩阵符号记为 通过这个式子由单元杆端位移 (1)
u1 = 1
F
e
= k
e
e
这就是局部座标系中的单元刚度方程。
1
M
2
其次，由杆端横向位移 v 1 , v 2 和转角
1 , 2 ,
Y1 Y2
可以用角变位移方程推导出相应的杆端
横向力 Y 1 e, Y 2 e 和杆端力矩
2013-4-20
M
1
e,M e
2
2 l l l 2 EI 4 EI 6 EI v1 - v 2 = 1 2 2 l l l 6 EI 12 EI 1 2 3 v 1 - v 2 = 2 l l 6 EI 12 EI 1 2 - 3 v 1 - v 2 = 2 l l = 4 EI
2 ×1
非 共形
b11 a11 a12 B A= ê ê b21 a21 a22
2 ×1 2 ×2
（2）不具有交换律，即
2013-4-20
AB BA
3
6、转置矩阵
将一个阶矩阵的行和列依次互换，所得的阶矩阵称之为
原矩阵的转置矩阵，如：
a11 a12 A= a21 a22 a31 a32
e
e
0 12 EI l 6 EI l
2 3
0 6 EI l 4 EI l 0 6 EI l 2 EI l
2 2
-
EA l 0 0 EA l -
0 12 EI l 6 EI l 0 12 EI l 6 EI l
2 3 2 3
0 12 EI l 6 EI l
2 3
0 0
-
6 EI 2 l 2 EI l 0 6 EI 2 l 4 EI l 0
1
2 EI
2
6 EI
v1
- v2
X1 EA l Y1 0 0 M1 = EA X 2 l 0 Y2 0 2013-4-20 M 2
y
EAI
2
e
l
1
u1
x
单元编号 杆端编号 局部座标 杆端位移编号
(b)
1
v1
2
2
u2
v2
(c) X 1 2013-4-20
1 M1
Y1
2
M2
X
2
杆端力编号
8
Y2
（1）单元杆端位移向量
1
u1
（2）单元杆端力向量
1 M1
X1
1
v1
(1) ( 2 ) ( 3) = ( 4 ) ( 5) ( 6)
4
8、 对 角 矩 阵
对角矩阵是除主对角元素外，其余元素全为零的方阵，如：
a 11 0 D= 0 0
0 a 22 0 0
0 0 O 0
0 0 0 a mm
9、 单 位 矩 阵
单位矩阵是一个对角矩阵，它的非零元素全为 1 用 I 表示 ，如
1 0 I = 0 0
e (3) k = (4)
(5)
2013-4-20
0
EA l 0 0
2EI l
0 -6EI l2
只与杆件本身性质有 关而与外荷载无关
0 0
-12EI -6EI l3 l2 6EI l2 2EI l
(6)
4EI l
13
二、单元刚度矩阵的性质
（1）单元刚度系数的意义
k ij —代表单元杆端第j个位移分量等于1时所引起的第i个杆端力分量。