中考数学单元达标测试(四)(第6章)新人教版
2024年江西中考数学中考模拟卷(四)及参考答案
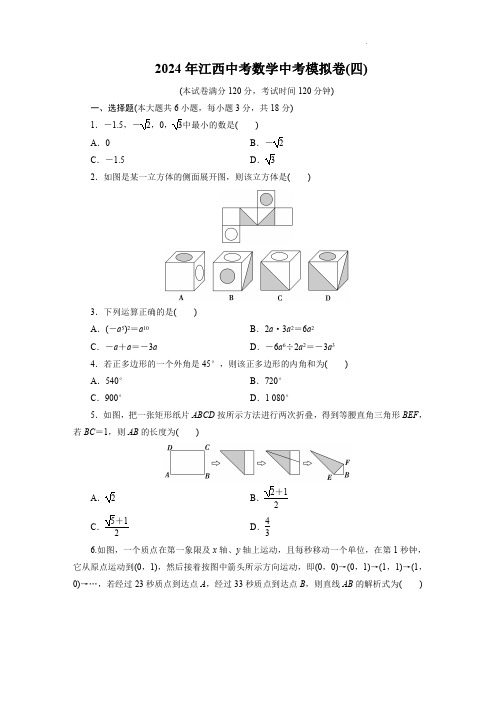
2024年江西中考数学中考模拟卷(四)(本试卷满分120分,考试时间120分钟)一、选择题(本大题共6小题,每小题3分,共18分)1.-1.5,-2,0,3中最小的数是()A .0B .-2C .-1.5D .32.如图是某一立方体的侧面展开图,则该立方体是()3.下列运算正确的是()A .(-a 5)2=a 10B .2a ·3a 2=6a 2C .-a +a =-3aD .-6a 6÷2a 2=-3a 34.若正多边形的一个外角是45°,则该正多边形的内角和为()A .540°B .720°C .900°D .1080°5.如图,把一张矩形纸片ABCD 按所示方法进行两次折叠,得到等腰直角三角形BEF ,若BC =1,则AB 的长度为()A .2B .2+12C .5+12D .436.如图,一个质点在第一象限及x 轴、y 轴上运动,且每秒移动一个单位,在第1秒钟,它从原点运动到(0,1),然后接着按图中箭头所示方向运动,即(0,0)→(0,1)→(1,1)→(1,0)→…,若经过23秒质点到达点A ,经过33秒质点到达点B ,则直线AB 的解析式为()A .y =12x +92B .y =-12x +92C .y =2x +9D .y =-2x +9二、填空题(本大题共6小题,每小题3分,共18分)7.因式分解:4a -4a 2-1=_________________________.8.(2023·抚州模拟)某品牌手机内部的A16芯片加入光线追踪功能,将宽度压缩到0.000000005米.将数字0.000000005用科学记数法表示为________.9.若关于x 的一元二次方程x 2+2x -k =0无实数根,则k 的取值范围是________________.10.如图,已知△ABC 是等边三角形,AD 是中线,E 在AC 上,AE =AD ,则∠EDC =________.11.已知一组数据x ,-2,4,1的中位数为1,则其方差为________.12.如图,在△ABC 中,∠ACB =90°,AC =BC =2,D 是边AC 的中点,CE ⊥BD 于E .若F 是边AB 上的点,且使△AEF 为等腰三角形,则AF 的长为________.三、解答题(本大题共5小题,每小题6分,共30分)13.(1)x -5<x +1,x -1)≥3x -4,并把它的解集在数轴上表示出来;(2)如图,在菱形ABCD 中,∠D =60°,E 是AD 上一点,M ,N 分别是CE ,AE 的中点,且MN =2,求菱形ABCD 的周长.14÷x 2-xx +1的过程:·x +1x (x -1)①·x +1x (x -1)②=x (2-x )x (x -1)③(1)小华的解答过程在第________步出现错误.(2)请你帮助小华写出正确的解答过程,并计算当x =5时分式的值.15.小惠家大门进门处有一个三位单极开关,如图,每个开关分别控制着A(楼梯),B(客厅),C(走廊)三盏电灯,其中走廊的灯已坏(对应的开关闭合也没有亮).(1)若小惠任意闭合一个开关,“客厅灯亮了”是________事件;若小惠闭合所有三个开关,“楼梯,客厅,走廊灯全亮了”是________事件;(填“不可能”“必然”或“随机”)(2)若任意闭合其中两个开关,试用画树状图或列表的方法求“客厅和楼梯灯都亮了”的概率.16.如图,点C是以AB为直径的半圆O内任意一点,连接AC,BC,点D在AC上,且AD=CD,请仅用无刻度的直尺分别按下列要求画图(保留画图痕迹).(1)在图1中,画出△ABC的中线AE;(2)在图2中,画出△ABC的角平分线AF.17.某家具厂生产一种餐桌和椅子,已知一张餐桌的售价比一把椅子的售价多480元,购买一套桌椅(一张餐桌和四把椅子)共需1280元.(1)分别求出一张餐桌和一把椅子的售价;(2)某经销商计划从该家具厂购进一批桌椅,已知购进椅子的数量比餐桌的数量的3倍多15个,且餐桌和椅子的总数不超过120个.该经销商计划把一半餐桌成套(每张餐桌配四把椅子)销售,每套1600元,其余桌椅按每张餐桌1000元,每把椅子300元零售.设该经销商购进餐桌x张,销售完这批桌椅获得的利润为y元.请你帮该经销商设计一种获利最大的进货方案,并求出最大利润.四、解答题(本大题共3小题,每小题8分,共24分)18.为进一步推进学校安全教育,切实增强广大学生的安全防范意识和自护自救能力,某校举行了安全知识网络竞赛活动,测试满分100分.为了解八、九年级学生此次竞赛成绩的情况,分别随机在八、九年级各抽取了20名参赛学生的成绩,已知抽取得到的八年级的数据如下:80、95、60、80、75、60、95、65、75、70、80、75、85、65、90、70、75、80、85、80.(分数80分以上、不含80分为优秀).为了便于分析数据,统计员对八年级数据进行了整理,得到了如表和直方图:成绩等级分数(单位:分)学生数D等级60≤x≤70aC等级70<x≤809B等级80<x≤90bA等级90<x≤1002八、九年级成绩的平均数、中位数如表:年级平均数中位数八年级77c九年级78.582.5(1)根据题目信息填空:a=________,b=________,c=________;补全八年级的频数分布直方图.(2)八年级小宇和九年级小乐的分数都为80分,请判断小宇、小乐在各自年级的排名哪位更靠前?请简述你的理由.(3)若九年级学生成绩的优秀率是八年级的两倍,且九年级共有600人参加参赛,请估计九年级获得优秀的学生人数.19.如图,一次函数y =ax +b 的图象与反比例函数y =kx 的图象交于A (2,2),B 两点.(1)求反比例函数与一次函数的关系式;(2)C 为y 轴负半轴上一动点.作CD ∥AB 交x 轴交于点D ,交反比例函数的图象于点E .当D 为CE 的中点时,求点C 的坐标.20.图1是某工厂生产的某种多功能儿童车,根据需要可变形为滑板车或三轮车,图2,图3是其示意图,已知前后车轮半径相同,车杆AB 的长为60cm ,点D 是AB 的中点,前支撑板DE =30cm ,后支撑板EC =40cm ,车杆AB 与BC 所成的∠ABC =53°.sin 53°≈45,cos 53°≈35,tan 53(1)如图2,当支撑点E 在水平线BC 上时,求支撑点E 与前轮轴心B 之间的距离BE 的长.(2)如图3,当座板DE 与地平面保持平行时,问变形前后两轴心BC 的长度有没有发生变化?若不变,请通过计算说明;若变化,请求出变化量.五、解答题(本大题共2小题,每小题9分,共18分)21.如图,在Rt △ABC 中,∠ABC =90°,以AB 为直径作⊙O ,交AC 于点E ,点D 为⊙O 上一点,且CD =CB .连接DO 并延长交CB 的延长线于点F .(1)求证:CD 是⊙O 的切线.(2)若AB =CB =6,连接BE .①求图中阴影部分的面积;②求DF 的长.22.如图,在等腰三角形ABC 中,∠BAC =90°,点A 在x 轴上,点B 在y 轴上,点C (3,1),二次函数y =13x 2+bx -32的图象经过点C .(1)求二次函数的解析式,并把解析式化成y=a(x-h)2+k的形式.(2)把△ABC沿x轴正方向平移,当点B落在抛物线上时,求△ABC扫过区域的面积.(3)在抛物线上是否存在异于点C的点P,使△ABP是以AB为直角边的等腰直角三角形?如果存在,请求出所有符合条件的点P的坐标;如果不存在,请说明理由.六、解答题(本大题共12分)23.我们把两条中线互相垂直的三角形称为“中垂三角形”.例如在图1,图2,图3中,AF,BE是△ABC的中线,AF⊥BE,垂足为P.像△ABC这样的三角形均为“中垂三角形”.设BC=a,AC=b,AB=c.特例探索:(1)①如图1,当∠ABE=45°,c=42时,a=________,b=________;②如图2,当∠ABE=30°,c=2时,求a和b的值.归纳证明:(2)请你观察(1)中的计算结果,猜想三者之间的关系,用等式表示出来,并利用图3证明你发现的关系式.(3)利用(2)中的结论,解答下列问题:在边长为3的菱形ABCD中,O为对角线AC,BD 的交点,E,F分别为线段AO,DO的中点,连接BE,CF并延长交于点M,BM,CM分别交AD于点G,H,如图4所示,求MG2+MH2的值.2024年江西中考数学中考模拟卷(四)答案1.C ∵-1.5<-2<0<3,∴最小的数是-1.5.2.D两个圆所在的面是相对的,不相邻,故A 错误;B ,C 中空白的圆圈不与白色的三角形相邻,故B ,C 错误;D.正确.3.AA.(-a 5)2=a 10,故正确;B.2a ·3a 2=6a 3,故错误;C.-2a +a =-a ,故错误;D.-6a 6÷2a 2=-3a 4,故错误.4.D正多边形的边数为360°÷45°=8,则这个多边形是正八边形,所以该正多边形的内角和为(8-2)×180°=1080°.5.A由折叠补全图形如图所示.∵四边形ABCD 是矩形,∴∠ADA ′=∠B =∠C =∠A =90°,AD =BC =1,CD =AB .由第一次折叠得∠DAE =∠A =90°,∠ADE =12∠ADC =45°,∴∠AED =∠ADE =45°,∴AE =AD =1.在Rt △ADE 中,根据勾股定理得,DE =2AD = 2.由第二次折叠可知,DC =DE ,∴AB = 2.6.B 3秒时到了(1,0);8秒时到了(0,2);15秒时到了(3,0);24秒到了(0,4);35秒到了(5,0);∴23秒到了(1,4),33秒到了(5,2),∴A (1,4),B (5,2).设直线AB 的解析式为y =kx +b ,+b=4,k+b=2,=-12,=92,∴直线AB的解析式为y=-12x+92.7.解析:原式=-(4a2-4a+1)=-(2a-1)2.答案:-(2a-1)28.解析:0.000000005=5×10-9.答案:5×10-99.解析:∵a=1,b=2,c=-k,由题意知,Δ=b2-4ac=22-4×1×(-k)=4+4k<0,解得k<-1.答案:k<-110.解析:∵AD是等边△ABC的中线,∴AD⊥BC,∠BAD=∠CAD=12∠BAC=12×60°=30°,∴∠ADC=90°.∵AD=AE,∴∠ADE=∠AED=12(180°-∠)=75°,∴∠EDC=∠ADC-∠ADE=90°-75°=15°.答案:15°11.解析:∵数据x,-2,4,1的中位数为1,∴①当这样排列时,x,-2,1,4,中位数不是1,舍去;②当这样排列时,-2,x,1,4,中位数为1,则x+12=1,解得x=1,③当这样排列时,-2,1,4,x,中位数不是1,舍去.综上,数据为-2,1,1,4,∴数据的平均数=-2+1+1+44=1,∴方差=(-2-1)2+2×(1-1)2+(4-1)24=92.答案:9212.解析:∵∠ACB =90°,AC =BC =2,D 是AC 的中点,∴AB =22,AD =CD =1,∴BD =5,∴CE =CD ·BC BD =255.∵∠DCB =90°,CE ⊥BD ,∴△CDE ∽△BDC ,∴CD 2=DE ·DB .∵AD =CD ,∴AD 2=DE ·DB ,∴AD DE =DB AD.∵∠ADE =∠ADB ,∴△DAE ∽△DBA ,∴AE AB =AD BD =55,∴AE =2105.∵DE =55,BD =5,∴BE =455.如图1中,若AE =AF 时,∴AF =2105.如图2中,若FE =AE 时,过点E 作EJ ⊥AB 于J .∵JE 2=AE 2-AJ 2=EB 2-BJ 2,∴4025-AJ 2=8025-(22-AJ )2,∴AJ =425.∵AE =EF ,EJ ⊥AF ,∴AF =2AJ =825.如图3中,若EF =AF 时,过点E 作EJ ⊥AB 于J .∵EJ 2=AE 2-AJ 2=EF 2-FJ 2,∴4025-3225=AF 2,∴AF =22.综上所述,AF 的长为2105或825或22.答案:2105或825或2213.解:x -5<x +1x -1)≥3x -4,②解不等式①,得x <3.解不等式②,得x ≥-2.所以原不等式组的解集为-2≤x <3.在数轴上表示如下:(2)如图,连接AC .∵M ,N 分别是CE ,AE 边的中点,∴MN 是△ACE 的中位线,∴AC =2MN =4.∵四边形ABCD 是菱形,且∠D =60°,∴AD =CD ,∴△ACD 为等边三角形,∴CD =AC =4,∴C 菱形ABCD =4CD =16,∴菱形ABCD 的周长为16.14.解:(1)小华的解答过程在第②步出现错误,在运算去括号时没有变号,·x +1x (x -1)故答案为②.(2)÷x (x -1)x +1=x x +1-x 2+x x +1·x +1x (x -1)·x +1x (x -1)=-x 2x +1·x +1x(x -1)=-x x -1,当x =5时,原式=-55-1=-54.15.解:(1)若小惠任意闭合一个开关,“客厅灯亮了”是随机事件.∵走廊的灯已坏,∴若小惠闭合所有三个开关,“楼梯,客厅,走廊灯全亮了”是不可能事件,故答案为随机;不可能.(2)设客厅灯亮了为事件A ,楼梯灯亮了为事件B ,走廊灯亮了为事件C ,则树状图如下:∴共有6种结果,其中“客厅灯和楼梯灯亮了”的有2种,∴P (客厅灯和楼梯灯都亮了)=26=13.16.解:(1)如图1,线段AE 即为△ABC 的中线.根据三角形三条中线交于一点即可证明.(2)如图2,线段AF 即为△ABC 的角平分线.证明:∵OA =OH ,∴∠HAO =∠H .∵点O 是AB 的中点,点E 是BC 的中点,∴OE 是△ABC 的中位线,∴OE ∥AC ,∴∠CAH =∠H ,∴∠CAF =∠BAF ,∴AF 为△ABC 的角平分线.17.解:(1)设一张餐桌和一把椅子的售价分别为a 元、b 元.-b =480,+4b =1280,=640,=160.答:一张餐桌和一把椅子的售价分别为640元、160元.(2)由题意得x +3x +15≤120,解得x ≤2614.由题意得y =x 2×1600+x 2×1000x +15-x 2×4-640x -(3x +15)×160=800x +500x +300x +4500-640x -480x -2400=480x +2100.∵480>0,∴y 随x 的增大而增大,∴当x =26时,y 取最大值,最大值为14580,此时3x +15=93.答:当购进26张餐桌,93把椅子时,销售完这批桌椅所获利润最大,最大利润为14580元.18.解:(1)根据频数统计的方法可得,成绩在60≤x ≤70的有6人,即a =6,成绩在80<x ≤90的有3人,即b =3,八年级20名学生成绩从小到大排列,处在中间位置的两个数的平均数为75+802=77.5(分),因此中位数是77.5,即c =77.5,补全图形如下:故答案为:6,3,77.5.(2)八年级小宇的排名更靠前.理由如下:因为八年级的中位数是77.5,九年级的中位数是82.5,所以八年级小宇和九年级小乐的分数都为80分,小宇的排名更靠前.(3)3+220×2×600=300(人),∴九年级获得优秀的学生人数为300人.19.解:(1)∵反比例函数y =k x的图象过点A (2,2),∴k =2×2=4,∴反比例函数的解析式为y∵反比例函数y =4x过点∴m =8,∴8∴把A ,B =2a +b ,-12=-8a +b ,=14,=32,∴一次函数解析式为y =14x +32.(2)∵CD ∥AB ,∴设直线CD 的解析式为y =14x -n (n >0).令x =0,则y =-n ,∴C (0,-n ),∴OC =n .∵D 为CE 的中点,∴E 的纵坐标为n ,代入y =14x -n (n >0),求得x =8n ,∴E (8n ,n ).∵反比例函数过点E ,∴n =48n,∴n =22(负数舍去),∴20.解:(1)如图1,过点D 作DF ⊥BE 于点F .由题意知BD =DE =30cm ,∴BF =BD cos ∠ABC ≈30×35=18(cm),∴BE =2BF =36(cm).答:BE 的长为36cm.(2)如图2,过点D 作DM ⊥BC 于点M ,过点E 作EN ⊥BC 于点N .由题意知四边形DENM 是矩形,∴MN =DE =30cm.在Rt △DBM 中,BM =BD cos ∠ABC ≈30×35=18(cm),EN =DM =BD sin ∠ABC ≈30×45=24(cm).在Rt △CEN 中,CE =40cm ,∴由勾股定理可得CN =EC 2-EN 2=402-242=32(cm),则BC =18+30+32=80(cm),原来BC =36+40=76(cm),80-76=4(cm),∴变形前后两轴心BC 的长度增加了4cm.21.(1)证明:如图1,连接OC .在△OCB 与△OCD 中,=CD ,=CO ,=OD ,∴△OCB ≌△OCD (SSS),∴∠ODC =∠OBC =90°,∴OD ⊥DC ,∴DC 是⊙O 的切线.(2)解:①如图2,连接OE .∵AB =CB =6,AB 为⊙O 的直径,∴∠AEB =90°,AE =EC ,∴OE =12BC =3,OE ∥BC ,∴OE =OB =3,∠EOB =90°,∴阴影部分的面积=S 扇形EOB -S △EOB =90π×32360-12×3×3=9π4-92②∵AB =CB =6,CD =CB ,∴CD =6.∵∠FBO =∠FDC =90°,∠F =∠F ,∴△FBO ∽△FDC ,∴OB CD =BF DF ,∴BF DF =12.设BF =x ,DF =2x ,∴OF =2x -3.∵OF 2=OB 2+BF 2,∴(2x -3)2=32+x 2,∴x =4,x =0(不合题意,舍去),∴BF =4,∴DF =8.22.解:(1)将点C (3,1)代入二次函数解析式y =13x 2+bx -32,可得3+3b -32=1,解得b =-16,故解析式为y =13x 2-16x -32,y =13x 2-16x -32=-7348.(2)作CK ⊥x 轴,如图.由题意可得∠BOA =∠CKA =∠BAC =90°,AB =AC ,OK =3,CK =1,∴∠BAO +∠CAK =∠BAO +∠OBA =90°,∴∠ABO =∠KAC ,∴△ACK ≌△BAO (AAS),∴OB =AK ,OA =CK =1,∴OB =AK =OK -OA =2,∴点B (0,2),A (1,0),则AB =OA 2+OB 2= 5.令13x 2-16x -32=2,解得x =72或x =-3(舍去),即ABC 向右平移的距离为72,即AE =72.由题意可得△ABC 扫过区域的面积为平行四边形ABDE 和△ABC 的面积和,即S ▱ABDE +S △ABC =AE ×OB +12AC ×AB =72×2+12×5×5=9.5.(3)当∠BAP =90°时,由题意可得AB =AP =AC ,∠BAC =∠BAP =90°,∴△BAP ≌△BAC (SAS).又∵A (1,0),C (3,1)∴P (-1,-1).当x =-1时,y =13+16-32=-1,点P (-1,-1)在抛物线上.当∠ABP =90°时,同理可求得P (-2,1)或P (2,3),当x =-2时,y =13×4+16×2-32≠1,P (-2,1)不在抛物线上,当x =2时,y =13×4-16×2-32≠1,P (2,3)不在抛物线上.综上所述,存在点P (-1,-1),使△ABP 是以AB 为直角边的等腰直角三角形.23.解:如图1,图2,图3,连接EF ,则EF 是△ABC 的中位线,则EF =12AB ,EF ∥AB ,∴△EFP ∽△BPA ,∴PB PE =PA PF =AB EF=2.(1)①如图1,在直角三角形ABP 中,PA =PB =AB sin 45°=4,∴PE =PF =2,∴a =b =2BF =2PB 2+PF 2=4 5.②如图2,在直角三角形ABP 中,PA =AB sin 30°=1,PB =AB cos 30°=3,∴PE =12PB =32,PF =12PA =12,则a =2BF =2PB 2+PF 2=13,b =2AE =2PA 2+PE 2=7.(2)关系为a 2+b 2=5c 2,证明:如图3,PF =12PA ,PE =12PB ,则a 2+b 2=(2BF )2+(2AE )2=4(BF 2+AE 2)=4(BP 2+PF 2+AP 2+PE 2)=2+54AP =5(BP 2+AP 2)=5c 2.(3)如图4,连接EF .在菱形ABCD 中,E ,F 分别为线段AO ,DO 的中点,则EF =12BC =12AD .∵AE =OE =13EC ,AG ∥BC ,∴AG =13BC =13AD .同理HD =13AD ,∴GH =13AD ,∴GH =23EF .∵GH ∥BC ,EF ∥BC ,∴HG ∥EF ,∴MG =23ME =13MB .同理MH =13MC ,则MG 2+MH 2=19(MB 2+MC 2)=19×5×BC 2=5.。
人教版初中数学九年级数学上册第四单元《圆》测试(包含答案解析)

一、选择题1.如图,在平面直角坐标系中,P 是直线y =2上的一个动点,⊙P 的半径为1,直线OQ 切⊙P 于点Q ,则线段OQ 的最小值为( )A .1B .2C .3D .52.如图,,AB AC 分别是O 的直径和弦,OD AC ⊥于点,D 连接,BD BC .若10,8AB AC ==,则BD 的长是( )A .25B .4C .213D .2453.如图,四个水平放置正方形的边长都为4,顶点A 、B 、C 是圆上的点,则此圆的面积为( )A .72πB .85πC .100πD .104π 4.点P 到圆上各点的最大距离为10cm ,最小距离为6cm ,则此圆的半径为( )A .8cmB .5cm 或3cmC .8cm 或2cmD .3cm 5.如图,一条公路的拐弯处是一段圆弧AB ,点O 是这段弧所在的圆的圆心,20cm AB =,点C 是AB 的中点,点D 是AB 的中点,且5cm CD =,则这段弯路所在圆的半径为( )A .10cmB .12.5cmC .15cmD .17cm 6.在平面直角坐标系中,以点()3,4-为圆心,半径为5作圆,则原点一定( ) A .与圆相切 B .在圆外 C .在圆上 D .在圆内 7.下列事件属于确定事件的为( )A .氧化物中一定含有氧元素B .弦相等,则所对的圆周角也相等C .戴了口罩一定不会感染新冠肺炎D .物体不受任何力的时候保持静止状态 8.如图,⊙O 的直径12CD =,AB 是⊙O 的弦,AB CD ⊥,垂足为P ,:1:2CP PO =,则AB 的长为( )A .45B .215C .16D .89.如图,A 、B 、C 三点在O 上,D 是CB 延长线上的一点,40ABD ∠=︒,那么AOC ∠的度数为( ).A .80°B .70°C .50°D .40° 10.如图,⊙O 的半径为2,四边形ADBC 为⊙O 的内接四边形,AB =AC ,∠D =112.5°,则弦BC 的长为( )A .2B .2C .22D .23 11.如图,大半圆中有n 个小半圆,若大半圆弧长为1L ,n 个小半圆弧长的和为2L ,大半圆的弦AB ,BC ,CD 的长度和为3L .则( )A .123L L L =>B .123L L L =<C .无法比较1L 、2L 、3L 间的大小关系D .132L L L >>12.如图,ABC 的顶点A 是O 上的一个动点,90ACB ∠=︒,30BAC ∠=︒,边AC ,AB 分别交O 于点E ,D ,分别过点E ,D 作O 的切线交于点F ,且点F 恰好在边BC 上,连接OC ,若O 的半径为6,则OC 的最大值为( )A 393B .2103C .353D .53二、填空题13.如图,在扇形AOB 中,90AOB ∠=︒正方形CDEF 的顶点C 是弧AB 的中点,点D 在OB 上,点E 在OB 的延长线上,当正方形CDEF 的边长为2时,阴影部分的面积为_______.14.如图,等腰直角△ABC中,∠BAC=90°,AB=AC=4.平面内的直线l经过点A,作CE⊥l 于点E,连接BE.则当直线l绕着点A转动时,线段BE长度的最大值是________.15.已知O的面积为π,则其内接正六边形的边长为______.16.如图,△ABC中,∠A=60°,若O为△ABC的内心,则∠BOC的度数为______度.17.已知,O的弦AB与O的半径相等,则弦AB所对的圆周角的度数为______.18.如图,AB是⊙O的直径,C是BA延长线上一点,点D在⊙O上,且CD=OA,CD的延长线交⊙O于点E,若∠BOE=54°,则∠C=______.19.如图,AB是O的直径,CD是O的弦,AB、CD的延长线交于点E,已知∠的度数为______︒.=,若CODAB DE2∆为直角三角形,则E20.如图,△ABC内接于O,∠BAC=45°,AD⊥BC于D, BD=6,DC=4,则AD的长是_____.三、解答题21.在平面直角坐标系中,ABC 的三个顶点分别为()5,2A -,()1,2B -,()4,5C -.(1)画出ABC 关于原点成中心对称的图形111A B C △,并写出点1B 的坐标; (2)将ABC 绕点B 顺时针旋转90°,求旋转过程中点A 走过的路径长.22.如图所示,AB 是⊙O 的直径,AC 是⊙O 的弦,∠ACB 的平分线交⊙O 于点D .若AB =10,AC =6,求BC 、BD 的长.23.已知:△ABC .(1)求作:△ABC 的外接圆⊙O (要求:尺规作图,保留作图痕迹,不写作法);(2)若已知△ABC 的外接圆的圆心O 到BC 边的距离OD =8,BC =12,求⊙O 的半径.24.如图,已知直线PT 与⊙O 相交于点T ,直线PO 与⊙O 相交于A 、B 两点,已知PTA B ∠=∠.(1)求证:PT 是⊙O 的切线;(2)若3PT BT ==,求图中阴影部分的面积. 25.如图,在Rt △ABC 中,∠C =90°,以BC 为直径的圆O 交AB 于点D ,切线DE 交AC 于点E .(1)求证:∠A =∠ADE ;(2)若AD =8,DE =5,求BC 的长.26.如图,AB 为O 的直径,C 为O 上一点,AD 和过点C 的切线互相垂直,垂足为D .(1)求证:AC 平分DAB ∠;(2)若4CD =,8AD =,试求O 的半径.【参考答案】***试卷处理标记,请不要删除一、选择题1.C解析:C【分析】连接PQ 、OP ,如图,根据切线的性质得:PQ ⊥OQ ,再利用勾股定理得出OQ ,利用垂线段最短,当OP 最小时,OQ 最小,即可求解.【详解】连接PQ 、OP ,如图,∵直线OQ 切⊙P 于点Q ,∴PQ ⊥OQ ,在直角OPQ △中,2221OQ OP PQ OP =-=-,当OP 最小时,OQ 最小,当OP ⊥直线y =2时,OP 有最小值2,∴OQ 的最小值为2213-=,故选:C .【点睛】本题考查了切线的性质:圆的切线垂直于经过切点的半径,也考查了勾股定理,熟练掌握切线的性质以及勾股定理是解答本题的关键.2.C解析:C【分析】先根据圆周角定理得∠ACB=90°,则利用勾股定理计算出BC=6,再根据垂径定理得到CD=AD=12AC=4,然后利用勾股定理计算BD 的长. 【详解】解:∵AB 为直径,∴∠ACB=90°, ∴22221086BC AB AC =-=-=,∵OD ⊥AC , ∴CD=AD=12AC=4, 在Rt △CBD 中,222246213BD BC CD =++=故选:C .【点睛】本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.也考查了垂径定理.3.B解析:B【分析】连接BC,作AB,BC的垂直平分线,交点为点O,连接OB,OC,根据垂直平分线可得AE=BE=2,DE=4×4=16,DC=4+2=6,设OD=x,则OE=16-x,再根据OB=OC即可列出方程求得x=7,最后再根据圆的面积公式计算即可.【详解】解:如图,连接BC,作AB,BC的垂直平分线,交点为点O,连接OB,OC,则OB=OC,AE=BE=2,DE=4×4=16,DC=4+2=6,设OD=x,则OE=16-x,∵OB=OC,∴OB2=OC2,∴22+(16-x) 2=62+x2,解得x=7,∴r2=OB2=22+92=85,∴圆的面积S=πr2=85π,故选:B.【点睛】本题考查了作三角形的外心,垂径定理的应用,圆的面积公式,熟练掌握垂径定理是解决本题的关键.4.C解析:C【分析】分析题意,本题应分两种情况讨论:(1)点P在圆内;(2)点P在圆外;根据“一个点到圆的最大距离和最短距离都在过圆心的直线上”可知,点P到圆的最大距离与最小距离的和或差即是圆的直径,进而即可得出半径的长.【详解】当点P在圆内时,圆的直径是10+6=16cm,所以半径是8cm.当点P在圆外时,圆的直径是10-6=4cm,所以半径是2cm.故选C.【点睛】本题考查了圆的有关性质,熟知一个点到圆的最大距离和最短距离都在过圆心的直线上是解题的关键.5.B解析:B【分析】根据题意,可以推出AD=BD=10,若设半径为r,则OD=r﹣5,OA=r,结合勾股定理可推出半径r的值.【详解】解:∵OC⊥AB,AB=20,∴AD=DB=10,在Rt AOD中,OA2=OD2+AD2,设半径为r得:r2=(r﹣5)2+102,解得:r=12.5,∴这段弯路的半径为12.5,故选:B.【点睛】本题主要考查垂径定理的应用、勾股定理的应用,关键在于设出半径为r后,用r表示出OD、OA的长度.6.C解析:C【分析】设点(-3,4)为点P,原点为点O,先计算出OP的长,然后根据点与圆的位置关系的判定方法求解.【详解】解:∵设点(-3,4)为点P,原点为点O,∴OP5,而⊙P的半径为5,∴OP等于圆的半径,∴点O在⊙P上.故选:C.【点睛】本题考查了点与圆的位置关系:点的位置可以确定该点到圆心距离与半径的关系,反过来已知点到圆心距离与半径的关系可以确定该点与圆的位置关系.7.A解析:A【分析】根据确定事件的概念,可知需找出必然事件或不可能事件即可.【详解】A、氧化物是含有两种元素其中一种是氧元素的化合物,必然事件;B、在同圆或等圆中,弦相等所对的圆周角相等或互补,不确定事件;C、戴了口罩一定不会感染新冠肺炎,不确定事件;D、物体不受任何力的时候保持静止状态或匀速运动,不确定事件.故选A.【点睛】本题考查事件的划分,必然事件和不可能事件统称为确定事件,确定事件中,必然出现的事情称为必然事件;不可能出现的事情称为不可能事件.8.A解析:A【分析】连接OA,先根据⊙O的直径CD=12,CP:PO=1:2求出CO及OP的长,再根据勾股定理可求出AP的长,进而得出结论.【详解】连接OA,∵⊙O的直径CD=12,CP:PO=1:2,∴CO=6,PO=4,∵AB⊥CD,∴22-22OA OP-5,64⨯=∴AB=2AP=22545故选:A.【点睛】本题考查了垂径定理和勾股定理的应用,解决与弦有关的问题时,往往需构造以半径、弦心距和弦长的一半为三边的直角三角形,若设圆的半径为r,弦长为a,这条弦的弦心距为d,则有等式2222ar d⎛⎫=+⎪⎝⎭成立,知道这三个量中的任意两个,就可以求出另外一个.9.A解析:A【分析】作弧ABC所对的圆周角∠AEC,如图,先利用邻补角计算出∠ABC=140°,再利用圆内接四边形的性质计算出∠E=40°,然后根据圆周角定理得到∠AOC的度数.【详解】解:作弧ABC所对的圆周角∠AEC,∵∠ABD=40°,∴∠ABC=180°-40°=140°,∵∠AEC+∠ABC=180°,∴∠E=40°,∴∠AOC=2∠AEC=2×40°=80°.故选:A.【点睛】本题考查了圆内接四边形对角互补,以及圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.10.C解析:C【分析】如图:连接OB、O C,先根据圆的内接四边形对角互补得到∠C=67.5°,再利用等腰三角形的性质和三角形内角和计算出∠BAC=45°,再根据圆周角定理可得∠BOC=90°,最后根据勾股定理求解即可.【详解】解:∵四边形ADBC为⊙O的内接四边形,∠D=112.5°∴∠C=180°-∠D=180°-112.5°=67.5°∵AC=AB∴∠BAC=180°-2∠C=45°∴∠BOC=90°∴22222222OB OC+=+=故答案为C .【点睛】本题考查了圆内接四边形的性质、等腰直角三角形的性质和圆周角定理,掌握圆内接四边形的对角互补是解答本题的突破口.11.A解析:A【分析】利用圆周长公式计算1L 和2L 的长.根据圆周长公式分别写出1L 和2L 的表达式进行比较,再根据“两点之间线段最短的性质”得出13L L >,即可选出答案.【详解】解:设n 个小半圆半径依次为1r ,2r ,⋯,n r .则大圆半径为()12n r r r ++⋯+()112n L r r r π∴=++⋯+,212n L r r r πππ=++⋯+()12n r r r π=++⋯+,12L L ∴=;根据“两点之间线段最短的性质”可得:13L L >,123L L L ∴=>..故选A .【点睛】本题考查了半圆弧长的计算,两点之间线段最短的性质,是基础题,难度不大. 12.A解析:A【分析】先推出∠DOE=2∠DAE=60°,连接OE,OD,OF,证明Rt△EFO≌Rt△DFO,得到∠EOF=∠DOF=30°,根据EO=6,在Rt△EFO中,∠EOF=30°,得出EF=23,推出点C在以EF为直径的半圆上,设EF中点为G,得出当OC经过半圆圆心G时,OC最长,即OC的值最大,求出OG,CG即可得出答案.【详解】在△ABC中,∠ACB=90°,∠BAC=30°,∠DAE是DE所对的圆周角,∠DOE是DE所对的圆心角,∴∠DOE=2∠DAE=60°,连接OE,OD,OF,∵过点E,D作O的切线交于点F,∴∠FEO=∠FDO=90°,∴在Rt△EFO和Rt△DFO中EO DO FO FO=⎧⎨=⎩,∴Rt△EFO≌Rt△DFO(HL),∴∠EOF=∠DOF=30°,又∵EO=6,在Rt△EFO中,∠EOF=30°,∴EF=23又∵点F恰好是腰BC上的点,∠ECF=90°,∴点C在以EF为直径的半圆上,∴设EF中点为G,则EG=FG=CG=12EF=12×233,∴当OC经过半圆圆心G时,OC最长,即OC的值最大,在Rt△OEG中,OE=6,3∴22OE EG+39,∴393故选:A.【点睛】本题考查了圆周角定理,全等三角形的判定和性质,勾股定理,圆的性质,证明Rt△EFO≌Rt△DFO是解题关键.二、填空题13.π﹣2【分析】连结OC根据勾股定理可求OC的长根据题意可得出阴影部分的面积=扇形BOC的面积﹣三角形ODC的面积依此列式计算即可求解【详解】解:连接OC∵在扇形AOB中∠AOB=90°正方形CDEF解析:π﹣2【分析】连结OC,根据勾股定理可求OC的长,根据题意可得出阴影部分的面积=扇形BOC的面积﹣三角形ODC的面积,依此列式计算即可求解.【详解】解:连接OC,∵在扇形AOB中,∠AOB=90°,正方形CDEF的顶点C是弧AB的中点,∴∠COD=45°,∴OC=2CD=22,∴阴影部分的面积=扇形BOC的面积﹣三角形ODC的面积=245(22)360π⨯⨯﹣12×22=π﹣2.故答案为:π﹣2..【点睛】本题考查了扇形面积的计算以及正方形的性质,解题的关键是得到扇形半径的长度.14.【分析】以AC为直径作圆O连接BO并延长交圆O于点可得BO+O>B从而可得BO+OE>B即BE为最大值再由勾股定理求出BO的长即可解决问题【详解】解:由题意知CE⊥l于点E∴以AC为直径作圆O∵CE解析:225+【分析】以AC为直径作圆O,连接BO,并延长交圆O于点E',可得BO+O E'>B E',从而可得BO+OE>B E',即BE为最大值,再由勾股定理求出BO的长即可解决问题.【详解】解:由题意知,CE⊥l于点E,∴以AC为直径作圆O,∵CE⊥AE,∴点E在圆O上运动,连接BO,并延长交圆O于点E',如图,∴BO+O E '>B E ',∵OE=O E ',∴BO+OE >B E ',∴BE 的长为最大值,∵AO=OC=OE ,且AB=AC=4, ∴122OE AC == 又∵∠BAC=90° ∴222224220BO AO AB =+=+=∴25BO =∴BE=252BO OE +=+故答案为:225+【点睛】此题主要考查了求线段的最大值,构造出△ACE 的外接贺是解答本题的关键. 15.1【分析】首先根据圆的面积求出圆的半径再证明△AOB 是等边三角形即可得到结论【详解】解:如图的面积为设半径为r ∴解得∵OA=OB 为等边三角形故故答案为:1【点睛】本题考查的是正多边形和圆熟知正六边形解析:1【分析】首先根据圆的面积求出圆的半径,再证明△AOB 是等边三角形即可得到结论.【详解】解:如图,O 的面积为π,设半径为r ,2S r ππ∴==,∴21r =,解得,1r =,∵360606AOB ︒∠==︒,OA=OB AOB ∴为等边三角形,故1AB OA ==.故答案为:1【点睛】本题考查的是正多边形和圆,熟知正六边形的半径与边长相等是解答此题的关键. 16.120【分析】根据三角形的内心是三角形角平分线的交点结合公式求出即可【详解】解:为的内心故答案是:120【点睛】注意此题中的结论:若是内心则熟记公式可简化计算解析:120【分析】根据三角形的内心是三角形角平分线的交点,结合公式1902BOC A ∠=+∠︒求出即可. 【详解】解:60A ∠=︒,O 为ABC ∆的内心,1190906012022BOC A , 故答案是:120.【点睛】注意此题中的结论:若O 是内心,则1902BOC A ∠=+∠︒.熟记公式可简化计算. 17.或【分析】由的半径为厘米弦的长为厘米可得等边三角形因此再利用圆周角定理和圆内接四边形的性质求出弦所对的圆周角注意所对的圆周角有两种情形【详解】解:如图为等边三角形则设弦所对的圆周角为当点在弦所对的优 解析:30或150︒【分析】由O 的半径为r 厘米,弦AB 的长为r 厘米,可得OAB 等边三角形,因此60AOB ∠=︒,再利用圆周角定理和圆内接四边形的性质求出弦AB 所对的圆周角.注意AB 所对的圆周角有两种情形.【详解】解:如图,OA OB AB r ===,ABO ∴为等边三角形,则60AOB ∠=︒.设弦AB 所对的圆周角为ACB ∠,当点C 在弦AB 所对的优弧上,则60230ACB ∠=︒÷=︒;当点C 在弦AB 所对的劣弧上,则18030150ACB ∠=︒-︒=︒.所以弦AB 所对的圆周角为30或150︒,故答案为:30或150︒.【点睛】本题考查了圆周角定理.同弧所对的圆周角相等,并且等于它所对的圆心角的一半.同时考查了圆内接四边形的对角互补和等边三角形的性质.18.18°【分析】连接OD 利用半径相等和等腰三角形的性质以及三角形的外角性质得到∠BOE=3∠C 即可解决问题【详解】连接OD ∵CD=OA=OD ∴∠C=∠DOC ∴∠ODE=∠C+∠DOC=2∠C ∵OD=O解析:18°.【分析】连接OD ,利用半径相等和等腰三角形的性质以及三角形的外角性质得到∠BOE=3∠C ,即可解决问题.【详解】连接OD ,∵CD=OA=OD ,∴∠C=∠DOC ,∴∠ODE=∠C+∠DOC=2∠C ,∵OD=OE ,∴∠E=∠EDO=2∠C ,∴∠EOB=∠C+∠E=3∠C=54°,∴∠C=18°,故答案为:18°.【点睛】本题考查了圆的认识及等腰三角形的性质及三角形的外角性质,熟练掌握等腰三角形的性质和三角形外角性质是关键.19.【分析】由于AB 是⊙O 的直径则AB =2DO 而AB =2DE 可得DO =DE 根据等腰三角形的性质得到∠DOE =∠E 又由于△COD 为直角三角形而OC =OD 所以△COD 为等腰直角三角形于是可得∠CDO =45°解析:22.5︒【分析】由于AB是⊙O的直径,则AB=2DO,而AB=2DE,可得DO=DE,根据等腰三角形的性质得到∠DOE=∠E,又由于△COD为直角三角形,而OC=OD,所以△COD为等腰直角三角形,于是可得∠CDO=45°,利用三角形外角性质有∠CDO=∠DOE+∠E,则∠E=1 2∠CDO=22.5°.【详解】解:∵AB是⊙O的直径,∵AB=2DO,而AB=2DE,∴DO=DE,∴∠DOE=∠E,∵△COD为直角三角形,而OC=OD,∴△COD为等腰直角三角形,∴∠CDO=45°,∵∠CDO=∠DOE+∠E,∴∠E=12∠CDO=22.5°.故答案为:22.5°.【点睛】本题考查了圆的认识:圆上任意两点的连线段叫圆的弦;过圆心的弦叫圆的直径;直径的长等于半径的2倍.也考查了等腰直角三角形的判定与性质以及等腰三角形的性质.20.12【分析】连接OAOBOC过点O作OE⊥AD于EOF⊥BC于F根据圆周角定理得到∠BOC=90°再根据等腰直角三角形的性质计算求出OB再由DF=BD-BF得出DF然后等腰直角三角形的性质求出OF根解析:12【分析】连接OA、OB、OC过点O作OE⊥AD于E,OF⊥BC于F,根据圆周角定理得到∠BOC=90°,再根据等腰直角三角形的性质计算,求出OB,再由DF=BD-BF得出DF,然后等腰直角三角形的性质求出OF,根据勾股定理求出AE,再根据AD=AE+OF得到答案.【详解】解:∵BD=6,DC=4,∴BC=BD+DC=10∵∠BAC=45°,∴∠BOC=90°,∴==OB BC连接OA 、OB 、OC 过点O 作OE ⊥AD 于E ,OF ⊥BC 于F ,∴BF=FC=5,∴DF=BD-BF=1,∵∠BOC=90°,BF=FC∴OF=12BC=5, ∵AD ⊥BC ,OE ⊥AD ,OF ⊥BC ,∴四边形OFDE 为矩形,∴OE=DF=1,DE=OF=5,在Rt △AOE 中,227,=-=AE OA OE∴AD=AE+DE=12.【点睛】本题考查的是三角形的外接圆,掌握圆周角定理、垂径定理、等腰直角三角形的性质是解题的关键.三、解答题21.(1)见解析,点1B 的坐标为()1,2-;(2)2π【分析】(1)根据中心对称的定义即可求解;(2)根据弧长公式即可求解.【详解】解:(1)111A B C △如图所示点1B 的坐标为()1,2-(2)∵()5,2A -,()1,2B -∴4AB =∴ABC 绕点B 顺时针旋转90°过程中,点A 走过的路径长为:9042180ππ⨯⨯=. 【点睛】 本题考查中心对称的定义、弧长公式,掌握以上基本概念是解题的关键. 22.BC =8,BD =52【详解】解:连接BD ,如图,∵AB 是直径,∴∠ACB =∠ADB =90°,在Rt △ABC 中,AB =10,AC =6,∴BC 22AB AC -22106-8,即BC =8;∵∠ACB 的平分线交⊙O 于点D ,∴∠DCA=∠BCD,∴AD BD=,∴AD=BD,∴在Rt△ABD中,AD=BD=22AB=22×10=52,即BD=52.【点睛】本题考查了勾股定理,圆周角定理,解题的关键是求出∠ACB=∠ADB=90°.23.(1)作图见解析;(2)10.【分析】(1)分别做AB、BC的垂直平分线且交于O,然后以O为圆心、OA为半径画圆即可;(2)如图:连接OB,然后根据垂径定理求得BD,最后根据勾股定理解答即可.【详解】解:(1)如图所示∴⊙O即为所求作的外接圆;(2)如图:连接OB∵已知△ABC的外接圆的圆心O到BC边的距离OD=8∵线段BC的垂直平分线交BC于点D,∴BD=CD=12BC=6,在Rt△BOD中,OB=2286+=10,∴⊙O的半径长10.【点睛】本题考查了三角形的外接圆的作法和垂径定理的应用,灵活应用相关知识成为解答本题的关键.24.(1)证明见解析;(2)3 64π-【分析】(1)先根据圆周角定理得:∠ATB=90°,则∠B+∠OAT=90°,根据同圆的半径相等和等腰三角形的性质得:∠OAT=∠2,从而得∠PTA+∠2=90°,即∠OTP=90°,所以直线PT与⊙O相切;(2)利用TP=TB 得到∠P=∠B ,而∠OAT=2∠P ,所以∠OAT=2∠B ,则利用∠ATB=90°可计算出∠B=30°,∠POT=60°,利用含30度的直角三角形三边的关系得到AT=12AB ,△AOT 为等边三角形,然后根据扇形的面积公式和图中阴影部分的面积=S 扇形OAT -S △AOT 进行计算.【详解】(1)证明:连接OT ,∵AB 是⊙O 的直径,∴∠ATB=90°,∴∠B+∠OAT=90°,∵OA=OT ,∴∠OAT=∠2,∵∠PTA=∠B ,∴∠PTA+∠2=90°,即∠OTP=90°,∴直线PT 与⊙O 相切;(2)∵3PT BT ==∴∠P=∠B=∠PTA ,∵∠TAB=∠P+∠PTA ,∴∠TAB=2∠B ,∵∠TAB+∠B=90°,∴∠TAB=60°,∠B=30°,在Rt △ABT 中,设AT=a ,则AB=2AT=2a ,∴a 232=(2a)2,解得:a=1,∴AT=1, ∵OA=OT ,∠TAO=60°,∴△AOT 为等边三角形, 1331224AOT S ∴=⨯⨯=. ∴阴影部分的面积2Δ 601333606AOT AOTS S ππ⨯=-==-扇形. 【点睛】本题考查了切线的判定、勾股定理,此类题常与方程结合,列方程求圆的半径和线段的长,也考查了扇形的面积公式.25.(1)证明见解析;(2)152. 【分析】 (1)只要证明90A B ∠+∠=︒,90ADE B ∠+∠=︒,即可解决问题;(2)首先证明210AC DE ==,在Rt △ADC 中,6DC =,设BD x =,在Rt △BDC 中,2226BC x =+,在Rt △ABC 中,()222810BC x =+-,可得()22226810x x +=+-,解方程即可解决问题;【详解】(1)证明:连接OD ,∵DE 是切线,∴90ODE ∠=︒,∴90ADE BDO ∠+∠=︒,∵90ACB ∠=︒,∴90A B ∠+∠=︒,∵OD=OB ,∴B BDO ∠=∠,∴ADE A ∠=∠;(2)连接CD ,∵ADE A ∠=∠,∴AE=DE ,∵BC 为圆O 的直径,90ACB ∠=︒,∴EC 是O 的切线,∴ED=EC ,∴AE=EC ,∵5DE =,∴210AC DE ==,在Rt △ADC 中,6DC =,设BD x =,在Rt △BDC 中,222=6BC x +,在Rt △ABC 中,()222810BC x =+-,∴()22226810x x +=+-, 解得:92x =,∴152BC ==.【点睛】本题主要考查了圆的基本性质,切线的性质,准确分析计算是解题的关键.26.(1)证明见解析;(2)5.【分析】(1)连接OC ,根据切线的性质可得OC CD ⊥,再证//AD OC ,然后再根据平行线的性质和等腰三角形的性质说明12∠=∠即可;(2)作OE AD ⊥于点E ,设O 的半径为x ,先证四边形OEDC 是矩形,进而求得OE 和AE ,然后根据勾股定理解答即可.【详解】(1)证明:如图1:连接OC ,∵CD 是切线,∴OC CD ⊥.∵AD CD ⊥,∴//AD OC ,∴13∠=∠.∵OA OC =,∴23∠∠=,∴12∠=∠,∴AC 平分DAB ∠;(2)解:如图2,作OE AD ⊥于点E ,设O 的半径为x .∵AD CD ⊥,OE AD ⊥,∴90OED EDC DCO ∠=∠=∠=︒,∴四边形OEDC 是矩形,∴4OE CD ==,8AE AD DE x =-=-,∴()22248x x +-=, ∴228016x x x -+=,解得5x =,∴O 的半径是5.【点睛】本题考查了圆的切线的性质、等腰三角形的性质、平行线的性质以及勾股定理等内容,灵活应用所学知识成为解答本题的关键.。
2024年人教版九年级下册数学第六单元课后练习题(含答案和概念)

2024年人教版九年级下册数学第六单元课后练习题(含答案和概念)试题部分一、选择题:1. 在直角坐标系中,点A(2, 3)关于原点对称的点是()A. (2, 3)B. (2, 3)C. (2, 3)D. (3, 2)2. 下列函数中,哪一个是一次函数?()A. y = 2x^2 + 1B. y = 3x + 4xC. y = x^2 3D. y = 5x3. 已知等腰三角形的底边长为8cm,腰长为5cm,则该三角形的周长为()A. 18cmB. 20cmC. 22cmD. 24cm4. 下列各数中,是无理数的是()A. √9B. √16C. √3D. 0.3333…5. 若a、b满足a+b=6,ab=8,则a^2+b^2的值为()A. 28B. 32C. 34D. 366. 下列关于x的不等式中,有解的是()A. x^2 < 0B. x^2 = 0C. x^2 > 0D. x^2 ≤ 07. 下列关于圆的命题中,正确的是()A. 圆的半径都相等B. 圆的直径都相等C. 圆上任意两点到圆心的距离相等D. 圆的周长与半径成正比8. 在平面直角坐标系中,点P(a, b)关于y轴对称的点是()A. (a, b)B. (a, b)C. (a, b)D. (a, b)9. 下列图形中,既是轴对称图形又是中心对称图形的是()A. 等腰三角形B. 正方形C. 等边三角形D. 长方形10. 下列关于一元二次方程的命题中,正确的是()A. 一元二次方程的解一定是实数B. 一元二次方程的解一定是整数C. 一元二次方程的解可以是负数D. 一元二次方程的解一定是正数二、判断题:1. 两条平行线的斜率相等。
()2. 任何两个等腰三角形的面积都相等。
()3. 两个无理数的和一定是无理数。
()4. 一元二次方程的解可以是两个相等的实数。
()5. 圆的半径与直径的比值为π。
()6. 一次函数的图像是一条直线。
()7. 两条直线的斜率相等,则这两条直线一定平行。
新人教版初中数学九年级数学上册第四单元《圆》测试题(答案解析)(5)

一、选择题1.如图,在ABC 中,90ACB ∠=︒,过B ,C 两点的O 交AC 于点D ,交AB 于点E ,连接EO 并延长交O 于点F .连接BF ,CF ,若135EDC ∠=︒,2AE =,4BE =,则CF 的值为( ).A .10B .22C .23D .3 2.如图,ABC 为O 的一个内接三角形,过点B 作O 的切线PB 与OA 的延长线交于点P .已知34ACB ∠=︒,则P ∠等于( )A .17°B .27°C .32°D .22°3.如图在ABC 中,∠B=90°,AC=10,作ABC 的内切圆圆O ,分别与AB 、BC 、AC 相切于点D 、E 、F ,设AD=x ,ABC 的面积为S ,则S 关于x 的函数图像大致为( )A .B .C .D .4.如图,AB 圆O 的直径,弦CD AB ⊥,垂足为M ,下列结论不成立的是( )A .CM DM =B .CB BD =C .ACD ADC ∠=∠ D .OM MB = 5.如图所示,AB 是O 的直径,点C ,D 在O 上,21BDC ∠=︒,则AOC ∠的度数是( )A .136°B .137°C .138°D .139° 6.已知⊙O 的直径为6,圆心O 到直线l 的距离为3,则能表示直线l 与⊙O 的位置关系的图是( ) A . B .C .D .7.如图,AB 为O 的弦,半径OC 交AB 于点D ,AD DB =,5OC =,3OD =,则AB 的长为( )A .8B .6C .4D .28.如图,在平行四边形ABCO 中,45C ∠=︒,点A ,B 在O 上,点D 在ADB 上,DA DB =,则AOD ∠的度数为( )A .112.5°B .120°C .135°D .150°9.如图,△ABC 内接于☉O ,若☉O 的半径为6,∠A=60°,则BC 的长为( )A .2πB .4πC .6πD .8π 10.如图,P 与y 轴交于点()0,4M -,()0,10N -,圆心P 的横坐标为4-,则P 的半径为( )A .3B .4C .5D .6 11.在扇形中,∠AOB =90°,面积为4πcm 2,用这个扇形围成一个圆锥的侧面,这个圆锥的底面半径为 ( )A .1cmB .2cmC .3nD .4cm12.如图,AB 是⊙O 的直径,AB=AC 且∠BAC=45°,⊙O 交BC 于点D ,交AC 于点E ,DF 与⊙O 相切,OD 与BE 相交于点H .下列结论错误的是( )A .BD=CDB .四边形DHEF 为矩形C .2AE DE= D .BC=2CE 二、填空题13.如图,PA ,PB 是O 的切线,A ,B 为切点,AC 是O 的直径,35BAC ∠=︒,则P ∠的度数为________.14.如图,四边形ABCD 是O 的内接四边形,对角线AC ,BD 交于点E ,且AC BD AB ==,若70AEB ∠=︒,则AOB ∠等于______︒.15.如图,⊙O 是ABC 的外接圆,64A ∠=︒,则OBC ∠=______°.16.如图,A 是半径为1的O 外一点,2OA =,AB 是O 的切线,点B 是切点,弦//BC OA ,连接AC ,则图中阴影部分的面积为________.17.如图所示,已知矩形ABCD 的边3AB cm =,4AD cm =.以点A 为圆心作圆,使B ,C ,D 三点中至少有一点在圆外,且至少有一点在圆内,此圆半径R 的取值范围是______.18.如图,已知AD 为半圆形O 的直径,点B ,C 在半圆形上,AB BC =,30BAC ∠=︒,8AD =,则AC 的长为________.19.如图,在⊙O 中,弦AC 、BD 相交于点E ,且AB BC CD ==,若∠BEC=130°,则∠ACD 的度数为_____20.如图,半径为3的⊙O 与边长为8的等边三角形ABC 的两边AB 、BC 都相切,连接OC ,则OC =_____.三、解答题21.已知:△ABC .(1)求作:△ABC 的外接圆⊙O (要求:尺规作图,保留作图痕迹,不写作法);(2)若已知△ABC 的外接圆的圆心O 到BC 边的距离OD =8,BC =12,求⊙O 的半径.22.已知:如图,ABC 中,BC AC =,以BC 为直径的O 交AB 于点O ,过点D 作DE AC ⊥于点E ,交BC 的延长线于点F .求证:(1)AD BD =,(2)DF 是O 的切线. 23.如图,AC 为O 的直径,4AC =,B 、D 分别在AC 两侧的圆上,60BAD ∠=︒,BD 与AC 的交点为E .(1)求点O 到BD 的距离及OBD ∠的度数;(2)若2DE BE =,求cos OED ∠的值和CD 的长.24.如图,已知AB 是O 的直径,四边形AODE 是平行四边形,请用无刻度直尺按下列要求作图.(1)如图1,当点D 在圆上时,作BAC ∠的平分线;(2)如图2,当点D 不在圆上时,作BAC ∠的平分线.25.对于平面上两点,A B ,给出如下定义:以点A 或B 为圆心,AB 长为半径的圆称为点,A B 的“共径圆”.点,A B 的“共径圆”的示意图如图所示.(1)已知点A 的坐标为(0,0),点B 的坐标为(3,4),则点,A B 的“共径圆”的面积为_______________;(2)已知点A 在以坐标原点为圆心,以1为半径的圆上,点B 在直线4y x =-+上,求点,A B 的“共径圆”的半径最小值;(3)已知点A 的坐标为(0,0),点B 是x 轴及x 轴上方的点,如果直线y x b =+上存在两个点B ,使得点,A B 的“共径圆”的面积为4π,直接写出满足条件的b 的取值范围.26.如图,一条公路的转弯处是一段圆弧CD ,点O 是CD 的圆心,E 为 CD 上一点,OE ⊥CD ,垂足为F .已知CD=300m ,EF=50m ,求这段弯路的半径.【参考答案】***试卷处理标记,请不要删除一、选择题1.A解析:A【分析】由四边形BCDE 内接于⊙O 知∠EFC=∠ABC=45°,据此得AC=BC ,由EF 是⊙O 的直径知∠EBF=∠ECF=∠ACB=90°及∠BCF=∠ACE ,再根据四边形BECF 是⊙O 的内接四边形知∠AEC=∠BFC ,从而证△ACE ≌△BCF 得AE=BF ,根据Rt △ECF 是等腰直角三角形知EF 2=20,继而可得答案.【详解】∵四边形BCDE 内接于O ,且135EDC ∠=︒, ∴18045EFC ABC EDC ︒∠=∠=-∠=︒, ∵90ACB ∠=︒,∴ABC 是等腰三角形,∴AC BC =, 又∵EF 是O 的直径, ∴90EBF ECF ACB ∠=∠=∠=︒,∴BCF ACE ∠=∠,∵四边形BECF 是O 的内接四边形,∴AEC BFC ∠=∠,∴()ACE BFC ASA ≅△△,∴AE BF =,Rt BEF △中,22222224220EF BF BE BE AE =+=+=+=,Rt ECF △中,45EFC ∠=︒,∴CE CF =,∴2222220CE CF CF EF +===,∴210CF =, ∴CF =故选:A .【点睛】本题主要考查圆周角定理,解题的关键是掌握圆内接四边形的性质、圆周角定理、全等三角形的判定与性质及勾股定理.2.D解析:D【分析】连接OB ,利用圆周角定理求得∠AOB ,再根据切线性质证得∠OBP=90°,利用直角三角形的两锐角互余即可求解.【详解】解:连接OB ,∵∠ACB=34°,∴∠AOB=2∠ACB=68°,∵PB 为O 的切线,∴OB ⊥PB ,即∠OBP=90°,∴∠P=90°﹣∠AOB=22°,故选:D .【点睛】本题考查了切线的性质、圆周角定理、直角三角形的两锐角互余,熟练掌握切线的性质和圆周角定理是解答的关键.3.A解析:A【分析】连接OD 、OE ,根据三角形内切圆证得四边形DBEO 是正方形,在根据勾股定理即可得解;【详解】连接OD 、OE ,如图,O 的半径为r ,∵△ABC 的内切圆O 分别于AB 、BC 、AC 相切与点D 、E 、F ,∴⊥OD AB ,OE BC ⊥,AF=AD=x ,CE=CF=10-x ,易得四边形DBEO 是正方形,∴DB BE OD r ===, ∵()()2△1110101022ABC S r AB BC AC r x r r x r r =++=+++-+=+,∵222AB BC AC +=,∴()()2221010x r x r ++-+=,∴221010r r x x +=-+, ∴()2210525S x x x =-+=--+(0<x <10). 故答案选A .【点睛】本题主要考查了切线的性质,三角形的内切圆与圆心,函数图像,准确分析判断是解题的关键.4.D解析:D【分析】根据垂径定理得到CM=DM ,BC BD =,AC AD =,然后根据圆周角定理得∠ACD=∠ADC ,而对于OM 与MB 的大小关系不能判断.【详解】解:∵AB 是⊙O 的直径,弦CD ⊥AB ,∴CM=DM ,BC BD =,AC AD =,∴∠ACD=∠ADC .而无法比较OM ,MB 的大小,故选:D .【点睛】本题考查了垂径定理:平分弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了圆周角定理.5.C解析:C【分析】利用圆周角定理求出∠BOC 即可解决问题.【详解】解:∵∠BOC=2∠BDC ,∠BDC=21°,∴∠BOC=42°,∴∠AOC=180°-42°=138°.故选:C .【点睛】本题考查了圆周角定理,解题的关键是熟练掌握圆周角定理,属于中考常考题型. 6.C解析:C【分析】因为⊙O 的直径为6,所以圆的半径是3,圆心O 到直线l 的距离为3即d=3,所以d=r ,所以直线l 与⊙O 的位置关系是相切.【详解】解:∵⊙O 的直径为6,∴r=3,∵圆心O 到直线l 的距离为3即d=3,∴d=r∴直线l 与⊙O 的位置关系是相切.故选:C .【点睛】本题考查直线与圆的位置关系,若圆的半径为r ,圆心到直线的距离为d ,d >r 时,圆和直线相离;d=r 时,圆和直线相切;d <r 时,圆和直线相交.7.A解析:A【分析】连接OB ,根据⊙O 的半径为5,CD =2得出OD 的长,再由垂径定理的推论得出OC ⊥AB ,由勾股定理求出BD 的长,进而可得出结论.【详解】解:连接OB ,如图所示:∵⊙O 的半径为5,OD =3,∵AD =DB ,∴OC ⊥AB ,∴∠ODB =90°, ∴2222.534BD OB OD -=-=,∴AB =2BD =8.故选:A .【点睛】本题考查的是垂径定理以及勾股定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.8.C解析:C【分析】延长DO 交AB 于点H ,连接OB ,证明△△AOD BOD ≅,OD 是AOB ∠的角平分线,求得290345∠=︒-∠=︒,进行求解即可;【详解】延长DO 交AB 于点H ,连接OB ,∵四边形ABCD 是平行四边形,45C ∠=︒,∴345∠=︒,∵DA DB =,OA OB =,∴△△AOD BOD ≅,∴OD 是AOB ∠的角平分线,又∵AO BO =,∴DH AB ⊥,∴290345∠=︒-∠=︒,又∵221∠=∠,∴18045135AOD ∠=︒-︒=︒.故选:C .【点睛】本题主要考查了与圆有关的计算,结合全等三角形的性质和角平分线的性质计算即可. 9.B解析:B【分析】连接OB ,OC ,根据圆周角定理求出∠BOC 度数,再由弧长公式即可得出结论.【详解】解:连接OB ,OC ,∵∠A=60°,∴∠BOC=2∠A=120°,∴BC =208161π⨯=4π. 故选:B .【点睛】 本题考查了三角形的外接圆与外心,根据题意作出辅助线,利用圆周角定理及弧长公式求解是解题的关键.10.C解析:C【分析】过点P 作PD ⊥MN ,连接PM ,由垂径定理得DM =3,在Rt △PMD 中,由勾股定理可求得PM 为5即可.【详解】解:过点P 作PD ⊥MN ,连接PM ,如图所示:∵⊙P 与y 轴交于M (0,−4),N (0,−10)两点,∴OM =4,ON =10,∴MN =6,∵PD ⊥MN ,∴DM =DN =12MN =3, ∴OD =7,∵点P 的横坐标为−4,即PD =4,∴PM 22PD DM +2243+5,即⊙P 的半径为5,故选:C .【点睛】本题考查了垂径定理、坐标与图形性质、勾股定理等知识;熟练掌握垂径定理和勾股定理是解题的关键. 11.A解析:A【分析】圆锥的底面周长等于侧面展开图的扇形弧长,因而要先求扇形的弧长,根据扇形的面积公式2360n R S π=,可以求出扇形的半径,就可以求出弧长. 【详解】 解:根据扇形的面积公式2360n R S π=得到:2904360R ππ=; ∴R=4,则弧长9042180cm ππ⋅==,设圆锥的底面半径为r,则2π=2πr;∴r=1cm.故选:A.【点睛】本题综合考查有关扇形和圆锥的相关计算.解题思路:解决此类问题时要紧紧抓住两者之间的两个对应关系:(1)圆锥的母线长等于侧面展开图的扇形半径;(2)圆锥的底面周长等于侧面展开图的扇形弧长.正确对这两个关系的记忆是解题的关键.12.D解析:D【分析】A、利用直径所对的圆周角是直角,以及等腰三角形的三线合一性质即可得出结论;B、根据中位线得出OD//AC,再根据矩形的判定即可得出结论C、根据垂径定理得出BD DE=,再根据等腰直角三角形的性质得出AE=BE,从而得出BD DE=,即可得出2=AE DED、不能得出BC=2CE【详解】解:连接AD∵AB为⊙O的直径,∴∠BDA=∠BEA =90°,即AD⊥BC,又∵AB=AC,∴BD=DC,∠BAD=∠DAE,故A正确;∵OA=OB∴OD是三角形ABC的中位线∴OD//AC∴∠DHE =90°=∠BEF,∵DF与⊙O相切,∴∠ODF =90°∴四边形DHEF为矩形故B正确;∵∠BEA =90°,∠BAC=45°,∴AE=BE∴AE BE=∵∠DHE =90°∴OD⊥BE∴BD DE=∴2AE DE故C正确;不能得出BC=2CE故选:D【点睛】本题考查了切线的性质、三线合一定理、三角形中位线定理、垂径定理;熟练掌握等腰三角形的性质和圆周角定理,并能进行推理论证是解决问题的关键.二、填空题13.70°【分析】根据题意可以求得∠OAP和∠OBP的度数然后根据∠BAC=35°即可求得∠P的度数【详解】解:连接OB:∵PAPB是⊙O的两条切线AB是切点AC是⊙O的直径∴∠OAP=∠OBP=90°解析:70°【分析】根据题意可以求得∠OAP和∠OBP的度数,然后根据∠BAC=35°,即可求得∠P的度数.【详解】解:连接OB:∵PA、PB是⊙O的两条切线,A、B是切点,AC是⊙O的直径,∴∠OAP=∠OBP=90°,∵∠BAC=35°,OA=OB,∴∠BAC=∠OBA=35°,∴∠PAB=∠PBA=55°,∴∠P=180°−∠PAB−∠PBA=70°,即∠P的度数是70°,故答案为:70°.【点睛】本题考查切线的性质,解答此类问题的关键是明确题意,找出所求问题需要的条件,利用切线的性质解答问题.14.125【分析】根据题意先求出∠ABE=∠BAE=55°然后由等腰三角形的定义和三角形的内角和定理求出∠C=625°即可求出的度数【详解】解:根据题意∵在圆中有∴∴∴在△ABE 中∴在等腰△ABC 中则∴解析:125【分析】根据题意,先求出∠ABE=∠BAE=55°,然后由等腰三角形的定义和三角形的内角和定理,求出∠C=62.5°,即可求出AOB ∠的度数.【详解】解:根据题意,∵在圆中,有AC BD AB ==,∴AC BD =,∴AD BC =,∴ABD BAC ∠=∠,在△ABE 中,70AEB ∠=︒, ∴1(18070)552ABD BAC ∠=∠=⨯︒-︒=︒, 在等腰△ABC 中,AC AB =则1(18055)62.52C ∠=⨯︒-︒=︒, ∴2125AOB C ∠=∠=︒;故答案为:125.【点睛】本题考查了圆内接四边形的性质,圆周角定理,三角形的内角和定理,等腰三角形的定义,解题的关键是熟练掌握所学的知识,正确的进行解题.15.26【分析】先利用圆周角定理得到∠BOC=2∠A=128°然后根据等腰三角形的性质和三角形内角和定理计算∠OBC 的度数【详解】解:∵∠A=64°∴∠BOC=2∠A=128°∵OB=OC ∴∠OBC=∠解析:26【分析】先利用圆周角定理得到∠BOC=2∠A=128°,然后根据等腰三角形的性质和三角形内角和定理计算∠OBC 的度数.【详解】解:∵∠A=64°,∴∠BOC=2∠A=128°,∵OB=OC ,∴∠OBC=∠OCB ,∴∠OBC=12(180°-128°)=26°. 故答案为26.【点睛】本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.16.【分析】连接OCOB 易证△OAB 为等边三角形由BC ∥OA 得S △OCB =S △ACB 把阴影部分的面积转化为扇形OBC 的面积【详解】连接OCOB ∵是的切线∴OB ⊥AB 在Rt △OBA 中∵OB=1OA=2∴∠解析:6π【分析】连接OC ,OB ,易证△OAB 为等边三角形,由BC ∥OA ,得S △OCB =S △ACB ,把阴影部分的面积转化为扇形OBC 的面积.【详解】连接OC ,OB∵AB 是O 的切线∴OB ⊥AB在Rt △OBA 中∵OB=1,OA=2∴∠AOB=60°又∵//BC OA∴∠OBC=60°∵OB=OC∴△OAB 为等边三角形又∵BC ∥OA ∴S △OCB =S △ACB∴S 阴=S 扇形OBC =2601360π⨯⨯ =6π故答案为:6π 【点睛】 本题考查扇形面积的求解,将不规则图形转化成规则的扇形是解题的关键.17.【分析】使BCD 三点至少有一个在圆内且至少有一个在圆外也就是说圆的半径不能小于AB 不能大于AC 可求得AC=5所以3<r<5【详解】如图连接AC ∵ 在矩形ABCD 中AB=3cmAD=4cm ∠ABC=9解析:35R <<【分析】使B 、C 、D 三点至少有一个在圆内,且至少有一个在圆外,也就是说圆的半径不能小于AB,不能大于AC ,可求得AC=5,所以3<r<5.【详解】如图,连接AC ,∵ 在矩形ABCD 中,AB=3cm ,AD=4cm ,∠ABC=90°,BD=AC ,∴AC=BD=2222345AB AD cm +=+=,∴AB<AD<AC ,∵B ,C ,D 三点中至少有一点在⊙A 内,且至少有一点⊙A 在外,∴点B 一定在⊙A 内,点C 一定在⊙A 外,∴⊙A 半径R 的取值范围应大于AB 的长,小于对角线AC 的长,即3<R<5.故答案为:3<R<5.【点睛】本题考查确定点与圆的位置关系,解题的关键是掌握确定点到圆心的距离与半径的大小关系,设点与圆心的距离d ,圆的半径为r ,则d >r 时,点在圆外;当d =r 时,点在圆上;当d <r 时,点在圆内.18.【分析】连接CD 由已知可以得到∠B=120°所以∠D=60°然后在Rt △ACD 中计算AC 即可【详解】解:如图所示连接CD ∵∴∠B=120°∴∠D=60°∵AD 为直径∴∠ACD=90°∴CD=4∴AC解析:43【分析】连接CD ,由已知可以得到∠B=120°,所以∠D=60°,然后在Rt △ACD 中计算AC 即可.【详解】解:如图所示,连接CD∵AB BC =,30BAC ∠=︒∴∠B=120°∴∠D=60°∵AD 为直径∴∠ACD=90°∴CD=4∴3【点睛】本题主要考查圆的内接四边形对角性质,掌握直径所对的圆周角是90°和圆的内接四边形对角互补是解题的关键.19.105°【分析】根据圆周角定理的推论可得∠BCA =∠CBD =∠CDB 然后根据三角形的内角和定理即可求出∠BCA 与∠CED 再在△CDE 中利用三角形的内角和求解即可【详解】解:∵∴∠BCA =∠CBD =∠解析:105°【分析】根据圆周角定理的推论可得∠BCA =∠CBD =∠CDB ,然后根据三角形的内角和定理即可求出∠BCA 与∠CED ,再在△CDE 中利用三角形的内角和求解即可【详解】解:∵AB BC CD ==,∴∠BCA =∠CBD =∠CDB ,∵∠BEC =130°,∴∠BCA =∠CBD =25°,∠CED =50°,∴∠CDB =25°,∴∠ACD =180°﹣50°﹣25°=105°.故答案为:105°.【点睛】本题考查了圆周角定理的推论和三角形的内角和定理,熟练掌握上述知识是解题的关键. 20.【分析】连接OB 作OD ⊥BC 于D 由等边三角形的性质得∠ABC =60°BC =8由⊙O与等边三角形ABC的两边ABBC都相切得出OD是⊙O的半径∠OBC=∠OBA=30°应用三角函数求出BD=3CD=B解析:27【分析】连接OB,作OD⊥BC于D,由等边三角形的性质得∠ABC=60°,BC=8,由⊙O与等边三角形ABC的两边AB、BC都相切,得出OD是⊙O的半径,∠OBC=∠OBA=30°,应用三角函数求出BD=3,CD=BC−BD=5,由勾股定理得出OC,即可得出答案.【详解】连接OB,作OD⊥BC于D,∵△ABC是边长为8的等边三角形,∴∠ABC=60°,BC=8,∵⊙O与等边三角形ABC的两边AB、BC都相切,∴OD是⊙O的半径,∠OBC=∠OBA=12∠ABC=30°,∵tan∠OBC=ODBD,∴BD=ODtan30=33=3,∴CD=BC−BD=8−3=5,OC=22OD+CD=()223+5=27,故填:27.【点睛】本题考查了切线的性质、等边三角形的性质、勾股定理、三角函数等知识;熟练掌握切线的性质是解题的关键.三、解答题21.(1)作图见解析;(2)10.【分析】(1)分别做AB、BC的垂直平分线且交于O,然后以O为圆心、OA为半径画圆即可;(2)如图:连接OB ,然后根据垂径定理求得BD ,最后根据勾股定理解答即可.【详解】解:(1)如图所示∴⊙O 即为所求作的外接圆;(2)如图:连接OB∵已知△ABC 的外接圆的圆心O 到BC 边的距离OD =8∵线段BC 的垂直平分线交BC 于点D ,∴BD =CD =12BC=6, 在Rt △BOD 中,OB =2286+=10,∴⊙O 的半径长10.【点睛】本题考查了三角形的外接圆的作法和垂径定理的应用,灵活应用相关知识成为解答本题的关键.22.(1)证明见解析;(2)证明见解析.【分析】(1)如图(见解析),先根据圆周角定理可得90BDC ∠=︒,再根据等腰三角形的三线合一即可得证;(2)先根据等腰三角形的三线合一可得ACD BCD ∠=∠,再根据等腰三角形的性质可得ODC BCD ∠=∠,从而可得ACD ODC ∠=∠,然后根据平行线的判定与性质可得OD DF ⊥,最后根据圆的切线的判定即可得证.【详解】(1)如图,连接CD ,BC 是O 的直径,90BDC ∴∠=︒,即CD AB ⊥,又BC AC =,CD ∴是AB 边上的中线(等腰三角形的三线合一),AD BD ∴=;(2)如图,连接OD ,,BC AC CD AB=⊥,ACD BCD∴∠=∠,OC OD=,ODC BCD∴∠=∠,ACD ODC∴=∠∠,//OD AC∴,DE AC⊥,即DF AC⊥,OD DF∴⊥,又OD是O的半径,DF∴是O的切线.【点睛】本题考查了等腰三角形的三线合一、圆周角定理、圆的切线的判定等知识点,较难的是题(2),熟练掌握圆的切线的判定定理是解题关键.23.(1)1,30º;(2)12,2【分析】(1)作OF⊥BD于点F,连接OD,根据圆周角定理可得出∠DOB=120º,再由OB=OD=12AC=2,可得出∠OBD的度数,也可以得出OF的长度,(2)设BF=2x,则可表示出DF、EF的长度,从而可解出x的值,在Rt△OEF中,利用三角函数值的知识可求出∠OED的度数,也可得出cos∠OED的值,判断出DO⊥AC,然后利用等腰直角三角形的性质可得出CD的长度.【详解】(1)作OF⊥BD于点F,连接OD,∵∠BAD=60º,∴∠BOD=2∠BAD=120º,又∵OB=OD,∴∠OBD=30º,∵AC为⊙O的直径,AC=4,∴OB=OC=2,在Rt△BOF中,∵∠OFB=90º,OB=2,∠OBF=30º,∴OF=12OB=1, 即点O 到BD 的距离等于1,(2)∵OB=OD ,OF ⊥BD 于点F ,∴BF=DF ,由DE=2BE ,设BE=2x ,则DE=4x ,BD=6x,EF =x,BF=3x ,∵3∴3333x EF ==, 在Rt △OEF 中,∠OFE=90º,∵tan ∠OED=OF =3EF∴∠OED=60º,cos ∠OED=12, ∴∠BOC=∠OED-∠OBD=30º,∴∠DOC=∠DOE-∠BOE=90º,∴∠C=45º,∴2OC=22【点睛】本题考查属于圆的综合题,涉及等腰三角形的性质,三角函数值,及勾股定理等知识,解答此类综合性题目,要求我们熟悉掌握一些小知识,做到将所学的知识融会贯通,难度较大.24.(1)见解析;(2)见解析.【分析】(1)由四边形AODE 是平行四边形,结合圆的 半径相等,可知四边形AODE 是菱形,利用菱形的性质即可做出BAC ∠的平分线;(2)延长OD 交于圆一点,连接该点与点A ,由此即可作出C BA ∠的平分线.【详解】解:(1)如图①:AD 即为所求.∵四边形AODE 是平行四边形点D 在圆上∴四边形AODE 是菱形∴AD 平分BAC ∠;(2)如图②:延长OD 交于圆一点P ,连接AP ,同理可证AP 即为所求.【点睛】此题考查尺规作图,关键是掌握圆的相关知识及角平分线的判定方法.25.(1) 25π;(2)221;(3)222b ≤<【分析】(1)由点A 、B 的坐标知,22345,=+=AB 由圆的面积公式得:“共径圆”的面积πr 2=25π;(2)如下图,当O 、A 、B 三点共线,且OB ⊥直线l 时,共径圆”的半径最小,即可求解; (3)设点B 的坐标为(x ,x+b ),设AB 之间的距离为r ,则πr 2=4π,解得r=2(负值已舍去),则AB=x 2+(x+b )2=22=4,满足条件的B 点有2个,故△=(2b )2-2×4(b 2-4)>0,进而求解.【详解】解:(1)A 的坐标为(0,0),点B 的坐标为(3,4), ∴22345,=+=AB由圆的面积公式得:“共径圆”的面积πr 2=25π,故答案为25π;(2)作OB ⊥直线l 于B 交圆O 于点A ,此时点,A B 的“共径圆”的半径最小值; 设直线4y x =-+与,x y 轴交于点,M N .()4,00,4()M N ∴,),则ON=OM=4,∴ MON △等腰直角三角形, ∴224244=+=MN∴О点到直线MN 的距离为22A 点在O 上,B 点在直线4y x =-+上,A B ∴间的最短距离是221-即,A B 的“共径圆”的最小半径是221-(3)设点B 的坐标为(x ,x+b ),设AB 之间的距离为r ,则πr 2=4π,解得r=2(负值已舍去),则AB=x 2+(x+b )2=22=4,化简得:2x 2+2bx+b 2-4=0,∵满足条件的B 点有2个,故△=(2b )2-2×4(b 2-4)>0,解得:2222,-<<b∵点B 是x 轴及x 轴上方的点,故b >0,而当b=2时,点B 在x 轴上,∴222b ≤<【点睛】本题为圆的综合题,涉及到一次函数的性质、根的判别式等,这种新定义类的题目,通常按照题设的顺序逐次求解,一般比较容易解答.26.这段弯路的半径为250米.【分析】设这段弯路的半径为R 米,可得50OFOE EF R .由垂径定理得 11300150()22CF CD m .由勾股定理可得222OC CF OF =+,解得 R 的值.【详解】解:连接OC .设这段弯路的半径为R 米则50OF OE EF ROE CD ⊥ 11300150()22CF CD m . 根据勾股定理,得222OC CF OF =+ 即()22215050R R =+- 解之,得250R =所以这段弯路的半径为250米.【点睛】本题考查了垂径定理及勾股定理的应用,熟悉相关性质是解题的关键.。
中考数学《第四章》单元达标测试(四)含答案

单元达标测试(四)(第四章)(时间:120分钟 满分:120分)一、选择题(每小题3分,共30分)1.长度分别为2,7,x 的三条线段能组成一个三角形,x 的值可以是CA .4B .5C .6D .92.如图,BD ∥AC ,BE 平分∠ABD ,交AC 于点E.若∠A =50°,则∠1的度数为AA .65°B .60°C .55°D .50°,第2题图) ,第3题图) ,第4题图) ,第6题图)3.如图,点P 是∠AOB 平分线OC 上一点,PD ⊥OB ,垂足为D ,若PD =2,则点P 到边OA 的距离是AA .2B .3C . 3D .44.在正方形网格中,△ABC 的位置如图所示,则cos B 的值为BA .12B .22C .32D .33 5.已知下列命题:①若a b>1,则a >b ;②若a +b =0,则|a|=|b|;③等边三角形的三个内角都相等;④底角相等的两个等腰三角形全等.其中原命题与逆命题均为真命题的个数是AA .1个B .2个C .3个D .4个6.某楼梯的侧面如图所示,已测得BC 的长约为3.5 m ,∠BCA 约为29°,则该楼梯的高度AB 可表示为AA .3.5sin 29° mB .3.5cos 29° mC .3.5tan 29° mD . 3.5cos 29°m 7.)如图:在△ABC 中,CE 平分∠ACB ,CF 平分∠ACD ,且EF ∥BC 交AC 于点M ,若CM =5,则CE 2+CF 2等于BA .75B .100C .120D .125,第7题图) ,第8题图) ,第9题图),第10题图)8.如图是由8个全等的矩形组成的大正方形,线段AB的端点都在小矩形的顶点上,如果点P是某个小矩形的顶点,连接PA,PB,那么使△ABP为等腰直角三角形的点P的个数是BA.2个B.3个C.4个D.5个9.如图,△ABC中,∠A=2∠B,CD⊥AB于点D,已知AB=10,AD=2,则AC 的长为BA.5 B.6 C.7 D.810.如图,将一个等腰Rt△ABC对折,使∠A与∠B重合,展开后得折痕CD,再将∠A 折叠,使C落在AB上的点F处,展开后,折痕AE交CD于点P,连接PF,EF,下列结论:①tan∠CAE=2-1;②图中共有4对全等三角形;③若将△PEF沿PF翻折,则点E 一定落在AB上;④PC=EC;⑤S四边形DFEP=S△APF.正确的个数是DA.1个B.2个C.3个D.4个二、填空题(每小题3分,共24分)11.在“三角尺拼角”实验中,小明同学把一副三角尺按如图所示的方式放置,则∠1=120°.,第11题图),第12题图),第13题图),第14题图)12.如图,四边形ABCD中,AD∥BC,∠A=110°,则∠B=70°.13.)如图,BC∥EF,AC∥DF,添加一个条件AB=DE或BC=EF或AC=DF或AD =BE(只需添加一个即可),使得△ABC≌△DEF.14.如图,在△ABC中,以点B为圆心,以BA长为半径画弧交边BC于点D,连接AD.若∠B=40°,∠C=36°,则∠DAC的度数是34°.15.如图,在直角△ABC中,∠BAC=90°,AB=8,AC=6,DE是AB边的垂直平分线,垂足为D,交边BC于点E,连接AE,则△ACE的周长为16.,第15题图),第16题图),第17题图),第18题图) 16.如图①,这个图案是我国汉代的赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”.此图案的示意图如图②,其中四边形ABCD 和四边形EFGH 都是正方形,△ABF 、△BCG 、△CDH 、△DAE 是四个全等的直角三角形.若EF =2,DE =8,则AB 的长为10.17.如图,在一笔直的沿湖道路l 上有A ,B 两个游船码头,观光岛屿C 在码头 A 北偏东60°的方向,在码头 B 北偏西45°的方向,AC =4 km .游客小张准备从观光岛屿C 乘船沿CA 回到码头A 或沿CB 回到码头B ,设开往码头A ,B 的游船速度分别为v 1,v 2,若回到 A ,B 所用时间相等,则v 1v 2=2(结果保留根号). 18.如图,在△ABC 中,AB =AC ,AD ,CE 是△ABC 的两条中线,P 是AD 上一个动点,则图中线段的长度等于BP +EP 最小值的是CE.(填图中的已知线段)三、解答题(共66分)19.(8分)如图,点E ,F 在BC 上,BE =FC ,AB =DC ,∠B =∠C.求证:∠A =∠D.证明:∵BE =FC ,∴BE +EF =CF +EF ,即BF =CE.又∵AB =DC ,∠B =∠C ,∴△ABF ≌△DCE(SAS ).∴∠A =∠D.20.(8分)如图,在△ABC 中,点D 是∠ACB 的平分线与∠ABC 的平分线的交点,BD 的延长线交AC 于点E.(1)∠AEB 、∠EDC 、∠DCB 的大小关系是∠AEB >∠EDC >∠DCB ,理由是三角形的一个外角大于任何一个和它不相邻的内角.(2)已知∠EDC =60°,求∠A 的度数.解:∵∠EDC 是△CDB 的一个外角,∴∠EDC =∠DCB +∠DBC.∵∠EDC =60°,∴∠DCB +∠DBC =60°.∵DC 平分∠ACB ,DB 平分∠ABC ,∴∠ACB =2∠DCB ,∠ABC =2∠DBC.∴∠ACB +∠ABC =2(∠DCB +∠DBC)=2×60°=120°.∴∠A =180°-(∠ACB +∠ABC)=60°.21.(8分)如图,线段AB ,CD 分别表示甲乙两建筑物的高,BA ⊥AD ,CD ⊥DA ,垂足分别为点A ,D.从D 点测到B 点的仰角α为60°,从C 点测得B 点的仰角β为30°,甲建筑物的高AB =30 m .(1)求甲、乙两建筑物之间的距离AD.(2)求乙建筑物的高CD.解:(1)在Rt △ABD 中,AD =AB tan α=303=103(m ). (2)作CE ⊥AB 于点E ,在Rt △BCE 中,CE =AD =10 3 m ,BE =CE·tan β=103×33=10(m ),则CD =AE =AB -BE =30-10=20(m ).答:乙建筑物的高度DC 为20 m .22.(10分)如图,已知AC ,BD 为竖直的墙面,一架梯子从点O 竖起,当靠在墙面AC 上时,梯子的另一端落在点A 处,此时∠AOC =60°,当靠在墙面BD 上时,梯子的另一端落在点B 处,此时∠BOD =45°,且OD =3 2 m .(1)求梯子的长;(2)求OC ,AC 的长.解:(1)∵由题意得,∠BDO =90°,∠BOD =45°,∴∠B =45°.∴OD =BD =32(m ).在Rt △OBD 中,OB =OD 2+BD 2=6(m ),∴梯子的长是6 m .(2)∵∠ACO =90°,∠AOC =60°,OA =OB =6 m ,∴∠CAO =30°.∴OC =12AO =3 m .在Rt △ACO 中,AC =AO 2-OC 2=27=3 3 m .23.(10分)如图,AD ∥BC ,∠BAC =70°,DE ⊥AC 于点E ,∠D =20°.(1)求∠B 的度数,并判断△ABC 的形状;(2)若延长线段DE 恰好过点B ,试说明DB 是∠ABC 的平分线.解:(1)∵DE ⊥AC 于点E ,∠D =20°,∴∠CAD =70°.∵AD ∥BC ,∴∠C =∠CAD =70°.∵∠BAC =70°,∴∠B =40°,BA =BC.∴△ABC 是等腰三角形.(2)∵延长线段DE 恰好过点B ,DE ⊥AC ,∴BD ⊥AC.∵△ABC 是等腰三角形,BA =BC ,∴DB 是∠ABC 的平分线.24.(10分))如图①所示,在△ABC 中,∠ACB 为锐角,点D 为射线BC 上一动点,连接AD ,以AD 为直角边,A 为直角顶点,在AD 左侧作等腰直角三角形ADF ,连接CF ,AB =AC ,∠BAC =90°.(1)当点D 在线段BC 上时(不与点B 重合),线段CF 和BD 的数量关系与位置关系分别是什么?请给予证明;(2)当点D 在线段BC 的延长线上时,(1)的结论是否仍然成立?请在图②中画出相应的图形,并说明理由.解:(1)CF =BD ,且CF ⊥BD ,证明如下:∵∠FAD =∠CAB =90°,∴∠FAC =∠DAB.在△ACF 和△ABD 中,⎩⎪⎨⎪⎧AB =AC ∠CAF =∠BAD AD =AF,∴△ACF ≌△ABD.∴CF =BD ,∠FCA =∠B.∴∠FCD =∠FCA +∠ACD =∠B +∠ACD =90°.∴CF ⊥BC ,故CF =BD ,且CF ⊥BD.(2)(1)的结论仍然成立,如图所示,∵∠CAB =∠DAF =90°,∴∠CAB +∠CAD =∠DAF +∠CAD ,即∠CAF =∠BAD ,在△ACF 和△ABD 中,⎩⎪⎨⎪⎧AB =AC ∠CAF =∠BAD AD =AF,∴△ACF ≌△ABD(SAS ).∴CF =BD ,∠ACF =∠B.∵AB =AC ,∠BAC =90°,∴∠B =∠ACB =45°.∴∠BCF =∠ACF +∠ACB =45°+45°=90°.∴CF ⊥BD.∴CF =BD ,且CF ⊥BD.25.(12分)定义:数学活动课上,李老师给出如下定义:如果一个三角形有一边上的中线等于这条边的一半,那么称这个三角形为“智慧三角形”.理解:(1)如图①,已知A ,B 是⊙O 上两点,请在圆上找出满足条件的点C ,使△ABC 为“智慧三角形”(画出点C 的位置,保留作图痕迹);(2)如图②,在正方形ABCD 中,E 是BC 的中点,F 是CD 上一点,且CF =14CD ,试判断△AEF 是否为“智慧三角形”,并说明理由;运用:(3)如图③,在平面直角坐标系xOy 中,⊙O 的半径为1,点Q 是直线y =3上的一点,若在⊙O 上存在一点P ,使得△OPQ 为“智慧三角形”,当其面积取得最小值时,直接写出此时点P 的坐标.解:(1)如图所示.(2)△AEF 为“智慧三角形”,理由如下:设正方形的边长为4a ,∵E 是BC 的中点,∴BE =CE =2a.∵DC ∶FC =4∶1,∴FC =a ,DF =4a -a =3a.在Rt △ABE 中,AE 2=(4a)2+(2a)2=20a 2,在Rt △ECF 中,EF 2=(2a)2+a 2=5a 2,在Rt △ADF 中,AF 2=(4a)2+(3a)2=25a 2,∴AE 2+EF 2=AF 2.∴△AEF 是直角三角形,∴斜边AF 上的中线等于AF 的一半,∴△AEF 为“智慧三角形”.(3)如图所示.由“智慧三角形”的定义可得△OPQ 为直角三角形,根据题意可得一条直角边为1,当斜边最短时,另一条直角边最短,则面积取得最小值,由垂线段最短可得斜边最短为3,由勾股定理可得PQ =32-12=22,PM =1×22÷3=223,由勾股定理可求得OM =13,故点P 的坐标(-223,13),(223,13).。
新人教版初中数学九年级数学上册第四单元《圆》检测卷(有答案解析)(1)

一、选择题1.如图,AC 为半圆的直径,弦3AB =,30BAC ∠=︒,点E 、F 分别为AB 和AC 上的动点,则BF EF +的最小值为( )A .3B .332C .3D .332+ 2.如图,A 是B 上任意一点,点C 在B 外,已知2AB =,4BC =,ACD △是等边三角形,则BCD △的面积的最大值为( )A .434+B .43C .438+D .63 3.已知正方形的边长a ,其内切圆的半径为r ,外接圆的半径为R ,则::R r a =( ) A .2:1:2B .2:1:1C .2:1:1D .2:2:4 4.已知O 的直径10CD cm ,AB 是O 的弦,AB CD ⊥,垂足为M ,且8AB cm =,则AC 的长为( ) A .25B .43C .25或45D .23或43 5.已知△ABC 的外心为O ,连结BO ,若∠OBA=18°,则∠C 的度数为( )A .60°B .68°C .70°D .72°6.如图,不等边ABC 内接于O ,下列结论不成立的是( )A .12∠=∠B .14∠=∠C .2AOB ACB ∠=∠D .23ACB ∠=∠+∠ 7.已知O 的半径为5,若4PO =,则点P 与O 的位置关系是( ) A .点P 在O 内 B .点P 在O 上 C .点P 在O 外 D .无法判断 8.如图,O 的半径为5,弦AB 的长为8,M 是弦AB 上的一个动点,则线段OM 可取的整数值有( )个A .1B .2C .3D .4 9.如图,⊙O 的半径为2,四边形ADBC 为⊙O 的内接四边形,AB =AC ,∠D =112.5°,则弦BC 的长为( )A .2B .2C .22D .23 10.如图,AB 为⊙O 的直径,,C D 为⊙O 上的两点,若7OB BC ==.则BDC ∠的度数是( )A .15︒B .30C .45︒D .60︒11.如图,在平行四边形ABCO 中,45C ∠=︒,点A ,B 在O 上,点D 在ADB 上,DA DB =,则AOD ∠的度数为( )A .112.5°B .120°C .135°D .150°12.如图,AB 是⊙O 的直径,AB=AC 且∠BAC=45°,⊙O 交BC 于点D ,交AC 于点E ,DF 与⊙O 相切,OD 与BE 相交于点H .下列结论错误的是( )A .BD=CDB .四边形DHEF 为矩形C .2AE DE= D .BC=2CE 二、填空题13.一排水管截面如图所示,截面半径13dm OA =,水面宽10dm AB =,则圆心O 到水面的距离OC =______dm .14.将面积为3πcm 2的扇形围成一个圆锥的侧面,若扇形的圆心角是120°,则该圆锥底面圆的半径为_____cm .15.已知O 的面积为π,则其内接正六边形的边长为______.16.如图,A 是半径为1的O 外一点,2OA =,AB 是O 的切线,点B 是切点,弦//BC OA ,连接AC ,则图中阴影部分的面积为________.17.如图,已知BD 是⊙O 的直径,点A ,C 在⊙O 上,58AOB ∠=,B 是弧AC 的中点,则BDC ∠的度数为___________.18.如图,O 是正方形ABCD 的外接圆,2,AB =点E 是劣弧AD 上的任意一点,连接BE ,作CF BE ⊥于点F ,连接,AF 则当点E 从点A 出发按顺时针方向运动到点D 时,AF 长的取值范围为________________.19.如图,直线33y x =+交x 轴于点A ,交y 轴于点B .以A 为圆心,以AB 为半径作弧交x 轴于点A 1;过点A 1作x 轴的垂线,交直线 AB 于点B 1,以A 为圆心,以AB 1为半径作弧交x 轴于点 A 2;…,如此作下去,则点n A 的坐标为___________;20.在半径为4cm 的圆中,长为4cm 的弦所对的圆周角的度数为________三、解答题21.如图,菱形ODCE 的顶点C 在扇形AOB 的弧AB 上,D 、E 在弦AB 上.(1)求证:AD BE =.(2)已知扇形的半径为2,当AD DO =时,求图中阴影部分的面积.22.如图,已知,90Rt ABC ACB ∆∠=︒.(1)请在图中用无刻度的直尺和圆规作一个圆,使得圆心О在边AC 上,且与边,AB BC 所在直线相切(不写作法,保留作图痕迹);(2)在(1)的条件下,若9,12AC BC ==,求O 的半径. 23.如图,AC 为O 的直径,4AC =,B 、D 分别在AC 两侧的圆上,60BAD ∠=︒,BD 与AC 的交点为E .(1)求点O 到BD 的距离及OBD ∠的度数;(2)若2DE BE =,求cos OED ∠的值和CD 的长.24.如图,在33⨯的网格中有一个圆,请仅用无刻度直尺作图(保留画图痕迹).(1)在图1中,圆过格点A ,B ,请作出圆心O ;(2)在图2中,⊙O 的两条弦AB CD =,请作一个45圆周角.25.如图,AB 为⊙O 的直径,C ,D 是⊙O 上的点,P 是⊙O 外一点,AC ⊥PD 于点E ,AD 平分∠BAC .(1)求证:PD 是⊙O 的切线;(2)若DE=3,,∠BAC=60°,求⊙O 的半径.26.已知PA 、PB 分别与O 相切于点A ,B 两点,76APB ∠=︒ ,C 为O 上一点. (1)如图,求ACB ∠的大小; (2)如图,AE 为O 的直径,AE 与BC 相交于点D ,若AB AD =,求EAC ∠的大小.【参考答案】***试卷处理标记,请不要删除一、选择题1.B解析:B【分析】作B 点关于直径AC 的对称点B′,过B′点作B′E ⊥AB 于E ,交AC 于F ,如图,利用两点之间线段最短和垂线段最短可判断此时FB +FE 的值最小,再判断△ABB′为等边三角形,然后计算出B′E 的长即可.【详解】解:作B 点关于直径AC 的对称点B′,过B′点作B′E ⊥AB 于E ,交AC 于F ,如图,则FB =FB′,∴FB +FE =FB′+FE =B′E ,此时FB +FE 的值最小,∵∠BAC =30°,∴∠B′AC =30°,∴∠BAB′=60°,∵AB =AB′,∴△ABB′为等边三角形,∵B′E ⊥AB ,∴AE =BE =32, ∴B′E 3=332, 即BF +EF 33. 故选:B .【点睛】本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.也考查了等腰三角形的性质.2.A解析:A【分析】以BC 为边作等边BCM ,连接DM ,则DCM CAB ≅△△,根据全等三角形的性质得到DM=AB=2为定值,即点D 在以M 为圆心,半径为2的圆上运动,当点D 运动至BC 为中垂线与圆的交点时,BC 边上的高取最大值为232,根据三角形的面积即可得到结论.【详解】解:以BC 为边作等边BCM ,连接DM ,∵60DCA MCB ==∠∠,∴DCM ACB =∠∠,∵DC=AC ,MC=BC ,∴DCM CAB ≅△△(SAS ),∴DM=AB=2为定值,即点D 在以M 为圆心,半径为2的圆上运动,当点D 运动至BC 为中垂线与圆的交点时,BC 边上的高取最大值为232+, 此时面积为:434+故选:A【点睛】本题考查了等边三角形的性质,三角形面积的计算,找出点D 的位置是解题的关键. 3.A解析:A【分析】经过圆心O 作正方形一边AB 的垂线OC ,垂足是C .连接OA ,则在直角△OAC 中,∠AOC=45°.OC 是边心距r ,OA 即半径R ,进而即可求解【详解】如图:作出正方形的边心距,连接正方形的一个顶点和中心可得到一直角三角形 在中心的直角三角形的角为360°÷4÷2=45°,∴内切圆的半径为2a ,外接圆的半径为2a , ∴::R r a =22a :2a :a=2:1:2 故选A【点睛】本题主要考查正多边形的外接圆与内切圆的半径,掌握相关概念,作出图形,是解题的关键.4.C解析:C【分析】连结OA ,由AB CD ⊥,根据垂径定理可以得到4AM =,结合勾股定理可以得到3OM =.在分类讨论,如图,当8CM =和2CM =时,再结合勾股定理即可求出AC .【详解】连结OA ,∵AB CD ⊥, ∴118422AM BM AB ===⨯=, 在Rt OAM 中,5OA =,∴223OA OM AM -==,当如图时,538CM OC OM =+=+=,在Rt ACM △中,2245AC AM CM =+=,当如图时,532CM OC OM =-=-=,在Rt ACM △中,2225AC AM CM +=故选C .【点睛】 本题考查垂径定理“垂直于弦的直径平分弦且平分这条弦所对的两条弧”.分类讨论思想也是解决本题的关键.5.D解析:D【分析】连接OA ,则OA=OB ,可得∠OBA=∠OAB ,再结合∠OBA=18°即可求得∠AOB=144°,再根据圆周角的性质即可求得∠C=72°.【详解】解:如图,连接OA ,∵点O为ABC的外心,∴OA=OB,∴∠OBA=∠OAB,又∵∠OBA=18°,∴∠OAB=∠OBA=18°,∴∠AOB=180°-∠OAB-∠OBA=144°,∠AOB=72°,∴∠C=12故选:D.【点睛】本题考查了三角形的外心,圆周角定理,熟练掌握相关定义及性质是解决本题的关键.6.B解析:B【分析】利用OB=OC可对A选项的结论进行判断;由于AB≠BC,则∠BOC≠∠AOB,而∠BOC=180°-2∠1,∠AOB=180°-2∠4,则∠1≠∠4,于是可对B选项的结论进行判断;根据圆周角定理可对C选项的结论进行判断;利用∠OCA=∠3,∠1=∠2可对D选项的结论进行判断.【详解】解:∵OB=OC,∴∠1=∠2,所以A选项的结论成立;∵OA=OB,∴∠4=∠OBA,∴∠AOB=180°-∠4-∠OBA=180°-2∠4,∵△ABC为不等边三角形,∴AB≠BC,∴∠BOC≠∠AOB,而∠BOC=180°-∠1-∠2=180°-2∠1,∴∠1≠∠4,所以B选项的结论不成立;∵∠AOB与∠ACB都对弧AB,∴∠AOB=2∠ACB,所以C选项的结论成立;∵OA=OC,∴∠OCA=∠3,∴∠ACB=∠1+∠OCA=∠2+∠3,所以D选项的结论成立.故选:B.本题考查了三角形的外接圆与外心:三角形外接圆的圆心是三角形三条边垂直平分线的交点,叫做三角形的外心.也考查了圆周角定理和等腰三角形的性质.7.A解析:A【分析】已知圆O的半径为r,点P到圆心O的距离是d,①当r>d时,点P在⊙O内,②当r=d 时,点P在⊙O上,③当r<d时,点P在⊙O外,根据以上内容判断即可.【详解】∵⊙O的半径为5,若PO=4,∴4<5,∴点P与⊙O的位置关系是点P在⊙O内,故选:A.【点睛】本题考查了点与圆的位置关系的应用,注意:已知圆O的半径为r,点P到圆心O的距离是d,①当r>d时,点P在⊙O内,②当r=d时,点P在⊙O上,③当r<d时,点P在⊙O外.8.C解析:C【分析】当M与A或B重合时,达到最大值;当OM⊥AB时,为最小,从而确定OM的取值范围即可解决问题.【详解】解:如图所示,过O作OM′⊥AB,连接OA,∵过直线外一点与直线上的所有连线中垂线段最短,∴当OM于OM′重合时OM最短,∵AB=8,OA=5,∴AM′=1×8=4,2∴在Rt△OAM′中,2222-'=3,OA AM=-54∴线段OM长的最小值为3,最大值为5.所以,OM的取值范围是:3≤OM≤5,故线段OM长的整数值为3,4,5,共3个.【点睛】本题考查的是勾股定理和最值.本题容易出现错误的地方是对点M的运动状态不清楚,无法判断什么时候会为最大值,什么时候为最小值.9.C解析:C【分析】如图:连接OB、O C,先根据圆的内接四边形对角互补得到∠C=67.5°,再利用等腰三角形的性质和三角形内角和计算出∠BAC=45°,再根据圆周角定理可得∠BOC=90°,最后根据勾股定理求解即可.【详解】解:∵四边形ADBC为⊙O的内接四边形,∠D=112.5°∴∠C=180°-∠D=180°-112.5°=67.5°∵AC=AB∴∠BAC=180°-2∠C=45°∴∠BOC=90°∴BC=2222+=+=.OB OC2222故答案为C.【点睛】本题考查了圆内接四边形的性质、等腰直角三角形的性质和圆周角定理,掌握圆内接四边形的对角互补是解答本题的突破口.10.B解析:B【分析】=,再根据等边三角形的判定与性质可得如图(见解析),先根据圆的性质可得OC OB∠=︒,然后根据圆周角定理即可得.BOC60【详解】如图,连接OC,=,由同圆半径相等得:OC OB==,OB BC7∴==,OC OB BCBOC ∴是等边三角形,60BOC ∴∠=︒, 由圆周角定理得:1230BOC BDC ∠=︒=∠, 故选:B .【点睛】本题考查了等边三角形的判定与性质、同圆半径相等、圆周角定理,熟练掌握等边三角形的判定与性质是解题关键.11.C解析:C【分析】延长DO 交AB 于点H ,连接OB ,证明△△AOD BOD ≅,OD 是AOB ∠的角平分线,求得290345∠=︒-∠=︒,进行求解即可;【详解】延长DO 交AB 于点H ,连接OB ,∵四边形ABCD 是平行四边形,45C ∠=︒,∴345∠=︒,∵DA DB =,OA OB =,∴△△AOD BOD ≅,∴OD 是AOB ∠的角平分线,又∵AO BO =,∴DH AB ⊥,∴290345∠=︒-∠=︒,又∵221∠=∠,∴18045135AOD ∠=︒-︒=︒.故选:C.【点睛】本题主要考查了与圆有关的计算,结合全等三角形的性质和角平分线的性质计算即可.12.D解析:D【分析】A、利用直径所对的圆周角是直角,以及等腰三角形的三线合一性质即可得出结论;B、根据中位线得出OD//AC,再根据矩形的判定即可得出结论C、根据垂径定理得出BD DE=,再根据等腰直角三角形的性质得出AE=BE,从而得出=,即可得出2BD DEAE DE=D、不能得出BC=2CE【详解】解:连接AD∵AB为⊙O的直径,∴∠BDA=∠BEA =90°,即AD⊥BC,又∵AB=AC,∴BD=DC,∠BAD=∠DAE,故A正确;∵OA=OB∴OD是三角形ABC的中位线∴OD//AC∴∠DHE =90°=∠BEF,∵DF与⊙O相切,∴∠ODF =90°∴四边形DHEF为矩形故B正确;∵∠BEA =90°,∠BAC=45°,∴AE=BE∴AE BE=∵∠DHE =90°∴OD⊥BE∴BD DE=∴2=AE DE故C正确;不能得出BC=2CE故选:D【点睛】本题考查了切线的性质、三线合一定理、三角形中位线定理、垂径定理;熟练掌握等腰三角形的性质和圆周角定理,并能进行推理论证是解决问题的关键.二、填空题13.12【分析】根据垂径定理求出AC=5dm 再根据勾股定理求出OC 即可【详解】∵OC ⊥AB ∴AC=5dm 在Rt △AOC 中∴OC==12dm 故答案为:12【点睛】此题考查垂径定理勾股定理熟记垂径定理是解题解析:12【分析】根据垂径定理求出AC=5dm ,再根据勾股定理求出OC 即可.【详解】∵OC ⊥AB ,10dm AB =,∴AC=5dm ,在Rt △AOC 中,13dm OA =,∴2222135OA AC -=-,故答案为:12【点睛】此题考查垂径定理,勾股定理,熟记垂径定理是解题的关键.14.1【分析】直接利用已知得出圆锥的母线长再利用圆锥侧面展开图与各部分对应情况得出答案【详解】解:设圆锥的母线长为Rcm 底面圆的半径为rcm ∵面积为3πcm2的扇形围成一个圆锥的侧面扇形的圆心角是120解析:1【分析】直接利用已知得出圆锥的母线长,再利用圆锥侧面展开图与各部分对应情况得出答案.【详解】解:设圆锥的母线长为Rcm ,底面圆的半径为rcm ,∵面积为3πcm 2的扇形围成一个圆锥的侧面,扇形的圆心角是120°, ∴2120360R π⨯=3π,解得:R =3,由题意可得:2πr =1203180π⨯, 解得:r =1.故答案为:1.【点睛】此题主要考查了圆锥的计算,正确得出母线长是解题关键. 15.1【分析】首先根据圆的面积求出圆的半径再证明△AOB 是等边三角形即可得到结论【详解】解:如图的面积为设半径为r ∴解得∵OA=OB 为等边三角形故故答案为:1【点睛】本题考查的是正多边形和圆熟知正六边形解析:1【分析】首先根据圆的面积求出圆的半径,再证明△AOB 是等边三角形即可得到结论. 【详解】解:如图,O 的面积为π,设半径为r ,2S r ππ∴==,∴21r =,解得,1r =,∵360606AOB ︒∠==︒,OA=OB AOB ∴为等边三角形,故1AB OA ==.故答案为:1【点睛】本题考查的是正多边形和圆,熟知正六边形的半径与边长相等是解答此题的关键. 16.【分析】连接OCOB 易证△OAB 为等边三角形由BC ∥OA 得S △OCB =S △ACB 把阴影部分的面积转化为扇形OBC 的面积【详解】连接OCOB ∵是的切线∴OB ⊥AB 在Rt △OBA 中∵OB=1OA=2∴∠解析:6π【分析】连接OC ,OB ,易证△OAB 为等边三角形,由BC ∥OA ,得S △OCB =S △ACB ,把阴影部分的面积转化为扇形OBC 的面积.【详解】连接OC ,OB∵AB 是O 的切线∴OB ⊥AB在Rt △OBA 中∵OB=1,OA=2∴∠AOB=60°又∵//BC OA∴∠OBC=60°∵OB=OC∴△OAB 为等边三角形又∵BC ∥OA ∴S △OCB =S △ACB∴S 阴=S 扇形OBC =2601360π⨯⨯ =6π故答案为:6π 【点睛】 本题考查扇形面积的求解,将不规则图形转化成规则的扇形是解题的关键.17.29°【分析】先由是弧的中点可得再根据圆周角定理可得结果【详解】解:连接OC ∵是弧的中点∴∴∠BOC=∠AOB=58°∴∠BDC==29°故答案为29°【点睛】本题考查了圆周角定理掌握圆周角定理是解解析:29°【分析】先由B 是弧AC 的中点,可得AB BC = ,再根据圆周角定理可得结果.【详解】解:连接OC ,∵B 是弧AC 的中点,∴AB BC =.∴∠BOC=∠AOB=58°∴∠BDC=1582⨯︒=29°. 故答案为29°.【点睛】 本题考查了圆周角定理,掌握圆周角定理是解题的关键.18.【分析】首先根据题意可知当点与点重合时最长的最大值为;再证明点的运动轨迹为以为直径的通过添加辅助线连接交于点连接由线段公理可知当点与点重合时最短的最小值为即可得解【详解】解:∵由题意可知当点与点重合 解析:512AF -≤≤【分析】首先根据题意可知,当点F 与点B 重合时AF 最长,AF 的最大值为2;再证明点F 的运动轨迹为以BC 为直径的'O ,通过添加辅助线连接'AO 交'O 于点M ,连接'O F ,由线段公理可知,当点F 与点M 重合时AF 最短,AF 的最小值为51-.即可得解.【详解】解:∵由题意可知,当点F 与点B 重合时AF 最长∴此时2AF AB ==,即AF 的最大值为2∵CF BE ⊥∴90CFB ∠=︒∴点F 的运动轨迹为以BC 为直径的'O ,连接'AO 交'O 于点M ,连接'O F ,如图:∵2AB =∴11'122BO BC AB === ∴在'Rt ABO 中,22''5AO AB BO =+=∴''51AM AO O M =-=∴由两点之间,线段最短可知,当点F 与点M 重合时AF 最短∴AF1∴AF≤≤.12【点睛】本题考查了正多边形和圆的动点问题、90︒的圆周角所对的弦为直径、勾股定理、线段公理等知识点,解题的关键是确定AF取最大值和最小值时点F的位置,属于中考常考题型,难度中等.19.(2n﹣10)【分析】根据题意先求出点AB的坐标再利用勾股定理求出AA1AA2AA3……AAn的长可得到点A1A2A3……An的坐标找到规律即可解答【详解】解:当x=0时y=当y=0时x=﹣1∴A(解析:(2n﹣1,0)【分析】根据题意,先求出点A、B的坐标,再利用勾股定理求出AA1、AA2、AA3……AA n的长,可得到点A1、A2、A3……A n的坐标,找到规律即可解答.【详解】解:当x=0时,y=0时,x=﹣1,∴A(﹣1,0),B(0,∴AA=,则点A1(1,0),B1(1,,12∴AA=,则点A2(3,0),B2(3,,2=AB14∴AA=,则点A3(7,0),B3(7,,3=AB28……∴可以得到A n的坐标为(2n﹣1,0),故答案为:(2n﹣1,0).【点睛】本题考查了一次函数图象上的点的坐标特征、图形的规律探究、圆的基本知识、勾股定理,解答的关键是利用勾股定理求得AA1、AA2、AA3……AA n的长,进而得到A1、A2、A3……A n的坐标的变化规律.20.或【分析】首先根据题意画出图形然后在优弧上取点C连接ACBC在劣弧上取点D连接ADBD易得是等边三角形再利用圆周角定理即可得出答案【详解】解:如图在优弧上取点C连接ACBC在劣弧上取点D连接ADBD解析:30或150︒【分析】首先根据题意画出图形,然后在优弧上取点C,连接AC、BC,在劣弧上取点D,连接AD、BD,易得OAB是等边三角形,再利用圆周角定理,即可得出答案.【详解】解:如图,在优弧上取点C,连接AC、BC,在劣弧上取点D,连接AD、BD,4,4OA OB cm AB cm OA OB AB===∴== OAB ∴是等边三角形,601302180150AOB C AOB D C ∴∠=︒∴∠=∠=︒∴∠=︒-∠=︒∴所对的圆周角度数为:30或150︒故答案为:30或150︒.【点睛】本题考查圆周角定理及等边三角形的判定与性质,注意两种情况.三、解答题21.(1)证明见解析;(2)2233π-【分析】(1)利用菱形的性质证明ODA OEB ∠=∠,接着证明(AAS)OAD OBE ≌,就可以得到结论;(2)连接OC 与AB 交于点F ,用勾股定理算出AF 的长,设DF EF x ==,列式求出x 的值,阴影部分的面积用扇形面积减去两个三角形面积和一个菱形面积进行求解.【详解】解:(1)∵四边形ODCE 是菱形, CDO CEO ∴∠=∠,DE 是菱形的对角线,ODE OED ∴∠=∠,180180ODE OED ∴︒-∠=︒-∠,即ODA OEB ∠=∠,OA OB =,OAD OBE ∴∠=∠,∴在OAD △和OBE △中,OAD OBE ODE OED OA OB ∠=∠⎧⎪∠=∠⎨⎪=⎩,(AAS)OAD OBE ∴≌△△,AD BE ∴=;(2)如图,连接OC 与AB 交于点F ,则DF EF =,2OA OB OC ===,OC DE ⊥,112122OF OC ==⨯=, 2222213AF OA OF ∴-=-,设DF EF x ==, 则2221OD DF OF x ++21AD OD x ∴==+21AF AD DF x x ∴=+=+,213x x +=33x =, 22313AD BE x OD ∴==+==,23223DE DF x ===, OD DE OE ∴==, ODE ∴是等边三角形,60DOE ODE OED ∴∠=∠=∠=︒,1302DAO DOA EDO ∴∠=∠=∠=︒, ∵由(1)知OAD OBE ≌△△,30AOD BOE ∴∠=∠=︒,120AOB AOD DOE BOE ∠=∠+∠+∠=︒,OAD OBE OAB ODCE S S S S S ∴=---阴影扇形菱形△△2OAD OAB ODCE S S S =--菱形菱形△120123602OA AD OF DE OC π⋅=-⨯⋅-⋅120212323212360233π⨯=-⨯⨯⨯-⨯ 22343333π=-- 2233π=-. 【点睛】本题考查几何综合题,解题的关键是掌握菱形的性质,圆的基本性质,扇形面积公式. 22.(1)见解析;(2)O 的半径为4 【分析】(1)先作∠ABC 的角平分线,交AC 于点O ,然后过O 作AB 的垂线,交AB 于E ,以O 为圆心,OE 为半径作圆即可;(2)先利用勾股定理求出AB ,然后由OBC ABO ABC S S S ∆∆∆+=即可求出O 的半径.【详解】解:(1)如图所示:(2)设直线AB 与O 切于点D ,连接OD ,则,OD AB ⊥90,ACB ∴∠=︒22222291215AB AC BC ∴=+=+=.15,AB ∴=设O 的半径为,r由得OBC ABO ABC S S S ∆∆∆+=1215912,r r +=⨯4,r ∴=即O 的半径为4【点睛】本题考查了尺规作图,切线的性质,理解题意熟练掌握角平分线和垂线的作图是解题的关键.23.(1)1,30º;(2)12,22 【分析】(1)作OF ⊥BD 于点F ,连接OD ,根据圆周角定理可得出∠DOB=120º,再由OB=OD=12AC=2,可得出∠OBD 的度数,也可以得出OF 的长度, (2)设BF=2x ,则可表示出DF 、EF 的长度,从而可解出x 的值,在Rt △OEF 中,利用三角函数值的知识可求出∠OED 的度数,也可得出cos ∠OED 的值,判断出DO ⊥AC ,然后利用等腰直角三角形的性质可得出CD 的长度.【详解】(1)作OF ⊥BD 于点F ,连接OD ,∵∠BAD=60º,∴∠BOD=2∠BAD=120º,又∵OB=OD ,∴∠OBD=30º,∵AC 为⊙O 的直径,AC=4,∴OB=OC=2,在Rt △BOF 中,∵∠OFB=90º,OB=2,∠OBF=30º,∴OF=12OB=1, 即点O 到BD 的距离等于1,(2)∵OB=OD ,OF ⊥BD 于点F ,∴BF=DF ,由DE=2BE ,设BE=2x ,则DE=4x ,BD=6x,EF =x,BF=3x ,∵BF=OB•cos30º=3, ∴33,33x EF ==, 在Rt △OEF 中,∠OFE=90º,∵tan ∠OED=OF =3EF, ∴∠OED=60º,cos ∠OED=12, ∴∠BOC=∠OED-∠OBD=30º,∴∠DOC=∠DOE-∠BOE=90º,∴∠C=45º,∴CD=2OC=22.【点睛】本题考查属于圆的综合题,涉及等腰三角形的性质,三角函数值,及勾股定理等知识,解答此类综合性题目,要求我们熟悉掌握一些小知识,做到将所学的知识融会贯通,难度较大.24.(1)见解析;(2)见解析.【分析】(1)如图3,连接AN 、BM ,通过圆内接三角形是直角三角形时,斜边就是直径来确定圆心位置;(2)连接BC 、AD 、BD ,通过同(等)弧所对圆周角相等推出ABD CDB ∠=∠,进而推出45BDC ∠=︒.【详解】(1)如图3,连接AN 、BM 交点O 即为圆心∵9090ABN BAM ∠=︒∠=︒,,∴AN 、BM 是直径,∴直径交点O 就是圆心.(2)如图4,连接BC 、AD 、BD∵AB=CD ,∴AB CD =,∴ADB CBD ∠=∠,又∵AC CA =,∴ABC CDA ∠=∠,∴ABD CDB ∠=∠,又∵90BED ∠=︒,∴45ABD CDB ∠=∠=︒,故连接BD ,则45BDC ∠=︒.【点睛】本题考查确定圆心和确定圆弧圆周角等问题,解题的关键是圆内接三角形是直角三角形时,斜边就是直径以及同(等)弧所对圆周角相等.25.(1)见解析;(2)2【分析】(1)连接OD ,根据角平分线的定义得到∠BAD=∠DAE ,根据等腰三角形的性质得到∠ODA=∠OAD ,由垂直的定义得到∠AEP=90°,根据切线的判定定理即可得到结论; (2)连接BD ,根据角平分线的定义得到∠BAD=∠DAE=30°,推出AB=2BD ,设BD=x ,则AB=2x ,根据勾股定理即可得到结论.【详解】(1)证明:连接OD ,∵AD 平分∠BAC ,∴∠BAD=∠DAE ,∵OA=OD ,∴∠ODA=∠OAD ,∴∠ODA=∠DAE ,∴OD ∥AE ,∵AC ⊥PD ,∴∠AEP=90°,∴∠ODP=∠AEP=90°,∴OD ⊥PE ,∵OD 是⊙O 的半径,∴PD 是⊙O 的切线;(2)解:连接BD ,∵AD 平分∠BAC ,∠BAC=60°,∴∠BAD=∠DAE=30°,∵AC ⊥PE ,∴AD=2DE=∵AB 为⊙O 的直径,∴∠ADB=90°,∴AB=2BD ,设BD=x ,则AB=2x ,∵AD 2+BD 2=AB 2,∴()222(2x x += ∴BD=2,AB=4,∴AO=2,∴⊙O 的半径为2.【点睛】本题考查了切线的判定和性质,勾股定理,角平分线的定义,圆周角定理,含30度角的直角三角形的性质,正确的作出辅助线是解题的关键.26.(1)52︒;(2)19︒【分析】(1)连接OA 、OB ,根据切线的性质得到90OAP OBP ∠=∠=︒,可以求出AOB ∠的度数,再根据圆周角定理得到ACB ∠的度数;(2)连接CE ,根据(1)的结论,先求出BCE ∠的度数,再由圆周角定理得到BAE BCE ∠=∠,再等腰三角形ABD 中求出底角ADB ∠的度数,再由外角和定理就可以求出EAC ∠的度数.【详解】解:(1)如图,连接OA 、OB ,∵PA 、PB 是O 的切线,∴90OAP OBP ∠=∠=︒,∴360909076104AOB ∠=︒-︒-︒-︒=︒, 根据圆周角定理,1522ACB AOB ∠=∠=︒;(2)如图,连接CE ,∵AE 是O 的直径, ∴90ACE ∠=︒,∵52ACB ∠=︒,∴905238BCE ∠=︒-︒=︒,∴38BAE BCE ∠=∠=︒,∵AB AD =,∴71ABD ADB ∠=∠=︒,∴19EAC ADB ACB ∠=∠-∠=︒.【点睛】本题考查圆周角定理和切线的性质,解题的关键是掌握这些性质定理进行求解.。
人教版中考数学考点系统复习 第六章 圆 微专题(六) 隐形圆在解题中的应用

8.★如图,在 Rt△ABC 中,∠C=90°,AC=6,BC=8,点 F 在边 AC 上,
且 CF=2,点 E 为边 BC 上的动点,将△CEF 沿直线 EF 翻折,点 C 落在点
P
处,则点
P
到边
AB
距离的最小值是5
66 5
.
微专(六) 隐形圆在解 题中的应用
模型一:定点定长模型 【模型分析】 平面内,点 A 为定点,点 B 为动点,且 AB 长度固定,则点 B 的轨迹在以 点 A 为圆心,AB 长为半径的圆上(如图①).依据的是圆的定义:圆是所 有到定点的距离等于定长的点的集合.
推广:如图②,点 E 为定点,点 F 为线段 BD 上的动点(不含点 B),将△ BEF 沿 EF 折叠得到△B′EF,则点 B′的运动轨迹为以点 E 为圆心,以线 段 BE 为半径的一段圆弧.
模型六:线圆最值
【模型分析】
已知⊙O 及直线 l,⊙O 的半径为 r,圆心 O 到直线 l 的距离为 d,点 Q 为
⊙O 上一动点.
位置
直线与⊙O
直线与⊙O
直线与⊙O
关系
相离
相切
相交
图示
点 Q 到直
线 l 的距
d+r
2r
d+r
离最大值
此时点 Q 过点 O 作直线 l 的垂线段,其反向延长线与⊙O 的交点,
模型五:点圆最值
【模型分析】
已知平面内一定点 D 和⊙O,点 E 是⊙O 上一动点,当 D,O,E 三点共线
时,线段 DE 有最大(小)值(依据:直径是圆中最长的弦).具体分以下三
种情况讨论(设点 O 与点 D 之间的距离为 d,⊙O 的半径为 r):
位置
点D在
中考数学第六单元测试题(含答案)

中考数学第六单元测试题(含答案)(时间:60分钟分值:100分得分:得分: )一、选择题(本大题10小题,每小题3分,共30分)1.已知⊙O的半径为4,直线l上有一点与⊙O的圆心的距离为4,则直线l与⊙O的位置关系为( )A.相离B.相切C.相交D.相切、相交均有可能2.下列叙述正确的是( )A.平分弦的直径必垂直于弦B.三角形的外心到三边的距离相等C.三角形的内心是三条角平分线的交点D.相等的圆周角所对的弧相等3.如图1,AB是⊙O的直径,点C,D是圆上两点,且∠AOC=126°,则∠CDB=( )图1A.54°B.64°C.27°D.37°4.如图2,△ABC内接于⊙O,AC是⊙O的直径,∠ACB=40°,点D是劣弧BC上一点,连接CD,BD,则∠D的度数是( )图2A.50°B.130°C.140°D.45°5.正多边形的中心角是36°,那么这个正多边形的边数是( )A.10 B.8C.6 D.56.用圆心角为120°,半径为6 cm的扇形纸片卷成一个圆锥形无底纸帽(如图3),则这个纸帽的底面周长是( )图3A.2π cm B.3π cmC.4π cm D.5π cm7.如图4,等边三角形ABC的边长为8,以BC上一点O为圆心的圆分别与边AB,AC相切,则⊙O的半径为( )图4A.2 3 B.3C.4 D.4- 38.如图5,在平面直角坐标系中,⊙A过原点O,分别与x轴、y轴交于点C、点D,点B在⊙A上,已知∠B=30°,⊙A的半径为2,则圆心A的坐标是( )图5A.(3,1) B.(1,3)C.(2,1) D.(1,2)9.如图6,AC是⊙O的直径,弦BD⊥AO于点E,连接BC,过点O作OF⊥BC于点F,若BD=8 cm,AE=2 cm,则OF的长度是( )图6A .3 cmB . 6 cmC .2.5 cmD . 5 cm10.如图7,在Rt △ABC 中,∠C =90°,∠A =30°,BC =2,⊙C 的半径为1,点P 是斜边AB 上的点,过点P 作⊙C 的一条切线PQ(点Q 是切点),则线段PQ 的最小值为( )图7A .1B . 2C . 3D .2 3二、填空题(本大题5小题,每小题4分,共20分)11.如图8,在⊙O 中,AB ︵ =AC ︵,∠B =70°,则∠A = .图812.已知扇形的圆心角的度数为120°,半径为4,则它的面积是 . 13.如图9,已知△ABC 内接于⊙O ,CD 是⊙O 的切线,与半径OB 的延长线交于点D ,若∠A =30°,则∠BCD 的度数为 .图914.如图10,半径为 3 的⊙O与边长为8的等边三角形ABC的两边AB,BC都相切,连接OC,则tan∠OCB=.图1015.如图11,在平行四边形ABCD中,AB<AD,∠A=150°,CD=4,以CD为直径的⊙O 交AD于点E,则图中阴影部分的面积为.图11三、解答题(本大题5小题,共50分)16.(8分)如图12,四边形ABCD内接于⊙O,延长AD,BC相交于点M,延长AB,DC相交于点N,∠M=40°,∠N=20°,求∠A的度数.图1217.(9分)如图13,△ABC是⊙O的内接三角形,AB为⊙O的直径,AB=6,AD平分∠BAC,交BC于点E,交⊙O于点D,连接BD.图13(1)求证:∠BAD =∠CBD ;(2)若∠AEB =125°,求BD ︵的长.(结果保留π)18.(9分)如图14,AC 是⊙O 的直径,AB 是⊙O 的一条弦,AP 是⊙O 的切线.作BM =AB 与AP 交于点M ,延长MB 交AC 于点E ,交⊙O 于点D ,连接AD .图14(1)求证:AB =BE ;(2)若⊙O 的半径R =5,AB =6,求AD 的长.19.(12分)如图15,AB 是⊙O 的直径,弦AC 与BD 交于点E ,且AC =BD ,连接AD ,BC . (1)求证:△ADB ≌△BCA ;(2)若OD ⊥AC ,AB =4,求弦AC 的长;(3)在(2)的条件下,延长AB 至点P ,使BP =2,连接PC .求证:PC 是⊙O 的切线.图1520.(12分)如图16,AB 为△ABC 的外接圆⊙O 的直径,CD =AC ,E 为CB 延长线上一点,DE 与⊙O 相切,交⊙O 于点D .图16(1)求证:CD 平分∠ADE ; (2)求证:DE 2=EB ·CE ;(3)若tan ∠CAB =12,且AB =5,求DE 的长.中考数学第六单元测试题参考答案1.D 2.C 3.C 4.B 5.A 6.C 7.A 8.A 9.D 10.B 11.40° 12.16π3 13.30° 14.35 15.2π3+ 316.∵四边形ABCD 内接于⊙O ,∴∠BCD +∠A =180°,即∠BCD =180°-∠A. ∵∠BCD =∠M +∠MDN =∠M +∠A +∠N , ∴180°-∠A =40°+∠A +20°. 解得∠A =60°.17.(1)证明:∵AD 平分∠BAC ,∴∠CAD =∠BAD. ∵∠CAD =∠CBD ,∴∠BAD =∠CBD.图1(2)如图1,连接OD.∵∠AEB =125°,∴∠AEC =55°. ∵AB 为⊙O 的直径,∴∠ACE =90°. ∴∠CAE =35°. ∴∠DAB =∠CAE =35°.∵OA =OD ,∴∠DAB =∠ADO =35°. ∴∠BOD =2∠BAD =70°. ∵AB =6,∴OB =3.∴BD ︵ 的长为 70×3π180=7π6.18.(1)证明:∵AP 是⊙O 的切线,∴∠EAM =90°. ∴∠BAE +∠MAB =90°,∠AEB +∠AMB =90°. 又AB =BM ,∴∠MAB =∠AMB. ∴∠BAE =∠AEB. ∴AB =BE.(2)如图2,连接BC.图2∵AC 是⊙O 的直径, ∴∠ABC =90°.在Rt △ABC 中,AC =2R =10,AB =6, ∴BC =AC 2-AB 2=8. ∵AB =BE =6,∠EAM =90°, ∴EM =2BE =12.由(1)知,∠BAE =∠AEB ,且∠ABC =∠EAM =90°, ∴△ABC ∽△EAM.∴∠C =∠AME ,EM AC =AM BC .∴1210=AM8.解得AM =485.又∠D =∠C ,∴∠D =∠AMD.∴AD =AM =485.19.(1)证明:∵AB 是⊙O 的直径,∴∠ACB =∠ADB =90°.在Rt △ADB 与Rt △BCA 中,⎩⎪⎨⎪⎧AB =BA ,BD =AC ,∴Rt △ADB ≌Rt △BCA(HL).(2)如图3,连接DC.图3∵OD ⊥AC ,∴AD ︵ =DC ︵. ∴AD =DC.∵△ADB ≌△BCA ,∴AD =BC. ∴AD =DC =BC. ∴∠ABC =60°. ∵AB =4,∴AC =AB ·sin ∠ABC =4×32=2 3. (3)证明:如图3,连接OC.由(1)知AC =23,∴BC =AB 2-AC 2=2. ∴BC =BP =2.∴∠BCP =∠P. ∵∠ABC =60°,∴∠BCP =30°. ∵OC =OB ,∴∠OCB =60°.∴∠OCP =∠OCB +∠BCP =60°+30°=90°. ∴OC ⊥PC.∴PC 是⊙O 的切线. 20.(1)证明:如图4,连接OC ,OD.∵DE 为⊙O 的切线,∠ODE =90°.∴∠EDC +∠CDO =90°. ∵CA =CD ,OA =OD ,OC =OC ,∴△ACO ≌△DCO(SSS). ∴∠CAO =∠CDO.∵AB 为⊙O 的直径,∴∠ACB =90°.∴∠CAO +∠CBA =90°. ∴∠CBA =∠EDC.∵∠CBA =∠CDA ,∴∠EDC =∠CDA. ∴CD 平分∠ADE.(2)证明:如图4,连接BD.∵∠DBE +∠CBD =180°,∠CBD +∠CAD =180°, ∴∠DBE =∠CAD.∵AC =CD ,∴∠CAD =∠CDA.由(1)知∠CDE =∠CDA ,∴∠DBE =∠CDE. ∵∠E =∠E ,∴△DBE ∽△CDE. ∴DE EB =CE DE . ∴DE 2=EB ·CE.图4(3)如图4,延长CO 交AD 于点G. ∵CA =CD ,OA =OD , ∴CG ⊥AD ,AG =GD.在Rt △ACB 中,tan ∠CAB =BC AC =12,AB =5,∴BC =5,AC =2 5. ∵OA =OC ,∴∠ACG =∠CAB ,在Rt △ACG 中,tan ∠ACG =tan ∠CAB =AG CG =12,∴AG =2,AD =4.在Rt △ADB 中,AB =5,∴BD =AB 2-AD 2=3. 由(2)知△DBE ∽△CDE ,∴BD DC =DE CE =32 5.设DE =3x ,则CE =2 5x.又DE 2=EB ·CE ,即(3x)2=(2 5x -5)·2 5x. 解得x =1011.∴DE =3×1011=3011.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
单元达标测试(四)(第六章)(满分:120分 时间:120分钟)一、选择题(每小题3分,共30分)1.如图,AB 和⊙O 相切于B ,∠AOB =60°,则∠A 的大小为( B )A .15°B .30°C .45°D .60°2.如图,线段AB 是⊙O 的直径,弦CD ⊥AB ,∠CAB =20°,则∠AOD 等于( C )A .160°B .150°C .140°D .120°,第1题图) ,第2题图),第3题图),第4题图)3.如图,在直角坐标系中,以原点为圆心,半径为5的圆内有一点P (0,-3),那么经过点P 的所有弦中,最短的弦的长为( C )A .4B .5C .8D .104.(2016·娄底)如图,已知AB 是⊙O 的直径,∠D =40°,则∠CAB 的度数为( C )A .20°B .40°C .50°D .70°5.如图,⊙O 是△ABC 的外接圆,若∠B =75°,∠C =60°,且BC ︵的长度为4π,则BC的长度( B )A .8B .8 2C .16D .16 26.(2016·临沂)如图,AB 是⊙O 的切线,B 为切点,AC 经过点O ,与⊙O 分别相交于点D ,C.若∠ACB=30°,AB =3,则阴影部分的面积是( C ) A.32 B.π6 C.32-π6 D.33-π6,第5题图) ,第6题图),第7题图) ,第8题图)7.(2016·昆明)如图,AB 为⊙O 的直径,AB =6,AB ⊥弦CD ,垂足为G ,EF 切⊙O 于点B ,∠A =30°,连接AD ,OC ,BC ,下列结论不正确的是( D )A .EF ∥CDB .△COB 是等边三角形C .CG =DG D.BC ︵的长为32π 8.(2016·泉州)如图,圆锥底面半径为r cm ,母线长为10 cm ,其侧面展开图是圆心角为216°的扇形,则r 的值为( B )A .3B .6C .3πD .6π9.(2016·襄阳)如图,I 是△ABC 的内心,AI 的延长线和△ABC 的外接圆相交于点D ,连接BI ,BD ,DC.下列说法中错误的一项是( D )A .线段DB 绕点D 顺时针旋转一定能与线段DC 重合B .线段DB 绕点D 顺时针旋转一定能与线段DI 重合C .∠CAD 绕点A 顺时针旋转一定能与∠DAB 重合D .线段ID 绕点I 顺时针旋转一定能与线段IB 重合10.如图,AB 是⊙O 是直径,⊙O 交BC 的中点于点D ,DE ⊥AC 于点E ,连接AD ,则下列结论:①AD ⊥BC ;②∠EDA =∠B ;③OA =12AC ;④DE 是⊙O 的切线,正确的个数是( D ) A .1个 B .2个 C .3个 D .4个二、填空题(每小题3分,共24分)11.(2016·湘西州)如图,在⊙O 中,圆心角∠AOB=70°,那么圆周角∠C=__35°__.12.(2015·淄博)如图,在⊙O 中,AB ︵=CD ︵,∠DCB =28°,则∠ABC=__28__度.,第11题图) ,第12题图),第13题图) ,第14题图)13.(2015·宿迁)如图,四边形ABCD 是⊙O 的内接四边形,若∠C=130°,则∠BOD=__100__度.14.如图,已知线段AB ,分别以点A 和点B 为圆心,大于12AB 的长为半径作弧,两弧相交于C ,D 两点,作直线CD 交AB 于点E ,在直线CD 上任取一点F ,连接FA ,FB.若FA =5,则FB =__5__.15.(2016·宁夏)已知正△ABC 的边长为6,那么能够完整覆盖这个正△ABC 的最小圆的半径是.16.(2016·台州)如图,△ABC 的外接圆O 的半径为2,∠C =40°,则AB ︵的长是__89π__.17.(2016·贵港)如图,在Rt △ABC 中,∠C =90°,∠BAC =60°,将△ABC 绕点A 逆时针旋转60°后得到△ADE,若AC =1,则线段BC 在上述旋转过程中所扫过部分(阴影部分)的面积是__π2__.(结果保留π),第16题图) ,第17题图),第18题图)18.(2016·随州)如图(1),PT 与⊙O 1相切于点T ,PAB 与⊙O 1相交于A ,B 两点,可证明△PTA∽△PBT,从而有PT 2=PA·PB.请应用以上结论解决下列问题:如图(2),PAB ,PCD分别与⊙O 2相交于A ,B ,C ,D 四点,已知PA =2,PB =7,PC =3,则CD =__53__. 三、解答题(共66分)19.(6分)如图,在△ABC 中,∠A =90°.(1)请用圆规和直尺作出⊙P,使圆心P 在AC 边上,且与AB ,BC 两边都相切;(保留作图痕迹,不写作法和证明)(2)若∠B =60°,AB =3,求⊙P 的面积.解:(1)作∠ABC 的平分线交AC 于点P ,以P 为圆心,PA 为半径即可作出⊙P (图略)(2)∵∠B =60°,BP 平分∠ABC ,∴∠ABP =30°,∵tan ∠ABP =AP AB,∴AP =3,∴S ⊙P =3π20.(8分)如图,A ,P ,B ,C 是半径为8的⊙O 上的四点,且满足∠BAC =∠APC=60°.(1)求证:△ABC 是等边三角形;(2)求圆心O 到BC 的距离OD.解:(1)证∠BAC =∠ABC =∠ACB =60°即可 (2)OD =421.(8分)如图,在⊙O 中,AB 是直径,点D 是⊙O 上的一点,点C 是AD ︵的中点,弦CM垂直AB 于点F ,连接AD ,交CF 于点P ,连接BC ,∠DAB =30°.(1)求∠A BC 的度数;(2)若CM =83,求AC ︵的长度.(结果保留π)解:(1)连接BD ,∵AB 为⊙O 的直径,∴∠ADB =90°,∵∠DAB =30°,∴∠ABD =90°-30°=60°.∵C 是AD ︵的中点,∴∠ABC =∠DBC =12∠ABD =30° (2)连接OC ,则∠AOC =2∠ABC =60°,∵CM ⊥直径AB 于点F ,∴CF =12CM =43,∴在Rt △COF 中,CO =CF sin60°=43÷32=8,∴AC ︵的长度为60π×8180=8π322.(10分)(2016·荆门)如图,AB 是⊙O 的直径,AD 是⊙O 的弦,点F 是DA 延长线的一点,AC 平分∠FAB 交⊙O 于点C ,过点C 作CE⊥DF,垂足为点E.(1)求证:CE 是⊙O 的切线;(2)若AE =1,CE =2,求⊙O 的半径.解:(1)连接CO ,∵OA =OC ,∴∠OCA =∠OAC ,∵AC 平分∠FAB ,∴∠CAE =∠OAC ,∴∠OCA =∠CAE ,∴OC ∥FD ,∵CE ⊥DF ,∴OC⊥CE ,∴CE 是⊙O 的切线 (2)连接BC ,在Rt △ACE 中,AC =AE 2+EC 2=22+12=5,∵AB 是⊙O 的直径,∴∠BCA =90°,∴∠BCA =∠CEA ,∵∠CAE =∠CAB ,∴△ABC ∽△ACE ,∴CA AB =AE AC , ∴5AB =15,∴AB =5,∴AO =2.5,即⊙O 的半径为2.523.(10分)(2016·丹东)如图,AB 是⊙O 的直径,点C 在AB 的延长线上,CD 与⊙O 相切于点D ,CE ⊥AD ,交AD 的延长线于点E.(1)求证:∠BDC=∠A;(2)若CE =4,DE =2,求AD 的长.解:(1)连接OD ,∵CD 是⊙O 切线,∴∠ODC =90°,即∠ODB +∠BDC =90°,∵AB 为⊙O 的直径,∴∠ADB =90°,即∠ODB +∠ADO =90°,∴∠BDC =∠ADO ,∵OA =OD ,∴∠ADO =∠A ,∴∠BDC =∠A(2)∵CE⊥AE ,∴∠E =∠ADB =90°,∴DB ∥EC ,∴∠DCE =∠BDC ,∵∠BDC =∠A ,∴∠A =∠DCE ,又∵∠E =∠E ,∴△AEC ∽△CED ,∴CE DE =AE CE,∴EC 2=DE·AE ,∴16=2(2+AD ),∴AD =624.(12分)(2016·泰州)如图,△ABC 中,∠ACB =90°,D 为AB 上一点,以CD 为直径的⊙O 交BC 于点E ,连接AE 交CD 于点P ,交⊙O 于点F ,连接DF ,∠CAE =∠ADF.(1)判断AB 与⊙O 的位置关系;(2)若PF∶PC=1∶2,AF =5,求CP 的长.解:(1)AB 是⊙O 切线.理由:连接DE ,CF.∵CD 是直径,∴∠DEC =∠DFC =90°,∵∠ACB =90°,∴∠DEC +∠ACE =180°,∴DE ∥AC ,∴∠DEA =∠EAC =∠DCF ,∵∠DFC =90°,∴∠FCD +∠CDF =90°,∵∠ADF =∠EAC =∠DCF ,∴∠ADF +∠CDF =90°,∴∠ADC =90°,∴CD ⊥AD ,∴AB 是⊙O 切线(2)∵∠CPF =∠CPA ,∠PCF =∠PAC ,∴△PCF ∽△PAC ,∴PC PA =PF PC,∴PC 2=PF ·PA.设PF =a ,则PC =2a ,∴4a 2=a (a +5),∴a =53,∴PC =2a =10325.(12分)(2016·雅安)如图1,AB 是⊙O 的直径,E 是AB 延长线上一点,EC 与⊙O 相切于点C ,OP ⊥AO 交AC 于点P ,交EC 的延长线于点D.(1)求证:△PCD 是等腰三角形;(2)如图2,CG ⊥AB 于点H ,交⊙O 于点G ,过点B 作BF∥EC,交⊙O 于点F ,交CG 于点Q ,连接AF ,若sin E =35,CQ =5,求AF 的值.解:(1)连接OC ,∵EC 切⊙O 于点C ,∴OC ⊥DE ,∴∠OCP +∠DCP =90°,又∵OP⊥OA ,∴∠OAP +∠OPA =90°,∵OA =OC ,∴∠OCP =∠OAP ,∴∠DCP =∠OPA ,又∵∠OPA =∠DPC ,∴∠DCP =∠DPC ,∴DP =DC ,即△PCD 为等腰三角形(2)连接OC ,BC ,∵DE 与⊙O 相切于点E ,∴∠OCB +∠BCE =90°,∵OC =OB ,∴∠OCB =∠OBC ,∴∠OBC +∠BCE =90°,又∵CG⊥AB ,∴∠OBC +∠BCG =90°,∴∠BCE =∠BCG ,∵BF ∥DE ,∴∠BCE =∠QBC ,∴∠BCG =∠QBC ,∴QC =QB =5,∵BF ∥DE ,∴∠ABF =∠E ,∵sinE =35,∴QH =3,BH =4,设⊙O 的半径为r ,在△OCH 中,r 2=82+(r -4)2,解得r =10,又∵∠AFB =90°,sin ∠ABF =35,∴AF =AB·sin ∠ABF =20×35=12。
