2013_北师大版六年级数学下册正比例课件
合集下载
北师大版六年级下册正比例ppt课件

“正比例,真和气。你扩大,他扩大, 你缩小,他缩小,一样倍数跟着你, 判断依据要记牢,快快乐乐正比例”。
18
比值
234 8 12 16
边长/cm 1 2 3 4
面积/cm2 1 4 9 16
周长与边 长的比
比值
2
比值相同
比值不同
7
小组合作二:
一辆汽车行驶的速度为90千米/时,汽车 行驶的时间和路程如下表
时间(时) 1 2 3 4 5 6 7 8 … 表格三 路程(千米) 90 180 270 360 450 540 630 720 …
讨论1:、表中有(时间)和(路程)两种相关联的量。
2、说说路程是怎样随着时间的变化而变化的?
3、任意写出三个相对应的路程和时间的比,
并算出它们的比值。
4、比值实际上表示( 它们的关系。
速度
),请用式子表示
路程÷时间=速度
8
时间是1,路程是90;
时间扩大,时间是2,路程是180;
路程随着 扩大。
时间是3,路程是270;
路程与时间的比值是一定的。
像这样,路程和时间两个量,时间变化,所行驶
的路程也随着变化,而且路程与时间的比值(也就是 速度)一定,我们就说路程和时间成正比例。
12
如何判断两种两个量是否成正比例?
(1)有两种相关联的量。 (2)一种量变化另一种量也随着变化。 (3)相对应的两个数的比值 一定。
这两种量就叫做成正比例的量, 它们的关系叫做正比例关系.
边长 /cm
1
2
3
周长 /cm
4
边长 /cm
1
2
3
面积 /cm2
1
4
小组合作-:
18
比值
234 8 12 16
边长/cm 1 2 3 4
面积/cm2 1 4 9 16
周长与边 长的比
比值
2
比值相同
比值不同
7
小组合作二:
一辆汽车行驶的速度为90千米/时,汽车 行驶的时间和路程如下表
时间(时) 1 2 3 4 5 6 7 8 … 表格三 路程(千米) 90 180 270 360 450 540 630 720 …
讨论1:、表中有(时间)和(路程)两种相关联的量。
2、说说路程是怎样随着时间的变化而变化的?
3、任意写出三个相对应的路程和时间的比,
并算出它们的比值。
4、比值实际上表示( 它们的关系。
速度
),请用式子表示
路程÷时间=速度
8
时间是1,路程是90;
时间扩大,时间是2,路程是180;
路程随着 扩大。
时间是3,路程是270;
路程与时间的比值是一定的。
像这样,路程和时间两个量,时间变化,所行驶
的路程也随着变化,而且路程与时间的比值(也就是 速度)一定,我们就说路程和时间成正比例。
12
如何判断两种两个量是否成正比例?
(1)有两种相关联的量。 (2)一种量变化另一种量也随着变化。 (3)相对应的两个数的比值 一定。
这两种量就叫做成正比例的量, 它们的关系叫做正比例关系.
边长 /cm
1
2
3
周长 /cm
4
边长 /cm
1
2
3
面积 /cm2
1
4
小组合作-:
北师大版六年级下册《正比例》课件

正比例的图像:正比例的图像是一条直线,斜率为k。
正比例的应用:在物理、化学、生物等学科中,正比例关系广泛存在, 如速度、密度、压强等。
正比例的性质证明
正比例的定义:如果两个变量x和y之间的关系可以表示为y=kx(k为常数,k≠0),那 么x和y成正比例。
正比例的性质:如果x和y成正比例,那么x和y的乘积为常数,即xy=k。
压强与面积:压强与面积成 正比,压强越大,面积越小
电阻与电流:电阻与电流成 正比,电阻越大,电流越小
正比例的性质
第四章
正比例的性质描述
正比例的定义:如果两个变量x和y之间的关系可以表示为y=kx(k为常 数,k≠0),那么x和y成正比例关系。
正比例的性质:当x增大时,y也增大;当x减小时,y也减小。
正比例解析式在 实际生活中有很 多应用,如物理 中的速度、加速 度、位移等关系, 化学中的反应速 率、浓度等关系, 经济学中的价格、 需求等关系。
正比例解析式的应用场景
解决实际问题:如计算速度、时间、距离等 数学建模:如物理、化学、生物等学科中的模型建立 数据分析:如统计、概率等学科中的数据处理 工程设计:如建筑、机械、电子等学科中的设计计算
正比例图像的特点
正比例图像是一条直线,表示两个变量之间的关系是正比例关系。 正比例图像的斜率是常数,表示两个变量之间的关系是线性关系。
正比例图像的横坐标和纵坐标的比例是常数,表示两个变量之间的关系是正比例关系。
正比例图像的斜率是正数,表示两个变量之间的关系是正比例关系。
正比例图像的应用场景
数学教学:帮助学生理解正比例的概念和图像 科学实验:用于表示实验数据之间的关系 商业分析:用于分析市场趋势和预测未来市场 工程设计:用于表示工程参数之间的关系和优化设计
正比例的应用:在物理、化学、生物等学科中,正比例关系广泛存在, 如速度、密度、压强等。
正比例的性质证明
正比例的定义:如果两个变量x和y之间的关系可以表示为y=kx(k为常数,k≠0),那 么x和y成正比例。
正比例的性质:如果x和y成正比例,那么x和y的乘积为常数,即xy=k。
压强与面积:压强与面积成 正比,压强越大,面积越小
电阻与电流:电阻与电流成 正比,电阻越大,电流越小
正比例的性质
第四章
正比例的性质描述
正比例的定义:如果两个变量x和y之间的关系可以表示为y=kx(k为常 数,k≠0),那么x和y成正比例关系。
正比例的性质:当x增大时,y也增大;当x减小时,y也减小。
正比例解析式在 实际生活中有很 多应用,如物理 中的速度、加速 度、位移等关系, 化学中的反应速 率、浓度等关系, 经济学中的价格、 需求等关系。
正比例解析式的应用场景
解决实际问题:如计算速度、时间、距离等 数学建模:如物理、化学、生物等学科中的模型建立 数据分析:如统计、概率等学科中的数据处理 工程设计:如建筑、机械、电子等学科中的设计计算
正比例图像的特点
正比例图像是一条直线,表示两个变量之间的关系是正比例关系。 正比例图像的斜率是常数,表示两个变量之间的关系是线性关系。
正比例图像的横坐标和纵坐标的比例是常数,表示两个变量之间的关系是正比例关系。
正比例图像的斜率是正数,表示两个变量之间的关系是正比例关系。
正比例图像的应用场景
数学教学:帮助学生理解正比例的概念和图像 科学实验:用于表示实验数据之间的关系 商业分析:用于分析市场趋势和预测未来市场 工程设计:用于表示工程参数之间的关系和优化设计
北师大版六年级下册《正比例》课件

对称性
正比例关系具有对称性,即当一 个变量增加时,另一个变量也按 相同的比例增加;反之亦然。这 种对称性在图像上表现为直线。
斜率恒定
正比例关系的直线斜率是恒定的 ,表示两个变量之间的固定比例 关系。斜率的大小直接反映了比
例的大小。
正比例图像的应用
理解比例关系
通过正比例图像,学生可以直观地理解比例关系,加深对正比例概 念的理解。
03
正比例的图像表示
正比例图像的绘制
绘制方法
在平面坐标系中,选择一个点作为原 点,然后根据正比例关系确定另一个 点的位置。通过连接这两个点,可以 得到一条直线,表示正比例关系。
注意事项
在绘制正比例图像时,需要确保坐标 轴的比例尺一致,以便准确反映比例 关系。
正比例图像的特点
直线表示
正比例关系在图像上表现为一条 通过原点的直线。随着一个变量 增加,另一个变量也按相同的比 例增加,图像呈45度角上升。
化时,另一个量也随之变化。
在实际问题中,可以通过观察和 实验的方法来验证两个量是否成
正比。
在数学中,可以通过代入法、图 像法和解析法等方法来判断两个
量是否成正比。
02
正比例的性质
正比例的性质
定义
正比例是指两个量之间的比值保 持不变,即y/x=k(k为常数)。
性质
当两个量成正比例时,它们的图像 是一条直线,并且这条直线经过原 点。
下节课预告
• 预告下一节课的主题和主要内容,让学生提前预习和准备 ,提高学习效果。
感谢观看
THANKS
正比例的意义
正比例关系在生活和生产中广泛存在 ,如速度、时间、距离之间的关系等 。
正比例关系是函数关系的一种特殊形 式,是数学中研究数量关系的重要基 础。
北师大版六年级下册数学《反比例》正比例与反比例PPT课件(第1课时)

请把上表补充完整,再回答下列问题。
⑴不同的人在打同一份稿件的过程中,哪个量 没有变? 不同的人在打同一份稿件的过程中,总字 数没有变。
⑵打字的速度和所用的时间有什么关系?
打字的速度随打字所用的时间的变化而变 化,并且它们的乘积一定(总字数为2400个),所 以它们成反比例。
⑶李老师打这份稿件用了24分,你知道她平均 每分打多少字吗? 平均1分钟打100个字。
返回作业设计
作业2
思维创新 提升培优 基础巩固
返回作业设计
1.(基础题)想一想,填一填。
(1)从甲城到乙城,不同车辆行驶的速度和所需时
间有如下关系。
速度/(千米/时) 6 15 20 30 60
时间/时
10 4 3 2 1
由表可知( 速度 )和( 时间 )是两种相关联的
量,( 时间 )随着( 速度 )的变化而变化,它们的
长方形的一条边长增加,相邻的边长减少。
表2 56 7 8
98 76 54 (1)在表2中,有哪几个变量? 长方形的相邻两边边长(即长和宽)这两个变量。
(2)这两个变量之间有什么关系呢?请完成表2。
长方形的一条边长增加,相邻的边长减少。
通过表1和表2我们发现,问题中的两个长方 形的相邻两边边长有着相同的变化规律。
题数成反比例。
(×)
3.(易错题)我是聪明的小法官。
(4)完成一项工程,工作效率和工作时间成反比例。 (√)
(5)将绳子剪成同样长的小段,剪成的段数和每
段的长度成正比例。
(× )
返回作业2
4.(变式题)a,b,c三种量的关系是 b×c=a。(a,b,c非零)
(1)如果a一定,那么b,c成( 反 )比例关系。
北师六年级下册数学《正比例》课件

引导学生理解正比例的定义,即 两个量之间的比值一定,从而理
解正比例的意义。
关系表达
引导学生理解正比例关系的数学表 达方式,即y/x=k(一定),帮助 学生建立数学思维。
实例说明
通过具体实例,如速度一定时路程 和时间的关系,让学生更好地理解 正比例的意义。
引导学生思考正比例的应用价值
生活中的正比例
引导学生思考生活中存在的正比 例关系,如身高和年龄的关系、 速度和时间的关系等,让学生认 识到正比例在生活中的普遍性和
北师六年级下册数学 《正比例》课件
目录
• 正比例的定义与特征 • 正比例关系的判定 • 正比例的应用 • 正比例与其他数学知识的联系 • 课堂互动与思考
01
正比例的定义与特征
什么是正比例
总结词
正比例是一种特殊的函数关系, 表示两个量之间的比值保持不变 。
详细描述
在数学中,正比例关系指的是两 个量之间的比值保持恒定,即当 一个量变化时,另一个量也按照 相同的比例变化。
重要性。
数学建模
通过正比例的数学建模过程,让 学生了解数学在解决实际问题中 的应用价值,培养学生的数学应
用能力。
其他学科中的应用
引导学生思考正比例在其他学科 中的应用,如物理学中的电阻定 律等,让学生认识到数学作为基
础学科的重要性。
THANKS
感谢观看
正比例的特征
总结词
正比例的特征是两个量的比值是一个 定值,且这个定值不为0。
详细描述
正比例关系的两个量x和y满足条件 y/x=k(k为定值且k≠0)。当k>0时 ,x和y同向变化;当k<0时,x和y反 向变化。
正比例的意义
总结词
正比例的意义在于揭示两个量之间的线性关系,并可用于描述现实生活中的许 多现象。
解正比例的意义。
关系表达
引导学生理解正比例关系的数学表 达方式,即y/x=k(一定),帮助 学生建立数学思维。
实例说明
通过具体实例,如速度一定时路程 和时间的关系,让学生更好地理解 正比例的意义。
引导学生思考正比例的应用价值
生活中的正比例
引导学生思考生活中存在的正比 例关系,如身高和年龄的关系、 速度和时间的关系等,让学生认 识到正比例在生活中的普遍性和
北师六年级下册数学 《正比例》课件
目录
• 正比例的定义与特征 • 正比例关系的判定 • 正比例的应用 • 正比例与其他数学知识的联系 • 课堂互动与思考
01
正比例的定义与特征
什么是正比例
总结词
正比例是一种特殊的函数关系, 表示两个量之间的比值保持不变 。
详细描述
在数学中,正比例关系指的是两 个量之间的比值保持恒定,即当 一个量变化时,另一个量也按照 相同的比例变化。
重要性。
数学建模
通过正比例的数学建模过程,让 学生了解数学在解决实际问题中 的应用价值,培养学生的数学应
用能力。
其他学科中的应用
引导学生思考正比例在其他学科 中的应用,如物理学中的电阻定 律等,让学生认识到数学作为基
础学科的重要性。
THANKS
感谢观看
正比例的特征
总结词
正比例的特征是两个量的比值是一个 定值,且这个定值不为0。
详细描述
正比例关系的两个量x和y满足条件 y/x=k(k为定值且k≠0)。当k>0时 ,x和y同向变化;当k<0时,x和y反 向变化。
正比例的意义
总结词
正比例的意义在于揭示两个量之间的线性关系,并可用于描述现实生活中的许 多现象。
新北师大版六年级数学下册正比例教学课件ppt
边长/cm 1 2 3 4 面积/cm2 1 4 9 16
正方形周长与边长的比不变,但面积与边长的 比是不相等的。
• 新知探究
下面是正方形周长与边长、面积与边长之间的变化情 况,请把表格填写完整。
边长/cm 1 2 3 4 周长/cm 4 8 12 16
边长/cm 1 2 3 4 面积/cm2 1 4 9 16
我列个表试一试:
圆的 面积
半径
3.14 12.56 28.26
1
2
3
比值不相等……
• 新知探究
试一试
乐乐和爸爸的年龄变化情况如下,把表填写完整。
乐乐的年龄/岁 6 7 8 爸爸的年龄/岁 32 33
9 10 11
他们的年龄成正比例吗?为什么?
• 新知探究
试一试
分别举一个成正比例和一个不成正比例的例子。
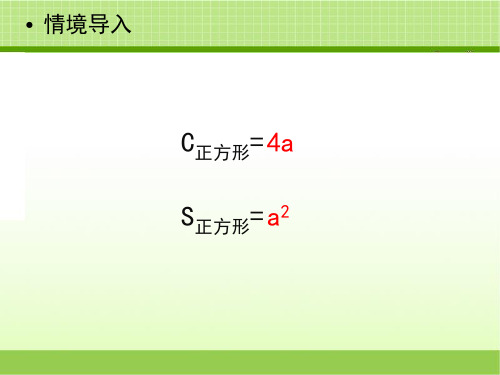
• 情境导入
C正方形= 4a S正方形= a2
• 新知探究
下面是正方形周长与边长、面积与边长之间的变化情 况,请把表格填写完整。
边长/cm 1 2 3 4 周长/cm 4 8 12 16
边长/cm 1 2 3 4 面积/cm2 1 4 9 16
说说你分别发现了什么?
• 新知探究
下面是正方形周长与边长、面积与边长之间的变化情 况,请把表格填写完整。
边长/cm 1 2 3 4 周长/cm 4 8 12 16
边长/cm 1 2 3 4 面积/cm2 1 4 9 16
先来说说周长与边长之间的变化情况吧?
• 新知探究
下面是正方形周长与边长、面积与边长之间的变化情 况,请把表格填写完整。
边长/cm 1 2 3 4 周长/cm 4 8 12 16
边长/cm 1 2 3 4 面积/cm2 1 4 9 16
六年级数学下册 正比例课件 北师大版

9.6
12.0
14.4
16.8
1、写出几组总价与相应数量的比,并比较比值的大小。 2、这个比值表示的意义是什么?
3、纯净水的总价和数量成正比例吗?为什么?
(3)、小明和爸爸的年龄变化情况如下,把表填写完整。
34
35
36
37
父子的年龄成正比例吗?为什么?
总结:
说说你这节课的收获。
•1、书籍是朋友,虽然没有热情,但是非常忠实。2022年3月2日星期三2022/3/22022/3/22022/3/2 •2、科学的灵感,决不是坐等可以等来的。如果说,科学上的发现有什么偶然的机遇的话,那么这种‘偶然的机遇’只能给那些学有素养的人,给那些善于独 立思考的人,给那些具有锲而不舍的人。2022年3月2022/3/22022/3/22022/3/23/2/2022 •3、书籍—通过心灵观察世界的窗口.住宅里没有书,犹如房间里没有窗户。2022/3/22022/3/2March 2, 2022 •4、享受阅读快乐,提高生活质量。2022/3/22022/3/22022/3/22022/3/2
讨论:路程是怎样随着时间的变化而变化的?有什么变化规律?
3、一些人买同一种苹果,购买苹果的数量和应付的钱数如下。把下表 填写完整。
21 18 15 12
9
从表中你发现了什么规律?
450 540 630 720
21 18 15 12
9
观察比较:它们的变化规律有什么共同特点?
450 540 630 720
谢谢观赏
You made my day!
我们,还在路上……
表中,时间增加,所走的路程也相应增加,而且路程与时间的
比值(速度)相同,那么,我们就说路程和时间成正比例。
正比例课件ppt_北师大版六年级数学下册课件

班 级:六年三班
学习目标
• 1. 结合实例,认识正比例。 • 2.能根据正比例的意义,判定俩
个相关联的量是不是正比例。
1.同学们,听过《数青蛙》这一首童谣吗?
青蛙只数 1 2 3 … n
嘴巴数
1
2
3
…
n
眼睛数
2
4
6
…
2n
腿数
4
8
12
…
4n
青蛙的只数和嘴巴数就是两种相关联的量 在这个表格中是否还存在着其它相关联的量呢?
450 540 630 720
21 18 15 12
9
观察比较:它们的变化规律有什么相同点?
450 540 630 720
21 18 15 12 9
两种相关联的量,一种量增加或(减少),另一 种量也相应增加或(减少),并且它们相应的比 值一定,像这样的两种量就成正比例。 现在你知道什么叫成正比例的量了吗? 要怎么样判断两种量是否成正比例?
口算练习:
0.6×1.2 = 0.72 0.84÷0.6= 1.4 4.5×0.1 = 0.45 0.7 × 1.6= 1.12 0.84÷0.3= 2.8 15 × 0.4= 6 0.1 × 0.5 = 0.05 2.8 ÷ 7= 0.4 100÷0.1= 1000 1.4 × 3= 4.2
正比例
元
1、写出几组总价与相应数量的比,并比较比值的大小。 2、这个比值表示的意义是什么? 3、纯净水的总价和数量成正比例吗?为什么?
(3)、小明和爸爸的年龄变化情况如下,把表填写完整。
34 35 36 37 父子的年龄成正比例吗?为什么?
总结:
说说你这节课的收获。
课堂检测
达标检测—正比例
学习目标
• 1. 结合实例,认识正比例。 • 2.能根据正比例的意义,判定俩
个相关联的量是不是正比例。
1.同学们,听过《数青蛙》这一首童谣吗?
青蛙只数 1 2 3 … n
嘴巴数
1
2
3
…
n
眼睛数
2
4
6
…
2n
腿数
4
8
12
…
4n
青蛙的只数和嘴巴数就是两种相关联的量 在这个表格中是否还存在着其它相关联的量呢?
450 540 630 720
21 18 15 12
9
观察比较:它们的变化规律有什么相同点?
450 540 630 720
21 18 15 12 9
两种相关联的量,一种量增加或(减少),另一 种量也相应增加或(减少),并且它们相应的比 值一定,像这样的两种量就成正比例。 现在你知道什么叫成正比例的量了吗? 要怎么样判断两种量是否成正比例?
口算练习:
0.6×1.2 = 0.72 0.84÷0.6= 1.4 4.5×0.1 = 0.45 0.7 × 1.6= 1.12 0.84÷0.3= 2.8 15 × 0.4= 6 0.1 × 0.5 = 0.05 2.8 ÷ 7= 0.4 100÷0.1= 1000 1.4 × 3= 4.2
正比例
元
1、写出几组总价与相应数量的比,并比较比值的大小。 2、这个比值表示的意义是什么? 3、纯净水的总价和数量成正比例吗?为什么?
(3)、小明和爸爸的年龄变化情况如下,把表填写完整。
34 35 36 37 父子的年龄成正比例吗?为什么?
总结:
说说你这节课的收获。
课堂检测
达标检测—正比例
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
用等式表示: 路程÷时间=速度(一定)
21
18
15
12
9
也就是说:当单价一定时,质量扩大几倍,应付的总钱数 也相应的扩大相同的倍数。质量缩小几倍,应付的总钱数 也相应的缩小相同的倍数。这时,应付的钱数与质量成正 比例。
用等式表示:
应付的钱数÷质量=单价(一定)
什么是正比例?
• 小结: • 两种相关联的量,一种量变化,另一种 量也随着变化,如果这两种量相对应的两 个数的商一定,这两种量就叫做成正比例 的量,它们的关系叫做正比例关系。 • 例:总重量÷袋数=每袋的重量(一定) • 则:总重量与袋数成正比例。
450
540
630
720
讨论:路程是怎样随着时间的变化而变化的?有什么变化规律?
发现:时间扩大几倍,所走的路程也相应的扩大相同的倍数。时间 缩小几倍,所走的路程也相应的缩小相同的倍数。 而360÷4=90 450÷5=90 540÷6=90 630÷7=90 ------
路程与时间的比值(速度)是一样的.
如果用X、Y字母表示两个相关联的量, K表示它们的比值,当K一定时。
用字母表示两个成正比例量的关系式:
用等式表示: X÷Y=K(一定) X 或: = K(一定) Y 所以 X与Y成正比例
想一想
(1)正方形的周长与边长成正比例吗? 面积与边长呢?为什么?
周长÷边长=4(一定)
当比值一定时,周长扩大几倍,边长也相应的扩大
用等式表示: 路程÷时间=速度(一定)
3、一些人买同一种苹果,购买苹果的数量和应付的钱数如下。把下表 填写完整。
21
18
15
12
9
从表中你发现了什么规律?
发现:质量扩大几倍,应付的总钱数也相应的扩大相同的倍数。质量缩小几倍, 应付的总钱数也相应的缩小相同的倍数。 而30÷10=3 27÷9=3 24÷8=3 21÷7=3-----应付的钱数与质量的比值(单价)是一样的.
1 2.4
2 4.8
3 7.2
4 9.6
5 12.0
6 14.4
7 16.8
1、写出几组总价与相应数量的比,并比较比值的大小。
2、这个比值表示的意义是什么?
3、纯况如下,把表填写完整。
34
35
36
37
父子的年龄成正比例吗?为什么?
相同的倍数。周长缩小几倍,边长也相应的缩小相
同的倍数。这时,周长与边长成正比例。 面积÷边长=边长(不一定) 比值不一定时,边长扩大几倍,面积扩大的倍数就是几 的平方倍;边长缩小几倍,面积缩小的倍数也是几的平 方倍。这时,面积与边长不成正比例。
(2)、下面是便民超市出售的纯净水数量与总价表。
数量/瓶 总价/元
1、下面分别是正方形的周长与边长、面积与边长的变化情况把表填完整。
2 3 4
8 12 16
2 3 4
4 9 16
讨论:正方形的周长与边长;面积与边长的变化情况各有 什么特点?它们的变化规律相同吗? 正方形的周长=边长×4 正方形的面积=边长×边长
2、一辆汽车行驶的速度为90千米/时,汽车行驶的时间和路程如下, 把下表补充完整。
用等式表示: 应付的钱数÷质量=单价(一定)
450
540
630
720
21
18
15
12
9
观察比较:它们的变化规律有什么共同特点?
450
540
630
720
表中,时间增加,所走的路程也相应增加,而且路程与时间的 比值(速度)相同,那么,我们就说路程和时间成正比例。
也就是说:当速度一定时,时间扩大 几倍,所走的路程也相应的扩大相同 的倍数。时间缩小几倍,所走的路程 也相应的缩小相同的倍数。这时,路 程与时间成正比例。
21
18
15
12
9
也就是说:当单价一定时,质量扩大几倍,应付的总钱数 也相应的扩大相同的倍数。质量缩小几倍,应付的总钱数 也相应的缩小相同的倍数。这时,应付的钱数与质量成正 比例。
用等式表示:
应付的钱数÷质量=单价(一定)
什么是正比例?
• 小结: • 两种相关联的量,一种量变化,另一种 量也随着变化,如果这两种量相对应的两 个数的商一定,这两种量就叫做成正比例 的量,它们的关系叫做正比例关系。 • 例:总重量÷袋数=每袋的重量(一定) • 则:总重量与袋数成正比例。
450
540
630
720
讨论:路程是怎样随着时间的变化而变化的?有什么变化规律?
发现:时间扩大几倍,所走的路程也相应的扩大相同的倍数。时间 缩小几倍,所走的路程也相应的缩小相同的倍数。 而360÷4=90 450÷5=90 540÷6=90 630÷7=90 ------
路程与时间的比值(速度)是一样的.
如果用X、Y字母表示两个相关联的量, K表示它们的比值,当K一定时。
用字母表示两个成正比例量的关系式:
用等式表示: X÷Y=K(一定) X 或: = K(一定) Y 所以 X与Y成正比例
想一想
(1)正方形的周长与边长成正比例吗? 面积与边长呢?为什么?
周长÷边长=4(一定)
当比值一定时,周长扩大几倍,边长也相应的扩大
用等式表示: 路程÷时间=速度(一定)
3、一些人买同一种苹果,购买苹果的数量和应付的钱数如下。把下表 填写完整。
21
18
15
12
9
从表中你发现了什么规律?
发现:质量扩大几倍,应付的总钱数也相应的扩大相同的倍数。质量缩小几倍, 应付的总钱数也相应的缩小相同的倍数。 而30÷10=3 27÷9=3 24÷8=3 21÷7=3-----应付的钱数与质量的比值(单价)是一样的.
1 2.4
2 4.8
3 7.2
4 9.6
5 12.0
6 14.4
7 16.8
1、写出几组总价与相应数量的比,并比较比值的大小。
2、这个比值表示的意义是什么?
3、纯况如下,把表填写完整。
34
35
36
37
父子的年龄成正比例吗?为什么?
相同的倍数。周长缩小几倍,边长也相应的缩小相
同的倍数。这时,周长与边长成正比例。 面积÷边长=边长(不一定) 比值不一定时,边长扩大几倍,面积扩大的倍数就是几 的平方倍;边长缩小几倍,面积缩小的倍数也是几的平 方倍。这时,面积与边长不成正比例。
(2)、下面是便民超市出售的纯净水数量与总价表。
数量/瓶 总价/元
1、下面分别是正方形的周长与边长、面积与边长的变化情况把表填完整。
2 3 4
8 12 16
2 3 4
4 9 16
讨论:正方形的周长与边长;面积与边长的变化情况各有 什么特点?它们的变化规律相同吗? 正方形的周长=边长×4 正方形的面积=边长×边长
2、一辆汽车行驶的速度为90千米/时,汽车行驶的时间和路程如下, 把下表补充完整。
用等式表示: 应付的钱数÷质量=单价(一定)
450
540
630
720
21
18
15
12
9
观察比较:它们的变化规律有什么共同特点?
450
540
630
720
表中,时间增加,所走的路程也相应增加,而且路程与时间的 比值(速度)相同,那么,我们就说路程和时间成正比例。
也就是说:当速度一定时,时间扩大 几倍,所走的路程也相应的扩大相同 的倍数。时间缩小几倍,所走的路程 也相应的缩小相同的倍数。这时,路 程与时间成正比例。
