第一章习题选解
无机及分析化学第一章课后习题

第1章思考题与习题参考答案一、选择题1.等压下加热5%的下列水溶液,最先沸腾的是()A. 蔗糖(C12H22O11)溶液B. 葡萄糖(C6H12O6)溶液C. 丙三醇(C 3H8O3)溶液D. 尿素((NH2)2 CO)溶液解:选D。
在等压下,最先沸腾就是指溶液的蒸气压最低。
根据难挥发非电解质稀溶液的依数性变化规律,溶液质量摩尔浓度增大,溶液的蒸气压下降。
这里,相同质量分数下,溶质的摩尔质量越小,质量摩尔浓度越大。
选项D中非电解质尿素的摩尔质量最小,尿素溶液的质量摩尔浓度最大,蒸气压最低,在等压下最先沸腾。
2.0.1mol·kg-1下列水溶液中凝固点最低的是()A. NaCl溶液B. C12H22O11溶液C. HAc溶液D. H2SO4溶液解:选D。
电解质溶液的依数性虽然不能用拉乌尔定律进行统一的定量计算,但仍然可以参照难挥发非电解质稀溶液的依数性进行定性描述。
即溶质的粒子数目增大,会引起溶液的蒸气压降低,沸点升高,凝固点下降和溶液的渗透压增大。
此题中,在相同质量摩尔浓度下,溶液中的粒子数目估算出来是H2SO4溶液最多,所以其凝固点最低。
3.胶体溶液中,决定溶胶电性的物质是()A. 胶团B. 电位离子C. 反离子D. 胶粒解:选D。
根据胶团结构,胶核和吸附层的整体称为胶粒,胶粒中反离子数比电位离子数少,故胶粒所带电荷与电位离子符号相同。
即胶粒带电,溶胶电性由胶粒决定。
4.溶胶具有聚结不稳定性,但经纯化后的Fe(OH)3溶胶可以存放数年而不聚沉,其原因是()A. 胶体的布朗运动B. 胶体的丁铎尔效应C. 胶团有溶剂化膜D. 胶粒带电和胶团有溶剂化膜解:选D。
溶胶具有动力学稳定性和聚结稳定性,而聚结稳定性是溶胶稳定的根本原因,它包含两个方面,胶粒带有相同电性的电荷,当靠近时会产生静电排斥,阻止胶粒聚结合并;而电位离子和反离子形成的溶剂化膜,也会阻隔胶粒的聚结合并。
由于纯化的Fe(OH)3溶胶具有这种聚结稳定性,从而可以存放数年而不聚沉。
第一章习题参考答案

第一章自我检测题参考答案一、填空题1.PN结具有单向导电性,正向偏置时导通,反向偏置时截止。
2. 2.U T为温度的电压当量,当温度为室温时,U T≈m v。
26mV。
3. 3.半导体二极管2AP7是半导体材料制成的,2CZ56是半导体材料制成的。
N型锗,N型硅。
二、判断题1.二极管的反向击穿电压大小与温度有关,温度升高反向击穿电压增大。
(×).2. .稳压二极管正常工作时必须反偏,且反偏电流必须大于稳定电流I Z。
(√)三、选择题1. 2CZ型二极管以下说法正确的是(B)A、点接触型,适用于小信号检波;B、面接触型,适用于整流;C、面接触型,适用于小信号检波2. 稳压二极管电路如图Z1.1所示,稳压二极管的稳压值U Z=6.3V,正向导通压降0.7V,则为U O(C)。
A.6.3VB.0.7VC.7VD.14V3.在图Z1.2所示各电路中,已知直流电压U I=3V,电阻,二极管的正向压降为0.7V,求U O=?解:(a)U O=0.7V (b)U O=1.5V (c)U O=4.3V第一章习题参考答案1.1判断题1.当二极管两端正向偏置电压大于死区电压,二极管才能导通。
()2.半导体二极管反向击穿后立即烧毁。
()1.√2.×1.2选择题1.硅二极管正偏时,正偏电压0.7V和正偏电压0.5V时,二极管呈现的电阻值()A、相同;B、不相同;C、无法判断。
2.二极管反偏时,以下说法正确的是()A、在达到反向击穿电压之前通过电流很小,称为反向饱和电流;B、在达到死区电压之前,反向电流很小;C、二极管反偏一定截止,电流很小,与外加反偏电压大小无关。
3.图P1.1所示电路,二极管导通时压降为0.7V,反偏时电阻为∞,则以下说法正确的是( C )。
A、VD导通,U AO=5.3V;B、VD导通,U AO=—5.3V;C、VD导通,U AO=—6V;D、VD导通,U AO=6V;E、VD截止,U AO=—9V。
清华大学《运筹学教程》胡运权主编课后习题答案

3 x1 x2 x5 3
st
4 x1 3 x2 x3 x6
x1
2 x2
x4
4
6
x j 0(, j 1,,4)
cj
CB
xB
b
-M x5 3
-M
x6
6
0
x4
4
cj zj
-4 x1 1
-M x6 2
0
x4
3
cj zj
-4
-1 0
x1
x2
x3
3
1
0
4
3 -1
1
20
7M-4 4M-1 -M
小于0 ,因此已经得到唯一最优解,最优解为:
X * 2 5 ,9 / 5,1,0T
max Z 10x1 15x2 12x3
5x1 3x2 x3 9
(4)
st
5x1 2x1
6x2 x2 x3
15x3 5
15
x j 0(, j 1,,3)
39
1.8 已知某线性规划问题的初始单纯形
表和用单纯形法迭代后得到下面表格,试求括
弧中未知数a∼l值。
项目
X1 X2 X3 X4 X5
X4 6 (b) (c) (d) 1 0
X5 1 -1 3 (e) 0 1
Cj-Zj
a -1 2 0 0
X1 (f) (g) 2 -1 1/2 0
X5 4 (h) (i) 1 1/2 1
Cj-Zj
0 -7 (j) (k) (l)
6 4
x1 , x2 0
无穷多最优解
(蓝 色 线 段 上 的 点 都 是 最优 解 )
x1
6 5
,
x2
大学物理习题答案解析第一章

第一章 质点运动学1 -1 质点作曲线运动,在时刻t 质点的位矢为r ,速度为v ,速率为v ,t 至(t +Δt )时间内的位移为Δr , 路程为Δs , 位矢大小的变化量为Δr ( 或称Δ|r |),平均速度为v ,平均速率为v .(1) 根据上述情况,则必有( ) (A) |Δr |= Δs = Δr(B) |Δr |≠ Δs ≠ Δr ,当Δt →0 时有|d r |= d s ≠ d r (C) |Δr |≠ Δr ≠ Δs ,当Δt →0 时有|d r |= d r ≠ d s (D) |Δr |≠ Δs ≠ Δr ,当Δt →0 时有|d r |= d r = d s (2) 根据上述情况,则必有( )(A) |v |= v ,|v |= v (B) |v |≠v ,|v |≠ v (C) |v |= v ,|v |≠ v (D) |v |≠v ,|v |= v分析与解 (1) 质点在t 至(t +Δt )时间内沿曲线从P 点运动到P′点,各量关系如图所示, 其中路程Δs =PP′, 位移大小|Δr |=PP ′,而Δr =|r |-|r |表示质点位矢大小的变化量,三个量的物理含义不同,在曲线运动中大小也不相等(注:在直线运动中有相等的可能).但当Δt →0 时,点P ′无限趋近P 点,则有|d r |=d s ,但却不等于d r .故选(B).(2) 由于|Δr |≠Δs ,故tst ΔΔΔΔ≠r ,即|v |≠v . 但由于|d r |=d s ,故tst d d d d =r ,即|v |=v .由此可见,应选(C). 1 -2 一运动质点在某瞬时位于位矢r (x,y )的端点处,对其速度的大小有四种意见,即(1)t r d d ; (2)t d d r ; (3)t s d d ; (4)22d d d d ⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛t y t x .下述判断正确的是( )(A) 只有(1)(2)正确 (B) 只有(2)正确 (C) 只有(2)(3)正确 (D) 只有(3)(4)正确分析与解trd d 表示质点到坐标原点的距离随时间的变化率,在极坐标系中叫径向速率.通常用符号v r 表示,这是速度矢量在位矢方向上的一个分量;td d r表示速度矢量;在自然坐标系中速度大小可用公式t s d d =v 计算,在直角坐标系中则可由公式22d d d d ⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛=t y t x v 求解.故选(D).1 -3 质点作曲线运动,r 表示位置矢量, v 表示速度,a 表示加速度,s 表示路程, a t表示切向加速度.对下列表达式,即(1)d v /d t =a ;(2)d r /d t =v ;(3)d s /d t =v ;(4)d v /d t |=a t. 下述判断正确的是( )(A) 只有(1)、(4)是对的 (B) 只有(2)、(4)是对的 (C) 只有(2)是对的 (D) 只有(3)是对的分析与解td d v表示切向加速度a t,它表示速度大小随时间的变化率,是加速度矢量沿速度方向的一个分量,起改变速度大小的作用;t r d d 在极坐标系中表示径向速率v r (如题1 -2 所述);tsd d 在自然坐标系中表示质点的速率v ;而td d v表示加速度的大小而不是切向加速度a t.因此只有(3) 式表达是正确的.故选(D).1 -4 一个质点在做圆周运动时,则有( ) (A) 切向加速度一定改变,法向加速度也改变 (B) 切向加速度可能不变,法向加速度一定改变 (C) 切向加速度可能不变,法向加速度不变 (D) 切向加速度一定改变,法向加速度不变分析与解 加速度的切向分量a t起改变速度大小的作用,而法向分量a n 起改变速度方向的作用.质点作圆周运动时,由于速度方向不断改变,相应法向加速度的方向也在不断改变,因而法向加速度是一定改变的.至于a t是否改变,则要视质点的速率情况而定.质点作匀速率圆周运动时, a t恒为零;质点作匀变速率圆周运动时, a t为一不为零的恒量,当a t改变时,质点则作一般的变速率圆周运动.由此可见,应选(B).*1 -5 如图所示,湖中有一小船,有人用绳绕过岸上一定高度处的定滑轮拉湖中的船向岸边运动.设该人以匀速率v 0 收绳,绳不伸长且湖水静止,小船的速率为v ,则小船作( )(A) 匀加速运动,θcos 0v v =(B) 匀减速运动,θcos 0v v = (C) 变加速运动,θcos 0v v =(D) 变减速运动,θcos 0v v = (E) 匀速直线运动,0v v =分析与解 本题关键是先求得小船速度表达式,进而判断运动性质.为此建立如图所示坐标系,设定滑轮距水面高度为h,t 时刻定滑轮距小船的绳长为l ,则小船的运动方程为22h l x -=,其中绳长l随时间t 而变化.小船速度22d d d d h l t llt x -==v ,式中t l d d 表示绳长l 随时间的变化率,其大小即为v 0,代入整理后为θlh l cos /0220v v v =-=,方向沿x 轴负向.由速度表达式,可判断小船作变加速运动.故选(C).讨论 有人会将绳子速率v 0按x 、y 两个方向分解,则小船速度θcos 0v v =,这样做对吗? 1 -6 已知质点沿x 轴作直线运动,其运动方程为32262t t x -+=,式中x 的单位为m,t 的单位为 s .求:(1) 质点在运动开始后4.0 s 内的位移的大小; (2) 质点在该时间内所通过的路程;(3) t =4 s 时质点的速度和加速度.分析 位移和路程是两个完全不同的概念.只有当质点作直线运动且运动方向不改变时,位移的大小才会与路程相等.质点在t 时间内的位移Δx 的大小可直接由运动方程得到:0Δx x x t -=,而在求路程时,就必须注意到质点在运动过程中可能改变运动方向,此时,位移的大小和路程就不同了.为此,需根据0d d =tx来确定其运动方向改变的时刻t p ,求出0~t p 和t p ~t 内的位移大小Δx 1 、Δx 2 ,则t 时间内的路程21x x s ∆+∆=,如图所示,至于t =4.0 s 时质点速度和加速度可用tx d d 和22d d t x两式计算.解 (1) 质点在4.0 s 内位移的大小m 32Δ04-=-=x x x(2) 由 0d d =tx得知质点的换向时刻为s 2=p t (t =0不合题意)则m 0.8Δ021=-=x x xm 40Δ242-=-=x x x所以,质点在4.0 s 时间间隔内的路程为m 48ΔΔ21=+=x x s(3) t =4.0 s 时1s0.4s m 48d d -=⋅-==t t xv2s0.422m.s 36d d -=-==t t x a1 -7 一质点沿x 轴方向作直线运动,其速度与时间的关系如图(a)所示.设t =0 时,x =0.试根据已知的v -t 图,画出a -t 图以及x -t 图.分析 根据加速度的定义可知,在直线运动中v -t 曲线的斜率为加速度的大小(图中AB 、CD 段斜率为定值,即匀变速直线运动;而线段BC 的斜率为0,加速度为零,即匀速直线运动).加速度为恒量,在a -t 图上是平行于t 轴的直线,由v -t 图中求出各段的斜率,即可作出a -t 图线.又由速度的定义可知,x -t 曲线的斜率为速度的大小.因此,匀速直线运动所对应的x -t 图应是一直线,而匀变速直线运动所对应的x –t 图为t 的二次曲线.根据各段时间内的运动方程x =x (t ),求出不同时刻t 的位置x ,采用描数据点的方法,可作出x -t 图.解 将曲线分为AB 、BC 、CD 三个过程,它们对应的加速度值分别为2s m 20-⋅=--=AB AB AB t t a v v (匀加速直线运动)0=BC a (匀速直线运动)2s m 10-⋅-=--=CD CD CD t t a v v (匀减速直线运动)根据上述结果即可作出质点的a -t 图[图(B)].在匀变速直线运动中,有2021t t x x ++=v由此,可计算在0~2s和4~6s时间间隔内各时刻的位置分别为用描数据点的作图方法,由表中数据可作0~2s和4~6s时间内的x -t 图.在2~4s时间内, 质点是作1s m 20-⋅=v 的匀速直线运动, 其x -t 图是斜率k =20的一段直线[图(c)].1 -8 已知质点的运动方程为j i r )2(22t t -+=,式中r 的单位为m,t 的单位为s.求: (1) 质点的运动轨迹;(2) t =0 及t =2s时,质点的位矢;(3) 由t =0 到t =2s内质点的位移Δr 和径向增量Δr ;*(4) 2 s 内质点所走过的路程s .分析 质点的轨迹方程为y =f (x ),可由运动方程的两个分量式x (t )和y (t )中消去t 即可得到.对于r 、Δr 、Δr 、Δs 来说,物理含义不同,可根据其定义计算.其中对s 的求解用到积分方法,先在轨迹上任取一段微元d s ,则22)d ()d (d y x s +=,最后用⎰=s s d 积分求s.解 (1) 由x (t )和y (t )中消去t 后得质点轨迹方程为2412x y -= 这是一个抛物线方程,轨迹如图(a)所示.(2) 将t =0s和t =2s分别代入运动方程,可得相应位矢分别为j r 20= , j i r 242-=图(a)中的P 、Q 两点,即为t =0s和t =2s时质点所在位置. (3) 由位移表达式,得j i j i r r r 24)()(Δ020212-=-+-=-=y y x x其中位移大小m 66.5)(Δ)(ΔΔ22=+=y x r而径向增量m 47.2ΔΔ2020222202=+-+=-==y x y x r r r r*(4) 如图(B)所示,所求Δs 即为图中PQ 段长度,先在其间任意处取AB 微元d s ,则22)d ()d (d y x s +=,由轨道方程可得x x y d 21d -=,代入d s ,则2s内路程为m 91.5d 4d 42=+==⎰⎰x x s s Q P1 -9 质点的运动方程为23010t t x +-= 22015t t y -=式中x ,y 的单位为m,t 的单位为s.试求:(1) 初速度的大小和方向;(2) 加速度的大小和方向.分析 由运动方程的分量式可分别求出速度、加速度的分量,再由运动合成算出速度和加速度的大小和方向.解 (1) 速度的分量式为t t xx 6010d d +-==v t ty y 4015d d -==v当t =0 时, v o x =-10 m·s-1 , v o y =15 m·s-1 ,则初速度大小为120200s m 0.18-⋅=+=y x v v v设v o 与x 轴的夹角为α,则23tan 00-==xy αv vα=123°41′(2) 加速度的分量式为2s m 60d d -⋅==ta xx v , 2s m 40d d -⋅-==t a y y v则加速度的大小为222s m 1.72-⋅=+=y x a a a设a 与x 轴的夹角为β,则32tan -==x ya a β β=-33°41′(或326°19′)1 -10 一升降机以加速度1.22 m·s-2上升,当上升速度为2.44 m·s-1时,有一螺丝自升降机的天花板上松脱,天花板与升降机的底面相距2.74 m .计算:(1)螺丝从天花板落到底面所需要的时间;(2)螺丝相对升降机外固定柱子的下降距离.分析 在升降机与螺丝之间有相对运动的情况下,一种处理方法是取地面为参考系,分别讨论升降机竖直向上的匀加速度运动和初速不为零的螺丝的自由落体运动,列出这两种运动在同一坐标系中的运动方程y 1 =y 1(t )和y 2 =y 2(t ),并考虑它们相遇,即位矢相同这一条件,问题即可解;另一种方法是取升降机(或螺丝)为参考系,这时,螺丝(或升降机)相对它作匀加速运动,但是,此加速度应该是相对加速度.升降机厢的高度就是螺丝(或升降机)运动的路程.解1 (1) 以地面为参考系,取如图所示的坐标系,升降机与螺丝的运动方程分别为20121at t y +=v20221gt t h y -+=v当螺丝落至底面时,有y 1 =y 2 ,即20202121gt t h at t -+=+v vs 705.02=+=ag ht (2) 螺丝相对升降机外固定柱子下降的距离为m 716.021202=+-=-=gt t y h d v解2 (1)以升降机为参考系,此时,螺丝相对它的加速度大小a ′=g +a ,螺丝落至底面时,有2)(210t a g h +-=s 705.02=+=ag ht (2) 由于升降机在t 时间内上升的高度为2021at t h +='v则 m 716.0='-=h h d1 -11 一质点P 沿半径R =3.0 m 的圆周作匀速率运动,运动一周所需时间为20.0s,设t =0 时,质点位于O 点.按(a )图中所示Oxy 坐标系,求(1) 质点P 在任意时刻的位矢;(2)5s时的速度和加速度.分析 该题属于运动学的第一类问题,即已知运动方程r =r (t )求质点运动的一切信息(如位置矢量、位移、速度、加速度).在确定运动方程时,若取以点(0,3)为原点的O′x′y′坐标系,并采用参数方程x′=x′(t )和y′=y′(t )来表示圆周运动是比较方便的.然后,运用坐标变换x =x 0 +x ′和y =y 0 +y ′,将所得参数方程转换至Oxy 坐标系中,即得Oxy 坐标系中质点P 在任意时刻的位矢.采用对运动方程求导的方法可得速度和加速度.解 (1) 如图(B)所示,在O′x′y′坐标系中,因t Tθπ2=,则质点P 的参数方程为t T R x π2sin=', t T R y π2cos -='坐标变换后,在O x y 坐标系中有t TR x x π2sin='=, R t TR y y y +-=+'=π2cos0 则质点P 的位矢方程为j i r ⎪⎭⎫ ⎝⎛+-+=R t T R t T R π2cos π2sinj i )]π1.0(cos 1[3)π1.0(sin 3t t -+=(2) 5s时的速度和加速度分别为j j i r )s m π3.0(π2sin π2π2cos π2d d 1-⋅=+==t TT R t T T R t vi j i r a )s m π03.0(π2cos )π2(π2sin )π2(d d 222222-⋅-=+-==t TT R t T T R t 1 -12 地面上垂直竖立一高20.0 m 的旗杆,已知正午时分太阳在旗杆的正上方,求在下午2∶00 时,杆顶在地面上的影子的速度的大小.在何时刻杆影伸展至20.0 m ?分析 为求杆顶在地面上影子速度的大小,必须建立影长与时间的函数关系,即影子端点的位矢方程.根据几何关系,影长可通过太阳光线对地转动的角速度求得.由于运动的相对性,太阳光线对地转动的角速度也就是地球自转的角速度.这样,影子端点的位矢方程和速度均可求得.解 设太阳光线对地转动的角速度为ω,从正午时分开始计时,则杆的影长为s =h tg ωt ,下午2∶00 时,杆顶在地面上影子的速度大小为132s m 1094.1cos d d --⋅⨯===tωωh t s v 当杆长等于影长时,即s =h ,则s 606034πarctan 1⨯⨯===ωh s ωt 即为下午3∶00 时.1 -13 质点沿直线运动,加速度a =4 -t2 ,式中a 的单位为m·s-2 ,t 的单位为s.如果当t =3s时,x =9 m,v =2 m·s-1 ,求质点的运动方程.分析 本题属于运动学第二类问题,即已知加速度求速度和运动方程,必须在给定条件下用积分方法解决.由t a d d v =和tx d d =v 可得t a d d =v 和t x d d v =.如a =a (t )或v =v (t ),则可两边直接积分.如果a 或v 不是时间t 的显函数,则应经过诸如分离变量或变量代换等数学操作后再做积分.解 由分析知,应有⎰⎰=tt a 0d d 0vv v得 03314v v +-=t t (1)由⎰⎰=txx t x 0d d 0v得 00421212x t t t x ++-=v (2) 将t =3s时,x =9 m,v =2 m·s-1代入(1) (2)得v 0=-1 m·s-1,x 0=0.75 m .于是可得质点运动方程为75.0121242+-=t t x 1 -14 一石子从空中由静止下落,由于空气阻力,石子并非作自由落体运动,现测得其加速度a =A -B v ,式中A 、B 为正恒量,求石子下落的速度和运动方程.分析 本题亦属于运动学第二类问题,与上题不同之处在于加速度是速度v 的函数,因此,需将式d v =a (v )d t 分离变量为t a d )(d =v v后再两边积分. 解 选取石子下落方向为y 轴正向,下落起点为坐标原点.(1) 由题意知 v vB A ta -==d d (1) 用分离变量法把式(1)改写为t B A d d =-vv(2)将式(2)两边积分并考虑初始条件,有⎰⎰=-t t B A 0d d d 0v vvvv得石子速度 )1(Bt e BA--=v 由此可知当,t →∞时,BA→v 为一常量,通常称为极限速度或收尾速度. (2) 再由)1(d d Bt e BAt y --==v 并考虑初始条件有 t e BA y t Bt y d )1(d 00⎰⎰--= 得石子运动方程)1(2-+=-Bt e BAt B A y 1 -15 一质点具有恒定加速度a =6i +4j ,式中a 的单位为m·s-2 .在t =0时,其速度为零,位置矢量r 0 =10 m i .求:(1) 在任意时刻的速度和位置矢量;(2) 质点在Oxy 平面上的轨迹方程,并画出轨迹的示意图.分析 与上两题不同处在于质点作平面曲线运动,根据叠加原理,求解时需根据加速度的两个分量a x 和a y 分别积分,从而得到运动方程r 的两个分量式x (t )和y (t ).由于本题中质点加速度为恒矢量,故两次积分后所得运动方程为固定形式,即20021t a t x x x x ++=v 和20021t a t y y y y ++=v ,两个分运动均为匀变速直线运动.读者不妨自己验证一下.解 由加速度定义式,根据初始条件t 0 =0时v 0 =0,积分可得⎰⎰⎰+==ttt t 0)d 46(d d j i a vvj i t t 46+=v又由td d r=v 及初始条件t =0 时,r 0=(10 m)i ,积分可得 ⎰⎰⎰+==tt r r t t t t 0)d 46(d d 0j i r vj i r 222)310(t t ++=由上述结果可得质点运动方程的分量式,即x =10+3t 2y =2t 2消去参数t ,可得运动的轨迹方程3y =2x -20 m 这是一个直线方程.直线斜率32tan d d ===αx y k ,α=33°41′.轨迹如图所示. 1 -16 一质点在半径为R 的圆周上以恒定的速率运动,质点由位置A 运动到位置B,OA 和OB 所对的圆心角为Δθ.(1) 试证位置A 和B 之间的平均加速度为)Δ(/)Δcos 1(22θR θa v -=;(2) 当Δθ分别等于90°、30°、10°和1°时,平均加速度各为多少? 并对结果加以讨论.分析 瞬时加速度和平均加速度的物理含义不同,它们分别表示为t d d v =a 和tΔΔv =a .在匀速率圆周运动中,它们的大小分别为Ra n 2v =,t a ΔΔv = ,式中|Δv |可由图(B)中的几何关系得到,而Δt 可由转过的角度Δθ 求出.由计算结果能清楚地看到两者之间的关系,即瞬时加速度是平均加速度在Δt →0 时的极限值. 解 (1) 由图(b)可看到Δv =v 2 -v 1 ,故θΔcos 2Δ212221v v v v -+=v)Δcos 1(2θ-=v而vv θR s t ΔΔΔ==所以θR θt a Δ)cos Δ1(2ΔΔ2v -==v (2) 将Δθ=90°,30°,10°,1°分别代入上式,得R a 219003.0v ≈,Ra 229886.0v ≈ R a 239987.0v ≈,Ra 24000.1v ≈ 以上结果表明,当Δθ→0 时,匀速率圆周运动的平均加速度趋近于一极限值,该值即为法向加速度R2v . 1 -17 质点在Oxy 平面内运动,其运动方程为r =2.0t i +(19.0 -2.0t 2 )j ,式中r 的单位为m,t 的单位为s .求:(1)质点的轨迹方程;(2) 在t 1=1.0s 到t 2 =2.0s 时间内的平均速度;(3) t 1 =1.0s时的速度及切向和法向加速度;(4) t =1.0s 时质点所在处轨道的曲率半径ρ.分析 根据运动方程可直接写出其分量式x =x (t )和y =y (t ),从中消去参数t ,即得质点的轨迹方程.平均速度是反映质点在一段时间内位置的变化率,即t ΔΔr =v ,它与时间间隔Δt 的大小有关,当Δt →0 时,平均速度的极限即瞬时速度td d r =v .切向和法向加速度是指在自然坐标下的分矢量a t 和a n ,前者只反映质点在切线方向速度大小的变化率,即t t te a d d v =,后者只反映质点速度方向的变化,它可由总加速度a 和a t 得到.在求得t 1 时刻质点的速度和法向加速度的大小后,可由公式ρa n 2v =求ρ.解 (1) 由参数方程x =2.0t , y =19.0-2.0t 2消去t 得质点的轨迹方程:y =19.0 -0.50x 2(2) 在t 1 =1.00s 到t 2 =2.0s时间内的平均速度j i r r 0.60.2ΔΔ1212-=--==t t t r v (3) 质点在任意时刻的速度和加速度分别为j i j i j i t ty t x t y x 0.40.2d d d d )(-=+=+=v v v j j i a 222220.4d d d d )(-⋅-=+=s m ty t x t 则t 1 =1.00s时的速度v (t )|t =1s=2.0i -4.0j切向和法向加速度分别为t t y x t t t tt e e e a 222s 1s m 58.3)(d d d d -=⋅=+==v v v n n t n a a e e a 222s m 79.1-⋅=-=(4) t =1.0s质点的速度大小为122s m 47.4-⋅=+=y x v v v 则m 17.112==na ρv 1 -18 飞机以100 m·s-1 的速度沿水平直线飞行,在离地面高为100 m 时,驾驶员要把物品空投到前方某一地面目标处,问:(1) 此时目标在飞机正下方位置的前面多远? (2) 投放物品时,驾驶员看目标的视线和水平线成何角度?(3) 物品投出2.0s后,它的法向加速度和切向加速度各为多少?分析 物品空投后作平抛运动.忽略空气阻力的条件下,由运动独立性原理知,物品在空中沿水平方向作匀速直线运动,在竖直方向作自由落体运动.到达地面目标时,两方向上运动时间是相同的.因此,分别列出其运动方程,运用时间相等的条件,即可求解.此外,平抛物体在运动过程中只存在竖直向下的重力加速度.为求特定时刻t 时物体的切向加速度和法向加速度,只需求出该时刻它们与重力加速度之间的夹角α或β.由图可知,在特定时刻t ,物体的切向加速度和水平线之间的夹角α,可由此时刻的两速度分量v x 、v y 求出,这样,也就可将重力加速度g 的切向和法向分量求得.解 (1) 取如图所示的坐标,物品下落时在水平和竖直方向的运动方程分别为x =v t , y =1/2 gt 2飞机水平飞行速度v =100 m·s -1 ,飞机离地面的高度y =100 m,由上述两式可得目标在飞机正下方前的距离m 4522==gy x v(2) 视线和水平线的夹角为 o 5.12arctan==x y θ (3) 在任意时刻物品的速度与水平轴的夹角为vv v gt αx yarctan arctan == 取自然坐标,物品在抛出2s 时,重力加速度的切向分量与法向分量分别为2s m 88.1arctan sin sin -⋅=⎪⎭⎫ ⎝⎛==v gt g αg a t 2s m 62.9arctan cos cos -⋅=⎪⎭⎫ ⎝⎛==v gt g αg a n 1 -19 如图(a)所示,一小型迫击炮架设在一斜坡的底端O 处,已知斜坡倾角为α,炮身与斜坡的夹角为β,炮弹的出口速度为v 0,忽略空气阻力.求:(1)炮弹落地点P 与点O 的距离OP ;(2) 欲使炮弹能垂直击中坡面.证明α和β必须满足αβtan 21tan =并与v 0 无关. 分析 这是一个斜上抛运动,看似简单,但针对题目所问,如不能灵活运用叠加原理,建立一个恰当的坐标系,将运动分解的话,求解起来并不容易.现建立如图(a)所示坐标系,则炮弹在x 和y 两个方向的分运动均为匀减速直线运动,其初速度分别为v 0cos β和v 0sin β,其加速度分别为g sin α和gcos α.在此坐标系中炮弹落地时,应有y =0,则x =OP .如欲使炮弹垂直击中坡面,则应满足v x =0,直接列出有关运动方程和速度方程,即可求解.由于本题中加速度g 为恒矢量.故第一问也可由运动方程的矢量式计算,即20g 21t t +=v r ,做出炮弹落地时的矢量图[如图(B)所示],由图中所示几何关系也可求得OP (即图中的r 矢量).(1)解1 由分析知,炮弹在图(a)所示坐标系中两个分运动方程为αgt βt x sin 21cos 20-=v (1) αgt βt y cos 21sin 20-=v (2) 令y =0 求得时间t 后再代入式(1)得)cos(cos sin 2)sin sin cos (cos cos sin 2220220βααg ββαβααg βx OP +=-==v v 解2 做出炮弹的运动矢量图,如图(b)所示,并利用正弦定理,有βgt αt βαsin 212πsin 2πsin 20=⎪⎭⎫ ⎝⎛+=⎪⎭⎫ ⎝⎛--v r 从中消去t 后也可得到同样结果.(2) 由分析知,如炮弹垂直击中坡面应满足y =0 和v x =0,则0sin cos 0=-=αgt βx v v (3)由(2)(3)两式消去t 后得αβsin 21tan = 由此可知.只要角α和β满足上式,炮弹就能垂直击中坡面,而与v 0 的大小无关.讨论 如将炮弹的运动按水平和竖直两个方向分解,求解本题将会比较困难,有兴趣读者不妨自己体验一下.1 -20 一直立的雨伞,张开后其边缘圆周的半径为R ,离地面的高度为h ,(1) 当伞绕伞柄以匀角速ω旋转时,求证水滴沿边缘飞出后落在地面上半径为g ωh R r /212+=的圆周上;(2) 读者能否由此定性构想一种草坪上或农田灌溉用的旋转式洒水器的方案?分析 选定伞边缘O 处的雨滴为研究对象,当伞以角速度ω旋转时,雨滴将以速度v 沿切线方向飞出,并作平抛运动.建立如图(a)所示坐标系,列出雨滴的运动方程并考虑图中所示几何关系,即可求证.由此可以想像如果让水从一个旋转的有很多小孔的喷头中飞出,从不同小孔中飞出的水滴将会落在半径不同的圆周上,为保证均匀喷洒对喷头上小孔的分布还要给予精心的考虑.解 (1) 如图(a)所示坐标系中,雨滴落地的运动方程为t ωR t x ==v (1)h gt y ==221 (2) 由式(1)(2)可得 g h ωR x 2222= 由图(a)所示几何关系得雨滴落地处圆周的半径为22221ωgh R R x r +=+= (2) 常用草坪喷水器采用如图(b)所示的球面喷头(θ0 =45°)其上有大量小孔.喷头旋转时,水滴以初速度v 0 从各个小孔中喷出,并作斜上抛运动,通常喷头表面基本上与草坪处在同一水平面上.则以φ角喷射的水柱射程为gR 2sin 0v = 为使喷头周围的草坪能被均匀喷洒,喷头上的小孔数不但很多,而且还不能均匀分布,这是喷头设计中的一个关键问题.1 -21 一足球运动员在正对球门前25.0 m 处以20.0 m·s-1 的初速率罚任意球,已知球门高为3.44 m .若要在垂直于球门的竖直平面内将足球直接踢进球门,问他应在与地面成什么角度的范围内踢出足球? (足球可视为质点)分析 被踢出后的足球,在空中作斜抛运动,其轨迹方程可由质点在竖直平面内的运动方程得到.由于水平距离x 已知,球门高度又限定了在y 方向的范围,故只需将x 、y 值代入即可求出.解 取图示坐标系Oxy ,由运动方程θt x cos v =, 221sin gt θt y -=v 消去t 得轨迹方程 222)tan 1(2tan x θg θx y +-=v以x =25.0 m,v =20.0 m·s-1 及3.44 m≥y ≥0 代入后,可解得71.11°≥θ1 ≥69.92°27.92°≥θ2 ≥18.89°如何理解上述角度的范围?在初速一定的条件下,球击中球门底线或球门上缘都将对应有两个不同的投射倾角(如图所示).如果以θ>71.11°或θ <18.89°踢出足球,都将因射程不足而不能直接射入球门;由于球门高度的限制,θ 角也并非能取71.11°与18.89°之间的任何值.当倾角取值为27.92°<θ <69.92°时,踢出的足球将越过门缘而离去,这时球也不能射入球门.因此可取的角度范围只能是解中的结果.1 -22 一质点沿半径为R 的圆周按规律2021bt t s -=v 运动,v 0 、b 都是常量.(1) 求t 时刻质点的总加速度;(2) t 为何值时总加速度在数值上等于b ?(3) 当加速度达到b 时,质点已沿圆周运行了多少圈?分析 在自然坐标中,s 表示圆周上从某一点开始的曲线坐标.由给定的运动方程s =s (t ),对时间t 求一阶、二阶导数,即是沿曲线运动的速度v 和加速度的切向分量a t,而加速度的法向分量为a n =v 2 /R .这样,总加速度为a =a te t+a n e n .至于质点在t 时间内通过的路程,即为曲线坐标的改变量Δs =s t -s 0.因圆周长为2πR,质点所转过的圈数自然可求得.解 (1) 质点作圆周运动的速率为bt ts -==0d d v v其加速度的切向分量和法向分量分别为b t s a t -==22d d , Rbt R a n 202)(-==v v 故加速度的大小为R )(402222bt b a a a a t tn -+=+=v 其方向与切线之间的夹角为⎥⎦⎤⎢⎣⎡--==Rb bt a a θt n 20)(arctan arctan v (2) 要使|a |=b ,由b bt b R R=-+4022)(1v 可得 bt 0v = (3) 从t =0 开始到t =v 0 /b 时,质点经过的路程为b s s s t 2200v =-= 因此质点运行的圈数为bRR s n π4π220v == 1 -23 一半径为0.50 m 的飞轮在启动时的短时间内,其角速度与时间的平方成正比.在t =2.0s 时测得轮缘一点的速度值为4.0 m·s-1.求:(1) 该轮在t′=0.5s的角速度,轮缘一点的切向加速度和总加速度;(2)该点在2.0s内所转过的角度.分析 首先应该确定角速度的函数关系ω=kt 2.依据角量与线量的关系由特定时刻的速度值可得相应的角速度,从而求出式中的比例系数k ,ω=ω(t )确定后,注意到运动的角量描述与线量描述的相应关系,由运动学中两类问题求解的方法(微分法和积分法),即可得到特定时刻的角加速度、切向加速度和角位移.解 因ωR =v ,由题意ω∝t 2 得比例系数322s rad 2-⋅===Rtt ωk v 所以 22)(t t ωω== 则t ′=0.5s 时的角速度、角加速度和切向加速度分别为12s rad 5.02-⋅='=t ω2s rad 0.24d d -⋅='==t tωα 2s m 0.1-⋅==R αa t总加速度n t t n R ωR αe e a a a 2+=+= ()()2222s m 01.1-⋅=+=R ωR αa在2.0s内该点所转过的角度rad 33.532d 2d 203202200====-⎰⎰t t t t ωθθ 1 -24 一质点在半径为0.10 m 的圆周上运动,其角位置为342t θ+=,式中θ 的单位为rad,t 的单位为s.(1) 求在t =2.0s时质点的法向加速度和切向加速度.(2) 当切向加速度的大小恰等于总加速度大小的一半时,θ 值为多少?(3) t 为多少时,法向加速度和切向加速度的值相等?分析 掌握角量与线量、角位移方程与位矢方程的对应关系,应用运动学求解的方法即可得到. 解 (1) 由于342t θ+=,则角速度212d d t tθω==.在t =2 s 时,法向加速度和切向加速度的数值分别为 22s 2s m 30.2-=⋅==ωr a t n 2s 2s m 80.4d d -=⋅==t ωr a t t(2) 当22212/t n t a a a a +==时,有223n t a a =,即 ()()422212243t r rt = 得 3213=t此时刻的角位置为 rad 15.3423=+=t θ(3) 要使t n a a =,则有()()422212243t r rt = t =0.55s1 -25 一无风的下雨天,一列火车以v 1=20.0 m·s-1 的速度匀速前进,在车内的旅客看见玻璃窗外的雨滴和垂线成75°角下降.求雨滴下落的速度v2 .(设下降的雨滴作匀速运动)分析 这是一个相对运动的问题.设雨滴为研究对象,地面为静止参考系S,火车为动参考系S′.v 1 为S′相对S 的速度,v 2 为雨滴相对S的速度,利用相对运动速度的关系即可解.解 以地面为参考系,火车相对地面运动的速度为v 1 ,雨滴相对地面竖直下落的速度为v 2 ,旅客看到雨滴下落的速度v 2′为相对速度,它们之间的关系为1'22v v v += (如图所示),于是可得 1o 12s m 36.575tan -⋅==v v 1 -26 如图(a)所示,一汽车在雨中沿直线行驶,其速率为v 1 ,下落雨滴的速度方向偏于竖直方向之前θ 角,速率为v 2′,若车后有一长方形物体,问车速v 1为多大时,此物体正好不会被雨水淋湿?分析 这也是一个相对运动的问题.可视雨点为研究对象,地面为静参考系S,汽车为动参考系S′.如图(a)所示,要使物体不被淋湿,在车上观察雨点下落的方向(即雨点相对于汽车的运动速度v 2′的方向)应满足hlαarctan ≥.再由相对速度的矢量关系122v v v -=',即可求出所需车速v 1.解 由122v v v -='[图(b)],有θθαcos sin arctan221v v v -= 而要使hlαarctan ≥,则 hl θθ≥-cos sin 221v v v ⎪⎭⎫ ⎝⎛+≥θh θl sin cos 21v v 1 -27 一人能在静水中以1.10 m·s-1 的速度划船前进.今欲横渡一宽为1.00 ×103 m 、水流速度为0.55 m·s-1 的大河.(1) 他若要从出发点横渡该河而到达正对岸的一点,那么应如何确定划行方向? 到达正对岸需多少时间? (2)如果希望用最短的时间过河,应如何确定划行方向? 船到达对岸的位置在什么地方?分析 船到达对岸所需时间是由船相对于岸的速度v 决定的.由于水流速度u 的存在, v 与船在静水中划行的速度v ′之间有v =u +v ′(如图所示).若要使船到达正对岸,则必须使v 沿正对岸方向;在划速一定的条件下,若要用最短时间过河,则必须使v 有极大值.解 (1) 由v =u +v ′可知v '=u αarcsin ,则船到达正对岸所需时间为。
第一章习题解析
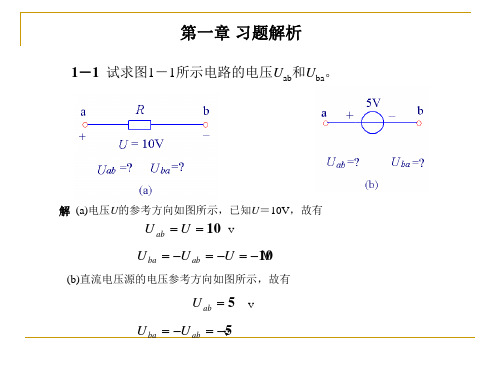
1-3 在图1-3所示电路中,试求: (1)若元件A吸收10W功率,求其电压UA; (2)若元件B吸收-10W功率,求其电流IB; (3)若元件C发出10W功率,求其电流IC; (4)若元件D发出10mW功率,求其电流ID。
+
4A
UA
A
-
+
IB
10V B
-
IC
P3 U3I 60 (10) 600w P4 U4I (80) (10) 800w
电路发出的功率为
P发出=1000 +400=1400
电路吸收的功率为
P吸收=600+800=1400
1-8 在图1-9(a)所示电路中,已知I1=0.2A,I2=0.3A, I6=1 A。试求电流I3、I4和I5。
I2
I6
I4
I2
I6
I4
I1
I3
I5
I1
I3
I5
(a)
(b)
图1-9
解 应用KCL对图1-9(a)电路中各结点列写电流方程,得
I3 I1 I2 0.2 0.3 0.5A
I4 I6 I2 1 0.3 0.7 A
由KVL,得
Ubc 5v
Uac Uab Ubc (20) 5 15v
Ucd 10I 10 (2) 20v
由KVL,得
Ude 3v
U ae U ac U cd U de (15) (20) (3) 38V
1-6 在图1-6所示电路中, 已知U1=10 V,Us1=4V,Us2=2V,R1=4Ω,R2=2Ω,R3=5Ω。 试计算端子1、2开路时流过电阻R2的电流I2和电压U2。
U x 6.3 V
电阻Rx的电流应为
数学分析习题选解第一章(华东师大版)

数学分析习题选解第一章 实数与函数 §1. 实数 习题Page. 41. 设a 为有理数,x 为无理数,证明:(1). a x +是无理数; (2)当0a ≠时,ax 是无理数。
证明:(用反证法) 3. 设,a b ∈R ,证明:若对任何正数ε有a b ε-<,则a b =。
证明:反证法,如果a b ≠,则取02a b ε-=>,有:a b ε-≥,矛盾。
6. 设,,a b c +∈R (+R 表示全体正实数的集合),证明:b c ≤-你能说明此不等式的几何意义吗? 证明:用分析法,b c ≤-22222222a b a c b c b c ⇐+++-≤+-22a cb c⇐≤-22a b c⇐+422242222a a b c bc a a ca bb c⇐++≤+++ 222bc c b ⇐≤+()20b c ⇐-≥(显然成立)几何意义,如图,在R t A B C ∆中,记B C a =,A C b =,在直角边A C 上,取一点D连接B D ,记D C c =,则A D b c =-,由勾股定理,A B =,B D =此结论说明,三角形的两边之和大于第三边。
7. 设0x >,0b >,a b ≠。
证明:a x b x++介于1与a b之间。
证明:1a x a b b xb x+--=++与a b -同号(注意,0x >,0b >);又()()x b a a x a b xbb b x -+-=++与b a -同号,故a x b x++介于1与a b之间。
8. 设p 为正整数,证明:若p证明:(反证法)设m n=,其中,n m ∈N ,(,)1n m =,于是,22p n m =。
由于大于1的整数能唯一地分解为素因数之积,若p 不是完全平方数,ac b D CBA则p 的素因数分解式中,必有r 是p 的具有奇指数的素因数。
则22p n m =的左端有奇数个素因数r ,而右端没有,与分解的唯一性矛盾,证毕 补充题:证明任何二个不同的有理数之间必有无理数。
第一章课后习题答案

第一章课后习题答案1、5个女生,7个男生进行排列,(a) 若女生在一起有多少种不同的排列?(b) 女生两两不相邻有多少种不同的排列?(c) 两男生A和B之间正好有3个女生的排列是多少?解:(a) 若女生在一起,可将5个女生看作一个整体参与排列,有8!种方式,然后5个女生再进行排列,有5!种方式,根据乘法法则,共有8!5!种方式。
(b) 若女生两两不相邻,可将7个男生进行排列,有7!种方式,考虑到两个男生之间的6个位置和两头的2个位置,每个位置安排一个女生均符合题意,故从中选出5个位置,然后5个女生再进行排列,按顺序安排到这5个位置,有C(8, 5)5!种方式,根据乘法法则,共有7!C(8, 5)5!=7!P(8, 5)种方式。
(c) 若两男生A和B之间正好有3个女生,可以按照顺序操作如下:首先将女生分为两组,一组3人,一组2人,有C(5, 3)种方式;将男生A和B看作一个整体,加上其他5个男生,2人一组的女生进行排列,有8!种方式;将3人一组的女生安排到男生A和B之间进行排列,有3!种方式;男生A和B进行排列,有2!种方式。
根据乘法法则,所求的排列方式为8!C(5, 3)3!2!=8!P(5, 3)2!2、求3000到8000之间的奇整数的数目,而且没有相同的数字。
解:设介于3000到8000之间的奇整数表示为abcd,则a∈{3, 4, 5, 6, 7}, d∈{1, 3, 5, 7, 9},对a进行分类如下:(1) 若a∈{3, 5, 7},则d有4种选取方式,bc有P(8, 2)种方式,根据乘法法则,此类数字有3⨯4⨯P(8, 2)=672个(2) 若a∈{4, 6},则d有5种选取方式,bc仍有P(8, 2)种方式,根据乘法法则,此类数字有2⨯5⨯P(8, 2)=560个根据加法法则,3000到8000之间数字不同的奇整数的数目为672+560=1232个3、证明nC(n-1, r)=(r+1)C(n, r+1),并给出组合解释。
高教社第一章习题及习题解答

习题一、判断题1、计算机区别于其他工具的本质特点是具有逻辑判断的能力。
()2、计算机的性能指标完全由CPU决定。
()3、RAM中的信息在计算机断电后会全部丢失。
()4、计算机软件包括系统软件和应用软件。
()5、声音、图片等属于计算机信息处理的表示媒体。
()6、存储地址是存储器存储单元的编号,CPU要存取某个存储单元的信息,一定要知道这个存储单元的地址。
()7、通常把计算机的运算器、控制器及内存储器称为主机。
()8、计算机的硬件和软件是互相依存、互相支持的,硬件的某些功能可以用软件来完成,而软件的某些功能也可以用硬件来实现。
()9、复制软件会妨害版权人的利益,是一种违法行为。
()10、计算机病毒可以通过光盘或网络等方式进行传播。
()二、选择题1、操作系统是一种()。
A、系统软件B、应用软件C、软件包D、游戏软件2、以下设备中不属于输出设备的是()。
A、打印机B、绘图仪C、扫描仪D、显示器3、计算机内所有的信息都是以()数字形式表示的。
A、八进制B、十六进制C、十进制D、二进制4、ASCII码是一种对()进行编码的计算机代码。
A、汉字B、字符C、图像D、声音5、个人计算机使用的键盘中,Shift键是()。
A、换档键B、退格键C、空格键D、回车换行键6、目前大多数计算机,就其工作原理而言,基本上采用的是科学家()提出的设计思想。
A、比尔.盖茨B、冯.诺依曼C、乔治.布尔D、艾仑.图灵7、现代信息技术的核心是()。
A、电子计算机和现代通信技术B、微电子技术和材料技术C、自动化技术和控制技术D、数字化技术和网络技术8、完整的计算机系统由()组成。
A、硬件系统B、系统软件C、软件系统D、操作系统9、计算机病毒是指()。
A、编制有错误的计算机程序B、设计不完善的计算机程序C、已被破坏的计算机程序D、以危害系统为目的的特殊计算机程序10、我国将计算机软件的知识产权列入()权保护范畴。
A、专利B、技术C、合同D、著作三、简答题1、计算机的特点有哪些?2、计算机的硬件系统分为哪五部分?3、什么是计算机软件?4、什么是多媒体计算机?5、试写出3种常见的计算机输入设备。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
习题选解第一章 习题选解.习 题 1-11.设x x x f +-=11)(,求)(x f -,)1(x f ,)(1x f ,)1(+x f . 解:1()1xf x x-=+ 1()1()1()1x x f x x x --+∴-==+--,1111()111x x f x x x --==++1111()11xx f x xx+==--+,1(1)(1)1(1)2x x f x x x -++==-+++ 2.下列各题中,函数)(x f 与)(x g 是否相同?为什么?(1)24)(2--=x x x f ,2)(+=x x g ;解:因为)(x f 的定义域为(,2)(2,)-∞⋃+∞,而()g x 的定义域为(,)-∞+∞,所以()f x 与()g x 定义域不同,因此()f x 与()g x 不相同.(2)2)13()(-=x x f ,13)(-=x x g ;解:因为()f x 与()g x 定义域相同,对应法则相同,故()f x 与()g x 相同.(3)11ln)(-+=x x x f ,)1ln()1ln()(--+=x x x g ; 解:由10101x x x -≠⎧⎪+⎨>⎪-⎩解出()f x 的定义域为(,1)(1,)-∞-⋃+∞,而由1010x x +>⎧⎨->⎩解出()g x 的定义域为(1,)+∞,所以()f x 与()g x 定义域不同,因此()f x 与()g x 不相同. (4)11ln)(2++=x x x f ,)1ln()1ln()(2+-+=x x x g . 解:因为()f x 与()g x 定义域相同,对应法则相同,故()f x 与()g x 相同.3.设⎩⎨⎧>+≤-=11121)(2x x x x x f , , ,求 )0(f ,)1(f ,)1(-f ,)23(f ,)23(-f .解:(0)1f =,(1)1f =-,(1)3f -=,313()24f =,313()24f -=.4.设x x f ln )(=,证明)]1([)1()(+=++x x f x f x f . 证:因为()(1)ln ln(1)f x f x x x ++=++,又[(1)]ln[(1)]ln ln(1)f x x x x x x +=+=++, 得证。
5.下列函数哪些是偶函数?哪些是奇函数?哪些是非奇非偶函数? (1) 532x x y -=; 解:因为5()23f x x x =-,于是55()23(23)f x x x x x -=-+=--,所以原函数为奇函数.(2) x x y 2sin sin +=;解:因为2()sin sin f x x x =+,于是22()sin()sin ()sin sin f x x x x x -=-+-=-+,不等于()f x 或()f x -,所以原函数为非奇非偶函数. (3) )sin(sin x y =;解:因为()sin(sin )f x x =, 于是()sin(sin())sin(sin )sin(sin )()f x x x x f x -=-=-=-=-,所以原函数为奇函数。
(4))1(2 >-=-a a a y xx ;解:因为()(1)2x xa a f x a --=> ,于是()()22x x x xa a a a f x f x -----==-=- ,所以原函数为奇函数.(5))1(2 >+=-a a a y xx ;解: 因为()(1)2x xa a f x a -+=> ,于是()()22x x x xa a a a f x f x --++-==-= ,所以原函数为偶函数.(6))1(11 >+-=a a a x y x x ;解: 因为1()1x x a f x x a -=+ ,于是111()()111x x x x x x a a a f x x x x f x a a a ------=--==+++= ,所以原函数为偶函数.(7)xxy +-=22lg; 解:因为2()lg 2xf x x-=+ ,于是 22()lg lg ()22x xf x f x x x+--=-=--+= ,所以原函数为奇函数.(8)1cos sin +-=x x y ;解:因为()sin cos 1f x x x =-+,于是()sin()cos()1sin cos 1f x x x x x -=---+=--+ ,不等于()f x 或()f x -,所以原函数为非奇非偶函数.(9)21cos xx y -=;解:因为()f x =()()f x f x -== ,所以原函数为偶函数.(10))1lg(2x x y ++=.解:因为()lg(f x x = ,于是()lg(lg lg(()1xf x x x f x -=-=-=-+=- =-,所以原函数为奇函数. 6.对于下列函数)(x f 与)(x g ,求复合函数)]([x g f 和[()]g f x ,并确定它们的定义域.(1) 1)(32)(2-=+=x x g x x f , ;解:22[()]2(1)321,(,)f g x x x x =-+=+∈-∞+∞;22[()](23)14128,(,)g f x x x x x =+-=++∈-∞+∞.(2)4)(1)(x x g x x f =-=, ;解:[()](,1][1,)f g x x =∈-∞-+∞ ;2[()](1),[1,)g f x x x =-∈+∞.(3))1sin()(2)(+==x x g x f x , .解:sin(1)[()]2,(,)x f g x x +=∈-∞+∞.[()]sin(21),(,)x g f x x =+∈-∞+∞.7.设b ax x f +=)(,满足x x f f =)]([,且1)2(-=f ,求)(x f .解:因为2[()]()(1)f f x a ax b b a x a b x =++=++=,得21,(1)0a a b =+=,当1a =时,0,()b f x x==,与1)2(-=f 矛盾;所以,1a =-,此时,()f x x b =-+,由1)2(-=f 知,1b =,故()1f x x =-+.8.设x v e u u y v -===, , arcsin ,试将y 表示成x 的函数.解:arcsin y e =.9.指出下列各复合函数是由哪些简单函数复合而成的. (1) 22)1(arcsin x y -=;解:由22,arcsin ,1y u u v v t x ====-复合而成.(2))11(sec 3xy -=;解:由31,sec ,1y u u v v x===-复合而成. (3)1sin log +=x a e y ;解:由log ,sin ,,1t a y u u v v e t x ====+复合而成.(4)321arctan -=x y .解:由21,,arctan 3-===x v v u u y 复合而成. 10.以下各对函数)(u f y =与)(x g u =中,哪些可以复合成复合函数)]([x g f ?哪些不能复合?为什么?(1)2)2arcsin(x u u y =+=, ;解:因为222x +≥不在arcsin t 的定义域内,所以)(u f y =与)(x g u =不能复合成复合函数)]([x g f .(2)21arccos x x u u y +==, ;解:因为2(1,1)1xx∈-+在arccos u 的定义域内,所以)(u f y =与)(x g u =能复合成复合函数)]([x g f .(3)211lnx u u y +==, ;解: 因为21ln01u x=≤+不在y =所以)(u f y =与)(x g u =不能复合成复合函数)]([x g f .(4)x u u y sin )1ln(=-=, .解: 因为1sin 0x -≥与ln y t =的定义域交集非空,所以)(u f y =与)(x g u =能复合成复合函数)]([x g f .11.设)(x f 的定义域为]10[,,问(1))(2x f ;(2))(sin x f ,(3))0)((>+a a x f ;(4))0)(()(>-++a a x f a x f 的定义域各是什么?解:(1)201x ≤≤,即11x -≤≤,所以)(2x f 的定义域为[1,1]-;(2)0sin 1x≤≤,即2(21)n x n ππ≤≤+,1,2,3n = 所以)(sin x f 的定义域为[2,(21)]n n ππ+,1,2,3n =(3)01x a ≤+≤,即1a x a -≤≤-,所以)0)((>+a a x f 的定义域为]1,[a a -- .(4)01x a ≤+≤且01x a ≤-≤,即1a x a -≤≤-且1a x a ≤≤+,所以)0)(()(>-++a a x f a x f 的定义域为:若210≤<a , 则为]1,[a a --;若21>a ,则为空集 .习 题 1-21.设lim nn x a →∞=,证明:lim n n x a→∞=.证 因为n n x a x a-≤-,所以0ε∀>,由lim n n x a →∞=知N ∃,当n N >时,有n n x a x a ε-≤-<成立,由定义知lim n n x a→∞=.2.根据数列极限的N -ε定义证明(1) 2)12(lim =+∞→nn ; (2)21lim0n n→∞=; (3) 1lim 11n n n →∞+=- ; (4)1n →∞=.证 (1) 由于11(2)2n n+-= ,所以ε∀>,取1N ε>,当n N>时,有111(2)2n n Nε+-=<< 成立,由定义知 2)12(lim =+∞→n n ;(2) 要使22110n n ε-=< ,只要n >0ε∀>,取N >当n N >时,有2221110n n Nε-=<< 成立,由定义知21lim0n n →∞=;(4)41n n nε--==<<,只要4n ε>即可.所以0ε∀>,取4N ε>,当n N >441n Nε-<<<成立,由定义知1n →∞=. 3.设 个, , , n n x x x 9999.099.09.021===,问 ?l i m =∞→n n x 求出N ,使Nn >时,n x 与其极限之差的绝对值小于0.0001.证10.99991n nx -=-= 110n,显然l i m n n x →∞=.要使1n x -= 10.000110n <, 只要4N>,当N n >,就有1n x -= 41110.0001101010n N <<=4.设数列{}n x 有界,又lim 0n n y →∞=,证明:lim 0n n n x y →∞=.证 因为数列{}n x 有界,故0M∃>,使得对一切n x ,有n x M≤,又lim 0nn y →∞=,故0,,N ε∀>∃当n N >时,有n y Mε<,于是,当nN >时,有n n n n x y x y M Mεε=<=,由定义知 lim 0n nn x y →∞=.5.对于数列{}n x ,若21k x a -→ ()k →∞,2k x a → ()k →∞,证明:n x a →()n →∞证 因为21k x a -→()k →∞,2k x a → ()k →∞,所以0ε∀>,0K ∃>,使得当k K >时,有21k x a ε--<,2k x a ε-<成立,令2N K =,则当n N >时,有n x a ε-<,由定义知 n x a →()n →∞.习 题 1-31.根据函数极限的定义证明(1) 5)13(lim 2=-→x x ;(2)212lim 31x x x x →---=-+.(3) 3131lim 33=+∞→x x x ; (4)lim0x →+∞= .证(1)(31)532x x --=-,0ε∀>要使32x ε-<,只要23x ε-<即可.于是取3εδ=,则当02x δ<-<时,就有(31)5323x x δε--=-<=,由定义知 5)13(lim 2=-→x x .(2)22(1)(2)33111x x x x x x x --+-+=+=+++,0ε∀>,要使2231x x x ε--+<+,只要1x ε+<即可.于是取δε=,则当01x δ<+<时,22311x x x x δε--+=+<=+成立,由定义知 212lim31x x x x →---=-+.(3)要使333333111113333x x x x x xε++--==<,只要x >即可.所以,0ε∀>,取X >,当x X>时,有333311113333x x Xx ε+-=<<成立,由定义知 3131lim 33=+∞→x x x . (40ε-≤< ,只要21x ε>即可.所以,0ε∀>,取21X ε>,则当x X >0ε-≤<< 成立,由定义知lim0x = .2.设⎩⎨⎧≥-<=3133)(x x x x x f , , ,讨论3→x 时)(x f 的左、右极限. 解:33lim()lim 3x x f x x --→→==,33lim ()lim(31)8x x f x x ++→→=-=.3.当∞→x 时,13122→+-=x x y ,问X 应为何值,才能使X x >时,01.01<-y ?解:要使222222134441110.01333x x y x x x x-+--=-=-=<<+++,只要20x >即可. 故取20X >,当X x >时,有01.01<-y .4.证明函数 ()f x x = 当0x →时极限为零.证:因为()000f x x x -=-=-,所以,0ε∀>,取δε=,当00x δ<-<时,有()00f x x δε-=-<=,由定义知 0lim ()0x f x →=5.证明:若x →+∞及x →-∞时,函数()f x 的极限都存在且都等于A ,则li m ()x f x A →∞=.证:因为x →+∞及x →-∞时,函数()f x 的极限都存在且都等于A ,所以,0ε∀>,10X ∃>,当1x X >时,有()f x A ε-<;又20X ∃>,当2x X <-时,有()f x A ε-<.取{}12max ,X X X =,当x X>时,就有()f x A ε-<成立,由定义知,lim()x f x A →∞=.6.设 lim()x f x A →∞=存在,证明:存在正数M及X,使得当x X>时,有()f x M <.证:由于lim()x f x A →∞=,所以对于1ε=,0X ∃>,当x X>时,有()1f x A -<,于是当x X >时,有()()()1f x f x A A f x A A A =-+≤-+<+,取1M A =+, 则当x X >时,有()f x M <.习 题 1-41.两个无穷小量的商是否一定是无穷小量?举例说明之。
