杠杆平衡条件的应用
杠杆的平衡原理应用

杠杆的平衡原理应用1. 杠杆的基本原理•杠杆是一种用于放大力量的简单机械装置。
•杠杆由一个固定点(支点)和两个或多个杠杆臂(力臂)组成。
•杠杆通过将力作用于一个杠杆臂上,产生平衡或运动。
2. 杠杆的平衡原理•杠杆的平衡原理是基于力矩的平衡。
•在平衡状态下,力矩总和为零。
•力矩是由力与力臂长度的乘积给出。
3. 杠杆的应用3.1 一级杠杆•一级杠杆是最简单的杠杆形式。
•一级杠杆用于放大力量或改变力的方向。
•例子:剪刀、锤子等。
3.2 二级杠杆•二级杠杆是由两个力臂组成的杠杆。
•二级杠杆提供了更大的机械优势。
•例子:推车手推杆、螺丝刀等。
3.3 三级杠杆•三级杠杆是由三个力臂组成的杠杆。
•三级杠杆可以提供更大的力量放大效果。
•例子:拨弦乐器、人体关节等。
4. 杠杆的应用案例4.1 制动系统•汽车制动系统利用了杠杆原理来放大制动力。
•当踩下制动踏板时,通过杠杆系统将力量传递给刹车鼓或刹车盘。
4.2 游乐设备•游乐设备如秋千、摇摆船等也应用了杠杆原理。
•通过调整不同的力臂长度,可以调节游乐设备的平衡性和运动性。
4.3 工具使用•许多工具如梯子、起重机等也利用了杠杆原理。
•通过调整杠杆的位置,可以轻松地提起重物或达到所需的高度。
5. 杠杆的平衡原理在生活中的应用•杠杆的平衡原理在日常生活中有很多应用。
•在家庭中,我们可以利用杠杆原理来搬运重物或调节家具的平衡。
•在体育运动中,例如举重和摔跤,运动员利用杠杆原理来提升力量和平衡能力。
•所有这些应用都基于杠杆的平衡原理,通过合理设计和调整力臂长度,实现了更高效和更轻松地完成任务的目标。
结论•杠杆的平衡原理是一种基本的物理原理,广泛应用于各个领域。
•了解和应用杠杆的平衡原理可以帮助我们更好地理解和利用力学原理。
•在日常生活和工作中,我们可以通过运用杠杆原理处理问题,提高工作效率和生活品质。
杠杆平衡的条件的原理应用

杠杆平衡的条件的原理应用一、什么是杠杆平衡杠杆平衡是物理学中的一个重要原理,也是机械原理的基础。
简单来说,杠杆平衡是指在一个平衡状态下,杠杆两端的力矩相等,使杠杆保持平衡。
这个原理被广泛应用在日常生活和工程领域中。
二、杠杆平衡的原理杠杆平衡的原理可以通过以下公式描述:力矩=力×距离根据这个公式,如果一个杠杆在一个点上保持平衡,那么这个点上的力矩总和为零。
可以表示为:$$ \\sum{力矩} = 0 $$根据力矩的定义,可以将上式改写为:$$ \\sum{力 × 距离} = 0 $$这意味着如果一个杠杆保持平衡,那么左边的力矩总和等于右边的力矩总和。
三、杠杆平衡的条件为了使杠杆保持平衡,需要满足以下两个条件:1. 力矩平衡在一个杠杆上的力矩总和必须为零。
这意味着杠杆两边的力矩相等。
用公式表示为:$$ \\sum{力 × 距离} = 0 $$2. 力的平衡在一个杠杆上的力总和必须为零。
这意味着杠杆两边的力相等。
用公式表示为:$$ \\sum{力} = 0 $$只有当上述两个条件同时满足时,杠杆才能保持平衡。
四、杠杆平衡的应用杠杆平衡的原理在很多领域都有应用。
下面是一些常见的应用示例:1. 手杖和拐杖手杖和拐杖是杠杆平衡原理的典型应用。
通过保持杠杆两端力的平衡,人们可以稳定地支撑身体重量。
2. 钳子和扳手钳子和扳手也是杠杆平衡的实际应用。
通过改变力的距离,人们可以在紧缩的状态下应用更大的力。
3. 制动系统制动系统中的刹车踏板和制动碟也运用了杠杆平衡的原理。
通过改变杠杆的长度,人们可以增加或减少制动力。
4. 剪刀和钳子剪刀和钳子也是杠杆平衡的实际应用,通过杠杆的力矩平衡,人们可以轻松地剪切纸张或夹紧物体。
5. 变焦镜头在摄影中,变焦镜头也是杠杆平衡的应用之一。
通过调整镜头的长度,人们可以调节焦距和放大倍数。
6. 机械辅助器具许多机械辅助器具,如起重机、推土机和叉车,都使用了杠杆平衡的原理。
杠杆平衡条件的应用

杠杆平衡条件的应用一、杠杆平衡条件的概述杠杆平衡条件是指在物理学和工程学中,当一个系统处于平衡状态时,各种力的作用力矩相互抵消。
这个概念在财务管理中也有应用,称为财务杠杆平衡条件。
它是指企业债务和股本结构的调整,以实现企业稳定运营和盈利的一种方法。
二、财务杠杆平衡条件的定义财务杠杆平衡条件是指企业通过调整债务和股本结构,使得企业运营所需的利息支出与企业经营收益之间达到最佳匹配状态,从而实现稳定运营和盈利。
三、影响财务杠杆平衡条件的因素1. 负债率:债务与股本比例越高,企业利润波动性越大。
2. 利息率:利息率越高,企业承担的财务风险越大。
3. 盈利能力:盈利能力越强,企业承担风险能力也就越强。
4. 经营周期:经营周期长短不同会影响到资金周转速度和流动性。
四、如何实现财务杠杆平衡条件1. 优化债务结构:企业应根据自身情况,适当调整债务与股本比例,以达到最佳匹配状态。
2. 提高盈利能力:企业应加强经营管理,提高产品质量和服务水平,增加市场份额和盈利能力。
3. 控制成本费用:企业应合理控制各项成本费用,减少浪费和不必要的支出。
4. 加强资金管理:企业应加强资金管理,提高资金使用效率和流动性。
五、财务杠杆平衡条件的意义1. 实现企业稳定运营:通过调整债务与股本比例,实现利息支出与经营收益之间的最佳匹配状态,可以使企业稳定运营。
2. 提高企业盈利能力:实现财务杠杆平衡条件可以降低企业承担的财务风险,从而提高企业盈利能力。
3. 增强企业竞争力:通过实现财务杠杆平衡条件,可以优化债务结构、提高盈利能力和控制成本费用等手段来增强企业竞争力。
六、财务杠杆平衡条件的应用案例以某公司为例,该公司债务结构不合理,负债率过高,导致企业经营风险加大。
为了实现财务杠杆平衡条件,该公司采取了以下措施:1. 优化债务结构:该公司通过增加股本比例和减少债务比例的方式来调整企业债务和股本结构。
2. 提高盈利能力:该公司加强产品研发和市场营销,提高产品质量和服务水平,增加市场份额和盈利能力。
杠杆平衡的应用

例1:如图是铁道检修工用的道钉撬,有关尺 寸见图.若在A点竖直向下作用200牛的力, 道钉撬对道钉会产生多大的力?如果还不能 将道钉撬出,在保持手的作用力和作用点不 变的情况下,采用什么方法可以增大道钉撬 对道钉的作用力?
使用费力杠杆的 目的是什么? F2 O F1
费力杠杆
由 F1L1=F2L2 ∵L1 〈 L2 ∴F1 〉 F2 这是费力杠杆
费力杠杆的特点
F1
O
B h
F2S=4h B F2
F1 A
A’
费力杠杆虽然费了力,但可以省距离
省力杠杆的特点: 省力、费距离
等臂杠杆的特点
由 F1L1=F2L2
O
动力臂L1
F A B O G
11、如图11所示,A端挂有重为G 1 的物体,B端 挂有重为G2的物体, OA>OB,此时杠杆处于平衡状态,现将G1、G2 的悬点都向里侧(支点O)移动,且移动的距离L 0 相等,则杠杆将( B )。
A.杠杆仍平衡
B.A端下降
C.B端下降
D.无法判断
end
想一想
图中的等臂杠杆处于水平位置并静止,B端绳子的拉力F 与A端重力G相比( ) A. F=G; B. F<G; A O B C. F>G; D. 无法比较。
G
F
9。如图,人体前臂可以视作杠杆,当曲肘将手 中重物举起时,阻力臂大小将 减小 (填“增 大”或“减小”)
练习二:
下列哪个杠杆是省距离的(
F1 O
l1<l2
F1 > F2
杠杆平衡条件的应用
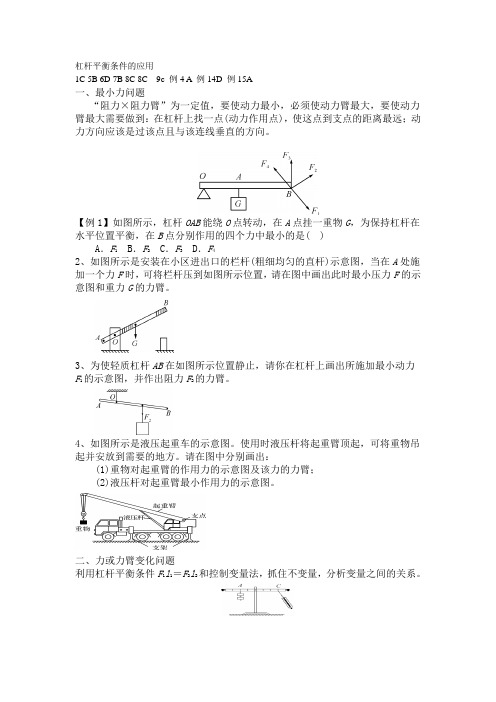
杠杆平衡条件的应用1C 5B 6D 7B 8C 8C 9c 例4 A 例14D 例15A一、最小力问题“阻力×阻力臂”为一定值,要使动力最小,必须使动力臂最大,要使动力臂最大需要做到:在杠杆上找一点(动力作用点),使这点到支点的距离最远;动力方向应该是过该点且与该连线垂直的方向。
【例1】如图所示,杠杆OAB能绕O点转动,在A点挂一重物G,为保持杠杆在水平位置平衡,在B点分别作用的四个力中最小的是( )A.F1 B.F2 C.F3 D.F42、如图所示是安装在小区进出口的栏杆(粗细均匀的直杆)示意图,当在A处施加一个力F时,可将栏杆压到如图所示位置,请在图中画出此时最小压力F的示意图和重力G的力臂。
3、为使轻质杠杆AB在如图所示位置静止,请你在杠杆上画出所施加最小动力F的示意图,并作出阻力F2的力臂。
14、如图所示是液压起重车的示意图。
使用时液压杆将起重臂顶起,可将重物吊起并安放到需要的地方。
请在图中分别画出:(1)重物对起重臂的作用力的示意图及该力的力臂;(2)液压杆对起重臂最小作用力的示意图。
二、力或力臂变化问题利用杠杆平衡条件F1l1=F2l2和控制变量法,抓住不变量,分析变量之间的关系。
5、小梦在做探究杠杆平衡条件的实验时,先在杠杆两端挂钩码进行实验探究,再用弹簧测力计取代一侧的钩码继续探究,如图所示,若仍然使杠杆保持平衡,拉力的变化情况是( )A.变小 B.变大 C.不变 D.无法确定6、如图所示,杠杆始终处于水平平衡状态,改变弹簧测力计拉力的方向,使其从①→②→③。
此过程中,弹簧测力计的示数将( )A.逐渐变大 B.逐渐变小C.先变大后变小 D.先变小后变大7、如图为吊车从图示位置向上起吊货物的工作示意图,利用伸缩撑杆可使吊臂绕O点缓慢转动,伸缩撑杆为圆弧状,伸缩时伸缩撑杆对吊臂的支持力始终与吊臂垂直。
下列说法正确的是( )A.匀速缓慢顶起吊臂的过程中,伸缩撑杆的支持力大小保持不变B.匀速缓慢顶起吊臂的过程中,伸缩撑杆的支持力渐渐变小C.匀速缓慢顶起吊臂的过程中,伸缩撑杆的支持力渐渐变大D.吊臂是一个省力杠杆8/如图所示,一根质地均匀的木杆可绕O点自由转动,在木杆的右端施加一个始终垂直于杆的作用力F,使杆从OA位置匀速转到OB位置的过程中,力F的大小将( )A.一直变大 B.一直变小C.先变大,后变小 D.先变小,后变大三、再平衡问题杠杆再平衡的问题,实际上就是判断杠杆在发生变化前后,力和力臂的乘积是否相等,乘积大的一端下降,乘积小的一端上升。
杠杆平衡的原理及应用

杠杆平衡的原理及应用1. 引言杠杆平衡是指通过调整杠杆的位置和力的大小,使得杠杆的两边能够保持平衡的原理。
在物理学中,杠杆平衡是一个重要的概念,我们可以通过掌握杠杆平衡的原理和应用,来解决实际生活中的问题。
2. 杠杆平衡的原理杠杆平衡的原理是基于物理学中的力和力矩的概念。
在一个平衡杠杆系统中,我们需要满足以下条件才能实现平衡: - 力的合力为零:即杠杆两边的力对称。
-力矩的和为零:即杠杆两边的力矩平衡。
3. 杠杆平衡的应用杠杆平衡的原理可以应用于多种实际场景中,以下是一些常见的应用: 1. 剪刀- 剪刀是一个常见的杠杆平衡应用的例子。
通过调整剪刀两边的杠杆长度和力的大小,我们可以轻松地剪断纸张或布料。
2. 门铰链 - 门铰链也是一个杠杆平衡应用的例子。
通过调整门的重心和力的大小,我们可以轻松地开关门。
3. 起重机 - 起重机是杠杆平衡应用的一个重要领域。
通过调整起重机吊臂的角度和杠杆长度,我们可以在不同位置上提起不同重量的物体。
4. 人体平衡 - 人体平衡也是一个杠杆平衡的应用。
当我们站立时,通过调整身体的重心和力的分配,我们能够保持平衡并保持站立的姿势。
5. 摇椅 - 摇椅是一个有趣的杠杆平衡应用。
通过调整身体的重心和力的大小,我们可以轻松地使摇椅前后摆动。
4. 杠杆平衡的优势杠杆平衡的应用有以下优势: - 简单且易于操作:只需要调整杠杆的位置和力的大小,就可以实现平衡。
- 灵活性高:可以应用于不同的场景和问题中,解决多种平衡问题。
- 节省力气:通过合理利用杠杆原理,可以达到减少力量消耗的效果。
5. 结论杠杆平衡是通过调整杠杆的位置和力的大小,使得杠杆两边能够保持平衡的原理。
在生活和工作中,我们可以通过掌握杠杆平衡的原理和应用,解决实际问题,提高效率。
无论是剪刀、门铰链还是起重机等等,杠杆平衡都有着广泛的应用。
通过合理利用杠杆原理,我们能够轻松地解决平衡问题,节约力气并提高工作效率。
【杠杆的平衡条件及其应用】杠杆平衡条件

【杠杆的平衡条件及其应用】杠杆平衡条件【杠杆的平衡条件及其应用】杠杆平衡条件1.探究杠杆的平衡条件(1)杠杆平衡是指杠杆处于静止状态或匀速转动.(2)实验前:应调节杠杆两端的螺母,使杠杆在水平位置平衡,这样做的目的是:可以消除杠杆自重对实验结果的影响;实验中:应调节杠杆两端的钩码的个数或位置,使杠杆在水平位置平衡,这样做的目的是:可以方便地从杠杆上直接量出力臂.(3)结论:杠杆的平衡条件(或杠杆原理)是:动力×动力臂=阻力×阻力臂.写成公式是:F1l1=F2l2,也可写成:F1/F2=l2/l1.2.杠杆平衡条件的应用方法(1)确认杠杆及其七要素.(2)利用公式F1l1=F2l2及变形公式F1=F2l2/l1解题.(3)要统一,即动力和阻力的单位要统一,动力臂和阻力臂的单位要统一,并不一定要用米,可以是厘米.3.典型题例(1)最小力问题例1如图1,一端弯曲的杠杆,O为支点,在B端挂一重为10N 的重物G,OB=AC=4cm,OC=3cm,在A端加一个作用力使杠杆平衡,这个力的最小值可能是().A.10NB.8NC.13.3ND.5N解析根据杠杆的平衡条件:F1l1=F2l2,因F2l2一定,则F1l1一定,所以l1越大,F1越小.由图2可知,OA是最长动力臂.由OA2 =OC2+AC2,AC=4cm,OC=3cm,则OA=5cm.由G·OB=F·OA,G=10N,OB=4cm,OA=5cm,则F=8N.故选项B正确.答案 B方法技巧实际生活中常遇到杠杆的最小力问题,注意要从实物中抽象出杠杆模型.解此类问题,关键是找到最长的动力臂,找到最小力的作用点和方向.解题时要明确两点:(1)明确已知条件(此题中尤其要注意动力臂和阻力臂的确定).(2)明确解题原理(F1l1=F2l2),解题时先把已知条件列出,再将已知条件代入公式解题.(2)杠杆的再平衡问题例2如图3,杠杆挂上钩码后刚好平衡,每个钩码的质量相同,在下列情况中,杠杆还能保持平衡的是().A.左右砝码各向支点移一格B.左右各减少一个砝码C.左右各减少一半砝码D.左右各增加两个砝码解析根据杠杆平衡条件,原来杠杆左边是2×4,右边是4×2,左右相等,杠杆平衡.情况变化后,A项的做法使左边是2×3,右边是4×1,杠杆不再平衡;B项的做法使左边是1×4,右边是3×2,杠杆不再平衡;D项的做法使左边是4×4,右边是6×2,杠杆不再平衡;C项的做法使左边是1×4,右边是2×2,杠杆平衡.故只有选项C正确.方法技巧杠杆的再平衡问题的特点是:原来杠杆是平衡的,当动力和阻力同时增减相等的力ΔF或动力臂和阻力臂同时增减相等的力臂ΔL时,杠杆不能平衡(等臂杠杆除外).(3)杠杆的动态平衡问题例3如图4所示,用始终与杠杆垂直的力F,将杠杆缓慢地由位置A拉至位置B,阻力G的力臂,动力F.(选填“变大”“变小”或“不变”)解析分别画出杠杆在A、B两位置的阻力G的力臂可看出,阻力臂lG将变大,由于F的方向始终与杠杆垂直,所以F的力臂始终等于杠杆长,故F的力臂lF不变.根据公式F×lF=G×lG,∵lF、G不变,lG变大,∴F变大.答案变大变大方法技巧杠杆的动态平衡是较为复杂的问题,实质在于考查杠杆的平衡条件和力臂的物理意义.解决的关键是明确哪些量变化,哪些量不变,先假设杠杆在某处静止,再用变动为静的处理方法.(4)杠杆与滑轮的组合问题例4如图5所示,质量为m的人站在轻质木板AB的中点,木板可以绕B端上下转动,要使木板静止于水平位置,人拉轻绳的力的大小为(摩擦阻力忽略不计).解析本题由于将杠杆与滑轮进行了组合,所以增加了分析思考问题的难度,木板可绕B端转动,说明B点为杠杆的支点,设人拉绳子的力为F,则由于天花板上的两个滑轮均为定滑轮,它们只能改变力的方向,不能改变力的大小,故A端所受绳子的拉力为F,方向竖直向上.人对杠杆的压力是G人-F.根据杠杆的平衡条件有:F·AB =(G人-F)·A B/2,F·AB=(mg-F)·AB/2,F=mg/3.答案mg/3方法技巧首先必须正确分析出作用在杠杆上的动力和阻力的大小,然后才能用杠杆平衡的条件得出答案.(5)实验探究过程中的经典问题例5在“研究杠杆平衡条件”的实验中,为了,应让杠杆在水平位置平衡.若实验前杠杆的位置如图6(甲)所示,欲使杠杆在水平位置平衡,则杠杆左端的平衡螺母应向(选填“左”或“右”)调.该实验得出的结论是:.某同学进一步用图6(乙)装置验证上述结论,若每个钩码重0.5N,当杠杆在水平位置平衡时,弹簧测力计的读数将4N(选填“<”“>”或“=”).解析经典实验通常是作为大的实验题来考的,问题多、分值大.今后中考也可能这样变化,为提高实验的覆盖面,一些重点实验将瘦身,问题减少,分值变小.但无论如何变形,其中的经典问题依然是命题的热点.杠杆不在水平位置平衡的话,杠杆本身的重力G杆对支点的力臂就不为零,这样会影响实验结论的正确得出.图甲所示的杠杆,左端下沉,右端上翘,说明左边偏重,应将平衡螺母向右调.若弹簧测力计竖直向下拉,则根据杠杆平衡的条件有:4G 钩·4l=F·2l,F=8G钩=8×0.5N=4N.弹簧测力计斜过来拉,力臂变短,力变大,应大于4N.答案消除杠杆自重对实验结果的影响(或使杠杆本身的重力对支点的力臂为0);右;动力×动力臂=阻力×阻力臂(或F1·l1=F2·l2);>.方法技巧探究杠杆平衡条件的题型,往往考查实验器材、过程、数据分析、结论以及对实验的反思.本题考查对实验注意事项的理解,要反思不注意这些事项的后果.许多同学只知道杠杆要在水平位置平衡,不清楚杠杆为什么要在水平位置平衡,阅读了这道题的解析后应该明白问题的答案了.(6)生产与生活中的杠杆问题例6商店里常用案秤称量货物质量,如图7所示,称量时,若在秤盘下粘一块泥,称量的结果比实际质量(选填“大”或“小”);若砝码磨损了,称量的结果比实际质量(选填“大”或“小”);若调零螺母的位置比正确位置向右多旋进了一些,称量的结果比实际质量.(选填“大”或“小”)解析案秤是一不等臂的杠杆,若秤盘下粘一块泥,相当于物体质量增大,此时就要增加砝码来平衡增加的物体,则读数就要比物体的实际质量大;若砝码磨损了,则砝码的质量比它实际的质量要小,用它去平衡物体时仍按其上标的示数进行读数,则结果比物体的实际质量大;若调零螺母的位置比正确位置向右多旋进了一些,则左侧的力与力臂的乘积减小,由于右侧的力臂不变,只有砝码的质量减小,此时称量的结果比实际量小.答案大大小方法技巧案秤的使用实质为教材中天平的使用的迁移,同学们一定要灵活运用所学的知识去解决实际问题.。
杠杆平衡原理的实际应用

杠杆平衡原理的实际应用引言杠杆平衡原理是物理学中的一个重要概念,它描述了一个杠杆在平衡状态下的运作规律。
尽管这个原理最初是由物理学家提出的,但它在实际生活中的应用却非常广泛。
本文将介绍一些杠杆平衡原理的实际应用,以帮助读者更好地理解这个概念。
1. 建筑领域杠杆平衡原理在建筑领域的应用非常常见。
例如,在建造大型桥梁或高楼大厦时,施工人员会使用起重机来搬运重物。
起重机通常通过杠杆平衡原理来实现高效、安全地工作。
通过调整杠杆的长度和角度,施工人员可以很容易地平衡起重机,使其能够轻松地操纵重物。
另外,杠杆平衡原理还可以应用在建筑物的设计中。
工程师会根据这个原理来确定支撑结构的位置和角度,以确保建筑物的稳定性和安全性。
通过合理利用杠杆原理,建筑物可以在外部力的作用下保持平衡,从而防止倒塌和损坏。
2. 机械工程杠杆平衡原理在机械工程领域也有广泛的应用。
例如,汽车发动机的活塞和曲轴系统就是通过杠杆平衡原理来传递动力的。
发动机的曲轴和活塞组成了一个杠杆系统,通过调整杠杆的长度和角度,可以实现发动机的平衡和高效工作。
此外,杠杆平衡原理还可以应用在机械装置的设计中。
例如,在一些复杂的机械装置中,需要使用多个杠杆来平衡各个部件的力。
通过调整不同杠杆的长度和角度,可以确保机械装置的正常工作并防止过度负载。
3. 运动器械杠杆平衡原理在运动器械中的应用既广泛又常见。
举个例子,健身房中的杠铃和哑铃就是通过这个原理来实现身体锻炼的。
运动员可以通过调整杠铃或哑铃的杠杆使其平衡,然后通过施加力量来进行训练。
此外,一些器械如跑步机、划船机等,也使用了杠杆平衡原理来实现人体运动。
这些器械通过调整杠杆的长度和角度,可以帮助运动员更好地控制身体的运动,从而实现锻炼效果。
4. 金融领域杠杆平衡原理在金融领域也有一些实际的应用。
例如,在投资领域有一种叫做杠杆交易的策略。
杠杆交易是指借入资金来增加投资额度,从而提高投资回报率的方法。
在杠杆交易中,投资者使用杠杆平衡原理来优化投资组合,以获得更高的收益。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
0.98
1.96 2.45
0.02 0.04 0.03
0.49
3.92 1.47
0.01
0.02 0.05
(1) 这三组数据中,有一组是错误的,请你判断它的实验序号为——— .
专题:杠杆平衡条 件的应用
例1:图中轻质杠杆能否平衡,如
不平衡,它将如何转动? 分析:如 F1l1= F2l2 ,则杠杆平衡
G1
G2
杠杆还能平衡吗?如不平衡,那端下沉?
小结:此类问题与两物体的质量、体积无关,也与
杠杆是否等臂无关,放入同种液体中后,都是密度
大端下沉。
练习.1.如图,在等臂杠杆左、右
端分别挂质量相等的实心铅块 和铝块,杠杆处于平衡状态, 若将铅块和铝块(ρ铅> ρ铝 全部浸入水中,则 ( A.杠杆仍然平衡 C.杠杆右端下沉
相信你能行!!!
4.有一等臂杠杆,两边分别挂有实心铜球A和实心铝
球B,当A球 浸没在水中,B球浸没在煤油中时,杠杆 恰好平衡,若将A、B两球分别从水和煤油中取出来, 这时( B ) A. 杠杆平衡 B. 杠杆失去平衡,B球一端下沉 C.杠杆失去平衡,A 球一端下沉 D.无法判断
铅
O
铝
B )
B.杠杆左端下沉 D.无法判断
2. 如图,轻质 杠杆两端分别挂有体积相同的物体M
和N,杠杆恰好平衡时的AO:OB=3:1,若将M和N 同 时浸没在水中,则杠杆B端将 ( A.下沉 C.不动 B.上升 D.无法判断
M N
A
)
O B
A
3.如图所示定滑轮两侧绳端分别挂 有铁块和铜块,并保持静止不动,现将 它们分别浸没在水中,(B ) A.它们仍保持静止
铜 铝
A
O
B
或“不动”)运动
小结:这节课我们主要学习了如何应用杠杆的 平衡条件解决实际问题,同学们可以记住一些 结论,在做这类选择或填空题的时候会给我们 带来极大的便利,但必须弄清结论成立的条件。 然而方法才是最重要的,只有掌握了哺鱼的方 法才能随时都有鱼吃。希望同学们能将在课堂 上学到的处理问题的方法不断的应用到自己的 学习过程中。
138中
杠杆平衡条件的应用
代荣芹
诊断检测: 1.力臂是指支点到力的作用线 的距离. 2.小明同学做研究杠杆平衡条件的实验,当杠杆平衡时,在 表格内计录了相应的数据,请你把表内空格处填上恰当的数 据。
实 验 次 数 动力 动力臂
动力×动力臂
阻力
阻力臂
动力×动力臂
F1(牛) L1(厘米)(牛· 厘米)
B .铜块下降,铁块上升
C.铜快上升,铁块下降来自D.无法判断铁铜
4.甲、乙两物体体积相等,它们的密度之比是
2:1,将它们挂在杠杆支点的两侧.杠杆平衡,如 果将甲、乙两物体没入水中,则杠杆( B ) A. 仍保持平衡 B .不能平衡,挂物体甲的一侧下沉 C.不能平衡,挂物体乙的一侧下沉 D.无法确定
5.如图所示杠杆两端分别挂
有铜块和铝块,恰好平衡,现 将它们同时浸没在同种液体的 两个容器内,则杠杆 ( C A.仍能平衡 B.不平衡,向左倾斜 C.不平衡,向右倾斜 )
A
O
B
铜
铝
D.无法判断
6.如图所示,轻质杠杆O,OA=OB,
A端挂实心铜块,B端挂实心铁块, 已知密度ρ铜> ρ铁,两金属块均 浸没在水中,此时杠杆平衡,若将 两盛水杯撤去,则杠杆的A端 将 向上 .(填“向上”、“向 下”
F1
l1
l2
F2
如 F1l1>F2l2 ,则杠杆不平衡,将逆时针转动 如 F1l1<F2l2 ,则杠杆不平衡,将顺时针转动
即:当杠杆不平衡时,杠杆如何转动取决 于 F与l 的乘积
例2:如图所示的杠杆两端分别挂有
l1
O
l2
实心金属块,恰好平衡,现将它们同
时浸没在同种液体的两个容器内,则
当 ρ2> ρ1时, ① <② ∴ ρ2端下沉 当 ρ2=ρ1时, ① =② ∴ ρ2仍平衡 当 ρ2<ρ1时, ① >② ∴ ρ1端下沉
厘米) F2(牛) L1(厘米) (牛·
1
1 2
5 30
5
0.5
10
5
2
60
3
20
60
根据实验,可得出杠杆的平衡条件是
( 是: 动力×动力臂 =阻力×阻力臂 F1l1= F2l2)
.
3.李明同学做 “研究杠杆平衡条件”实验时,分别三次调节杠 杆在水平位置平衡以后记录三组实验数据,如下表所示:
实验序号 动力F1(牛) 动力臂L1(米) 阻力F2(米) 阻力臂L2(米) (1)
