最新基本初等函数经典总结
(完整版),基本初等函数公式总结,推荐文档
( f g)dx f dx gdx kfdx k f dx
运算公式：
fg dx f dg fg g df
分部积分法计算法则
对
幂
指
三
ln x
x
ex
sin x 、 cos x
两两组合，位置排在前面的选 f ，排列在后面的选 g
dx c dx
1 dx d ln x x
凑微分公式 1 dx 2d x x
导数公式
(c) 0 (0) 0
(x) 1 (x2 ) 2x
(log a
x)
1 x ln a
(ln x) 1 x
(sin x) cos x (cos x) sin x
1 0
1 x
1 x2
(a x ) a x ln a
( f g) ( f ) (g) ( fg) ( f )g f (g) (kf ) k( f )
0 dx c
1 dx x c
x
dx
1 2
x2
c
1 x2
dx 1 c x
不定积分公式
1 x
dx 2
x c
ax dx ax c
ln a
不定积分运算法则： 加减法，数乘
x
dx
2
3
x2
c
3
xa dx 1 xa1 c
a 1
1 x
dx
ln |
x | c
ex dx ex c sin x dx cos x c cos x dx sin x c
(x a ) ax a1
( x) 1 2x
(e x ) e x
f g
(
f
)g g2
f
(g)
高考数学中基本初等函数的图像及性质总结
高考数学中基本初等函数的图像及性质总结数学作为一门基础学科，在高中阶段的学习中占据非常重要的地位，而在高考数学中，基本初等函数更是赫赫有名。
基本初等函数包括常数函数、幂函数、指数函数、对数函数、三角函数和反三角函数等，除了常数函数外，每个函数都有其特点的图像及性质，下面将对其进行总结。
幂函数幂函数是指函数y=x^a，其中a为常数，当a>0时，函数的图像经过(1,1)，在第一象限上单调递增；当a<0时，在第一象限上单调递减。
当a=1时，函数为y=x，图像为一条直线。
此外，当a为偶数时，函数在第一象限上为关于y轴对称的，当a为奇数时，函数在第一象限上为关于坐标原点对称的。
指数函数指数函数是指函数y=a^x，其中a为正实数且不等于1。
当a>1时，函数的图像在x轴右侧单调递增，当0<a<1时，在x轴右侧单调递减。
其图像在y轴上通过(0,1)，在x轴上不存在渐近线。
对数函数对数函数是指函数y=loga x，其中a为正实数且不等于1，且x>0。
当a>1时，函数在x轴右侧单调递增，当0<a<1时，在x轴右侧单调递减。
其图像在y轴上通过(0,0)，在x轴上不存在渐近线。
三角函数三角函数包括正弦函数、余弦函数和正切函数。
正弦函数和余弦函数的图像均为周期函数，其周期为2π，其函数值均在[-1,1]之间。
正弦函数的图像在点(π/2,1)和(3π/2,-1)处取得极值；余弦函数的图像在点(0,1)和(π,-1)处取得极值。
正切函数是一个奇函数，其在点π/2、3π/2、5π/2等处有无穷大趋势。
反三角函数反三角函数包括反正弦函数、反余弦函数和反正切函数。
反正弦函数的定义域为[-1,1]，值域为[-π/2,π/2]；反余弦函数的定义域为[-1,1]，值域为[0,π]；反正切函数的定义域为实数集，值域为[-π/2,π/2]。
以上是基本初等函数的图像及性质总结，希望能够对数学学习者有所帮助。
基本初等函数知识点总结
基本初等函数知识点总结基本初等函数是数学中常见的一类函数，包括多项式函数、指数函数、对数函数、三角函数和反三角函数等。
它们在数学和实际问题中具有广泛的应用，因此掌握基本初等函数的性质和特点对于学习和理解数学非常重要。
下面将对基本初等函数的知识点进行总结。
一、多项式函数多项式函数是由常数乘以各个整数幂的变量构成的函数。
它的一般形式为：$$f(x) = a_nx^n + a_{n-1}x^{n-1} + \dots + a_1x+a_0$$其中，$a_n, a_{n-1},\dots,a_1,a_0$为常数，$n$为正整数，$a_n \neq 0$。
多项式函数的特点包括：定义域为实数集，值域为实数集，可导且导函数为次数比原来次数低一的多项式函数。
二、指数函数指数函数的一般形式为：$$f(x) = a^x$$其中，$a$为正实数且不等于1。
指数函数的特点包括：定义域为实数集，值域为正实数集，可导且导函数为$a^x\ln a$。
三、对数函数对数函数的一般形式为：$$f(x) = \log_a x$$其中，$a$为正实数且不等于1，$x$为正实数。
对数函数的特点包括：定义域为正实数集，值域为实数集，可导且导函数为$\frac{1}{x\ln a}$。
四、三角函数三角函数包括正弦函数、余弦函数、正切函数等。
它们的一般形式为：$$\sin x, \cos x, \tan x$$其中，$x$为实数。
三角函数的特点包括：定义域为实数集，值域为闭区间[-1, 1]，具有周期性，可导且导函数是相关三角函数的倍数。
五、反三角函数反三角函数包括反正弦函数、反余弦函数、反正切函数等。
它们的一般形式为：$$\arcsin x, \arccos x, \arctan x$$其中，$x$在相应的定义域内。
反三角函数的特点包括：定义域为闭区间[-1, 1]，值域为实数集，可导且导函数是相关函数的倒数。
基本初等函数的性质还包括：1. 奇偶性对于函数$f(x)$，如果对于定义域内的任意$x$，有$f(-x)=-f(x)$，则称函数为奇函数；如果对于定义域内的任意$x$，有$f(-x)=f(x)$，则称函数为偶函数。
六大基本初等函数图像及其性质
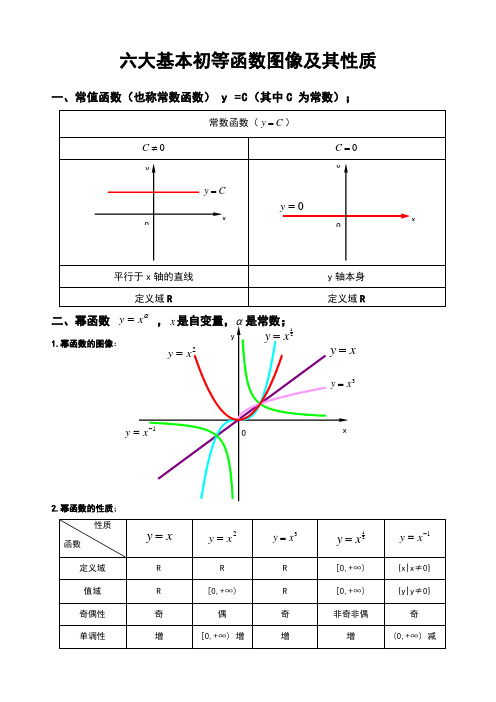
六大基本初等函数图像及其性质一、常值函数（也称常数函数） y =C （其中C 为常数）；二、幂函数 αy =1.幂函数的图像：2.幂函数的性质；3y1）当α为正整数时，函数的定义域为区间为),(+∞-∞∈x ，他们的图形都经过原点，并当α>1时在原点处与x 轴相切。
且α为奇数时，图形关于原点对称；α为偶数时图形关于y 轴对称；2）当α为负整数时。
函数的定义域为除去x=0的所有实数； 3）当α为正有理数nm时，n 为偶数时函数的定义域为（0, +∞），n 为奇数时函数的定义域为（-∞,+∞），函数的图形均经过原点和（1 ,1）；4）如果m>n 图形于x 轴相切，如果m<n,图形于y 轴相切，且m 为偶数时，还跟y 轴对称；m ，n 均为奇数时，跟原点对称；5）当α为负有理数时，n 为偶数时，函数的定义域为大于零的一切实数；n 为奇数时，定义域为去除x=0以外的一切实数。
三、指数函数xa y =(x 是自变量,a 是常数且0>a ，1≠a )，定义域是R ；[无界函数]1.指数函数的图象：2.指数函数的性质；1(1）当1>a 时函数为单调增,当10<<a 时函数为单调减； 2）不论x 为何值,y 总是正的,图形在x 轴上方； 3）当0=x 时,1=y ,所以它的图形通过(0,1)点。
3.（选，补充）指数函数值的大小比较*N ∈a ；a.底数互为倒数的两个指数函数x a x f =)(，xa x f ⎪⎭⎫ ⎝⎛=1)(的函数图像关于y 轴对称。
.当1>a 时，a 值越大，x a y =的图像越靠近y 轴；.当10<<a 时，a 值越大，xa y =的图像越远离y 轴。
4.指数的运算法则（公式）；a.整数指数幂的运算性质),,0(Q n m a ∈≥；(1) n m n m a a a +=⋅(2)n m n m a a a -=÷(3)()()mn nmnm aaa ==xf x xxx g ⎪⎫⎛=1)((4)()n n n b a ab =b.根式的性质； (1)()a a nn= ； (2)当n 为奇数时，a a nn =当n 为偶数时，⎩⎨⎧<-≥==)0(0)(a a a a a a nnc.分数指数幂；(1))1,,,0(*>∈>=n Z n m a a a n m nm(2))1,,,0(11*>∈>==-n Z n m a a aanmnm nm 四、对数函数x y a log =(a 是常数且1,0≠>a a )，定义域),0(+∞∈x [无界]1.对数的概念：如果a(a ＞0，a ≠1)的b 次幂等于N ，就是 N a b=，那么数b 叫做以a 为底N 的对数，记作b N a =log ,其中a 叫做对数的底数，N 叫做真数，式子N a log 叫做对数式。
基本初等函数对称性总结
基本初等函数对称性总结
函数的对称性
函数的对称性是指函数在某种变换下保持不变的性质。
对称性
在数学中起到了重要的作用，它可以帮助我们简化问题，提供更方
便的解法，并为各个数学领域的研究提供了基础。
平移对称性
如果一个函数 f(x) 在坐标平面上的图像关于 y 轴对称，则称该
函数具有平移对称性。
也就是说，对于任意实数x，有f(x) = f(-x)。
奇偶对称性
如果一个函数 f(x) 在坐标平面上的图像关于原点对称，则称该
函数具有奇偶对称性。
也就是说，对于任意实数x，有f(x) = -f(-x)。
周期性
如果一个函数 f(x) 对于某个正数 T ，对于任意实数 x，有
f(x+T) = f(x)，则称该函数具有周期性。
周期性函数在数学和物理学中都有重要的应用，可以用于描述各种重复现象。
对数函数的对称性
对数函数具有平移对称性。
例如，logx = log(-x)。
三角函数的对称性
正弦函数和余弦函数具有奇偶对称性。
例如，sin(x) = -sin(-x)。
而正切函数具有周期性。
例如，tan(x+π) = tan(x)。
指数函数的对称性
指数函数具有平移对称性。
例如，exp(x) = exp(-x)。
总结
基本初等函数具有不同的对称性特点，包括平移对称性、奇偶对称性和周期性。
这些对称性可帮助解决数学问题，并为各个数学领域的研究提供了基础。
以上为基本初等函数对称性的总结。
基本初等函数知识总结
基本初等函数知识总结含义:常数函数、幂函数、指数函数、对数函数、三角函数和反三角函数统称为基本初等函数1.常数函数（y=C）（1）定义域: D（f）＝（-∞，+∞）（2）值域: Z(f)=C(3) 性质: 它的图像是一条平行于x轴并通过点(0，C)在y轴上截距为C的直线(4 )图像：(5)周期性：常值函数是一个周期函数. 因对于任何x∈(-∞,+∞)和实数T，f(x+T)=f(x)=T,但并无最小正周期【注】常值函数不含自变量且不存在反函数2.幂函数(1)定义：形如y=x^a(a为常数）的函数，即以底数为自变量，幂为因变量，指数为常量的函数称为幂函数.(2)性质：在(0，+∞)内总有意义①当α＞0时函数图像过点(0，0)和(1，1)，在(0，+∞)内单调增加且无界②当α＜0时函数图像过点(1，1)，在(0，+∞)内单调减少且无界(3)图像：3.指数函数y=a^x(a>0且a≠1)(1)定义域：x∈R(2)值域：(0，+∞)(3)性质：①单调性：1.当0＜a＜1时，在(-∞，+∞)内单调减少 2.当a ＞1时，在(-∞，+∞)内单调增加②奇偶性：非奇非偶函数③周期性：非周期函数④有界性：无界函数(4)图像：①由指数函数y=a^x与直线x=1相交于点（1，a)可知：在y轴右侧，图像从下到上相应的底数由小变大。
②由指数函数y=a^x与直线x=-1相交于点（-1，1/a）可知：在y轴左侧，图像从下到上相应的底数由大变小。
③指数函数的底数与图像间的关系可概括的记忆为：在y轴右边“底大图高”；在y轴左边“底大图低” 如图：(5)运算法则：①②③④4.对数函数y=logax（a>0 且a≠1）(1)定义：如果a^x=N（a>0，且a ≠1），那么数x叫做以a为底N的对数，记作x=logaN，读作以a为底N的对数，其中a叫做对数的底数，N叫做真数一般地，函数y=logax（a>0，且a ≠1）叫做对数函数，也就是说以幂（真数）为自变量，指数为因变量，底数为常量的函数，叫对数函数(2)定义域：(0，+∞)，即x>0(3)值域：R(4)性质：①单调性：1.当0＜a＜1时，在(0，+∞)内单调减少 2.当a ＞1时，在(0，+∞)内单调增加②奇偶性：非奇非偶函数③周期性：非周期函数④有界性：无界函数(5)图像：【注】①负数和零没有对数②1的对数是零③底数的对数等于1(6)常用法则/公式：5.三角函数⑴正弦函数y=sin x(1)定义：对边与斜边的比(2)定义域：R(3)值域：【-1，1】(4)最值：1.当X=2Kπ(K∈Z)时，Y 取最大值1 2.当X=2Kπ+3π/2(K∈Z时，Y取最小值－1(5)性质：①周期性：最小正周期都是2πT=2π②奇偶性：奇函数③对称性：对称中心是(Kπ,0)，K ∈Z；对称轴是直线x=Kπ+π/2，K ∈Z④单调性：在[2Kπ-π/2,2Kπ+π/2]，K∈Z上单调递增；在[2Kπ+π/2,2Kπ+3π/2]，K∈Z上单调递减⑤有界性：有界函数(6)图像：(2)余弦函数y=cos x(1)定义：邻边与斜边之比(2)定义域：R(3)值域：【-1，1】(4)最值：1.当X=2Kπ +π /2(K∈Z)时，Y取最大值1 2.当X=2Kπ +π (K∈Z)时，Y取最小值－1(5)性质：①周期性：最小正周期都是2πT=2π②奇偶性：偶函数③对称性：对称中心是(Kπ+π/2,0)，K∈Z；对称轴是直线x=Kπ，K∈Z④单调性：在[2Kπ,2Kπ+π]，K∈Z上单调递减；在[2Kπ+π,2Kπ+2π]，K∈Z上单调递增⑤有界性：有界函数(6)图像：(3)正切函数y=tan x(1)定义：对边与邻边之比(2)定义域：{x∣x≠Kπ+π/2,K∈Z}(3)值域：R(4)最值：无最大值和最小值(5)性质：①周期性：最小正周期都是πT=π②奇偶性：奇函数③对称性：对称中心是(Kπ/2,0)，K∈Z④单调性：在[Kπ-π/2,Kπ+π/2]，K∈Z上单调递增⑤有界性：无界函数(6)图像：(4)余切函数y=cot x(1)定义：在直角三角形中，某锐角的相邻直角边和相对直角边的比，叫做该锐角的余切。
基本初等函数总结表格
基本初等函数总结表格基本初等函数总结表格篇一：基本初等函数图像及其性质表 ??y篇二：基本初等函数归纳(表格)篇三：基本初等函数知识点总结基本初等函数知识点总结一、指数函数（一）指数与指数幂的运算1．根式的概念：一般地，如果xn?a，那么x叫做a的n次方根， * 其中n 1，且n∈N．? 负数没有偶次方根；0的任何次方根都是0，记作0?0。
当na n 当na?a， n (a?0)?a ?|a|?? ?a(a?0)? 2．分数指数幂正数的分数指数幂的意义，规定：m aa n ? mn a(a?0,m,n?N,n?1)1 m n m* ， * ? ?? 1 a ?0的正分数指数幂等于0，0的负分数指数幂没有意义3．实数指数幂的运算性质 a m (a?0,m,n?N,n?1)（1）a〃a?a r s rsrrr?s (a?0,r,s?R)；(a?0,r,s?R)；（2）(a)?a（3） (ab)?aa r r s (a?0,r,s?R)．（二）指数函数及其性质1、指数函数的概念：一般地，函数y?ax(a?0,且a?1)叫做指数函数，其中x是自变量，函数的定义域为R．注意：指数函数的底数的取值范围，底数不能是负数、零和1．注意：利用函数的单调性，结合图象还可以看出：（1）在[a，b]上，f(x)?ax(a?0且a?1)值域是[f(a),f(b)]或[f(b),f(a)]；（2）若x?0，则f(x)?1；f(x)取遍所有正数当且仅当x?R；（3）对于指数函数f(x)?ax(a?0且a?1)，总有f(1)?a；二、对数函数（一）对数1．对数的概念：一般地，如果ax?N(a?0,a?1)，那么数x叫做以．a为底．．N的对数，记作：x?lg数，lg aa N（a—底数，N—真 N—对数式）说明：○1 注意底数的限制a?0，且a?1；2 a?N?lgN?x；○ 3 注意对数的书写格式．○x a 两个重要对数：1 常用对数：以10为底的对数lgN；○ 2 自然对数：以无理数e?2.71828?为底的对数的对数ln N○ ? 指数式与对数式的互化幂值真数．指数对数（二）对数的运算性质如果a?0，且a?1，M?0，N?0，那么： 1 lga(M〃N)?lgaM＋lga N；○ 2 lg○3 lg○ M aNM n ?lg a M －lg a aN； a ?nlgM (n?R)．注意：换底公式lgcb c?0，l gab? （a?0，且a?1；且c?1；b?0）． lgca 利用换底公式推导下面的结论（1）lg a m b?n nm lg a（2）lgb； a b? 1lgb a ．（二）对数函数1、对数函数的概念：函数y?lg a x(a?0，且a?1)叫做对数函数，其中x是自变量，函数的定义域是（0，+∞）．注意：○1 对数函数的定义与指数函数类似，都是形式定义，注意辨别。
基本初等函数知识点总结
基本初等函数知识点总结1.常数函数：常数函数是指函数的值在定义域内都保持不变的函数。
表示为f(x)=c，其中c是常数。
常数函数的图像是一条平行于x轴的直线。
常数函数的性质是恒等性，即f(x)=f(x')，对于任意x和x'都成立。
2.平方函数：平方函数是指函数的值与自变量的平方成正比的函数。
表示为f(x)=x²。
平方函数的图像是一条开口向上的抛物线。
平方函数的性质是奇偶性，即f(-x)=f(x)，对于任意实数x都成立。
3.立方函数：立方函数是指函数的值与自变量的立方成正比的函数。
表示为f(x)=x³。
立方函数的图像是一条通过原点且存在于所有象限的曲线。
立方函数的性质是单调性，即在定义域内，当x₁<x₂时，有f(x₁)<f(x₂)或f(x₁)>f(x₂)成立。
4.绝对值函数：绝对值函数是指函数的值与自变量的绝对值成正比的函数。
表示为f(x)=，x。
绝对值函数的图像是一条以原点为顶点且对称于y轴的V字形曲线。
绝对值函数的性质是非负性，即对于任意实数x，有f(x)≥0成立。
5.指数函数：指数函数是指函数的值与自变量的指数幂成正比的函数。
表示为f(x)=aˣ，其中a是一个正实数且a≠1、指数函数的图像是一条通过点(0,1)且与x轴和y轴都无交点的曲线。
指数函数的性质是增长性，即在定义域内，当x₁<x₂时，有f(x₁)<f(x₂)成立。
6. 对数函数：对数函数是指函数的值与自变量的对数成正比的函数。
表示为f(x)=logₐ(x)，其中a是一个正实数且a≠1、对数函数的图像是一条通过点(1, 0)且与x轴和y轴都无交点的曲线。
对数函数的性质是单调性，即在定义域内，当x₁<x₂时，有f(x₁)<f(x₂)成立。
7. 三角函数：三角函数包括正弦函数、余弦函数、正切函数等。
正弦函数表示为f(x)=sin(x)，余弦函数表示为f(x)=cos(x)，正切函数表示为f(x)=tan(x)。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
精品文档 精品文档 第十二讲 基本初等函数 一：教学目标 1、掌握基本初等函数（指数函数、对数函数、幂函数）的基本性质； 2、理解基本初等函数的性质； 3、掌握基本初等函数的应用，特别是指数函数与对数函数 二：教学重难点 教学重点：基本初等函数基本性质的理解及应用； 教学难点：基本初等函数基本性质的应用
三：知识呈现 1.指数与指数函数
1).指数运算法则：（1）rsrsaaa； （2）srrsaa； （3）rrrabab；
（4）mnmnaa； （5）1mnnmaa （6）,||,nnanaan奇偶 2). 指数函数：形如(01)xyaaa且
2.对数函数 1）对数的运算：
1、互化：NbNaablog
2、恒等：NaNalog 3、换底： abbccalogloglog
指数函数 01 图 象 表达式 xya
定义域 R
值 域 (0,)
过定点 (0,1)
单调性 单调递减 单调递增 精品文档
精品文档 推论1 abbalog1log 推论2 logloglogababcc• 推论3 loglogmnaanbbm)0(m 4、NMMNaaalogloglog
logloglogaaaMMNN 5、MnManaloglog 2）对数函数：
3.幂函数 一般地，形如 ayx（aR）的函数叫做幂函数，其中a 是常数 1)性质： (1) 所有的幂函数在(0,+∞)都有定义，并且图象都通过点(1, 1);
对数函数 01
图 象 表达式 logayx
定义域 (0,)
值 域 R
过定点 (1，0) 单调性 单调递减 单调递增 精品文档
精品文档 (2) 如果α＞０，则幂函数图象通过（0，0），并且在区间[0,+∞)上是增函数； (3) 如果α＜０，则幂函数在区间(0,+∞)上是减函数，在第一象限内，当x从右边趋向于原点时，图象在y轴右方无限地逼近y轴，当x趋于+∞时，图象在x轴上方无限逼近x轴。
四：典型例题 考点一：指数函数
例1 已知2321(25)(25)xxaaaa，则x的取值范围是___________． 分析：利用指数函数的单调性求解，注意底数的取值范围． 解：∵2225(1)441aaa≥，
∴函数2(25)xyaa在()，∞∞上是增函数， ∴31xx，解得14x．∴x的取值范围是14，∞． 评注：利用指数函数的单调性解不等式，需将不等式两边都凑成底数相同的指数式，并判断底数与1的大小，对于含有参数的要注意对参数进行讨论．
例2 函数221(01)xxyaaaa且在区间[11]，上有最大值14，则a的值是_______． 分析：令xta可将问题转化成二次函数的最值问题，需注意换元后t的取值范围． 解：令xta，则0t，函数221xxyaa可化为2(1)2yt，其对称轴为1t．
∴当1a时，∵11x，， ∴1xaaa≤≤，即1taa≤≤． ∴当ta时，2max(1)214ya． 解得3a或5a（舍去）； 当01a时，∵11x，，
∴1xaaa≤≤，即1ata≤≤，
∴ 1ta时，2max11214ya， 解得13a或15a（舍去），∴a的值是3或13． 评注：利用指数函数的单调性求最值时注意一些方法的运用，比如：换元法，整体代入等．
例3 求函数216xy的定义域和值域． 解：由题意可得2160x≥，即261x≤， ∴20x≤，故2x≤． ∴函数()fx的定义域是2，∞． 精品文档 精品文档 令26xt，则1yt， 又∵2x≤，∴20x≤． ∴2061x≤，即01t≤． ∴011t≤，即01y≤．
∴函数的值域是01，． 评注：利用指数函数的单调性求值域时，要注意定义域对它的影响．
例4 求函数y＝23231xx的单调区间. 分析 这是复合函数求单调区间的问题 可设y＝u31,u＝x2-3x+2，其中y＝u31为减函数 ∴u＝x2-3x+2的减区间就是原函数的增区间(即减减→增) u＝x2-3x+2的增区间就是原函数的减区间(即减、增→减)
解：设y＝u31,u＝x2-3x+2,y关于u递减， 当x∈(-∞，23)时，u为减函数， ∴y关于x为增函数；当x∈［23，+∞)时，u为增函数，y关于x为减函数.
考点二：对数函数 例5 求下列函数的定义域 （1）y=log2（x2-4x-5）; （2）y=logx+1（16-4x）
（3）y= ． 解：（1）令x2-4x-5＞0，得（x-5）（x+1）＞0， 故定义域为 ｛x｜x＜-1，或x＞5｝．
（2）令 得 故所求定义域为｛x｜-1＜x＜0，或0＜x＜2｝． 精品文档 精品文档 （3）令 ，得 故所求定义域为
｛x｜x＜-1- ，或-1- ＜x＜-3,或x≥2｝． 说明 求与对数函数有关的定义域问题，首先要考虑，真数大于零．底数大于零不等于1，若处在分母的位置，还要考虑不能使分母为零． 例6 比较大小： （1）log0．71．3和log0．71．8． （2）（lgn）1．7和（lgn）2（n＞1）． （3）log23和log53． （4）log35和log64． 解：（1）对数函数y=log0．7x在（0，+∞）内是减函数．因为1．3＜1．8，所以 log0．71．3＞log0．71．8． （2）把lgn看作指数函数的底，本题归为比较两个指数函数的函数值的大小，故需对底数lgn讨论． 若1＞lgn＞0，即1＜n＜10时，y=（lgn） x在R上是减函数，所以（lgn）1．2＞（lgn）2； 若lgn＞1，即n＞10时，y=（lgn）2在R上是增函数，所以（lgn）1．7＞（lgn）2． （3）函数y=log2x和y=log5x当x＞1时，y=log2x的图像在y=log5x图像上方．这里x=3，所以log23＞log53． （4）log35和log64的底数和真数都不相同，须找出中间量“搭桥”，再利用对数函数的单调性即可求解． 因为log35＞log33=1=log66＞log64，所以log35＞log64． 评析 要注意正确利用对数函数的性质，尤其是第（3）小题，可直接利用例2中的说明得到结论． 例7 已知f（x）=2+log3x，x∈［1，9］，求y=［f（x）］2+f（x2）的最大值，及y取最大值时，x的值． 分析 要求函数y=［f（x）］2+f（x2）的最大值，要做两件事，一是要求其表达式；二是要求出它的定义域，然后求值域． 解：∵f（x）=2+log3x， ∴y=［f（x）］2+f（x2）=（2+log3x）2+2+log3x2 精品文档 精品文档 =（2+log3x）2+2+2log3x =log23x+6log3x+6 =（log3x+3）2-3． ∵函数f（x）的定义域为［1，9］，
∴要使函数y=［f（x）］2+f（x2）有定义，就须91912xx ， ∴1≤x≤3． ∴0≤log3x≤1 ∴6≤y=（log3x+3）2-3≤13 ∴当x=3时，函数y=［f（x）］2+f（x2）取最大值13． 说明 本例正确求解的关键是：函数y=［f（x）］2+f（x2）定义域的正确确定．如果我们误认为［1，9］是它的定义域．则将求得错误的最大值22． 其实我们还能求出函数y=［f（x）］2+f（x2）的值域为［6，13］．
例8 求函数y=log0．5（-x2+2x+8）的单调区间． 分析 由于对函数的底是一个小于1的正数，故原函数与函数u=-x2+2x+8（-2＜x＜4）的单调性相反．
解．∵-x2+2x+8＞0， ∴ -2＜x＜4，
∴ 原函数的定义域为（-2，4）． 又∵ 函数u=-x2+2x+8=-（x-1）2+9在（-2，1］上为增函数，在［1，4）上为减函数， ∴函数y=log0．5（-x2+2x+8）在（-2，1］上为减函数，在［1，4）上为增函数．
评析 判断函数的单调性必须先求出函数的定义域，单调区间应是定义域的子集．
考点三：幂函数 精品文档
精品文档 例9．比较大小：
（1）11221.5,1.7 （2）33(1.2),(1.25)（3）1125.25,5.26,5.26（4）30.530.5,3,log0.5 解：（1）∵12yx在[0,)上是增函数，1.51.7，∴11221.51.7 （2）∵3yx在R上是增函数，1.21.25，∴33(1.2)(1.25) （3）∵1yx在(0,)上是减函数，5.255.26，∴115.255.26； ∵5.26xy是增函数，12，∴125.265.26； 综上，1125.255.265.26 （4）∵300.51，0.531，3log0.50， ∴30.53log0.50.53 例10．已知幂函数223mmyx（mZ）的图象与x轴、y轴都无交点，且关于原点对称，求m的值． 解：∵幂函数223mmyx（mZ）的图象与x轴、y轴都无交点，
∴2230mm，∴13m； ∵mZ，∴2(23)mmZ，又函数图象关于原点对称， ∴223mm是奇数，∴0m或2m． 例11、求函数y＝52x＋2x51＋4（x≥－32）值域． 解析：设t＝x51，∵x≥－32，∴t≥－2，则y＝t2＋2t＋4＝（t＋1）2＋3． 当t＝－1时，ymin＝3．
∴函数y＝52x＋2x51＋4（x≥－32）的值域为［3，＋）． 点评：这是复合函数求值域的问题，应用换元法． 五：课后练习
1、若a＞1在同一坐标系中，函数y=ax和y=logxa的图像可能是（ ）