普通年金终值的计算公式为
年金终值和年金现值的计算

一、年金终值:年金终值是指在一段时间内,定期支付一定金额的现金流,经过一定的利率增长后所积累的总金额。
年金终值计算的目的是评估未来一段时间内现金流的价值。
年金终值的计算可以通过如下的公式进行:FV=P*((1+r)^n-1)/r其中,FV表示年金终值,P表示每期支付的金额,r表示每期支付的利率,n表示支付的期数。
例如,每年支付1000元,利率为5%,持续支付10年,则年金终值的计算为:年金终值的计算方法可以应用于各种不同的现金流情况,如每月、每季度、每半年等的现金支付。
二、年金现值:年金现值是指将未来一段时间内的现金流按照一定的利率折算到现在的价值,将未来的现金流所得到的总金额。
年金现值的计算的目的是评估未来现金流的现值,以便做出更加准确的投资决策。
年金现值的计算可以通过如下的公式进行:PV=P*(1-(1+r)^(-n))/r其中,PV表示年金现值,P表示每期支付的金额,r表示每期支付的利率,n表示支付的期数。
例如,每年支付1000元,利率为5%,持续支付10年,则年金现值的计算为:所以,每年支付1000元,利率为5%,持续支付10年,年金现值为7721.73元。
年金现值的计算方法也可以适用于各种不同的现金流情况。
三、年金终值和年金现值的应用:在投资决策中,投资者可以利用年金终值和年金现值来比较不同投资方案的收益。
通过计算不同方案的年金终值和年金现值,可以判断哪种投资方案更加有利可图,从而做出更加明智的决策。
在退休规划中,个人可以利用年金终值和年金现值来评估自己的退休金需求和储蓄目标。
通过计算所需的年金终值和现值,可以规划合理的退休储蓄计划,确保在退休时有足够的资金支持。
总之,年金终值和年金现值是评估一定时间内或一系列现金流价值的重要工具。
通过运用年金终值和年金现值的计算方法,可以帮助人们做出更加准确的投资决策和退休规划。
普通年金终值系数表

年金终值系数是指一定时期内,每期期末等额收入或支出的本利和。
年金终值系数为[(1+i)^n-1]/i。
多应用于经济学;金融学;建筑工程经济等领域。
年金是每隔相等时间间隔收到或支付相同金额的款项,如每年年末收到养老金10000元,即为年金。
年金终值(普通年金终值)也就是将每一期的金额,按复利换算到最后一期期末的终值,然后加总,就是该年金终值。
利率为i,经过n期的年金终值系数记作(F/A,i,n), 年金终值系数为[(1+i)^n-1]/iF=A(F/A,i,n)什么是年金终值系数?年金终值系数指固定的间隔时间相等的期间(如以年为单位)分期支付(存入)1元金额,经过若干年后按复利计算的累计本利之和。
而年金按其每次收付发生的时点(即收付当日日是在①有限期的首期期末、②有限期的首期期初、③有限期的若干期后的期末、④无限期)的不同,可分为:普通年金(后付年金)、先付年金、递延年金、永续年金等几种,故年金终值亦可分为:普通年金终值、先付年金终值、递延年金终值。
(注:永续年金只有现值,不存在终值。
)复利年金终值系数公式年金终值系数公式如下:年金终值系数(Future value of an annuity factor)=F/A=(F/A,i,n)F/A=(F/A,i,n)=\frac{(1+i)^n-1}{i}这里F/A=(F/A,i,n)代表年金终值系数,i代表利率,n代表年数。
复利终值和年金复利终值的区别1、投入方式不同:复利终值是不需要连续同期投入资金,一次性存入;年金复利终值是相同期限间隔(如每月,每季)等额存入固定金额,不是一次性存入。
2、计算数额不同:复利终值在计算时每一期本金的数额是不同的;年金复利终值在计算时每一期本金的数额是相同的。
完整复利年金终值系数表一览复利年金终值系数表一复利年金终值系数表二(接上表)复利年金终值系数表三(接上表)。
普通年金终值的计算公式为

v 年金是指一定时期内每次等额收付的系列款 项,即如果每次收付的金额相等,则这样的 系列收付款项便称为年金,通常记作A 。
v 年金终值是指一定时期内每期等额发生款项 的复利终值的累加和。——零存整取
v 年金现值是指一定时期内每期等额发生款项 的复利现值的累加和。——整存零取
精选PPT
13
v 年金按其每次收付发生的时点不同,可分为:
v P = 70000 × (P/A,12%,8) v = 70000 × 4.968 v = 347760 (元)
精选PPT
20
v 【例8】某企业现在存入银行347760元,准 备在今后的8年内等额取出,用于发放职工奖 金,若年利率为12%,问每年年末可取出多 少钱?
v 很明显,此例是已知年金现值 ,倒求年金A, 是年金现值的逆运算。
F = 50000 × (F/A,6%,6) = 50000 × 6.975 = 348750 (元)
精选PPT
17
v 【例6】某企业准备在6年后建造某一福利设 施,届时需要资金348750元,若年利率为 6%,则该企业从现在开始每年年末应存入多 少钱?即年偿债基金是多少?
很明显,此例是已知年金终值F,倒求年金A, 是年金终值的逆运算。
年金终值和年金现值的计算

六、年金终值和年金现值的计算(一)年金的含义年金是指一定时期内每次等额收付的系列款项。
通常记作A 。
具有两个特点:一是金额相等;二是时间间隔相等。
也可以理解为年金是指等额、定期的系列收支。
在现实工作中年金应用很广泛。
例如,分期付款赊购、分期偿还贷款、发放养老金、分期支付工程款、每年相同的销售收入等,都属于年金收付形式。
老师手写板:①②年、月、半年、2年1年 2年 3年1年 1年 1年(二)年金的种类年金按其每次收付款项发生的时点不同,可以分为四种:普通年金(后付年金):从第一期开始每期期末收款、付款的年金。
预付年金(先付年金、即付年金):从第一期开始每期期初收款、付款的年金。
与普通年金的区别仅在于付款时间的不同。
递延年金:从第二期或第二期以后开始每期期末收付的年金。
永续年金:无限期的普通年金。
注意:各种类型年金之间的关系(1)普通年金和即付年金区别:普通年金的款项收付发生在每期期末,即付年金的款项收付发生在每期期初。
联系:第一期均出现款项收付。
【例题1·单选题】2007年1月1日,甲公司租用一层写字楼作为办公场所,租赁期限3年,每年12月31日支付租金10万元,共支付3年。
该租金有年金的特点,属于( )。
(2010年考试真题)A .普通年金B .即付年金C .递延年金D .永续年金【答案】A【解析】每年年末发生等额年金的是普通年金。
(2)递延年金和永续年金二者都是在普通年金的基础上发展演变起来的,它们都是普通年金的特殊形式。
它们与普通年金的共同点有:它们都是每期期末发生的。
区别在于递延年金前面有一个递延期,也就是前面几期没有现金流,永续年金没有终点。
在年金的四种类型中,最基本的是普通年金,其他类型的年金都可以看成是普通年金的转化形式。
【提示】1.这里的年金收付间隔的时间不一定是1年,可以是半年、一个季度或者一个月等。
A A A A A A A A A A 300万 200万 100万2.这里年金收付的起止时间可以是从任何时点开始,如一年的间隔期,不一定是从1月1日至12月31日,可以是从当年7月1日至次年6月30日。
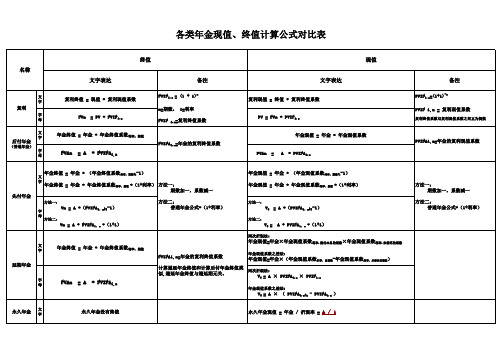
各类年金终值 现值计算公式对比表
两次折现法:
年金现值=年金×年金现值系数利率,偿付本息的期数×年金现值系数利率,未偿还的期数
FVIFAi,n=年金的复利终值系数
计算递延年金终值和计算后付年金终值类 似,递延年金终值与递延期无关。
年金现值系数之差法:
年金现值=年金×(年金现值系数利率,总期数-年金现值系数利率,未偿还的期数)
方法二: 普通年金公式*(1+利率)
年金现值 = 年金 * (年金现值系数利率,期数+1-1) 年金现值 = 年金 * 年金现值系数利率,期数 *(1+利率)
方法一:
V0 = A *(PVIFAi,n+1-1)
方法二:
V0 = A * PVIFAi,n *(1+i)
文 字
延期年金
字 母
年金终值 = 年金 * 年金终值系数利率,期数
各类年金现值、终值计算公式对比表
名称
文 字
复利
字 母
文 字
后付年金
(普通年金) 字 母
终值
文字表达
复利终值 = 现值 * 复利现值系数 FVn = PV * FVIFi,n
年金终值 = 年金 * 年金终值系数利率,期数
FVAn = A * FVIFAi,n
备注
FVIFi,n = (1 + i)n n=期数, i=利率 FVIF i,n=复利终值系数
PVIFAi,n=年金的复利现值系数
先付年金
文 年金终值 = 年金 * (年金终值系数利率,期数+1-1)
字
年金终值 = 年金 * 年金终值系数利率,期数 *(1+利率) 方法一: 期数加一,系数减一
年金终值与限制的计算范例

年金终值与限制的计算范例1、普通年金现值和终值的计算1)普通年金的概念 P66普通年金,又称后付年金,是指每期期末有等额的收付款项的年金。
2)普通年金终值的计算 P66n,,(1,i),1普通年金终值(FVA),A(公式8),,i,,(1,i)n,1i被称为年金终值系数,用FVIFA表示 i,n则FVA=A×FVIFA公式8 i,n3) 普通年金现值的计算 P6811,,普通年金现值(PVA),A,(公式9)n,,ii(1,i),,11,被称为年金现值系数,用PVIFA表示i,nnii(1,i)则:PVA,A,PVIHA(公式9)i,n4)普通年金的应用例1:拟在5年后还清10000元债务,从现在起每年等额存入一笔款项,假如银行存款利率5%,问每年需要存入多少钱,解题思路:1)分析题目所给的资料,判断已知条件2)分析题目要求求解的问题3)选择适用公式进行计算或利用公式推导解: 解:已知年金终值FVA=10000,I=5%,n=5; 求年金A用公式8 n5 FVA=A[(1+i)-1]]/i=A[(1+5%)-1]/5%=10000A=1809.63或(查年金终值系数):FVA=A×FVIFA =A×5.526=10000 i,nA=1809.63例2:某人出国三年,请你代付房租,每年租金5000元,银行存款利率为5%,问他应当现在给你在银行存入多少钱,解:已知年金A=5000,n=3,I=5%;求年金现值PVA用公式9PVA=A×PVIFA=5000×2.7232=13615 ,in或:直接计算例3:某人在未来10年中,每年底存入3000元,他想拥有60912元,则年利率为多少,解:已知A=3000,n=10,FVA=60912;求利率IFVA=A×FVIFA=3000 ×FVIFA=60912 i,ni,nFVIFA=20.304 i,n查表可知当n=10,I=15%时,FVIFA=20.304 i,n所以 I=15%或: 用插入法计算。
年金的计算公式的

年金的计算公式的年金的计算公式。
年金是一种定期给付的金融产品,通常用于退休金、养老金等用途。
年金的计算公式是非常重要的,它可以帮助人们了解年金的计算方式,帮助他们做出合理的规划和决策。
本文将介绍年金的计算公式,并对其进行详细的解释和应用。
年金的计算公式通常包括三个主要因素,本金、利率和时间。
根据这三个因素的不同组合,可以得到不同类型的年金。
最常见的年金类型包括普通年金、年金现值、年金终值、年金付款、年金付款期数等。
下面我们将分别介绍这些年金类型的计算公式。
1. 普通年金的计算公式。
普通年金是指在每个支付期末支付利息的年金。
其计算公式为:A = P (1 + r)^n。
其中,A表示每期支付的金额,P表示本金,r表示利率,n表示支付期数。
2. 年金现值的计算公式。
年金现值是指将未来的一系列支付转换为当前的等值金额。
其计算公式为:PV = P [1 (1 + r)^(-n)] / r。
其中,PV表示年金现值,P表示每期支付的金额,r表示利率,n表示支付期数。
3. 年金终值的计算公式。
年金终值是指在未来某一时间点的一系列支付的总金额。
其计算公式为:FV = P [(1 + r)^n 1] / r。
其中,FV表示年金终值,P表示每期支付的金额,r表示利率,n表示支付期数。
4. 年金付款的计算公式。
年金付款是指在一定时间内的一系列支付。
其计算公式为:PMT = P r / (1 (1 + r)^(-n))。
其中,PMT表示每期支付的金额,P表示本金,r表示利率,n表示支付期数。
5. 年金付款期数的计算公式。
年金付款期数是指在一定时间内的支付期数。
其计算公式为:n = -log(1 (PV r / P)) / log(1 + r)。
其中,n表示支付期数,PV表示年金现值,P表示每期支付的金额,r表示利率。
以上就是年金的常见计算公式,通过这些公式,我们可以对年金进行各种复杂的计算和分析。
在实际应用中,我们可以根据具体情况选择合适的计算公式,帮助我们做出明智的决策。
