北理工《信号与系统》习题答案第2章答案(纯手写)
《信号与系统》课后习题参考答案

《信号与系统》课后习题参考答案第二章 连续信号与系统的时域分析2-9、(1)解:∵系统的微分方程为:)(2)(3)(t e t r t r '=+',∴r(t)的阶数与e(t) 的阶数相等,则h(t)应包含一个)(t δ项。
又∵系统的特征方程为:03=+α,∴特征根3-=α∴)()(2)(3t u Ae t t h t -+=δ∴)]()(3[)(2)(33t e t u e A t t h t t δδ--+-+'=')()(3)(23t A t u Ae t t δδ+-'=-将)(t h 和)(t h '代入微分方程(此时e(t)= )(t δ),得:)()(3)(23t A t u Ae t t δδ+-'-+3)(2)]()(2[3t t u Ae t t δδ'=+-∴A=-6则系统的冲激响应)(6)(2)(3t u et t h t --=δ。
∴⎰⎰∞--∞--==t td ue d h t g τττδτττ)](6)(2[)()(3⎰∞-=t d ττδ)(2⎰∞---t d u e τττ)(63 )()(6)(203t u d e u t t ⎰-∞--=τττ )()3(6)(203t u e t u t --=-τ)()1(2)(23t u e t u t -+=- )(23t u e t -=则系统的阶跃响应)(2)(3t u et g t -=。
2-11、解:①求)(t r zi : ∵系统的特征方程为:0)3)(2(652=++=++αααα,∴特征根:21-=α,32-=α ∴t t zi e C eC t r 3221)(--+= (t ≥0) ②求)(t r zs :t t e A eA t h 3221)(--+= (t ≥0),可求得:11=A ,12-=A (求解过程略) ∴)()()(32t u e e t h t t ---=∴)(*)()(*)()]()[(*)()(*)()(3232t u e t u e t u e t u e t u e e t u e t h t e t r t t t t t t t zs --------=-==)()2121()()(21)()(3232t u e e e t u e e t u e e t t t t t t t -------+-=---= ③求)(t r :)(t r =)(t r zi +)(t r zs ++=--)(3221t te C e C )2121(32t t t e e e ---+- t tt e C e C e 3221)21()1(21---++-+= (t ≥0) ∵)()(t u Ce t r t -=,21=C 21=C ∴ 011=-C , ∴ 11=C0212=+C 212-=C ∴=-)0(r 21211)0(21=-=+=+C C r zi , ='-)0(r 2123232)0(21-=+-=--='+C C r zi 2-12、解:(1)依题意,得:)(2)(*)()(t u e t h t u t r tzi -=+)()()(t t h t r zi δ=+∴)(2)]()([*)()(t u e t r t t u t r t zi zi -=-+δ)(2)()()()1(t u e t r t u t r t zi zi --=-+∴)()12()()()1(t u e t r t r t zi zi -=---,两边求导得:)()12()(2)()(t e t u e t r t r t t zi ziδ-+-=-'-- )(2)()()(t u e t t r t r t zi zi--=-'δ ∴)(11)(112)()()1(t p p t p t t r p zi δδδ+-=+-=- ∴)()(11)(t u e t p t r t zi -=+=δ (2)∵系统的起始状态保持不变,∴)()(t u e t r t zi -=∵)()()(t t h t r zi δ=+,∴)()()(t u e t t h t--=δ∴)]()([*)()()(*)()()(33t u e t t u e t u e t h t e t r t r t t t zi ----+=+=δ )()()(t u te t u e t u e tt t ----+=)()2(t u e t t --= 2-16、证:∑∑∞-∞=--∞-∞=--=-=k k t k t k t u e k t t u e t r )3()3(*)()()3(δ∑∞-∞=--=k k t k t u e e )3(3 ∵当t-3k>0即3t k <时:u(t-3k)为非零值 又∵0≤t ≤3,∴k 取负整数,则:3003311)(---∞=∞=----===∑∑e e e e e et r t k k k t k t 则t Ae t r -=)(,且311--=e A 。
北理工-信号与系统-第三版-第三章-作业参考答案
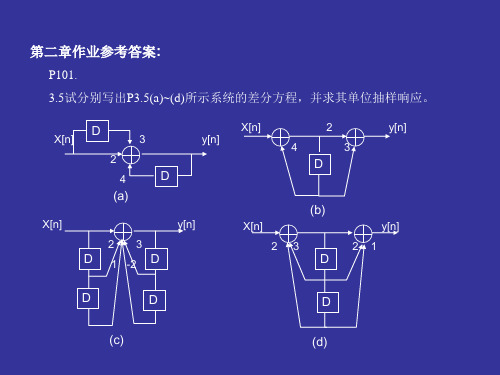
k
| u[k ] | ,有界
是非稳定系统
(e) 显然n<0时,h[n]=0,所以是因果系统;
k
| h[k ] | | u[k ] / n | ,无界
k
是非稳定系统
(f) 显然n<0时,h[n]=0,所以是因果系统;
| h[k ] |
(d)
y[n] x[n] h[n]
k
[k n ] [n k n ]
1 2
[n n1 n2 ]
3.11在LTI离散时间系统中 已知x[n]=u[n]时的零状态响应(单位阶跃响应)为s[n],求单位抽样响应h[n]; 已知h[n],求s[n].
y[n] - 4y[n-1] =2x[n]+3x[n-1];
令x[n]=δ[n],则有 h[n] – 4h[n-1] =2 δ[n]+3 δ[n-1];当n<0时,h[n]=0,得h[0]=2,h[1]=11,
特征方程为 λ-4=0, 得λ=4,
h[n]=c(4)nu[n],由h[1]=4c=11,c=11/4得 h[n]=(11/4)(4)nu[n-1]=11 (4)n-1u[n-1],考虑h[0]=2=2 δ[n],得 h[n]=2 δ[n]+11 (4)n-1u[n-1]。(n>0的解) (b).据图有同(a)一样的结果…。 (c).据图 y[n]=3y[n-1]- 2y[n-2]+ x[n]+2x[n-1]+x[n-2] ,即差分方程为 y[n] -3y[n-1]+2y[n-2] = x[n]+2x[n-1]+x[n-2], 先求
北理工《信号与系统》同步习题答案(与曾禹教材配套)
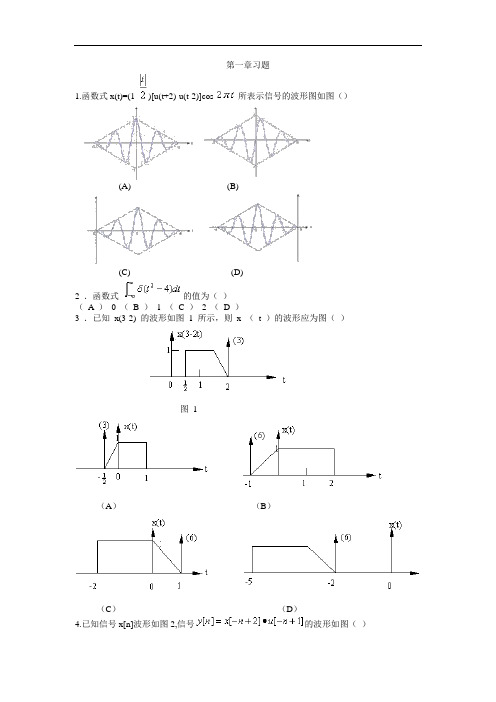
第一章习题1.函数式x(t)=(1-)[u(t+2)-u(t-2)]cos所表示信号的波形图如图()(A) (B)(C) (D)2 .函数式的值为()(A )0 (B ) 1 (C ) 2 (D )3 .已知x(3-2) 的波形如图1 所示,则x (t )的波形应为图()图1(A)(B)(C)(D)4.已知信号x[n]波形如图2,信号的波形如图()图2(A)(B)(C) (D)5 .卷积积分等于()(A)(B)-2 (C)(D)-2 (E)-26 .卷积和x[n] u[n-2] 等于()(A )( B )( C )(D )(E )7 .计算卷积的结果为()(A )( B )(C )(D )8 .已知信号x(t) 的波形如图3 所示,则信号的波形如图()图3(A)(B)(C) (D)9 .已知信号x (t )如图所示,其表达式为()(A)(B)(C)(D)10 .已知x(t)为原始信号,y(t)为变换后的信号,y(t) 的表达式为()(A )( B )(C )(D )11 .下列函数中()是周期信号(A )( B )(C )(D )(E )12 .函数的基波周期为()。
(A )8 (B )12 ( C )16 (D )2413 .某系统输入—输出关系可表示为,则该系统是()系统。
(A )线性(B )时不变(C )无记忆(D )因果(E )稳定14 .某系统输入—输出关系可表示为,则系统为()系统。
(A )线性(B )时不变(C )无记忆(D )因果(E )稳定15.某系统输入—输出关系可表示为,则系统为()系统。
(A )线性(B )时不变(C )无记忆(D )因果(E )稳定16.某系统输入—输出关系可表示为,则系统为()系统。
(A )线性(B )时不变(C )无记忆(D )因果(E )稳定17 .某系统输入—输出关系可表示为,则系统为()系统(A )线性(B )时不变(C )无记忆(D )因果()稳定18 .下列系统中,()是可逆系统(A )y[n]=nx[n] (B )y[n]=x[n]x[n-1](C )y(t)=x(t-4) ( D )y(t)=cos[x(t)](E )y[n]=19 .如图系统的冲激响应为()(A )(B )(C )(D )20 .某系统的输入x (t )与输出y (t )之间有如下关系,则该系统为()(A)线性时变系统(B)线性非时变系统(C)非线性时变系统(D)非线性非时变系统21 .一个LTI 系统在零状态条件下激励与响应的波形如图,则对激励的响应的波形()(A) (B)(C) (D)22. 线形非时变系统的自然(固有)响应就是系统的()(A )零输入响应(B )原有的储能作用引起的响应(C )零状态响应(D )完全的响应中去掉受迫(强制)响应分量后剩余各项之和23 .零输入响应是()(A )全部自由响应(B )部分零状态响应(C )部分自由响应(D )全响应与强迫响应之差24 .下列叙述或等式正确的是()(A)(B)(C) 若, 则(D) 若x(t) 和h(t) 是奇函数,则是偶函数25.设是一离散信号,,,则下列说法( )是正确的(A) 若是周期的,则也是周期的(B) 若是周期的,则也是周期的(C) 若是周期的,则也是周期的(D) 若是周期的,则也是周期的26 .有限长序列经过一个单位序列响应为的离散系统,则零状态响应为()(A) (B)(C) (D)第一章习题答案1.A提示:这是三角形为包络的余弦调制信号 ----§1.2-----2.C提示:原式=------§1.2-------3.A提示:反转——伸缩——移位x(3+2t) x(3+t) x(t) ----§1.4----4.B提示:是将x[n]反转右移;是将u[n]反转右移;= ------§1.6-------5.D提示:=()’=-2------§2.4-------6.E提示:将u[n-2]反转,u[k-n-2],k从到n-2,u[k-n-2]=1,其余为0 x[n] u[n-2]= ------§3.5-------7.C提示:原式=,为偶函数------§2.5-------8.D提示:------§2.5-------9.B10.D提示:信号波形扩展了,只有(D)对------§1.4-------11.C提示:q为正整数------§1.6-------12.C提示:最小公倍数为N=16------§1.6-------13.B,C,D,E 14.A,B,D 15.A 16.A,B,E 17.B,C,D,E18.C,E提示:不满足非线性如x(t)= ------§1.8-------19.D20.D示:不满足非线性如x(t)= ------§1.8-------21.C 22.D 23.C 24.B,C,D 25.B,C 26.C第二章习题1. 某 LTI 连续时间系统具有一定的起始状态,已知激励为 x ( t )时全响应, t 0 ,起始状态不变,激励为时,全响应 y ( t )= 7e + 2e, t 0 ,则系统的零输入响应为()( A )( B )( C )( D )2 .微分方程的解是连续时间系统的()(A) 零输入响应 (B) 零状态响应(C) 自由响应 (D) 瞬态响应(E)全响应3 .单位阶跃响应是()(A) 零状态响应 (B) 瞬态响应(C) 稳态响应 (D) 自由响应(E) 强迫响应4 .已知系统如图所示,其中 h (t) 为积分器,为单位延时器, h (t) 为倒相器,则总系统的冲激响应 h (t) 为()( A )( B )( C )( D )5 .如图所示电路以为响应,其冲激响应 h (t) 为()(A)(B)(C)(D)6. 某 LTI 系统如图所示,该系统的微分方程为()(A ) (B)(C) (D)7 .已知系统的微分方程 , 则求系统单位冲激响应的边界条件 h(0 ) 等于()(A) - 1 (B) 0 (C) 2 (D) + 18 .已知系统的微分方程则系统的单位冲激响应为()(A) (B)(C) (D)9 .已知描述系统的微分方程和初始状态 0 值如下;y (0 ) = 2 ,, , ,则初始条件 0 值为()(A) (B)(C) (D)10 .已知描述系统的微分方程和初始状态 0 值如下 y (t) + 6 y (t) +8 y (t) = x (t) + 2x (t) ,y (0 ) = 1 , y (0 ) = 2 , x (t) =( t )则初始条件 0 值为()。
北京理工大学信号与系统试题

1 .按照信号的能量或功率为有限值,信号可分为和。
2 .一个离散时间系统可由、、等基本部件组成。
3 .如图所示 LTIS ,若, , ,则系统的输出为。
4 .应用卷积积分的方法可以得到系统的。
5 .6 .试写出下列函数的频谱密度函数(a) , 所以(b) , 所以7. x(n) 的离散时间傅立叶变换为 X(e ), 则 y(n)= 的傅立叶变换为8. 果而稳定的 LTI 系统,单位冲击响应为 h(t) , 系统 H(s) 有一极点在s= -2, 则是9. 知一因果而稳定系统的单位脉冲响应为 h(n),H(z) 是有理的,且, 则10 .二、计算题1 .设三个因果 LTI 系统的级联如图 1 所示,其中冲激响应而总的冲激响应如图 2 所示,求(a)冲激响应(b) 整个系统对输入的响应2 .考虑一个 LTI 系统它对输入的响应为(a) 求该系统的频率响应(b) 确定该系统的冲激响应(c) 求出联系输入、输出的微分方程,并用积分器、相加器和系数相乘器实现该系统。
3 .如图所示,系统(1) 以为状态变量列出其状态方程与输出方程(2) 求状态转移矩阵4.的单边拉氏反变换5.已知信号 x(n) 的傅立叶变换, 求的傅立叶反变换试题一答案一. 填空题1 .答案:(能量信号,功率信号)2 .答案:(单位延时器、相加器、倍乘器)3 .4 .答案:(零状态响应)5 .答案:6 .答案:(a)7.8.9.10 .二、计算题1 .答案:2 .解 :(a)(b)(c)3 .解 :(1)(2)4.解:(分子阶次与分母阶次相同,降阶)(分母多项式带有重根的部分分式展开法)又因为求单边拉氏变换所得信号为因果信号5.解:(注:文档可能无法思考全面,请浏览后下载,供参考。
)。
信号与系统课后习题参考答案

1试分别指出以下波形是属于哪种信号?题图1-11-2试写出题1-1图中信号的函数表达式。
1-3已知信号)(1t x 与)(2t x 波形如题图1-3中所示,试作出下列各信号的波形图,并加以标注。
题图1-3⑴)2(1-t x ⑵)1(1t x -⑶)22(1+t x⑷)3(2+t x ⑸)22(2-t x ⑹)21(2t x - ⑺)(1t x )(2t x -⑻)1(1t x -)1(2-t x ⑼)22(1t x -)4(2+t x 1-4已知信号)(1n x 与)(2n x 波形如题图1-4中所示,试作出下列各信号的波形图,并加以标注。
题图1-4⑴)12(1+n x ⑵)4(1n x -⑶)2(1n x ⑷)2(2n x -⑸)2(2+n x ⑹)1()2(22--++n x n x⑺)2(1+n x )21(2n x -⑻)1(1n x -)4(2+n x ⑼)1(1-n x )3(2-n x1-5已知信号)25(t x -的波形如题图1-5所示,试作出信号)(t x 的波形图,并加以标注。
题图1-51-6试画出下列信号的波形图:⑴)8sin()sin()(t t t x ΩΩ=⑵)8sin()]sin(211[)(t t t x ΩΩ+= ⑶)8sin()]sin(1[)(t t t x ΩΩ+=⑷)2sin(1)(t tt x = 1-7试画出下列信号的波形图:⑴)(1)(t u e t x t -+=⑵)]2()1([10cos )(---=-t u t u t e t x t π⑶)()2()(t u e t x t --=⑷)()()1(t u e t x t --=⑸)9()(2-=t u t x ⑹)4()(2-=t t x δ1-8试求出以下复变函数的模与幅角,并画出模与幅角的波形图。
⑴)1(1)(2Ω-Ω=Ωj e j X ⑵)(1)(Ω-Ω-Ω=Ωj j e e j X ⑶Ω-Ω---=Ωj j e e j X 11)(4⑷21)(+Ω=Ωj j X 1-9已知信号)]()([sin )(π--=t u t u t t x ,求出下列信号,并画出它们的波形图。
信号与系统课后习题与解答第二章
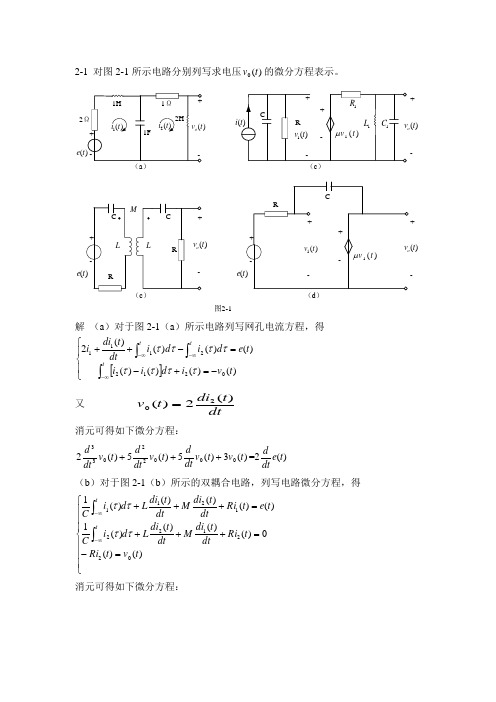
2-1 对图2-1所示电路分别列写求电压)(0t v 的微分方程表示。
2(t ei )(t +-(e )(e )(t +-图2-1解 (a )对于图2-1(a )所示电路列写网孔电流方程,得[]⎪⎩⎪⎨⎧-=+-=-++⎰⎰⎰∞-∞-∞-t t t t v i d i i t e d i d i dt t di i )()()()()()()()(202122111ττττττττ 又 dtt di t v )(2)(20= 消元可得如下微分方程:)(3)(5)(5)(200022033t v t v dt dt v dtd t v dt d +++=2)(te dt d(b )对于图2-1(b )所示的双耦合电路,列写电路微分方程,得⎪⎪⎪⎩⎪⎪⎪⎨⎧=-=+++=+++⎰⎰∞-∞-)()(0)()()()(1)()()()()(10221221211t v t Ri t Ri dt t di M dt t di L d i Ct e t Ri dtt di M dt t di L d i C ttττττ 消元可得如下微分方程:)()(1)(2)(2)(2)()(22020022203304422t e dtd MR t v C t v dt d C R t v dtd R R L t v dtd RL t v dt d M L =++⎪⎭⎫ ⎝⎛+++- (c )对于图2-1(c )所示电路列写电路方程,得⎪⎪⎩⎪⎪⎨⎧=⎥⎦⎤⎢⎣⎡+++=⎰∞-)()()(1)()()()(10101011t v t v dt d C dt t v L R t v R t v t v dt d C t i t μ 消元可得如下微分方程:)()(1)(1)()(101011022110331t i dt dR t v RL t v dt d R R L C t v dt d R C R C t v dt d CC μ=+⎪⎪⎭⎫ ⎝⎛++⎪⎪⎭⎫ ⎝⎛++ (d )对图2-1(d )所示电路列写电路方程,电流)(t i 如图2-2所示,得⎪⎪⎩⎪⎪⎨⎧==+=++⎰∞-)()()()()()()()(1)(1011t v t v t e t v t Ri t e t v d i C t Ri t μμττ 消元可得如下微分方程:(t e )(t +-图2-2)()(1)()1(00t e Rt v R t v dt d Cμμ=+-2-2 图2-3所示为理想火箭推动器模型。
信号与系统课后答案 第2章 习题解

第2章 习 题2-1 求下列齐次微分方程在给定起始状态条件下的零输入响应(1)0)(2)(3)(22=++t y t y dt d t y dt d ;给定:2)0(,3)0(==--y dt dy ; (2)0)(4)(22=+t y t y dt d ;给定:1)0(,1)0(==--y dtd y ;(3)0)(2)(2)(22=++t y t y dt d t y dt d ;给定:2)0(,1)0(==--y dt dy ; (4)0)()(2)(22=++t y t y dt d t y dt d ;给定:2)0(,1)0(==--y dtdy ; (5)0)()(2)(2233=++t y dt d t y dt d t y dt d ;给定:2)0(,1)0(,1)0(22===---y dt d y dt d y 。
(6)0)(4)(22=+t y dt d t y dt d ;给定:2)0(,1)0(==--y dtdy 。
解:(1)微分方程的特征方程为:2320λλ++=,解得特征根:121, 2.λλ=-=- 因此该方程的齐次解为:2()t th y t Ae Be --=+.由(0)3,(0)2dy y dt--==得:3,2 2.A B A B +=--=解得:8, 5.A B ==- 所以此齐次方程的零输入响应为:2()85tty t e e--=-.(2)微分方程的特征方程为:240λ+=,解得特征根:1,22i λ=±.因此该方程的齐次解为:()cos(2)sin(2)h y t A t B t =+.由(0)1,(0)1d y y dx --==得:1A =,21B =,解得:11,2A B ==. 所以此齐次方程的零输入响应为:1()cos(2)sin(2)2y t t t =+.(3)微分方程的特征方程为:2220λλ++=,解得特征根:1,21i λ=-± 因此该方程的齐次解为:()(cos()sin())th y t e A t B t -=+.由(0)1,(0)2dy y dx--==得:1,2,A B A =-= 解得:1,3A B ==.所以齐次方程的零输入响应为:()(cos()3sin())ty t e t t -=+.(4)微分方程的特征方程为:2210λλ++=,解得二重根:1,21λ=-.因此该方程的齐次解为:()()th y t At B e -=+. 由(0)1,(0)2dy y dx--==得:1,2,B A B =-=解得:3, 1.A B == 所以该方程的零输入响应为:()(31)ty t t e -=+.(5)微分方程的特征方程为:3220λλλ++=,解得特征根: 1,21λ=-,30λ=. 因此该方程的齐次解为:()()th y t A Bt C e -=++.由22(0)1,(0)1,(0)2d d y y y dx dt---===得:1,1,22A C B C C B +=-=-=. 解得:5,3,4A B C ==-=-.所以方程的零输入响应为:()5(34)ty t t e -=-+.(6)微分方程的特征方程为:240λλ+=,解得特征根:120,4λλ==-. 因此该方程的齐次解为:4()th y t A Be -=+.由(0)1,(0)2d y y dx --==得:1,42A B B +=-=.解得:31,22A B ==-. 所以此齐次方程的零输入响应为:431()22ty t e -=-.2-2 已知系统的微分方程和激励信号,求系统的零状态响应。
2信号与系统-每章课后答案第二章作业PPT课件

21.11.2020
7
2.7 写出下列信பைடு நூலகம்的波形图。
(a)f(t)u(4t2)
( b ) f( t ) ( t 2 ) 3 ( t 2 ) 2 ( t )
(c) f (t) (34t) 1 (t - 3)
-4 4
1(t - 3)
44
21.11.2020
8
2.8 设 f (t) 在 t 0 及 t 8 时 f(t), 0 , f(0 )且 4 ;已知 f(t)f(2t) 的波形如图所示,试确定 f (t) 的波形。
请对以下连续时间系统确定哪些性质成立、哪些不成立,
并陈述你的理由。下列中 y(t) 和 x (t ) 分别记作系统的输出和
输入。
(a)y(t) dx(t) dt
时不变、线性、因果、 稳定
( b) y(t)co3t)sx((t) 时变、线性、因果、稳 定
(c)y(t) 2t x()d
(d)y(t) x(t ) 3
的波形。
21.11.2020
6
2.6 写出信号 f1(t) 和 f2 (t) 的表达式。
f1(t)u(t)u(t2) f 2 ( t ) - u ( t 1 ) ( t 1 ) u ( t 1 ) ( t 1 ) u ( t 1 ) 2 u ( t 1 ) u ( t 2 )
- 0(t)3(t)d t-3
(3)4(t-5)(t)dt4(t5 )22(t)d t4(-1 -)4
-3
2
-3
( 4)(t2t2)(2t)dt(t2t2)1(t)d t121
-
-
2
2
(5)t (t2)(t2)dt4t (t2)d t4u(t2)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
xt*)*?23 u.D
k,r*t-^ at+L (aN)
hLt-4nb)
)= qa)(4t*x t&xI
L tt-t1=Gt + z
=) l, 'xt = ({'- e-121 ) u,t*1
btl L ul = + (e-t- u-%) LtLt)
@) | ht ft) = a{m+ cyte
{) a=o
(I C, =l
\ lU Ur= C e-c atrr 7 C,ito;t
,
hnttl:
t
+
O-l) ,at
ht-r{*/-t)+--e "tr;t +e "C.rDt
) i, Lt) = 0o D i,,*t
)l =
dr (-b-A) ryz/L) clx = 1z Lt)x 4, th)
t Crto
-o) (D'-+?/D+zl!/ot=o t flr.o)=1, g'ttro)=z
; ; :t,r,il,Aln= co-m + cro''6 -J
) h,n*)= L'vt-o-'t-tzo
0, kl = d N bt) l,u*) = lw> u u,4,L) = ,f! U
= Lb, ct+t) _ 2 + g *-,., ] *, J -I r/" Lzr) al t -, I-t*r,ol,
-t,-ttt-itUt --;t,e---*rkt) = (+L-t-)tu-'+*wt ) t,LLt)
(l'+ ) ro nt I f w, = o-+ sat
= (nu'trot + br/wr )+st -autrat
04ro lo tr;t + t-h-ps ttu+t + Lb-A) /*:cF,+)
c , t <o
(-e
+
'
o(T't
2 - e-f t- e'/'-t-, lztz-y
t + e a-t - €* - e/-0, uctz f
ea-*_ e*r_L?t+ o{-t, t>f
9r-41 = CrA' f C>O
'A. (.O_l = h,/to_) =_o
\ rt t*S= c,*+ C,tt
+
e-
d-"**r,
ffrrat= lm^ N tu)
U,t*+ >) - uL,L -D
h, w>t rx b*7 = ) f:: e-t^') ol'
= Lo-'-[' , t>v
h, tt+>) - lr, h->) + h, (tt t) - h, tt-l )
( t- e,t )wb * (r- LY-t) utr*g 1 (t- et-t ) u/t-t )
u,th)
- Lt-z) tL uL -z) /+t1>t?o fus=o
>/ll t zf WA
l,r, ,*t + h, wt * h*q x ht &l
WiDt tt{*S+ 9U-t t-*(3Ut)
arl @t
l,tWl
=
=
h, Lts 1 5r4*ts * l.rrl:tl
h,t*t -t h, Lt-t) = e-u^"u,*->)
o-tet - Boaaht
L-'r4f
tB==Y0' =) hL *, = - ft rat
.\ Urw)= te-'-u-tE;t
fi
tn
+
= (Dlr
L'+c+I
p+t ) !p6s =
- c,y)'b ) + e:'
O-b ct-sAt1 ft ct-c.,,t ) - c p
e-t o?
c-a)O -
l!, u cTL) t{. L- z-t tzs o{z
+v+ b -- Q-)t
u47- ^L\)
lt c ->- t+z;
u,Lz. l)
= CtLLt ) t t,u.rt-t) - zul*-z;)x [ 8 o*; - zf *ll -r tut-r;) = lruW t w.t*t)- zu,,t*-2, -buc,t-ts+)u)h->)- 4u*->t )
= _4tCz=3 -) C.=b
,',t'*)= (r+bt )e-* uwc)
:.,/l ( o5+D'-D-l ) Jb)=o ,Jtq=t,J,tttD -1, )tr,rr=-2
z\'(A+ r)- (A1) = o
( A' t) cz\ + t)'= o
Ar:l , Ar=A r=-l
., W*et + cro-b + (cfie-t )"= (c>a
e-t +
>ehrt
-
z a4rt
-t-
t)1,-L
=
L
45,^rt-Ab>n/t,+e-u
='.aA I o,= L Sout 3 w-t) t 9t t-zs I "- hfi) = h*l+ k,t t-t tt k U ->)
z-)
h, cO - lr', Lt -r> l, tt->;
= 8 ut-t1* [L*'r ert ) u*t-z;
': \il1) v tt-Tdz
Y, lrx,4tx x
= T-x, Ltl x N,*t) x 4+ tk ) :c) Xt k) * I ,>'(ht + 't*,+l )
(^ x, Q) {z tb4 c/t +
+ (- e_+'crf+t
*fffi+
h, W) = h,"l wtt h, (*) = 3' wt - 29 h) t elr O
€-. www,ekaisa,com
rr .leibo+ftlwt--o , !{01 =1 !',,,0)=)
r.A+))'=0 Ar =r\2=-) yLt)=c,e-fr+ Crt(_-%
f-u1S"'t=o1g== I
- ) c, (,-u lr=o t cr{* [ ,=o ) qfi e-4't [ ,=,
'e'nl .- + g
-t + at2.-f ,tro fisAt + Bc-et A o-'ro b r b o- tont + v{4@)t - >b9dt + ba,l
ct{tr+sAt
flu*1= a =e
llhc't= -c+ c,+)=o
,;Jtus= -lto-t+ 4rrAt
-jn-t+ /te-t+ /ant)
= Z*2e:1,+O-u+=j-O1-+ro
=
-(- i-,= _ L_L+t) nl-t*
I
u
l, T<o
* 3 ,t^ l
cl+t'
o* l;'
L)=e WL)
(*) - >8 w-,2
Lz)
L
e/ /t t ct tka /wt= J: >o/t* J':'- r rtz
l@= J;, -z dt = z *->)
lIlLlo)= A+Cy=-Q
'7a-)c''= )
=(L-+*Ze--1h + e'w ) U/*2
e4 (L-fi4 )
[,,,1*t- A@zfi+ C>q,^1f
lrr'Lor, = 2c>'-l
-
Je
+u
^+-
I,t)e'(
(
a>x.J
k)>u
olz
+,0
5 /t tt =
DnTtI E;vt-
*{7
et cru*)
+ L-+"-fth-+b-t=+ te-' - { " (/- aht) = (t-t Se + e "Ntt
,t>o
t\u-t) - w Lt -a-Q )
l: 'A)tuT
o<t <
, t.o,
L-lt , -lrt ,0
[kl= l'vwl+ ct( lu)=.
+-lL- z ) t <-l lilt=4-yfr , t2z-zcf-l )-l ltzo
A'b , 6-6t-Ztt-L=> octztp
