相似三角形的几种模型

相似三角形的常见模型(地总结)

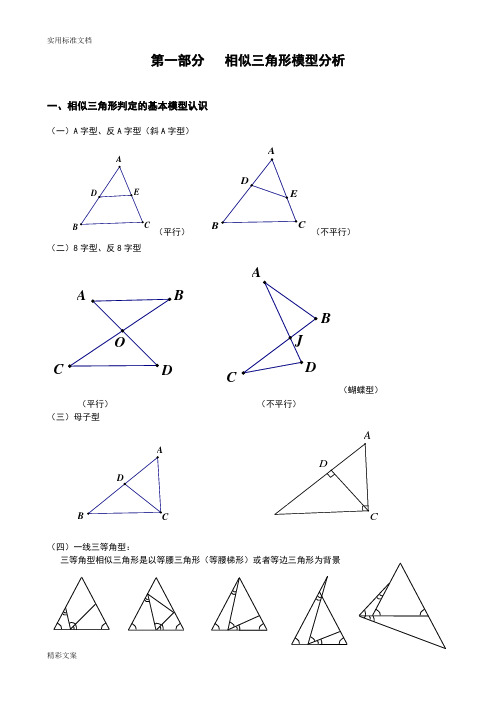
第一部分相似三角形模型分析一、相似三角形判定的基本模型认识（一）A 字型、反A 字型（斜A 字型）ABCDE（平行）CBA DE（不平行）（二）8字型、反8字型J OADBCAB CD（蝴蝶型）（平行）（不平行）（三）母子型ABCDCAD（四）一线三等角型：三等角型相似三角形是以等腰三角形（等腰梯形）或者等边三角形为背景（五）一线三直角型：（六）双垂型：CAD二、相似三角形判定的变化模型旋转型：由A 字型旋转得到。

8字型拓展CB EDA共享性GABCEF一线三等角的变形一线三直角的变形第二部分相似三角形典型例题讲解母子型相似三角形例1：如图，梯形ABCD 中，AD ∥BC ，对角线AC 、BD 交于点O ，BE ∥CD 交CA 延长线于E ．求证：OE OA OC ⋅=2．例2：已知：如图，△ABC 中，点E 在中线AD 上, ABC DEB ∠=∠．求证：（1）DA DE DB ⋅=2；（2）DAC DCE ∠=∠．例3：已知：如图，等腰△ABC 中，AB ＝AC ，AD ⊥BC 于D ，CG ∥AB ，BG 分别交AD 、AC 于E 、F ．求证：EG EF BE ⋅=2．相关练习：1、如图，已知AD 为△ABC 的角平分线，EF 为AD 的垂直平分线．求证：FC FB FD ⋅=2．AC D E B2、已知：AD 是Rt △ABC 中∠A 的平分线，∠C=90°，EF 是AD 的垂直平分线交AD 于M ，EF 、BC 的延长线交于一点N 。

求证：(1)△AME ∽△NMD; (2)ND 2=NC ·NB3、已知：如图，在△ABC 中，∠ACB=90°，CD ⊥AB 于D ，E 是AC 上一点，CF ⊥BE 于F 。

求证：EB ·DF=AE ·DB4.在∆ABC 中，AB=AC ，高AD 与BE 交于H ，EF BC ⊥，垂足为F ，延长AD 到G ，使DG=EF ，M 是AH 的中点。

中考数学几何专项——相似模型(相似三角形)

中考数学几何专项——相似模型(相似三角形)相似模型相似模型一：A字型特征：DE∥BC模型结论：根据A字型相似模型，可以得出以下结论：C∠B=∠XXXAC²=AD×AB相似模型二：X型特征：AC∥BD模型结论：根据X型相似模型，可以得出以下结论：AO×OB=OC×ODBOC∽△DOACAOC∽△DOB相似模型三：旋转相似特征：成比例线，段共端点模型结论：根据旋转相似模型，可以得出以下结论：BEF∽△BCDDEF∽△DABAEB∽△DEC相似模型四：三平行模型特征：AB∥EF∥CD模型结论：根据三平行模型，可以得出以下结论：ABE∽△CDF相似模型五：半角模型特征：90度，45度；120度，60度模型结论：根据半角模型，可以得出以下结论：ABN∽△MAN∽△MCAABD∽△CAE∽△CBA相似模型六：三角形内接矩形模型特征：矩形EFGH或正方形EFGH内接与三角形模型结论：根据三角形内接矩形模型，可以得出以下结论：ABC∽△EFH相似模型七：十字模型特征：正方形HDGB模型结论：根据十字模型，可以得出以下结论：若AF=BE，则AF⊥BE，且为长方形若AF⊥BE，则AF=BEBDBC平行四边形，且△GME∽△HNF，△MED≌△BFA。

下面给出几个几何问题。

1.在△ABC中，AB＝AC，且有以下七个结论：①D为AC中点；②AE⊥BD；③BE：EC＝2：1；④∠ADB＝∠CDE；⑤∠AEB＝∠CED；⑥∠BMC＝135°；⑦BM：MC＝2：1.求AC和CD的比值。

2.在平行四边形ABCD中，AB∥CD，线段BC，AD相交于点F，点E是线段AF上一点且满足∠BEF=∠C，其中AF=6，DF=3，CF=2，求AE的长度。

3.在Rt△ABD中，过点D作CD⊥BD，垂足为D，连接XXX于点E，过点E作EF⊥BD于点F，若AB=15，CD=10，求4.在□ABCD中，E为BC的中点，连接AE，AC，分别交BD于M，N，求5.在平行四边形ABCD中，AB∥CD，AD，BC相交于点E，过E作EF∥AB交BD于点F。

三角形相似题型大全

三角形相似题型大全
三角形相似是数学几何中的一个重要概念，涉及到的题型非常多样。

以下是几种常见的三角形相似题型：
1. 平行线型：当两条平行线被第三条线段所截，所形成的三角形是相似的。

这是三角形相似的一个基本题型。

2. 角相等型：当两个三角形中有两个对应的角相等时，这两个三角形是相似的。

这也是一个比较常见的题型。

3. 边长比例型：当两个三角形的对应边长之间存在一定的比例关系时，这两个三角形是相似的。

这种题型在解决实际问题时经常出现。

4. 综合型：结合以上几种情况，可能需要在多个条件下判断三角形是否相似。

这种题型较为复杂，需要综合考虑各种因素。

在解决三角形相似问题时，需要灵活运用三角形相似的判定定理和性质定理，同时结合题目给出的条件进行推理和计算。

此外，对于一些比较复杂的题型，可能需要采用一些特殊的解题方法，如代数法、几何法等。

希望这些题型能够帮助你更好地理解和掌握三角形相似的知识，提高解决实际问题的能力。

相似三角形的几种模型

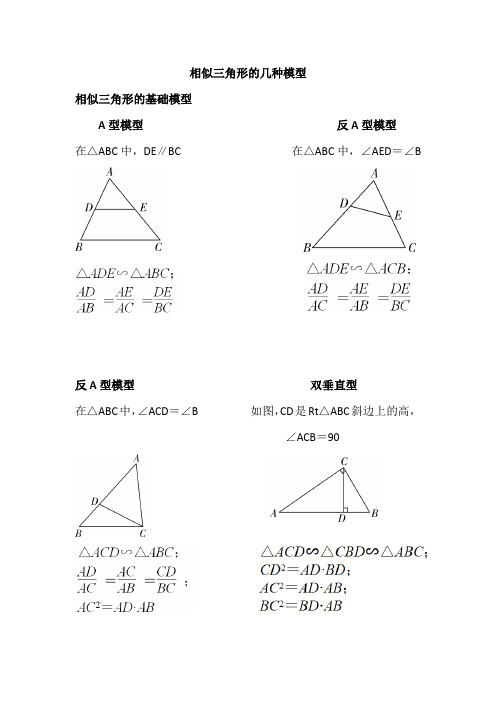
相似三角形的几种模型相似三角形的基础模型A型模型反A型模型在△ABC中，DE∥BC 在△ABC中，∠AED＝∠B反A型模型双垂直型在△ABC中，∠ACD＝∠B 如图，CD是Rt△ABC斜边上的高，∠ACB＝90一直线三等角模型在Rt△ABC与Rt△CDE中，A，C，D三点共线，△A＝△BCE＝△D＝90在△ABC与△CDE中，B，C，D三点共线，△B＝△ACE＝△D半角模型正方形ABCD中，点E，F分别在边AB，AD上，且△ECF＝45°，连接AC，EF，GH，CH，CF相交弦定理△O中，弦AB与弦CD相交与点PAP·BP＝CP·DP切割线定理PA为△O切线，PCB为△O割线PA2＝PB·PC割线定理PAB，PCD分别为△O割线PA·PB＝PC·PD模型应用1. (2017·深圳改编)如图，线段AB是△O的直径，弦CD△AB于点H，点M是上任意一点，直线BM交直线CD于点E，直线MH交△O 于点N，连接BN交CE于点F，AH＝2，HB＝8，求HE·HF的值．2. (2018·深圳改编)如图，△ABC内接于△O，BC＝2，AB＝AC＝，点D为上的动点，在点D的运动过程中，弦AD的延长线交BC 延长线于点E，问AD·AE的值是否变化？若不变，请求出AD·AE的值；若变化，请说明理由．GE·GF是否为定值？如果是，求出该定值；如果不是，请说明理由．4. 如图，以△ABC的BC边上一点O为圆心的圆，经过A，C两点，与BC边交于点E，点D为CE的下半圆弧的中点，连接AD交线段EO于点F.AB＝BF，CF＝4，DF＝，AB是△O的切线．(1)求△O的半径r；(2)设点P是BA延长线上的一个动点，连接DP交CF于点M，交弧AC于点N(N与A，C不重合).试问DM·DN是否为定值？如果是，求出该定值；如果不是，请说明理由．。

相似三角形的几种模型

相似三角形的几种模型Revised on November 25, 2020相似三角形的几种模型一、A 字型练习：1.如图,在△ABC 中，∠C=90°,在AB 边上取一点D,使BD=BC ，过D 作DE ⊥AB 交AC 于E ，AC=8，BC=6，求DE 的长。

2.如图，∠C=∠1，则下列各式不成立的是（）A 、BC BD AB AD = B 、BCBD AC AB = C 、AC AD AD ⋅=2 D 、BC AD AB ⋅=23.如图，在四边形ABCD 中，AB=AD ，AC 与BD 交于点E ，∠ADB=∠ACB.求证：△ABE ∽△ACB ．二、8字型1.将一副三角板如图叠放在一起，若OB=2，则OD=2.已知，如图∠ADE=∠ACB ，BD=8，CE=4,CF=2,求DF 的长 3.如图，在△ABC 中，∠ACB=90°,点F 在边AC 的延长线上，且FD ⊥AB,垂足为点D ，如果AD=6，AB=10，ED=2，那么FD=___．4.将三角形纸片（△ABC ）按如图所示的方式折叠,使点B 落在边AC 上,记为点B ′,折痕为EF ，已知AB=AC=6，BC=8，若以点B ′，F ，C 为顶点的三角形与△ABC 相似，那么BF 的长度是三、双垂图：1.如图，AD 和BE 是锐角△ABC 的两条高，P 是两条高的交点，请你写出图中所有的相似三角形2.在△ABC 中，D 为AB 边上一点，且∠BCD=∠A,已知BC=22,AB=3，则BD=3.如图，△ABC 中，∠ACB=90°,CD 是斜边AB 上的高，AD=9,BD=4，那么CD= AC=四、一线三等角如图，在正方形ABCD中，E为边AD上的点，点F在边CD上，且CF=3FD, ∠BEF=90°求证：△ABE∽△DEF．。

中考数学几何专项——相似模型(相似三角形)

相似模型【相似模型一：A 字型】特征模型结论DE ∥BCCBCBBC D E ADA E DA AD:AB=AE:AC=DE:BC 顺着比∠B=∠AEDCB CBDA EDAAD:AC=AE:AB=DE:BC 反着比AD×AB=AE×AC 顺着乘∠B =∠ACDCBED AAD:AC=AC:AB=CD:BC AC²=AD×AB当∠ BAC=90°AD B CB①△ABD ∽△CBA AB ²=BD×BC ②△ACD ∽△BCAAC²=CD×BC③△ADB ∽△CDA AD²=BD×CD特征模型结论AC ∥BDAD B CO DB A CC A OD BAD B CODBACCAO D B① △BD0∽△ACO ② DO:0C=BO:0A=BD:AC 交叉比③ △AOD 与△C0B 不相似∠B=∠C（也叫蝴蝶型相似）A D BC ODBACCAD B CODBACC① △AOC ∽△DOB② AO:OD=0C:0B=AC:BDAO×OB=OC×0D 顺着比，交叉乘 ③ △BOC∽△DOA特征模型结论成比例线段共端点① △ABC ∽△ADE② △ABD∽△ACE特征模型结论AB ∥EF ∥CDFEBCD AF EDCBA图2① 有两对A 字型相似△BEF ∽△BCD △DEF∽△DAB ② 有一对X 型相似△AEB ∽△DEC ③111AB CD EF+=特征模型结论ECD BAA BDC EEDCBA90度，45度； 120度，60度60°45°图2图1旋转N M 60°120°E D CB A 45°ED C B A ①△ABN ∽△MAN ∽△MCA ②△ABD ∽△CAE ∽△CBA【相似模型六：三角形内接矩形模型】特征模型结论矩形EFGH 或正方形EFGH 内接与三角形H G FED C BA【相似模型七：十字模型】特征模型结论正方形①若AF=BE,则AF ⊥BE ②若AF ⊥BE ，则AF=BE,长方形PEAB CD矩形ABCD 中，CE ⊥BD ，则△CDE ∽△BCD ，CE CDBD BC平行四边形△GME ∽△HNF△MED ≌△BFA三角形MED CAB在△ABC 中，AB ＝AC ，AB ⊥AC ，①D 为中点，②AE ⊥BD ，③BE ：EC＝2：1，④∠ADB ＝∠CDE ，⑤∠AEB ＝∠CED ，⑥∠BMC ＝135°，⑦2BMMC =，这七个结论中，“知二得五”【A 型，X 型，三平行模型】1.如图，在△ABC 中，EF ∥DC ，∠AFE =∠B ，AE =6，ED =3，AF =8，则AC =_________，CDBC=_________．F E DCBABCDE FA2．如图，AB ∥CD ，线段BC ，AD 相交于点F ，点E 是线段AF 上一点且满足∠BEF =∠C ，其中AF =6，DF =3，CF =2，则AE =_________．3.如图，在Rt △ABD 中，过点D 作CD ⊥BD ，垂足为D ，连接BC 交AD 于点E ，过点E 作EF ⊥BD 于点F ，若AB =15，CD =10，则BF :FD =_____________．FEBCAN MEDCBA4.如图，在□ABCD 中，E 为BC 的中点，连接AE ，AC ，分别交BD 于M ，N ，则BM :DN =_____________．5.如图所示，AB ∥CD ，AD ，BC 相交于点E ，过E 作EF ∥AB 交BD 于点F ．则下列结论：①△EFD ∽△ABD ；②EF BF CD BD =；③1EF EF FD BF AB CD BD BD +=+=；④111AB CD EF+=．其中正确的有___________． F EDCBA图26.在△ABC 中，AB=9，AC=6，点M 在边AB 上，且AM=3，点N 在AC 边上.当AN= 时，△AMN 与原三角形相似.7.如图，在△ABC 中，∠C=90°，AC=8，BC=6，D 是边AB 的中点，现有一点P 位于边AC 上，使得△ADP 与△ABC 相似，则线段AP 的长为 .8.如图，已知O 是坐标原点，点A.B 分别在y x 、轴上，OA=1，OB=2，若点D 在x 轴下方，且使得△AOB 与△OAD 相似，则这样的点D 有个.9.如图，在Rt △ACB 中，∠C=90°，AC=16cm ，BC=8cm ，动点P 从点C 出发，沿CA 方向运动；动点Q 同时从点B 出发，沿BC 方向运动,如果点P 的运动速度均为4cm/s ，Q 点的运动速度均为2cm/s ，那么运动几秒时，△ABC 与△PCQ 相似.10.将△ABC的纸片按如图所示的方式折叠，使点B落地边AC上，记为点B＇，折叠痕为EF，已知AB=AC=8，BC=10,若以点B＇.F.C为顶点的三角形与△ABC相似，那么BF的长度是.11.如图,在中,,,是角平分线.求证:(1)(2)12.如图，四边形中，平分，，，为的中点．（1）求证：；（2）与有怎样的位置关系？试说明理由；（3）若，，求的值．13.如图，在中，为上一点，，，，于，连接．（1）求证：；（2）找出图中一对相似三角形，并证明．14.如图，在中，，分别是，上的点，，的平分线交于点，交于点．（1）试写出图中所有的相似三角形，并说明理由（2）若，求的值．15.如图，在平行四边形ABCD中，对角线AC、BD交于点O．M为AD中点，连接CM交BD于点N，且ON=1．（1）求BD的长；（2）若△DCN的面积为2，求四边形ABNM的面积．16.如图,在中,于点,于点,连接,求证: ..17.如图,在△ABC中,DE∥FG∥BC,AD∶DF∶FB=1∶2∶3,若EG=3,则AC=________.图1 图218..如图,平行于BC的直线DE把△ABC分成的两部分面积相等.则ADAB= _________.19.如图所示，AD=DF=FB, DE∥FG∥BC,则S1:S2:S3=__________.20.如图，在矩形ABCD中，对角线AC，BD相交于点O，OE⊥BC于点E，连接DE交OC于点F，作FG⊥BC于点G，则线段BG与GC的数量关系是___.21. 如图，已知点C 为线段AB 的中点，CD ⊥AB 且CD=AB=4，连接AD ，BE ⊥AB ，AE 是∠DAB 的平分线，与DC 相交于点F ，EH ⊥DC 于点G ，交AD 于点H ，则HG 的长为 .22.如图1，在△ABC 中，点D 、E 、Q 分别在边AB 、AC 、BC 上，且DE ∥BC ，AQ 交DE 于点P ．（1）求证：；（2）如图，在△ABC 中，∠BAC =90°，正方形DEFG 的四个顶点在△ABC 的边上，连接AG 、AF ，分别交DE 于M 、N 两点．如图2，若AB =AC =1，直接写出MN 的长；如图3，求证MN 2=DM【母子型】1、已知：如图，△ABC 中，∠ACB=90°，CD ⊥AB 于D ，S △ABC=20，AB=10。

相似三角形的九大模型

相似三角形的九大模型模型一：A 字型1．如图，在ABC △中，:2:3AF FB =，延长BC 至点D ，使得2BC CD =，求AEEC的值．2．如图，在ABC △中，已知CD 为边AB 上的高，正方形EFGH 的四个顶点分别在ABC △上，求证：111AB CD EF+=．3．如图，在矩形ABCD 中，2AB =，3BC =，点E 、F 、G 、H 分别在矩形ABCD 的各边上，EF HG AC ∥∥，EH FG BD ∥∥，则四边形EFGH 的周长是_________．4．如图，ABC △中，M 是AC 的中点，E 是AB 上一点，且3BE AE =，求BCCD的值．模型二：反A 字型5．如图，D 、E 分别为ABC △的边AB 、AC 上的点，且ADE ACB ∠=∠．（1）求证：AD AB AE AC ⋅=⋅；（2）如果ABC △的面积为m ，3DE =，5BC =，求ADE △的面积．6．如图，在ABC △中，点D 、E 分别在边AB 、AC 上，DE 、BC 的延长线相交于点F ，且EF DF BF CF ⋅=⋅．（1）求证：AD AB AE AC ⋅=⋅；（2）当12AB =，9AC =，8AE =时，求BD 的长与ADEECFS S △△的值．7．将三角形纸片()ABC △按如图所示的方式折叠，使点C 落在AB 边上的点D ，折痕为EF ．已知3AB AC ==，4BC =，若以点B 、D 、F 为顶点的三角形与ABC △相似，那么CF 的长度是（）A ．2B ．127或2 C ．127D ．125或2 8．将ABC △纸片按如图所示的方式折叠，使点B 落在边AC 上，记为点B '，折痕为EF ．已知6AB AC ==，8BC =．（1）求ABC △的周长；（2）若以点B '，F ，C 为顶点的三角形与ABC △相似，求BF 的长．9．如图，在ABC △中，6AB =，8BC =．点D 以每秒1个单位长度的速度由B 向A 运动，同时点E 以每秒2个单位长度的速度由C 向B 运动，当点E 停止运动时，点D 也随之停止．设运动时间为t 秒，当以B ，D ，E 为顶点的三角形与ABC △相似时，求t 的值．10．如图，在锐角三角形ABC 中，点D ，E 分别在边AC ，AB 上，AG BC ⊥于点G ，AF DE ⊥于点F ，EAF GAC ∠=∠．（1）求证：ADE ABC △∽△；（2）若3AD =，5AB =，求AFAG的值．模型三：8字型11．如图，E 是ABCD □的边BA 延长线上一点，连接EC ，交AD 于点F ．在不添加辅助线的情况下，请你写出图中所有的相似三角形，并任选一对相似三角形给予证明．12．如图，平行四边形ABCD 中，过点B 的直线与对角线AC 、边AD 分别交于点E 和F ．过点E 作EG BC ∥，交AB 于G ，则图中相似三角形有（）A ．7对B ．6对C ．5对D ．4对13．已知DE AB ∥，2OA OC OE =⋅，求证：AD BC ∥．14．学校门口的栏杆如图所示，栏杆从水平位置BD 绕O 点旋转到AC 位置，已知AB BD ⊥，CD BD ⊥，垂足分别为B ，D ，4m AO =， 1.6m AB =，1m CO =，则栏杆C 端应下降的垂直距离CD 为（）A ．0.2mB ．0.3mC ．0.4mD ．0.5m15．如图，E ，F 是平行四边形ABCD 对角线AC 上两点，14AE CF AC ==．连接DE ，DF 并延长，分别交AB 、BC 于点G 、H ，连接GH ，则ADGBGHS S ∆∆的值为（）A ．12B ．23C ．34D ．116．如图所示，在平行四边形ABCD 中，AC 与BD 相交于点O ，E 为OD 的中点，连接AE 并延长交DC 于点F ，则:DF FC =（）A ．1:4B ．1:3C ．2:3D ．1:217．如图，在矩形ABCD 中，E 是边AB 的中点，连接DE 交对角线AC 于点F ，若4AB =，3AD =，则CF 的长为．18．如图，直线a b ∥，:3:5AF FB =，:3:1BC CD =，则:AE EC 为（）A ．5:12B ．9:5C ．12:5D ．3:219．如图，在平行四边形ABCD 中，E 是BA 延长线上一点，CE 分别与AD ，BD 交于点G ，F ．下列结论：①EG AG GC GD =②EF BF FC FD =；③FC BFGF FD=；④2CF GF EF =⋅，其中正确的个数是（）A ．1B ．2C ．3D ．4模型四：蝴蝶型20．如图，四边形ABCD 的对角线AC 、BD 相交于O ，且将这个四边形分成①、②、③、④四个三角形．若::OA OC OB OD =，则下列结论中一定正确的是（）A ．①与②相似B ．①与③相似C ．①与④相似D ．③与④相似21．如图，AB CD ∥，线段BC 、AD 相交于点F ，点E 是线段AF 上一点，且满足BEF C ∠=∠，其中9AF =，3DF =，2CF =，则AE =_________．FEDCBA22．如图，在ABC △中，AB AC =，AD BC ⊥，DE AC ⊥，M 为DE 的中点，AM 与BE 相交于点N ，AD 与BE 相交于点F ．求证：（1）DE ADCE CD=；（2）BCE ADM △∽△；（3）猜想AM 与BE 的位置关系，并说明理由．23．点D 为Rt ABC △的斜边AB 上一点，点E 在AC 上，连接DE ，CD ，且ADE BCD ∠=∠，CF CD ⊥交DE 的延长线于点F ，连接AF（1）如图1，若AC BC =，求证：AF AB ⊥；（2）如图2，若AC BC ≠，当点D 在AB 上运动时，求证：AF AB ⊥．N FMEDCBA模型五：共边共角型24．如图，在ABC △中，点D 是边AB 上的一点，ADC ACB ∠=∠，2AD =，6BD =，则边AC 的长为（）A ．2B ．4C ．6D ．825．已知：如图，ABC △中，AD 是BAC ∠的平分线，AD 的垂直平分线交AD 于E ，交BC 的延长线于F ．求证：（1）2FD FB FC =⋅；（2）22::AB AC BF CF =．26．如图，在ABC △中，AB AC a ==，()BC b a b =>．在ABC △内依次作CBD A ∠=∠，DCE CBD ∠=∠，EDF DCE ∠=∠．则EF 等于（）A ．32b aB ．32a bC ．43b aD ．43a b27．如图，在矩形ABCD 中，对角线AC 、BD 相交于点G ，E 为AD 的中点，连接BE 交AC 于F ，连接FD ，若90BFA ∠=︒，则下列四对三角形：①BEA △与ACD △；②FED △与DEB △；③CFD △与ABG △；④ADF △与CFB △．其中相似的为（）A ．①④B ．①②C ．②③④D ．①②③28．如图，点P 是菱形ABCD 的对角线BD 上一点，连结CP 并延长，交AD 于E ，交BA 的延长线于点F ．试问：（1）图中APD △与哪个三角形全等？并说明理由．（2）猜想：线段PC 、PE 、PF 之间存在什么关系？并说明理由．模型六：射影定理29．在Rt ABC △中，90C ∠=︒，CD AB ⊥于D ，下列等式中错误的是（） A ．2AD BD CD ⋅= B ．AC BD CB AD ⋅=⋅C ．2AC AD AB =⋅ D ．222AB AC BC =+30．在Rt ABC △中，CD 是斜边AB 上的高．（1）求证：2CD AD DB =⋅；（2）求证：2CB DB AB =⋅．31．如图，在Rt ABC △中，90CAB ∠=︒，30B ∠=︒，AD CB ⊥于D ，3CD =，则CB = ．32．如图，90ADC ACB ∠=∠=︒，ACD B ∠=∠，5AC =，6AB =，则AD = ．33．如图，在Rt ABC △中，CD 为斜边AB 上的高，如果3AC =，6AB =，求BD 的值．34．在Rt ABC △中，CD 是斜边AB 上的高线，DE AC ⊥于E ，DF BC ⊥于F ，求证：33BC BFAC AE=．35．在ABC △中，90ACB ∠=︒，CE AB ⊥于点E ，D 在AB 延长线上，且DCB A ∠=∠，:1:2BD CD =，AE =BCD S △．36．如图，在Rt ABC △中，90ABC ∠=︒，BA BC =．点D 是AB 的中点，连接CD ，过点B 作BG CD ⊥，分别交CD 、CA 于点E 、F ，与过点A 且垂直于AB 的直线相交于点G ，连接DF ．给出以下四个结论： ①AG FGAB FB=； ②点F 是GE 的中点；③AF AB =； ④5ABC BDF S S =△△，其中正确的结论序号是．模型七：三垂直模型37．如图，矩形ABCD中，E是BC的中点，连接AE，过点E作EF AE⊥交DC于点F，连接AF．设ABkAD=，下列结论：（1）ABE ECF△∽△，（2）AE平分BAF∠，（3）当1k=时，ABE ADF△∽△，其中结论正确的是（）A．（1）（2）（3）B．（1）（3）C．（1）（2）D．（2）（3）38．如图，一个长方形的ABCD长为8cm，宽为6cm，E为边CD上的一点，现把Rt ADE△沿AE对折使得D点恰好落在边BC上的中点D'处．（1）请说明Rt ABD'△与Rt ECD'△相似；（2）求CE的长．39．(1) 如图1 ，已知AB l∠=︒，ACD⊥，垂足分别为B、E，且C是l上一点，90⊥，DE l△∽△；求证：ABC CED(2) 如图2 ，在四边形ABCD中，已知90BC=，10CD=，∠=︒，3ABCAB=，4DA=BD的长．40．如图，在直角梯形ABCD中，//∠=︒，AD BC，90BC=，CD=BAD=，3 P在线段AB上．若PCD△是以点P为直角顶点的直角三角形，则AP=．模型八：一线三等角41．如图，ABC △中，8AB AC ==，D 为BC 上一点，3BD =，30ADE B ∠=∠=︒，则AE 的长为_________．42．如图，D 是等边ABC △边AB 上的一点，且:1:2AD DB =，现将ABC △折叠，使点C 与D 重合，折痕为EF ，点E ，F 分别在AC 和BC 上，则:CE CF =（）A ．34B ．45C ．56D ．6743．已知：如图，ABC △中，90BAC ∠=︒，1AB AC ==，点D 是BC 边上的一个动点（不与B ，C 点重合），45ADE ∠=︒．（1）求证：ABD DCE △∽△；（2）设BD x =，AE y =，求y 关于x 的函数关系式；（3）当ADE △是等腰三角形时，求AE 的长．44．如图，四边形ABCD 中，AD BC ∥，AB DC =，3cm AD =，7cm BC =，60B ∠=︒，P 为BC 边上一点（不与B ，C 重合），连接AP ，过P 点作PE 交DC 于E ，使得APE B ∠=∠．（1）求证：ABP PCE △∽△；（2）求AB 的长；（3）在边BC 上是否存在一点P ，使得:5:3DE EC =？如果存在，求BP 的长；如果不存在，请说明理由．45．如图，M 为线段AB 上一点，AE 与BD 交于点C ，DME A B α∠=∠=∠=，且DM 交AE 于点F ，ME 交BD 于点G ．（1）写出图中的三对相似三角形；（2）连接FG ，当AM MB =时，求证：MFG BMG △∽△；（3）在（2）条件下，若45α=︒，AB =，3AF =，求FG 的长．模型九：手拉手46．如图，12∠=∠，要使ABC ADE △∽△，只需要添加一个条件即可，这个条件不可能是（）A ．B D ∠=∠ B ．C E ∠=∠ C ．AD ABAE AC= D ．AC BCAE DE= 47．如图，把ABC △绕点A 旋转到ADE △，当点D 刚好落在BC 上时，连结CE ，设AC ，DE ，相交于点F ，则图中相似三角形（不含全等）的对数有（）A ．1B ．2C ．3D ．448．如图，在ABC △中，ABC C ∠=∠，将ABC △绕点B 逆时针旋转得DBE △，点E 在AC 上，若3ED =，1EC =，则EB =（）AB ．32C D ．249．将一幅三角尺（Rt ACB △中，90ACB ∠=︒，60B ∠=︒，在Rt EDF △中，90EDF ∠=︒，45E ∠=︒）如图摆放，点D 为AB 的中点，DE 交AC 于点P ，DF 经过点C ，将EDF △绕点D 顺时针方向旋转角(060)αα︒<<︒，DE '交AC 于点M ，DF '交BC 于点N ，则PMCN的值为（）AB C ．12D 50．如图，点A 在线段BD 上，在BD 的同侧作30︒角的直角三角形ABC 和30︒角的直角三角形ADE ，CD 与BE ，AE 分别交于点P ，M ，连接PA 对于下列结论：①BAE CAD △∽△；②M P M D M A M E ⋅=⋅；③图中有5对相似三角形；④AP CD ⊥其中结论正确的个数是（）A ．1个B ．2个C ．4个D ．3个51．如图，ABC △为等腰直角三角形，90BAC ∠=︒，1BC =，E 为直角边AB 上任意一点，以线段CE 为斜边作等腰Rt CDE △，连接AD ，下列说法：①AC ED ⊥；②BCE ACD ∠=∠；③AED ECB △∽△；④AD BC ∥；⑤四边形ABCD 面积的最大值为38，其中正确的是__________．52．如图，ABC △中，45BAC ∠=︒，30ACB ∠=︒，将ABC △绕点A 顺时针旋转得到11AB C △，当点1C 、1B 、C 三点共线时，旋转角为α，连接1BB ，交AC 于点D ，下面结论：①1AC C △为等腰三角形；②1AB D BCD △∽△；③135α=︒；④1CA CB =；⑤1AB B C =中，正确结论的个数是（）A ．2个B ．3个C ．4个D ．5个53．如图，在正方形ABCD 中，AEF △的顶点E ，F 分别在BC ，CD 边上，高AG 与正方形的边长相等，连接BD 分别交AE ，AF 于点M ，N ，下列说法： ①45EAF ∠=︒；②连接MG ，NG ，则MGN △为直角三角形； ③AMN AFE △∽△；④若2BE =，3FD =，则MN（）A ．4B ．3C ．2D ．154．如图，在Rt ABC △中，90ACB ∠=︒，BC aAC b=，CD AB ⊥于点D ，点E 是直线AC 上一动点，连接DE ，过点D 作FD ED ⊥，交直线BC 于点F ．（1）探究发现：如图①，若a b =，点E 在线段AC 上，则DEDF= ．（2）数学思考①如图②，若点在线段AC 上，则DEDF= ，（用含a ，b 的代数式表示）； ②当点E 在直线AC 上运动时，①中的结论是否仍然成立？请仅就图③的情形给出证明；（3）拓展应用：若AC BC =DF =CF 的长．。

中考中相似三角形的常见模型及典型例题

1.相似的基本模型：
（1）A字、8字；（3）角平分线；（5）一线三等角；（7）内接矩形；
2.基本辅助线：
（2）反A、反8；（4）旋转型；（6）线束模型；（8）相似比与面积比。
（1）作平行线构造A字、8字；（2）作垂线构造直角三角形相似
3.基本问题类型：
（1）证明相似；
（2）求线段长；
（1）若点P在线段CB上，且BP=6，求线段CQ的长；（2）若BP=x，CQ=y,求y与x的关系式，并求出自变量x的取值范围。
例 9 如图,△ABC是等边三角形,点D、E分别在BC、AC上,且BD=CD，
AD与BE相交于点F. （1）求证：△ABD≌△BCE；（2）求证：△ABE∽△FAE；
（3）当AF=7，DF=1时，求BD的长。
（量得BN=70cm）
C
C
DME
DME
A PN F
B
A PN F
B
1.如图,△ABC是一块锐角三角形余料,边BC=120毫米,高AD=80 毫米，要把它加工成正方形零件，使正方形的一边在BC上，其余两个顶点分别在AB、AC上，这个正方形零件的边长是多少？
A
A
M
EN
H
KG
∟
B Q DPC
B
E
DF C
E
AB AC BC
B
C （2）公共边平方=共线边之积：AC 2 AE • AB
反A字型【模型2】反“A”字型＆反“8”字型
（Ⅱ）DE拉下来经过点C，又称之为母子型，为相似常考模型：
A
A
E
B
C
AC2 AED • BC
AC2 CD • CB
AD2 BD • CD

相似三角形的九大模型

相似三角形的九大模型1.在三角形ABC中，已知2.在三角形ABC中，CD为边AB上的高，正方形EFGH 的四个顶点分别在三角形ABC上，证明：111+EF^2=AB^2+BC^2+AC^2.3.在矩形ABCD中，AB=2，BC=3，点E、F、G、H分别在矩形ABCD的各边上，且EF∥HG∥AC，EH∥FG∥BD，则四边形EFGH的周长是10.4.在三角形ABC中，M是AC的中点，E是AB上一点，且BE=3AE，求BC的值。

5.在三角形ABC中，D、E分别为边AB、AC上的点，且∠ADE=∠ACB。

证明：AD×AB=AE×AC。

如果三角形ABC的面积为m，DE=3，BC=5，求三角形ADE的面积。

6.在三角形ABC中，点D、E分别在边AB、AC上，DE、BC的延长线相交于点F，且EF×DF=BF×CF。

证明：AD×AB=AE×AC。

当AB=12，AC=9，AE=8时，求BD的长与△ADE的面积。

7.将三角形纸片△ABC按如图所示的方式折叠，使点C落在AB边上的点D，折痕为EF。

已知AB=AC=3，BC=4，若以点B、D、F为顶点的三角形与△ABC相似，那么CF的长度是2/7.8.将三角形ABC纸片按如图所示的方式折叠，使点B落在边AC上，记为点B'，折痕为EF。

已知AB=AC=6，BC=8.求△ABC的周长。

若以点B'、F、C为顶点的三角形与△XXX 相似，求BF的长。

9.在三角形ABC中，AB=6，BC=8.点D以每秒1个单位长度的速度由B向A运动，同时点E以每秒2个单位长度的速度由C向B运动，当点E停止运动时，点D也随之停止。

设运动时间为t秒，当以B、D、E为顶点的三角形与△ABC相似时，求t的值。

10.在锐角三角形ABC中，AG⊥BC于点G，点D、E分别在XXX、AB上，XXX⊥DE于点F，且∠EAF=∠GAC。

证明：△ADE∽△ABC。

相似三角形常见模型总结

相关练习：
1、如图，在△ ABC 中， AB AC 8 ， BC 10 ， D 是 BC 边上的一个动点，点 E 在 AC 边上，且
ADE C ．
A
E
F
B
D
C
例 2：（ 1）在 ABC 中， AB AC 5 ， BC 8 ，点 P 、 Q 分别在射线 CB 、 AC 上（点 P 不与点 C 、点 B 重合），且保持 APQ ABC .
①若点 P 在线段 CB 上（如图），且 BP 6 ，求线段 CQ 的长； ②若 BP x ， CQ y ，求 y 与 x 之间的函数关系式，并写出函数的定义域；
求证： BE 2 EF EG ．
相关练习：
1、如图，已知 AD 为△ ABC 的角平分线， EF 为 AD 的垂直平分线．求证： FD 2 FB FC ．
.
2、已知： AD是 Rt △ ABC中∠ A 的平分线，∠ C=90°， EF 是 AD的垂直平分线交 AD于 M， EF、 BC的延长线交于一点 N。求证： (1) △ AME∽△ NMD; (2)ND 2 =NC· NB
①当点 Q 在线段 DC 的延长线上时，设 AP＝ x， CQ＝ y，求 y 关于 x 的函数解析式，并写出函数的
定义域；
②当 CE＝ 1 时，写出 AP 的长．
A
A
D
D
B
B
C
C
例 4：如图，在梯形 ABCD 中， AD ∥ BC ， AB CD BC 6 ， AD 3 ．点 M 为边 BC 的中点，以 M 为顶点作 EMF B ，射线 ME 交腰 AB 于点 E ，射线 MF 交腰 CD 于点 F ，联结 EF ．（ 1）求证：△ MEF ∽△ BEM ；（ 2）若△ BEM 是以 BM 为腰的等腰三角形，求 EF 的长；（ 3）若 EF CD ，求 BE 的长．

模型05 相似三角形中的常见五种基本模型(解析版)

模型探究相似三角形考查范围广，综合性强，其模型种类多，其中有关一线三垂直模型在前面的专题已经很详细的讲解，这里就不在重复.模型一、A字型相似模型A字型（平行）反A字型（不平行）模型二、8字型与反8字型相似模型模型三、AX型相似模型（A字型及X字型两者相结合）模型四、共边角相似模型（子母型）模型五、手拉手相似模型例题精讲考点一、A字相似模型【例1】．如图，在△ABC中，∠A＝78°，AB＝4，AC＝6，将△ABC沿图示中的虚线剪开，剪下的阴影三角形与原三角形不相似的是（）A．B．C．D．解：A、阴影部分的三角形与原三角形有两个角相等，故两三角形相似，故本选项错误；B、阴影部分的三角形与原三角形有两个角相等，故两三角形相似，故本选项错误；C、两三角形的对应边不成比例，故两三角形不相似，故本选项正确．D、两三角形对应边成比例且夹角相等，故两三角形相似，故本选项错误；故选：C．变式训练【变式1-1】．如图，在△ABC中，DE∥BC，AH⊥BC于点H，与DE交于点G．若，则＝．解：∵，∴，∵DE∥BC，∴△ADE∽△ABC，∴，故答案为．【变式1-2】.如图，在△ABC中，M是AC的中点，E是AB上一点，AE＝AB，连接EM并延长，交BC的延长线于D，则＝__________.解：如图，过C点作CP∥AB，交DE于P，∵PC∥AE，∴△AEM∽△CPM，∴＝，∵M是AC的中点，∴AM＝CM，∴PC＝AE，∵AE＝AB，∴CP＝AB，∴CP＝BE，∵CP∥BE，∴△DCP∽△DBE，∴＝＝，∴BD＝3CD，∴BC＝2CD，即＝2．【变式1-3】．如图，在△ABC中，点D在边AB上，AD＝9，BD＝7．AC＝12．△ABC的角平分线AE交CD于点F．（1）求证：△ACD∽△ABC；（2）若AF＝8，求AE的长度．解：（1）∵AD＝9，BD＝7，AC＝12，∴AB＝AD+BD＝16，∵＝＝，＝＝，∴＝，∵∠BAC＝∠CAD，∴△ACD∽△ABC；（2）由（1）可知，△ACD∽△ABC，∴∠ABE＝∠ACF，∵AE平分∠BAC，∴∠BAE＝∠CAF，∴△ABE∽△ACF，∴＝，即＝，∴AE＝＝．考点二、8字与反8字相似模型【例2】．如图，AG∥BD，AF：FB＝1：2，BC：CD＝2：1，求的值解：∵AG∥BD，∴△AFG∽△BFD，∴＝，∵，∴CD＝BD，∴，∵AG∥BD，∴△AEG∽△CED，∴．变式训练【变式2-1】．如图，AB∥CD，AE∥FD，AE、FD分别交BC于点G、H，则下列结论中错误的是（）A．B．C．D．解：A、∵AB∥CD，∴＝，故本选项不符合题目要求；B、∵AE∥DF，∴△CEG∞△CDH，∴＝，∴＝，∵AB∥CD，∴＝，∴＝，∴＝，∴＝，故本选项不符合题目要求；∵AB∥CD，AE∥DF，∴四边形AEDF是平行四边形，∴AF＝DE，∵AE∥DF，∴，∴＝，故本选项不符合题目要求；D、∵AE∥DF，∴△BFH∞△BAG，∴，故本选项符合题目要求；故选：D．【变式2-2】．如图，在平行四边形ABCD中，E为边AD的中点，连接AC，BE交于点F．若△AEF的面积为2，则△ABC的面积为（）A．8B．10C．12D．14解：如图，∵四边形ABCD是平行四边形，∵EA∥BC，∴△AEF∽△CBF，∵AE＝DE＝AD，CB＝AD，∴＝＝＝＝，∴AF＝AC，EF＝BF，＝S△ABC，∴S△ABF＝S△ABF＝×S△ABC＝S△ABC，∴S△AEF＝2，∵S△AEF＝6S△AEF＝6×2＝12，故选：C．∴S△ABC【变式2-3】.如图，锐角三角形ABC中，∠A＝60°，BE⊥AC于E，CD⊥AB于D，则DE：BC＝1：2．解：如图，∵在△ADC中，∠A＝60°，CD⊥AB于点D，∴∠ACD＝30°，∴＝．又∵在△ABE中，∠A＝60°，BE⊥AC于E，∴∠ABE＝30°，∴＝，∴＝．又∵∠A＝∠A，∴△ADE∽△ACB，∴DE：BC＝AD：AC＝1：2．故答案是：1：2．考点三、AX型相似模型（A字型及X字型两者相结合）【例3】.如图，在△ABC中，点D和E分别是边AB和AC的中点，连接DE，DC与BE交于点O，若△DOE的面积为1，则△ABC的面积为（）A．6B．9C．12D．13.5解：∵点D和E分别是边AB和AC的中点，∴O点为△ABC的重心，∴OB＝2OE，＝2S△DOE＝2×1＝2，∴S△BOD＝3，∴S△BDE∵AD＝BD，＝2S△BDE＝6，∴S△ABE∵AE＝CE，＝2S△ABE＝2×6＝12．故选C．∴S△ABC变式训练【变式3-1】.如图，DE是△ABC的中位线，F为DE中点，连接AF并延长交BC于点G，＝1，则S△ABC＝24．若S△EFG解：方法一：∵DE是△ABC的中位线，∴D、E分别为AB、BC的中点，如图过D作DM∥BC交AG于点M，∵DM∥BC，∴∠DMF＝∠EGF，∵点F为DE的中点，∴DF＝EF，在△DMF和△EGF中，，∴△DMF≌△EGF（AAS），＝S△EGF＝1，GF＝FM，DM＝GE，∴S△DMF∵点D为AB的中点，且DM∥BC，∴AM＝MG，∴FM＝AM，＝2S△DMF＝2，∴S△ADM∵DM为△ABG的中位线，∴＝，＝4S△ADM＝4×2＝8，∴S△ABG＝S△ABG﹣S△ADM＝8﹣2＝6，∴S梯形DMGB＝S梯形DMGB＝6，∴S△BDE∵DE是△ABC的中位线，＝4S△BDE＝4×6＝24，∴S△ABC方法二：连接AE，∵DE是△ABC的中位线，∴DE∥AC，DE＝AC，∵F是DE的中点，∴＝，∴＝＝，＝1，∵S△EFG＝16，∴S△ACG∵EF∥AC，∴＝＝，∴＝＝，＝S△ACG＝4，∴S△AEG＝S△ACG﹣S△AEG＝12，∴S△ACE＝2S△ACE＝24，故答案为：24．∴S△ABC【变式3-2】．如图：AD∥EG∥BC，EG交DB于点F，已知AD＝6，BC＝8，AE＝6，EF ＝2．（1）求EB的长；（2）求FG的长．解：（1）∵EG∥AD，∴△BAD∽△BEF，∴＝，即＝，∴EB＝3．（2）∵EG∥∥BC，∴△AEG∽△ABC，∴＝，即＝，∴EG＝，∴FG＝EG﹣EF＝．【变式3-3】.如图，已知AB∥CD，AC与BD相交于点E，点F在线段BC上，，．（1）求证：AB∥EF；：S△EBC：S△ECD．（2）求S△ABE（1）证明：∵AB∥CD，∴＝＝，∵，∴＝，∴EF∥CD，∴AB∥EF．（2）解：设△ABE的面积为m．∵AB∥CD，∴△ABE∽△CDE，∴＝（）2＝，＝4m，∴S△CDE∵＝＝，＝2m，∴S△BEC：S△EBC：S△ECD＝m：2m：4m＝1：2：4．∴S△ABE模型四、子母型相似模型【例4】.如图，点C，D在线段AB上，△PCD是等边三角形，且∠APB＝120°，求证：（1）△ACP∽△PDB，（2）CD2＝AC•BD．证明：（1）∵△PCD是等边三角形，∴∠PCD＝∠PDC＝∠CPD＝60°，∴∠ACP＝∠PDB＝120°，∵∠APB＝120°，∴∠APC+∠BPD＝60°，∵∠CAP+∠APC＝60°∴∠BPD＝∠CAP，∴△ACP∽△PDB；（2）由（1）得△ACP∽△PDB，∴，∵△PCD是等边三角形，∴PC＝PD＝CD，∴，∴CD2＝AC•BD．变式训练【变式4-1】.如图，点P在△ABC的边AC上，要判断△ABP∽△ACB，添加一个条件，不正确的是（）A．∠ABP＝∠C B．∠APB＝∠ABC C．D．解：在△ABP和△ACB中，∠BAP＝∠CAB，∴当∠ABP＝∠C时，满足两组角对应相等，可判断△ABP∽△ACB，故A正确；当∠APB＝∠ABC时，满足两组角对应相等，可判断△ABP∽△ACB，故B正确；当时，满足两边对应成比例且夹角相等，可判断△ABP∽△ACB，故C正确；当时，其夹角不相等，则不能判断△ABP∽△ACB，故D不正确；故选：D．【变式4-2】.如图，在△ABC中，点D在AC边上，连接BD，若∠ABC+∠BDC＝180°，AD＝2，CD＝4，则AB的长为（）A．3B．4C．D．2解：∵∠ABC+∠BDC＝180°，∠ADB+∠BDC＝180°，∴∠ADB＝∠ABC，∵∠A＝∠A，∴△ABC∽△ADB，∴，∵AD＝2，CD＝4，∴，∴AB2＝12，∴AB＝2或﹣2（不合题意，舍去），故选：D．【变式4-3】．如图，边长为4的正方形，内切圆记为圆O，P为圆O上一动点，则PA+PB的最小值为2．解：设⊙O半径为r，OP＝r＝BC＝2，OB＝r＝2，取OB的中点I，连接PI，∴OI＝IB＝，∵，，∴，∠O是公共角，∴△BOP∽△POI，∴，∴PI＝PB，∴AP+PB＝AP+PI，∴当A、P、I在一条直线上时，AP+PB最小，作IE⊥AB于E，∵∠ABO＝45°，∴IE＝BE＝BI＝1，∴AE＝AB﹣BE＝3，∴AI＝＝，∴AP+PB最小值＝AI＝，∵PA+PB＝（PA+PB），∴PA+PB的最小值是AI＝＝2．故答案是2．模型五、手拉手相似模型【例5】.如图，△ABC与△DEF均为等边三角形，O为BC、EF的中点，则AD：BE的值为．解：连接OA、OD，∵△ABC与△DEF均为等边三角形，O为BC、EF的中点，∴AO⊥BC，DO⊥EF，∠EDO＝30°，∠BAO＝30°，∴OD：OE＝OA：OB＝：1，∵∠DOE+∠EOA＝∠BOA+∠EOA即∠DOA＝∠EOB，∴△DOA∽△EOB，∴OD：OE＝OA：OB＝AD：BE＝：1＝，故答案为：．变式训练【变式5-1】.如图，在△ABC与△ADE中，∠BAC＝∠DAE，∠ABC＝∠ADE．求证：（1）△BAC∽△DAE；（2）△BAD∽△CAE．证明：（1）∵∠BAC＝∠DAE，∠ABC＝∠ADE．∴△BAC∽△DAE；（2）∵△BAC∽△DAE，∴，∴，∵∠BAC＝∠DAE，∴∠BAD＝∠CAE，∴△BAD∽△CAE．【变式5-2】.如图，点D是△ABC内一点，且∠BDC＝90°，AB＝2，AC＝，∠BAD＝∠CBD＝30°，AD＝．解：如图，过点A作AB的垂线，过点D作AD的垂线，两垂线交于点M，连接BM，∵∠BAD＝30°，∴∠DAM＝60°，∴∠AMD＝30°，∴∠AMD＝∠DBC，又∵∠ADM＝∠BDC＝90°，∴△BDC∽△MDA，∴，又∠BDC＝∠MDA，∴∠BDC+∠CDM＝∠ADM+∠CDM，即∠BDM＝∠CDA，∴△BDM∽△CDA，∴＝，∵AC＝，∴BM＝3，在Rt△ABM中，AM＝＝＝，∴AD＝AM＝．【变式5-3】．如图，在四边形ABCD中，AE⊥BC，垂足为E，∠BAE＝∠ADC，BE＝CE＝2，CD＝5，AD＝kAB（k为常数），则BD的长为．（用含k的式子表示）解：如图中，∵AE⊥BC，BE＝EC，∴AB＝AC，将△ABD绕点A逆时针旋转得到△ACG，连接DG．则BD＝CG，∵∠BAD＝∠CAG，∴∠BAC＝∠DAG，∵AB＝AC，AD＝AG，∴∠ABC＝∠ACB＝∠ADG＝∠AGD，∴△ABC∽△ADG，∵AD＝kAB，∴DG＝kBC＝4k，∵∠BAE+∠ABC＝90°，∠BAE＝∠ADC，∴∠ADG+∠ADC＝90°，∴∠GDC＝90°，∴CG＝＝．∴BD＝CG＝，故答案为：．实战演练1．如图，已知DE∥BC，EF∥AB，则下列比例式中错误的是（）A．＝B．C．D．解：A、∵EF∥AB，∴＝，∵DE∥BC，∴＝，∴＝，故A正确，B、易知△ADE∽△EFC，∴＝，∴＝，故B正确．C、∵△CEF∽△CAB，∴＝，∴＝，故C正确．D、∵DE∥BC，∴＝，显然DE≠CF，故D错误．故选：D．2．如图，梯形ABCD中，AD∥BC，∠B＝∠ACD＝90°，AB＝2，DC＝3，则△ABC与△DCA的面积比为（）A．2：3B．2：5C．4：9D．：解：∵AD∥BC，∴∠ACB＝∠DAC又∵∠B＝∠ACD＝90°，∴△CBA∽△ACD＝＝＝，∵＝（）2＝∴△ABC与△DCA的面积比为4：9．故选：C．3．如图，菱形ABCD中，E点在BC上，F点在CD上，G点、H点在AD上，且AE∥HC ∥GF．若AH＝8，HG＝5，GD＝4，则下列选项中的线段，何者长度最长？（）A．CF B．FD C．BE D．EC解：∵AH＝8，HG＝5，GD＝4，∴AD＝8+5+4＝17，∵四边形ABCD为菱形，∴BC＝CD＝AD＝17，∵AE∥HC，AD∥BC，∴四边形AECH为平行四边形，∴CE＝AH＝8，∴BE＝BC﹣CE＝17﹣8＝9，∵HC∥GF，∴＝，即＝，解得：DF＝，∴FC＝17﹣＝，∵＞9＞8＞，∴CF长度最长，故选：A．4．如图，在△ABC中，BC＝6，E，F分别是AB，AC的中点，动点P在射线EF上，BP 交CE于点D，∠CBP的平分线交CE于点Q，当CQ＝CE时，EP+BP的值为（）A．6B．9C．12D．18解：如图，延长BQ交射线EF于M，∵E、F分别是AB、AC的中点，∴EF∥BC，∴∠M＝∠CBM，∵BQ是∠CBP的平分线，∴∠PBM＝∠CBM，∴∠M＝∠PBM，∴BP＝PM，∴EP+BP＝EP+PM＝EM，∵CQ＝CE，∴EQ＝2CQ，由EF∥BC得，△MEQ∽△BCQ，∴＝2，∴EM＝2BC＝2×6＝12，即EP+BP＝12．故选：C．5．如图，在四边形ABCD中，AD∥BC，∠ABC＝90°，AB＝2，AD＝2，将△ABC绕点C顺时针方向旋转后得△A′B′C，当A′B′恰好经过点D时，△B′CD为等腰三角形，若BB′＝2，则AA′等于（）A．B．2C．D．解：过D作DE⊥BC于E，则BE＝AD＝2，DE＝2，设B′C＝BC＝x，则DC＝x，∴DC2＝DE2+EC2，即2x2＝28+（x﹣2）2，解得：x＝4（负值舍去），∴BC＝4，AC＝，∵将△ABC绕点C顺时针方向旋转后得△A′B′C，∴∠DB′C＝∠ABC＝90°，B′C＝BC，A′C＝AC，∠A′CA＝∠B′CB，∴∴△A′CA∽△B′CB，∴，即∴AA′＝，故选：A．6．如图，已知，△ABC中边AB上一点P，且∠ACP＝∠B，AC＝4，AP＝2，则BP＝6．解：∵∠A＝∠A，∠ACP＝∠B，∴△ACP∽△ABC，∴AC2＝AP•AB，即AB＝AC2÷AP＝16÷2＝8，∴BP＝AB﹣AP＝6．7．如图，在▱ABCD中，AC、BD相交于点O，点E是OA的中点，联结BE并延长交AD 于点F，如果△AEF的面积是4，那么△BCE的面积是36．解：∵在▱ABCD中，AO＝AC，∵点E是OA的中点，∴AE＝CE，∵AD∥BC，∴△AFE∽△CBE，∴＝＝，＝4，＝（）2＝，∵S△AEF＝36，故答案为36．∴S△BCE8．如图，在△ABC中，点G为ABC的重心，过点G作DE∥AC分别交边AB、BC于点D、E，过点D作DF∥BC交AC于点F，如果DF＝4，那么BE的长为8．解：连接BG并延长交AC于H，∵G为ABC的重心，∴＝2，∵DE∥AC，DF∥BC，∴四边形DECF是平行四边形，∴CE＝DF＝4，∵GE∥CH，∴△BEG∽△CBH，∴＝2，∴BE＝8，故答案为：8．9．如图，已知Rt△ABC中，两条直角边AB＝3，BC＝4，将Rt△ABC绕直角顶点B旋转一定的角度得到Rt△DBE，并且点A落在DE边上，则sin∠ABE＝．解：∵将Rt△ABC绕直角顶点B旋转一定的角度得到Rt△DBE，∴BD＝AB，BC＝BE，∠ABD＝∠CBE，∠DEB＝∠ACB，∴∠D＝∠BAC＝∠BAD＝（180°﹣∠ABD），∴∠BEC＝（180°﹣∠CBE），∴∠D＝∠BEC，∵∠ABC＝∠DBE＝90°，∴∠DEB+∠BEC＝90°，∴∠AEC＝90°，∵∠AGB＝∠EGC，∴∠ACE＝∠ABE，∵在Rt△ABC中，AB＝3，BC＝4，∴AC＝DE＝5，过B作BH⊥DE于H，则DH＝AH，BD2＝DH•DE，∴DH＝＝，∴AD＝，∴AE＝DE﹣AD＝，∴sin∠ABE＝sin∠ACE＝＝＝，故答案为：．10．如图，在Rt△ABC中，∠ACB＝90°，∠BAC＝60°，AC＝6，AD平分∠BAC，交边BC于点D，过点D作CA的平行线，交边AB于点E．（1）求线段DE的长；（2）取线段AD的中点M，联结BM，交线段DE于点F，延长线段BM交边AC于点G，求的值．解：（1）∵AD平分∠BAC，∠BAC＝60°，∴∠DAC＝30°，在Rt△ACD中，∠ACD＝90°，∠DAC＝30°，AC＝6，∴CD＝2，在Rt△ACB中，∠ACB＝90°，∠BAC＝60°，AC＝6，∴BC＝6，∴BD＝BC﹣CD＝4，∵DE∥CA，∴，∴DE＝4；（2）如图，∵点M是线段AD的中点，∴DM＝AM，∵DE∥CA，∴，∴DF＝AG，∵DE∥CA，∴，∴，∵BD＝4，BC＝6，DF＝AG，∴．11．如图，在菱形ABCD中，∠ADE、∠CDF分别交BC、AB于点E、F，DF交对角线AC 于点M，且∠ADE＝∠CDF．（1）求证：CE＝AF；（2）连接ME，若＝，AF＝2，求ME的长．解：（1）∵四边形ABCD是菱形，∴AD＝CD，∠DAF＝∠DCE，又∵∠ADE＝∠CDF，∴∠ADE﹣∠EDF＝∠CDF﹣∠EDF，∴∠ADF＝∠CDE，在△ADF和△CDE中，，∴△ADF≌△CDE，∴CE＝AF．（2）∵四边形ABCD是菱形，∴AB＝BC，由（1）得：CE＝AF＝2，∴BE＝BF，设BE＝BF＝x，∵＝，AF＝2，∴，解得x＝，∴BE＝BF＝，∵＝，且CE＝AF，∴＝＝，∵∠CMD＝∠AMF，∠DCM＝∠AMF，∴△AMF∽△CMD，∴，∴＝，且∠ACB＝∠ACB∴△ABC∽△MEC∴∠CAB＝∠CME＝∠ACB∴ME＝CE＝212．[问题背景]（1）如图①，已知△ABC∽△ADE，求证：△ABD∽△ACE．[尝试应用]（2）如图②，在△ABC和△ADE中，∠BAC＝∠DAE＝90°∠ABC＝∠ADE＝30°，AC与DE相交于点F，点D在BC边上，＝，①填空：＝1；②求的值．（1）证明：如图①，∵△ABC∽△ADE，∴∠BAC＝∠DAE，＝，∴∠BAC﹣∠CAD＝∠DAE﹣∠CAD，＝，∴∠BAD＝∠CAE，∴△ABD∽△ACE．（2）解：①如图②，∵∠DAE＝90°，∠ADE＝30°，∴DE＝2AE，∴AD＝＝＝AE，∵＝，∴AD＝BD，∴AE＝BD，∴＝1，故答案为：1．②如图②，连接CE，∵∠BAC＝∠DAE＝90°，∠ABC＝∠ADE，∴△BAC∽△CAE，∴＝，∴＝，∵∠BAD＝∠CAE＝90°﹣∠CAD，∴△BAD∽△CAE，∴∠ABC＝∠ACE，∴∠ADE＝∠ACE，∵∠AFD＝∠EFC，∴△AFD∽△EFC，∴＝，由①得AD＝AE，AD＝BD，∴＝＝，∴BD＝CE，∴AD＝×CE＝3CE，∴＝3，∴＝3，∴的值是3．13．如图，在正方形ABCD中，AB＝4，E、F分别是BC、CD上的点，且∠EAF＝45°，AE、AF分别交BD于点M、N，连接EN、EF．（1）求证：△ABN∽△MBE；（2）求证：BM2+ND2＝MN2；（3）①求△CEF的周长；②若点G、F分别是EF、CD的中点，连接NG，则NG的长为．（1）证明：如图1，∵四边形ABCD是正方形，∴AB＝AD，∠BAD＝∠ABC＝90°，∴∠ABD＝∠ADB＝45°，∴∠ABN＝∠MBE＝45°，∠BME＝∠ABD+∠BAM＝45°+∠BAM，∵∠EAF＝45°，∴∠BAN＝∠EAF+∠BAM＝45°+∠BAM，∴∠BAN＝∠BME，∴△ABN∽△MBE．（2）证明：如图1，将△ADN绕点A顺时针旋转90°得到△ABH，连接MH，∴∠BAH＝∠DAN，AH＝AN，HB＝ND，∵∠MAN＝∠EAF＝45°，∴∠MAH＝∠BAH+∠BAM＝∠DAN+∠BAM＝45°，∴∠MAH＝∠MAN，∵AM＝AM，∴△MAH≌△MAN（SAS），∴MH＝MN，∵∠ABH＝∠ADN＝45°，∴∠MBH＝∠ABD+∠ABH＝90°，∴BM2+HB2＝MH2，∴BM2+ND2＝MN2．（3）解：①如图2，将△ADF绕点A顺时针旋转90°得到△ABK，∴AK＝AF，∠BAK＝∠DAF，BK＝DF，∠ABK＝∠ADF＝90°，∴∠ABK+∠ABE＝180°，∴点K、点B、点E在同一条直线上，∵∠EAK＝∠BAE+∠BAK＝∠BAE+∠DAF＝45°，∴∠EAK＝∠EAFM，∵AE＝AE，∴△EAK≌△EAF（SAS），∴EK＝EF，∴BE+DF＝BE+BK＝EK＝EF，∵CB＝CD＝AB＝4，∴CE+EF+CF＝CE+BE+DF+CF＝CB+CD＝4+4＝8，∴△CEF的周长是8．②如图2，∵F是CD的中点，∴CF＝DF＝CD＝2，∵∠C＝90°，∴CF2+EF2＝CE2，∵EF＝BE+DF＝BE+2，CE＝CB﹣BE＝4﹣BE，∴22+（4﹣BE）2＝（BE+2）2，解得BE＝，∴EF＝+2＝，∵∠MBE＝∠MAN＝45°，∠BME＝∠AMN，∴△BME∽△AMN，∴＝，∴＝，∴∠AMB＝∠NME，∴△AMB∽△NME，∴∠NEM＝∠ABM＝45°，∴∠ENF＝∠MAN+∠NEM＝90°，∵G是EF的中点，∴NG＝EF＝×＝，故答案为：．14．问题背景如图（1），已知△ABC∽△ADE，求证：△ABD∽△ACE；尝试应用如图（2），在△ABC和△ADE中，∠BAC＝∠DAE＝90°，∠ABC＝∠ADE＝30°，AC与DE相交于点F，点D在BC边上，＝，求的值；拓展创新如图（3），D是△ABC内一点，∠BAD＝∠CBD＝30°，∠BDC＝90°，AB ＝4，AC＝2，直接写出AD的长．问题背景证明：∵△ABC∽△ADE，∴，∠BAC＝∠DAE，∴∠BAD＝∠CAE，，∴△ABD∽△ACE；尝试应用解：如图1，连接EC，∵∠BAC＝∠DAE＝90°，∠ABC＝∠ADE＝30°，∴△ABC∽△ADE，由（1）知△ABD∽△ACE，∴，∠ACE＝∠ABD＝∠ADE，在Rt△ADE中，∠ADE＝30°，∴，∴＝3．∵∠ADF＝∠ECF，∠AFD＝∠EFC，∴△ADF∽△ECF，∴＝3．拓展创新解：如图2，过点A作AB的垂线，过点D作AD的垂线，两垂线交于点M，连接BM，∵∠BAD＝30°，∴∠DAM＝60°，∴∠AMD＝30°，∴∠AMD＝∠DBC，又∵∠ADM＝∠BDC＝90°，∴△BDC∽△MDA，∴，又∠BDC＝∠MDA，∴∠BDC+∠CDM＝∠ADM+∠CDM，即∠BDM＝∠CDA，∴△BDM∽△CDA，∴，∵AC＝2，∴BM＝2＝6，∴在Rt△ABM中，AM＝＝＝2，∴AD＝．15．如图1，四边形ABCD是正方形，G是CD边上的一个动点（点G与C、D不重合），以CG为一边在正方形ABCD外作正方形CEFG，连接BG，DE．我们探究下列图中线段BG、线段DE的长度关系及所在直线的位置关系：（1）①猜想如图1中线段BG、线段DE的数量关系BG＝DE及所在直线的位置关系BG⊥DE；②将图1中的正方形CEFG绕着点C按顺时针（或逆时针）方向旋转任意角度α，得到如图2，如图3情形．请你通过观察、测量等方法判断①中得到的结论是否仍然成立，并选取图2证明你的判断；（2）将原题中正方形改为矩形（如图4﹣6），且AB＝a，BC＝b，CE＝ka，CG＝kb（a≠b，k＞0），则线段BG、线段DE的数量关系＝及所在直线的位置关系BG ⊥DE；（3）在第（2）题图5中，连接DG、BE，且a＝4，b＝3，k＝，直接写出BE2+DG2的值为．解：（1）①猜想：BG ⊥DE ，BG ＝DE ；故答案为：BG ＝DE ，BG ⊥DE ；②结论成立．理由：如图2中，∵四边形ABCD 和四边形CEFG 是正方形，∴BC ＝DC ，CG ＝CE ，∠BCD ＝∠ECG ＝90°，∴∠BCG ＝∠DCE ，∴△BCG ≌△DCE （SAS ），∴BG ＝DE ，∠CBG ＝∠CDE ，又∵∠CBG +∠BHC ＝90°，∴∠CDE +∠DHG ＝90°，∴BG ⊥DE ．（2）∵AB ＝a ，BC ＝b ，CE ＝ka ，CG ＝kb ，∴＝＝，又∵∠BCG ＝∠DCE ，∴△BCG ∽△DCE ，∴∠CBG ＝∠CDE ，＝＝，又∵∠CBG +∠BHC ＝90°，∴∠CDE +∠DHG ＝90°，∴BG⊥DE．故答案为：＝，BG⊥DE．（3）连接BE、DG．根据题意，得AB＝4，BC＝3，CE＝2，CG＝1.5，∵BG⊥DE，∠BCD＝∠ECG＝90°∴BE2+DG2＝BO2+OE2+DO2+OG2＝BC2+CD2+CE2+CG2＝9+16+2.25+4＝．。

模型05相似三角形中的常见五种基本模型(原卷版)

模型探究相似三角形考查范围广，综合性强，其模型种类多，其中有关一线三垂直模型在前面的专题已经很详细的讲解，这里就不在重复.模型一、A字型相似模型A字型（平行）反A字型（不平行）模型二、8字型与反8字型相似模型模型三、AX型相似模型（A字型及X字型两者相结合）模型四、共边角相似模型（子母型）模型五、手拉手相似模型考点一、A 字相似模型【例1】．如图，在△ABC 中，∠A ＝78°，AB ＝4，AC ＝6，将△ABC 沿图示中的虚线剪开，剪下的阴影三角形与原三角形不相似的是（）A ．B ．C ．D ．➢变式训练【变式1-1】．如图，在△ABC 中，DE ∥BC ，AH ⊥BC 于点H ，与DE 交于点G ．若，则＝．例题精讲【变式1-2】.如图，在△ABC中，M是AC的中点，E是AB上一点，AE＝AB，连接EM并延长，交BC 的延长线于D，则＝__________.【变式1-3】．如图，在△ABC中，点D在边AB上，AD＝9，BD＝7．AC＝12．△ABC的角平分线AE交CD于点F．（1）求证：△ACD∽△ABC；（2）若AF＝8，求AE的长度．考点二、8字与反8字相似模型【例2】．如图，AG∥BD，AF：FB＝1：2，BC：CD＝2：1，求的值➢变式训练【变式2-1】．如图，AB∥CD，AE∥FD，AE、FD分别交BC于点G、H，则下列结论中错误的是（）A．B．C．D．【变式2-2】．如图，在平行四边形ABCD中，E为边AD的中点，连接AC，BE交于点F．若△AEF的面积为2，则△ABC的面积为（）A．8B．10C．12D．14【变式2-3】.如图，锐角三角形ABC中，∠A＝60°，BE⊥AC于E，CD⊥AB于D，则DE：BC＝．考点三、AX型相似模型（A字型及X字型两者相结合）【例3】.如图，在△ABC中，点D和E分别是边AB和AC的中点，连接DE，DC与BE交于点O，若△DOE的面积为1，则△ABC的面积为（）A．6B．9C．12D．➢变式训练【变式3-1】.如图，DE是△ABC的中位线，F为DE中点，连接AF并延长交BC于点G，若S△EFG＝1，则S△ABC＝．【变式3-2】．如图：AD∥EG∥BC，EG交DB于点F，已知AD＝6，BC＝8，AE＝6，EF＝2．（1）求EB的长；（2）求FG的长．【变式3-3】.如图，已知AB∥CD，AC与BD相交于点E，点F在线段BC上，，．（1）求证：AB∥EF；（2）求S△ABE：S△EBC：S△ECD．模型四、子母型相似模型【例4】.如图，点C，D在线段AB上，△PCD是等边三角形，且∠APB＝120°，求证：（1）△ACP∽△PDB，（2）CD2＝AC•BD．➢变式训练【变式4-1】.如图，点P在△ABC的边AC上，要判断△ABP∽△ACB，添加一个条件，不正确的是（）A．∠ABP＝∠C B．∠APB＝∠ABC C．D．【变式4-2】.如图，在△ABC中，点D在AC边上，连接BD，若∠ABC+∠BDC＝180°，AD＝2，CD＝4，则AB的长为（）A．3B．4C．D．2【变式4-3】．如图，边长为4的正方形，内切圆记为圆O，P为圆O上一动点，则P A+PB的最小值为．模型五、手拉手相似模型【例5】.如图，△ABC与△DEF均为等边三角形，O为BC、EF的中点，则AD：BE的值为．➢变式训练【变式5-1】.如图，在△ABC与△ADE中，∠BAC＝∠DAE，∠ABC＝∠ADE．求证：（1）△BAC∽△DAE；（2）△BAD∽△CAE．【变式5-2】.如图，点D是△ABC内一点，且∠BDC＝90°，AB＝2，AC＝，∠BAD＝∠CBD＝30°，AD＝．【变式5-3】．如图，在四边形ABCD中，AE⊥BC，垂足为E，∠BAE＝∠ADC，BE＝CE＝2，CD＝5，AD ＝kAB（k为常数），则BD的长为．（用含k的式子表示）实战演练1．如图，已知DE∥BC，EF∥AB，则下列比例式中错误的是（）A．＝B．C．D．2．如图，梯形ABCD中，AD∥BC，∠B＝∠ACD＝90°，AB＝2，DC＝3，则△ABC与△DCA的面积比为（）A．2：3B．2：5C．4：9D．：3．如图，菱形ABCD中，E点在BC上，F点在CD上，G点、H点在AD上，且AE∥HC∥GF．若AH＝8，HG＝5，GD＝4，则下列选项中的线段，何者长度最长？（）A．CF B．FD C．BE D．EC4．如图，在△ABC中，BC＝6，E，F分别是AB，AC的中点，动点P在射线EF上，BP交CE于点D，∠CBP的平分线交CE于点Q，当CQ＝CE时，EP+BP的值为（）A．6B．9C．12D．185．如图，在四边形ABCD中，AD∥BC，∠ABC＝90°，AB＝2，AD＝2，将△ABC绕点C顺时针方向旋转后得△A′B′C，当A′B′恰好经过点D时，△B′CD为等腰三角形，若BB′＝2，则AA′等于（）A．B．2C．D．6．如图，已知，△ABC中边AB上一点P，且∠ACP＝∠B，AC＝4，AP＝2，则BP＝．7．如图，在▱ABCD中，AC、BD相交于点O，点E是OA的中点，联结BE并延长交AD于点F，如果△AEF的面积是4，那么△BCE的面积是．8．如图，在△ABC中，点G为ABC的重心，过点G作DE∥AC分别交边AB、BC于点D、E，过点D作DF∥BC交AC于点F，如果DF＝4，那么BE的长为．9．如图，已知Rt△ABC中，两条直角边AB＝3，BC＝4，将Rt△ABC绕直角顶点B旋转一定的角度得到Rt△DBE，并且点A落在DE边上，则sin∠ABE＝．10．如图，在Rt△ABC中，∠ACB＝90°，∠BAC＝60°，AC＝6，AD平分∠BAC，交边BC于点D，过点D作CA的平行线，交边AB于点E．（1）求线段DE的长；（2）取线段AD的中点M，联结BM，交线段DE于点F，延长线段BM交边AC于点G，求的值．11．如图，在菱形ABCD中，∠ADE、∠CDF分别交BC、AB于点E、F，DF交对角线AC于点M，且∠ADE＝∠CDF．（1）求证：CE＝AF；（2）连接ME，若＝，AF＝2，求ME的长．12．[问题背景]（1）如图①，已知△ABC∽△ADE，求证：△ABD∽△ACE．[尝试应用]（2）如图②，在△ABC和△ADE中，∠BAC＝∠DAE＝90°∠ABC＝∠ADE＝30°，AC与DE相交于点F，点D在BC边上，＝，①填空：＝；②求的值．13．如图，在正方形ABCD中，AB＝4，E、F分别是BC、CD上的点，且∠EAF＝45°，AE、AF分别交BD于点M、N，连接EN、EF．（1）求证：△ABN∽△MBE；（2）求证：BM2+ND2＝MN2；（3）①求△CEF的周长；②若点G、F分别是EF、CD的中点，连接NG，则NG的长为．14．问题背景如图（1），已知△ABC∽△ADE，求证：△ABD∽△ACE；尝试应用如图（2），在△ABC和△ADE中，∠BAC＝∠DAE＝90°，∠ABC＝∠ADE＝30°，AC与DE 相交于点F，点D在BC边上，＝，求的值；拓展创新如图（3），D是△ABC内一点，∠BAD＝∠CBD＝30°，∠BDC＝90°，AB＝4，AC＝2，直接写出AD的长．15．如图1，四边形ABCD是正方形，G是CD边上的一个动点（点G与C、D不重合），以CG为一边在正方形ABCD外作正方形CEFG，连接BG，DE．我们探究下列图中线段BG、线段DE的长度关系及所在直线的位置关系：（1）①猜想如图1中线段BG、线段DE的数量关系BG＝DE及所在直线的位置关系BG⊥DE；②将图1中的正方形CEFG绕着点C按顺时针（或逆时针）方向旋转任意角度α，得到如图2，如图3情形．请你通过观察、测量等方法判断①中得到的结论是否仍然成立，并选取图2证明你的判断；（2）将原题中正方形改为矩形（如图4﹣6），且AB＝a，BC＝b，CE＝ka，CG＝kb（a≠b，k＞0），则线段BG、线段DE的数量关系＝及所在直线的位置关系BG⊥DE；（3）在第（2）题图5中，连接DG、BE，且a＝4，b＝3，k＝，直接写出BE2+DG2的值为．。

相似三角形模型(全)

A
• 5、如图，已知锐角△ABC，AD、CE分别是BC、AB边上的高，△ABC和△BDE的面积分别是27和3，DE=6，求：点B到直线 AC的距离。
A
E
B
D
C
七、共享型
A
A E G F
D
B
C
E
B
C
• 1、已知：如图，在Rt△ABC中，AB=AC， ∠DAE=45°． • 求证：（1）△ABE∽△DCA；（2）．BC 2 2BE CD
A P D
E B
C
• 4、在△ABC中，∠C=90°， AC=4 ， AO 2 BC=3，O是AB上的一点且 AB 5 ，点P 是AC上的一个动点，PQ OP 交线段BC于点Q，（不与点B,C重合），设 AP x, CQ y ，试求y关于x的函数关系，并写出定义域
C Q P
B
O
E
D
C
A
• 2：如图，等边△ABC中，边长为6，D是 BC上动点，∠EDF=60° • （1）求证：△BDE∽△CFD • （2）当BD=1，FC=3时，求BE
AEFB NhomakorabeaD
C
• 3、已知矩形ABCD中，CD=2，AD=3，点 P是AD上的一个动点，且和点A,D不重合，过点P作，交边AB于点E, 设 PE CP ，求y关于x的函数关系式，并写出 xx 的取值范围。 PD , AE y
A D
D
B
C
B
C
（四）旋转型（手拉手）:
A E E' B F
E F E'
F'
F'
A
C AEF旋转到 AE‘F’
B

相似三角形的基本模型

相似三角形是指具有相同形状但可能不同尺寸的三角形。

两个三角形相似的条件是它们的对应角相等，而对应边的比例相等。

相似三角形的基本模型包括比例、角的对应关系和性质等。

1. 相似三角形的定义：两个三角形ABC 和DEF 是相似的，记作∆ABC ∼ ∆DEF ，如果它们的对应角相等，即∠A = ∠D ，∠B = ∠E ，∠C = ∠F 。

2. 相似三角形的基本性质：• 对应边的比例：如果两个三角形相似，那么它们的对应边的长度比是相等的，即AB DE =BC EF =CA FD 。

• 高与底的比例：两个相似三角形的高与底的比例等于它们的对应边的比例。

•角平分线：如果在一个三角形的两个角上分别引一条角平分线，这两条平分线所夹的角的正弦比等于与这两个角对应的边的比例。

3. 相似三角形的求解问题：•相似三角形的判定：给定两个三角形的三个角，判断它们是否相似。

•相似三角形的边长求解：已知一个三角形和一个角，求另一个相似三角形的边长。

• 相似三角形的角度求解：已知两个相似三角形的边长比，求它们的角度。

4. 模型示例：考虑两个相似三角形ABC 和DEF ，其中∠A = ∠D ，∠B = ∠E 。

已知AB DE =BC EF =CA FD =k 。

• 已知边长求解：如果已知AB=6，找出DE 、BC 和EF 。

DE =AB k , BC =AB k , EF =AB k• 已知一个角和边长比求解：如果已知∠A=40°，找出∠D ，∠B 和∠E 。

∠D =40°, ∠B =40°, ∠E =40°•已知角度求解：如果已知∠A=30°，∠B=60°，找出∠D 和∠E 。

∠D =30°, ∠E =60°这是一个基本的相似三角形模型，可以根据具体的已知条件和问题求解未知量。

在实际应用中，相似三角形的模型经常出现在几何问题中，例如测量远近、影子问题、光学等领域。

(完整版)相似三角形模型分析大全(非常全面-经典)

相似三角形模型分析大全1、相似三角形判定的基本模型认识（一）A字型、反A字型（斜A字型）B（平行）B（不平行）（二）8字型、反8字型BCBC（蝴蝶型）（平行）（不平行）（三）母子型B（四）一线三等角型：三等角型相似三角形是以等腰三角形（等腰梯形）或者等边三角形为背景（五）一线三直角型：（6）双垂型：2、相似三角形判定的变化模型旋转型：由A 字型旋转得到。

8字型拓展B一线三等角的变形一线三直角的变形第二部分相似三角形典型例题讲解母子型相似三角形例1：如图，梯形ABCD 中，AD ∥BC ，对角线AC 、BD 交于点O ，BE ∥CD 交CA 延长线于E ．求证：．OE OA OC ⋅=2例2：已知：如图，△ABC 中，点E 在中线AD 上, ．ABC DEB ∠=∠求证：（1）；（2）．DA DE DB ⋅=2DAC DCE ∠=∠ACDEB例3：已知：如图，等腰△ABC 中，AB ＝AC ，AD ⊥BC 于D ，CG ∥AB ，BG 分别交AD 、AC 于E 、F ．求证：．EG EF BE ⋅=2相关练习：1、如图，已知AD 为△ABC 的角平分线，EF 为AD 的垂直平分线．求证：．FC FB FD ⋅=22、已知：AD 是Rt△ABC 中∠A 的平分线，∠C=90°，EF 是AD 的垂直平分线交AD 于M ，EF 、BC 的延长线交于一点N 。

求证：(1)△AME∽△NMD; (2)ND =NC·NB23、已知：如图，在△ABC中，∠ACB=90°，CD⊥AB于D，E是AC上一点，CF⊥BE于F。

求证：EB·DF=AE·DB⊥，垂足为F，延长AD到G，使DG=EF，M是AH的中点。

4.在∆ABC中，AB=AC，高AD与BE交于H，EF BCGBM90求证：∠=︒5．（本题满分14分，第（1）小题满分4分，第（2）、（3）小题满分各5分）已知：如图，在Rt△ABC 中，∠C =90°，BC =2，AC =4，P 是斜边AB 上的一个动点，PD ⊥AB ，交边AC于点D （点D 与点A 、C 都不重合），E 是射线DC 上一点，且∠EPD =∠A ．设A 、P 两点的距离为x ，△BEP 的面积为y ．（1）求证：AE =2PE ；（2）求y 关于x 的函数解析式，并写出它的定义域；（3）当△BEP 与△ABC 相似时，求△BEP 的面积．双垂型1、如图，在△ABC 中，∠A=60°，BD 、CE 分别是AC 、AB 上的高A（第25题图）求证：（1）△ABD∽△ACE；（2）△ADE∽△ABC；(3)BC=2ED2、如图，已知锐角△ABC ，AD 、CE 分别是BC 、AB 边上的高，△ABC 和△BDE 的面积分别是27和3，DE=6，求：点B 到直线AC 的距离。

相似三角形的九大模型

相似三角形的九大模型相似三角形是几何学中一类重要的图形，它具有一些独特的性质和模型。

这些模型可以用来解决各种实际问题，从简单的长度关系到复杂的空间结构。

本文将介绍相似三角形的九大模型，并给出相应的例子和应用场景。

相似三角形是指两个三角形形状相同，大小成比例。

相似三角形的对应边成比例，对应角相等。

相似三角形还有一些其他的性质，例如，相似三角形的中线、角平分线、高的比等于它们的相似比。

平行线模型：两个三角形分别在两条平行线上，它们的对应边平行且成比例。

这种模型经常用于解决一些与长度和角度相关的问题。

共顶点模型：两个三角形有一个共同的顶点，且它们的对应边成比例。

这种模型常用于证明两个三角形相似，以及求解一些角度问题。

角平分线模型：一个三角形的角平分线将这个三角形分成两个小的相似三角形。

这种模型可以用于证明两个三角形相似，以及求解一些角度问题。

平行四边形模型：一个平行四边形被它的两条对角线分成四个小的相似三角形。

这种模型可以用于解决一些与面积和长度相关的问题。

位似模型：一个相似变换将一个三角形映射到另一个三角形，这种变换称为位似变换。

这种模型可以用于解决一些与长度、角度和面积相关的问题。

旋转模型：一个三角形绕着它的一个顶点旋转一定的角度后得到另一个三角形，这两个三角形是相似的。

这种模型可以用于解决一些与角度和长度相关的问题。

镜像模型：一个三角形沿一条直线翻折后得到另一个三角形，这两个三角形是相似的。

这种模型可以用于解决一些与长度和角度相关的问题。

传递模型：如果一个三角形与另一个三角形相似，那么这个三角形的每一个部分都与另一个三角形的对应部分相似。

这种模型可以用于解决一些与长度和角度相关的问题。

扩展模型：如果一个三角形与另一个三角形相似，那么这个三角形的每一个部分都与另一个三角形的对应部分成比例。

这种模型可以用于解决一些与长度和角度相关的问题。

相似三角形的九创作者是几何学中一类重要的模型，它们具有广泛的应用价值。

中考数学相似三角形的几种模型

2. (2018·深圳改编)如图，△ABC内接于⊙O，
BC＝2，AB＝AC＝，点D为上的动点，在点D的运动过程中，弦AD的延长线交BC延长线于点E，问AD·AE的值是否变化？若不变，请求出AD·AE的值；若变化，请说明理由．
GE·GF是否为定值？如果是，求出该定值；如果不是，请说明理由．
请说明理由．
模型5 相似三角形的几种模型
相似三角形的基础模型
已知
A型模型在△ABC中，DE∥BC 图形
求法
已知反A型模型在△ABC中，∠AED＝∠B
图形
求法
已知在△ABC中，∠ACD＝∠B 图形
求法
已知
双垂直型如图，CD是Rt△ABC斜边上的高，∠ACB＝ 90°
图形
求法
△ACD∽△CBD∽△ABC； CD2＝AD·BD；ห้องสมุดไป่ตู้AC2＝AD·AB； BC2＝BD·AB
已知
一直线三等角模型在Rt△ABC与Rt△CDE中，A，C，D三点共线，∠A＝∠BCE＝∠D＝90°
图形
求法
已知在△ABC与△CDE中，B，C，D三点共线， ∠B＝∠ACE＝∠D
图形
求法
已知
半角模型正方形ABCD中，点E，F分别在边AB，AD上，且∠ECF＝45°，连接AC，EF，GH，CH， CF
图形
求法
∠AHC＝∠ACG； △AHC∽△ACG； AC2＝AG·AH
已知相交弦定理 ⊙O中，弦AB与弦CD相交与点P
图形
求法 AP·BP＝CP·DP
已知切割线定理 PA为⊙O切线，PCB为⊙O割线
图形
求法 PA2＝PB·PC
已知割线定理 PAB，PCD分别为⊙O割线