计量经济学第二次作业---异方差检验
计量经济学异方差实验报告及心得体会

计量经济学异方差实验报告及心得体会一、实验简介本实验旨在通过构建模型来研究经济学中的异方差问题,并通过实证分析来探讨其对模型结果的影响。
实验数据采用随机抽样方法自真实经济数据中获取,共包括两个自变量和一个因变量。
在实验中,我将对模型进行两次回归分析,一次是假设无异方差问题,一次是考虑异方差问题,并比较两个模型的结果。
二、实验过程1.数据准备:根据实验设计,我根据随机抽样方法,从真实经济数据中抽取了一部分样本数据。
2.模型建立:我将自变量Y和X1、X2进行回归分析。
首先,我假设模型无异方差问题,得到回归结果。
然后,我将检验异方差性,若存在异方差问题,则建立异方差模型继续回归分析。
3.模型估计:利用最小二乘法进行参数估计,并计算回归结果的标准差和假设检验。
4.模型比较:对比两个模型的回归结果,分析异方差对模型拟合程度和参数估计的影响。
三、实验结果1.无异方差假设模型回归结果:回归方程:Y=0.9X1+0.5X2+2.1标准差:0.3显著性水平:0.05拟合优度:0.852.考虑异方差问题模型回归结果:回归方程:Y=0.7X1+0.4X2+1.9标准差:0.6显著性水平:0.05拟合优度:0.75四、实验心得体会通过本次实验,我对计量经济学中的异方差问题有了更深入的了解,并进一步认识到其对模型结果的影响。
1.异方差问题的存在会对统计推断结果产生重要影响。
在本次实验中,考虑异方差问题的模型相较于无异方差模型,参数估计值差异较大,并且拟合优度也有所下降。
因此,我们在实证分析中应尽可能考虑异方差问题。
2.在实际应用中,异方差问题可能较为普遍。
经济学中的许多变量存在异方差性,例如,个体收入、消费支出等。
因此,在进行经济学研究时,我们应当警惕并尽量排除异方差问题。
3.针对异方差问题,我们可以采用多种方法进行调整,例如,利用异方差稳健标准误、加权最小二乘法等。
在本次实验中,我们采用了异方差模型进行调整,并得到了相对较好的结果。
异方差检验结果解读

异方差检验结果解读
异方差检验(Heteroscedasticity test)是一种用于检验不同组之间是否存在方差
差异的统计方法。
该检验通常用于回归分析中,以确定回归模型的合理性和精确性。
异方差性可能导致回归模型的预测能力下降,因此解读异方差检验结果对于正确分析数据非常重要。
在异方差检验中,常用的检验方法包括Park、White、Goldfeld-Quandt等。
检
验结果通常以显著性水平为基准进行判断。
检验结果显示显著性水平小于或等于设定的阈值(通常为0.05),则可以认为不存在异方差;反之,如果显著性水平大于阈值,则可以认为存在异方差。
异方差检验的结果还提供了其他有用的信息,如异方差性的模式或形式。
一种
常用的方法是绘制残差图,通过观察残差与预测值的关系,可以初步判断异方差性的模式。
常见的异方差性模式包括上升或下降斜线、漏斗形状等。
在图形分析的基础上,可以进一步使用更专业的统计方法,如白噪声检验(White noise test)或Breusch-Pagan检验,来验证异方差性的模式。
在回归分析中,若检验结果显示存在异方差,需要采取相应的纠正措施。
常用
的纠正方法包括回归模型的转换、加权最小二乘法等。
这些方法可以有效地纠正异方差性,提高模型的准确性和稳定性。
总结来说,异方差检验结果的解读需要关注显著性水平、残差图以及其他专业
统计方法的检验结果。
通过综合分析这些信息,我们能够确定回归模型是否受到异方差性的影响,进而采取相应的纠正措施。
正确解读异方差检验结果对于准确分析数据和得出可靠的结论至关重要。
异方差练习题

异方差练习题在统计学中,方差是用来衡量一组数据的离散程度的统计量。
如果我们要比较两组数据的方差是否相等,就需要进行异方差检验。
本文将介绍一些异方差检验的练习题,帮助读者巩固对于异方差的理解和应用。
题目一:某研究人员想要比较两种不同药物在治疗头痛方面的效果。
为此,他随机选取了两组患者,第一组患者接受药物A的治疗,第二组患者接受药物B的治疗。
研究人员在治疗结束后,记录了患者的头痛缓解时间(单位:分钟)如下:药物A: 40, 45, 50, 55, 60药物B: 20, 25, 30, 35, 40请用适当的统计方法检验这两组数据的方差是否相等,并给出相应的结论。
解答一:为了比较这两组数据的方差是否相等,我们可以使用F检验。
F检验的零假设是两组数据的方差相等。
首先,我们计算两组数据的方差。
对于药物A组的数据,方差为:方差A = ((40-50)^2 + (45-50)^2 + (50-50)^2 + (55-50)^2 + (60-50)^2) / (n-1) = 62.5对于药物B组的数据,方差为:方差B = ((20-30)^2 + (25-30)^2 + (30-30)^2 + (35-30)^2 + (40-30)^2) / (n-1) = 62.5其中n为每组的样本数,这里为5。
然后,我们计算F统计量:F = 方差A / 方差B = 62.5 / 62.5 = 1接下来,我们需要根据自由度来查找F分布表中的临界值。
在这个例子中,自由度为4和4(n-1),显著性水平选择为α = 0.05。
根据F分布表可以查到,当自由度为4和4,显著性水平为0.05时,临界值为2.866。
由于计算得到的F统计量(1)小于临界值(2.866),因此我们无法拒绝零假设,即两组数据的方差相等。
结论:根据F检验结果,我们无法拒绝两组数据的方差相等的零假设。
题目二:某市场调研公司想要研究某产品在不同年龄段消费者中的满意度是否存在差异。
计量经济学实验二
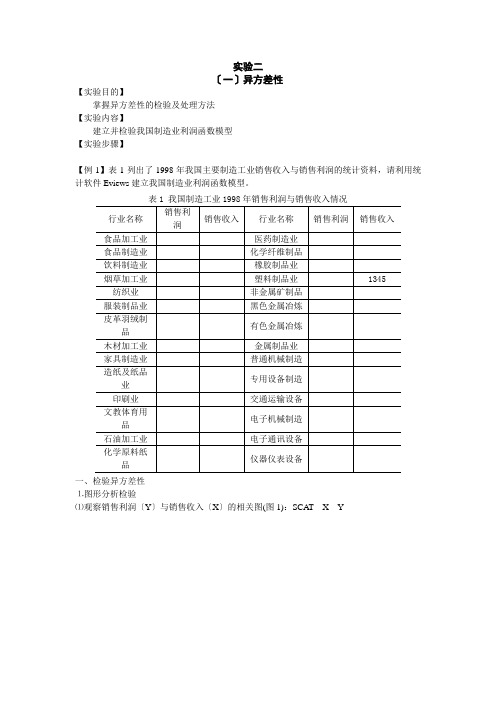
实验二〔一〕异方差性【实验目的】掌握异方差性的检验及处理方法【实验内容】建立并检验我国制造业利润函数模型【实验步骤】【例1】表1列出了1998年我国主要制造工业销售收入与销售利润的统计资料,请利用统计软件Eviews建立我国制造业利润函数模型。
一、检验异方差性⒈图形分析检验⑴观察销售利润〔Y〕与销售收入〔X〕的相关图(图1):SCAT X Y图1 我国制造工业销售利润与销售收入相关图从图中可以看出,随着销售收入的增加,销售利润的平均水平不断提高,但离散程度也逐步扩大。
这说明变量之间可能存在递增的异方差性。
⑵残差分析首先将数据排序〔命令格式为:SORT 解释变量〕,然后建立回归方程。
在方程窗口中点击Resids按钮就可以得到模型的残差分布图〔或建立方程后在Eviews工作文件窗口中点击resid对象来观察〕。
图2 我国制造业销售利润回归模型残差分布图2显示回归方程的残差分布有明显的扩大趋势,即说明存在异方差性。
⒉Goldfeld-Quant检验⑴将样本安解释变量排序〔SORT X〕并分成两部分〔分别有1到10共11个样本合19到28共10个样本〕⑵利用样本1建立回归模型1〔回归结果如图3〕,其残差平方和为。
SMPL 1 10LS Y C X图3 样本1回归结果⑶利用样本2建立回归模型2〔回归结果如图4〕,其残差平方和为。
SMPL 19 28 LS Y C X图4 样本2回归结果⑷计算F 统计量:12/RSS RSS F ==,21RSS RSS 和分别是模型1和模型2的残差平方和。
取05.0=α时,查F 分布表得44.3)1110,1110(05.0=----F ,而44.372.2405.0=>=F F ,所以存在异方差性⒊White 检验⑴建立回归模型:LS Y C X ,回归结果如图5。
图5 我国制造业销售利润回归模型⑵在方程窗口上点击View\Residual\Test\White Heteroskedastcity,检验结果如图6。
计量经济学--异方差性讲解

图1:我国税收和GDP
图2:1998年我国制造工业和利润
X-GDP Y-税收
X-销售收入 Y-销售利润
两个散点图有共同的特征,随着自变量增加,因变量也 增加,但是图2中,当X比较小时,数据点相对集中,随 着X增大,数据点变得相对分散。而图1中数据分布却没 有出现这一特征。
异方差的性质
➢经典线形回归模型的一个重要假定是同方差性:
PRF的干扰项 u i 是同方差的(homoscedastic)
即: E(ui2) 2
i 1, 2, , n (3.3.1)
➢异方差性是指,ui 的条件方差(= Yi 的条件方差)
随着X的变化而变化,用符号表示为:
E (ui2
)
2 i
(3.3.2)
Var(Yi ) Var(ui )
异方差产生的主要原因
——这就是GLS方法,得到的是GLS估计量
•模型函数形式存在设定误差 •模型中遗漏了一些重要的解释变量 •随机因素本身的影响
异方差较之 同方差更为
常见
7
异方差的具体理由
➢按照边错边改学习模型(error—learning models),人 们的行为误差随时间而减少。
➢随着收入的增长,人们在支出和储蓄中有更大的灵活
性。在做储蓄对收入的回归中, i2与收入俱增
此时如果仍采用
计算斜率参数的方差,将会
产生估计偏误,偏误的大小取决与因子值的大小。
17
3.t检验的可靠性降低
由于异方差的存在,无法正确估计参数的方差和标 志误差,因此也影响到t检验的效果
4.模型的预测误差增大
模型的预测区间和随机误差项的方差有着紧密联 系,随着随机误差项方差的增大,模型的预测区 间也随之增大,模型的预测误差也会相应增加。
计量经济学:异方差性

计量经济学:异方差性异方差性在现实经济活动中,最小二乘法的基本假定并非都能满足,上一章介绍的多重共线性只是其中一个方面,本章将讨论违背基本假定的另一个方面——异方差性。
虽然它们都是违背了基本假定,但前者属于解释变量之间存在的问题,后者是随机误差项出现的问题。
本章将讨论异方差性的实质、异方差出现的原因、异方差的后果,并介绍检验和修正异方差的若干方法。
第一节异方差性的概念一、异方差性的实质第二章提出的基本假定中,要求对所有的i (i=1,2,…,n )都有2)(σ=i u Var (5.1)也就是说i u 具有同方差性。
这里的方差2σ度量的是随机误差项围绕其均值的分散程度。
由于0)(=i u E ,所以等价地说,方差2σ度量的是被解释变量Y 的观测值围绕回归线)(i Y E =ki k i X X βββ+++ 221的分散程度,同方差性实际指的是相对于回归线被解释变量所有观测值的分散程度相同。
设模型为n i u X X Y iki k i i ,,2,1221 =++++=βββ (5.2)如果其它假定均不变,但模型中随机误差项i u 的方差为).,,3,2,1(,)(22n i u Var i i ==σ (5.3)则称i u 具有异方差性。
由于异方差性指的是被解释变量观测值的分散程度是随解释变量的变化而变化的,如图5.1所示,所以进一步可以把异方差看成是由于某个解释变量的变化而引起的,则)()(222i i i X f u Var σσ== (5.4)图5.1二、产生异方差的原因由于现实经济活动的错综复杂性,一些经济现象的变动与同方差性的假定经常是相悖的。
所以在计量经济分析中,往往会出现某些因素随其观测值的变化而对被解释变量产生不同的影响,导致随机误差项的方差相异。
通常产生异方差有以下主要原因:1、模型中省略了某些重要的解释变量异方差性表现在随机误差上,但它的产生却与解释变量的变化有紧密的关系。
计量经济学--异方差的检验及修正

经济计量分析实验报告一、实验项目异方差的检验及修正二、实验日期2015.12.06三、实验目的对于国内旅游总花费的有关影响因素建立多元线性回归模型,对变量进行多重共线性的检验及修正后,进行异方差的检验和补救。
四、实验内容建立模型,对模型进行参数估计,对样本回归函数进行统计检验,以判定估计的可靠程度,包括拟合优度检验、方程总体线性的显著性检验、变量的显著性检验,以及参数的置信区间估计。
检验变量是否具有多重共线性并修正。
检验是否存在异方差并补救。
五、实验步骤1、建立模型。
以国内旅游总花费Y 作为被解释变量,以年底总人口表示人口增长水平,以旅行社数量表示旅行社的发展情况,以城市公共交通运营数表示城市公共交通运行状况,以城乡居民储蓄存款年末增加值表示城乡居民储蓄存款增长水平。
2、模型设定为:t t t t t μβββββ+X +X +X +X +=Y 443322110t 其中:t Y — 国内旅游总花费(亿元) t 1X — 年底总人口(万人) t 2X — 旅行社数量(个) t 3X — 城市公共交通运营数(辆)t 4X — 城乡居民储蓄存款年末增加值(亿元)3、对模型进行多重共线性检验。
4、检验异方差是否存在。
六、实验结果(一)、消除多重共线性之后的模型多元线性回归模型估计结果如下:4321000779.0053329.0151924.0720076.0-99.81113ˆX +X +X +X =Y i SE=(26581.73) (0.230790) (0.108223) (0.013834) (0.020502) t =(3.051494) (-3.120046) (1.403805) ( 3.854988) (0.038020)R2=0.969693R2=0.957571F=79.98987(1)拟合优度检验:可决系数R 2=0.969693较高,修正的可决系数R 2=0.957571也较高,表明模型拟合较好。
计量经济学:异方差

(1)布罗施-帕甘(Breusch-Pagan)检验
例4.2 使用BP检验对例4.1的回归模型进行异方差检验。 解:EViews中进行BP检验的结果如下:
从中可以看出,无论是使用F检验还是LM检验,在5%的显著性水 平下,均可拒绝随机误差项不存在异方差的原假设
2)怀特(White)检验
20000 X
30000
40000
(2)用 X e%i2 的散点图进行判断
第三节 异方差的检验
方法2:作X-ei2散点图
从图中可以看出,随着居 民可支配收入X的提高,随 机误差项平方ei2呈递增趋 势。表明随机误差项存在 递增型异方差。
ESQU
320000 280000 240000 200000 160000 120000
概 率 密 度
X1 X2 X3
同方差
概
率
Y
密
Y
度
E(Y|X) = β0 + β 1X
X
X1 X2 X3 异方差
E(Y|X) = β 0 + β 1X
X
异方差的矩阵表示
2 1
Var(u)
0 M
0
2 2
M
L L M
0
0
0
0
0
L
2 n
2、异方差的类型
•同方差性假定的意义是:每个ui围绕其零均值的离差,并不随解释 变量X的变化而变化,不论解释变量X的观测值是大还是小,每个ui
E(ˆ )(ˆ ) E ( X X )1 X Y ( X X )1 X Y
E ( X X )1 X X U ( X X )1 X X U
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三章13题 下表列出了中国某年按行业分的全部制造业国有企业及规模以上制造业非国有企业
的工业总产值Y ,资产合计K 及职工人数L 。
序号 工业总产值 Y (亿元) 资产合计 K (亿元) 职工人数L (万人) 序号 工业总产值Y (亿元) 资产合计K (亿元) 职工人数
L (万人) 1 3722.7 3078.22 113 13 4429.19 3785.91 61 2 1442.52 1684.43 67 14 5749.02 8688.03 254 3 1752.37 2742.77 84 15 1781.37 2798.9 83 4 1451.29 1973.82 27 16 1243.07 1808.44 33 5 5149.3 5917.01 327 17 812.7 1118.81 43 6 2291.16 1758.77 120 18 1899.7 2052.16 61 7 1345.17 939.1 58 19 3692.85 6113.11 240 8 656.77 694.94 31 20 4732.9 9228.25 222 9 370.18 363.48 16 21 2180.23 2866.65 80 10 1590.36 2511.99 66 22 2539.76 2545.63 96 11 616.71 973.73 58 23 3046.95 4787.9 222 12 617.94 516.01 28 24 2192.63 3255.29 163
解:
⑴ 先对Y AK L e αβμ=左右两边同时取对数得:
ln ln ln ln ln Y C K L
C A e αβμ=++=+
相应的数据变为:
通过Eviews 软件进行回归分析得到如下结果:
于是得到回归方程为:
首先可决系数20.892388
R=和修正的可决系数20.882139
R=都是接近于1的,故该回归方程的模拟情况还是比较好的。
在5%的显著性水平下,自由度为(2,21)的F分布的临界值为
0.05(2,21) 3.47
F=,该回归分析的统计量87.07231
F=显著大于3.47,因此ln Y与lnK、lnL有显著
的关系;再看t分布,因为
0.05(21) 1.721
t=,其常数项
02,410253 1.721
β=>、lnK的系数
15.692170 1.721
β=>说明这两项已经通过检验,但是lnL的回归系数没有通过检验。
⑵这个题不知道怎么做,只能根据答案提示做出结果,具体不知道怎么分析。
第四章8题下表列出了某年中国部分省市城镇居民家庭平均每个全年可支配收入(X)与消费性支出(Y)的统计数据。
地区
可支配
收入(X)
消费性
支出(Y)
地区
可支配
收入(X)
消费性
支出(Y)
北京10349.69 8493.49 浙江9279.16 7020.22
天津8140.5 6121.04 山东6489.97 5022
河北5661.16 4348.47 河南4766.26 3830.71
山西4724.11 3941.87 湖北5524.54 4644.5
内蒙古5129.05 3927.75 湖南6218.73 5218.79
辽宁5357.79 4356.06 广东9761.57 8016.91
吉林4810 4020.87 陕西5124.24 4276.67
黑龙江4912.88 3824.44 甘肃4916.25 4126.47
上海11718.01 8868.19 青海5169.96 4185.73
江苏6800.23 5323.18 新疆5644.86 4422.93
解:
⑴最小线性二乘估计的检验结果和回归方程为:
⑵异方差检验
X与Y散点图,从下图可以看出方差基本一致。
怀特检验结果:(这个表有些项看不懂,故也不知道怎么分析)
G-Q检验:
两个样本的估计结果为:
于是得到如下的F 统计量:10.052/4295354.3
4.09883268(4,4) 6.39/472058.15
RSS F F RSS ===<=,故接受原假
设,即不是异方差的。
⑶ 通过上面的检验是不存在异方差性的,不需要纠正异方差性的后果了。
当然,如果显著性水平再高一点的话,该回归模型就不能通过同方差的假设性检验了,此时就需要对此进行一定的修改。
权的确定这部分是看参考答案的,为什么选它目前还没完全明白。
可以得到加权最小最小二乘估计的结果为:
接下来对加权最小二乘得到的回归方程进行怀特检验,有如下结果:。
