第二章 电阻电路的等效变换
合集下载
第二章电阻电路的等效变换

ab
20 100 60
120 60
ab 20 100
100 Rab=70
ab
20 100 60
40
例2 求: Rab
5
15 6
a 20
b
缩短无
电阻支路
7
6
Rab=10
4 a b
15
10
20
5
a
15 b
7 6 6 4 a
b
15 7
3
例6
求: Rab c
对称电路 c、d等电位
R
R
R
c R
a R
断路 a
+a
2 +
U
6V –
(a)
b
3 9V +
(b)
解: a
+
+a U b
a +
3A 2 U
3A 3 U
b
(a)
b
(b)
例1: 求下列各电源等效变换
+a
3A 1 U
解:
(c)
b
a
+
1 +
U
3V –
(c)
b
+a
2A 5 U
(d) b
a
+
5 -
U
10V +
(d)
b
例2: 试用电压源与电流源等效变换的方法,计算2
2.1 概述
1 一些概念
1)电阻电路 仅由电源和线性电阻构成的电路。
2)等效的概念:
若结构、元件参数不相同的两部分电路N1、N2,具 有相同的电压、电流关系,则称它们彼此等效。
i
二章电阻电路等效变换
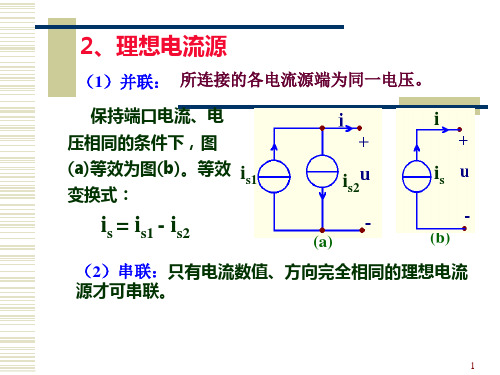
2、理想电流源
(1)并联: 所连接的各电流源端为同一电压。
保持端口电流、电 压相同的条件下,图
(a)等效为图(b)。等效 is1
变换式:
i
is2
is
is = is1 - is2
(a)
(b)
(2)串联:只有电流数值、方向完全相同的理想电流 源才可串联。
1
二、实际电源模型:
1、实际电压源模型
(1)伏安关系:
i=1.5A Uab=6(i-1)=3V R=Uab/1=3Ω
13
四、三个电阻的星形、三角形连接及等效变换 1、电阻的星形、三角形连接
(a) 星形连接(T形、Y形)
(b) 三角形连接(形、形)
14
2、从星形连接变换为三角形连接
R1
R3
R2
R31 R12 R23
变换式:R12
R1
R2
R1R2 R3
∴i3=i2/3 KCL: i2+i3=I
∴i3=i/4 ∴u=3i+2i = 5i
- 2i0 +
i0
i1 i2
i3
R= u/I=5Ω
21
二、含受控源简单电路的分析:
基本分析思想:运用等效概念将含受控源电路化简、 变换为只有一个单回路或一个独立节点的最简形式, 然后进行分析计算。 例1:求电压u、电流i。
R23
R2
R3
R2 R3 R1
15
3、从三角形连接变换为星形连接
R1
R3
R2
变换式:R1
R12
R12 R31 R23
R31
R31 R12 R23
R2
R12
R23 R23
R31
(1)并联: 所连接的各电流源端为同一电压。
保持端口电流、电 压相同的条件下,图
(a)等效为图(b)。等效 is1
变换式:
i
is2
is
is = is1 - is2
(a)
(b)
(2)串联:只有电流数值、方向完全相同的理想电流 源才可串联。
1
二、实际电源模型:
1、实际电压源模型
(1)伏安关系:
i=1.5A Uab=6(i-1)=3V R=Uab/1=3Ω
13
四、三个电阻的星形、三角形连接及等效变换 1、电阻的星形、三角形连接
(a) 星形连接(T形、Y形)
(b) 三角形连接(形、形)
14
2、从星形连接变换为三角形连接
R1
R3
R2
R31 R12 R23
变换式:R12
R1
R2
R1R2 R3
∴i3=i2/3 KCL: i2+i3=I
∴i3=i/4 ∴u=3i+2i = 5i
- 2i0 +
i0
i1 i2
i3
R= u/I=5Ω
21
二、含受控源简单电路的分析:
基本分析思想:运用等效概念将含受控源电路化简、 变换为只有一个单回路或一个独立节点的最简形式, 然后进行分析计算。 例1:求电压u、电流i。
R23
R2
R3
R2 R3 R1
15
3、从三角形连接变换为星形连接
R1
R3
R2
变换式:R1
R12
R12 R31 R23
R31
R31 R12 R23
R2
R12
R23 R23
R31
[工学]第2章 电阻电路的等效变化
![[工学]第2章 电阻电路的等效变化](https://img.taocdn.com/s3/m/e885ad12f111f18583d05a67.png)
2、电压源、电流源 、受控源
US 3、KCL—— IS ∑ i=0 或 ∑ i入= ∑ i出 推广到闭合面
KVL——
∑ u=0
或 ∑u压降= ∑ u压升
沿不同路径两点间的压降相同
二、电阻电路的等效变换
1、电阻串并联: Req、分压、分流 2、Y—△ :
R Δ相邻电阻乘积 R GΔ Y相邻电导乘积 GY
Rn + un _ _ 等效 i
Req
u
Req=( R1+ R2 +…+Rn) = Rk 结论: 串联电路的总电阻等于各分电阻之和。 3. 串联电阻上电压的分配 º + + u1 u u2 _ + º
例:两个电阻分压, 如下图 i
R1
R1 u1 u R1 R2
R2 u2 u R1 R2
即 R IS R 2R R 2R RL + UL _
I S RRL UL 4 R RL
P44例2-4.
求UR 2
受控源和独立源一样可以进行电源转换,但要 注意保存控制量。
12V
+ _
+u _
R
i
2 uR 12V
2
2
+
_
+u _
R
i
2 + 4 uR _
U R 2i 4U R 2i 2i 8i 12V
i = i1+ i2+ …+ ik+ …+in
2. 等效电阻Req
i
i i2 Rk ik Rn in 等效 + u _
+ u _ R1
i1 R2
电阻电路的等效变换

三. 电阻星形联接、三角形联接旳等效互换 由三角形联接求等效星形联接旳公式
比较(1)式和(4)式,可得:
R1
R12
R31 R12 R23 R31
R2
R12
R23 R12 R23
R31
R3
R12
R23 R31 R23 R31
R12
1
i1
R1
2
R2
i2
R31
R3
R23
i3
3
若 R12=R23=R31=R ,则 R1=R2=R3=RT , 且 RT= (1/3) R 。
在分析含受控源旳电路时,也可用以上多 种等效变换措施化简电路。
但要注意:变换过程中不能让控制变量 消失。
例: 求图示二端 电路旳开路 电压Uab。
解:原电路
4Ω
2Ω
a
2A
+
5Ω
U1
-
2U1 b
4Ω
2Ω
+-
4U1
a
2A
+
5Ω
U1
-
b
Uab 4U1 2 (4 5) U1 2 5 10
Uab 4 10 18 22 (V )
第二章 电阻电路旳等效变换
❖ 2.1 等效二端网络 ❖ 2.2 电压源及电流源串、并联电路旳等效变换 ❖ 2.3 实际电源旳两种模型及其等效变换 ❖ 2.4 电阻星形连接与三角形连接旳等效变换 ❖ 2.5 例题
2.1 等效二端网络
电阻电路
仅由电源和线性电阻构成旳 电路
分析措施
(1)欧姆定律和基尔霍夫定律 是分析电阻电路旳根据;
2.1.2 单口网络端口伏安关系(VAR)旳求取
将单口网络从电路中分离出来,标好其端 口电流、电压旳参照方向;
电阻电路的等效变换

+
u
_
各电阻顺序连接,流过同一电流 (判断电路是否为串联的依据)
2)等效电阻
R1
Rk
_
_
i
+ u1
+ uk
+
u
由KVL和VAR得:
Rn
_
+ un
_
等效
Req
i
+u
_
u R1i Rki Rni (R1 Rk Rn )i Reqi
n
等效电阻: Req R1 Rk Rn Rk Rk k 1
电阻元件的串、并联对偶记忆
电阻元件
串联
并联
等效变换 分压/分流 公式
功率比
i相同
u相同
Req R1 R2 Rn Geq G1 G2 ... Gn
uk
Rk Req
u
ik
Gk Geq
i
pk1 Rk1 pk 2 Rk 2
pk1 Gk1 pk 2 Gk 2
三、电阻的混联
电路中有电阻的串联,又有电阻的并联,这种连接方式称电阻的串并 联(混联)。
如果一个电路(网络)向外引出一对端钮,这 对端钮可以作为测量用,也可以用来与外部的电源 或其他电路连接用。这类具有一对端钮的电路称为 一端口电路(网络)或二端电路(网络)。
i
+
N
u
i
N0-无源二端网络 Ns-含源二端网络
2.等效二端电路(网络)
N1 i
+
u
i
-
i
+
N2
u
i
若两个二端网络N1和N2与同一个外部相连,当 相接端钮处的电压、电流关系完全相同时,称N1和 N2互为等效的二端网络。
第2章电阻电路的等效变换

总电流
U S 18 I= = A = 6A R 3
由分流公式得
6 I1 = I = × 6A = 4A 4× 4 9 6 + (1 + ) 4+4
再分流得
6
1 I x = I 1 = 2A 2
返回
电路分析基础
第2章 电阻电路的等效变换
2.2.4 Y形电路和Δ形电路之间 的等效变换
返回
电路分析基础
如何等效化简电桥测温电路? 如何等效化简电桥测温电路?
返回
电路分析基础
第2章 电阻电路的等效变换
2.1 等效变换
电阻电路
线性电阻电路
非线性电阻电路
简化线性电阻电路的主要依据是等效变换
返回
电路分析基础
第2章 电阻电路的等效变换
2.1.1 一端口网络的定义
二端网络
一端口网络
流入一个端子的电流必定等于流出另一端子的电流
Ig =
Rp Rg + R p
× 10 × 10 −3 = 1 × 10 −3 mA
解之得应并联的电阻为
0.1RG 2 × 10 3 Rp = = Ω ≈ 222.22Ω 0.9 9
返回
电路分析基础
第2章 电阻电路的等效变换
2.2.3 电阻的混联
判别电路的串并联关系根据以下原则: 判别电路的串并联关系根据以下原则: (1)看电路的结构特点。 看电路的结构特点。 (2)看电压、电流关系。 看电压、电流关系。 (3)对电路作变形等效。 对电路作变形等效。 (4)找出等电位点。 找出等电位点。
R4 R5 R2(R3 + ) R4+R5 R = R1 + R4 R5 R2 + (R3 + ) R4 + R5
02第二章电阻电路的等效变换

12
12
12
8 //(4 4) 4
R
R eq R
R
R
例6.求Req。
解:
R
R
R
R R
Req
R 8
例7.
R R I1 I2
I3
I4 求:I1 ,I4 ,U4
12V
2R 2R
2R
U4 2R
解:
I1
12 R
I4
1 2
I
3
1 4
I2
1 8
I1
1 8
12 R
3 2R
0.04
16.5mA
10mA
I3
G1
G3 G2
G3
Is
0.04 0.025 0.1
0.04
16.5mA
4mA
三、 电阻的串并联(混联)
电阻的串联和并联相结合的联接方式叫电阻的串并联 (或混联)。
要求:弄清楚串、并联的概念。
计算举例:
4
º
例1.
Req
2 3
Req
i1
i' 1
,
i2
i' 2
,
i3
i' 3
i' 2
2
对,各个电阻的电流分别为:
R31
'
i ' 31
i3 3
1 i'
1
i' 12
i' u12 R 12
12
R 12
R23
第二章电阻电路的等效变换

(2)R1增大,Uis增大,对其它元件均无影响
26
$2-5 电压源及电流源串联和并联(39)
1、电压源串联(如图): 1 + 等效电压源符号: 1 + Us 2 +Us1+ Us2 Us 2 +Usn -
Us=Us1+Us2+….+Usn Usk与Us方向一致取“+”,否则,取“-”
27
2、电流源并联(如图)
22
R 23 R 31
R23
2
2、 △ 型连接等效变换为Y型连接
1
23
R13
R23
R12 2
R R
1
R R R
3
12
R 1 2 R 31 R 23 R R 12 R 23 R 23 R R 31 R 23 R 23 R
31
2
1 R1 R3 3 R2 2
12
31
R
3
• 端口施加电压法求Rin: 端口施加电压源U,则有端口电流I, 求出端口伏安特性表达式:U=IR 则Rin=R=U/I
C)若端口内部有独立电源 先将电压源短路,电流源开路, 求输入电阻归结为 a)b)情况 34
二、实例: 例2-5( 44页)(自学)
练习题 2-12 :试求图(a)图(b)中的Rab
则: I Req=U 等效电路: 结论:串联电阻,等效电阻为各电阻之和。
例2-3-1 电路如图,求U1
I + U1 R1 R2 -
+
Us -
KVL:IR IR U 1 2 S + US I U2 R1 R2 R 1 U R *I Us 1 1 R R 1 2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
-
C
i
+ u
-
对A电路Hale Waihona Puke 言,C代替B后BA
C
A
(1)等效变换的条件
结 论 (2)仅仅是对外等效
(3)对内不等效
两电路具有相同的VCR
即外电路A中的电压、 电流和功率不变。
C是B的简化。
2.3 电阻的串联、并联
1. 电阻串联( Series Connection of Resistors )
(1) 电路特点
R31
R1
R2
R3
2
R23
3
2
3
形网络
Y形网络
R2
b
R4
三端 网络
,Y 网络的变形:
形电路 ( 形)
T 形电路 (Y形)
这两个电路当它们的电阻满足一定的关系时, 能够相互等效。
2. —Y 变换的等效条件
1 +– i1
1 +i1Y –
u12 R12
– i2
2+
R23 u23
等效条件:
i1 =i1Y ,
第二章 电阻电路的等效变换
2.2 电路的等效变换
1. 二端电路(网络)
任何一个复杂的电路, 向外引出两个端钮,且从一个 端子流入的电流等于从另一端子流出的电流,则称这一电 路为二端网络(或一端口网络)。
i i
2. 电路等效的概念
两个二端电路,端口具有相同的伏安特性,则两电路等效
B
i
+ u
等效
i3 =u31 /R31 – u23 /R23
根据等效条件,比较式(3)与式(1),得Y型型的变换条件:
R12
R1R2R2R3R3R1 R3
R23
R1R2R2R3R3R1 R1
R31
R1R2R2R3R3R1 R2
G 12
G 1G 2 G1 G2 G3
或
G 23
G 2G 3 G1 G2 G3
G 31
u31 R31
i3 + –3
u12Y – i2Y R2
2+
R1 u31Y R3 i3Y +
u23Y
–3
i2 =i2Y , i3 =i3Y ,
u12 =u12Y , u23 =u23Y , u31 =u31Y
1 +– i1
1 +i1Y –
u12 R12 – i2 2+
R23 u23
R3u1 31
n
ReqR1R2 Rn Rk k1
结论: 串联电路的总电阻等于各分电阻之和。
R1
R2
Rn
i
+ u1 _ + U 2 _ + un _
等效
i
+
u
_
+
R eq u_
(3) 各电阻的电压
uk
Rki
Rk
u Req
Rk u u Req
说明串联的每个电阻,其电压与电阻值成正比。 串联电阻电路可作分压电路
例i
两个电阻的分压:
º ++
u-1 R1
u1
R1 R1 R2
u
u_ u+2 R2 º
u2
R2 R1 R2
u
注意方向 !
2. 电阻并联 (Parallel Connection)
(1) 电路特点
ii
+
i1 i2
ik
in
u
R1 R2
Rk
Rn
_
(a) 各电阻两端分别接在一起,两端为同一电压 (KVL); (b) 总电流等于流过各并联电阻的电流之和 (KCL)。
-
18
165V
18
9
4 i4
i5
-
12
i11656515A
u 15i15 1575 V
i2 1 5 99 1 8 5 Ao r i216575185A
u26i118i290 V
i315510 A
u3 6i3 60V
i4 1 01 21 24 7 .5 A
i5107.52.5A
u4u53i330V
i
R1
R2
Rn
+
+ u1 _ + u 2 _ + un _ u
_
(a) 各电阻顺序连接,流过同一电流 (KCL);
(b) 总电压等于各串联电阻的电压之和 (KVL)。
u u 1 u k u n
(2) 等效电阻
由欧姆定律 uu 1u ku n
u R 1 i R K i R n i ( R 1 R n ) i R e iq
例 求: Rab
对称电路 c、
c
d等电位
c
R
R
R
i
R
i
a
短路
R
b
R
a i1 R d
根据电
R i2 b
d
c
R
R
流分配
1
i1
2
i
1
i2
1
a
R
uabi1Ri2R(2i2i)RiR
d
R
b
Rab
uab i
R
Rab R
2.4 电阻的Y形连接与Δ连接的
等效变换
c
1.电阻的 ,Y连接
R1
包含 1
a
R3
1d
R12
(2)
i 3 u31 R31u23R23
i1Yi2Yi3Y 0
由式(2)解得:
i1Y
u12YR3u31YR2 R1R2R2R3R3R1
i2Y
u23YR1u12YR3 R1R2R2R3R3R1
i3Y R1uR321YRR 22Ru323YR R31R1
i1 =u12 /R12 – u31 /R31 (3) i2 =u23 /R23 – u12 /R12 (1)
G 3G 1 G1 G2 G3
类似可得到由型 Y型的变换条件:
G1
G 12
G 31
G 12 G 31 G 23
G2
G 23
G 12
G 23 G 12 G 31
G3
G 31
G 23
G 31 G 23 G 12
R1
R 12
R 12 R 31 R 23
R 31
或 R2
R 12
R 23 R 12 R 23 R 31
R3
R 12
R 31 R 23 R 23
R 31
简记方法:
R 相邻电阻乘积 或
R
GΔY相邻 G电Y 导乘积
变Y
Y变
特例:若三个电阻相等(对称),则有
R = 3RY
注意
外大内小
R12 R1 R2
ik
Gku
Gk Geq
i
每个电阻的电流与 其电导值成正比
例 i
º R1
º
i1 R2
Req
1
1R11R2
R1R2 R1R2
i2
i1
G1 Geq
i
R2 R1 R2
i
i2G G e2qiR1R1 R2i(ii1)
例 计算各支路的电压和电流。 i1 5
i1 5
6
+
i2 6 i3
+
i2
i3
165V
ii1 i2 ik in
(2) 等效电阻
由欧姆定律: ii1 i2 ik in
G 1uG 2u G ku G nu
G 1G 2 G k G nuG equ
n
GeqG1G2 Gn Gk k1
并联电路的总电导等于各电导之和
i
i
+
i1 i2
ik
in等效 +
u R1 R2
Rk
Rn
u
Req
_
_
(3) 各电阻的电流
i3 + –3
u12Y – i2Y R2
2+
R1 u31Y R3 i3Y +
u23Y – 3
接: 用电压表示电流
Y接: 用电流表示电压
i1 u12 R 12u31 R31
u 12 Y
R1i1Y R2i2Y
u 2 3 Y R2i2Y R3i3Y
i 2 u23 R23u12R 12 (1) u 3 1 Y R3i3Y R1i1Y
