高斯投影坐标正反算VB程序
坐标反算(VB编程代码)
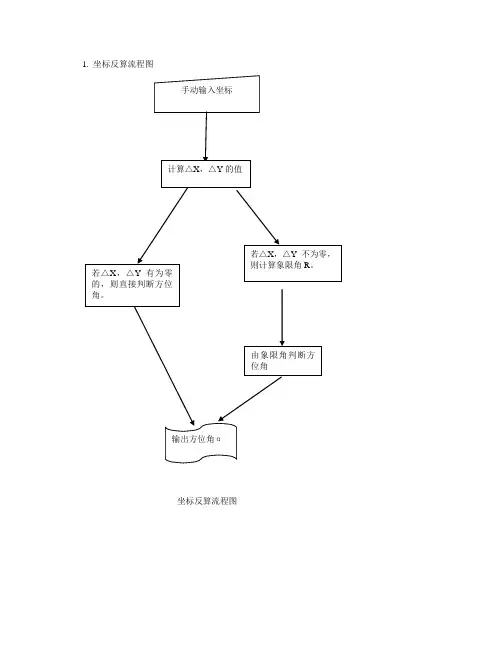
计算△X，△Y 的值
若△X，△Y 有为零 的，则直接判断方位 角。
若△X，△Y 不为零， 则计算象限角 R。
由象限角判断方 位角
输出方位角α
坐标反Sub Command3_Click() Dim Xa, Ya, Xb, Yb, M, N, Rab, R, F, R1, R2, R3 As Single pi = 3.1415926 Xa = Text1.Text Ya = Text4.Text Xb = Text2.Text Yb = Text5.Text M = Xb - Xa '求纵坐标增量 N = Yb - Ya '求横坐标增量 Rab = Math.Atn(Abs(N / M)) * 180 / pi '计算象限角 If M > 0 And N > 0 Then F = Rab '由象限角判断方位角 If M < 0 And N > 0 Then F = 180 - Rab If M < 0 And N < 0 Then F = 180 + Rab If M > 0 And N < 0 Then F = 360 - Rab If M = 0 And N > 0 Then F = 90 If M = 0 And N < 0 Then F = 270 If N = 0 And M > 0 Then F = 0 If N = 0 And M < 0 Then F = 180 R1 = Fix(F) '把弧度化为度 R2 = Fix((F - R1) * 60) R3 = Fix((((F - R1) * 60) - R2) * 60) Text3.Text = R1 & "°" & R2 & "′" & R3 & "″" Text6 = Sqr(M ^ 2 + N ^ 2) End Sub Private Sub Command2_Click() Text1 = "" Text2 = "" Text3 = "" Text4 = "" Text5 = "" Text6 = "" End Sub
高斯投影正算与反算的理论方法与实
高斯投影正算与反算的理论方法与实现代码高斯投影是正形投影的一种，同一坐标系中的高斯投影换带计算公式是根据正形投影原理推导出的两个高斯坐标系间的显函数式。
在同一大地坐标系中(例如1954北京坐标系或1980西安坐标系)，如果两个高斯坐标系只是主子午线的经度不同，那么显函数式前的系数可以根据坐标系使用的椭球元素和主子午线经度唯一确定。
但如果两个高斯坐标系除了主子午线的经度不同以外，还存在其他线性系，则将线性变换公式代入换带计算的显函数式中，仍然可以得到严密的坐标变换公式。
此时显函数式前的系数等价于使用两个坐标系主子午线的经度和线性变换参数联合求解得到的，可以唯一确定。
//6度带宽54北京坐标系//高斯投影由大地坐标(Unit:Metres)反算经纬度(Unit:DD)void GaussProjInvCal(double X, double Y, double *longitude, double *latitude){int ProjNo; int ZoneWide; ////带宽double longitude1,latitude1, longitude0,latitude0, X0,Y0, xval,yval;double e1,e2,f,a, ee, NN, T,C, M, D,R,u,fai, iPI;iPI = 0.0174532925199433; ////3.1415926535898/180.0;a = 6378245.0; f = 1.0/298.3; //54年北京坐标系参数////a=6378140.0; f=1/298.257; //80年西安坐标系参数ZoneWide = 6; ////6度带宽ProjNo = (int)(X/1000000L) ; //查找带号longitude0 = (ProjNo-1) * ZoneWide + ZoneWide / 2;longitude0 = longitude0 * iPI ; //中央经线X0 = ProjNo*1000000L+500000L;Y0 = 0;xval = X-X0; yval = Y-Y0; //带内大地坐标e2 = 2*f-f*f;e1 = (1.0-sqrt(1-e2))/(1.0+sqrt(1-e2));ee = e2/(1-e2);M = yval;u = M/(a*(1-e2/4-3*e2*e2/64-5*e2*e2*e2/256));fai = u+(3*e1/2-27*e1*e1*e1/32)*sin(2*u)+(21*e1*e1/16-55*e1*e1*e1*e1/32)*sin( 4*u)+(151*e1*e1*e1/96)*sin(6*u)+(1097*e1*e1*e1*e1/512)*sin(8*u);C = ee*cos(fai)*cos(fai);T = tan(fai)*tan(fai);NN = a/sqrt(1.0-e2*sin(fai)*sin(fai));R = a*(1-e2)/sqrt((1-e2*sin(fai)*sin(fai))*(1-e2*sin(fai)*sin(fai))*(1-e2*sin(fai)*sin(fai)));D = xval/NN;//计算经度(Longitude) 纬度(Latitude)longitude1 =longitude0+(D-(1+2*T+C)*D*D*D/6+(5-2*C+28*T-3*C*C+8*ee+24*T*T)*D*D*D*D*D/120)/cos(fai);latitude1 = fai -(NN*tan(fai)/R)*(D*D/2-(5+3*T+10*C-4*C*C-9*ee)*D*D*D*D/24+(61+90*T+298*C+45*T*T-256*ee-3*C*C)*D*D*D*D*D*D/720);//转换为度DD*longitude = longitude1 / iPI;*latitude = latitude1 / iPI;}//高斯投影由经纬度(Unit:DD)正算平面坐标(含带号，Unit:Metres)void GaussProjCal(double longitude, double latitude, double *X, double *Y) {int ProjNo=0; int ZoneWide; ////带宽double longitude1,latitude1, longitude0,latitude0, X0,Y0, xval,yval; double a,f, e2,ee, NN, T,C,A, M, iPI;iPI = 0.0174532925199433; ////3.1415926535898/180.0;ZoneWide = 6; ////6度带宽a=6378245.0; f=1.0/298.3; //54年北京坐标系参数////a=6378140.0; f=1/298.257; //80年西安坐标系参数ProjNo = (int)(longitude / ZoneWide) ;longitude0 = ProjNo * ZoneWide + ZoneWide / 2;longitude0 = longitude0 * iPI ;latitude0=0;longitude1 = longitude * iPI ; //经度转换为弧度latitude1 = latitude * iPI ; //纬度转换为弧度e2=2*f-f*f;ee=e2*(1.0-e2);NN=a/sqrt(1.0-e2*sin(latitude1)*sin(latitude1));T=tan(latitude1)*tan(latitude1);C=ee*cos(latitude1)*cos(latitude1);A=(longitude1-longitude0)*cos(latitude1);M=a*((1-e2/4-3*e2*e2/64-5*e2*e2*e2/256)*latitude1-(3*e2/8+3*e2*e2/32+45*e2 *e2*e2/1024)*sin(2*latitude1)+(15*e2*e2/256+45*e2*e2*e2/1024)*sin(4*latitude1)-(3 5*e2*e2*e2/3072)*sin(6*latitude1));xval = NN*(A+(1-T+C)*A*A*A/6+(5-18*T+T*T+72*C-58*ee)*A*A*A*A*A/120); yval = M+NN*tan(latitude1)*(A*A/2+(5-T+9*C+4*C*C)*A*A*A*A/24+(61-58*T+T*T+600*C-330*ee)*A*A*A*A*A*A/720);X0 = 1000000L*(ProjNo+1)+500000L;Y0 = 0;xval = xval+X0; yval = yval+Y0;*X = xval;*Y = yval;}NN卯酉圈曲率半径，测量学里面用N表示M为子午线弧长，测量学里用大X表示fai为底点纬度，由子午弧长反算公式得到，测量学里用Bf表示R为底点所对的曲率半径，测量学里用Nf表示。
vb课程课件测绘程序设计8(八)解析教学提纲
W 1e2si2nB
Ma(1W3e2) Vc3
M─子午圈曲率半径
t tan B 2 e 2 cos 2 B
e2
a2 b2 b2
N a 2 (1 e 2 sin 2 B )
四、工程测量投影面与投影带选择
3、地图投影的分类
等角投影——投影后角度不变，保持小范围内图形相似。 等面积投影——用于某些专题地图，投影后面积不变。 平面投影——投影平面与椭球面在某一点相切，按数学投影建立函数关系。 圆锥面投影——圆锥面与椭球体在某一纬圈相切或某两纬圈相割，按数学 投影。 圆柱面投影——圆柱面或椭圆柱面与椭球面在赤道或某一子午面上相切， 按数字投影。 正轴投影——圆柱面中心轴与椭球短轴重合，圆柱面与赤道相切。 横轴投影——圆柱面中心轴与椭球长轴重合，圆柱面与某一子午圈相切。 斜轴投影——圆柱面中心轴与椭球长、短轴都不重合，位于两者之间。
式中:
A 1 3 e 2 45 e 4 175 e 6 11025 e 8 43659 e10 693693 e12
4 64 256 16384
65536
1048576
B 3 e 2 15 e 4 525 e 6 2205 e 8 72765 e10 297297 e12
6°带带号N和中央子午线经度 LN的关系式：LN=6N-3 3°带带号n和中央子午线经度 Ln的关系式：Ln=3n
6°带与3°带带号之间的关系为 n2N1
三、高斯投影正算和反算
高斯投影坐标正算——由（B，L）求（x，y） 高斯投影坐标反算——由（x，y）求（B，L）
1、由（B，L）计算（x，y）－－正算
1048576
E
315 e 8 3465 e10 99099 e12
坐标正算、反算计算方法及在Excel中的VBA编程
坐标正算、反算计算方法及在Excel 中的VBA 编程测量中经常需要将某点相对坐标系坐标转换成线路的里程、偏距，或根据线路某一里程偏距计算出对应的相对坐标系坐标，为寻求一种快速简单高效的计算方法，本文对线路正算反算的原理进行了阐述，并结合Excel VBA 编程，将编程和Excel 的拖拽的功能相结合，编制出实用计算表，特别适用于需要大量计算边桩、围护桩的情况。
关键词：坐标方位角坐标正算坐标反算 V AB 编程循环迭代直接算法一、坐标方位角的反算1.坐标方位角反算如图1所示，已知点A 、B 的坐标，求直线AB坐标方位角α。
图1坐标方位角反算直线AB 之间的坐标增量：AB B AAB B Ax x x y y y ∆=−∆=−当0,0AB AB x y ∆>∆>时，角α位于第一象限角：arctan ABABy x α∆=∆当0,0AB AB x y ∆<∆>时，角α位于第二象限角：arctan 180AB ABy x α∆=+°∆当0,0AB AB x y ∆<∆<时，角α位于第三象限角：arctan 180AB ABy x α∆=+°∆当0,0AB AB x y ∆>∆<时，角α位于第二象限角：arctan360AB AB y x α∆=+°∆2.坐标方位角反算的VBA 编程可用VBA 将上述过程定义为一个名为angel()的函数，代码如下：Function angel(x0As Double, y0 As Double, x1 As Double, y1 As Double) As Double dx = x1- x0dy = y1- y0If dx > 0 And dy > 0 Thenangel = Atn(dy / dx)End IfIf dx < 0 And dy > 0 Thenangel = Atn(dy / dx) + 3.14159265358979End IfIf dx < 0 And dy < 0 Thenangel = Atn(dy / dx) + 3.14159265358979End IfIf dx > 0 And dy < 0 Thenangel = Atn(dy / dx) + 3.14159265358979 * 2End IfEnd Function二、直线段坐标正算与反算1.直线段正算图2直线段计算已知HZ 点坐标（x1,y1）、里程N HZ ，ZH 点坐标（x2,y2），正算时已知P 点对应的中桩里程Np 和偏距e （规定沿着线路前进方向，左边偏距为负，右边偏距为正），Np>N HZ ，求P 点对应的坐标。
高斯正反算代码 vb
a4 = m4 / 8 + 3 / 16 * m6 + 7 / 32 * m8
a6 = m6 / 32 + m8 / 16
r = x / a0
π = 4 * Atn(1)
If Option1.Value = True And Option3.Value = True Then '国家2000坐标正算
p2 = 0 - a2 / (2 * a0)
p4 = a4 / (a0 * 4)
p6 = 0 - a6 / (6 * a0)
q2 = 0.5 * p2 ^ 3 - p2 - p2 * p4
x3 = 1 / 24 * x1 + 1 / 720 * x2 * m ^ 2
y1 = 1 - t ^ 2 + G ^ 2
y2 = 5 - 18 * t ^ 2 + t ^ 4 + 14 * G ^ 2 - 58 * G ^ 2 * t ^ 2
m = Cos(B) * L
m0 = a * (1 - e ^ 2)
m2 = 1.5 * e ^ 2 * m0
m4 = 5 / 4 * e ^ 2 * m2
m6 = 7 / 6 * e ^ 2 * m4
m2 = 1.5 * e ^ 2 * m0
m4 = 5 / 4 * e ^ 2 * m2
m6 = 7 / 6 * e ^ 2 * m4
m8 = 9 / 8 * e ^ 2 * m6
a0 = m0 + m2 / 2 + 3 / 8 * m4 + 5 / 16 * m6 + 35 / 128 * m8
Gauss投影正反算程序
#include<stdio.h>#include<math.h>#include<stdlib.h>double trans1() //由度分秒到弧度{double B1,B11,B12,B13,B111;scanf("%lf°%lf′%lf″",&B11,&B12,&B13);B111=fabs(B11); //B11可能为负值B1=B111+B12/60.0+B13/3600.0;B1=B1*atan(1)/45.0;if(B11<0)B1=-B1;return B1;}void trans2(double B) //由弧度到度分秒并输出角度值{int a,b;double B0;B0=fabs(B); //B可能为负值double c;B0=B0*45.0/atan(1);a=int(B0);b=int((B0-a)*60);c=(B0-a)*3600-b*60;if((int)(c)==60) //为了避免出现59′60″这种情况，不过好像不起作用，不知道为什么,原来是int没有加括号{b=b+1;c=0.0;}if(b==60){b=0;a=a+1;}if(B<0)a=-a;printf("%d°%d′%.4f″\n",a,b,c);}void Gauss1() //高斯投影坐标正算，克拉索夫斯基椭球{double B,L; //输入经纬度并转换成弧度printf("请输入大地纬度B=\n");B=trans1();printf("请输入大地经度L=\n");L=trans1();double L0,l;printf("请以度分秒的形式（如10°10′10″）输入中央子午线L0=\n");L0=trans1();l=L-L0; //经度与中央子午线之差……坑爹的书上居然又错了!!114°20′0″-117°0′0″=3°20′0″FUCK! 原来是我误会了……人家的L0=111°double R; //平面子午线收敛角γ（仅与B和l有关）R=(1+((0.33333+0.00674*cos(B)*cos(B))+(0.2*cos(B)*cos(B)-0.0067)*l*l)*l*l*cos(B)*cos(B))* l*sin(B);double N,a0,a4,a6,a3,a5; //求解一些常数以及系数N=6399698.902-(21562.267-(108.973-0.612*cos(B)*cos(B))*cos(B)*cos(B))*cos(B)*cos(B);a0=32140.404-(135.3302-(0.7092-0.004*cos(B)*cos(B))*cos(B)*cos(B))*cos(B)*cos(B);a4=(0.25+0.00252*cos(B)*cos(B))*cos(B)*cos(B)-0.04166;a6=(0.166*cos(B)*cos(B)-0.084)*cos(B)*cos(B);a3=(0.3333333+0.001123*cos(B)*cos(B))*cos(B)*cos(B)-0.1666667;a5=0.0083-(0.1667-(0.1968+0.004*cos(B)*cos(B))*cos(B)*cos(B))*cos(B)*cos(B);double x,y; //求解Gauss投影平面坐标想，x,yx=6367558.4969*B-(a0-(0.5+(a4+a6*l*l)*l*l)*l*l*N)*sin(B)*cos(B);y=(1+(a3+a5*l*l)*l*l)*l*N*cos(B);printf("平面坐标系中的坐标\nx=%.4fM\n",x);printf("平面坐标系中的坐标\ny=%.4fM\n",y);printf("平面子午线收敛角R=\n");trans2(R);}void Gauss2() //Gauss投影坐标反算，克拉索夫斯基椭球{double x,y,L0; //输入平面坐标x,y及中央子午线L0=printf("请输入平面坐标系中的坐标x=\n");scanf("%lf",&x);printf("请输入平面坐标系中的坐标y=\n");scanf("%lf",&y);printf("请以度分秒的形式输入（如10°10′10″）输入中央子午线L0=\n");L0=trans1();double beta,Bf,Nf,Z;beta=x/6367558.4969;Bf=beta+(50221746+(293622+(2350+22*cos(beta)*cos(beta))*cos(beta)*cos(beta))*cos(beta)*co s(beta))*1e-10*cos(beta)*sin(beta);Nf=6399698.902-(21562.267-(108.973-0.612*cos(Bf)*cos(Bf))*cos(Bf)*cos(Bf))*cos(Bf)*cos(B f);Z=y/(Nf*cos(Bf));double b2,b3,b4,b5;b2=(0.5+0.003369*cos(Bf)*cos(Bf))*cos(Bf)*sin(Bf);b3=0.333333-(0.166667-0.001123*cos(Bf)*cos(Bf))*cos(Bf)*cos(Bf);b4=0.25+(0.16161+0.00562*cos(Bf)*cos(Bf))*cos(Bf)*cos(Bf);b5=0.2-(0.1667-0.0088*cos(Bf)*cos(Bf))*cos(Bf)*cos(Bf);double B,L,l,R;B=Bf-(1-(b4-0.12*Z*Z)*Z*Z)*Z*Z*b2;l=(1-(b3-b5*Z*Z)*Z*Z)*Z;L=L0+l;R=(1+((0.33333+0.00674*cos(B)*cos(B))+(0.2*cos(B)*cos(B)-0.0067)*l*l)*l*l*cos(B)*cos(B))* l*sin(B);printf("大地纬度B=\n");trans2(B);printf("大地经度L=\n");trans2(L);printf("平面子午收敛角R=\n");trans2(R);}void Gauss3() //换带计算，克拉索夫斯基椭球{double x1,y1,L10;printf("请输入平面坐标系中的原坐标x1=\n");scanf("%lf",&x1);printf("请输入平面坐标系中的原坐标y1=\n");scanf("%lf",&y1);printf("请以度分秒的形式输入（如10°10′10″）原中央子午线L10=\n");L10=trans1();double beta,Bf,Nf,Z;beta=x1/6367558.4969;Bf=beta+(50221746+(293622+(2350+22*cos(beta)*cos(beta))*cos(beta)*cos(beta))*cos(beta)*co s(beta))*1e-10*cos(beta)*sin(beta);Nf=6399698.902-(21562.267-(108.973-0.612*cos(Bf)*cos(Bf))*cos(Bf)*cos(Bf))*cos(Bf)*cos(B f);Z=y1/(Nf*cos(Bf));double b2,b3,b4,b5;b2=(0.5+0.003369*cos(Bf)*cos(Bf))*cos(Bf)*sin(Bf);b3=0.333333-(0.166667-0.001123*cos(Bf)*cos(Bf))*cos(Bf)*cos(Bf);b4=0.25+(0.16161+0.00562*cos(Bf)*cos(Bf))*cos(Bf)*cos(Bf);b5=0.2-(0.1667-0.0088*cos(Bf)*cos(Bf))*cos(Bf)*cos(Bf);double B,L,l1;B=Bf-(1-(b4-0.12*Z*Z)*Z*Z)*Z*Z*b2;l1=(1-(b3-b5*Z*Z)*Z*Z)*Z;L=L10+l1;double L20,l2,R;printf("请以度分秒的形式（如10°10′10″）输入新中央子午线L20=\n");L20=trans1();l2=L-L20; //R=(1+((0.33333+0.00674*cos(B)*cos(B))+(0.2*cos(B)*cos(B)-0.0067)*l2*l2)*l2*l2*cos(B)*cos (B))*l2*sin(B);//子午线收敛角γ（仅与B和l有关）double N,a0,a4,a6,a3,a5; //求解一些常数以及系数N=6399698.902-(21562.267-(108.973-0.612*cos(B)*cos(B))*cos(B)*cos(B))*cos(B)*cos(B);a0=32140.404-(135.3302-(0.7092-0.004*cos(B)*cos(B))*cos(B)*cos(B))*cos(B)*cos(B);a4=(0.25+0.00252*cos(B)*cos(B))*cos(B)*cos(B)-0.04166;a6=(0.166*cos(B)*cos(B)-0.084)*cos(B)*cos(B);a3=(0.3333333+0.001123*cos(B)*cos(B))*cos(B)*cos(B)-0.1666667;a5=0.0083-(0.1667-(0.1968+0.004*cos(B)*cos(B))*cos(B)*cos(B))*cos(B)*cos(B);double x2,y2;x2=6367558.4969*B-(a0-(0.5+(a4+a6*l2*l2)*l2*l2)*l2*l2*N)*sin(B)*cos(B);y2=(1+(a3+a5*l2*l2)*l2*l2)*l2*N*cos(B);printf("平面坐标系中的坐标x2=%.4fM\n",x2);printf("平面坐标系中的坐标y2=%.4fM\n",y2);printf("平面子午线收敛角R=\n");trans2(R);printf("大地纬度B=\n");trans2(B);printf("大地经度L=\n");trans2(L);}void main(){int k;printf("请输入k=\n");printf("注：k=1表示正算（BL→xy）k=2表示反算（xy→BL）k=3表示换带（x1y1→x2y2）\n");scanf("%d",&k);if(k==1)Gauss1();if(k==2)Gauss2();if(k==3)Gauss3();}。
基于VB6.0的高斯投影坐标转换的实现
收 稿 日期 ：０ ０— ２ ２ ２１Leabharlann １ — ２作 者简 介 ： 安
卫 （９４一 ）男 ， １８ ， 彝族 ， 州大 方人 ， 贵 助理工 程 师 ， 士 ， 学 主要从 事城镇 地籍 测量 及 Ｃ Ｄ与 ＧＳ 面 的二次 开发 工作 。 Ａ Ｉ方
我国规定按经差 ６ 和 ３进行分 带 ， 。 。 一般 情况下 ， 在进行
ｎ—ｂ
（） ９
采用式 （ ２）～式 （ ９）即 － 计 算 出 高 斯 投 影 的 正 算 ． ｊ
大 比例尺测 图和工程测量时 采用 ３带投影 。在特殊 的情况 。 下， 工程测量控制 网 也可 以采 用 １５ 带或 任 意带 。但 是 为 ．。
Ｏ 引 言
在 日常 的 测 量 工 作 中 ， 业 测 量 的 坐 标 一 般 为 外 ＷＧ Ｓ一８ ４坐标 ， 也称 经纬 度坐 标 ， 而最终 的测 图 成果 均为 平面 直 角坐标 系 ， 因此 这 就 涉 及 经 纬 度 坐标 与平 面 直 角
㈩
＝ Ｙ （ 曰） ， Ｊ
Ｐ ｏｅｔ ｎ Ｕｓ ｇＶＢ ６ ０ ｒｊｃｉ ｉ ． ｏ ｎ
ＡＮ Ｗ ｅ 。 ＧＥ Ｙａ ｇ ， ＡＯ Ｗ ｅ ， ＯＮＧ ｉ ｎ Ｃ ｉ Ｓ Ｂｏ
，
（ ． ｉｎｉ ｎｔ ｕｅｏ ｕ ｖｙｎ ｎ ａ ｐｎ ， ｉｎｉ ０ ３ １ Ｃ ｉａ １ Ｔａｊ Ｉｓｉ ｔ ｆ ｒｅｉｇａ ｄＭ ｐ ｉｇ Ｔａ ｊ ３０ ８ ， ｈｎ ； ｎ ｔ Ｓ ｎ ２ Ｔ ｅＸ ｑｎ ｒｎｈ ｏ ｉｎｉ ｎｃ ａ Ｂ ｒａ ｆ ａ ｄ Ｒ ｓｕ ｃｓａ ｄＨｏ ｎ ａ ａ ｅ ｎ ， ｉｎｉ ０ ３ １ Ｃ ｎ ） ． ｈ ｉｉｇＢ ａ ｃ ｆ ａ ｊ Ｍｕ ｉｉ ｌ ｕｅ ｕｏ ｎ ｅｏ ｒｅ ｍｉｇＭ ｎ ｇ ｍｅ ｔＴａ ｊ ３０ ８ ， ｈ ａ Ｔ ｎ ｐ Ｌ ｎ ｎ ｉ
vb坐标正算程序
VB坐标正算程序简介VB坐标正算程序是一种用于计算地理坐标的计算机程序，使用VB语言编写。
本文将深入探讨VB坐标正算程序的原理、功能以及使用方法。
原理VB坐标正算程序基于数学和地理学的原理，通过输入已知的地理坐标和相关参数，计算出目标点的地理坐标。
其原理主要包括以下几个步骤：1. 坐标系统转换VB坐标正算程序支持不同的坐标系统，如经纬度坐标、UTM坐标等。
在进行计算之前，需要将输入的坐标转换为程序所使用的统一坐标系统。
2. 大地测量模型大地测量模型是VB坐标正算程序中的核心算法，用于计算地球上两点之间的距离和方位角。
常用的大地测量模型有球面模型和椭球模型，根据实际需求选择合适的模型进行计算。
3. 参数输入在进行坐标正算之前，需要输入已知的地理坐标和相关参数。
已知的地理坐标可以是已知点的经纬度或UTM坐标，相关参数包括大地测量模型的参数、椭球模型的参数等。
4. 坐标计算根据已知的地理坐标和相关参数，通过大地测量模型进行计算，得出目标点的地理坐标。
功能VB坐标正算程序具有以下主要功能：1. 坐标系统转换VB坐标正算程序可以实现不同坐标系统之间的转换，如经纬度坐标转换为UTM坐标，UTM坐标转换为经纬度坐标等。
通过这个功能，用户可以方便地在不同坐标系统之间进行转换。
2. 大地测量计算VB坐标正算程序可以根据已知的地理坐标和相关参数，通过大地测量模型计算目标点的地理坐标。
用户只需输入已知点的坐标和相关参数，程序即可自动计算出目标点的坐标。
3. 参数设置VB坐标正算程序提供了参数设置功能，用户可以根据实际需求设置大地测量模型的参数、椭球模型的参数等。
通过参数设置，用户可以根据实际需求进行精确的坐标计算。
4. 结果输出VB坐标正算程序可以将计算结果以文本形式输出，用户可以方便地查看计算结果。
输出结果包括目标点的经纬度坐标、UTM坐标等。
使用方法以下是VB坐标正算程序的使用方法：1. 安装程序首先，用户需要将VB坐标正算程序安装到计算机上。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
高斯投影坐标正反算V B程序文件编码（GHTU-UITID-GGBKT-POIU-WUUI-8968）高斯投影坐标正反算学院：班级：学号：姓名：课程名称:指导老师：实验目的：1.了解高斯投影坐标正反算的基本思想；2.学会编写高斯正反算程序，加深了解。
实验原理：高斯投影正算公式中应满足的三个条件：1. 中央子午线投影后为直线；2. 中央子午线投影后长度不变；3. 投影具有正形性质，即正形投影条件。
高斯投影反算公式中应满足的三个条件：1. x坐标轴投影成中央子午线，是投影的对称轴；2. x轴上的长度投影保持不变；3. 正形投影条件，即高斯面上的角度投影到椭球面上后角度没有变形，仍然相等。
操作工具：计算机中的代码：Dim a As Double, b As Double, x As Double, y As Double, y_#Dim l_ As Double, b_ As Double, a0#, a2#, a4#, a6#, a8#, m2#, m4#, m6#, m8#, m0#, l0#, e#, e1#Dim deg1 As Double, min1 As Double, sec1 As Double, deg2 As Double, min2 As Double, sec2 As DoublePrivate Sub Command1_Click()Dim x_ As Double, t#, eta#, N#, W#, k1#, k2#, ik1%, ik2%, dh% deg1 = Valmin1 = Valsec1 = Valdeg2 = Valmin2 = Valsec2 = Vall_ = (deg1 * 3600 + min1 * 60 + sec1) / 206265b_ = (deg2 * 3600 + min2 * 60 + sec2) / 206265dh = Valk1 = ((l_ * 180 / + 3) / 6)k2 = (l_ * 180 / / 3)ik1 = Round(k1, 0)ik2 = Round(k2, 0)If dh = 6 Thenl0 = 6 * ik1 - 3ElseIf dh = 3 Thenl0 = 3 * ik2ElseMsgBox "error", 48, "error": Exit SubEnd IfEnd Ifl = l_ - l0 * / 180e = Sqr(a * a - b * b) / am0 = a * (1 - e * e)m2 = e * e * m0 * 3 / 2m4 = e * e * m2 * 5 / 4m6 = m4 * e * e * 7 / 6m8 = e * e * m6 * 9 / 8a0 = m0 + m2 / 2 + m4 * 3 / 8 + m6 * 5 / 16 + m8 * 35 / 128a2 = m2 / 2 + m4 / 2 + m6 * 15 / 32 + m8 * 7 / 16a4 = m4 / 8 + m6 * 3 / 16 + m8 * 7 / 32a6 = m6 / 32 + m8 / 16a8 = m8 / 128x_ = a0 * b_ - a2 * Sin(2 * b_) / 2 + a4 * Sin(4 * b_) / 4 - Sin(6 * b_) * a6 / 6 + Sin(8 * b_) * a8 / 8t = Tan(b_)e1 = Sqr((a * a - b * b) / (b * b))eta = Sqr(e1 * e1 * Cos(b) * Cos(b))W = Sqr(1 - e * e * Sin(b_) * Sin(b_))N = a / Wx = x_ + N * Sin(b_) * Cos(b_) * l * l / 2 + N * Sin(b_) *Cos(b_) ^ 3 * (5 - t * t + 9 * eta * eta + 4 * eta ^ 4) * l ^ 4 / 24 + N * Sin(b_) * Cos(b_) ^ 5 * (61 - 58 * t * t + t ^ 4) * l ^ 6 / 720y = N * Cos(b_) * l + N * Cos(b_) ^ 3 * (1 - t * t + eta * eta) * l * l * l / 6 + N * Cos(b_) ^ 5 * (5 - 18 * t * t + t ^ 4 + 14 * eta * eta - 58 * eta * eta * t * t) * l ^ 5 / 120Text7 = xIf dh = 6 Theny_ = y + 500000 + 1000000 * ik1ElseIf dh = 3 Theny_ = y + 500000 + 1000000 * ik2ElseMsgBox "error", 48, "error": Exit SubEnd IfEnd IfText8 = y_End SubPrivate Sub Command2_Click()Dim bf#, j%, Wf#, Vf#, Nf#, Mf#, c#, tf#, etaf#, dh%, ik%x = Valy_ = Vale = Sqr((a * a - b * b) / (a * a))m0 = a * (1 - e * e)m2 = e * e * m0 * 3 / 2m4 = e * e * m2 * 5 / 4m6 = m4 * e * e * 7 / 6m8 = e * e * m6 * 9 / 8a0 = m0 + m2 / 2 + m4 * 3 / 8 + m6 * 5 / 16 + m8 * 35 / 128 a2 = m2 / 2 + m4 / 2 + m6 * 15 / 32 + m8 * 7 / 16a4 = m4 / 8 + m6 * 3 / 16 + m8 * 7 / 32a6 = m6 / 32 + m8 / 16a8 = m8 / 128bf = x / a0For j = 1 To 10bf = (x + a2 / 2 * Sin(2 * bf) - a4 * Sin(4 * bf) / 4 + a6 * Sin(6 * bf) / 6 - a8 * Sin(8 * bf) / 8) / a0Next je1 = Sqr(a * a - b * b) / bVf = Sqr(1 + e1 * e1 * Cos(bf) * Cos(bf))Wf = Sqr(1 - e * e * Sin(bf) * Sin(bf))Nf = a / Wfc = a * a / bMf = c / Vf ^ 3tf = Tan(bf)e1 = Sqr((a * a - b * b) / (b * b))etaf = Sqr(e1 * e1 * Cos(bf) * Cos(bf))ik = Int(y_ / 1000000)y = y_ - ik * 1000000 - 500000b_ = bf - tf * y * y / (2 * Mf * Nf) + tf * (5 + 3 * tf *tf + etaf * etaf - 9 * etaf * etaf * tf * tf) * y * y * y * y / (24 * Mf * Nf * Nf * Nf) + tf * (61 + 90 * tf * tf + 45 * tf * tf * tf * tf) * y * y * y * y * y * y / (720 * Mf * Nf * Nf * Nf * Nf * Nf)l = y / (Nf * Cos(bf)) - (1 + 2 * tf * tf + etaf * etaf) * y * y * y / (6 * Nf * Nf * Nf * Cos(bf)) + (5 + 28 * tf * tf + 24 * tf * tf * tf * tf + 6 * etaf * etaf + 8 * etaf * etaf * tf * tf) * y * y * y * y * y / (120 * Nf * Nf * Nf * Nf * Nf * Cos(bf))dh = ValIf dh = 6 Thenl0 = 6 * ik - 3ElseIf dh = 3 Thenl0 = 3 * ikElseMsgBox "error", 48, "error": Exit Sub End IfEnd Ifl_ = l0 * / 180 + lsec1 = l_ * 206265deg1 = Int(sec1 / 3600)min1 = Int((sec1 - deg1 * 3600) / 60) sec1 = sec1 - deg1 * 3600 - min1 * 60 sec2 = b_ * 206265deg2 = Int(sec2 / 3600)min2 = Int((sec2 - deg2 * 3600) / 60) sec2 = sec2 - deg2 * 3600 - min2 * 60 Text1 = deg1Text2 = min1Text3 = Round(sec1, 5)Text4 = deg2Text5 = min2Text6 = Round(sec2, 5) End SubPrivate Sub Command3_Click() EndEnd SubPrivate Sub Command4_Click() = ""= ""= ""= ""= ""= ""= ""= ""= ""= ""End SubPrivate Sub Option1_Click() a = 6378245b =End SubPrivate Sub Option2_Click()a = 6378140b = 6356755.End SubPrivate Sub Option3_Click()a = 6378137b =End SubPrivate Sub Option4_Click()a = 6378137b =End SubPrivate Sub Option5_Click()a = Val(InputBox("a", "plsase input"))b = Val(InputBox("b", "please input")) End Sub界面截图如下：使用方法：1.如下所示，高斯投影坐标正算时，在经度纬度相应的文本框里输入经纬度，再在度号对应的文本框里输入是六度带还是三度带，最后按坐标正算按钮即可，答案会显示在X，Y相应的文本框里；2.如果要进行坐标反算，则输入X，Y与度号，最后按坐标反算按钮即可得到所需的大地经纬度；3.注意选择需要的椭球。