(完整版)定积分的应用--平面图形的面积
合集下载
定积分的简单应用__平面图形的面积

的面积。
y
y=x-2
解:阴影部分面积
2
S=S1+S2.
S1由y= x ,y= - x , 1
x=1围成:
s1 s2
o 12
4
x
S2由y= x,y= x-2 , -1
x=1围成:
-2 x=1
y2
x=
1
s1
[
0
x (
x )]dx,
4
s2
[
1
x (x 2)]dx,
1
4
s 0 2 xdx 1 ( x x 2)dx.
例 1 计算由两条抛物线 y2 x和 y x2所围成的
图形的面积.
解
y y
x x2
x
0及x
1
两曲线的交点 O(0,0) B(1,1)
y
y2 x
B
C y x2
D
o
Ax
S S曲梯形OABC - S曲梯形OABD
1 xdx 1 x2dx
0
0
S
1
(
0
x - x2 )dx
2 3 x3 1 3 x 2 3 0
9 2
学习小结: 求在直角坐标系下平面图形的面积步骤: 1.作图象; 2.求交点的横坐标,定出积分上、下限; 3.确定被积函数,用定积分表示所求的面积, 特别注意分清被积函数的上、下位置; 4.用牛顿-莱布尼茨公式求定积分.
课外练习
作业:课本 P67 A 组 T2
y x4
4
y 2x
2 S1
S2 y x 4
S1
8
2
S 2S1 S2 2 0
8
2xdx ( 2
2x x 4)dx
定积分的简单应用__平面图形的面积

的面积。
y
y=x-2
解:阴影部分面积
2
S=S1+S2.
S1由y= x ,y= - x , 1
x=1围成:
s1 s2
o 12
4
x
S2由y= x,y= x-2 , -1
x=1围成:
-2 x=1
y2
x=
1
s1
[
0
x (
x )]dx,
4
s2
[
1
x (x 2)]dx,
1
4
s 0 2 xdx 1 ( x x 2)dx.
y x4
4
y 2x
2 S1
S2 y x 4
S1
8
2
S 2S1 S2 2 0
8
2xdx ( 2
2x x 4)dx
y2 2x
2
8
0 2 2xdx 2 ( 2x x 4)dx
42 3
3
x2
|02
(2 2 3
3
x2
1 2
x2
4x)
|82
16 3
64 3
26 3
18
例3.求曲线x= y2 和直线y=x-2所围成的图形
4
8
8
8
8
(0 2xdx 4 2xdx) 4 (x 4)dx 0 2xdx 4 (x 4)dx
2
2 3
3
x2
|80
( 1 2
x2
4x)
|84
40 3
练习1
练习2
练习 1(课本变式题):
计算由曲线 y2 2x和直线 y x 4所围成的图形的面积.
解: 两曲线的交点
定积分的应用§1平面图形的面积§2由平行截面面积求体积省名师优质课赛课获奖课件市赛课一等奖课件

1
4
A1
[
0
x (
x )]dx , 3
所以A=A1+A2=
32 3
.
A2
9 1
x
x
2
3
dx
28 3
首页 ×
(ii)设平面图形由左、右两条连续曲线x=g1 (y) ,x=g2 ( y ) 及上、下两条平行直线y=c,y=d(c< d)所围成,
其面积计算公式为
A=
d c
g2
y
g1
y
dy
射线 = i(i=1,2,…,n-1)把扇形提成n个 小扇形.
首页 ×
(ii)因为r( )是连续旳,所以当 T 很小时,在
每一种 i [i1,i ] 上r( )旳值变化也很小.任取
便有 r( ) r(i ),i i ,
i=1,2,…,n.
这时,第i个小扇形旳面积
于是
Ai
1 2
r 2 (i
f1 x dx
(1)
注 当两条直线其中之一或两条缩为点时,仍可用公式(1).
首页 ×
例1 求由抛物线 y2 x 与直线x-2y-3=0所围平面
图形旳面积A.
y x=1
解 先求出抛物线与直线旳
交点P(1,-1)与Q(9,3).
用x=1把图形分为左、 O
x
右两部分,应用公式(1)
分别求得它们旳面积为
)
i ,
A
n i 1
1 2
r 2 (i
)
.
(iii)由定积分旳定义和连续函数旳可积性,当
T →0时,上式右边旳极限即为公式(5)中 旳定积分.
首页 ×
.
上面例1中也可把抛物线方程和直线方程改写成
第六章 定积分(2)
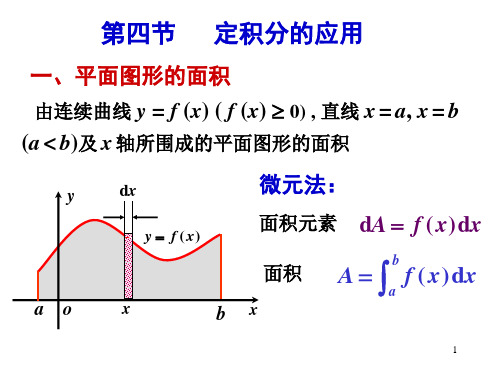
若 f ( x ) g( x ) ,
y
y f ( x)
y g( x )
a o
x x dx
b
x
面积元素: dA [ f ( x ) g( x )] dx ,
A [ f ( x ) g( x )] dx
a
b
3
一般地,
y
y f ( x)
y g( x )
a o
b
围成的平面图形的面积. 解 交点 x 1 , 由对称性,
x2 y 2
2
y
1 y 1 x2
3Βιβλιοθήκη 1 213o
2
1
3
x
x 1 1 x ) dx S 2 ( ) dx 2 ( 2 2 1 0 1 x 2 1 x 2 2 3 . 3 3
16
二、平行截面面积为已知的立体的体积 一个立体, 夹在平面 x a 和 x b 之间, 被垂直于 x 轴的平面所截的截面积为A( x ) ,则该立体的体积为
a
27
b
y
y f ( x)
V y 2 x f ( x ) dx
a
b
o a
b
x
y
上例:
2
1 2 0
y 2x2
Vy 2 x 2 x dx .
o
1
x
28
例13 求由曲线 y ( x 1)( x 2) 和 x 轴所围平面图 形绕 y 轴旋转一周而成的旋转体体积. 2 解 V y 2 x( x 1)( x 2) dx . 1 2 y y
y
a x
利 用 圆 面 积
9
第十章定积分的应用§1平面图形的面积

轴所围成的曲边梯形的面积为
y
y f (x)
0 a
bx
2 、 若 f ( x )在 [a , b ]上 不 都 是 非 负 的 ,
则所围成图形(如右图)
y
b
的 面 积 为 A f (x) dx.
a
c
d
f (x)dx f (x)dx
o
a
c
a c od
e
b
f (x)dx f (x)dx.
a
4、若平面区域是 y—区域:
由左曲线 x1 g1( y) 、 右曲线 x2 g2 ( y) 、下 直线 y a 、上直线 y b
所围成, 则其面积公式为:
y b
xg1(y) g1( y) dy. 如
o
a
图所示。
xg2(y) x
5、如果平面区域既不是x—型区域,也 不是y—型区域,则用一组平行于坐标 轴的直线,把平面区域分成尽可能少的 若干个x—型区域与y—型区域,然后计 算每一区域的面积,则平面区域总的面 积等于各区域面积之和。如右下图:
A
B
D
C
a
o
F E
b x
G
显然:由图可以知道上部分曲线由三
条不同的曲线:AB、BC与CD 构成;下 部分曲线由两条不同曲线:EF与FG所构 成。为计算其面积,可分别过点B、C与 F作平行于 y轴的直线,这样则把平面区 域分成4个x—型区域,然后利用前面的X ——型区域的公式就可以计算了。
下面看几个计算的例子我们就清楚利
计算公式得面积
A
3
2
1
y
3
y 2 d y
10
y
y f (x)
0 a
bx
2 、 若 f ( x )在 [a , b ]上 不 都 是 非 负 的 ,
则所围成图形(如右图)
y
b
的 面 积 为 A f (x) dx.
a
c
d
f (x)dx f (x)dx
o
a
c
a c od
e
b
f (x)dx f (x)dx.
a
4、若平面区域是 y—区域:
由左曲线 x1 g1( y) 、 右曲线 x2 g2 ( y) 、下 直线 y a 、上直线 y b
所围成, 则其面积公式为:
y b
xg1(y) g1( y) dy. 如
o
a
图所示。
xg2(y) x
5、如果平面区域既不是x—型区域,也 不是y—型区域,则用一组平行于坐标 轴的直线,把平面区域分成尽可能少的 若干个x—型区域与y—型区域,然后计 算每一区域的面积,则平面区域总的面 积等于各区域面积之和。如右下图:
A
B
D
C
a
o
F E
b x
G
显然:由图可以知道上部分曲线由三
条不同的曲线:AB、BC与CD 构成;下 部分曲线由两条不同曲线:EF与FG所构 成。为计算其面积,可分别过点B、C与 F作平行于 y轴的直线,这样则把平面区 域分成4个x—型区域,然后利用前面的X ——型区域的公式就可以计算了。
下面看几个计算的例子我们就清楚利
计算公式得面积
A
3
2
1
y
3
y 2 d y
10
高等数学- 定积分的应用

x
0 L(x)dx c0
L(x) x2 L(x)dx x1
例1 设固定成本为50万元,R(Q) 100 - 2Q, C(Q) 14Q 20,试确定厂商的最大利润
四、小结
求在直角坐标系下、参数方程形式 下、极坐标系下平面图形的面积.
(注意恰当的选择积分变量有助于简化 积分运算)
绕 x轴旋转一周
Vx
b (f 2 (x) g2 (x))dx
a
(3) x (y),y c,y d围成图形绕 y轴旋转而成的体积为
Vy
d 2 (y)dy
c
y
d
x ( y) c
o
x
例1 求 x2 y 2 1 (1)绕x轴,(2)绕y轴旋转产 a2 b2
生的旋转体体积
解 : (1)绕x轴
y b a2 x2 a
Vx
a y 2dx
a
2
a b2 0 a2
(a2
x2 )dx
2b 2 a2
(a2x
1 3
x
3
)
|a0
4 ab2 3
(2)绕y轴
Vy
2 2
a x | f (x) | dx
0
4
a b2 0 a2
x
a2 x2dx 4 a2b 3
例2 求y x2 ,x y2围成平面图形绕x轴旋转
而成的旋转体体积.
练习题答案
一、1、1;
2、32 ; 3
4、 y ;
5、e 1 2 ; e
二、1、3 ln 2; 2
2、7 ; 6
4、3a2 ;
5、5 ; 4
三、9 . 4
四、e . 2
3、2;
6、1 . 2
定积分的应用:平面图形面积

一、 填空题: 1、由曲线 y e x , y e 及 y 轴所围成平面区域的面积 是______________ . 2、由曲线 y 3 x 2 及直线 y 2 x 所围成平面区域的 面积是_____ . 3、由 曲 线 y x 1 x 2 , y 1 , x 1 , x 1 所 围 成平面区域的面积是_______ . 4 、计算 y 2 2 x 与 y x 4 所围的区域面积时,选用 ____作变量较为简捷 . 5 、由曲线 y e x , y e x 与直线x 1 所围成平面区 域的面积是_________ .
r ( )
d
o 1 面积元素 dA [ ( )]2 d 2 1 曲边扇形的面积 A [ ( )]2 d .
x
2
例 4
求双纽线 a cos 2 所围平面图形
2 2
的面积.
解 由对称性知总面积=4倍第 一象限部分面积
y x
A 4 A1
在(0,1) 内的一条切线, 使它与
两坐标轴和抛物线所围图形的面积最小.
B M
它与 x , y 轴的交点分别为
A
所指面积
得[ 0 , 1] 上的唯一驻点
B M
A
且为最小点 . 故所求切线为
x (t ) 如果曲边梯形的曲边为参数方程 y (t )
曲边梯形的面积
A ( t ) ( t )dt .
练习题答案
32 一、1、1; 2、 ; 3、2; 3 1 1 y e 2 4、 ; 5、 ; 6、 . e 2 3 7 2 a 二、1、 ln 2 ; 2、 ; 3、 ; 2 6 5 3 2 2 3 a 4、 ; 5、 ; 6、 a . 2 4 9 e 8 2 三、 . 四、 . 五、 a . 4 2 3
r ( )
d
o 1 面积元素 dA [ ( )]2 d 2 1 曲边扇形的面积 A [ ( )]2 d .
x
2
例 4
求双纽线 a cos 2 所围平面图形
2 2
的面积.
解 由对称性知总面积=4倍第 一象限部分面积
y x
A 4 A1
在(0,1) 内的一条切线, 使它与
两坐标轴和抛物线所围图形的面积最小.
B M
它与 x , y 轴的交点分别为
A
所指面积
得[ 0 , 1] 上的唯一驻点
B M
A
且为最小点 . 故所求切线为
x (t ) 如果曲边梯形的曲边为参数方程 y (t )
曲边梯形的面积
A ( t ) ( t )dt .
练习题答案
32 一、1、1; 2、 ; 3、2; 3 1 1 y e 2 4、 ; 5、 ; 6、 . e 2 3 7 2 a 二、1、 ln 2 ; 2、 ; 3、 ; 2 6 5 3 2 2 3 a 4、 ; 5、 ; 6、 a . 2 4 9 e 8 2 三、 . 四、 . 五、 a . 4 2 3
定积分应用求面积
y2 2
4
y3
4
4y 2
6
2
18
8
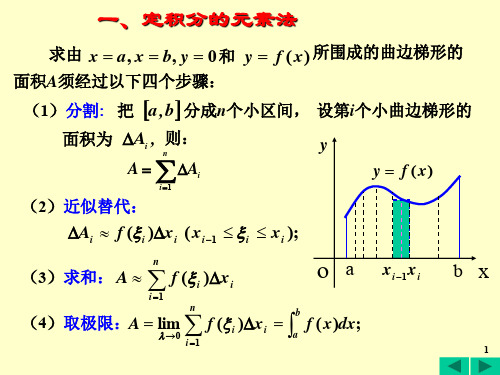
注:如果取x为积分变量
X型 在 0,8 上任取小区间x, x dx,
则 dA 2 x1xdx
A
8
0
2 x
y穿出
1 x
y穿入
dx
y
dA
o (2,2)
(8,4)
以 f ( x)dx作为 A的近似值。
即: A f ( x)dx
f ( x)dx 叫做面积元素, 记为
dA f ( x)dx
Oa
y f (x)
A
dx
x x dx
b
x
b
(3)写出A的积分表达式,即:A f ( x)dx a
3
一般地,如果某一实际问题中的所求量 U符合下列条件:
以极点O为圆心,以 a为半径的的圆的极坐标方程: r a.
P(r, )
P(r, )
r
O
(a,0) x O (a,0)
x
P(r, )
3
3
O
x
以点(a,0) 为圆心,以 a 为半径的的圆的极坐标方程 r 2a cos
过极点O,且与极轴的夹角为 的直线方程 .
(1)U是与一个变量x的变化区间[a,b]有关的量; (2)U对于区间[a,b]具有可加性;
(3)部分量
U
的近似值可表为
i
f i xi
那么这个量就
可以用积分来表示。
具体步骤是:
(1)确定积分变量,和它的变化区间[a,b]; (2)写出积分元素
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
C3x
跨度为6米, 高为3米,此抛物
线形拱桥的横截面积为多少?
解:如图建立平面直角坐标系,
A
-3
B
可设抛物线方程为
y ax2 (a 0)
于是抛物线形拱桥的横截面积
S= S长方形 - S曲边梯形
点 (3,3)代入方程,得
a 1
所以抛物线方程
3 y
1
x2
3
= 18 -
3 1 x2dx 3 3
=12 - 3 1 x2dx
3 3
计算
问题情境
b
a f ( x)dx 的几何意义是什么?
几何意义
y
当 f (x) ≥ 0,定积分
b
a f (x)dx
0
a
表示曲线 y = f (x),直线 x = a,
x = b和 x 轴所围成的曲边梯形
的面积
y f (x)
bx
几何意义
ya
b
当函数 f (x) 0 , 定积分 x
b
a f (x)dx
1 2
y2)d
y
所围图形
y y2 2x (8, 4)
o
yx4 x
(2, 2)
18
定积分在几何上的应用
y
y y 2 (x)
y 1(x)
oa x b
x
X —型:
a x b
d
y
cx 1( y) o
x 2 ( y)
x
Y —型:
c yd
h 2 (x) 1(x) h 2 ( y) 1( y)
y f (x)
就是位于x轴下方的曲边梯形
面积的相反数. 即
b
a f (x)dx S
几何意义
对于函数值有正有负的连续函数 f ( x)
定积分
b
f (x)dx
a
y
S1
C
d
S3
b
a
S2
x
b
a f ( x)d x S1 S2 S3
热身练习
1.用定积分求下列图形的面积
1
y
y 1 x2
-1
o 1x
求由曲线围成的平面图形面积
情境回归
如图所示, 一抛物线形拱桥的
跨度为6米, 高为3米,此抛物 线形拱桥的横截面积为多少? 解:如图建立平面直角坐标系,
可设抛物线方程为
y ax2 (a 0)
-3
点 (3,3)代入方程,得
a 1
于是抛物线方程
3 y
1
x2
3
(3,3)
3米
6米
y
o
3x
-3
(3,3)
情境回归
热身练习
y y sin x
x
0
范例
1、 计算:由曲线 f ( x) x2 ,直线
x 2, x 2和 x 轴所围成的
-2
曲边梯形的面积
解:
S
=-
2 x2dx
2
2 x2dx
2
1 3
x3
2 2
1 23 (2)3 16
3
3
y
oБайду номын сангаас
2
x
f (x) x2
变式
2、如图所示由 y 4和 f ( x) x2所围图形的
1.通过本堂课的学习,你获得了什么数学知识? 定积分解决平面上曲边形面积的问题
一 般
①根据题意画出图形;
步 ②确定积分上下限和被积函数,
骤 写出相应的积分表达式
③计算定积分,得出所求图形
的面积
情境回归
如图所示, 一抛物线形拱桥的
跨度为6米, 高为3米,此抛物
3米
线形拱桥的横截面积为多少?
6米
建立平面直角坐标系 确定抛物线方程
面积是多少?
y
s 解:
S
S - ABCD
曲 边 梯 形ABCD
44 - 16
2
2
x
2dx
A
-2
o
16
3
-4
32
C
3
B
2
x
y 4
D f (x) x2
y
AS
0a
b X0
曲边形
抽象
S1
长方形
面积 S=S1-S2
S2
曲边梯形
例2 求 y x 3 与直线 x 1, x 2 及 x 轴所围成的
如图所示, 一抛物线形拱桥的
跨度为6米, 高为3米,此抛物 线形拱桥的横截面积为多少? 解:如图建立平面直角坐标系,
可设抛物线方程为
y ax2 (a 0)
-3
点 (3,3)代入方程,得
a 1
于是抛物线方程
3 y
1
x2
3
(3,3)
3米
6米
y
o
3x
-3
(3,3)
情境回归
y
如图所示, 一抛物线形拱桥的 -3 D o
平面图形的面积。
y
解 所围成的图形如图所示:
y x3
则
s
0 1
x
3dx
2 0
x
3dx
17 4
1
0 2x
范例
3.计算由曲线y x2 与 y x所围图形的面积
解:作出草图,所求面积为阴影部分的面积
y2 x
解方程组y x2得交点横坐标为
x
0
及
x
1
S S -S y y x2 y x
= 曲边梯形OABC
{y
2x
(8,4).
y x4
y2 2x
思考题:
计算由 y2 2x和 y x 4所围图形的面积.
解 先求两曲线的交点。
y x4
y2 2x
y2 2x
(2,2), (8,4).
y x4
法二: 的面积 .
解: 由
得交点
(2, 2) , (8, 4)
此平面图形为Y—型
则有
4
A
2
(
y
4
曲边梯形OABD
1
B
C
D
-1 O
1A
x
= 1 x dx 1 x 2 dx
0
0
-1
=
2
3
x2
1
1
x3
1=
2
1
=1
3
3
0
033
3
y
A
0a
bX
曲边形
提升
1
a
b
A2
a
b
曲边梯形
面积 A=A1-A2
巩固练习
例3计算由 y 2x 和 y x 4及 x 轴所围图形
的面积.
解 先求两曲线的交点。
y x4
