大学物理实验课后习题答案-西安交大张永利主编
大学物理实验课后习题答案-西安交大张永利主编

第一章误差估算与数据处理方法课后习题答案1.指出下列各量有效数字的位数。
(1)kV 有效位数:4 (2)mm 有效位数:3 (3)kg 有效位数:5 (4)自然数有效位数:无限位2.判断下列写法是否正确,并加以改正。
(1)A mA错,0.0350A 有效位数为3位,而35mA 有效位数为2位,二者物理意义不同,不可等同,应改为A mA 。
(2)kg错,测量结果(即最佳估计值)有效数字的最后一位应与不确定度的末位对齐。
测量结果有效数字取位时,应遵循“四舍六入五凑偶”的原则;而且,不确定度应记为“”的形式。
故应将上式改成kg 。
(3)km错,当采用科学计数法表示测量结果时,最佳估计值与不确定度应同时用科学计数法表示,并且10的指数应取一致,还要保证最佳估计值的最后一位与不确定度的末位对齐。
因此,上式应改为。
(4)A 正确。
3.试按有效数字修约规则,将下列各数据保留三位有效数字。
3.8547,2.3429,1.5451,3.8750,5.4349,7.6850,3.6612,6.26383.85 2.34 1.54 3.88 5.43 7.68 3.66 6.26 4.按有效数字的确定规则,计算下列各式。
(1)000.1=U 000123.0=L 010.10=m 40350.0=I 35=0350.0=I 11050.3⨯=()3.0270.53+=m 270.53=m ±()3.03.53±=m ()2000103.274±⨯=h ()kmh 4102.03.27⨯±=()004.0325.4±=x ?6386.08.7537.343=++解:原式 (2)解:原式 (3)解:原式 (4)解:原式5.分别写出下列各式的不确定度传播公式。
(1)(K 为常数)解:(a )绝对不确定度:(b )相对不确定度:其中,、分别表示A 、B 量的合成不确定度。
西安交大版大学物理上学习指导作业及选择题答案参考答案
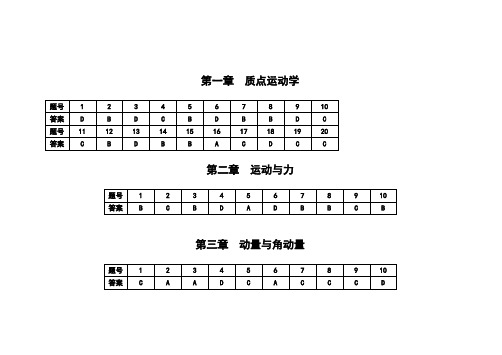
第一章质点运动学第二章运动与力第三章动量与角动量第四章功和能第五章刚体的转动第六章狭义相对论基础- 2 -第七章振动第八章波动- 3 -第九章温度和气体动理论第十章热力学第一定律- 4 -- 5 -第十一章 热力学第二定律第一章 质点运动学课 后 作 业1、一质点沿x 轴运动,其加速度a 与位置坐标x 的关系为 a =2+6 x 2 (SI)如果质点在原点处的速度为零,试求其在任意位置处的速度.解:设质点在x 处的速度为v ,62d d d d d d 2x txx t a +=⋅==v v 2分- 6 - ()x x xd 62d 020⎰⎰+=v v v 2分()2 213xx +=v 1分2、一质点沿x 轴运动,其加速度为a = 4t (SI),已知t = 0时,质点位于x 0=10 m 处,初速度v 0 = 0.试求其位置和时间的关系式.解: =a d v /d t 4=t , d v 4=t d t⎰⎰=vv 0d 4d tt tv 2=t 2 3分v d =x /d t 2=t 2 t t x txx d 2d 020⎰⎰=x 2= t 3 /3+x 0 (SI) 2分3、一质点沿半径为R 的圆周运动.质点所经过的弧长与时间的关系为221ct bt S += 其中b 、c 是大于零的常量,求从0=t 开始到切向加速度与法向加速度大小相等时所经历的时间.- 7 -解: ct b t S +==d /d v 1分c t a t ==d /d v 1分()R ct b a n /2+= 1分根据题意: a t = a n 1分即 ()R ct b c /2+=解得 cbc R t -=1分4、如图所示,质点P 在水平面内沿一半径为R =2 m 的圆轨道转动.转动的角速度ω与时间t 的函数关系为2kt =ω (k 为常量).已知s t 2=时,质点P 的速度值为32 m/s .试求1=t s 时,质点P 的速度与加速度的大小.- 8 - 解:根据已知条件确定常量k()222/rad 4//s Rt t k ===v ω 1分24t =ω, 24Rt R ==ωvs t 1=时, v = 4Rt 2 = 8 m/s 1分 2s /168/m Rt dt d a t ===v 1分22s /32/m R a n ==v 1分()8.352/122=+=nt a a a m/s 2 1分5、一敞顶电梯以恒定速率v =10 m/s 上升.当电梯离地面h =10 m 时,一小孩竖直向上抛出一球.球相对于电梯初速率200=v m/s .试问:(1) 从地面算起,球能达到的最大高度为多大? (2) 抛出后经过多长时间再回到电梯上?解:(1) 球相对地面的初速度=+='v v v 030 m/s 1分抛出后上升高度 9.4522='=gh v m/s 1分- 9 - 离地面高度 H = (45.9+10) m =55.9 m 1分(2) 球回到电梯上时电梯上升高度=球上升高度2021)(gt t t -+=v v v 1分08.420==gt vs 1分6、在离水面高h 米的岸上,有人用绳子拉船靠岸,船在离岸S 处,如图所示.当人以0υ(m ·1-s )的速率收绳时,试求船运动的速度和加速度的大小.解: 设人到船之间绳的长度为l ,此时绳与水面成θ角,由图可知222s h l +=将上式对时间t 求导,得题1-4图tss t l ld d 2d d 2=- 10 - 根据速度的定义,并注意到l ,s 是随t 减少的,∴ t sv v t l v d d ,d d 0-==-=船绳即 θcos d d d d 00v v s l t l s l t s v ==-=-=船 或 sv s h s lv v 02/1220)(+==船 将船v 再对t 求导,即得船的加速度320222022002)(d d d d d d sv h s v s l s v slv s v v s t sl t l st v a =+-=+-=-==船船- 11 - 第二章 运动与力 课 后 作 业1、 一人在平地上拉一个质量为M 的木箱匀速前进,如图. 木箱与地面间的摩擦系数μ=0.6.设此人前进时,肩上绳的支撑点距地面高度为h =1.5 m ,不计箱高,问绳长l 为多长时最省力?解:设绳子与水平方向的夹角为θ,则l h /sin =θ. 木箱受力如图所示,匀速前进时, 拉力为F , 有F cos θ-f =0 2分F sin θ+N -Mg =0 f =μN得 θμθμsin cos +=MgF 2分- 12 - 令0)sin (cos )cos sin (d d 2=++--=θμθθμθμθMg F ∴ 6.0tg ==μθ,637530'''︒=θ 2分且 0d d 22>θF∴ l =h / sin θ=2.92 m 时,最省力.m 1m 22、一质量为60 kg 的人,站在质量为30 kg 的底板上,用绳和滑轮连接如图.设滑轮、绳的质量及轴处的摩擦可以忽略不计,绳子不可伸长.欲使人和底板能以1 m/s 2的加速度上升,人对绳子的拉力T 2多大?人对底板的压力多大? (取g =10 m/s 2)g M P =θFNf- 13 -解:人受力如图(1) 图2分a m g m N T 112=-+ 1分 底板受力如图(2) 图2分 a m g m N T T 2221=-'-+ 2分212T T = 1分 N N ='由以上四式可解得 a m m g m g m T )(421212+=--∴ 5.2474/))((212=++=a g m m T N 1分 5.412)(21=-+=='T a g m N N N 1分3、一条轻绳跨过一轻滑轮(滑轮与轴间摩擦可忽略),在绳的一端挂一质量为m 1的物体,在另一侧有一质量为m 2的环,求当环相对于绳以恒定的加速度a 2沿绳向下滑动时,物体和环相对地面的加速度各是多少?环与绳间的摩擦力多大?- 14 - m 1m 22a解:因绳子质量不计,所以环受到的摩擦力在数值上等于绳子张力T .设m 2相对地面的加速度为2a ',取向上为正;m 1相对地面的加速度为a 1(即绳子的加速度),取向下为正. 1分111a m T g m =- 2分 222a m g m T =-2分 212a a a -=' 2分 解得 2122211)(m m a m g m m a ++-= 1分21212)2(m m m m a g T +-=1分2121212)(m m a m g m m a +--=' 1分- 15 - 4、一条质量分布均匀的绳子,质量为M 、长度为L ,一端拴在竖直转轴OO ′上,并以恒定角速度ω在水平面上旋转.设转动过程中绳子始终伸直不打弯,且忽略重力,求距转轴为r 处绳中的张力T ( r ).解:取距转轴为r 处,长为d r 的小段绳子,其质量为 ( M /L ) d r . (取元,画元的受力图) 2分由于绳子作圆周运动,所以小段绳子有径向加速度,由牛顿定律得:T ( r )-T ( r + d r ) = ( M / L ) d r r ω2 令 T ( r )-T (r + d r ) = - d T ( r ) 得 d T =-( M ω2 / L ) r d r 4分由于绳子的末端是自由端 T (L ) = 0 1分有r r L M T Lrr T d )/(d 2)(⎰⎰-=ω ∴ )2/()()(222L r L M r T -=ω 3分OO- 16 - 第三章 动量与角动量 课 后 作 业hAv1、如图,用传送带A 输送煤粉,料斗口在A 上方高h =0.5 m 处,煤粉自料斗口自由落在A 上.设料斗口连续卸煤的流量为q m =40 kg/s ,A 以v =2.0 m/s 的水平速度匀速向右移动.求装煤的过程中,煤粉对A 的作用力的大小和方向.(不计相对传送带静止的煤粉质重)解:煤粉自料斗口下落,接触传送带前具有竖直向下的速度gh 20=v 1分设煤粉与A 相互作用的∆t 时间内,落于传送带上的煤粉质量为 t q m m ∆=∆1分设A 对煤粉的平均作用力为f,由动量定理写分量式:0-∆=∆v m t f x 1分)(00v m t f y ∆--=∆ 1分- 17 - 将 t q m m ∆=∆代入得 v m x q f =, 0v m y q f =∴ 14922=+=y x f f f N 2分 f与x 轴正向夹角为α = arctg (f x / f y ) = 57.4° 1分由牛顿第三定律煤粉对A 的作用力f ′= f = 149 N ,方向与图中f相反.2分30°F2、质量为1 kg 的物体,它与水平桌面间的摩擦系数μ = 0.2 .现对物体施以F = 10t (SI)的力,(t 表示时刻),力的方向保持一定,如图所示.如t = 0时物体静止,则t = 3 s 时它的速度大小v 为多少?解:由题给条件可知物体与桌面间的正压力mg F N +︒=30sin 1分物体要有加速度必须 N F μ≥︒30cos 2分即 mg t μμ≥-)3(5, 0s 256.0t t =≥ 1分物体开始运动后,所受冲量为 ⎰-︒=tt t N F I 0d )30cos (μ- 18 - )(96.1)(83.3022t t t t ---= t = 3 s, I = 28.8 N s 2分则此时物体的动量的大小为 I m =v速度的大小为 8.28==mIv m/s 2分3、一炮弹发射后在其运行轨道上的最高点h =19.6 m 处炸裂成质量相等的两块.其中一块在爆炸后1秒钟落到爆炸点正下方的地面上.设此处与发射点的距离S 1=1000 m ,问另一块落地点与发射地点间的距离是多少?(空气阻力不计,g =9.8 m/s 2)解:因第一块爆炸后落在其正下方的地面上,说明它的速度方向是沿竖直方向的.利用 2t g t h '+'=211v , 式中t '为第一块在爆炸后落到地面的时间. 可解得v 1=14.7 m/s ,竖直向下.取y 轴正向向上, 有v 1y =-14.7 m/s 2分设炮弹到最高点时(v y =0),经历的时间为t ,则有S 1 = v x t ① h=221gt ② 由①、②得 t =2 s , v x =500 m/s 2分- 19 - 以2v表示爆炸后第二块的速度,则爆炸时的动量守恒关系如图所示.x v v m m x =221③0==+y y m m m v v v 1y 22121 ④解出 v 2x =2v x =1000 m/s , v 2y =-v 1y =14.7 m/s 3分 再由斜抛公式 x 2= S 1 +v 2x t 2 ⑤y 2=h +v 2y t 2-22gt 21 ⑥落地时 y 2 =0,可得 t 2 =4 s , t 2=-1 s (舍去) 故 x 2=5000 m 3分mv4、质量为M =1.5 kg 的物体,用一根长为l =1.25 m 的细绳悬挂在天花板上.今有一质量为m =10 g 的子弹- 20 - 以v 0=500 m/s 的水平速度射穿物体,刚穿出物体时子弹的速度大小v =30 m/s ,设穿透时间极短.求: (1) 子弹刚穿出时绳中张力的大小; (2) 子弹在穿透过程中所受的冲量.解:(1) 因穿透时间极短,故可认为物体未离开平衡位置.因此,作用于子弹、物体系统上的外力均在竖直方向,故系统在水平方向动量守恒.令子弹穿出时物体的水平速度为v ' 有 m v 0 = m v +M v 'v ' = m (v 0 - v )/M =3.13 m/s 2分 T =Mg+M v 2/l =26.5 N 2分(2) s N 7.40⋅-=-=∆v v m m t f (设0v方向为正方向) 2分负号表示冲量方向与0v方向相反. 2分- 21 - 课 后 作 业1、一质量为m 的质点在Oxy 平面上运动,其位置矢量为j t b i t a rωωsin cos +=(SI)式中a 、b 、ω是正值常量,且a >b . (1)求质点在A 点(a ,0)时和B 点(0,b )时的动能;(2)求质点所受的合外力F 以及当质点从A 点运动到B 点的过程中F的分力x F 和y F 分别作的功.解:(1)位矢 j t b i t a rωωsin cos += (SI) 可写为 t a x ωcos = , t b y ωsin =t a t x x ωωsin d d -==v , t b ty ωωcos d dy-==v在A 点(a ,0) ,1cos =t ω,0sin =t ωE KA =2222212121ωmb m m y x =+v v 2分在B 点(0,b ) ,0cos =t ω,1sin =t ωE KB =2222212121ωma m m y x=+v v 2分 (2) j ma i ma F y x +==j t mb i t ma ωωωωsin cos 22-- 2分- 22 - 由A →B ⎰⎰-==020d cos d a a x x x t a m x F W ωω=⎰=-022221d a ma x x m ωω 2分⎰⎰-==b b y y t b m y F W 020dy sin d ωω=⎰-=-b mb y y m 022221d ωω 2分2、劲度系数为k 的轻弹簧,一端固定,另一端与桌面上的质量为m 的小球B 相连接.用外力推动小球,将弹簧压缩一段距离L 后放开.假定小球所受的滑动摩擦力大小为F 且恒定不变,滑动摩擦系数与静摩擦系数可视为相等.试求L 必须满足什么条件时,才能使小球在放开后就开始运动,而且一旦停止下来就一直保持静止状态.解:取弹簧的自然长度处为坐标原点O ,建立如图所示的坐标系.在t =0时,静止于x =-L 的小球开始运动的条件是kL >F ① 2分小球运动到x 处静止的条件,由功能原理得- 23 - 222121)(kL kx x L F -=+- ② 2分 由② 解出kFL x 2-= 使小球继续保持静止的条件为 F k FL k x k ≤-=2 ③ 2分 所求L 应同时满足①、③式,故其范围为 k F <L kF3≤ 2分3、一链条总长为l ,质量为m ,放在桌面上,并使其部分下垂,下垂一段的长度为a .设链条与桌面之间的滑动摩擦系数为μ.令链条由静止开始运动,则 (1)到链条刚离开桌面的过程中,摩擦力对链条作了多少功?- 24 -al -a(2)链条刚离开桌面时的速率是多少?解:(1)建立如图坐标.某一时刻桌面上全链条长为y ,则摩擦力大小为g l ym f μ= 1分 摩擦力的功 ⎰⎰--==00d d a l al f y gy l my f W μ 2分=022al y lmg-μ =2)(2a l lmg --μ 2分(2)以链条为对象,应用质点的动能定理 ∑W =2022121v v m m -其中 ∑W = W P +W f ,v 0 = 0 1分- 25 - W P =⎰la x P d =la l mg x x l mg la 2)(d 22-=⎰ 2分由上问知 la l mg W f 2)(2--=μ所以222221)(22)(v m a l l mg l a l mg =---μ 得 []21222)()(a l a l lg ---=μv 2分αh0v4、一物体与斜面间的摩擦系数μ = 0.20,斜面固定,倾角α = 45°.现给予物体以初速率v 0 = 10 m/s ,使它沿斜面向上滑,如图所示.求: 物体能够上升的最大高度h ;该物体达到最高点后,沿斜面返回到原出发点时的速率v .- 26 - 解:(1)根据功能原理,有 mgh m fs -=2021v 2分 ααμαμsin cos sin mgh Nh fs ==mgh m mgh -==2021ctg v αμ 2分)ctg 1(220αμ+=g h v =4.5 m 2分(2)根据功能原理有 fs m mgh =-221v 1分αμctg 212mgh mgh m -=v 1分[]21)ctg 1(2αμ-=gh v =8.16 m/s 2分第五章 刚体的转动课 后 作 业- 27 - 1、一轻绳跨过两个质量均为m 、半径均为r 的均匀圆盘状定滑轮,绳的两端分别挂着质量为m 和2m 的重物,如图所示.绳与滑轮间无相对滑动,滑轮轴光滑.两个定滑轮的转动惯量均为221mr .将由两个定滑轮以及质量为m 和2m 的重物组成的系统从静止释放,求两滑轮之间绳内的张力.解:受力分析如图所示. 2分 2mg -T 1=2ma 1分T 2-mg =ma 1分 T 1 r -T r =β221mr 1分 T r -T 2 r =β221mr 1分 a =r β 2分解上述5个联立方程得: T =11mg / 8 2分- 28 -2、一轻绳绕过一定滑轮,滑轮轴光滑,滑轮的半径为R ,质量为M / 4,均匀分布在其边缘上.绳子的A 端有一质量为M 的人抓住了绳端,而在绳的另一端B 系了一质量为21M 的重物,如图.设人从静止开始相对于绳匀速向上爬时,绳与滑轮间无相对滑动,求B 端重物上升的加速度?(已知滑轮对通过滑轮中心且垂直于轮面的轴的转动惯量J =MR 2 / 4 )解:受力分析如图所示.设重物的对地加速度为a ,向上.则绳的A 端对地有加速度a 向下,人相对于绳虽为匀速向上,但相对于地其加速度仍为a 向下. 2分 根据牛顿第二定律可得:对人: Mg -T 2=Ma ① 2分对重物: T 1-21Mg =21Ma ② 2分根据转动定律,对滑轮有(T2-T1)R=Jβ=MR2β / 4 ③2分因绳与滑轮无相对滑动,a=βR④1分①、②、③、④四式联立解得a=2g / 7 1分3、一质量为m的物体悬于一条轻绳的一端,绳另一端绕在一轮轴的轴上,如图所示.轴水平且垂直于轮轴面,其半径为r,整个装置架在光滑的固定轴承之上.当物体从静止释放后,在时间t内下降了一段距离S.试求整个轮轴的转动惯量(用m、r、t和S表示).解:设绳子对物体(或绳子对轮轴)的拉力为T,则根据牛顿运动定律和转动定律得:mgT=ma①2分T r=Jβ②2分由运动学关系有:a = rβ③2分- 29 -- 30 - 由①、②、③式解得: J =m ( g -a ) r 2 / a ④ 又根据已知条件 v 0=0式代入④式得:J =mr 2(Sgt 22∴ S =221at , a =2S / t 2 ⑤ 2分将⑤-1) 2分Am 1 ,l1v2俯视图4、有一质量为m 1、长为l 的均匀细棒,静止平放在滑动摩擦系数为μ的水平桌面上,它可绕通过其端点O 且与桌面垂直的固定光滑轴转动.另有一水平运动的质量为m 2的小滑块,从侧面垂直于棒与棒的另一端A 相碰撞,设碰撞时间极短.已知小滑块在碰撞前后的速度分别为1v 和2v,如图所示.求碰撞后从细棒开始转动到停止转动的过程所需的时间.(已知棒绕O 点的转动惯量2131l mJ =)- 31 -解:对棒和滑块系统,在碰撞过程中,由于碰撞时间极短,所以棒所受的摩擦力 矩<<滑块的冲力矩.故可认为合外力矩为零,因而系统的角动量守恒,即1分m 2v 1l =-m 2v 2l +ω2131l m ① 3分碰后棒在转动过程中所受的摩擦力矩为gl m x x l m g M l f 10121d μμ-=⋅-=⎰ ② 2分由角动量定理 ω210310l m dt M tf -=⎰ ③ 2分由①、②和③解得 gm m t 12122μv v += 2分第六章 狭义相对论基础课 后 作 业1、一体积为V 0,质量为m 0的立方体沿其一棱的方向相对于观察者A 以速度v 运动.求:观察者A 测得其密度是- 32 - 多少?解:设立方体的长、宽、高分别以x 0,y 0,z 0表示,观察者A 测得立方体的长、宽、高分别为 221cx x v -=,0y y =,0z z =.相应体积为 2201cV xyz V v -== 3分观察者A测得立方体的质量 2201cm m v -=故相应密度为 V m /=ρ22022011/c V c m v v --=)1(2200cV m v -=2分2、在O 参考系中,有一个静止的正方形,其面积为 100 cm 2.观测者O '以 0.8c 的匀速度沿正方形的对角线运动.求O '所测得的该图形的面积.- 33 -解:令O 系中测得正方形边长为a ,沿对角线取x 轴正方向(如图),则边长在坐标轴上投影的大小为a a x 221=,a a y 221= 面积可表示为: x y a a S ⋅=2 2分在以速度v 相对于O 系沿x 正方向运动的O '系中2)/(1c a a x x v -=' =0.6×a 221 a a a yy 221==' 在O '系中测得的图形为菱形,其面积亦可表示为606.022=='⋅'='a a a S x y cm 2 3分 3、一艘宇宙飞船的船身固有长度为L 0 =90 m ,相对于地面以=v 0.8 c (c 为真空中光速)的匀速度在地面观测站的上空飞过.(1) 观测站测得飞船的船身通过观测站的时间间隔是多少? (2) 宇航员测得船身通过观测站的时间间隔是多少?解:(1) 观测站测得飞船船身的长度为 =-=20)/(1c L L v 54 maaO y x- 34 - 则 ∆t 1 = L /v =2.25×10-7 s 3分(2) 宇航员测得飞船船身的长度为L 0,则∆t 2 = L 0/v =3.75×10-7 s 2分4、半人马星座α星是距离太阳系最近的恒星,它距离地球S = 4.3×1016 m .设有一宇宙飞船自地球飞到半人马星座α星,若宇宙飞船相对于地球的速度为v = 0.999 c ,按地球上的时钟计算要用多少年时间?如以飞船上的时钟计算,所需时间又为多少年?解:以地球上的时钟计算: 5.4≈=∆vSt 年 2分以飞船上的时钟计算: ≈-='∆∆221ct t v 0.20 年 3分5、在惯性系S 中,有两事件发生于同一地点,且第二事件比第一事件晚发生∆t =2s ;而在另一惯性系S '中,观测第二事件比第一事件晚发生∆t '=3s .那么在S '系中发生两事件的地点之间的距离是多少?解:令S '系与S 系的相对速度为v ,有- 35 - 2)/(1c tt v -='∆∆, 22)/(1)/(c t t v -='∆∆则 2/12))/(1(t t c '-⋅=∆∆v ( = 2.24×108 m ·s -1 ) 4分那么,在S '系中测得两事件之间距离为:2/122)(t t c t x ∆∆∆∆-'='⋅='v = 6.72×108 m 4分6、要使电子的速度从v 1 =1.2×108 m/s 增加到v 2 =2.4×108 m/s 必须对它作多少功? (电子静止质量m e =9.11×10-31 kg)解:根据功能原理,要作的功 W = ∆E根据相对论能量公式 ∆E = m 2c 2- m 1c 2 2分根据相对论质量公式 2/12202])/(1/[c m m v -=2/12101])/(1/[c m m v -= 1分 ∴ )1111(22122220cc c m W v v ---==4.72×10-14 J =2.95×105 eV 2分 第七章 振动课 后 作 业1、一个轻弹簧在60 N 的拉力作用下可伸长30 cm .现将一物体悬挂在弹簧的下端并在它上面放一小物体,它们的总质量为4 kg .待其静止后再把物体向下拉10 cm ,然后释放.问: (1) 此小物体是停在振动物体上面还是离开它?(2) 如果使放在振动物体上的小物体与振动物体分离,则振幅A 需满足何条件?二者在何位置开始分离?- 36 -解:(1) 小物体受力如图.设小物体随振动物体的加速度为a ,按牛顿第二定律有(取向下为正) ma N mg =- 1分)(a g m N -=当N = 0,即a = g 时,小物体开始脱离振动物体,已知 1分A = 10 cm ,N/m 3.060=k有 50/==m k ω rad ·s -1 2分 系统最大加速度为 52max ==A a ω m ·s -2 1分 此值小于g ,故小物体不会离开. 1分(2) 如使a > g ,小物体能脱离振动物体,开始分离的位置由N = 0求得x a g 2ω-== 2分 6.19/2-=-=ωg x cm 1分即在平衡位置上方19.6 cm 处开始分离,由g A a >=2max ω,可得2/ωg A >=19.6 cm . 1分2、一质点在x 轴上作简谐振动,选取该质点向右运动通过A 点时作为计时起点( t = 0 ),经过2秒后质点第一次经过B 点,再经过2秒后质点第二次经过B 点,若已知该质点在A 、B 两点具有相同的速率,且AB = 10 cm 求: (1) 质点的振动方程;- 37 - (2) 质点在A 点处的速率.解: T = 8 s , ν = (1/8) s -1, ω = 2πν = (π /4) s -1 3分(1) 以AB 的中点为坐标原点,x 轴指向右方. t = 0时, 5-=x cm φcos A = t = 2 s 时, 5=x cm φφωsin )2cos(A A -=+=由上二式解得 tg φ = 1因为在A 点质点的速度大于零,所以φ = -3π/4或5π/4(如图) 2分 25cos /==φx A cm 1分 ∴ 振动方程 )434cos(10252π-π⨯=-t x (SI) 1分(2) 速率 )434sin(41025d d 2π-π⨯π-==-t t x v (SI) 2分 当t = 0 时,质点在A 点 221093.3)43sin(10425d d --⨯=π-⨯π-==t x v m/s 1分3、在一轻弹簧下端悬挂m 0 = 100 g 砝码时,弹簧伸长8 cm .现在这根弹簧下端悬挂m = 250 g 的物体,构成弹簧振子.将物体从平衡位置向下拉动4 cm ,并给以向上的21 cm/s 的初速度(令这时t = 0).选x 轴向下, 求振动方- 38 - 程的数值式.解: k = m 0g / ∆l 25.12N/m 08.08.91.0=⨯=N/m11s 7s 25.025.12/--===m k ω 2分 5cm )721(4/2222020=+=+=ωv x A cm 2分 4/3)74/()21()/(tg 00=⨯--=-=ωφx v ,φ = 0.64 rad 3分)64.07cos(05.0+=t x (SI) 1分4、有一轻弹簧,当下端挂一个质量m 1 = 10 g 的物体而平衡时,伸长量为4.9 cm .用这个弹簧和质量m 2 = 16 g 的物体组成一弹簧振子.取平衡位置为原点,向上为x 轴的正方向.将m 2从平衡位置向下拉 2 cm 后,给予向上的初速度v 0 = 5 cm/s 并开始计时,试求m 2的振动周期和振动的数值表达式.解:设弹簧的原长为l ,悬挂m 1后伸长∆l ,则 k ∆l = m 1g ,k = m 1g/ ∆l = 2 N/m 1分取下m 1挂上m 2后,2.11/2==m k ω rad/s 2分ω/2π=T =0.56 s 1分t = 0时, φcos m 10220A x =⨯-=-- 39 - φωsin m/s 10520A -=⨯=-v解得 220201005.2m )/(-⨯=+=ωv x A m 2分=-=-)/(tg 001x ωφv 180°+12.6°=3.36 rad也可取 φ = -2.92 rad 2分 振动表达式为 x = 2.05×10-2cos(11.2t -2.92) (SI) 2分或 x = 2.05×10-2cos(11.2t +3.36) (SI)- 40 - 5、在竖直悬挂的轻弹簧下端系一质量为 100 g 的物体,当物体处于平衡状态时,再对物体加一拉力使弹簧伸长,然后从静止状态将物体释放.已知物体在32 s 内完成48次振动,振幅为5 cm . (1) 上述的外加拉力是多大?(2) 当物体在平衡位置以下1 cm 处时,此振动系统的动能和势能各是多少?解一:(1) 取平衡位置为原点,向下为x 正方向.设物体在平衡位置时弹簧的伸长量为∆l ,则有l k mg ∆=, 加拉力F 后弹簧又伸长x 0,则0)(0=+-+∆x l k mg F解得 F = kx 0 2分 由题意,t = 0时v 0 = 0;x = x 0则 0202)/(x x A =+=ωv 2分 又由题给物体振动周期4832=T s, 可得角频率 Tπ=2ω, 2ωm k = ∴ 444.0)/4(22=π==A T m kA F N 1分 (2) 平衡位置以下1 cm 处: )()/2(2222x A T -π=v 2分221007.121-⨯==v m E K J 2分2222)/4(2121x T m kx E p π== = 4.44×10-4 J 1分解二:(1) 从静止释放,显然拉长量等于振幅A (5 cm ),- 41 - kA F = 2分2224νωπ==m m k ,ν = 1.5 Hz 2分 ∴ F = 0.444 N 1分(2) 总能量 221011.12121-⨯===FA kA E J 2分当x = 1 cm 时,x = A /5,E p 占总能量的1/25,E K 占24/25. 2分∴ 21007.1)25/24(-⨯==E E K J , 41044.425/-⨯==E E p J 1分6、如图,有一水平弹簧振子,弹簧的劲度系数k = 24 N/m ,重物的质量m = 6 kg ,重物静止在平衡位置上.设以一水平恒力F = 10 N 向左作用于物体(不计摩擦),使之由平衡位置向左运动了0.05 m 时撤去力F .当重物运动到左方最远位置时开始计时,求物体的运动方程.解:设物体的运动方程为 )cos(φω+=t A x .恒外力所做的功即为弹簧振子的能量: F ×0.05 = 0.5 J . 2分当物体运动到左方最远位置时,弹簧的最大弹性势能为0.5 J ,即:5.0212=kA J , ∴ A = 0.204 m . 2分- 42 - A 即振幅. 4/2==m k ω (rad/s)2ω = 2 rad/s . 2分 按题目所述时刻计时,初相为φ = π.∴ 物体运动方程为 2分)2cos(204.0π+=t x (SI). 2分第八章 波动课 后 作 业1、一平面简谐波沿x 轴正向传播,波的振幅A = 10 cm ,波的角频率ω = 7π rad/s.当t = 1.0 s 时,x = 10 cm 处的a 质点正通过其平衡位置向y 轴负方向运动,而x = 20 cm 处的b 质点正通过y = 5.0 cm 点向y 轴正方向运动.设该波波长λ >10 cm ,求该平面波的表达式.解:设平面简谐波的波长为λ,坐标原点处质点振动初相为φ,则该列平面简谐波的表达式可写成 )/27cos(1.0φλ+π-π=x t y (SI) 2分 t = 1 s 时 0])/1.0(27cos[1.0=+π-π=φλy 因此时a 质点向y 轴负方向运动,故π=+π-π21)/1.0(27φλ ① 2分而此时,b 质点正通过y = 0.05 m 处向y 轴正方向运动,应有05.0])/2.0(27cos[1.0=+π-π=φλy且 π-=+π-π31)/2.0(27φλ ② 2分由①、②两式联立得 λ = 0.24 m 1分 3/17π-=φ 1分 ∴ 该平面简谐波的表达式为]31712.07cos[1.0π-π-π=x t y (SI) 2分或 ]3112.07cos[1.0π+π-π=x t y (SI)(m) -2、图示一平面简谐波在t = 0 时刻的波形图,求 (1) 该波的波动表达式; (2) P 处质点的振动方程.解:(1) O 处质点,t = 0 时0cos 0==φA y , 0sin 0>-=φωA v所以 π-=21φ 2分又 ==u T /λ (0.40/ 0.08) s= 5 s 2分故波动表达式为 ]2)4.05(2cos[04.0π--π=x t y (SI) 4分(2) P 处质点的振动方程为]2)4.02.05(2cos[04.0π--π=t y P )234.0cos(04.0π-π=t (SI) 2分3、沿x 轴负方向传播的平面简谐波在t = 2 s 时刻的波形曲线如图所示,设波速u = 0.5 m/s . 求:原点O 的振动方程.解:由图,λ = 2 m , 又 ∵u = 0.5 m/s ,∴ ν = 1 /4 Hz , 3分T = 4 s .题图中t = 2 s =T 21.t = 0时,波形比题图中的波形倒退λ21,见图. 2分此时O 点位移y 0 = 0(过平衡位置)且朝y 轴负方向运动,∴ π=21φ 2分∴ )2121cos(5.0π+π=t y (SI) 3分4、一平面简谐波沿Ox 轴正方向传播,波的表达式为 )/(2cos λνx t A y -π=, 而另一平面简谐波沿Ox 轴负方向传播,波的表达式为 )/(2cos 2λνx t A y +π= 求:(1) x = λ /4 处介质质点的合振动方程;(2) x = λ /4 处介质质点的速度表达式.解:(1) x = λ /4处)212cos(1π-π=t A y ν , )212cos(22π+π=t A y ν 2分∵ y 1,y 2反相 ∴ 合振动振幅 A A A A s =-=2 , 且合振动的初相φ 和y 2的初相一样为π21. 4分合振动方程 )212cos(π+π=t A y ν 1分(2) x = λ /4处质点的速度 )212sin(2/d d π+ππ-== v t A t y νν)2cos(2π+ππ=t A νν 3分5、设入射波的表达式为 )(2cos 1Ttx A y +π=λ,在x = 0处发生反射,反射点为一固定端.设反射时无能量损失,求(1) 反射波的表达式; (2) 合成的驻波的表达式; (3) 波腹和波节的位置.解:(1) 反射点是固定端,所以反射有相位突变π,且反射波振幅为A ,因此反 射波的表达式为 ])//(2cos[2π+-π=T t x A y λ 3分 (2) 驻波的表达式是 21y y y +=)21/2cos()21/2cos(2π-ππ+π=T t x A λ 3分(3) 波腹位置: π=π+πn x 21/2λ, 2分λ)21(21-=n x , n = 1, 2, 3, 4,…波节位置: π+π=π+π2121/2n x λ 2分λn x 21= , n = 1, 2, 3, 4,…6、如图所示,一平面简谐波沿x 轴正方向传播,BC 为波密媒质的反射面.波由P 点反射,OP = 3λ /4,DP = λ /6.在t = 0时,O 处质点的合振动是经过平衡位置向负方向运动.求D 点处入射波与反射波的合振动方程.(设入射波和反射波的振幅皆为A ,频率为ν.)解:选O 点为坐标原点,设入射波表达式为 ])/(2cos[1φλν+-π=x t A y 2分 则反射波的表达式是 ])(2cos[2π++-+-π=φλνxDP OP t A y 2分合成波表达式(驻波)为 )2cos()/2cos(2φνλ+ππ=t x A y 2分 在t = 0时,x = 0处的质点y 0 = 0, 0)/(0<∂∂t y ,故得 π=21φ 2分因此,D 点处的合成振动方程是)22cos()6/4/32cos(2π+π-π=t A y νλλλt A νπ=2sin 3 2分第九章 温度和气体动理论 课 后 作 业1、黄绿光的波长是5000A (1A =10 -10 m).理想气体在标准状态下,以黄绿光的波长为边长的立方体内有多少个分子?(玻尔兹曼常量k =1.38×10- 23J ·K -1)解:理想气体在标准状态下,分子数密度为n = p / (kT )=2.69×1025 个/ m 3 3分 以5000A 为边长的立方体内应有分子数为N = nV =3.36×106个. 2分2、已知某理想气体分子的方均根速率为 400 m ·s -1.当其压强为1 atm 时,求气体的密度.解: 223131v v ρ==nm p∴ 90.1/32==v p ρ kg/m 3 5分 3、一瓶氢气和一瓶氧气温度相同.若氢气分子的平均平动动能为 w = 6.21×10-21 J .试求:(1) 氧气分子的平均平动动能和方均根速率. (2) 氧气的温度.(阿伏伽德罗常量N A =6.022×1023 mol -1,玻尔兹曼常量k =1.38×10-23 J ·K -1)解:(1) ∵ T 相等, ∴氧气分子平均平动动能=氢气分子平均平动动能w=6.21×10-21 J .且 ()()483/22/12/12==m w vm/s 3分(2) ()k w T 3/2==300 K . 2分 4、某理想气体的定压摩尔热容为29.1 J ·mol -1·K -1.求它在温度为273 K 时分子平均转动动能. (玻尔兹曼常量k =1.38×10-23 J ·K -1 )解: R R iR i C P +=+=222, ∴ ()5122=⎪⎭⎫⎝⎛-=-=R C R R C i P P , 2分可见是双原子分子,只有两个转动自由度.211077.32/2-⨯===kT kT r ε J 3分5、一超声波源发射超声波的功率为10 W .假设它工作10 s ,并且全部波动能量都被1 mol 氧气吸收而用于增加其内能,则氧气的温度升高了多少? (氧气分子视为刚性分子,普适气体常量R =8.31 J ·mol -1·K -1 )解: A = Pt = T iR v ∆21, 2分∴ ∆T = 2Pt /(v iR )=4.81 K . 3分6、1 kg 某种理想气体,分子平动动能总和是1.86×106 J ,已知每个分子的质量是3.34×10-27 kg ,试求气体的温度. (玻尔兹曼常量 k =1.38×10-23 J ·K -1)解: N = M / m =0.30×1027 个 1分 ==N E w K / 6.2×10-21 J 1分kwT 32== 300 K 3分第十章 热力学第一定律 课 后 作 业1、一定量的单原子分子理想气体,从初态A 出发,沿图示直线过程变到另一状态B ,又经过等容、等压两过程回到状态A . (1) 求A →B ,B →C ,C →A 各过程中系统对外所作的功W ,内能的增量∆E 以及所吸收的热量Q .(2) 整个循环过程中系统对外所作的总功以及从外界吸收的总热量(过程吸热的代数和).1 2 3 12 OV (10-3 m 3) p (105 Pa) A BC解:(1) A →B : ))((211A B A B V V p p W -+==200 J . ΔE 1=ν C V (T B -T A )=3(p B V B -p A V A ) /2=750 JQ =W 1+ΔE 1=950 J . 3分B →C : W 2 =0ΔE 2 =ν C V (T C -T B )=3( p C V C -p B V B ) /2 =-600 J .Q 2 =W 2+ΔE 2=-600 J . 2分 C →A : W 3 = p A (V A -V C )=-100 J .150)(23)(3-=-=-=∆C C A A C A V V p V p T T C E ν J .Q 3 =W 3+ΔE 3=-250 J 3分 (2) W = W 1 +W 2 +W 3=100 J . Q = Q 1 +Q 2 +Q 3 =100 J 2分 2、1 mol 双原子分子理想气体从状态A (p 1,V 1)沿p -V 图所示直线变化到状态B (p 2,V 2),试求: 气体的内能增量.气体对外界所作的功. 气体吸收的热量.此过程的摩尔热容.解:(1) )(25)(112212V p V p T T C E V -=-=∆ 2分(2) ))((211221V V p p W -+=, W 为梯形面积,根据相似三角形有p 1V 2= p 2V 1,则)(211122V p V p W -=. 3分 (3) Q =ΔE +W =3( p 2V 2-p 1V 1 ). 2分 (4) 以上计算对于A →B 过程中任一微小状态变化均成立,故过程中ΔQ =3Δ(pV ). 由状态方程得 Δ(pV ) =R ΔT , 故 ΔQ =3R ΔT ,摩尔热容 C =ΔQ /ΔT =3R . 3分BAOVp 1p 2p V 1V 2(摩尔热容C =T Q ∆∆/,其中Q ∆表示1 mol 物质在过程中升高温度T ∆时所吸收的热量.)3、一定量的理想气体,由状态a 经b 到达c .(如图, abc 为一直线)求此过程中1 2 3 1 2 3 a bcV (L)p (atm)气体对外作的功; 气体内能的增量;气体吸收的热量.(1 atm =1.013×105 Pa)解:(1) 气体对外作的功等于线段c a 下所围的面积W =(1/2)×(1+3)×1.013×105×2×10-3 J =405.2 J 3分 (2) 由图看出 P a V a =P c V c ∴T a =T c 2分 内能增量 0=∆E . 2分(3) 由热力学第一定律得Q =E ∆ +W =405.2 J . 3分 4、如图所示,abcda 为1 mol 单原子分子理想气体的循环过程,求:Oadcbp (×105 Pa)V (×10-3 m 3)2312(1) 气体循环一次,在吸热过程中从外界共吸收的热量; (2) 气体循环一次对外做的净功;(3) 证明 在abcd 四态, 气体的温度有T a T c =T b T d .解:(1) 过程ab 与bc 为吸热过程, 吸热总和为 Q 1=C V (T b -T a )+C p (T c -T b ))(25)(23b b c c a a b b V p V p V p V p -+-==800 J 4分 (2) 循环过程对外所作总功为图中矩形面积W = p b (V c -V b )-p d (V d -V a ) =100 J 2分 (3) T a =p a V a /R ,T c = p c V c /R , T b = p b V b /R ,T d = p d V d /R , T a T c = (p a V a p c V c )/R 2=(12×104)/R 2 T b T d = (p b V b p d V d )/R 2=(12×104)/R 2∴ T a T c =T b T d 4分 5、一定量的理想气体经历如图所示的循环过程,A →B 和C →D 是等压过程,B →C 和D →A 是绝热过程.已知:T C = 300 K ,T B = 400 K . 试求:此循环的效率.(提示:循环效率的定义式η =1-Q 2 /Q 1,Q 1为循环中气体吸收的热量,Q 2为循环中气体放出的热量)ABCD OVp解: 121Q Q -=η Q 1 = ν C p (T B -T A ) , Q 2 = ν C p (T C -T D ))/1()/1(12B A B C D C A B D C T T T T T T T T T T Q Q--=--= 4分根据绝热过程方程得到:γγγγ----=D D A A T p T p 11, γγγγ----=C C B B T p T p 11 ∵ p A = p B , p C = p D ,∴ T A / T B = T D / T C 4分故 %251112=-=-=B C T T Q Qη 2分6、一卡诺热机(可逆的),当高温热源的温度为 127℃、低温热源温度为27℃时,其每次循环对外作净功8000 J .今维持低温热源的温度不变,提高高温热源温度,使其每次循环对外作净功 10000 J .若两个卡诺循环都工作在相同的两条。
《大学物理实验》绪论部分习题答案

U U r 4.3 10 3 6.659 0.029 g/cm3
所以 6.659 0.029 g/cm3 或
6.66 0.03 g/cm3
1
3. 用分度值为 0.002cm 的游标尺测量一端封闭的空心圆柱体,得下列测量数据 测量次数 1 2 3 4 5 6 解:实验数据表格 空心圆柱体体积的测量 测量次数 1 2 3 4 5 6 平均值 标准偏差 S △ins 不确定度 U 直接测量结果 测量结果 高 H/cm 4.810 4.802 4.808 4.806 4.804 4.806 4.8060 0.0028 0.002 0.0035
4
(2 3.30 4.81 0.0031) 2 (3.30 2 0.0035 ) 2 (2 1.50 3.79 0.0054 ) 2 (1.50 2 0.013) 2
=0.099cm3 所以 V V U V (34.46 0.10) cm3 红字部分不确定度保留一位是正确的。
y A y B 2.66 0.17 0.0369 mV/℃ xA xB 72.5 5.0
所以实验方程可写为
t 0.0369 (t t 0 ) mV
2)利用计算器对实验数据进行最小二乘法运算可得直线的斜率 a 0.0368 mV/℃
3
ε
t
/mV 热电偶温度计温差电动势曲线
3.0
⊕A(72.5,2.66)
+ +
+
2.0
+ + 作者: ××× 日期:2007.3.10
1.0
+
+
⊕B(5.0,0.17)
西安交大大学物理2_3-1

m
ar
mg sin m(ar a0 sin ) N mg cos ma0 cos
y
a0
N m( g a0 ) cos ar ( g a0 ) sin
mg
N
ar
x
方法(二)以升降机参考系
mg N ma0 mar
dA F dr
F 在ab一段上的功:
在直角坐标系中 在自然坐标系中 注意:
b
A
A
b aL
b
F dr
aL
(Fx dx Fy dy Fz dz) A
b aL
dr ds
F cos ds
(1)合力的功等于各分力的功的代数和
A ( F1 F2 Fn ) dr aL b b F1 dr F2 dr
2
2
0
0
2 P F v 12t 3t 288W
例 已知用力 F 缓慢拉小球,F 保持方向不变 求 = 0 时, F 作的功。 解 Y
F T sin 0
T cos mg 0
L
X
T
F mgtg A F dr F cos ds
二. 惯性力
一般把在非惯性系中来自参照系本身加速效应的力称为惯性 体m 受到的惯性力 F' ma F F' 0 F ma 非惯性系 F F ' mar 牛二律在非惯性系形式上成立
取整个绳为研究对象 设压力为 N
y
l
v 2 2 g (l y) v 2 yg 2 g (l y) yg N 3g (l y ) d(yv ) gl v 2 yg (l y ) v 2 讨论 N gl dt
大学物理1-6章课后习题答案1

二、课后习题解答1-1、一飞轮直径为0.2m ,质量为5.00kg ,t 边缘饶一轻绳,现用恒力拉绳子的一端,使其有静止均匀地加速,经0.50s 转速达10转/s 。
假定飞轮可看作实心圆柱体。
求; 飞轮的角加速度及在这段时间转过的转数 拉力及拉力所做的功从拉动后t=10s 时飞轮的角速度及边缘上一点的速度和切向加速度及发向速度。
解:,/1058.1,/6.12,/126,/1026.1)3(3.4921212125232202s m r a s m r a s m r v s t J J J J A t n t t z z z ⨯======⨯====-=ωβωβωωωωτ1-2、有一根长为l 、质量为m 的匀质细杆,两端各牢固的连接一个质量为m 的小球,整个系统可绕一过O 点并垂直于杆的水平轴无摩察的转动,如图。
当系统转到水平位置时,求: 系统所受的和力矩 系统的转动惯量 系统的角加速度解: (1)设垂直纸面向里为z 轴的正方向(即力矩的正方向),合力矩为两小球及杆的重力矩之和。
mgl M M M M lmg r g dr rg rgdm M l mlmg M lmg M F r M z z zz l l l l z zzz 4341243,4190,4/34/24/34/0=+'+'=∴======'-='=⨯=--⎰⎰杆右左杆右左杆所受重力矩:其中两小球所受重力矩:ρρρθ224/34/34/34/24/34/222483748731)41(,)43()2(ml J J J J ml r dr r dm r J l m J l m J z z zz l l l l l l z z z=+'+'=∴====='='---⎰⎰杆右左杆右左杆的转动惯量:两小球的转动惯量:转动惯量之和,小球的转动惯量和杆的系统的转动惯量等于两λλ(3)由转动定理lg J M J M z z z z 3736==⇒=ββ1-3、有一质量为m 1、 m 2(m 1>m 2)两物体分别悬挂在两个半径不同的组 合轮上,如图。
大学物理(交大3版)答案(21-23章)

n = k +1
v 习题 22
22-1.计算下列客体具有 10MeV 动能时的物质波波长,(1)电子; (2)质子。 解:(1) 电子高速运动,设电子的总能量可写为:= E EK + m0 c 2
2 4 = E 2 c 2 p 2 + m0 c 可得
用相对论公式,
p=
1 1 1 2 4 2 4 2 ( EK + m0 c 2 ) 2 − = E 2 − m0 c = m0 c EK + 2m0 c 2 EK c c c
E 1.6 × 10−13 = = 1.78 × 10− 30 kg c 2 (3 × 108 ) 2
P=
m=
21-6. 100 W 钨丝灯在 1800K 温度下工作。假定可视其为黑体,试计算每秒钟内,在
5000 A 到 5001 A 波长间隔内发射多少个光子?
解:设钨丝灯的发射面积为 S ,由斯特藩-玻耳兹曼定律可得辐射总功率 P = σT ⋅ S
N =
P∆λ 2π cλ −4 S ∆λ = = 5.7 ×1013 hc e e λ kT − 1
21-7.波长为 1 A 的 X 光在石墨上发生康普顿散射,如在 θ = (1)散射光的波长 λ ' ; (2)反冲电子的运动方向和动能。 解:(1)
π
2
处观察散射光。试求:
θ Δλ = λ′ − λ0 = 2 λc sin 2 ( ) 2
= λ
h = p
h = 2mE
6.63 ×10−34 = 9.1×10−15 m −27 −19 6 2 ×1.67 ×10 ×10 ×10 ×1.6 ×10
−2
A )的光子的能量、动量和质量。
大学物理实验 部分思考题答案

实验八用拉脱发测定液体的表面张力系数1.对公式, 是要在水面与金属表面的接触角趋于0时满足的, 即在金属框恰好脱离液体前。
公式中的重力是金属框和它所粘附的液体的总重量, 但在公式中我们忽略了水对框架的浮力和水膜的重量。
2.“三线对齐”是因为朱利秤的下端是固定的,上端为自由端,因而我们在用朱利秤测量弹簧的伸长时也要固定弹簧的下端,这样才能在朱利秤上读到弹簧的伸长量。
“三线对齐”中的三线是指小镜子上的水平线和玻璃罐上的水平线以及玻璃罐上的水平线在小镜子里成的像。
实验十牛顿环干涉现象的研究和测量思考题1.牛顿环实验中, 假如平玻璃板上有微小的凸起, 则凸起处空气薄膜厚度变小, 这时的牛顿环是局部外凸的, 因为在平玻璃板上的突起位置的空气薄膜厚度变小, 此点的光程差也就变小, 那么此级暗条纹的光程差都要比该点的大, 因而该级暗条纹就会饶向外面一级的位置, 这时表现出此暗条纹就要外凸。
2.用白光照射时,我们是可以看到牛顿环干涉条纹的,而且是以赤橙黄绿蓝靛紫这样的顺序依次排列,只是在偏离中心位置越远,条纹级数之间会重叠越厉害。
实验十二迈克耳逊干涉仪数据处理参见P19的内容。
思考题1. 图形见书P115。
2.所以条纹变密。
实验十三超声波在空气中传播速度的测定数据处理中相对误差的有效位数参见P19的内容。
思考题1.因为在测量过程中, 我们要想在两个换能器之间形成驻波, 就一定要求S1发出的波和经S2发射的波是同频率, 同振幅, 而且是传播方向相反并在一条直线上, 这就要求两个换能器的发射面要保持相互平行。
2.略。
3.用“逐差法”处理数据是为了更充分地,最大限度地利用所测得的数据,保持多次测量的优点,减少测量误差。
实验十四密立根油滴实验数据处理表格1中最后要求的量是表格中的量求了平均以后的值, 比如量中的应该是对表格中的求5次测量的平均值。
而这其中的相对误差的表示参见P19。
思考题1.选择平衡点压在250V左右, 新仪器在12s-24s时间内匀速下降1.6mm的油滴(旧仪器在15s-30s时间内匀速下降2mm的油滴)的原因是在这个范围内的油滴体积不大, 带的电量也不是很多, 因而在下降时的速度不是很快, 下降的时间就比较容易测准确, 而且这样的油滴也不是很小, 不会因为太小而作布朗运动。
西安交通大学大物仿真实验

课程名称:大学物理实验 名称:密立根油滴法测电子电荷 班级:姓 名:学号: 一.实验目的。
1.学习测量元电荷的方法。
二.实验原理。
1. 平衡测量法.平衡测量法的出发点是,使油滴在均匀电场中静止在某一位置,或在重力场中作匀速运动。
当油滴在电场中平衡时,油滴在两极板间受到的电场力qE ,重力m 1g 和浮力m 2g 达到平衡,从而静止在某一位置,即. (1)油滴在重力场中作匀速运动时,设油滴以匀速下落,则有 (2)若此油滴带电荷为q ,并处在场强为E 的均匀电场中,设电场力qE 方向与重力方向相反, 油滴以匀速上升,则有 (3)由喷雾器喷出的小油滴半径r 是微米量级,直接测量其质量m 1也是困难的,为此希望消去m 1,而带之以容易测量的量。
设油与空气的密度分别为ρ1,ρ2,于是半径为r 的油滴的视重为 (4)由斯托克斯定律,粘滞流体对球形运动物体的阻力与物体速度成正比,其比例系数K 为6πηr ,η为粘度,r 为物体半径. prb Vrr f r +=16ηπ (5) b 是修正常数, b=0.00823N/m, p 为大气压强,单位为厘米汞高。
实验中常常固定油滴运动的距离,通过测量它通过此距离s 所需的时间来求得其运动速度,且电场强度E=U/d ,d 为平行板间的距离,U 为所加的电压,因此U d g g s pr b t g q g 2321213^)1(1218⎥⎦⎤⎢⎣⎡-⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+=ρρηπ (6) 三.实验仪器及注意事项。
1.密立根 CCD 一体化屏显油滴仪。
2.实验前应检查油滴仪是否水平,如果不水平可能造成落油孔被堵。
四.实验内容。
1. 选择适当的油滴并测量油滴上所带电荷,调整油滴实验装置。
2. 当油雾从喷雾口喷入油滴室内后,视场中将出现大量清晰的油滴,试加上平衡电压,改变其大小和极性,练习控制其中一颗油滴的运动。
当油滴处于平衡位置,选定测量的一段距离(一般取l=0.200cm 比较合适),然后把开关拨向“下降”,使油滴自由下落。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章误差估算与数据处理方法课后习题答案1.指出下列各量有效数字的位数。
(1)kV 有效位数:4 (2)mm 有效位数:3 (3)kg 有效位数:5 (4)自然数有效位数:无限位2.判断下列写法是否正确,并加以改正。
(1)A mA错,0.0350A 有效位数为3位,而35mA 有效位数为2位,二者物理意义不同,不可等同,应改为A mA 。
(2)kg错,测量结果(即最佳估计值)有效数字的最后一位应与不确定度的末位对齐。
测量结果有效数字取位时,应遵循“四舍六入五凑偶”的原则;而且,不确定度应记为“”的形式。
故应将上式改成kg 。
(3)km错,当采用科学计数法表示测量结果时,最佳估计值与不确定度应同时用科学计数法表示,并且10的指数应取一致,还要保证最佳估计值的最后一位与不确定度的末位对齐。
因此,上式应改为。
(4)A 正确。
3.试按有效数字修约规则,将下列各数据保留三位有效数字。
3.8547,2.3429,1.5451,3.8750,5.4349,7.6850,3.6612,6.26383.85 2.34 1.54 3.88 5.43 7.68 3.66 6.26 4.按有效数字的确定规则,计算下列各式。
(1)000.1=U 000123.0=L 010.10=m 40350.0=I 35=0350.0=I 11050.3⨯=()3.0270.53+=m 270.53=m ±()3.03.53±=m ()2000103.274±⨯=h ()kmh 4102.03.27⨯±=()004.0325.4±=x ?6386.08.7537.343=++解:原式 (2)解:原式 (3)解:原式 (4)解:原式5.分别写出下列各式的不确定度传播公式。
(1)(K 为常数)解:(a )绝对不确定度:(b )相对不确定度:其中,、分别表示A 、B 量的合成不确定度。
(2)解:(a )绝对不确定度:(b )相对不确定度:8.41981.41964.08.7537.343==++=?543.76180.845.88=--73.3727.3543.76180.845.88==--=?5.20725.0=⨯18.05.20725.0=⨯=()?001.247.0052.042.8=÷-+()00.4001.200.8001.247.0052.042.8=÷=÷-+=()2221BA K Q +=()()()()()()()2222222222222221 21BABABA B A C u B u A Ku B u A KuB BA uA BA K uB Q u A Q Q u +=+=⎪⎪⎭⎫⎝⎛∂+∂+⎪⎪⎭⎫ ⎝⎛∂+∂=⎪⎭⎫⎝⎛∂∂+⎪⎭⎫⎝⎛∂∂=()()()()()()22222222221BA uB u A BA K uB u A KQQ u E bAbAC ++=++==A uB u ()FDC B AN 2112--=()()()()()222222222222222222222221211 212111 ⎪⎭⎫ ⎝⎛+⎥⎦⎤⎢⎣⎡-+⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫⎝⎛-=⎪⎭⎫ ⎝⎛-+⎥⎦⎤⎢⎣⎡-+⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛+⎥⎦⎤⎢⎣⎡--=⎪⎭⎫⎝⎛∂∂+⎪⎭⎫ ⎝⎛∂∂+⎪⎭⎫ ⎝⎛∂∂+⎪⎭⎫ ⎝⎛∂∂+⎪⎭⎫ ⎝⎛∂∂=F D C B A F D C B A F D C B A C u u C B A D u D A u D A u A DC B u uD C B A u D A u D A u D C B A u F N u D N u C N u B N u A N N u其中,、、、、分别表示A 、B 、C 、D 、F 量的合成不确定度。
(3)解:(a )绝对不确定度:(b )相对不确定度:其中,、分别表示A 、B 量的合成不确定度。
(4)解:(a )绝对不确定度:()()()()F C B A u u C B A D u D A u D A u A D C B NN u E F D C B A C 21121211 222222222--⎪⎭⎫ ⎝⎛+⎥⎦⎤⎢⎣⎡-+⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛-==A uB uC uD u Fu AB A f 422-=()()[]()[]()()222222222222222222222141 //41 4/4/4/4/ 44⎪⎪⎭⎫⎝⎛+⎥⎦⎤⎢⎣⎡⎪⎪⎭⎫ ⎝⎛+=⎪⎪⎭⎫ ⎝⎛∂-∂+⎪⎪⎭⎫ ⎝⎛∂-∂=⎪⎪⎭⎫ ⎝⎛∂-∂+⎪⎪⎭⎫ ⎝⎛∂-∂=⎪⎪⎪⎪⎪⎭⎫⎝⎛∂⎪⎪⎭⎫⎝⎛-∂+⎪⎪⎪⎪⎪⎭⎫⎝⎛∂⎪⎪⎭⎫⎝⎛-∂=⎪⎭⎫⎝⎛∂∂+⎪⎭⎫ ⎝⎛∂∂=B A B A B A B A B AC u A B u A B u B A B A u A A B A u B A B A u A A B A u BA B A u A A BA uB f u A f f u ()()222222222222242141BA uB u A B A AB A u A B u A B ff u E B A B A C -+⎥⎦⎤⎢⎣⎡⎪⎪⎭⎫ ⎝⎛+=-⎪⎪⎭⎫ ⎝⎛+⎥⎦⎤⎢⎣⎡⎪⎪⎭⎫ ⎝⎛+==A uB u 42h d V π=(b )相对不确定度:其中,、分别表示d 、h 量的合成不确定度。
6.用最小刻度为0.1cm 的米尺对物体进行长度测量,其数据为9.92,9.94,9.87,9.86,9.91,若置信概率为,则测量结果应该表示为?解: (1)最佳值(2)不确定度A 类分量:()()()()222222224424hdh d h d C u d u h d u d u d h u h V u d V V u +=⎪⎪⎭⎫ ⎝⎛+⎥⎦⎤⎢⎣⎡⋅=⎪⎭⎫⎝⎛∂∂+⎪⎭⎫ ⎝⎛∂∂=πππ()()()222222424⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=+==h u d u h d u d u h d VV u E h d hdC ππdu hu ()=cm L %5.95L )(900.9550.49591.986.987.994.992.9551cm LL i i==++++==∑=du ()()()()()()()()cmL LS L u i iL A 016.010516.11030.210.20460.201046 200.1160.9160.4102014342102001.004.003.004.002.0 45900.991.9900.994.9900.992.9 1552224422222422222222512=⨯=⨯=⨯=⨯=++++=++++=++++=⨯-++-+-=--==------=∑ 平均值有效数字的位数可比原数据有效数字的位数多取一位。
加、减法中间计算结果的末位与运算各数据中末位数数量级最大的那一位对齐(如9.92),不必再多取一位。
乘方、开方运算的中间计算结果的有效数字位数可比被乘方、被开方数的有效数字加、减法中间计算结果的末位与运算各数据中末位数数量级最大的那一位对齐(如16),不必中间过程的不确定度可多取一位有效数字(两位),且遵常数可根据具体计算需要多取几位有效数3米尺的仪器误差取其最小刻度的一半,即0.05cm 。
B 类分量:L 的合成不确定度:由于置信概率为,则扩展不确定度(3)测量结果表示7.用量程为20mA ,准确度等级为0.5级的电流表测量某电流的指示值为15.00mA ,其测量结果的最大误差为?解:测量结果的最大误差即仪器误差。
仪器误差=量程准确度等级%,而与测量指示值15.00mA 无关。
该题测量结果的最大误差。
注意,仪器误差通常取一位有效数字。
8.用千分尺(仪器极限误差为mm )测量一钢球直径6次,测量数据为:14.256、14.278、14.262、14.263、14.258、14.272(mm );用天平(仪器极限误差为g )测量它的质量1次,测量值为:g ,试求钢球密度的最佳值与不确定度。
解:密度为间接测量量,直径d 与质量m 为直接测量量,故应按间接测量数据处理方法来求测量结果。
1.直径d 的处理 (1)最佳值(2)不确定度A 类分量:()cmL u B 028.0732.105.03==∆=仪()()cmL u L u u B A C 04.01040.101084.756.2108.26.12322222=⨯=⨯+=⨯+=+=---%5.95%80.0900.908.008.004.022====⨯=⨯=LU E cmu U C ()()%80.0%5.95 /08.090.93==±=E P cm g ρ⨯)(1.0%5.020mA =⨯=004.0±06.0±84.11ρd mmdd i i2648.146272.14278.14256.14661=+++==∑= 平均值有效数字的位数可比原数据有效数字的位数多取一位。
乘方、开方运算的中间计算结果的有效数字位数可比被乘方、被开方数的有效数字绝对不确定度保留一位有效数字,且遵循“只进不舍”的取舍原则。
B 类分量:d 的合成不确定度:2.质量m 的处理由于质量m 为单次测量值,因此不存在标准不确定度的A 类分量,并且B 类分量,则质量m 的合成不确定。
3.密度ρ的处理 (1)最佳值(2)合成不确定度密度与质量和直径之间的函数为简单乘除关系,可先计算相对不确定度E 。
()()()()()()()()mmddS d u i id A 0035.01003.121000.3036100.3010361 3049490.40.916981103077231391030007.0007.0002.0003.0013.0009.0 562648.14272.142648.14278.142648.14256.14 16633662222226222222222612=⨯=⨯=⨯=+++++=+++++=+++++=⨯-++-+-=--==-----=∑ ()mmd u B 0023.0732.1004.03==∆=仪()()mmd u d u u B A d 0042.0105.171029.52.12103.25.33332222=⨯=⨯+=⨯+=+=---()m u A ()gm u B 06.0=∆==仪仪σ()gm u u B m 06.0==ρ()333/790.79028.21416.384.116 90279.214159.384.1164265.114159.384.1166cmg cm g dm=⨯⨯=⨯⨯=⨯⨯==πρ()ρC u 应比运算各数中有效数字位数最多的(如1.42648)还多取一位。
