数字图像处理-灰度变换
数字图像处理_课件_3
21
航拍图像的幂律变换增强
数第 字三 图章 像灰 处度 理变
换 与 空 间 滤 波
a. 原始图像
b. C=1, =3.0 c. C=1, =4.0 (最佳) d. C=1, =5.0
s cr c 1
22
电子显微镜扫描
3.2.4 对比度拉伸
的 放 大 约 700 倍 的花粉图像
➢ 因此，归一化后的直方图由 p(rk ) nk / MN 给 出，其中k＝0, 1, …, L-1。
29
数第 字三
➢ p(rk)是灰度级rk在图像中出现的概率的一
图 章 个估计。
像灰
处 度 ➢ 归一化直方图的所有分量之和应等于1。
理变
换 与
➢ 直方图是多种空间域处理技术的基础。
空
间
滤
波
30
数第 字三 图章 像灰 处度 理变
换 与 空 间 滤 波
4. 一般情况下，从输入图像的左上角开始处理，以 水平扫描的方式逐像素地处理，每次一行
5. 当该邻域的原点位于图像的边界上时，部分邻域 将位于图像的外部。此时，可以用0或者其它指定 的灰度值填充图像的边缘，被填充边界的厚度取 决于邻域的大小。
以上处理称为空间滤波，邻域与预定义的操作一 起称为空间滤波器。
与 为输出中较宽范围的灰度值，可以扩展图像
空 间
中暗像素的值，同时压缩高灰度级的值。
滤 波
➢ 反对数变换的作用与此相反。
17
傅里叶频谱及其对数变换
数第
字三
图章
像灰
处度
理变
换
与
空
间 滤
傅立叶频谱的对数变换，s
c
灰度变换的基本原理
灰度变换的基本原理灰度变换是数字图像处理中一种常见的操作技术，它通过改变图像中每个像素的亮度值，从而实现图像的增强或调整。
灰度变换的基本原理是将原始图像的灰度级映射到一个新的灰度级，使得图像的视觉效果更加理想。
在进行灰度变换之前，我们需要了解一些基本概念。
首先，灰度级是指图像中每个像素的亮度值，通常用0到255的整数表示，其中0代表黑色，255代表白色。
其次，灰度变换函数是将原始图像的灰度级映射到新的灰度级的函数，它决定了图像的最终效果。
常用的灰度变换函数包括线性变换、对数变换、幂律变换等。
线性变换是最简单的一种灰度变换方法，它通过一条直线的斜率和截距来调整图像的亮度。
对数变换和幂律变换则是非线性变换方法，它们通过对原始图像的灰度级取对数或幂次来改变图像的亮度分布。
灰度变换的具体步骤如下：首先，读入原始图像，并将其转换为灰度图像。
然后，选择合适的灰度变换函数，并根据函数的定义计算每个像素的新灰度级。
最后，将新的灰度级赋值给每个像素，并生成处理后的图像。
灰度变换在图像处理中有着广泛的应用。
首先，它可以用于图像增强，即通过调整图像的亮度和对比度，使图像更加清晰和鲜明。
其次，灰度变换可以用于图像的调整和校正，例如校正图像的曝光不足或过度曝光的问题。
此外，灰度变换还可以用于图像的压缩和编码，从而减少图像的存储空间和传输带宽。
灰度变换虽然简单，但在实际应用中需要根据具体情况选择合适的变换函数和参数。
例如，在图像增强中，可以根据图像的亮度分布选择线性变换、对数变换或幂律变换。
对于高动态范围图像，可以采用自适应灰度变换方法，根据图像的局部特征进行变换。
需要注意的是，灰度变换可能会引入一些副作用，例如图像的噪声会被放大，导致图像质量的下降。
因此，在进行灰度变换时，需要考虑图像的特点和应用需求，避免不必要的变换和误操作。
灰度变换是数字图像处理中一种重要的操作技术，它通过改变图像的灰度级来实现图像的增强和调整。
灰度变换的基本原理是将原始图像的灰度级映射到一个新的灰度级，从而改变图像的亮度分布和视觉效果。
数字图像处理名词解释
•名词解释（每小题5分,本题共20分）数字图像数字图像是指由被称作像素的小块区域组成的二维矩阵。
将物理图像行列划分后，每个小块区域称为像素（PiXeI）O 数字图像处理指用数字计算机及其它有关数字技术，对图像施加某种运算和处理，从而达到某种预想目的的技术.8-连通的定义-对于具有值V的像素P和q ,如果q在集合N&p）中,则称这两个像素是8-连通的。
灰度直方图是指反映•幅图像各灰度级像元出现的频率。
灰度自方图是灰度级的函数，描述的是图像中该灰度级的像素个数。
即：横坐标农示灰度级，纵坐标衣示图像中该灰度级出现的个数。
性质：直方图是•幅图像中各像素灰度值出现次数（或频数）的统计结果，它只反映该图像中不同灰度值出现的次数（或频数），而未反映某•灰度值像素所在位置。
也就是说，它只包含了该图像中某•灰度值的像素出现的概率，而丢失了其所在位置的信息。
用途：用于判断图像量化是否恰当直方图给出了•个简单可见的指示，用来判断•幅图象是否合理的利用了全部被允许的灰度级范圉。
•般•幅图应该利用全部或几乎全部可能的灰度级，否则等于增加了量化间隔。
丢失的信息将不能恢复。
数字图像通常有两种表示形式：位图，矢量图位图和矢量图的比较：1、点位图由像素构成，矢量图由对象构成点位图的基本构图单位是像素，像素包含了色彩信息。
包含不同色彩信息的像素的矩阵组合构成了千变万化的图像。
矢量图形指由代数方程定义的线条或曲线构成的图形。
如:农示-个圆形,矢量图像保存了• 个画圆的命令、圆心的坐标、半径的长度等等。
欲显示该圆，矢量绘图软件则根据圆的坐标、半径等信息，经过方程式计算，将圆“画”在屏幕上。
矢量图像由许多矢量图形元素构成, 这些图形元素称为“对象”。
2、点位图面向像素绘画,矢量图面向对象“构画”两种图像的构成方式不同，其绘画力式也存在差别。
点位图是通过改变像素的色彩实现绘画和画面的修改。
点位图软件捉供了模拟手绘习惯的工具实现绘画。
数字图像处理-图像基本运算
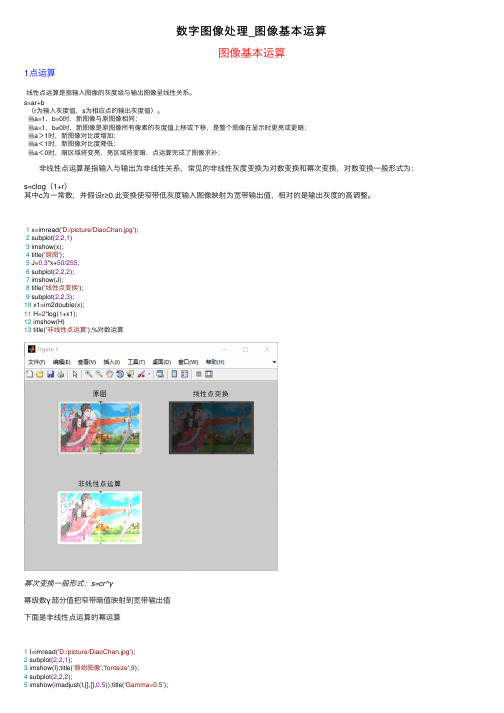
数字图像处理_图像基本运算图像基本运算1点运算线性点运算是指输⼊图像的灰度级与输出图像呈线性关系。
s=ar+b（r为输⼊灰度值，s为相应点的输出灰度值）。
当a=1，b=0时，新图像与原图像相同；当a=1，b≠0时，新图像是原图像所有像素的灰度值上移或下移，是整个图像在显⽰时更亮或更暗；当a＞1时，新图像对⽐度增加；当a＜1时，新图像对⽐度降低；当a＜0时，暗区域将变亮，亮区域将变暗，点运算完成了图像求补； ⾮线性点运算是指输⼊与输出为⾮线性关系，常见的⾮线性灰度变换为对数变换和幂次变换，对数变换⼀般形式为：s=clog（1+r）其中c为⼀常数，并假设r≥0.此变换使窄带低灰度输⼊图像映射为宽带输出值，相对的是输出灰度的⾼调整。
1 x=imread('D:/picture/DiaoChan.jpg');2 subplot(2,2,1)3 imshow(x);4 title('原图');5 J=0.3*x+50/255;6 subplot(2,2,2);7 imshow(J);8 title('线性点变换');9 subplot(2,2,3);10 x1=im2double(x);11 H=2*log(1+x1);12 imshow(H)13 title('⾮线性点运算');%对数运算幂次变换⼀般形式：s=cr^γ幂级数γ部分值把窄带暗值映射到宽带输出值下⾯是⾮线性点运算的幂运算1 I=imread('D:/picture/DiaoChan.jpg');2 subplot(2,2,1);3 imshow(I);title('原始图像','fontsize',9);4 subplot(2,2,2);5 imshow(imadjust(I,[],[],0.5));title('Gamma=0.5');7 imshow(imadjust(I,[],[],1));title('Gamma=1');8 subplot(2,2,4);9 imshow(imadjust(I,[],[],1.5));title('Gamma=1.5');2代数运算和逻辑运算加法运算去噪处理1 clear all2 i=imread('lenagray.jpg');3 imshow(i)4 j=imnoise(i,'gaussian',0,0.05);5 [m,n]=size(i);6 k=zeros(m,n);7for l=1:1008 j=imnoise(i,'gaussian',0,0.05);9 j1=im2double(j);10 k=k+j1;11 End12 k=k/100;13 subplot(1,3,1),imshow(i),title('原始图像')14 subplot(1,3,2),imshow(j),title('加噪图像')15 subplot(1,3,3),imshow(k),title(‘求平均后的减法运算提取噪声1 I=imread(‘lena.jpg’);2 J=imnoise (I,‘lena.jpg’,0,0.02);3 K=imsubtract(J,I);4 K1=255-K;5 figure;imshow(I);7 figure;imshow(K1);乘法运算改变图像灰度级1 I=imread('D:/picture/SunShangXiang.jpg')2 I=im2double(I);3 J=immultiply(I,1.2);4 K=immultiply(I,2);5 subplot(1,3,1),imshow(I);subplot(1,3,2),imshow(J);6 subplot(1,3,3);imshow(K);逻辑运算1 A=zeros(128);2 A(40:67,60:100)=1;3 figure(1)4 imshow(A);5 B=zeros(128);6 B(50:80,40:70)=1;7 figure(2)8 imshow(2);9 C=and(A,B);%与10 figure(3);11 imshow(3);12 D=or(A,B);%或13 figure(4);14 imshow(4);15 E=not(A);%⾮16 figure(5);17 imshow(E);3⼏何运算平移运算实现图像的平移1 I=imread('lenagray.jpg');2 subplot(1,2,1);3 imshow(I);4 [M,N]=size(I);g=zeros(M,N);5 a=20;b=20;6for i=1:M7for j=1:N8if((i-a>0)&(i-a<M)&(j-b>0)&(j-b<N)) 9 g(i,j)=I(i-a,j-b);10else11 g(i,j)=0;12 end13 end14 end15 subplot(1,2,2);imshow(uint8(g));⽔平镜像变换1 I=imread('lena.jpg');2 subplot(121);imshow(I);3 [M,N]=size(I);g=zeros(M,N);4for i=1:M5for j=1:N6 g(i,j)=I(i,N-j+1);7 end8 end9 subplot(122);imshow(uint8(g));垂直镜像变换1 I=imread('lena.jpg');2 subplot(121);imshow(I);3 [M,N]=size(I);g=zeros(M,N);4for i=1:M5for j=1:N6 g(i,j)=I(M-i+1,j);7 end8 end9 subplot(122);imshow(uint8(g));图像的旋转1 x=imread('D:/picture/DiaoChan.jpg');2 imshow(x);3 j=imrotate(x,45,'bilinear');4 k=imrotate(x,45,'bilinear','crop');5 subplot(1,3,1),imshow(x);6 title(‘原图')7 subplot(1,3,2),imshow(j);8 title(‘旋转图(显⽰全部)')9 subplot(1,3,3),imshow(k);10 title(‘旋转图(截取局部)')⼏种插值法⽐较1 i=imread('lena.jpg');2 j1=imresize(i,10,'nearest');3 j2=imresize(i,10,'bilinear');4 j3=imresize(i,10,'bicubic');5 subplot(1,4,1),imshow(i);title(‘原始图像')6 subplot(1,4,2),imshow(j1);title(‘最近邻法')7 subplot(1,4,3),imshow(j2);title(‘双线性插值法')8 subplot(1,4,4),imshow(j3);title(‘三次内插法')放缩变换1 x=imread('D:/picture/ZiXia.jpg')2 subplot(2,3,1)3 imshow(x);4 title('原图');5 Large=imresize(x,1.5);6 subplot(2,3,2)7 imshow(Large);8 title('扩⼤为1.5');9 Small=imresize(x,0.1);10 subplot(2,3,3)11 imshow(Small);12 title('缩⼩为0.3');13 subplot(2,3,4)14 df=imresize(x,[600700],'nearest');15 imshow(df)16 title('600*700');17 df1=imresize(x,[300400],'nearest');18 subplot(2,3,5)19 imshow(df1)20 title('300*400');后记：（1）MATLAB基础知识回顾1：crtl+R是对选中的区域注释，ctrl+T是取消注释2：有的代码中点运算如O=a.*I+b/255 ，其中b除以255原因是：灰度数据有两种表式⽅法：⼀种是⽤unit8类型，取值0~255；另⼀种是double类型，取值0~1。
数字图像处理图像变换实验报告
实验报告实验名称:图像处理姓名:刘强班级:电信1102学号:1404110128实验一图像变换实验——图像点运算、几何变换及正交变换一、实验条件PC机数字图像处理实验教学软件大量样图二、实验目的1、学习使用“数字图像处理实验教学软件系统”,能够进行图像处理方面的简单操作;2、熟悉图像点运算、几何变换及正交变换的基本原理,了解编程实现的具体步骤;3、观察图像的灰度直方图,明确直方图的作用与意义;4、观察图像点运算与几何变换的结果,比较不同参数条件下的变换效果;5、观察图像正交变换的结果,明确图像的空间频率分布情况。
三、实验原理1、图像灰度直方图、点运算与几何变换的基本原理及编程实现步骤图像灰度直方图就是数字图像处理中一个最简单、最有用的工具,它描述了一幅图像的灰度分布情况,为图像的相关处理操作提供了基本信息。
图像点运算就是一种简单而重要的处理技术,它能让用户改变图像数据占据的灰度范围。
点运算可以瞧作就是“从象素到象素”的复制操作,而这种复制操作就是通过灰度变换函数实现的。
如果输入图像为A(x,y),输出图像为B(x,y),则点运算可以表示为:B(x,y)＝f[A(x,y)]其中f(x)被称为灰度变换(Gray Scale Transformation,GST)函数,它描述了输入灰度值与输出灰度值之间的转换关系。
一旦灰度变换函数确定,该点运算就完全确定下来了。
另外,点运算处理将改变图像的灰度直方图分布。
点运算又被称为对比度增强、对比度拉伸或灰度变换。
点运算一般包括灰度的线性变换、阈值变换、窗口变换、灰度拉伸与均衡等。
图像几何变换就是图像的一种基本变换,通常包括图像镜像变换、图像转置、图像平移、图像缩放与图像旋转等,其理论基础主要就是一些矩阵运算,详细原理可以参考有关书籍。
实验系统提供了图像灰度直方图、点运算与几何变换相关内容的文字说明,用户在操作过程中可以参考。
下面以图像点运算中的阈值变换为例给出编程实现的程序流程图,如下:2、图像正交变换的基本原理及编程实现步骤数字图像的处理方法主要有空域法与频域法,点运算与几何变换属于空域法。
数字图像处理基本操作及灰度调整实验报告
一．实验目的1.掌握读、写图像的基本方法；2.掌握MATLAB 语言中图像数据与信息的读取方法；3.理解图像灰度变换处理在图像增强的作用；4．掌握绘制灰度直方图的方法，理解灰度直方图的灰度变换及均衡化的方法。
二．实验基本原理1. 灰度变换灰度变换是图像增强的一种重要手段，它常用于改变图象的灰度范围及分布，是图象数字化及图象显示的重要工具。
1) 图像反转灰度级范围为[0, L-1]的图像反转可由下式获得r L s --=12) 对数运算：有时原图的动态范围太大，超出某些显示设备的允许动态范围，如直接使用原图，则一部分细节可能丢失。
解决的方法是对原图进行灰度压缩，如对数变换：s = c log(1 + r )，c 为常数，r ≥ 03) 幂次变换：0,0,≥≥=γγc cr s4) 对比拉伸：在实际应用中,为了突出图像中感兴趣的研究对象，常常要求局部扩展拉伸某一范围的灰度值，或对不同范围的灰度值进行不同的拉伸处理，即分段线性拉伸：其对应的数学表达式为：2. 直方图均衡化灰度直方图的横坐标是灰度级，纵坐标是该灰度级出现的频度，它是图像最基本的统计特征。
依据定义，在离散形式下， 用r k 代表离散灰度级，用p r (r k )代表p r (r )，并且有下式成立：nn r P k k r =)( 1,,2,1,010-=≤≤l k rk式中：n k 为图像中出现r k 级灰度的像素数，n 是图像像素总数，而n k /n 即为频数。
直方图均衡化处理是以累积分布函数变换法为基础的直方图修正法。
假定变换函数为ωωd p r T s r r)()(0⎰==(a) Lena 图像 (b) Lena 图像的直方图图1-1 Lena 图像及直方图当灰度级是离散值时，可用频数近似代替概率值，即1,,1,010)(-=≤≤=l k r nn r p k k k r式中：l 是灰度级的总数目，p r (r k )是取第k 级灰度值的概率，n k 是图像中出现第k 级灰度的次数，n 是图像中像素总数。
实验报告---实验三图像灰度变换处理模板
计算机科学与工程学院天津理工大学计算机科学与工程学院实验报告2016 至2017 学年第二学期实验三图像灰度变换处理课程名称数字图像处理学号学生姓名卢洪利年级2014专业计算机科学与技术教学班号2实验地点主7-215实验时间2016年4月4日第1节至第2 节主讲教师杨淑莹实验成绩软件运行特色算法分析流程设计报告成绩总成绩实验（三）实验名称图像灰度变换处理软件环境OpenSUSE Leap 42.2Qt 5.6.1硬件环境PC实验目的掌握图像的灰度变换原理，编程实现图像的灰度变换功能。
实验内容（应包括实验题目、实验要求、实验任务等）1．实现灰度直方图。
要求：了解灰度直方图基本原理，实现灰度直方图。
说明：灰度直方图基本原理1 灰度直方图简介2 基本原理任务：（1）在左视图中打开一幅位图。
（2）制作一个【灰度直方图】菜单，将消息映射到右视图中，在右视图中实现灰度直方图。
2．实现灰度线性变换。
要求：了解灰度线性变换基本原理，实现灰度线性变换。
说明：灰度线性变换基本原理任务：（1）在左视图中打开一幅位图。
（2）制作一个【灰度线性变换】菜单，将消息映射到右视图中，在右视图中实现灰度线性变换。
3．实现灰度非线性变换。
要求：了解灰度非线性变换基本原理，实现灰度非线性变换。
说明：灰度非线性变换基本原理1灰度对数变换2灰度幂次变换3灰度指数变换任务：（1）在左视图中打开一幅位图。
（2）制作一个【灰度对数变换】菜单，将消息映射到右视图中，在右视图中实现灰度对数变换。
（3）制作一个【灰度幂次变换】菜单，将消息映射到右视图中，在右视图中实现灰度对数变换。
（4）制作一个【灰度指数变换】菜单，将消息映射到右视图中，在右视图中实现灰度指数变换。
4．实现阈值变换。
要求：了解阈值变换图基本原理，实现灰度阈值变换说明：灰度阈值变换基本原理任务：（1）在左视图中打开一幅位图。
（2）制作一个【阈值变换】菜单，将消息映射到右视图中，在右视图中实现阈值变换。
数字图像处理实验报告：灰度变换与空间滤波(附带程序,不看后悔)
1.灰度变换与空间滤波一种成熟的医学技术被用于检测电子显微镜生成的某类图像。
为简化检测任务，技术决定采用数字图像处理技术。
发现了如下问题：（1）明亮且孤立的点是不感兴趣的点；（2）清晰度不够，特别是边缘区域不明显；（3）一些图像的对比度不够；（4）技术人员发现某些关键的信息只在灰度值为I1-I2的范围，因此，技术人员想保留I1-I2区间范围的图像，将其余灰度值显示为黑色。
（5）将处理后的I1-I2范围内的图像，线性扩展到0-255灰度，以适应于液晶显示器的显示。
请结合本章的数字图像处理处理，帮助技术人员解决这些问题。
1.1问题分析及多种方法提出（1）明亮且孤立的点是不够感兴趣的点对于明亮且孤立的点，其应为脉冲且灰度值为255(uint8)噪声，即盐噪声，为此，首先对下载的细胞图像增加盐噪声，再选择不同滤波方式进行滤除。
均值滤波：均值滤波是典型的线性滤波算法，它是指在图像上对目标像素给一个模板，该模板包括了其周围的临近像素（以目标像素为中心的周围8个像素，构成一个滤波模板，即去掉目标像素本身），再用模板中的全体像素的平均值来代替原来像素值。
优点：速度快，实现简单；缺点：均值滤波本身存在着固有的缺陷，即它不能很好地保护图像细节，在图像去噪的同时也破坏了图像的细节部分，从而使图像变得模糊，不能很好地去除噪声点。
其公式如下：使用矩阵表示该滤波器则为：中值滤波：滤除盐噪声首选的方法应为中值滤波，中值滤波法是一种非线性平滑技术，它将每一像素点的灰度值设置为该点某邻域窗口内的所有像素点灰度值的中值。
其过程为：a 、存储像素1，像素2.....像素9的值；b 、对像素值进行排序操作；c 、像素5的值即为数组排序后的中值。
优点：由于中值滤波本身为一种利用统计排序方法进行的非线性滤波方法，故可以滤除在排列矩阵两边分布的脉冲噪声，并较好的保留图像的细节信息。
缺点：当噪声密度较大时，使用中值滤波后，仍然会有较多的噪声点出现。
数字图像灰度变换技术总结
数字图像灰度变换技术总结篇一：图像的灰度变换昆明理工大学（数字图像处理）实验报告实验名称：图像的灰度变换专业：电子信息科学与技术姓名：学号：成绩：[实验目的]1、理解并掌握灰度变换的基本原理和方法。
2、编程实现图像灰度变换。
3、分析不同的灰度变换方法对最终图像效果的影响。
[实验内容]1、灰度的线性变换；2、灰度的非线性变换；3、图像的二值化；4、图像的反色处理；[实验原理]图像的灰度变换(grayscaletransformation,GST)处理是图像增强处理技术中一种非常基础、直接的空间域图像处理方法,也是图像数字化软件和图像显示软件的一个重要组成部分。
灰度变换是指根据某种目标条件按一定变换关系逐点改变原图像中每一个像素灰度值的方法。
目的是为了改善画质,使图像的显示效果更加清晰。
灰度变换有时又被称为图像的对比度增强或对比度拉伸。
从图像输入装置得到的图像数据,以浓淡表示,(:数字图像灰度变换技术总结)各个像素与某一灰度值相对应。
设原图像像素的灰度值d=f(x,y),处理后图像像素的灰度值d′=g(x,y),则灰度增强可表示为:g(x,y)=T[f(x,y)]或d′=T(d)要求d和d′都在图像的灰度范围之内。
函数T(d)称为灰度变换函数,它描述了输入灰度值和输出灰度值之间的转换关系。
灰度变换主要针对独立的像素点进行处理,通过改变原始图像数据所占据的灰度范围而使图像在视觉上得到良好的改观,没有利用像素点之间的相互空间关系。
因此,灰度变换处理方法也叫做点运算法。
点运算可以按照预定的方式改变一幅图像的灰度直方图。
除了灰度级的改变是根据某种特定的灰度变换函数进行之外,点运算可以看做是“从像素到像素”的复制操作。
根据g(x,y)=T[f(x,y)],可以将灰度变换分为线性变换和非线性变换。
1、灰度的线性变换若g(x,y)=T[f(x,y)]是一个线性或分段线性的单值函数,例如g(x,y)=T[f(x,y)]=af(x,y)+b则由它确定的灰度变换称为灰度线性变换,简称线性变换。
数字图像处理 第5章 灰度变换与色彩校正
图像处理
低分辨 传统方法插值 率图像
边缘检测 边缘以及 特殊处理 附近像素
插值图像
◎区域指导的图像插值算法
输入原始 图像f(x,y)
区域分割
2020/9/23
确定插值 位置
设计插值 公式
输出插值 图像g(x,y)
36
三、灰度变换技术
灰度变换——图像增强手段之一—— 点处理方式
0.03
14
r7=1
180
0.04
解：由变换函数公式得到对应的灰度等级：
s2
s0
s1
T (r
1
2
i0
ni
) CP(rk )
0 i0
ni n
0.17
ni 0.17 0.25 0.42
n
0.17 0.25 0.19 0.61
i0 n
s3
3 i0
ni n
0.17 0.25 0.19 0.18
2020/9/23
5
一、基本概念
1.阶调与色调
①阶调：
描述一种颜色区别与另一种颜色的特征
高光：图像中最亮的部分。灰度等级约在240 左右 中间调：图像中的主要部分。 暗调：图像中最暗的部分。灰度等级约在12 左右
层次：灰度亮化的等级（明暗程度）
注意：对灰度图像，阶调与层次的概念是相同的
阶调与层次的复制状况决定了图像中各种颜
HA(r)
dr
T ' (r) ds dr
0
255
CL
2020/9/23
s T (r)
A0
H A(r)dr
0
CP(r)
13
设：一幅像素总数为n，灰度等级为[0,L]的图像
数字图像处理03_灰度变换及空间滤波
2020年5月28日
数字图像处理
13
频率域方法
在图像的某种变换域内，对图像的变换值进行处理。如， 先对图像进行二维傅立叶变换，再对图像的频谱进行某 种修正（滤波），最后将修正后的变换值逆变换到空间 域，从而获得增强后的图像。
2020年5月28日
数字图像处理
6
图像增强的主要方法
图像增强的处理方法
空间域方法:直接以图像中的像素操作为基础。
灰度变换（强度映射、点处理）
➢ 直接灰度变换(图像反转、对数变换、幂次变换、分段线性变换) ➢ 直方图处理（直方图均衡化、直方图匹配、局部直方图） ✓ 关键是寻找一个合适的变换函数T
（b）模板系数以及与图像 像素对应位置关系
f(x,y-1) f(x, y) f(x, y+1) f(x+1,y-1) f(x+1, y) f(x+1,y+1)
（a）模板下的图像像素
ab
g(x, y) w(s,t) f (x s, y t) sa tb
空域滤波的基本原理
2020年5月28日
数字图像处理
例如,伪彩色图像增强：将不同灰度的图像赋以不同的彩色,以 增强人类的视觉感知,在医学图像处理中经常采用；
又如，假彩色增强：不同波段获取的图像赋以不同的彩色,用 在对多波段遥感图像的假彩色显示等
图像的增强是综合和一般性地改善图像质量，解决图像 由于噪声、模糊退化和对比度降低等三类问题,获得最 好的视觉效果。
低质量图像(低对比度、高噪声、低清晰度)
2020年5月28日
数字图像处理
3
3.1 背景知识
数字图像处理基本操作及灰度调整实验报告
数字图像处理基本操作及灰度调整实验报告实验目的1.掌握数字图像处理的基本概念和原理。
2.学会使用Python编程语言进行图像处理。
3.理解并实现图像灰度调整的方法。
4.分析实验结果，讨论图像处理方法的优缺点。
2.1 数字图像处理概述数字图像处理（Digital Image Processing，DIP）是一门研究使用计算机对图像进行处理的技术。
它的目的是改善图像的质量，使之更适合人类或计算机对图像进行观察和分析。
数字图像处理涉及到图像采集、存储、传输、分析以及图像的恢复等方面。
2.2 图像的表示和描述数字图像由图像元素（像素）组成，每个像素有一个对应的灰度值。
灰度值表示像素的亮度，通常用8位二进制数表示，其范围为0~255。
像素的灰度值越高，亮度越高。
数字图像可以表示为一个矩阵，矩阵中的每个元素对应一个像素的灰度值。
彩色图像通常采用RGB颜色模型，每个像素包含三个分量，分别对应红色、绿色和蓝色通道的亮度。
2.3 图像灰度调整图像灰度调整是指调整图像像素的灰度值，以改善图像的质量。
常用的图像灰度调整方法有：1.线性灰度变换：通过线性映射关系改变图像灰度值，可以实现图像亮度的调整和对比度的拉伸。
2.直方图均衡化：通过调整图像的灰度直方图，使其均匀分布，可以提高图像的对比度。
•操作系统：Windows 10•编程语言：Python 3.8•图像处理库：OpenCV 4.5.2•集成开发环境：Visual Studio Code4.1 图像读取和显示首先，我们需要使用OpenCV库读取和显示图像。
以下是读取和显示图像的Python代码：4.2 图像灰度化为了便于后续的灰度调整操作，我们需要将彩色图像转换为灰度图像。
以下是图像灰度化的Python代码：4.3 灰度调整接下来，我们将对图像进行灰度调整。
首先，实现线性灰度变换。
以下是线性灰度变换的Python代码：4.4 图像直方图均衡化直方图均衡化是一种能够提高图像对比度的方法。
图像的基本灰度变换
Digital Image Processing 数字图像处理实验DIP Lab 2数字图像处理实验2 —空间域增强(1):图像的灰度变换实验目的1.学习常见的图像增强的方法并实际体会图像增强前后画质的变化；2.了解几种不同增强方式用于不同图像处理所取得的效果；3.培养处理实际图像的能力并为课堂教学提供配套的实践机会。
实验要求1.利用MatLab工具箱中关于图像增强的函数对本指导书中的指定图像进行灰度增强处理；2.自己编制程序实现MatLab工具箱中函数以外的图像增强算法，对于本指导书中指定的图像进行处理。
实验内容一：灰度变换1.运用亮度变换函数imadjust对图像进行增强处理，观察图像对比度的变化。
实验教材P63 -642.学习教材【例2-21】和【例2-22】，实现对图像进行分段线性变换：编程实验：对图pout.tif ,将其小于30的灰度值不变,将30到150的灰度值拉伸到30到200,同时压缩150到255的灰度值到200到255之间.3.编程实验：对图像Fig3.04(a).jpg进行求反，观察图像处理前后的变化；4.验证实验：对图像进行对数变换，观察图像处理前后的变化；5.总结灰度变换增强方法处理的特点；常见图像格式数据类操作提示(续)w贴图时可以点击图像窗口的Edit，然后在下拉菜单中点击Copy Figure，即可将图像放入减切板，然后就可以在WORD文档中粘贴。
灰度变换原图像f(m,n) 的灰度范围[a,b] 线形变换为图像g(m,n),灰度范围[a’,b’]公式：g(m,n)=a’+(b’-a’)* f(m,n) /(b-a)运用灰度变换函数imadjustJ = imadjust(I,[low in;high in],[low out;high out],gamma)反转实验：思考用matlab自带函数imadjust实现图像反转，图3.4（a）思考题/问答题1.小结一下本实验所用的增强方法。
图像处理实验3-4
数字图像处理实验1. 直方图修正灰度变换是图像增强的一种重要手段，使图像对比度扩展，图像更加清晰，特征更加明显。
灰度级的直方图给出了一幅图像概貌的描述，通过修改灰度直方图来得到图像增强。
（1）计算出一幅灰度图像的直方图clearclose allI=imread(' rice.png');imhist(I)title('实验一（1）直方图');（2）对灰度图像进行简单的灰度线形变换，figuresubplot(2,2,1)imshow(I);title('试验2-灰度线性变换');subplot(2,2,2)histeq(I);（3）看其直方图的对应变化和图像对比度的变化原图像f(m,n) 的灰度范围[a,b] 线形变换为图像g(m,n),灰度范围[a’,b’] 公式：g(m,n)=a’+(b’-a’)* f(m,n) /(b-a)figuresubplot(2,2,1)imshow(I)J=imadjust(I,[0.3,0.7],[0,1],1);title(' 实验一（3）用g(m,n)=a’+(b’-a’)* f(m,n)/(b-a)进行变换');subplot(2,2,2)imshow(J)subplot(2,2,3)imshow(I)J=imadjust(I,[0.5 0.8],[0,1],1);subplot(2,2,4)imshow(J)(4) 图像二值化（选取一个域值，将图像变为黑白图像）figuresubplot(2,2,1)imshow(I)J=find(I<150);I(J)=0;J=find(I>=150);I(J)=255;title(' 实验一（4）图像二值化( 域值为150 ）');subplot(2,2,2)imshow(I)clc;I=imread(‘rice.png');bw=im2bw(I,0.5);%选取阈值为0.5figure;imshow(bw) %显示二值图像2. 图像处理变换1．傅立叶变换熟悉其概念和原理,实现对一幅灰度图像的快速傅立叶变换,并求其变换后的系数分布. 2．离散余弦变换熟悉其概念和原理,实现对一幅灰度和彩色图像作的离散余弦变换,选择适当的DCT系数阈值对其进行DCT反变换.% 图像的FFT变换clc;I=imread('rice.png');subplot(1,2,1)imshow(I);title('原图');subplot(1,2,2)imhist(I);title('直方图');colorbar;J=fft2(I);figure;subplot(1,2,1)imshow(J);title('FFT变换结果');subplot(1,2,2)K=fftshift(J);imshow(K);title('零点平移');figure;imshow(log(abs(K)),[]),colormap(jet(64)),colorbar;title('系数分布图');% 图像的DCT变换RGB=imread('onion.png');figure;subplot(1,2,1)imshow(RGB);title('彩色原图');a=rgb2gray(RGB);subplot(1,2,2)imshow(a);title('灰度图');figure;b=dct2(a);imshow(log(abs(b)),[]),colormap(jet(64)),colorbar; title('DCT变换结果');figure;b(abs(b)<10)=0;% idctc=idct2(b)/255;imshow(c);title('IDCT变换结果');3. 小波变换实验内容：熟悉小波变换的概念和原理,熟悉matlab小波工具箱主要函数的使用.利用二维小波分析对一幅图像作2层小波分解,并在此基础上提取各层的低频信息实现图像的压缩.程序如下：clcclose allcleara=imread('deblur1.png ');subplot(1,2,1);imshow(a);title('原始图像');I=rgb2gray(a);subplot(1,2,2);imshow(I);title('原始图像的灰度图');% 进行二维小波变换[a,b] = wavedec2(I, 2, 'bior3.7');% 提取各层低频信息figure;c = appcoef2( a, b, 'bior3.7', 1 );subplot(1,2,1);imshow(c, []);title('一层小波变换结果');d = appcoef2( a, b, 'bior3.7', 2 );subplot(1,2,2);imshow(d, []);title('二层小波变换结果');4. 模板运算一、实验内容：（1）平滑：平滑的目的是模糊和消除噪声。
灰度变换 对数变换
灰度变换对数变换灰度变换是数字图像处理中常用的一种技术，它可以改变图像的亮度分布，使得图像更加清晰、易于分析和处理。
而对数变换则是灰度变换的一种特殊形式，它通过对图像的灰度值取对数来改变图像的亮度分布。
本文将介绍灰度变换和对数变换的原理、应用以及优缺点。
一、灰度变换的原理灰度变换是指通过改变图像的灰度值来改变图像的亮度分布。
在灰度变换过程中，我们可以根据需要调整图像的对比度、亮度和色彩等属性，从而使图像更加清晰、鲜艳或者更适合特定的应用场景。
对数变换是一种常用的灰度变换方法之一。
它的原理是通过对图像的灰度值取对数，来改变图像的亮度分布。
对数变换可以将原始的灰度值域映射为更广的范围，从而增强图像的对比度和细节。
二、对数变换的应用对数变换在数字图像处理中有着广泛的应用。
以下是对数变换的几个常见应用场景：1.图像增强：对数变换可以增强图像的对比度和细节，使得图像更加清晰。
在医学影像、卫星遥感等领域，对数变换常用于提高图像的可视化效果和分析能力。
2.图像压缩：对数变换可以将原始图像的灰度值域映射到更广的范围，从而增加图像的动态范围，提高图像的可压缩性。
在图像压缩算法中，对数变换常用于提高压缩比和保持图像质量。
3.图像分割：对数变换可以改变图像的亮度分布，使得图像的前景和背景更加明确。
在图像分割算法中，对数变换常用于增强图像的边缘和纹理信息，从而提高分割的准确性和效果。
三、对数变换的优缺点虽然对数变换在图像处理中有着广泛的应用，但它也存在一些优缺点。
优点：1.对数变换可以增强图像的对比度和细节，使得图像更加清晰；2.对数变换可以增加图像的动态范围，提高图像的可压缩性；3.对数变换可以增强图像的边缘和纹理信息，提高图像分割的效果。
缺点：1.对数变换可能导致图像的亮度失真，使得图像变得过亮或过暗；2.对数变换的计算复杂度较高，对大型图像的处理速度较慢；3.对数变换对图像的噪声敏感，可能导致噪声的增强。
四、总结灰度变换是数字图像处理中常用的一种技术，对数变换是灰度变换的一种特殊形式。
【数字图像处理】灰度变换
【数字图像处理】灰度变换原⽂链接：作者：图像的空间域滤波，其对像素的处理都是基于像素的某⼀邻域进⾏的。
本⽂介绍的图像的灰度变换则不同，其对像素的计算仅仅依赖于当前像素和灰度变换函数。
灰度变换也被称为图像的点运算（只针对图像的某⼀像素点）是所有图像处理技术中最简单的技术，其变换形式如下：s=T(r)s=T(r)其中，T是灰度变换函数；r是变换前的灰度；s是变换后的像素。
图像灰度变换的有以下作⽤：改善图像的质量，使图像能够显⽰更多的细节，提⾼图像的对⽐度（对⽐度拉伸）有选择的突出图像感兴趣的特征或者抑制图像中不需要的特征可以有效的改变图像的直⽅图分布，使像素的分布更为均匀常见的灰度变换灰度变换函数描述了输⼊灰度值和输出灰度值之间变换关系，⼀旦灰度变换函数确定下来了，那么其输出的灰度值也就确定了。
可见灰度变换函数的性质就决定了灰度变换所能达到的效果。
⽤于图像灰度变换的函数主要有以下三种：线性函数（图像反转）对数函数:对数和反对数变换幂律函数：n次幂和n次开⽅变换上图给出了⼏种常见灰度变换函数的曲线图，根据这⼏种常见函数的曲线形状，可以知道这⼏种变换的所能达到的效果。
例如，对数变换和幂律变换都能实现图像灰度级的扩展/压缩，另外对数变换还有⼀个重要的性质，它能压缩图像灰度值变换较⼤的图像的动态范围（例如，傅⽴叶变换的频谱显⽰）。
线性变换令r为变换前的灰度，s为变换后的灰度，则线性变换的函数：s=a⋅r+bs=a⋅r+b其中，a为直线的斜率，b为在y轴的截距。
选择不同的a，b值会有不同的效果：a>1a>1，增加图像的对⽐度a<1a<1，减⼩图像的对⽐度a=1且b≠0a=1且b≠0，图像整体的灰度值上移或者下移，也就是图像整体变亮或者变暗，不会改变图像的对⽐度。
a<0且b=0a<0且b=0，图像的亮区域变暗，暗区域变亮a=1且b=0a=1且b=0，恒定变换，不变a=−1且b=255a=−1且b=255，图像反转。
数字图像处理基础 第3章 灰度级变换
(i 1, 2,..., m; j 1, 2,..., n)
Potoshop 演示对比度线性展宽(近似实现）
已知一幅图像F如下，其中灰度变化范围为0～7，
请对其进行线性对比度展宽处理。假设fa=3, fb=5,
ga=2, gb=6。求新图像G。 解： ga / fa 0.667 (1) (gb ga) /( fb fa) 2
g(i,j)=9/5×[f(i,j)-2]
34 56 24 57
27 074
79 005 0 9 0 7 0 C=26.2895
3.4.2 非线性动态范围调整
灰度映射关系通常采用对数运算。原因是人眼 对信号的处理是有一个近似对数算子的环节。
g(i, j) c lg(1 f (i, j))
当f (i, j) 0,则g(i, j)＝0； 当f (i, j) 255,则g(i, j)＝255；
L C I1/
• 因此，γ校正的关键是确定γ值。
3.1.4 γ校正方法
1. γ值的确定
1）测试靶图法
I C L
log I r log L C
• 即logI与logL成线性关系。通过测试靶图，即： 设置光图像，检测电信号图像，选取一组logI 与logL的数据，用于计算γ的值。
2）基于γ估计与校正的逐步调整法 通常CCD的γ值在0.4～0.8之间，γ值越小，
第三章 图像增强
• 图像增强的目的是为了改善画质，使图 像的显示效果更加清晰。本章中主要介 绍的内容包括：
• γ校正 • 对比度展宽 • 动态范围调整 • 直方图均衡化处理 • 伪彩色技术
3.1 图像的γ校正
3.1.1 对比度的概念
• 对比度：通俗地讲，就是亮暗的对比程度。 • 对比度大的图像通常层次感强，清晰度高。 • 对比度的计算公式如下：
c语言数字图像处理（四）：灰度变换
c语⾔数字图像处理（四）：灰度变换灰度变换灰度变换函数 s = T(r) 其中r为输⼊图像在(x, y)点处的灰度值，s为输出图像在(x, y)点处的灰度值灰度变换的作⽤上图所⽰的两幅T(s)函数的图像曲线，第⼀幅图可以增强图像对⽐度，第⼆幅图可以对图像进⾏⼆值化处理灰度变换函数反转函数1void reverse(short** in_array, short** out_array, long height, long width)2 {3for (int i = 0; i < height; i++){4for (int j = 0; j <width; j++)5 out_array[i][j] = GRAY_LEVELS - in_array[i][j];6 }7 }最简单的灰度变换函数，将图像中的每个像素点处的颜⾊值反转，对于8位灰度图⽚，⽤255减去原灰度值原图反转图对数变换s = clog(1 + r) c为常数，本次测试中c取101void logarithm(short** in_array, short** out_array, long height, long width) 2 {3for (int i = 0; i < height; i++){4for (int j = 0; j <width; j++)5 out_array[i][j] = (short)(10 * log((1 + in_array[i][j])));6 }7 }可以看出，对数变换降低了图像的对⽐度幂律（伽马）变换s = crγ其中 c 和γ为正常数其中γ<1时，降低对⽐度，γ>1时，提⾼对⽐度γ = 1.21void gamma(short** in_array, short** out_array, long height, long width)2 {3for (int i = 0; i < height; i++){4for (int j = 0; j <width; j++)5 out_array[i][j] = (short)pow(in_array[i][j], 1.2);6 }7 }直⽅图均衡化直⽅图为离散函数h(r k) = n k, 其中r k是第k级灰度值，n k是图像中h灰度为r k的像素个数现在给出上⾯⼏幅图像的直⽅图可以明显看出，对⽐度越⾼的图像，直⽅图的分布越均衡，因此直⽅图均衡化算法可以显著提⾼图像对⽐度直⽅图均衡化算法推导（需⼀定⾼等数学及概率论知识）算法实现1void calculate_histogram(long height, long width, short **image, unsigned long histogram[]) 2 {3short k;4for(int i=0; i < height; i++){5for(int j=0; j < width; j++){6 k = image[i][j];7 histogram[k] = histogram[k] + 1;8 }9 }10 }1112void histogram_equalization(short** in_array, short** out_array, long height, long width)13 {14 unsigned long sum, sum_of_h[GRAY_LEVELS];15double constant;16 unsigned long histogram[GRAY_LEVELS] = {};1718 calculate_histogram(height, width, in_array, histogram);19 sum = 0;20for(int i=0; i < GRAY_LEVELS; i++){21 sum = sum + histogram[i];22 sum_of_h[i] = sum;23 }2425 constant = (double)(GRAY_LEVELS)/(double)(height*width);26for(int i = 0, k = 0; i < height; i++){27for(int j = 0; j < width; j++){28 k = in_array[i][j];29 out_array[i][j] = sum_of_h[k] * constant;30 }31 }32 }。
数字图像灰度变换技术的研究总结
数字图像灰度变换技术的研究总结数字图像处理一直是计算机科学中最重要的方向之一，而灰度变换则是处理数字图像时常用的一种技术。
灰度变换是数字图像处理中广泛应用的一种方法，其主要功能是将原始数字图像像素映射为新的像素值，从而改变数字图像的亮度、对比度等特征。
在数字图像处理中，灰度变换被广泛应用于医学图像处理、遥感图像处理和计算机视觉等领域。
灰度变换技术主要有三种基本方法：对数变换、幂次变换和分段线性变换。
其中，对数变换和幂次变换实质上是两种相反的变换方法，它们可以将原始图像的亮度分布在灰度直方图上向左或向右平移。
分段线性变换更为常用，它可以通过使用多个不同的线性转换阶段，将原始图像的亮度细分为多个不同的阶段来映射。
在实践应用中，无论是对数变换还是幂次变换都常常与分段线性变换配合使用。
常见的使用方法是先使用对数变换或幂次变换来改变原始图像的亮度分布，然后使用分段线性变换来将新图像细分为相应的灰度级别。
数图像灰度变换的具体应用范围很广，例如在医学图像处理中，医生可以通过对CT、MRI或X光图像进行灰度变换来显示相关组织和器官。
在遥感图像处理中，可以使用灰度变换来显示地表的不同特征，例如冰川、水体和植被等。
在计算机视觉中，灰度变换可以被用来提高图像质量和增强特定特征，例如边缘、纹理等。
然而，灰度变换技术也存在一些缺陷。
灰度变换过程中会产生信息丢失，图像的动态范围会变小。
此外，灰度变换直接影响图像的亮度和对比度，但不是所有的图像特征都可以用这两个参数来描述。
因此，需要其他先进的技术来处理数字图像的其他特征。
数字图像灰度变换技术是数字图像处理中最基本、最重要的技术之一。
灰度变换可以改变原始图像的亮度、对比度等特性，以及提高图像质量和增强图像特征。
但是，这种技术也存在缺陷，如信息丢失等，因此需要进一步研究和发展其他技术来满足数字图像处理的需求。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
1000
800
600
400
200
0
0
50
100
150
200
250
4
Gray-Level Transformation
The principal objective of image enhancement is to create a better image representation with unwanted information suppressed/removed and wanted information enhanced. This can be achieved in the spatial domain by graylevel transformation which maps the original set of gray-levels in an image Where T denotes the transformation or mapping function which can be either a linear or non-linear function. It is useful to visualize the transformation in two dimensions with the x-axis representing the old gray-levels and the y-axis the new gray-levels. For example, if the slope of the transformation function equals 1 , then gout T(gin)
gin
5
Gray-Level Transformation
if the slope of the transformation function is greater or less than 1 , then
T(gin) with slope>1 gout T(gin) with slope<1
数字图像处理-灰度变换
1
Displaying Gray-Level Information
There are a number of useful Matlab functions for displaying the graylevel/color information of an image (a) Pixel information An interactive display of pixel co-ordinate and gray/color information in the current figure can be turned on or off by entering pixval on and pixval off
12
Bit-plane Slicing
The image is thought of as a stack of bit-planes and each bit-plane represents the contribution made by a particular bit to the overall image appearance.
14
Bit-plane Slicing
load imdemos bit7=bitget(flower,8);imshow(bit7>0) bit6=bitget(flower,7);imshow(bit6>0) bit5=bitget(flower,6);imshow(bit5>0) bit1=bitget(flower,2);imshow(bit1>0) bit0=bitget(flower,1);imshow(bit0>0)
gout
1
T(gin)
TL
TU
gin
11
Gray-level slicing
load imdemos A=double(alumgrns)/255; B= (img>0.5)& (img<0.8);
AA= (1-(img>0.5)& (img<0.8)).*img; imshow(AA) imshow(AA+B);
top 1
gamma<1 gamma>1
bottom low high 1
gin
8
Gray-level slicing
The essentially perform a double thresholding operation to highlight a particular range of gray-levels in an image. Two approaches are possible depending on whether it is desirable to remove other features in the image. (a) Double thresholding with background removed This approach produces a binary image with all gray levels in the range of interest mapped to white and all other gray levels mapped to black. That is
7
Gamma Correction
The input-output relationship of an image acquisition or display system is generally non-linear and is frequently of the form
G out cG in
where c is constant, and is an exponent (known as the gamma of the system) varying in practice between about 0.5 to nearly 3 The camera, the display and the eye all have non-unity gammas. In Matlab, the effect can be inversely compensated by using B = IMADJUST(A,[LOW_IN HIGH_IN],[LOW_OUT HIGH_OUT],GAMMA) gout
1 B(i, j ) A(i, j ) TL A(i, j ) T otherwise
U
Where A(i,j) and B(i,j) denote respectively the gray-level of input image A and output image B at point (i,j) and TL and TU denote the lower and upper threshold as shown below
0 1 2 3 4
1 2 3 4 5
2 3 -plane 2(MSB) Bit-plane 1 Bit-plane 0(LSB)
Image with 8 gray-levels
3 Bit-planes representation
13
Bit-plane Slicing
1
T(gin)
Tl
TU
gin
9
Gray-level slicing
load imdemos imshow(alumgrns) imhist(alumgrns)
imshow((alumgrns>128)& (alumgrns<192))
10
Gray-level slicing
(b) Double thresholding with background preserved This approach brightness all gray levels in the range of interest with all other gray levels remained at their original values. That is
190
180
170
160
150
140
130
120
110
100
0
10
20
30 40 Dis tance a long profile
50
60
70
3
Displaying Gray-Level Information
(c) Image Information The distribution of the gray-level/color values in an image can be displayed and computed using Matlab function imhist
gin
6
Gray-Level Transformation
The transformation function can be either a continuous function or piecewise continuous function with different expressions over different intervals. For example, if the contrast of an image in the middle range is to be stretched at the expense of compressing the contrast for high and low gray-levels, then
T(gin) gout gout T(gin)