市场需求预测模型
六章市场需求的测量与预测

市场试验法
●多用于投资大、风险高和有新奇特色产品的预测。
时间序列分析法
●即把某种经济统计指标的数值,按时间先后顺序排成序 列,再将此序列数值的变化加以延伸,进行推算,预测未 来发展趋势。
●这种方法的根据是: ⒈过去的统计数据之间存在着一定的关系,而且这种关系
利用统计方法可以揭示出来; ⒉过去的销售状况对未来的销售趋势有绝对的影响,销售
5%
潜在市场
市场需求[1]
●某一产品的市场总需求,是指在一定的营销努力水平 下,一定时期内在特定地区、特定营销环境中,特定顾 客群体可能购买的该种产品总量。
市场需求
市场需求对产品价格、产品改进、促销和分销 等一般都表现出某种程度的弹性。
其影响力可以分为四个层次: ⑴市场营销支出水平; ⑵市场营销组合; ⑶市场营销配置; ⑷市场营销效率。
优点: ⑴预测过程迅速,成本较低; ⑵在预测过程中,各种不同观点都可以表达并加以调
和; ⑶如果缺乏基本数据,可以运用这些方法加以弥补; 缺点: ⑴专家意见法未必能反应客观现实; ⑵责任较为分散,估计值的权数相同; ⑶一般仅适用于总额的预测,而用于区域、顾客群、
产品大类等的预测时,可靠性较差。
德尔菲法及其特点
德尔菲法是在二十世纪60年代由美国兰德 (RAND)公司首创和使用的一种特殊的调 查方法,在西方非常流行。德尔菲是古西腊 的一个地名,因阿波罗神殿而闻名。由于传 说中的阿波罗有着非凡的预测未来的能力, 故德尔菲成了预言家的代名词。
德尔菲法是指按规定的程序,采用函询的方式, 依靠分布在各地的专家小组背对背地作出判断 分析,经过反复征询使不同意见趋于一致得到 调查结果。
意识到,就公司的长期生存能力而言,肯德基重新进行形象定位是至关重要的, 因为家庭是快餐行业最大且增长最快的一部分消费者。由此,肯德基营销管理 层即刻面临的问题是:如何使公司对英国的母亲们具有足够的吸引力,以及如 何使她们经常购买肯德基的食品作为家庭膳食。所以,英国肯德基面临的两个 主要问题是:①相似的“家庭宴会’是否会吸引英国的母亲们?②“家庭宴会的 推出是否会使肯德基的品牌在英国的整体形象及知名度有所提高?
市场需求预测模型的构建与应用研究

市场需求预测模型的构建与应用研究第一章研究背景市场需求预测模型是企业制定市场营销策略和生产计划的重要依据,它的准确性直接影响企业的经济效益和市场竞争力。
在当前复杂多变的市场环境下,如何构建和使用更为精准的市场需求预测模型,一直是企业和研究机构关注的热点问题。
本文将从市场需求预测模型的构建方法、应用场景以及精度评估等方面进行研究探讨,旨在为相关研究提供理论参考和实践指导。
第二章市场需求预测模型的构建方法2.1 线性回归模型线性回归模型是一种常用的市场需求预测模型,其基本思想是通过变量之间的线性关系来预测目标变量的未来走势。
在实际应用中,需要选取适当的自变量和因变量,并通过数据建立回归方程,然后运用该方程进行预测。
2.2 协整分析模型协整分析模型是指两个或多个时间序列变量之间存在长期均衡关系,且误差项具有稳定的时序性质。
通过建立协整关系,可以实现变量之间的联动预测,其精度相对较高。
在应用中,需要进行协整检验和模型建立,然后运用该模型进行预测。
2.3 时间序列分析模型时间序列分析模型是以时间为自变量,对目标变量进行观测和预测的一种方法。
该模型一般包括三个部分:趋势分析、季节性调整和随机扰动。
在实际应用中,需要选取合适的时间序列模型,并对其进行参数估计和模型拟合,然后进行预测。
第三章市场需求预测模型的应用场景3.1 新品上市预测对于新品上市的情况,由于缺乏历史数据和市场反馈,通常难以采用传统的预测方法。
此时可以借助先进的市场需求预测模型,结合产品特性、竞争格局等因素,对新品上市的市场需求进行科学预测和合理估计。
3.2 供应链管理预测在供应链管理中,准确的市场需求预测模型可以帮助企业制定优化的生产计划和库存管理策略,充分利用企业资源。
同时,预测模型还可以帮助企业及时发现和应对市场变化,保持市场竞争优势。
3.3 营销推广预测市场需求预测模型可以帮助企业设计和实施精准的营销方案,提高广告宣传的效果和投资回报率。
基于多元线性回归的市场需求预测模型

基于多元线性回归的市场需求预测模型市场需求预测一直是企业决策的重要环节,它的准确性直接影响着企业的销售额和利润。
基于多元线性回归的市场需求预测模型,是一种常用的数据分析方法,可以帮助企业了解市场需求,预测销售量,并提供决策依据。
多元线性回归是一种用于分析多个自变量对一个因变量的影响的统计方法,其核心思想是寻找一条线来描述多个自变量和因变量之间的关系。
对于市场需求预测而言,我们可以将销售量作为因变量,将各种潜在影响因素(如广告投入、产品特征、竞争对手销售量等)作为自变量,建立一个多元线性回归模型,从而预测市场需求量。
在构建多元线性回归模型之前,我们需要收集相关的数据。
这些数据包括历史销售量、广告投入、产品特征、竞争对手销售量等信息。
在收集数据时需要尽量确保数据的准确性和完整性,以提高预测模型的准确性。
在建立多元线性回归模型之前,还需要进行一些预处理步骤。
首先,我们需要对数据进行清洗,排除异常值和缺失值。
然后,对自变量进行标准化处理,以消除不同变量之间的量纲差异。
最后,我们可以使用相应的统计软件,如R、Python等,来进行模型的构建和分析。
构建多元线性回归模型的关键是选择合适的自变量。
在选择自变量时,我们可以根据经验和领域知识进行初步筛选,然后使用逐步回归或其他变量选择方法进行进一步选择。
选择自变量时要注意自变量之间的相关性,尽量选择与因变量有高度相关性的自变量。
在建立模型后,我们可以利用已有数据对模型进行验证和评估。
常用的评估指标包括决定系数(R^2)、均方根误差(RMSE)、平均绝对误差(MAE)等。
通过评估模型的准确性,我们可以判断模型的可靠性,并对模型进行必要的修正和改进。
一旦构建好的多元线性回归模型具有较高的预测准确性,我们就可以利用该模型进行市场需求预测。
预测的结果可以帮助企业制定合理的市场策略,调整产品定价,优化广告投入以及与竞争对手的竞争策略。
然而,多元线性回归模型也存在一些限制。
市场需求预测模型研究

市场需求预测模型研究如何有效地预测市场需求,一直是企业市场营销中的难题。
因为市场需求随时间、地域和消费者需求的变化而变化,所以需要寻找一种科学有效的方法对市场需求进行预测。
本文将介绍市场需求预测模型的研究。
一、市场需求预测模型概述市场需求预测模型是基于历史销售数据和市场环境数据进行分析和建模,从而预测未来市场需求的模型。
市场需求预测模型的应用范围非常广泛,如消费品、服务、房地产等行业都可以使用。
常用的市场需求预测模型有时间序列分析模型、回归分析模型,以及神经网络模型等。
其中,时间序列分析模型是最古老的市场需求预测模型,经历了几十年的发展。
但是,它也存在一些问题,如对趋势、季节性和周期性数据的处理可能不太稳定,这导致了市场需求预测的不确定性。
二、时间序列分析模型时间序列分析模型是通过对历史数据的分析来预测未来市场需求的模型。
其基本假设是,历史数据的趋势、季节性和周期性特征在未来仍然有效。
时间序列分析模型主要有ARIMA自回归移动平均模型和指数平滑模型两种。
1、ARIMA自回归移动平均模型ARIMA是一种时间序列预测模型,它是通过对数据的自相关和偏自相关分析来找出合适的模型。
ARIMA模型基于三个参数来建模,它们分别是AR(p)模型、MA(q)模型和I(d)模型。
AR(p)模型和MA(q)模型是基本的自回归模型和移动平均模型,它们都是平稳时间序列的建模方法。
I(d)模型是阶差分模型,用来处理非平稳时间序列。
2、指数平滑模型指数平滑模型是一种常用的时间序列预测模型,主要用于数据平稳且具有周期性的时间序列。
该模型通过对历史数据进行某些平均处理,从而得出未来的预测值。
常用的指数平滑模型有简单指数平滑模型、二次指数平滑模型和三次指数平滑模型。
这些模型根据所使用的加权系数和历史数据的平滑程度的不同而具有不同的性质。
三、回归分析模型回归分析模型是一种基于自变量和因变量之间关系的建模方法,其目标在于通过建立合适的数学模型来表达两个变量之间的函数关系,从而预测未来市场需求。
市场需求预测模型介绍分析详解

市场需求预测模型介绍分析详解市场需求预测模型是指通过收集和分析市场数据,以预测消费者需求的工具和方法。
它对于企业制定战略、制定生产计划和预测市场变化具有重要意义。
本文将详细介绍市场需求预测模型的各种类型、应用案例以及优缺点。
市场需求预测模型的类型多种多样,其中最常见的包括时间序列分析、回归分析、群体决策模型和机器学习模型等。
时间序列分析主要基于历史数据的趋势和周期性,通过统计和数学方法来预测未来的需求。
回归分析则是建立变量之间的关系模型,通过分析不同因素对市场需求的影响来进行预测。
群体决策模型则是基于开展市场调研和消费者调查,通过统计和随机抽样方法得到市场需求的预测结果。
机器学习模型是近年来发展起来的一种模型,通过训练机器学习算法来预测市场需求。
市场需求预测模型作为一种实用工具,在各个行业都有广泛的应用。
以零售业为例,市场需求预测模型可以帮助企业预测季节性需求波动,从而合理安排库存和销售计划。
在制造业中,市场需求预测模型可以帮助企业调整生产计划,避免过剩或不足的产能。
而在互联网行业,市场需求预测模型可以为平台提供个性化推荐和精准营销,提高用户体验和销售效果。
然而,市场需求预测模型也存在一些挑战和限制。
首先,模型预测的准确性受到数据的质量和完整性的影响,如果数据收集不全或者存在错误,模型的预测结果可能会出现偏差。
其次,市场需求本身具有一定的不确定性,因此模型仅能提供一种预测结果,不能完全代替人的判断和决策。
此外,市场需求模型的建立和维护需要投入大量的人力和技术资源,对于中小企业而言,这可能是一项巨大的负担。
为了提高市场需求预测模型的准确性和实用性,企业可以考虑以下几点措施。
首先,加强数据的质量管理,确保收集到的数据准确、完整且具有代表性。
其次,建立多种模型的组合,通过不同模型之间的比对和融合,提高预测的准确性和可靠性。
此外,及时更新模型中的参数和算法,使其能够适应市场需求的变化。
在应用市场需求预测模型时,企业应该根据自身的情况和需求选择合适的模型,并结合其他定性分析和专业知识进行判断和决策。
预测市场需求的模型和技术应用

预测市场需求的模型和技术应用一、引言在当今竞争激烈的市场环境下,企业需要不断提升市场敏感度和反应速度,以及更精准地预测市场需求,以满足消费者的多样化需求。
因此,建立一套可靠的预测市场需求的模型和技术应用愈加重要。
本文将介绍预测市场需求的模型和技术应用,并探讨其在不同领域中的实际应用。
二、预测市场需求的模型1.时间序列分析模型时间序列分析模型是一种基于历史数据对未来趋势进行预测的模型。
该模型主要有下列3种方法:- 移动平均法:通过前一天或前几天的销售数据来预测未来的销量,以适应瞬息万变的市场需求,尤其适用于季节性产品;- 指数平滑法:通过对历史数据进行加权平均的方式,对未来销售情况进行推测。
该模型适用于快速变化的市场环境;- 自回归模型:此方法是预测未来销售数据的常用方法,通过对销售数据的一阶(一度)或二阶(二次)自回归,进行推测分析。
2.因素分析模型因素分析模型是根据一定的假设来分析不同影响因素对市场的影响程度,并将这些因素的权重逐一加入到模型计算中,进行市场需求的预测。
因素分析模型主要分为3种:- 常规线性回归:基于对“自变量”(放在X轴上)与“因变量”(放在Y轴上)的线性回归分析,计算出斜率和截距等参数,进行市场预测;- ARIMA模型:是传统的时间序列分析模型,可以同时处理趋势、周期和随机事件产生的影响;- 神经网络模型:是一种非线性模型,它可以通过处理大量的数据进行模型训练,以达到更好的预测效果。
三、预测市场需求的技术应用1.电商行业电商行业是最早将预测市场需求模型应用于实际业务的行业。
通过数据挖掘、人工智能等技术,对用户的购买行为进行分析,形成用户画像、购买路径等数据图像,进而预测市场需求,精准地进行产品推荐。
2.物流行业以快递行业为代表的物流行业,也是依托预测市场需求的模型和技术,实现了高效精准的配送服务。
物流企业通过对用户需求的大数据分析,优化物流运输方案,实现“时效达、准确率高”的服务。
基于ARIMA预测模型的人才市场需求分析
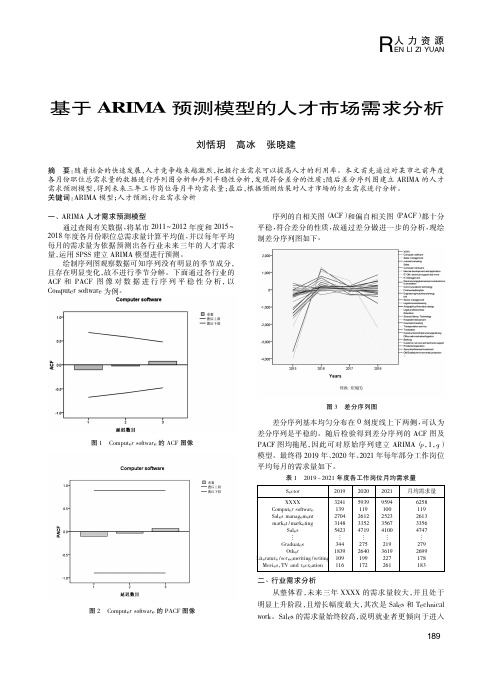
3241
Computer software
139
Sales management
2704
market / marketing
3148
Sales
5423
Graduates
344
Other
1839
Literature / screenwriting / writing 109
越高。
作者简介: [1]崔振辉,李林川,赵承利,杨挺. 基于 ARIMA 的电
力视频流量分析和预测[J]. 天津大学学报,2015,48( 01) : 50-54.
作者简介: 刘恬玥,华北 理 工 大 学 经 济 学 院,河 北 唐 山,高 冰,华
北理工大学经济学院,河北唐山,张晓建,华北理工大学中 医学院,河北唐山。
( 上接第 188 页) 术的要求。 四、智能化时代管理会计人才培养模式存在问题的对策
高校培养懂 管 理、善 决 策、会 分 析 的 复 合 型 管 理 会 计 人才,离不开课程体系建设、教师队伍建设、教学手段方法 改革等方面,具体措施如下。
( 一) 智能课程体系建设 实现人才培养目标的核心是与之匹配、完善的课程体 系,随着财务机器人的应用,财务共享中心的普及,会计人 才培养目标由核算能力转为决策分析能力,在课程体系设 置中应加入智能化课程内容。如: 大数据分析技术与工 具、大数据财务分析、财务共享中心模拟实践、云会计平台 实训等课程,培 养 学 生 大 数 据 分 析 能 力,能 够 从 多 维 度 的 视角分析一个组织利益相关者的行为并进行关联性分析 和决策支持。 ( 二) 智能教师团队建设 通过引进和培养相结合的原则,建设一支由高校与企 业教师、企业高级技术人员组成的多元化、高水平、结构合 理、梯队完整、特色鲜明的教师团队。智能教师主要是教 师利用智能设备参与教学; 定期学习更新知识库,能够将 最新的会计理论与实务、前沿动态热点分享给学生。授课 教师应包括专职教师和兼职教师。①理论课程模块化,由 专职教师组成授课团队,融入慕课、微课、云课堂等手段, 提高网络对教学的促进作用; ②实训课程由专职老师主要 负责规则讲解,兼职教师通过智能型设备对实训内容进行 讲解和指导,提高教学的效率和效果。 ( 三) 教学手段、教学方法改革 1. 翻转课堂教学模式 突破传统“填 鸭 式”“一 言 堂 ”教 学 模 式,教 学 回 归 中 心、回归主体,课程主角由“教师”转为“学生”,全方位培养 学生的综合能力。翻转课堂主要由教师创建管理会计教 学资源库,学生 课 外 自 主 学 习 教 学 资 源( “微 课”“慕 课” “学习通”等教学资源) ,然后再回到课堂进行师生、生生间 面对面的分享、交 流 学 习 成 果 与 心 得,以 实 现 教 学 目 标 为
pricemuller模型介绍

Pricemuller模型介绍一、背景介绍1.1 Pricemuller模型的由来Pricemuller模型是由经济学家Pricemuller在20世纪提出的,主要用于分析市场结构和市场行为的模型。
该模型主要从价格形成和市场行为的角度出发,分析市场上的供求关系以及价格的变动规律,为企业和政府的决策提供理论依据。
1.2 Pricemuller模型的重要性Pricemuller模型可以帮助我们更好地理解市场经济的运行规律,预测价格变动趋势,指导企业正确预测市场需求,合理制定价格策略,提高市场竞争力。
政府也可以借助Pricemuller模型来监管市场价格,维护市场秩序,确保消费者利益。
二、Pricemuller模型的基本原理2.1 市场需求曲线Pricemuller模型中的市场需求曲线表示不同价格水平下市场上的总需求量。
通常情况下,需求曲线呈现出负斜率的特征,即价格上升时,需求量下降;价格下降时,需求量上升。
2.2 市场供给曲线Pricemuller模型中的市场供给曲线表示不同价格水平下企业的总供给量。
一般情况下,供给曲线呈现出正斜率的特征,即价格上升时,供给量上升;价格下降时,供给量下降。
2.3 平衡价格和平衡数量Pricemuller模型认为,市场达到供求平衡时,即市场需求量等于市场供给量时,所对应的价格和数量分别为平衡价格和平衡数量。
2.4 市场价格变动的原因Pricemuller模型指出,市场价格的变动主要是由市场需求量和市场供给量的变动引起的。
当市场需求量增加或市场供给量减少时,市场价格上升;反之,市场价格下降。
三、Pricemuller模型的应用3.1 企业定价策略根据Pricemuller模型,企业可以根据市场需求曲线和市场供给曲线来分析市场需求和供给的变化趋势,选择合适的定价策略,以获取更大的市场份额和利润。
3.2 政府价格监管政府可以借助Pricemuller模型来监测市场价格的变动情况,及时发现价格垄断和操纵行为,采取措施维护市场秩序,保护消费者合法权益。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
•
(3-28)
• 再计算平均季节指数 f j :
fj•
fj
fj T
fj 2T ,...,fj (m 1)T m
,j
1(,2,3..-2.,9T)
• 最后,计算规范平均季节指数 fj`:
• 从理论上讲,T个平均季节指数的平均值应该为1,但实际 上却常常不是,所以需要规范化处理,以使其平均值为1。
变量相互的假设条件约束。
• 2 MA移动平均模型形式
• MA模型主要是通过过去的干扰值和现在的干扰值的线 性组合进行预测,移动平均模型的数学公式是:
•
(3-50)
• 公式中q为模型的阶数,
为模型的移动
平均项系数,et为误差,Yt为观测值。
• MA(p)模型用过去各个时期的随机干扰或预测误差的
线性组合来反映当前的预测值,当AR(p)的假设条件
• 设有一组时间序列为{Yt}:y1,y2,…,yt。令Mt(1)为时间序列Yt的 一次移动平均序列,其中N为移动平均的时段长:
•
(3-13)
• 2 二次加权平均法
• 二次移动平均法,是对一次移动平均数进行第二次移动平
均,再以一次移动平均值和二次移动平均值为基础建立预 测模型,计算预测值的方法。
• 将时间序列{Yt}的移动平均序列Mt(1)为再取一次移动平均,
不满足时我们可以考虑采用MA(p)形式。
• 3 ARMA模型
• 自回归模型和移动平均模型的组合就构成了用于描述平 稳随机过程的自回归移动平均模型ARMA,数学公式为:
Yt• 1Yt 1 2Yt 2 ,...,pYt p et 1et 1 2et 2 ,(...3,-51qY)t q
用,因而更能刻画出近期经济现象变化的情况;②可以充 分利用全部数据,而移动平均法只能用到部分数据。
•
• 3.2.3 季节变动预测法
• 1 季节指数法
• 季节指数法预测模型为:
(3-26)
• 式中,xt—时间序列Yt的长期趋势变动函数,如向上、向下 或第者j个保季持节稳的定季;节T指—数一,个它完表整示周季期节所性包变含动的幅季度节的个大数小;,fj—它 以趋势值xi为基准,表示上下波动的振幅的相对值。
• 一般的时间序列模型是由上述四种变动形式组合而成的模 型,表现为以下几种类型:
• 加法型:y(t)=T(t)+S(t)+C(t)+R(t)
(3-8)
• 乘法型:y(t)=T(t) × S(t) × C(t) × R(t)
(3-9)
• 混合型: y(t)=T(t) × S(t)+C(t)+R(t)
用预测误差之和来衡量偏差。如果误差真的是随机的,不朝这个或那
个方向偏离,偏差就是0。
n
•
biasn E n (3-6)
t 1
• 路径信号(TS)是偏差与平均绝对离差的比值。
•
(3-7)
• 如果任何一个时期的TS在+6或-6之间的范围之外,这就说 明预测出现了偏差,说明低估或高估了。
• 3.2 时间序列法
(3-10)
•
y(t)=T(t) × S(t)+R(t)
(3-11)
•
y(t)=T(t) × S(t) × C(t)+R(t)
(3-12)
• 3.2.1 移动平均法
• 1 一次移动平均法
• 一次移动平均法是收集一组观察值,计算这组观察值的均 值,利用这一均值作为下一期的预测值,它是对时间序列
的数据按一定周期进行移动,逐个计算其移动平均值,取 最后一个移动平均值作为预测值的方法。
• 设时间序列yt长度为n,共有m个季节,则有n=mT。 • 具体算法共三步:
• (1)计算长期趋势变动函数。一般用线性函数近似表示长
• 期趋势变动函数。
(3-27)
• 通过(3-27)式可以得到t=1,2,…,n时的趋势值x1,x2,…,xn。 • (2)计算季节指数fi。首先,计算各期样本季节指数值ft:
• (2) 二次曲线趋势模型。如果时间序列存在非线性趋势, 则需用到一次、二次和三次指数平滑序列。预测模型为:
(3-24)
at
3St(1)
3St(2)
S (3) t
ytl at bt l ct l 2
•
bt
a 2(1 a)2
6
5a
S (1) t
25
ARMA模型进行拟合。 • (4)估计模型中的未知参数。 • (5)检验模型的有效性。 • (6)模型优化。 • (7)利用拟合模型进行预测。
• 假定需求是正态分布的,MAD可以用来预测随机需求部分的标准差。
在这种情况下,需求的标准差可以表示为: 1.25MAD (3-4)
• 平均绝对百分比误差,MAPE是平均绝对误差与需求的百分比。
•
MAPE n
n
t 1
Et Dt
n
100
(3-5)
• 偏差(bias)主要是为了判断预测方法是否高估或低估了需求,可以利
得已有数据真实值和预测值误差最小,也即最佳平滑系数
需要满足序列的方差S2为最小。
•
(3-19)
• 令Y`t=aYt+(1-a)y`t-1
(3-20)
• 式中,N—时间序列项数;Yt—第t期真实值;Y`t—指数平 滑的第t期预测值; --真实值的平均。
• 3 预测模型
• (1)线性趋势模型。如果时间序列存在线性趋势,则需用 到一次和二次指数平滑序列。根据式(3-18)可得:
• 显然,AR模型和MA模型是该模型的特殊情况,q=0时, ARMA模型即为AR(p)模型,p=0时, ARMA模型即为 MA(q)模型
• 4 ARMA模型的基本预测步骤 • (1)时间序列的处理,判断该序列是否为平稳非纯随机
序列。 • (2)计算出观察值序列的样本自相关系数。 • (3)根据样本自相关系数和偏自相关系数,选恰当的
• 1 AR自回归模型形式
• AP(p)模型主要是通过过去的预测值和现在的干扰值 的线性组合来进行预测,自回归模型的数学公式是:
•
(3-49)
• 公式中的p为自回归模型的阶数,
为模型
的自回归系数, et为误差,为一个时间序列。
• AR(p)模型的意义在于它主要通过时间序列变量自身的历
史观测值来反映有关因素对预测目标的影响。不受模型
所得序列称为 式为:
y1的二次移动平均序列,记为Mt(2)
,计算公
•
(3-14)
• 设二次移动平均法线性预测模型为:
•
(3-15)
•
(3-16)
• 式b时t—中段预,的测t预—方测当程值前斜。时率期。;最l后--通预过测式时(段3长-1;5)at—就预可测以方预程测截出距所;需
• 3 移动加权平均法
• 数v相t同。估y计t季节变x差t 为(v3j-,34计)算公式如下:
• 计算平均季节变差 v j :
•v j
Vj
Vj T ,...,Vj (m 1)T m
,j
1,2,..(.,T3-35)
• 规范化平均季节变差 • •
: (3-36) (3-37)
• 以预规测范模化型平为均:y季t` 节变x差t vj`作v j`为(季3-3节8)变差vj的估计值。因此,
• •
F为平均季节指数
F
1
T
(f1
f2
fj 的算术平均值:
,...,fT )
(3-30)
•
fj`
fj F
(3-31)
• (3)预测。预测模型修改为:
•
(3-32)
• 式中,y`t依次对应第j个季节。 • 2 季节变差法
• 季节变差法预测模型为:
•
(3-33)
• 同样的,xt为趋势变动函数,只是vj为第j个季节的季节变差, 它表示季节性变动幅度的绝对值大小。 xt的求法同季节指
4aS (2) t源自 (43(a)S3t(-32) 5)
ct
a2 2(1 a)2
S (1) t
2St(2)
S (3) t
• 式数中平,滑值St(;1)、-S-预t(2)测、时S段t(3)长--。当期t时的一次、二次、三次指
• 相比移动平均法指数平滑法具有以下优点:①指数平滑法 采用加权平均,体现了近期数据较远期具有更大的影响作
• 指数平滑法基本模型如下:设有一组时间为 {Yt}:y1,y2,…,yt。 St 1 Yt (1 )St (3-18)
• 式中,St+1—t+1期时间序列的预测值;Yt—t期时间序列 的实际值;St—t时期时间序列的预测值;a—平滑指数
(0≤a≤1)初始值的确定,即第一期的预测值,项数较
• 3.1.3 需求预测误差测定
• 需求预测误差是某期预测需求与实际需求之间的差值,一般用Et表示, Et=Ft-Dt。
• 平均方差,表示误差的离散程度。
(3-1)
• 绝对离差,为t期的误差的绝对值。
(3-2)
• 平均绝对离差,指各期绝对离差的平均值。
•
MAD n
1 n
n t 1
At
(3-3)
• 3.2.4 ARMA模型
• ARMA模型利用大量的历史数据来建模,经过模型识别、
参数估计来确定一个能够描述所研究时间序列的数学模
型,最后再由该模型推导出预测模型,进而达到预测的 目的。 ARMA模型是目前公认的最好的单一变量随机时 间序列预测模型。 ARMA模型作为一种比较成熟的随机
