大学物理计算题_08[1]
《大学物理》习题库试题及答案__08_电学习题答案

一、选择题1.1003:下列几个说法中哪一个是正确的?(A) 电场中某点场强的方向,就是将点电荷放在该点所受电场力的方向 (B) 在以点电荷为中心的球面上,由该点电荷所产生的场强处处相同(C) 场强可由q F E / =定出,其中q 为试验电荷,q 可正、可负,F 为试验电荷所受的电场力(D) 以上说法都不正确 [ ]2.1405:设有一“无限大”均匀带正电荷的平面。
取x 轴垂直带电平面,坐标原点在带电平面上,则其周围空间各点的电场强度E 随距离平面的位置坐标x 变化的关系曲线为(规定场强方向沿x 轴正向为正、反之为负):[ B ]3.1551:关于电场强度定义式0/q F E=,下列说法中哪个是正确的?(A) 场强E 的大小与试探电荷q 0的大小成反比(B) 对场中某点,试探电荷受力F与q 0的比值不因q 0而变(C) 试探电荷受力F 的方向就是场强E的方向(D) 若场中某点不放试探电荷q 0,则F =0,从而E=0[ ]4.1558:下面列出的真空中静电场的场强公式,其中哪个是正确的? [ D ](A)点电荷q 的电场:204r qE επ=(r 为点电荷到场点的距离)(B)“无限长”均匀带电直线(电荷线密度λ)的电场:r r E 302ελπ=(r点的垂直于直线的矢量)(C)“无限大”均匀带电平面(电荷面密度σ)的电场:02εσ=E(D) 半径为R 的均匀带电球面(电荷面密度σ)外的电场:r r R E 302εσ=(r 为球心到场点的矢量)5.1035:有一边长为a 的正方形平面,在其中垂线上距中心O 点a /2处,有一电荷为q 的正点电荷,如图所示,则通过该平面的电场强度通量为(A) 03εq (B) 04επq (C) 03επq (D) 06εq[ D ]6.1056:点电荷Q 被曲面S 所包围,从无穷远处引入另一点电荷q (A)(C)( D (B) q1035图 q图所示,则引入前后:(A) 曲面S 的电场强度通量不变,曲面上各点场强不变 (B) 曲面S 的电场强度通量变化,曲面上各点场强不变 (C) 曲面S 的电场强度通量变化,曲面上各点场强变化(D) 曲面S 的电场强度通量不变,曲面上各点场强变化 [ ]7.1255:图示为一具有球对称性分布的静电场的E ~r 关系曲线。
华南理工大学2008级大学物理(I)期末试卷解答(A卷)

2008级大学物理(I )期末试卷A 卷答案及评分标准考试日期:2009年7月6日+一、选择题(每题3分)B ,B ,A ,B ,E ,D ,E ,C ,B ,B二、填空题(每题3分)11. 212. `21C B A B m m m gm ++ 13.()1225p p V - 14.⎰∞p f v v v d )( 15. 25%16. 017. 5 J18. 3.019. 13.920. 3三、计算题(每题10分)21.解:(1) 设摆球与细杆碰撞时速度为v 0,碰后细杆角速度为ω,系统角动量守恒得:J ω = m v 0l 2分由于是弹性碰撞,所以单摆的动能变为细杆的转动动能2202121ωJ m =v 2分 代入J =231Ml ,由上述两式可得 M =3m 2分(2) 由机械能守恒式mgl m =2021v 及 ()θωc o s 121212-=M g l J 2分 并利用(1) 中所求得的关系可得 31a r c c o s =θ 2分22.解:设c 状态的体积为V 2,则由于a ,c 两状态的温度相同,p 1V 1= p 1V 2 /4故 V 2 = 4 V 1 2分 循环过程 ΔE = 0 , Q =A . 而在a →b 等体过程中功 A 1= 0.在b →c 等压过程中功A 2 =p 1(V 2-V 1) /4 = p 1(4V 1-V 1)/4=3 p 1V 1/4 2分在c →a 等温过程中功A 3 =p 1 V 1 ln (V 2/V 1) = -p 1V 1ln 4 2分 ∴ A =A 1 +A 2 +A 3 =[(3/4)-ln4] p 1V 1 2分Q =A=[(3/4)-ln4] p 1V 1 2分23.解:入射波在x = 0处引起的振动方程为 t A y ωc o s 10=,由于反射端为固定端,∴反射波在 x = 0处的振动方程为)cos(20π+=t A y ω 或 )c o s (20π-=t A y ω 2分 ∴反射波为 )2cos(2λωxt A y π-π+=或 )2cos(2λωx t A y π-π-= 4分驻波表达式为 21y y y += 2分 )2cos(λωxt A π+=)2cos(λωx t A π-π-+ )21cos()212cos(2π+π-π=t xA ωλ 2 或 )21cos()212cos(2π-π+π=t x A y ωλ24.解:第四条明条纹满足以下两式:λλθ42124=+x ,即()θλ4/74=x 2分 λλθ42124=+''x ,即()θλ'='4/74x 1分 第4级明条纹的位移值为∆x =()()θθθθλ''-=-'4/744x x 2分 (也可以直接用条纹间距的公式算,考虑到第四明纹离棱边的距离等于3.5 个明纹间距.)25.解:(1) 由光栅衍射主极大公式()sin a b k θλ+= 1分得()1330sin λ=+b a cm 1036.330sin 341-⨯==+ λb a 2分 (2) ()2430sin λ=+ b a()4204/30sin 2=+= b a λnm 2分。
大学物理试题及答案

大学物理试题及答案一、单项选择题(每题3分,共30分)1. 光年是天文学中用来表示距离的单位,它表示的是()。
A. 时间单位B. 光在一年内传播的距离C. 光在真空中一年内传播的距离D. 光在一年内传播的距离,但与介质有关答案:C2. 根据相对论,当物体的速度接近光速时,其质量会()。
A. 保持不变B. 增加C. 减少D. 先增加后减少答案:B3. 在理想气体状态方程 PV=nRT 中,P、V、n、R、T 分别代表()。
A. 压强、体积、摩尔数、气体常数、温度B. 功率、速度、质量、加速度、时间C. 动量、位置、质量、力、时间D. 电流、电压、电荷、电阻、电势答案:A4. 根据麦克斯韦方程组,电场和磁场的关系是()。
A. 电场是磁场的源头B. 磁场是电场的源头C. 电场和磁场相互独立D. 电场和磁场相互产生答案:D5. 以下哪种现象不属于量子力学范畴()。
A. 光电效应B. 原子光谱C. 布朗运动D. 超导现象答案:C6. 根据热力学第一定律,系统内能的变化等于系统吸收的热量与对外做的功之差,即()。
A. ΔU = Q - WB. ΔU = Q + WC. ΔU = W - QD. ΔU = Q/W答案:A7. 以下哪种波是横波()。
B. 电磁波C. 光波D. 以上都是答案:D8. 根据牛顿第三定律,作用力和反作用力的关系是()。
A. 方向相同,大小相等B. 方向相反,大小相等C. 方向相同,大小不等D. 方向相反,大小不等答案:B9. 在电路中,欧姆定律描述了电压、电流和电阻之间的关系,其公式为()。
A. V = IRC. R = VID. V = RI答案:A10. 根据能量守恒定律,能量在转化和传递过程中()。
A. 可以被创造B. 可以被消灭C. 总量保持不变D. 总量不断增加答案:C二、填空题(每题4分,共20分)11. 光在真空中的传播速度是_______m/s。
答案:3×10^812. 根据普朗克关系式,E=hv,其中E代表能量,h代表普朗克常数,v代表频率,普朗克常数的值是______。
大学物理同步训练第08章电磁感应

(D)线圈中感应电流方向不确定
答案:B
分析:利用极限法,可将离金属线圈较远的直导线忽略不计,只考虑离金属线圈较近的直导
线。由右手定则可知,金属线圈内的磁场垂直直面向外,随着电流 I 增加,穿过金属线圈的
向外的磁通量增加;根据楞次定律可知,金属线圈产生的感应电流要阻止磁通量的增加(即
产生相反的磁场),由右手定则可知,感应电流的方向为顺时针,答案 B 正确。
故 B 选项正确。
������1: ������2 = ������1: ������2 = ������12: ������22 = 1: 16
二、填空题
1. 半径为 r 的无限长密绕螺线管,单位长度上的匝数为 n,通以交变电流������ = ������������cos������������,则 围在管外的同轴圆形回路(半径为 R)上的感生电动势为________。
2. 如图 2 所示,一载流螺线管的旁边有一圆形线圈,欲使线圈产生图示方向的感应电流 i,
下列哪一种情况可以做到?
(A)载流螺线管向线圈靠近
(B)载流螺线管离开线圈
(C)载流螺线管中电流减小
(D)抽出载流螺线管中的铁芯
答案:A
分析:(1)B、C、D 选项都会使得穿过线圈的磁通量减小,故 A 选项正确(单项选择题的
4/7
同步训练答案
第八章 电磁感应
许照锦
电动势为最小。
答案:导线端点;导线中点
分析:(参考选择题 4)设转轴位置与长为 L 导线一端的距离为 x(0 ≤ ������ ≤ ������),则导线的电
动势大小为
|������|
=
1 |2
������������[������2
大学物理 第08章 恒定磁场习题
第八章 电磁感应与电磁场
5
物理学
第五版
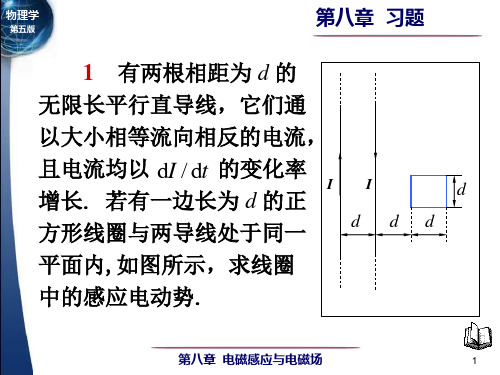
第八章 习题
(2)如 dB 0.010 T s1,求距螺线管中心 dt
轴 r 5.0 cm 处感生电场的大小和方向.
第八章 电磁感应与电磁场
6
物理学
第五版
第八章 习题
6 在半径为 R 的圆柱形空间中存在
着均匀磁场 B 的方向与柱的轴线平行. 如
图所示,有一长为 l 的
电动势E 大小. 哪一端电
势较高?
第八章 电磁感应与电磁场
2
物理学
第五版
第八章 习题
3 如图所示,长为 L 的导体棒 OP, 处于均匀磁场中, 并绕 OO’ 轴以角速
度 旋转,棒与转
轴间夹角恒为 ,
磁感强度 B 与转轴 平行. 求 OP 棒在图 示位置处的电动势.
第八章 电磁感应与电磁场
3
物理学
第八章 电磁感应与电磁场
11
物理学
第五版
10 如图所示,一 面积为 4.0cm2 共 50 匝 的小圆形线圈 A ,放 在半径为 20cm共 100 匝的大圆形线圈 B 的 正中央,此两线圈同 心且同平面.
第八章 习题
第八章 电磁感应与电磁场
12
物理学
第五版
第八章 习题
设线圈 A 内该各点的磁 感强度可看作是相同的. 求:(1)两线圈的互感; (2)当线圈 B 中电流的 变化率为 50A s1 时,线圈 A 中感应电动 势的大小和方向.
第五版
第八章 习题
4 如图所示,金属杆
AB 以匀速率 v = 2.0 m s1
平行于一长直导线移动,
v
此导线通有电流 I = 40 A .
大学物理 下 计算题参考答案

大学物理 下 复习题 部分计算题 参考答案 答案来自网络 仅供参考1四条平行的载流无限长直导线,垂直通过一边长为a 的正方形顶点,每条导线中的电流都是I ,方向如图,求正方形中心的磁感应强度。
⎪⎭⎫⎝⎛a I πμ02解0222Iaμπ=2.如图所示的长空心柱形导体半径分别为1R 和2R ,导体内载有电流I ,设电流均匀分布在导体的横截面上。
求 (1)导体内部各点的磁感应强度。
(2)导体内壁和外壁上各点的磁感应强度。
解:导体横截面的电流密度为2221()IR R δπ=-在P 点作半径为r 的圆周,作为安培环路。
由0B dl I μ∙=∑⎰得 222201012221()2()I r R B r r R R Rμπμδπ-=-=-即 22012221()2()I r R B r R R μπ-=- 对于导体内壁,1r R =,所以 0B = 对于导体外壁,2r R =,所以 022IB R μπ=3. 如图, 一根无限长直导线,通有电流I , 中部一段弯成圆弧形,求图中O 点磁感应强度的大小。
解:根据磁场叠加原理,O 点的磁感应强度是)A (-∞、)ABC (和)C (∞三段共同产生的。
)A (-∞段在O 点磁感应强度大小:)cos (cos x4IB 2101θθπμ-=将6021πθθ==,,a 213cosa x ==π代入 得到:)231(a 2IB 01-=πμ,方向垂直于纸面向里; )C (∞段在O 点磁感应强度大小:)cos (cos x4IB 2102θθπμ-=将πθππθ=-=216,,a 213cos a x ==π带入得到:)231(a 2I B 02-=πμ,方向垂直向里;)ABC (段在O 点磁感应强度大小:⎰=203a Idl 4B πμ,)a 32(a I 4B 203ππμ=,a6IB 03μ=,方向垂直于纸面向里。
O 点磁感应强度的大小:321B B B B ++=,)231(a I a6IB 00-+=πμμ, 方向垂直于纸面向里。
大学物理计算题

m x 100=00=v 00=x 00=v m x 100=物理复习题总编三、计算题★1、一质点沿x 轴运动,其加速度为a=4t (SI),已知t=0时,质点位于 处,初速度。
试求其位置和时间的关系式。
★2、一质点沿x 轴运动,其加速度a 与位置坐标x 的关系为a=2+6x 2(SI)。
如果质点在原点处的速度为零,试求其在任意位置处的速度。
★ 3、已知一质点绕半径为0.2米的圆周运动,其转过的弧长随时间变化的关系式是S=2t 2+3t+1(式中t 以秒计,S 以米计)。
求:(1)前2秒内质点的平均速率;(2)质点在第2秒末的瞬时速率;(3)质点在第2秒末的切向加速度、法向加速度和总加速度的大小。
★4、质点m=2kg 的物体沿x 轴作直线运动,所受合外力F=10+6x 2(SI)。
如果在处时速度 ;试求该物体运动到x=4m 处时速度的大小。
★5、已知质点的运动方程为x=5-3t 3,y=3t 2+2t-8(SI)求:(1)任意时刻质点的位置矢量、速度和加速度;(2)质点在第二秒内的位移、平均速度和平均加速度。
★6、质量为2.0kg 的质点沿x 轴运动,其速度v=5+t2,当t=0时,质点坐标为 。
试求:(1) t=3s 时质点的加速度和加速度和所受的力(2) 质点的运动方程(3) 前2秒内,力对质点所作的功。
★7、有一个水平的弹簧振子,振幅A=2.0×10-2米,周期为0.5秒,当t=0时,(1)物体经过x=1.0×10-2米处,且向负方向运动,(2)物体过x=-1.0×10-2米处,且向正方向运动。
请分别用旋转矢量图来表示它们各自运动的初相位,同时分别写出以上两种运动情况下的振动表达式;振动速度表达式;振动加速度表达式。
★8、如果所示,以P点在平衡位置向正方向运动作计时零点,已知圆频率为ω,振幅A,简谐波以速度u向x轴的正方向传播,试求:(1)P点振动方程。
(2)波动方程。
大学物理计算题

大学物理计算题1.一质点沿半径为R 的圆周运动,运动学方程为20bt 21t v s -=,其中0v 、b 都是常数,求: (1) 在时刻t ,质点的加速度a ; (2) 在何时刻加速度的大小等于b ;(3)到加速度大小等于b 时质点沿圆周运行的圈数。
1.解:(1)由用自然坐标表示的运动学方程可得bt v d d v 0ts-==b d d a 2ts 2-==τ故有 a b b R )bt v (a 2220=+⎥⎦⎤⎢⎣⎡-=(2)令b b R )bt v (a2220=+⎥⎦⎤⎢⎣⎡-=解得 0bt v 0=-bv t 0=即bv t 0=时,加速度大小为b 。
(3))0(s )t (s s -=∆2bv 2b v b 21b v v 22000=⎪⎭⎫⎝⎛-=运行的圈数为Rb4v R 2sn 2ππ=∆=2、一质点运动学方程为2t x =,2)1(-=t y ,其中x ,y 以m 为单位,t 以s 为单位。
(1)质点的速度何时取极小值?(2)试求当速度大小等于s m /10时,质点的位置坐标(3)试求时刻t 质点的切向和法向加速度的大小。
解:(1)t 时刻质点的速度为 )1(22-====t dt dy V t ;dtdxV y x速度大小为 v=22yx v v +=令 ,得t=0.5,即0.5s 时速度取极小值。
(2)令得t=4,带入运动学方程,有 (3)切向加速度为总加速度为因此,法向加速度为3、一沿x 轴正方向的力作用在一质量为3.0kg 的质点上。
已知质点的运动学方程为x=3t-4t 2+t 3,这里x 以m 为单位,时间t 以s 为单位。
试求: (1)力在最初4.0s 内的功; (2)在t=1s 时,力的瞬间功率。
解 (1)由运动学方程先求出质点的速度,依题意有 V=dtdx =3-8t+3t 2质点的动能为 E k (t)= 21mv 2 =21×3.0×(3-8t-3t 2 )2 根据动能定理,力在最初4.0s 内所作的功为A=△E K= E K (4.0)- E K (0)=528Jdv=6t-8(2)a=dtF=ma=3×(6t-8)功率为P(t)=Fv=3×(6t-8) ×(3-8t-3t2 )P(1)=12W这就是t=1s时力的瞬间功率。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
计算题练习
一 计算题 (共156分) 1. (本题 5分)(0265)
有一质点沿 x 轴作直线运动,t 时刻的坐标为 x = 4.5 t2 – 2 t3 (1) 第 2 秒内的平均速度; (2) 第 2 秒末的瞬时速度; (3) 第 2 秒内的路程.
(SI) .试求:
2. (本题 5分)(0513)
O m,r
m′, r′
A
B
一系统从静止开始运动,绳与盘无相对滑动,绳的长度不变.已知 r = 10 cm.求:
(1) 组合轮的角加速度β;
(2) 当物体 A 上升 h=40 cm 时,组合轮的角速度ω.
10. (本题 5分)(5427)
电荷为 q1=8.0×10-6 C 和 q2=-16.0×10-6 C 的两个点电荷相距 20 cm,求 离它们都是 20 cm 处的电场强度. (真空介电常量ε0=8.85×10-12 C2N-1m-2 )
质点 M 在水平面内的运动轨迹如图所示,
MB
OA 段为直线,AB、BC 段分别为不同半径的
两个 1/4 圆周.设 t =0 时,M 在 O 点,已知运 S
15 m
动学方程为
A
30 m
S =30t+5t2 (SI)
15 m C
求 t =2 s 时刻,质点 M 的切向加速度和法向加 O
速度.
3. (本题 5分)(0516)
如图所示线框,铜线横截面积 S = 2.0 mm2,其中 OA 和 DO'两段保持水平不动,ABCD 段是边长为 a O
v
A
B
D
O'
的正方形的三边,它可绕
导线放在匀强磁场
v B
中,
BvO的O'方轴向无竖摩直擦向转上动..已整知个铜
α B
α C
的密度ρ = 8.9×103 kg/m3,当铜线中的电流 I =10 A 时,导线处于平衡状态,AB 段和 CD 段与竖直方向的夹角α
17. (本题10分)(2251)
有一条载有电流 I 的导线弯成如图示 abcda 形状.其
中 ab、cd 是直线段,其余为圆弧.两段圆弧的长度和半
径分别为 l1、R1 和 心 O 处的磁感强度
Bvl2的、大R2小,.且两段圆弧共面共心.求圆
l2
I ab
l1 c
R1
d
R2
O
第 3页
18. (本题 8分)(2592)
15. (本题10分)(0392)
两导体球 A、B.半径分别为 R1 = 0.5 m,
R2 =1.0 m,中间以导线连接,两球外分别包以
A
B R2
内半径为 R =1.2 m 的同心导体球壳(与导线绝
R R1
R
缘)并接地,导体间的介质均为空气,如图所
示.已知:空气的击穿场强为 3×106 V/m,今
使 A、B 两球所带电荷逐渐增加,计算:
第 4页
24. (本题 5分)(2225)
给电容为 C 的平行板电容器充电,电流为 i = 0.2e-t ( SI ),t = 0 时电容器极 板上无电荷.求:
(1) 极板间电压 U 随时间 t 而变化的关系. (2) t 时刻极板间总的位移电流 Id (忽略边缘效应).
第 5页
的距离变为 1 l 时,两质点的速度各为多少? 2
8. (本题 5分)(0120)
一作匀变速转动的飞轮在 10s 内转了 16 圈,其末角速度为 15 rad /s,它的角 加速度的大小等于多少?
9. (本题10分)(0780)
两个匀质圆盘,一大一小,同轴地粘结在一起,构成一个组合
轮.小圆盘的半径为 r,质量为 m;大圆盘的半径 r′ =2r,质量 m′ =2m.组合轮可绕通过其中心且垂直于盘面的光滑水平固定轴 O 转动,对 O 轴的转动惯量 J=9mr2 / 2.两圆盘边缘上分别绕有轻 质细绳,细绳下端各悬挂质量为 m 的物体 A 和 B,如图所示.这
11. (本题 5分)(1059)
图中虚线所示为一立方形的高斯面,已知空间
的场强分布为: Ex=bx, Ey=0, Ez=0. 高斯面边长 a=0.1 m,常量 b=1000 N/(C·m).试 求该闭合面中包含的净电荷.(真空介电常数ε0= 8.85×10-12 C2·N-1·m-2 )
z
y
a O
v B
0.5 T).圆形线圈可绕通过圆心的轴 O1O2 转动, 转速 n =600 rev/min.求圆线圈自图示的初始 O1
ω r
O2
位置转过
1 2
π
时,
(1) 线圈中的瞬时电流值(线圈的电阻 R 为 100 Ω,不计自感);
(2) 圆心处的磁感强度.(μ0 =4π×10-7 H/m)
22. (本题 5分)(2512)
如图所示,有一中心挖空的水平金属圆盘,内圆半 角径速为度R1ω,匀外速圆转半动径.为均R匀2.磁圆场盘B绕v 的竖方直向中为心竖轴直O向′上O″.求以 圆盘的内圆边缘处 C 点与外圆边缘 A 点之间的动生电 动势的大小及指向.
O′
R1
R2 A C
ω
v B
O″
23. (本题 5分)(2532)
一螺绕环单位长度上的线圈匝数为 n =10 匝/cm.环心材料的磁导率μ =μ0.求 在电流强度 I 为多大时,线圈中磁场的能量密度 w =1 J/ m3? (μ0 =4π×10-7 T·m/A)
有两根半径都是 R 的“无限长”直导线,彼此平
行放置,两者轴线的距离是 d (d≥2R),沿轴线方向单
R
位长度上分别带有+λ和-λ的电荷,如图所示.设两 &#间的电势差.
d
R -λ
14. (本题 5分)(1369)
电荷为+q 和+2q 的两个点电荷分别置于 x=0 和 x=l 处,一试验电荷置于 x 轴上何处,它受到的合力为零?
一飞机驾驶员想往正北方向航行,而风以 60 km/h 的速度由东向西刮来, 如果飞机的航速(在静止空气中的速率)为 180 km/h,试问驾驶员应取什么 航向?飞机相对于地面的速率为多少?试用矢量图说明.
4. (本题 5分)(5391)
如图所示,质量为 m 的钢球 A 沿着中心在 O、 半径为 R 的光滑半圆形槽下滑.当 A 滑到图示的位 置时,其速率为 v ,钢球中心与 O 的连线 OA 和竖直 方向成θ角,求这时钢球对槽的压力和钢球的切向加 速度.
x a aa
第 2页
12. (本题 5分)(1216)
如图所示两个平行共轴放置的均匀带电圆环,它 -λ
+λ
们的半径均为 R,电荷线密度分别是+λ和-λ,相距
R
为 l.试求以两环的对称中心 O 为坐标原点垂直于环
RO
x
面的 x 轴上任一点的电势(以无穷远处为电势零点).
l
13. (本题 5分)(1052)
螺绕环中心周长 l = 10 cm,环上均匀密绕线圈 N = 200 匝,线圈中通有电流 I = 0.1 A.管内充满相对磁导率μr = 4200 的磁介质.求管内磁场强度和磁感强度的 大小.
21. (本题12分)(2119)
形线如圈图,所匝示数,N有=1一00半,径置为于r均=匀10磁cm场的Bv 多中匝(B圆=
(1) A、B 起动后,经多长时间 C 也开始运动?
(2)C 开始运动时速度的大小是多少?(取 g=10 m/s2)
第 1页
6. (本题 8分)(0102)
劲度系数为 k 的轻弹簧,一端固定,另一端与桌面
上的质量为 m 的小球 B 相连接.用外力推动小球,将
k
弹簧压缩一段距离 L 后放开.假定小球所受的滑动摩擦
O
A m
vvθ R
5. (本题10分)(0375)
A、B、C 为质量都是 M 的三个物体,B、C 放在光滑 水平桌面上,两者间连有一段长为 0.4 m 的细绳,原先松
CB
放着.B、C 靠在一起,B 的另一侧用一跨过桌边定滑轮
的细绳与 A 相连(如图).滑轮和绳子的质量及轮轴上的
A
摩擦不计,绳子不可伸长.问:
力大小为 F 且恒定不变,滑动摩擦系数与静摩擦系数可
视为相等.试求 L 必须满足什么条件时,才能使小球在
放开后就开始运动,而且一旦停止下来就一直保持静止状态.
BO L
7. (本题 8分)(0204)
设想有两个自由质点,其质量分别为 m1 和 m2,它们之间的相互作用符合万 有引力定律.开始时,两质点间的距离为 l,它们都处于静止状态,试求当它们
=15°.求磁感强度Bv
的大小.
19. (本题 5分)(2443)
一无限长导线弯成如图形状,弯曲部分是一半径为 R
I
的半圆,两直线部分平行且与半圆平面垂直,如在导线上 I O 通有电流 I,方向如图.(半圆导线所在平面与两直导线所 R
I
在平面垂直)求圆心 O 处的磁感强度.
20. (本题 5分)(5910)
(1) 此系统何处首先被击穿?这里场强为何值?
(2) 击穿时两球所带的总电荷 Q 为多少?
(设导线本身不带电,且对电场无影响.)
(真空介电常量ε 0 = 8.85×10-12 C2·N-1·m-2 )
16. (本题 5分)(5682)
一绝缘金属物体,在真空中充电达某一电势值,其电场总能量为 W0.若断 开电源,使其上所带电荷保持不变,并把它浸没在相对介电常量为εr 的无限大的 各向同性均匀液态电介质中,问这时电场总能量有多大?
