第八章 位移法习题解答
《结构力学习题集》第8章位移法

第8章 位移法习 题一、判断题:1、位移法未知量的数目与结构的超静定次数有关。
( )2、位移法的基本结构可以是静定的,也可以是超静定的。
( ) 4、位移法典型方程的物理意义反映了原结构的位移协调条件。
( )5、图示结构,当支座B 发生沉降∆时,支座B 处梁截面的转角大小为12./∆l ,方向为顺时针方向,设EI =常数。
( )6、图示梁之 EI =常数,当两端发生图示角位移时引起梁中点C 之竖直位移为(/)38l θ(向下)。
( )2θθC7、图示梁之EI =常数,固定端A 发生顺时针方向之角位移θ,由此引起铰支端B 之转角(以顺时针方向为正)是-θ/2 。
( )8、用位移法可求得图示梁B 端的竖向位移为ql EI 324/。
( )q9、结 构 按 位 移 法 计 算 时 , 其 典 型 方 程 的 数 目 与 结 点 位 移 数 目 相 等 。
( ) 10、位移法求解结构内力时如果P M 图为零,则自由项1P R 一定为零。
( ) 11、超 静 定 结 构 中 杆 端 弯 矩 只 取 决 于 杆 端 位 移 。
( ) 12、图示梁之 EI =常数,当两端发生图示角位移时引起梁中点C 之竖直位移为(/)38l θ(向下)。
2θθC二、填空题:13、判断下列结构用位移法计算时基本未知量的数目。
(1) (2) (3)(4) (5) (6)EIEIEIEI 2EI EI EIEIEA EA ab EI=EI=EI=24442第13题14、位移法可解超静定结构、静定结构,位移法典型方程体现了_______条件。
15、图示梁A 截面的角位移φA = ____________。
(杆长l,荷载作用在中点)16、图示结构,M AB = __________。
17、图示刚架,各杆线刚度i 相同,不计轴向变形,用位移法求得 M AD = ,M BA =___________。
Di i i A4518、图示结构M BA 的值为_____________,________________侧受拉。
位移法对称结构例题

位移法对称结构例题
以下是一个位移法求解对称结构问题的例题:
一个对称的矩形薄板,长为6m,宽为4m,在两端承受均匀分布的压力:P=10kPa。
求矩形薄板的挠曲形状。
解:首先,由于结构是对称的,因此可以将其分为一半进行计算。
假设矩形薄板在x方向上的挠度为u(x),则在y方向上的挠度为:
y = u(x) + u(-x)
由于压力是均匀分布的,因此可以将其表示为:
P = P0 * x
其中,P0是压力的常量。
根据力学平衡方程,可以得到:
-P0 * x * (u(x) + u(-x)) = -M(x)
其中,M(x)是矩形薄板在x方向的弯矩。
由于压力是均匀分布的,因此可以将其表示为:
M(x) = P0 * x^3 / 12
将上述两个方程联立,可以得到:
-P0 * x * (u(x) + u(-x)) = P0 * x^3 / 12 化简得:
u(x) + u(-x) = -x^2 / 12
将上式代入y的表达式中,可以得到:y = u(x) + u(-x) = -x^2 / 12
因此,矩形薄板的挠曲形状为:
y = -x^2 / 12 (0 <= x <= 6m)。
位移法习题课

6i
6i
1
Pl
lC
lD
8C
D
i
i
k13
6i k23
6i
l
l 3 k331
A
21i2i
B 12i
l
l
2i
2i
Pi
i
F1P 1
1 Pl F2 P 8
F3 P
8 Pl A
2i
B
P
2i
2i
12i E
12i
F
l
l
E
1 Pl 8
F
k 33
72i l2
F1P 0 F2 P 0 F3P P
(3)列经典方程:20i1
M BA
1 2
ql 2
q
F 0.5l
i ql
0.5l
M BC 4i1 2i 2 M BD 4i1
M CB 2i1 4i 2
M CE
3i 2
3 ql 2 16
A iB
i
C 0.5l
i
i ql 0.5l
D
E
M CF
i 2
3 ql 2 8
l
l
(3)基本方程:
M B 0 M BA M BC M BD 0 MC 0 M CB M CE M CF 0
位移法习题课
1、超静定构造
力法:多出未知力,变形协调条件 位移法:结点位移,静力平衡条件
相对每一种独立旳结点角位移,可列一种结点力矩平衡方程 相对每一种独立旳结点线位移,可列一种截面力矩平衡方程
2、基本未知量鉴定
结点角位移:构造内部刚结点数;支座位移不作为基本未知量。
结点线位移:将构造中全部结点均改为铰结(点弹(性涉支及座固除定外端)),
三根杆的位移法例题

三根杆的位移法例题
摘要:
一、位移法简介
1.位移法的定义
2.位移法的基本原理
二、三根杆的位移法例题解析
1.问题描述
2.位移法解题步骤
2.1 确定基本未知量
2.2 建立位移方程
2.3 求解位移方程
2.4 计算杆件内力
3.答案与解析
正文:
位移法是一种求解杆件内力的方法,其基本原理是通过位移来建立内力与位移之间的关系。
接下来,我们将通过一个三根杆的位移法例题来详细解析位移法的解题过程。
题目描述:一个刚性三根杆件结构,其中两根杆固定,另一根杆在两端受力,求解杆件的内力分布。
位移法解题步骤如下:
1.确定基本未知量:首先需要确定一个基本未知量,通常选择一个杆件的
位移作为基本未知量。
2.建立位移方程:根据位移法原理,我们需要建立一个关于位移的方程。
这个方程通常包括两部分:刚度方程和边界条件。
刚度方程反映了杆件的弹性特性,而边界条件则反映了杆件与外部结构的连接关系。
3.求解位移方程:通过求解位移方程,我们可以得到杆件的位移分布。
这一步通常需要使用数值方法,如牛顿法或梯度下降法。
4.计算杆件内力:在得到杆件的位移分布后,我们可以通过力学平衡方程计算出杆件的内力分布。
根据以上步骤,我们可以得出三根杆的位移法例题的解答。
结构力学 第八章 作业参考答案
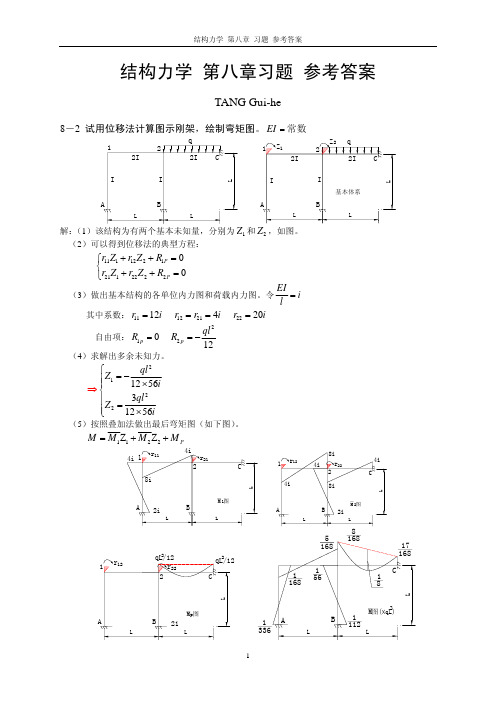
D
Z2
B
2I 2FL/9 I
M图
D
L
B
A
L
B
2FL/9
A
L
FL/9
B
解: (1)该结构为有两个基本未知量,分别为 Z1 和 Z 2 ,如图。 (2)可以得到位移法的典型方程:
⎧r11Z1 + r12 Z 2 + R1P = 0 ⎨ ⎩r21Z1 + r22 Z 2 + R2 P = 0
(3)做出基本结构的各单位内力图和荷载内力图。令 其中系数: r11 = 14i 自由项: R1 p = 0 (4)求解出多余未知力。
4
1m
E
E
E r12 2I
4m
I
I
4m
I
I
1m
0.75 E
1m
结构力学 第八章 习题 参考答案
(2)可以得到位移法的典型方程:
⎧r11Z1 + r12 Z 2 + R1P = 0 ⎨ ⎩r21Z1 + r22 Z 2 + R2 P = 0
(3)做出基本结构的各单位内力图和荷载内力图。 其中系数: r11 = r22 =
8-7 试用位移法计算连续梁,绘制弯矩图。 EI = 常数
A Z1 B 6m 6m
基本体系
Z1 C 6m
A B 6m 6m C 6m
D
D
解: (1)该结构为有两个基本未知量,分别为 Z1 和 Z 2 ,如图。 (2)可以得到位移法的典型方程:
⎧r11Z1 + r12 Z 2 + R1P = 0 ⎨ ⎩r21Z1 + r22 Z 2 + R2 P = 0
结构力学习题集(下)矩阵位移法习题及答案
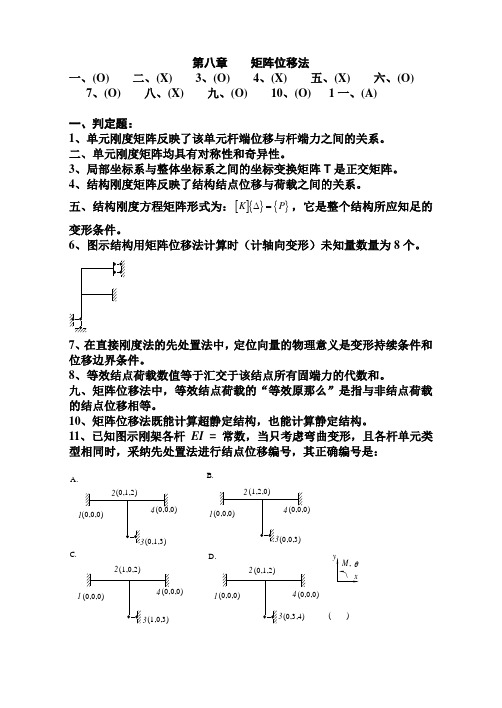
第八章 矩阵位移法一、(O) 二、(X) 3、(O) 4、(X) 五、(X) 六、(O) 7、(O) 八、(X) 九、(O) 10、(O) 1一、(A)一、判定题:1、单元刚度矩阵反映了该单元杆端位移与杆端力之间的关系。
二、单元刚度矩阵均具有对称性和奇异性。
3、局部坐标系与整体坐标系之间的坐标变换矩阵T 是正交矩阵。
4、结构刚度矩阵反映了结构结点位移与荷载之间的关系。
五、结构刚度方程矩阵形式为:[]{}{}K P ∆=,它是整个结构所应知足的变形条件。
6、图示结构用矩阵位移法计算时(计轴向变形)未知量数量为8个。
7、在直接刚度法的先处置法中,定位向量的物理意义是变形持续条件和位移边界条件。
8、等效结点荷载数值等于汇交于该结点所有固端力的代数和。
九、矩阵位移法中,等效结点荷载的“等效原那么”是指与非结点荷载的结点位移相等。
10、矩阵位移法既能计算超静定结构,也能计算静定结构。
11、已知图示刚架各杆EI = 常数,当只考虑弯曲变形,且各杆单元类型相同时,采纳先处置法进行结点位移编号,其正确编号是:(0,1,2)(0,0,0)(0,0,0)(0,1,3)(0,0,0)(1,2,0)(0,0,0)(0,0,3)(1,0,2)(0,0,0)(0,0,0)(1,0,3)(0,0,0)(0,1,2)(0,0,0)(0,3,4)A.B.C.D.2134123412341234( )二、计算题:12、用先处置法计算图示结构刚度矩阵的元素133322,,K K K 。
123ll4l5EI2EIEA(0,0,0)(0,0,1)(0,2,3)(0,0,0)(0,2,4)(0,0,0)EI13、用先处置法计算图示刚架结构刚度矩阵的元素153422,,K K K 。
EI ,EA 均为常数。
l14、计算图示结构整体刚度矩阵的元素665544,,K K K 。
E 为常数。
l l1342A , I AA /222A I , 2A1五、写出图示结构以子矩阵形式表达的结构原始刚度矩阵的子矩阵[][]K K 2224,。
结构力学(5.1.2)--位移法习题及参考答案
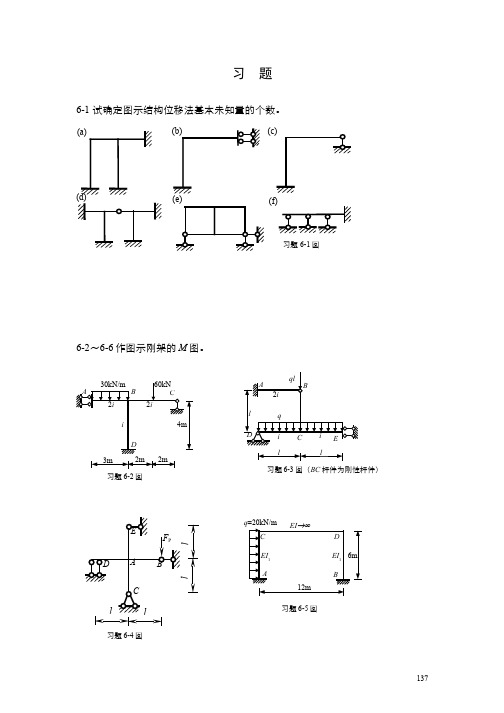
习 题6-1 试确定图示结构位移法基本未知量的个数。
6-2~6-6作图示刚架的M 图。
(a)(f)习题6-1图(d)习题6-2图习题6-5图习题6-3图(BC 杆件为刚性杆件)习题6-4图6-6 试用位移法计算图示结构,并作内力图。
6-7 试用位移法计算图示结构,并作内力图。
6-8 试用位移法计算图示结构,并作内力图。
EI 为常数。
6-9试用位移法计算图示结构,并作弯矩图。
EI 为常数。
6-10 试用位移法计算图示结构,并作弯矩图(提示:结构对称)。
习题6-9图习题6-7图6-11作图示刚架的体系内力图。
6-12 设支座 B 下沉0.5cm B D =,试作图示刚架的M 图。
6-13如图所示连续梁,设支座C 下沉淀1cm ,试作M 图。
6-14图示等截面正方形刚架,内部温度升高+t°C ,杆截面厚度h ,温度膨胀系数为 ,试作M 图。
10 kN/m( a )( b)40 kN习题6-10图BGH习题6-11图(a )(b )q6-15试作图示有弹性支座的梁的弯矩图,332EIk l=,EI =常数。
6-16 试用弯矩分配法计算图示连续梁,并作M 图。
6-176-18 用力矩分配法计算图示结构,并作M 图。
6-19 已知图示结构的力矩分配系数1238/13,2/13,3/13,A A A m m m ===作M 图。
6-20 求图示结构的力矩分配系数和固端弯矩。
已知q=20kN/m,各杆EI 相同。
习题6-17图习题6-13图习题6-14图6-21~6-22 用力矩分配法计算图示连续梁,作M 图,并计算支座反力。
EI=常数。
6-23~6-25用力矩分配法计算图示刚架,作M 图。
EI=常数。
参考答案6.1 (a) 2 (b) 1 (c) 2 (d) 3 (e) 6 (f) 26.2 15BD M =kN·m (右侧受拉)20kN/m 40kN习题6-22图习题6-21图15kN/m习题6-23图F P =10kN 习题6-24图习题6-25图6.321112AB M ql =(上侧受拉)6.4P 0.4AD M F l =(上侧受拉)6.5150AC M =kN·m (左侧受拉)6.651.3AB M =kN·m (左侧受拉)6.780AB M =kN·m (上侧受拉)6.816.9AB M =kN·m (左侧受拉)6.9 (a) 10.43CA M =kN·m (左侧受拉) (b) 56.84CE M =kN·m (下侧受拉)6.10 (a) 8.5AB M =kN·m (上侧受拉) (b) 34.3AC M =kN·m (左侧受拉)6.11 (a) 20.794DC M ql =(右侧受拉) (b) 6.14GD M q =(右侧受拉)6.1223.68AC M =kN·m (右侧受拉)6.1359.3310BA M =ᅲkN·m (上侧受拉)6.142/M EIt h a =(外侧受拉)6.152/32BA M ql =(下侧受拉)6.1617.5CB M =kN·m (下侧受拉)6.1778.75CD M =kN·m (上侧受拉)6.1827/12AB M ql =(上侧受拉)6.191117.95A M =kN·m (上侧受拉)6.200.34AD m =,13.33AD M =kN·m 6.2142.3BA M =kN·m (上侧受拉)6.2217.35BA M =kN·m (上侧受拉)6.2357.4BA M =kN·m (上侧受拉)6.2428.5BA M =kN·m (上侧受拉)6.2573.8BD M =kN·m (左侧受拉)。
位移法解题步骤(精)

位移法解题步骤1.位移法解题步骤⑴ 确定位移法基本未知量数目,作出位移法基本体系图。
⑵ 列位移法基本方程。
⑶ 求系数和自由项。
作位移法基本结构单独在各个单位位移作用下的弯矩图(1M 、2M …n M 图),作位移法基本结构单独在荷载作用下的弯矩图(P M 图)。
依据结点的平衡条件,应用式∑=ij e M M 、式∑∑-+-=Qik Qij e F F F 求系数和自由项。
⑷ 解算方程组,求出各基本未知量。
⑸ 根据叠加法作弯矩图。
⑹ 取各个杆为对象,根据各杆的杆端弯矩和杆上的作用荷载,依据杆件的平衡条件,求各杆端剪力。
取各个结点为对象,根据各杆对结点作用的剪力,应用平衡条件求各杆的轴力。
作结构体系的剪力图和轴力图。
2.例题用位移法计算图(a )所示结构,并作弯矩图。
结构中各杆EI 为常数。
解:(1)作位移法基本体系图。
此结构只有一个刚结点B ,即只有一个角位移1Z 。
作位移法基本体系图如图(b )所示。
各杆的线刚度都为4EI i =。
(2)列位移法方程。
将基本体系可看待成固定状态和位移状态之叠加。
根据附加刚臂上约束力偶矩为零的条件建立方程。
01111=+P R Z r(3) 作固定状态下的弯矩图,求自由项。
作位移法基本结构单独在荷载作用下的弯矩图,如图(d )所示。
根据载常数得固定状态下各杆端弯矩,0====F DB F BD F CB F ABM M M M ).(10)81(2m kN ql M F BA =--= ).(40m kN l F M F BC-=⨯-= 考虑结点B 的平衡条件,得F BC F BD F BA e P M M M M R ++=+1).(4212400101m kN M M M M R eF BC F BD F BA P -=--+=-++=作单位位移状态下的弯矩图,求系数。
作位移法基本结构单独在单位正向位移状态下的弯矩图,如图(d )所示。
根据形常数得基本结构单独在单位正向位移状态下各杆端弯矩, 0===CB BC AB M M M i M BA 3= i M BD 4= i M DB 2=考虑结点B 的平衡条件,得 i M M M r BC BD BA 711=++=(4) 解方程。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
8-2、清华8-2c 试用位移法计算图示结构,并作内力图。
题8-2c (a )方法一:列位移法典型方程解:(1)D 处定向支座与AD 段不平行,视为固定端。
AB 段剪力、弯矩是静定的,弯矩图、剪力图直接可以画出来,DA 杆D 端支座与杆轴线不平行,视为固定端。
结构只有一个转角位移法基本未知量。
基本结构如图(b)。
(2)建立典型方程:11110P k z R ⋅+=(3)画基本结构的P M 、1M 的弯矩图:如图(c) 、(d) 所示。
(4)利用结点的力矩平的平衡求系数:1110;k i =1P R P l =-⋅(5)将系数,自由项代入典型方程得z 1。
110P lz i⋅=(6)利用叠加法求各杆端的最后弯矩,如图(f ):11P M M M z =+⋅30.3()1040.4()20.2()101030.3()10AC AD DA AEP lM i Pl i P l P lM i Pl M i Pl i iP l M i Pl i⋅=+⋅=⋅⋅=+⋅==+⋅=⋅=+⋅=左拉上拉下拉右拉方法二:转角位移法(c)ACMAB(d)(b)(e)Q ABF Q解:(1)确定结构的基本未知量。
有一个角位移z1,如图所示(b)。
(2)列杆端的转角位移方程:AB段剪力和弯矩静定,DA杆D端支座与杆轴线不平行,视为固定端。
C1111,,3,3,4,2 FAB AB A AE AD DAM Pl M Pl M i z M i z M i z M i z =-=-=⋅=⋅=⋅=⋅(3)根据刚结点的力矩平衡,列位移方程,求未知量z1:111100343010AB AC AD AEPl M M M M M Pl i z i z i z zi =→+++=→-+⋅+⋅+⋅=→=∑(4)将所求位移代回转角位移方程求各杆端力,并作结构的弯矩图,如图(c)所示。
C1111,,330.3,330.3,1010440.4,220.21010FAB ABA AEAD DAM Pl M PlPl PlM i z i Pl M i z i Pli iPl PlM i z i Pl M i z i Pli i=-=-=⋅=⨯==⋅=⨯==⋅=⨯==⋅=⨯=讨论;本题将D处的滑动支座改为与杆轴线平行。
(b)(e)(d)MABAC(c)Q ABF Q解:(1)确定结构的基本未知量。
有一个线位移z1,如图所示(b)。
(2)列杆端的转角位移方程:AB段剪力和弯矩静定。
C 1111,,3,3,,F AB AB A AE AD DA M Pl M Pl M i z M i z M i z M i z =-=-=⋅=⋅=⋅=-⋅(3)根据刚结点的力矩平衡,列位移方程,求未知量z 1:1111003307AB AC AD AE PlM M M M M Pl i z i z i z z i=→+++=→-+⋅+⋅+⋅=→=∑ (4)将所求位移代回转角位移方程求各杆端力,并作结构的弯矩图,如图(c)所示。
C 1111,,3333,33,777711,7777F AB AB A AE ADDA M Pl M Pl Pl Pl M i z i Pl M i z i Pl i i Pl Pl M i z i Pl M i z i Pli i =-=-=⋅=⨯==⋅=⨯==⋅=⨯==-⋅=-⨯=- 类8-2 d 、试用位移法典型方程计算图示结构,并作内力图。
4q =20k N /mq =20k N /m解:1)基本结构如图(b),有两个位移法未知量。
2)列典型方程:111122*********0P Pk z k z R k z k z R ⋅+⋅+=⎧⎨⋅+⋅+=⎩ 3)画基本结构在下述情况的弯矩图:荷载单独作用下的P M 图、只让刚臂1单独转过正的单位转角的1M 图以及只让刚臂2发生正的单位转角的2M 图,如图(c) 、(d) 、 (e)。
4)利用结点的力矩平衡,和横梁力的平衡求系数: (c):1225;0P P R R =-⋅=kN m ;(d):11125;2k i k i ==(e):21222;11k i k i ==5)将系数,自由项代入典型方程得z 1、z 2。
12275505151z z ii-==6)利用叠加法求各杆端的最后弯矩,如图(f ):2211z M z M M M P ⋅+⋅+=27550150217()()515127550150411.1()()515150003 2.9()()512755015248.1()()515127550154234.6()()5151AB BA BC BD DB DE M i kN m i i M i kN m i i M i kN m i M i i kN m i i M i i kN m i iM -=-+⋅+⋅=-⋅-=++⋅+⋅=⋅-=++⋅=-⋅-=-+⋅+⋅=-⋅-=++⋅+⋅=⋅左拉左拉上拉左拉左拉2755.4()()512755.4()()51ED i kN m i M i kN m i =⋅=⋅=-⋅=-⋅下拉下拉 3、清华5-3a 试用位移法典型方程计算图示结构,并作内力图。
4i清华 题5-3(a )解:(1)DE 段剪力、弯矩是静定的,弯矩图、剪力图直接可以画出来。
结构有两个位移法基本未知量。
基本结构如图(b)。
(2)建立典型方程:111122*********P P k z k z R k z k z R ⋅+⋅+=⎧⎨⋅+⋅+=⎩(3)画基本结构在下述情况的弯矩图:荷载单独作用下的P M 图、只让刚臂1单独转过正的单位转角的1M 图以及只让附加连杆2发生正的单位线位移的2M 图,如图(c) 、(d) 、 (e)。
(4)利用结点的力矩平衡,和横梁力的平衡求系数:1230;0P P R R =-⋅=kN m ;1122122121567;;i ik i k k k l l====-(5)将系数,自由项代入典型方程得z 1、z 2。
1215060;2323lZ Z i i== (6)利用叠加法求各杆端的最后弯矩,如图(f ):2211z M z M M M P ⋅+⋅+=15066002 2.61()()23231506600410.43()()232315030310.43()()2320()()360007.83()()23AC CA CD DC DE BD i lM i kN m i l i i lM i kN m i l i M i kN m iM kN m M i lM kN m l i=+⋅-⋅=-⋅=+⋅-⋅=⋅=-+⋅=-⋅=⋅=-=+-⋅=-⋅左拉左拉上拉上拉左拉8-3c 、试用位移法典型方程计算图示刚架,并做弯矩图,EI =常量。
解:(1)外伸段剪力、弯矩是静定的,弯矩图、剪力图直接可以画出来。
结构有两个位移法基本未知量。
基本结构如图(b)。
(2)建立典型方程: 111122*********P P k z k z R k z k z R ⋅+⋅+=⎧⎨⋅+⋅+=⎩BA (d )(e )(b )lV (c )(a )(3)画基本结构在下述情况的弯矩图:荷载单独作用下的P M 图、只让刚臂1单独转过正的单位转角的1M 图以及只让附加连杆2发生正的单位转角的2M 图,如图(c) 、(d) 、 (e)。
(4)利用结点的力矩平衡,和横梁力的平衡求系数:12353104()30;1026.875248P P c R R ⨯⨯=⋅=-⨯--=-⋅:kN m kN m ;1111k i =(d )22122122624() 1.875;344i ie k i k k i =+===-(5)将系数,自由项代入典型方程得z 1、z 2。
11111221122112222122 2.097011330003 1.87526.875017.688P P Z k z k z R i z i z ik z k z R i z i z Z i ⎧=⎪⋅+⋅+=⋅-⋅+=⎧⎧⎪→→⎨⎨⎨⋅+⋅+=-⋅+⋅-=⎩⎩⎪=⎪⎩(6)利用叠加法求各杆端的最后弯矩,如图(f ):2211z M z M M M P ⋅+⋅+=2.097617.68817.5044.03()()42.09717.688303036.29()()AB CBi M kN m i i M i kN m i i=-+⨯-⨯=-⋅=+⨯-⋅=⋅左拉上拉2.0971217.6880836.29()()42.0971217.6880444.68()()4CD DCi M i kN m i i i M i kN m i i=+⨯-⨯=-⋅=+⨯-⨯=-⋅右拉左拉讨论:试用力法典型方程计算图示刚架,并做弯矩图,EI =常量。
图15-15(a )(d )x(e )(b )(c )解:(1)外伸段段剪力、弯矩是静定的,弯矩图、剪力图直接可以画出来。
结构有两个力法基本未知量。
基本结构如图(b)。
(2)建立典型方程:111122*********0P Pz z z z δδδδ⋅+⋅+∆=⎧⎨⋅+⋅+∆=⎩(3)画基本结构在下述情况的弯矩图:画荷载单独作用下的P M 图、两单位力分别单独的单位弯矩1M 图和2M 图,如图(c) 、(d) 、 (e)。
4)图乘求系数:12112215412111254570(204)6323311111330(408)(12541)22211482331181412033P P EI EI EI EI EI EI EIEI EIEI EI EI δδ⨯⨯⨯⨯∆=--⨯⨯⨯+=∆=⨯⨯⨯+⨯⨯⨯=⨯⨯=⨯=⨯⨯⨯⨯=+=;5)将系数,自由项代入典型方程得x 1、x 2。
12111122112112222212825700044.03233022033036.2903P P x x x x x EI EI EIx x x x x EIEI EI δδδδ⎧⋅+⋅+=⎪⋅+⋅+∆==-⎧⎧⎪→→⎨⎨⎨⋅+⋅+∆==-⎩⎩⎪⋅+⋅+=⎪⎩ 6)利用叠加法求各杆端的最后弯矩,如图(f ):1212P M M M x M x =+⋅+⋅01(44.032)0(36.29)44.03()()5()()00(44.032)1(36.29)36.29()()00(44.032)1(36.29)36.29()()1251(44.032)1(36.29)44.68()()AB BA CB CD DC M kN m M kN m M kN m M kN m M kN m =+⨯-+⨯-=-⋅=⋅=+⨯--⨯-=⋅=+⨯-+⨯-=-⋅=--⨯--⨯-=-⋅左拉左拉上拉右拉左拉8-4c 、试用位移法典型方程计算图示结构,并作内力图。
