祁皑结构力学 第8章 位移法
福大结构力学课后习题详细答案(祁皑).. - 副本
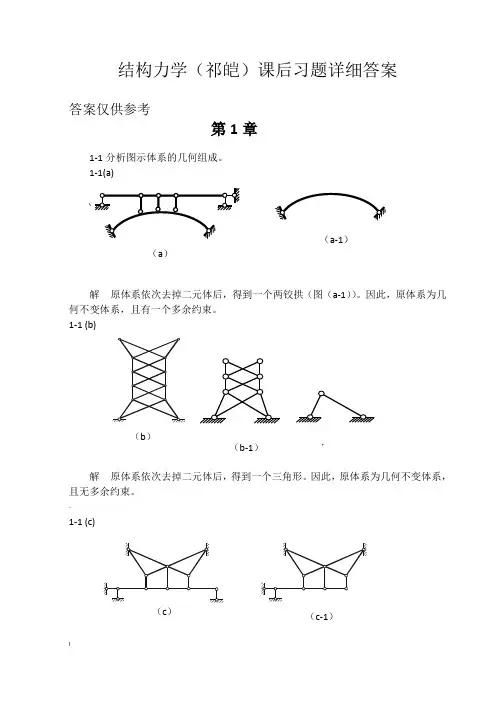
结构力学（祁皑）课后习题详细答案答案仅供参考第1章1-1分析图示体系的几何组成。
1-1(a)(解原体系依次去掉二元体后，得到一个两铰拱（图（a-1））。
因此，原体系为几何不变体系，且有一个多余约束。
1-1 (b)解原体系依次去掉二元体后，得到一个三角形。
因此，原体系为几何不变体系，且无多余约束。
1-1 (c)[（c-1）（a）（a-1）（b）（b-1）*（c-2） （c-3）解 原体系依次去掉二元体后，得到一个三角形。
因此，原体系为几何不变体系，且无多余约束。
1-1 (d)!（d-1） （d-2） （d-3）解 原体系依次去掉二元体后，得到一个悬臂杆，如图（d-1）-（d-3）所示。
因此，原体系为几何不变体系，且无多余约束。
注意：这个题的二元体中有的是变了形的，分析要注意确认。
1-1 (e)~解 原体系去掉最右边一个二元体后，得到（e-1）所示体系。
在该体系中，阴影所示的刚片与支链杆C 组成了一个以C 为顶点的二元体，也可以去掉，得到（e-2）所示体系。
在图（e-2）中阴影所示的刚片与基础只用两个链杆连接，很明显，这是一个几何可变体系，缺少一个必要约束。
因此，原体系为几何可变体系，缺少一个必要约束。
1-1 (f)[解 原体系中阴影所示的刚片与体系的其它部分用一个链杆和一个定向支座相（d ）（e ）（e-1）AB}AB （e-2）（f ）（f-1）连，符合几何不变体系的组成规律。
因此，可以将该刚片和相应的约束去掉只分析其余部分。
很明显，余下的部分（图（f-1））是一个几何不变体系，且无多余约束。
因此，原体系为几何不变体系，且无多余约束。
1-1 (g)解 原体系中阴影所示的刚片与体系的其它部分用三个链杆相连，符合几何不变体系的组成规律。
因此，可以将该刚片和相应的约束去掉，只分析其余部分。
余下的部分（图（g-1））在去掉一个二元体后，只剩下一个悬臂杆（图（g-2））。
因此，原体系为几何不变体系，且无多余约束。
福大结构力学课后习题详细问题详解(祁皑).. - 副本
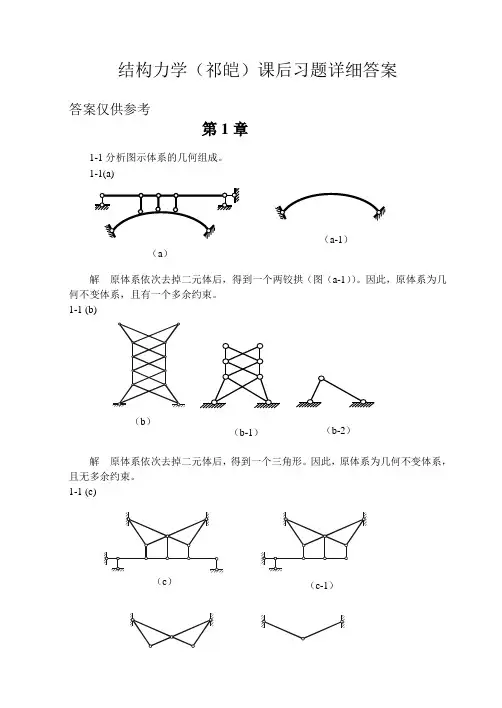
结构力学（祁皑）课后习题详细答案答案仅供参考第1章1-1分析图示体系的几何组成。
1-1(a)解 原体系依次去掉二元体后，得到一个两铰拱（图（a-1））。
因此，原体系为几何不变体系，且有一个多余约束。
1-1 (b)解 原体系依次去掉二元体后，得到一个三角形。
因此，原体系为几何不变体系，且无多余约束。
1-1 (c)（c-1）（a ）（a-1）（b ）（b-1）（b-2）（c-2） （c-3）解 原体系依次去掉二元体后，得到一个三角形。
因此，原体系为几何不变体系，且无多余约束。
1-1 (d)（d-1） （d-2） （d-3）解 原体系依次去掉二元体后，得到一个悬臂杆，如图（d-1）-（d-3）所示。
因此，原体系为几何不变体系，且无多余约束。
注意：这个题的二元体中有的是变了形的，分析要注意确认。
1-1 (e)解 原体系去掉最右边一个二元体后，得到（e-1）所示体系。
在该体系中，阴影所示的刚片与支链杆C 组成了一个以C 为顶点的二元体，也可以去掉，得到（e-2）所示体系。
在图（e-2）中阴影所示的刚片与基础只用两个链杆连接，很明显，这是一个几何可变体系，缺少一个必要约束。
因此，原体系为几何可变体系，缺少一个必要约束。
1-1 (f)解原体系中阴影所示的刚片与体系的其它部分用一个链杆和一个定向支座相连，符合几何不变体系的组成规律。
因此，可以将该刚片和相应的约束去掉只分析其余部分。
很明显，余下的部分（图（f-1））是一个几何不变体系，且无多余约束。
因此，原体系为几何不变体系，且无多余约束。
1-1 (g)（d ） （e ）（e-1）A（e-2）（f ）（f-1） （g ） （g-1） （g-2）解 原体系中阴影所示的刚片与体系的其它部分用三个链杆相连，符合几何不变体系的组成规律。
因此，可以将该刚片和相应的约束去掉，只分析其余部分。
余下的部分（图（g-1））在去掉一个二元体后，只剩下一个悬臂杆（图（g-2））。
结构力学-位移法PPT学习教案
F
有两个刚结点E、F、D、C，由于忽
略轴向变形， 点的竖向 E、F、D、C
C
位移为零， 点及 的水平
E、F
D、C 点
位移相等，因此该结构的未知量为：
E F C D EF CD
B
第10页/共96页
§8-2 位移法未知量的确定
结论： 刚架（不带斜杆的）一个结点一个转角，一层一个侧移。
例5：
A B
例6： A
荷载作用下，杆端弯矩表达式：
3
EI L
B
qL2 8
M AB 0
第27页/共96页
§8-3 杆端力与杆端位移的关系
FP
例：
BA杆：
B 2EI
q EI
可看作两端固定的梁，在B端支座发
C
生了转角B水平位移 ，BC还有均 L 布荷载作用下，杆端弯矩表达式
：
A
L/2
L/2
M BA
4
EI L
B
6EI L2
BC
B 排架结构，有两个铰结点A、B， 由于忽略轴向变形，A、B两点的竖 向位移为零，A、B两点的水平位移
D
相等，因此该结构的未知量为： AB
例8：
A
B
EA=∞
C
E
F
两跨排架结构，有四个结点 A、B、C、D，同理A与B点、D与 D C点的水平位移相同，各结点的 竖向位移为零，但D结点有一转 角，因此该结构的未知量为：
下面开始对单跨超静定梁在支座位移及荷载作用 下的杆端弯矩用力法进行逐个求解。
第16页/共96页
§8-3 杆端力与杆端位移的关系
第17页/共96页
§8-3 杆端力与杆端位移的关系
第18页/共96页
结构力学第八章位移法
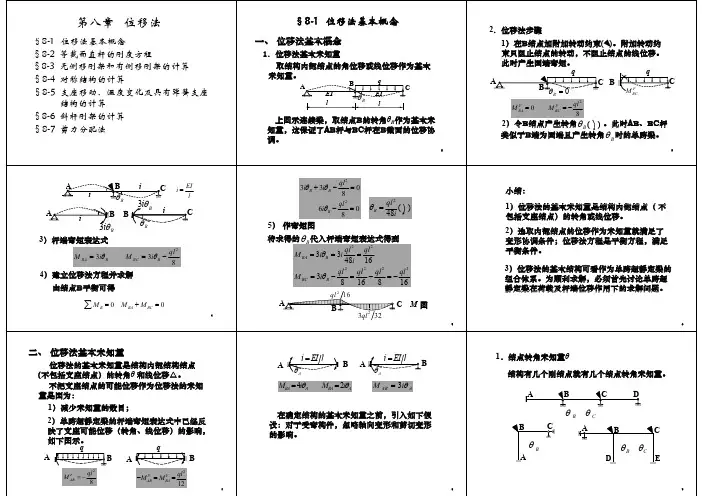
二、等截面直杆的刚度方程
D
EI 1. 两端固定梁 i l
MAB 4iA M BA 2i A
由上图可得： i
A
M AB 4i A 2i B
M BA
B( ) 3．杆件两端相对侧移 杆件两端相对侧移
C ( )
A A
EI
B
A
B 可写成：
6i l 6i 2i A 4i B l
F M BA 0 F M BC
B
EI
C
上图示连续梁，取结点B的转角θB作为基本未 知量，这保证了AB杆与BC杆在B截面的位移协 这保 与 在 截 位移协 调。
2
2）令 ）令B结点产生转角 结点产生转角 B ( ) 。此时 。此时AB、BC杆 杆 类似于B端为固端且产生转角 B 时的单跨梁。
l
MAB
B
MBA
MAB 2iB M BA 4i B
杆件两端相对侧移△，其与弦转角β 的正负 号一致。而β以顺时针方向为正，逆时针方向 为负。 为负 l B A A B
l
13
A
i
MAB
B
B
A
A
EI
B
l
B
A
i
MBA
M AB 4i 2i 6i A l B M 2i 4i 6i BA l
F M AB
A
i EI l
A
B
A
i EI l
A
B
1．结点转角未知量θ 结构有几个刚结点就有几个结点转角未知量。 A B C D
MBA 4iA
MBA 2iA
结构力学 第8章 位移法
6
杆端内力、位移的符号规定： 杆端内力、位移的符号规定：
●
杆端弯矩: 表示AB杆 端的弯矩 绕杆端顺时针 端的弯矩。 顺时针为正 杆端弯矩: MAB表示 杆A端的弯矩。绕杆端顺时针为正 杆端剪力：绕隔离体顺时针转为正(同前) 杆端剪力：绕隔离体顺时针转为正(同前)。 顺时针转为正 结点转角： 顺时针转为正。 结点转角：以顺时针转为正。 转为正 杆端的相对线位移：使杆件弦转角顺时针转动为正。 杆端的相对线位移：使杆件弦转角顺时针转动为正。 弦转角顺时针转动为正
1 2 3
杆14, 36: 两端固定
4 5 6
基本未知量3个。 基本未知量 个
杆12, 23, 25: 一端固定 一端铰结
23
又例:
m m
原结构
次超静定） （4次超静定） 次超静定
基本结构
次超静定） （5次超静定） 次超静定
24
§8—4 位移法的典型方程及计算步骤 4
基本未知量为: 基本未知量为:Z1、Z2 。 基本结构如图。 基本结构如图。 R1—附加刚臂上的反力矩 附加刚臂上的反力矩 F R2—附加链杆上的反力 附加链杆上的反力 l 据叠加原理, 则有 据叠加原理, 2 R1=R11+R12+R1P=0 R2=R21+R22+R2P=0
EI
可见， 不独立, 代入第一式: 可见，B=f (A、△AB), 不独立 代入第一式 MAB=3iA 式中 （转角位移方程） 转角位移方程） （固端弯矩） 固端弯矩）
l
t2
16
§8—3 位移法的基本未知量和基本结构 3
1.位移法的基本未知量 1.位移法的基本未知量
位移法的基本未知量是各结点的角位移和线位移, 位移法的基本未知量是各结点的角位移和线位移, 计算时应 各结点的角位移 独立的角位移和 数目。 首先确定独立的角位移 线位移数目 首先确定独立的角位移和线位移数目。 (1) 独立角位移数目 同一刚结点,各杆端转角相等一个独立的角位移未知量。 一个独立的角位移未知量 同一刚结点,各杆端转角相等一个独立的角位移未知量。 固定支座处，转角=0,已知量; =0,已知量 固定支座处，转角=0,已知量; 铰结点或铰支座各杆端的转角不独立，不必作为基本未知量。 铰结点或铰支座各杆端的转角不独立，不必作为基本未知量。 独立角位移数目= 独立角位移数目=结构刚结点的数目
结构力学8位移法
一端固定、一端简支
M AB
Δ AB 3iθ A 3i MF AB L
3iθ A Δ AB F FQAB 3i 2 FQAB L L 3iθ A Δ AB F F 3i 2 FQBA QBA L L
一端固定、一端定向
M AB iθ A iθ B M F AB F M BA iθ A iθ B M BA
1 qL2 41.7kN m 12
MF BC
F MCB
1 qL2 41.7kN m 12
设 EI 0 1
i BA i BE
4EI0 1 4 3EI0 3 4 4
i BC i CF
5EI0 1 5
i CD
4EI0 1 4
3EI0 0.5 6
§8-2 等截面杆件的刚度方程
两端固定 1、由杆端位移求杆端力 一端固定、一端简支 一端固定、一端定向
F M F FQij ij 2、荷载作用下求固端力
两端固定 3、等截面杆件的刚度方程 4、算例 5、计算步骤 一端固定、一端简支 一端固定、一端定向
弦转角
两端固定
Δ AB M AB 4iθ A 2iθ B 6i L M 2iθ 4iθ 6i Δ AB A B BA L
3iθ B 9
M BC 3iθB M F BC
MF Bc
1 2 2 62 qL 9kN m 8 8
算例2 求图示梁的弯矩图。
解： 1、基本未知量 θ B θ C 2、求各杆端弯矩 AB杆： BE杆：
M BA 3iBA θB M F BA
M BE 4iBE θ B M EB 2iBE θ B
结构力学第8章 矩阵位移法
单元两端的杆端位移分别在单元坐标系和整体坐标系 下分解，其位移分量就构成上面的杆端位移向量。
与坐标轴的正方向一致者为正;
返回目录
作业1：已知单元的内力图，列出单元坐标下 及整体坐标下的杆端力向量。
3.04
1.24
y 0.43
4.38N)
x
作业2：已知单元的杆端力如图，写出单元坐 标及整体坐标表示的单元杆端力向量，并 作出单元的内力图。
2EI
l
x
2EI EI
l 6EIl x x
l2
EuIj 1
6EIl
x
l 2 uj 1
EA
l
x
EI
EuIj 1
l
平l面梁单元ul j 的1 x单元刚度矩阵
l
y
ui=1
6EI
l2
N ElA i y
6EI
l
12 2EI l3
12EI
Qi
0l 3
y
2EI
0 Ml iy
2EI 6EI
l
l2
vi =1 θi=1
等截面直杆的刚度方程
适用于两端都是刚结点的杆， 基本未知量为杆两端的转角和侧移；
刚度方程：
M AB
4i A
2i B
6i
l
M BA
2i A
4i B
6i
l
QAB
QBA
1 l
(
M
AB
M BA)
QAB
QBA
6i l
A
6i l
B
1 2i l2
4i
❖ 写成矩阵的形式：
❖ 杆端弯矩、剪力、杆端 侧移均以绕杆端顺时针 为正。关键掌握每个系
结构力学 位移法
n EAi 2 ∑ ⋅ sin α i ∆ = F p li i =1
荷载之间的关系。 荷载之间的关系。 由基本方程得
(e)
上式就是位移法的基本方程 位移法的基本方程， 上式就是位移法的基本方程，它反映了结构的结点位移与结构的结点
Fp ∆= n EAi ⋅ sin2 αi ∑l i =1 i
由虎克定律得
(b)
图(a)
ui =
则：FN i
FN i l i EAi
(c)
∆
ui
EAi = u i (u i = ∆ sin α i ) (d) li
图(c)
上式就是拉压杆的刚度方程 它反映了杆端力F 与杆端位移u 拉压杆的刚度方程， 上式就是拉压杆的刚度方程，它反映了杆端力 N i与杆端位移 i 之间的 关系。 式代入(a)式得 关系。把(d)式代入 式得 式代入
F
p
2 1
Z
1
Z
1
Z
1
3
图(b) 图(a)
图(c)
如果能求出转角Z 则各杆（ 杆 如果能求出转角 1，则各杆（12杆、13杆）的内力均可按前面的 杆 力法求得。因此，在位移法中，以结点位移 作为基本未知量 作为基本未知量， 力法求得。因此，在位移法中，以结点位移Z作为基本未知量，并以 单跨超静定梁作为基本计算单元，由此可知，用位移法分析刚架时， 单跨超静定梁作为基本计算单元，由此可知，用位移法分析刚架时， 需要解决下面三个问题： 需要解决下面三个问题： (1)位移法的基本未知量的数目（至少要求出多少个位移未知量） 位移法的基本未知量的数目（至少要求出多少个位移未知量） 位移法的基本未知量的数目 (2)单跨超静定梁分析 单跨超静定梁分析 (3)相应于基本未知量的位移法方程如何建立和求解。 相应于基本未知量的位移法方程如何建立和求解。 相应于基本未知量的位移法方程如何建立和求解
结构力学第8章 4-2
位移法基本方程是：附加刚臂的反力矩和附加链杆反力应为零的 630 r11Z1 r12 Z 2 R1P 0 平衡条件。 Z1
r21Z1 r22 Z 2 R2 P 0
23i
Z2
r11 4i 3i 7i 3i r21 2 3i 3i 15i r22 16 4 16
1
2
8-4 位移法算例
例1 试用位移法绘制图示刚架的弯矩图。
30kN 30kN
20kN/m
EI=常数
2m
4m
此刚架B点的左边部分为静定悬臂梁，其B端的弯矩 和剪力可由静力平衡条件得出，并将它们反向作用于 结点B上。
3
4m
R1P 30
R2 P 3 20 4 30 8 60
为计算系数项和自由项，绘出单位和荷载弯矩图， 如下：
14
单位弯矩图及荷载弯矩图
r11 12i r12 r21 4i
r22 20i
R1P 0
ql 2 3ql 2 Z1 , Z2 672i 672i 15
R2 P
ql 2 12
例4 用位移法计算排架
r11 Z1 R1P 0
r11 Z1 R1P 0
23
12i 18i 12i r11 2 2 2 l l l
R1P P
P Pl 2 Z1 12i 18i 12i 42i 2 2 2 l l l
24
用叠加法作弯矩图，即
M M1Z1 M P M1Z1 0 M1Z1
30
位移法典型方程为
r11Z1 r12 Z 2 R1P 0 r21Z1 r22 Z 2 R2 P 0
第8章位移法b
求出各系数后，不难进行具体计算。
§8.7*用位移法计算有斜柱的刚架
用位移法计算有斜柱的刚架时，在分析原理上与前面所述的矩形
刚架的计算方法是一样的，只是在计算典型方程的系数和自由项时要 复杂些。常用的方法有几何法和方程法两种。下面举例说明。如图
(a)所示带斜柱的刚架，作M图。
Fp
Z1
C 2EI EI D
(3)建立位移法方程
MBA
B
图(a) Z1 Z2
MBC
MCB
C
图(b) MCD
MBE
MCF
(a) 两端为固定
M AB 4i A 2i B M BA FQAB 6i F AB M AB l 6i F 2i A 4i B AB M BA l 6i 6i 12i F A B 2 AB FQAB l l l 6i 6i 12i F A B 2 AB FQBA l l l
如图(a)所示对称结构，受一般荷载作用。利用对称性可将荷载 分解成两组：对称荷载和反对称荷载两种情况。
2Fp
Fp
Fp
Fp
Fp
=
图(a)
Fp
+
图(b)
Fp
图(c)
图(d)
图(e)
正对称荷载部分：力法分析时有两个基本未知量，位移法分析时有 一个基本未知量，因此采用位移法计算较为方便。 反对称荷载部分：力法分析时有一个基本未知量，位移法分析时有两 个基本未知量，因此采用力法计算较为方便。
l
Fp
B 2i
Z2
C
1 几何法
B EI A
l
Z3
基本结构如图(b)所示 位移法典型方程为
福大结构力学课后习题详细答案(祁皑).. - 副本
结构力学（祁皑）课后习题详细答案答案仅供参考第1章1-1分析图示体系的几何组成。
1-1(a)解 原体系依次去掉二元体后，得到一个两铰拱（图（a-1））。
因此，原体系为几何不变体系，且有一个多余约束。
1-1 (b)解 原体系依次去掉二元体后，得到一个三角形。
因此，原体系为几何不变体系，且无多余约束。
1-1 (c)（c-1）（a ）（a-1）（b ）（b-1）（b-2）（c-2） （c-3）解 原体系依次去掉二元体后，得到一个三角形。
因此，原体系为几何不变体系，且无多余约束。
1-1 (d)（d-1） （d-2） （d-3）解 原体系依次去掉二元体后，得到一个悬臂杆，如图（d-1）-（d-3）所示。
因此，原体系为几何不变体系，且无多余约束。
注意：这个题的二元体中有的是变了形的，分析要注意确认。
1-1 (e)解 原体系去掉最右边一个二元体后，得到（e-1）所示体系。
在该体系中，阴影所示的刚片与支链杆C 组成了一个以C 为顶点的二元体，也可以去掉，得到（e-2）所示体系。
在图（e-2）中阴影所示的刚片与基础只用两个链杆连接，很明显，这是一个几何可变体系，缺少一个必要约束。
因此，原体系为几何可变体系，缺少一个必要约束。
1-1 (f)解 原体系中阴影所示的刚片与体系的其它部分用一个链杆和一个定向支座相连，符合几何不变体系的组成规律。
因此，可以将该刚片和相应的约束去掉只分析其余部分。
很明显，余下的部分（图（f-1））是一个几何不变体系，且无多余约束。
因此，原体系为几何不变体系，且无多余约束。
1-1 (g)（d ） （e ）（e-1）ABCAB （e-2）（f ）（f-1）解 原体系中阴影所示的刚片与体系的其它部分用三个链杆相连，符合几何不变体系的组成规律。
因此，可以将该刚片和相应的约束去掉，只分析其余部分。
余下的部分（图（g-1））在去掉一个二元体后，只剩下一个悬臂杆（图（g-2））。
因此，原体系为几何不变体系，且无多余约束。
结构力学中的位移法ppt课件
MBA
M B AM BC 0.........1 ..a .)....(
1i0 B 1i 540 .......1 .) ..(...
MBC6iB
MDC0.75 i MBC
B B
QBA
B
23
C
QCD
x0
QAB
QDC
QBA + QCD =0…………...(2a)
MAB
MDC
6iB3.7i 52 40....2.)...(
B
A31iMAB61iMBA
7
MBA MBA
B61iMAB31iMBA
（2）由于相对线位移引起的A和B
A
B
l
以上两过程的叠加
A3 1iMAB 6 1iMBA l
A B
我们的任务是要由杆端位移求 杆端力，变换上面的式子可得：
B6 1iMAB 3 1iM BA l
MAB4iA MBA2iA
2iB 4iB
（4）由杆件的单元刚度方程求出杆件内力，画内力图。
关于刚架的结点未知量
A
P C
A
q
B
A
M AB
P A
A
M AC
A
C
B
.
§8-2 等截面杆件的计算
6
一、由杆端位移求杆端弯矩
杆端力和杆端位移的正负规定
MAB
EI
① 杆端转角θA、θB ，弦转角
β＝Δ/l 都以顺时针为正。
A
MAB
A
MAB
1
l
B
MBA
A 4I0 B 5I0 C 4I0
3I0
D
3I0
E
F
4m
《结构力学》第八章-位移法
(5) 按叠加法绘制最后弯矩图。
18
例 8—1 图示刚架的支座A产生了水平位移a、竖向位移b=4a
及转角=a/L，试绘其弯矩图。
L
解：基本未知量 Z 1(结点C转角)； C EI
B C Z1
B
基本结构如图示；
2EI
建立位移法典型方程： r11Z1+R1△=0
A Z1
基本结构 A
为计算系数和自由项，作
链为了杆能数简，捷即地为确定原出结结构构的的独独立立线线位
(b)
移位移数数目目(见，可图以b)。
11
2.位移法的基本结构
用位移法计算超静定结构时，每一根杆件都视为一根单跨超静
定梁。因此，位移法的基本结构就是把每一根杆件都暂时变为一根
单跨超静定梁(或可定杆件)。通常 的做法是，在每个刚结点上假想 1
构在荷载等外因和各结点位移共同作用下，各附加联系上的反力矩
或反力均应等于零的条件，建立位移法的基本方程。
(3) 绘出基本结构在各单位结点位移作用下的弯矩图和荷载作
用下(或支座位移、温度变化等其它外因作用下)的弯矩图，由平衡
条件求出各系数和自由项。
(4) 结算典型方程，求出作为基本未知量的各结点位移。
正。
B
B
B′
X2
X3
M1图
1
M
图
2
7
将以上系数和自由项代入典型方程，可解得 X1=
X2=
令
称为杆件的线刚度。此外，用MAB代替X1，用
MBA代替X2，上式可写成
MAB= 4iA+2i B－ MBA= 4i B +2i A－
(8—1）
是此两端固定的梁在荷载、温度变化等外因作用下的杆
结构力学第8章位移法
注意：在忽略的直杆的轴向变形时，受弯直杆两 端之间的距离保持不变。
§8-3 位移法的基本未知量和基本结构
图a所示刚架独立结点角位移数目为2
§8-3 位移法的基本未知量和基本结构
（2）确定独立结点线位移的方法—— 观察法、换铰法 观察法
略去受弯杆件的轴向变形，设弯矩变形是微小的。 如图a， 4、5、6点不动，三根柱子长度不变，故1、2、3点均无竖向位移。 两根横梁长度不变。因而，1、2、3点有相同的平位移。 独立结点线位移数目为1。
§8-3 位移法的基本未知量和基本结构
图a所示刚架，结点角位移数目=4（注意结点2）
结点线位移数目=2
加上4个刚臂，两根支座链杆，可得基本结构如图b。
§8-3 位移法的基本未知量和基本结构
特例：1、（1）考虑轴向变形
图a所示刚架，结点线位移数目=2
（2）受弯曲杆 图b所示刚架，结点角位移数目=2 结点线位移数目=2
6i F M AB 4i A 2i B ΔAB M AB l 6i F M BA 4i B 2i A ΔAB M BA l
转角位移方程
§8-2 等截面直杆的转角位移方程
对于一端固定另一端铰支的等截面梁，设B端为铰支，则有
A
A
F
B
由图e可得 Δ1 Δ Δ2 Δ AB
ΔAB l
βAB—弦转角，顺时针方向为正。
4 EI 2 EI 6 EI X1 A B 2 ΔAB l l l 解典型方程得 4 EI 2 EI 6 EI X2 B A 2 ΔAB l l l
§8-2 等截面直杆的转角位移方程
B
B
ql/2
F M AB ql 2 / 12 F M BA ql 2 / 12
福大结构力学课后习题详细答案(祁皑)..---副本
结构力学（祁皑）课后习题详细答案答案仅供参考第1章1-1分析图示体系的几何组成。
1-1(a)解 原体系依次去掉二元体后，得到一个两铰拱（图（a-1））。
因此，原体系为几何不变体系，且有一个多余约束。
1-1 (b)解 原体系依次去掉二元体后，得到一个三角形。
因此，原体系为几何不变体系，且无多余约束。
'1-1 (c)…（c-1）（a ）（a-1）（b ）（b-1）%（c-2） （c-3）解 原体系依次去掉二元体后，得到一个三角形。
因此，原体系为几何不变体系，且无多余约束。
1-1 (d)(（d-1） （d-2） （d-3）解 原体系依次去掉二元体后，得到一个悬臂杆，如图（d-1）-（d-3）所示。
因此，原体系为几何不变体系，且无多余约束。
注意：这个题的二元体中有的是变了形的，分析要注意确认。
1-1 (e)；解 原体系去掉最右边一个二元体后，得到（e-1）所示体系。
在该体系中，阴影所示的刚片与支链杆C 组成了一个以C 为顶点的二元体，也可以去掉，得到（e-2）所示体系。
在图（e-2）中阴影所示的刚片与基础只用两个链杆连接，很明显，这是一个几何可变体系，缺少一个必要约束。
因此，原体系为几何可变体系，缺少一个必要约束。
1-1 (f).解 原体系中阴影所示的刚片与体系的其它部分用一个链杆和一个定向支座相（d ）（e ）（e-1）AB"AB （e-2）（f ）（f-1）连，符合几何不变体系的组成规律。
因此，可以将该刚片和相应的约束去掉只分析其余部分。
很明显，余下的部分（图（f-1））是一个几何不变体系，且无多余约束。
因此，原体系为几何不变体系，且无多余约束。
1-1 (g)解 原体系中阴影所示的刚片与体系的其它部分用三个链杆相连，符合几何不变体系的组成规律。
因此，可以将该刚片和相应的约束去掉，只分析其余部分。
余下的部分（图（g-1））在去掉一个二元体后，只剩下一个悬臂杆（图（g-2））。
因此，原体系为几何不变体系，且无多余约束。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
B 5I0 3I0 E
5m
C 4I0 D 3I0
F 4m
4m 6m
MCB 2iBC 1 4iBC 2 MCFB 21 42 41.7
MCD 3iCD 2 3 2
MBE 4iBE 1 3 1
MEB 2iEB 1 1.5 1
MCF 4iCF 2 2 2
MFC 2iFC 2 2
8-2位移法Ⅰ——直接平衡法
q=20kN/m
A 4I0 4m
B 5I0 3I0 E
5m
C 4I0 D 3I0
F 4m
4m 6m
M BA
3iBA
1
M
F BA
3
4EI0 4
1
20 42 8
3 1
40
MBC 4iBC 1 2iBC 2 MBFC 41 2 2 41.7
8-2位移法Ⅰ——直接平衡法
q=20kN/m
A 4I0 4m
12i/l2
A
B
FQ 12i / l 2
8-1 形常数和载常数
1
A
BA
B
A
B
3i
3i/l
M AB 3i
FQ 3i / l
A
B
3i/l
1
3i/l2
A
B
A
B
M AB 3i / l
FQ 3i / l 2
1 A
A
B
i
BA
i
B
M AB i MBA i
FQ 0
8-1 形常数和载常数
2 载常数
F AB
FP l
/2
M
F BA
FP l
/
2
FQF FP
BA
BA
B
M
F AB
EI
t1
t2
/
h
M
F BA
EI
t1
t2
/
h
FQF 0
8-1 形常数和载常数
1
A
B
A
B
1
1
A
B
A
B
1
1
A
B
8-1 形常数和载常数
q A
B
A
FP B
A
t1 t2
B
l/2 l/2
l
q A
FP
A
B
A
B
l/2 l/2
t1 t2
2 4.89
8-2位移法Ⅰ——直接平衡法
（4）求杆端弯矩
MBA 43.5kNm
MCD 14.7 kNm MCF 9.78kNm
（5）按照区段叠加法 作出弯矩图
MBC 46.9kNm MBE 3.4kNm MFC 4.89kNm
MCB 24.5kNm MEB 1.73kNm
11FP/16
B
A
B
5FP/16
M
F AB
3FPl
/ 16
FF Q AB
11FPl
/ 16
FF Q BA
5FPl
/ 16
A
t1 t2
B
A
B A
B
l
M
F AB
3EI t1
2h
t2
M
F BA
3EI t1
2h
t2
FQF
3EI t1
2hl
t2
8-1 形常数和载常数
q
ql2/3
ql
A
BA
BA
B
l
ql2/6
（3）建立隔离体平衡方程，求基本未知量
M BA
B
M BC
M BE
M BA M BE M BC 0
10 1 2 2 1.7 0L L L L L L (a)
C
M CB
MCD
MCF
MCB MCF MCD 0
2 1 9 2 41.7 0L L L L L L (b)
解（a）和（b），得 1 1.15
B点转角位移Δ1
8-2位移法Ⅰ——直接平衡法
（2）写出杆端弯矩
FP Δ1
A
B
M AB
2i
1
20 6 8
2i
1
15
M BA
4i
1
20 8
6
4i
1
15
q
B
C
Δ1
M BC
3i
1
2 62 8
3i
1 9
（3）利用隔离体的平衡方程求结点位移。
取B点为隔离体，建立B点的力矩平衡方程
M BA B M BC
解得
MBA MBC 0
q A
ql2/12
ql2/12
B
A
B
M
F AB
ql 2
/ 12
M
F BA
ql 2
/ 12
FP
A
B
l/2 l/2
FP l/8 A
FP l/8 B
M
F AB
FP l
/8
M
F BA
FP l
/
8
ql/2
A
B
ql/2
FF Q AB
ql
/
2
FF Q BA
ql
/
2
FP/2
A
B
FP/2
FF Q AB
FP
/
2
FF Q BA
1
6 7i
7i 1 6 0
8-2位移法Ⅰ——直接平衡法
（4）将结点位移代回杆端弯矩表达式。
M AB
2i
6 7i
15
16.72kN m
M BA
4i
6 7i
15
11.57 kN m
M BC
3i
6 7i
9
11.57 kN m
（5）按照区段叠加法作出弯矩图
16.72
11.57
3.21 15.85
第8章 位移法 8-1 形常数与载常数 8-2 位移法Ⅰ—直接平衡法 8-3 位移法Ⅱ—典型方程法 8-4 对称性利用 8-5 支座位移和温度变化时的计算
8-1 形常数与载常数
基本构件
形常数 三类基本构件由杆端单位位移引起的杆端弯矩和剪力. 载常数 三类基本构件在荷载作用下的杆端弯矩和剪力
要求:熟练背诵形常数和载常数,并能正确画 出相应的弯 矩图和剪力图
M
F AB
ql 2
/3
M
F BA
ql 2
/
6
FF Q AB
ql
FF Q BA
0
FP A
l/2 l/2
3FPl/8
FP
B
A
BA
B
FP l/8
M
F AB
3FPl
/8
M
F BA
FP l
/
8
FF Q AB
FP
FF Q BA
0
8-1 形常数和载常数
FP
FPl/2
A l
B
A
FP
BA
B
FPl/2
A
t1 t2
l
M
M图（kNm）
8-2位移法Ⅰ——直接平衡法
【例题】 试做图示刚架的弯矩图。各杆E相同。
4m 6m
q=20kN/m
A 4I0 4m
B 5I0 3I0 E
5m
C 4I0 D 3I0
F 4m
解 （1）基本未知量 B点顺时针转角位移Δ1
C点顺时针转角位移Δ2
8-2位移法Ⅰ——直接平衡法
（2）写出杆端弯矩 设EI0=1
l
B
8-1 形常数和载常数
q
A l
FP
B
A
B
l/2 l/2
A
FP B
A
t1 t2
B
l
l
8-2位移法Ⅰ——直接平衡法
1 无侧移结构
【例题】 试做图示刚架的弯矩图。各杆EI相同，i=EI/6。 FP=20kN，q=2kN/m。
FP
q
A
B
C
3m 3m
6m
FP Δ1
A
B
q
B
C
Δ1
【解】 （1）基本未知量
8-1 形常数和载常数
符号 结点转角、杆轴弦转角：顺时针为正。 杆端弯矩：绕杆端顺时针为正、绕结点逆时针为正。 ★ ★
剪力：以绕隔离体顺时针转动为正。
8-1 形常数和载常数
1 形常数
1
2i
A
B
ห้องสมุดไป่ตู้
A
BA
B
4i
6i/l
M AB 4i MBA 2i
FQ 6i / l
A
B
1
6i/l
A
B
6i/l
M AB 6i / l MBA 6i / l
FP
/
2
8-1 形常数和载常数
A
t1 t2
B
A
B A
B
l
M
F AB
EI
t1
t2
/
h
M
F BA
EI
t1
t2
/
h
FQF 0
q A
ql2/8
B
A
5ql/8
B
A
B 3ql/8
M
F AB
ql 2
/
8
FF Q AB
5ql
/8
FF Q BA
3ql
/
8
8-1 形常数和载常数
FP
A
B
l/2 l/2
3FP l/16 A