结构力学第07章位移法-1补(形常数载常数)
合集下载
结构力学-位移法
则梁端结点转角为0；若柱子不平行，则梁端结
点转角可由柱顶侧移表示出来。
（4）对于平行柱刚架不论横梁是平的，还是斜的， 柱子等高或不等高，柱顶线位移都相等。
a
Δ Δ
§7.4 位移法举例
例1:
q
B EI C
EI
杆长为：l
A
解：1.确定未知量
未知量为: B
2.写出杆端力的表达式
BC杆
M Bc
3
EI L
二、基本未知量的确定
1.无侧移结构基本未知量：所有刚结点的转角
1
2
1
2.有侧移结构
1
2
3
例1. B
C 例2. B
C
A
A
只有一个刚结点B，由于忽 略轴向变形，B结点只有 B
只有一个刚结点B， 由于忽略轴向变形及C 结点的约束形式，B结 点有一个转角和水平位 移 B BH
例3. B
l
A
F11
4EI A l
4EI A l
B
2
E l
I
A
θA
4i
2
E l
I
A
A
ql3 96 EI
4E l
I
A
基本体系法解题要点：
（1）位移法的基本未知量是结点位移；
（2）位移法的基本结构----单跨梁系； （3）位移法的基本方程是平衡方程； （4）建立基本方程的过程分为两步：
1）把结构拆成杆件，进行杆件分析； 2）再把杆件综合成结构，进行整体分析； （5）杆件分析是结构分析的基础。
第7章 位移法
基本要求：熟练掌握位移法解题的基本原理和超静定梁、刚架在荷 载作用下内力的计算。 掌握位移法方程建立的两种途径：一是利用直接平衡法 建立平衡方程，便于理解和手算；二是利用基本体系建 立典型方程，为矩阵位移法打基础，便于用计算机电算。 掌握对称性的利用。
点转角可由柱顶侧移表示出来。
（4）对于平行柱刚架不论横梁是平的，还是斜的， 柱子等高或不等高，柱顶线位移都相等。
a
Δ Δ
§7.4 位移法举例
例1:
q
B EI C
EI
杆长为：l
A
解：1.确定未知量
未知量为: B
2.写出杆端力的表达式
BC杆
M Bc
3
EI L
二、基本未知量的确定
1.无侧移结构基本未知量：所有刚结点的转角
1
2
1
2.有侧移结构
1
2
3
例1. B
C 例2. B
C
A
A
只有一个刚结点B，由于忽 略轴向变形，B结点只有 B
只有一个刚结点B， 由于忽略轴向变形及C 结点的约束形式，B结 点有一个转角和水平位 移 B BH
例3. B
l
A
F11
4EI A l
4EI A l
B
2
E l
I
A
θA
4i
2
E l
I
A
A
ql3 96 EI
4E l
I
A
基本体系法解题要点：
（1）位移法的基本未知量是结点位移；
（2）位移法的基本结构----单跨梁系； （3）位移法的基本方程是平衡方程； （4）建立基本方程的过程分为两步：
1）把结构拆成杆件，进行杆件分析； 2）再把杆件综合成结构，进行整体分析； （5）杆件分析是结构分析的基础。
第7章 位移法
基本要求：熟练掌握位移法解题的基本原理和超静定梁、刚架在荷 载作用下内力的计算。 掌握位移法方程建立的两种途径：一是利用直接平衡法 建立平衡方程，便于理解和手算；二是利用基本体系建 立典型方程，为矩阵位移法打基础，便于用计算机电算。 掌握对称性的利用。
结构力学 位移法
1
第七章 位移法
7-1 位移法的基本概念
2
求解超静定结构的两种最基本的方法：
力法 位移法
力法适用性广泛，解题灵活性较大。（可选 用各种各样的基本结构）。
位移法在解题上比较规范，具有通用性，因 而计算机易于实现。
位移法可分为：手算——位移法 电算——矩阵位移法
力法与位移法最基本的区别： 3
基本未知量不同
（位移法基本方程）
在(1)(2)条件成立条件下，基本结构 的内力和位移与原结构相同。
解位移法基本方程
结点位移 未知量
内力
适用范围：
6
力法: 超静定结构
位移法： 超静定结构，也可用于静定结构。 一般用于结点少而杆件较多的刚架。
例：
7
P
力法计算,9个基本未知量
位移法计算, 1个基本未知量
位移法的准备工作
力法：以多余未知力基本未知量
位移法：以某些结点位移基本未知量
力法和位移法的解题思路：
力法：
先求多余未知力
结构 内力
结构 位移
力法的解题过程
4
力法的全部计算均在基本结构上
原结构
超静定结构
确定基本未知量： 多余未知力Xi
基本结构
施加条件:
原结构的变形协调条件
（力法基本方程）
在变形条件成立条件下，基本体 系的内力和位移与原结构相同。
8
三种单跨超静定梁作为基本构件
常用的形常数：杆轴弦转角
9
三类基本构件由杆端单位位移引起的杆端弯矩和剪力.
1
A
B
+
−
i
i = EI 线刚度
l
M AB = i MBA = −i
第七章 位移法
7-1 位移法的基本概念
2
求解超静定结构的两种最基本的方法：
力法 位移法
力法适用性广泛，解题灵活性较大。（可选 用各种各样的基本结构）。
位移法在解题上比较规范，具有通用性，因 而计算机易于实现。
位移法可分为：手算——位移法 电算——矩阵位移法
力法与位移法最基本的区别： 3
基本未知量不同
（位移法基本方程）
在(1)(2)条件成立条件下，基本结构 的内力和位移与原结构相同。
解位移法基本方程
结点位移 未知量
内力
适用范围：
6
力法: 超静定结构
位移法： 超静定结构，也可用于静定结构。 一般用于结点少而杆件较多的刚架。
例：
7
P
力法计算,9个基本未知量
位移法计算, 1个基本未知量
位移法的准备工作
力法：以多余未知力基本未知量
位移法：以某些结点位移基本未知量
力法和位移法的解题思路：
力法：
先求多余未知力
结构 内力
结构 位移
力法的解题过程
4
力法的全部计算均在基本结构上
原结构
超静定结构
确定基本未知量： 多余未知力Xi
基本结构
施加条件:
原结构的变形协调条件
（力法基本方程）
在变形条件成立条件下，基本体 系的内力和位移与原结构相同。
8
三种单跨超静定梁作为基本构件
常用的形常数：杆轴弦转角
9
三类基本构件由杆端单位位移引起的杆端弯矩和剪力.
1
A
B
+
−
i
i = EI 线刚度
l
M AB = i MBA = −i
结构力学第七章-位移法(一)
由 M B = 0 同理可得，
FQAB 6i 6i 12i F A B 2 FQAB l l l
结构力学 第七章 位移法
2015年9月12日星期六
§7-2 等截面直杆的转角位移方程
等截面直杆的转角位移方程：
一端固端一端铰支的等截面直杆：
B端角位移不独立。
C
B A
AB：一端固定一端定向滑动 BC：一端固定一端定向滑动 BD：一端固定一端铰支
C
EI=c D B A
AB：两端固定 BC：一端固定一端定向滑动 BD：一端固定一端铰支
C
EI=c D B A
AB：两端固定 BC：两端固定 BD：一端固定一端铰支
C
EI=c D EI=c B A
AB：两端固定 BC：一端固定一端定向滑动 BD：两端固定
R1 = 0 R2 = 0 R3 = 0
R11 Z1
R21
R31
R12
R22 Z2
R32
R13
R23
R1P R33
R2P
P2
R3P
D EI=c A
E
F
D EI=c
E
F
D EI=c
E
F
P1
D EI=c A
E
F
B
C
A
B
C
A
B
C
B
C
(a)基本结构只发生 Z1
(b)基本结构只发生 Z 2
EI 1
B’ O
B
A’
EI
EI
EI
A EI
EI 1
不考虑杆件伸缩变形，AB 不能转动，无结点角位移
结构力学 第七章 位移法
结构力学课件--7位移法1资料教程
梁 MBC4B2C41.741.1524.8941.746.9kNm
..............................................
柱 MBE443B3B31.153.45kNm
MCF412C2C2(4.89)9.8kNm
43.5 46.9
24.5 14.7
A
3.45 B
Q
F BA
B
D
i1
q
i
i
A
C
其中
x 0 Q B A Q D C 0
QBAl32i
3ql 8
3i QDC l 2
6i l2
3ql 8
0
ql 3 16 i
QBA q
QDC
绘制弯矩图的方法：
（1）直接由外荷载及剪力计算；
（2）由转角位移方程计算。
课件
例：作图示刚架的弯矩图。忽略梁的轴向变形。
MBA4iB15 MBC3iB9
4、位移法基本方程（平衡条件） 5、各杆端弯矩及弯矩图
MB 0
MBAMBC 0
4iB 153iB 90
B
6 7i
16.72
11.57
M AB 2i7 6i1 51.7 6k2N m
M BA 4i7 6i1 51.5 1k7N m M BC 3i7 6i91.5 1k7N m
A31iMAB61iMBA
7
B61iMAB31iMBA
（2）由于相对线位移引起的A和B
A
B
l
以上两过程的叠加
A3 1iMAB 6 1iMBA l
A B
我们的任务是要由杆端位移求 杆端力，变换上面的式子可得：
B6 1iMAB 3 1iM BA l
..............................................
柱 MBE443B3B31.153.45kNm
MCF412C2C2(4.89)9.8kNm
43.5 46.9
24.5 14.7
A
3.45 B
Q
F BA
B
D
i1
q
i
i
A
C
其中
x 0 Q B A Q D C 0
QBAl32i
3ql 8
3i QDC l 2
6i l2
3ql 8
0
ql 3 16 i
QBA q
QDC
绘制弯矩图的方法：
（1）直接由外荷载及剪力计算；
（2）由转角位移方程计算。
课件
例：作图示刚架的弯矩图。忽略梁的轴向变形。
MBA4iB15 MBC3iB9
4、位移法基本方程（平衡条件） 5、各杆端弯矩及弯矩图
MB 0
MBAMBC 0
4iB 153iB 90
B
6 7i
16.72
11.57
M AB 2i7 6i1 51.7 6k2N m
M BA 4i7 6i1 51.5 1k7N m M BC 3i7 6i91.5 1k7N m
A31iMAB61iMBA
7
B61iMAB31iMBA
（2）由于相对线位移引起的A和B
A
B
l
以上两过程的叠加
A3 1iMAB 6 1iMBA l
A B
我们的任务是要由杆端位移求 杆端力，变换上面的式子可得：
B6 1iMAB 3 1iM BA l
位移法--形常数、载常数
M AC
4iq A
PL 8
3 56
PL
＝
M CA
2iq A
PL 8
9 56
PL
＋
M AB
3iq A
3 56
PL
M BA 0
qA
PL 56i
第 八 章 位移法
§8-1 位移法的概念
位移法要点: 一、基本未知量： 位移
结点线位移和结点角位移
二、基本结构：无结点位移的结构
特殊的单根杆
三、基本方程： 平衡方程
P
P
由位移连续条件： 1 sin1
2 2
2
N1 k11
EA L1EA 2L
N2
由平衡条件：
N1 sin1 N2 sin2＝P
EA 2L
22 2
回代： N1 N2
2P 2
2L P EA
第 八 章 位移法
§8-1 位移法的概念
P
i sini
Ni kii
EA Li
sini ki sini
由平衡条件： Ni sini＝P ki sin2i
ki
P
sin2 i
回代：
Ni
ki sini
kisin2 i
P
第 八 章 位移法
§8-1 位移法的概念
基本思路:
拆 1. 各杆内力由结点位移(未知)表示
合 2. 建立内力与荷载之间平衡方程
3. 解方程,求位移 4. 回代求各杆内力
弯矩：
杆端——顺时针为正 结点——逆时针为正
当结点上有荷载时,仍以顺时针为正
第 八 章 位移法
§8-2 等截面直杆的转角位移方程
2. 杆端力与杆端位移的关系 ——刚度方程 即：由杆端位移求杆端力 以下讨论中，杆长均为Ｌ，EI为常数
第七章 位移法(结构力学)
4m
用位移法计算并作图示结构M图，横梁 为无穷刚梁EI→∞，两柱刚度均为EI
7.5
典型方程法
↓↓↓↓↓↓↓↓↓↓
位移法典型方程
↓↓↓↓↓↓↓↓↓↓
q C
F1
q C
A l
βA EI=常数
A θA
F1=0
A A
B
A A A A
F1 0 F1 0
B l
基本体系 转化为原结构的 条件：基本结构 在给定荷载以及 结点位移∆1作用 下，附加约束反 力应等于零。
M AB
A
EI
B
M AB 3i A
A
A
A
i
B
l EI i l
A
M AB
i
3i l
B
M AB
3i 3i A l
3). 一端固定、一端滑动支座的梁
MAB
EI
MBA
A
A
B
EI i l
M AB i A
M BA i A
4). 等截面直杆只要两端的杆端位移对应相同， 则相应的杆端力也相同。
EI MBA A i l
MAB MAB
1) A
B
A
EI MBA A i l
B
M AB
6i 4i A l
M BA
6i 2i A l
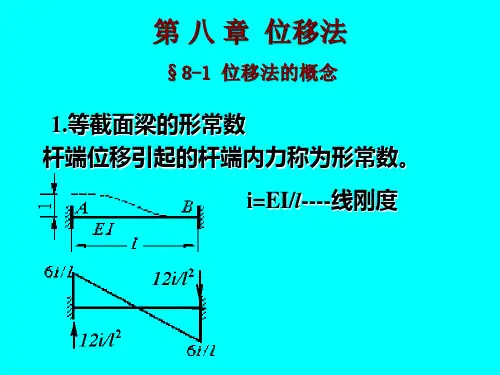
单位杆端位移引起的杆端内力称为形常数. i=EI/l----线刚度
2.由荷载求固端弯矩（载常数教材表8-1）
荷载引起的杆端内力称为载常数.
• 主系数 kii── 基本体系在Δi=1单独作用时，在第 i个附加约 束中产生的约束力矩和约束力，恒为正； • 付系数 kij= kji── 基本体系在Δj=1单独作用时，在第 i个 附 加约束中产生的约束力矩和约束力，可正、可负、可为零； • 自由项 FiP── 基本体系在荷载单独作用时，在第 i个 附加约 束中产生的约束力矩和约束力，可正、可负、可为零；
结构力学-7 位移法1
第一种梁（两端固定）：
MAFB,
MBFA,
FF QBA
第二种梁（另一端铰支）：
MF AB
MAFB12MBFA
13
第二、三种梁的固端弯矩与第一种梁固端内力的关系
第一种梁（两端固定）：
MAFB,
MBFA,
FF QBA
第三种梁（另一端滑动）：
MF AB
MAFB
2l FQFBA
MF BA
MBFA2l FQFBA
B
l
以上两过程的叠加
A3 1iMAB 6 1iMBA l
A B
由杆端位移求杆端力，变换上 面的式子可得转角位移方程：
B6 1iMAB 3 1iM BA l
MAB4iA MBA2iA
2iB 4iB
6i 6i
l (1) l
q
EI l q
EI l
mABq82l
Q BA
mBA
Q BA
mBA
ql 2 8
Q AB
5 8
ql
Q BA
3 ql 8
Q AB
3 8
ql
Q BA
5 ql 8
»在已知荷载及杆端位移的共同作用下的杆端力一般公式（转角
位移方程）：
MAB
4iA
14
Q A BQ B A 6 li A 6 li B 1 l2 i 2 6 (2 )
方法二：用力法求解单跨超静定梁
Δ
11X112X21CA 21X122X22CB
θA
X1
θB
X2
结构力学
因 B 0, QAB QBA 0 EI l MBA
1 A 代入（2）式可得 l 2
M AB i A M BA i A
A
由单位杆端位移引起的杆端力称为形常数(即刚度系数， 是只与截面尺寸和材料性质有关的常数)。
单跨超静定梁简图
A A
MAB
B
MBA
QAB= QBA
关于刚架的结点未知量
A P C
q
B A
A
A
B
M AB
A
P C
M AB
A
q
↓↓↓↓↓↓↓↓↓↓
↓↓↓↓↓↓↓↓↓↓
F1
θA
q
ql2/12 ↓↓↓↓↓↓↓↓↓↓
F1P
q
ql2/12
A
C F1P
ql 2 F1P 12
ql2/12
2 EI A l
A l
βA EI=常数
C
A
C
F1=0
ql2/48
2
2 EI A l
B
2 EI A l
4i
2 EI A l
B
ql3 A 96EI
4 EI θA A l
§2 等截面杆件的刚度方程
杆端力和杆端位移的正负规定
①杆端转角θA、θB ，弦转角β＝Δ/l都以顺时针为正。 ②杆端力的表示方法和正负号的规定 1、弯矩：MAB表示AB杆A端的弯矩。对杆端而言，顺时针为 正，逆时针为负；对结点而言，顺时针为负，逆时针为正。 P B A MBA0 MAB0 2、剪力：QAB表示AB杆A端的剪力。正负号规定同前。 P B A QAB0 QBA0
A A
A A F1 0 A A F1 0
结构力学第7章位移法讲解
内力与位移的关系式；整体分析（组合）建立位 移法基本方程，解方程求出基本未知量; （4）由杆件的内力与位移关系式求出各杆件内力。
关于刚架的计算思路
A
P C
q
A
A
M AB
P A
A
M AB
A
C
B
B
第一种位移法的基本思路：
将结构拆成杆件，推导各杆件的内力和位 移的关系；再把杆件组装成结构，通过各 杆件在结点处的受力平衡列基本方程。
l
l
(1)
l FQBA
6i l
A
6i l
B
12i l2
(2)
几种不同远端支座的刚度方程
（1）远端为固定支座
MAB
A
EI l
（2）远端为固定铰支座
MAB
A
EI l
（3）远端为定向支座
MAB
A
EI
l
MBA
M M
AB BA
4i A 2i A
M BA
（2）由于相对线位移引起的A和B
A 2 B 2
A2 B2 l
以上两过程的叠加
A
1 3i
M
AB
1 6i
M
BA
l
M AB M BA
4i A 2i A
B
2iB 6i
4iB 6i
FQAB
1
1
6i
M AB
3i
M BA
BA
8
8
关于刚架的计算思路
A
P C
q
A
A
M AB
P A
A
M AB
A
C
B
B
第一种位移法的基本思路：
将结构拆成杆件，推导各杆件的内力和位 移的关系；再把杆件组装成结构，通过各 杆件在结点处的受力平衡列基本方程。
l
l
(1)
l FQBA
6i l
A
6i l
B
12i l2
(2)
几种不同远端支座的刚度方程
（1）远端为固定支座
MAB
A
EI l
（2）远端为固定铰支座
MAB
A
EI l
（3）远端为定向支座
MAB
A
EI
l
MBA
M M
AB BA
4i A 2i A
M BA
（2）由于相对线位移引起的A和B
A 2 B 2
A2 B2 l
以上两过程的叠加
A
1 3i
M
AB
1 6i
M
BA
l
M AB M BA
4i A 2i A
B
2iB 6i
4iB 6i
FQAB
1
1
6i
M AB
3i
M BA
BA
8
8
第7章 位移法
两端为固定结点
3i M AB 3i A AB l
c
一端为固定结点，一端铰支
c M AB i A c M BA i A
一端为固定结点，一端滑动支承
§7-2 杆件单元的形常数和载常数——位移法的前期工作
力法方程：
2、由荷载求固端内力——载常数 两端固定梁
F M AB F M BA
ui sini
几何条件
EAi sin i li FNi FP EAi 2 sin i li
FNi sin i FP
综合各杆件，得平衡条件
EAi 2 sin i FP li
FP EA i sin 2 i li
§7-1 位移法的基本概念
（2）杆端弯矩Mi j
3I0 E
4m 5m
F
4m
2m
4m
D
2 2 ql 20 4 F M BA 40 8 8
F M BC
ql 2 41.7 12
F M CB 41.7
计算线性刚度i，设EI0=1，则
E 4I 0 EI iAB AB 1 l AB 4
iBC 1, iCD 1, iBE
C
P
基本未知量 （如图所示刚架有几个
独立结点位移参数？） 在刚架分析中，通常只考虑弯曲变形， 忽略剪切和拉伸变形。 因此，取独立节点位移参数A和作为基本未知量。
A
B A
M AB
建立基本方程分两步
A
B
A
M AB
P C
A
（1）单元分析（拆分）确 定单杆的杆端内力与杆端 位移及杆件上荷载的关系；
力法方程：
结构力学第7章 位移法(27-30)
第 7 章 位移法
Displacement Method
第 7 章 位移法
教学内容 7-1 等截面杆件的形常数和载常数 7-2 位移法的基本概念
7-3 无侧移刚架的计算
7-4 有侧移刚架的计算
7-5 对称结构的计算
7-1 等截面杆件的形常数和载常数
知识点：
等截面梁的形常数 等截面梁的载常数
（1）结构的独立结点位移
（2）结构拆成杆件，做杆件分析—荷载、变形
（3）平衡方程，求解
（4）回代，求杆端弯矩
小结
7-1 等截面杆件的形常数和载常数
知识点： 等截面梁的形常数
等截面梁的载常数 重点： 记忆等截面梁的形常数和载常数。
7-2 位移法的基本概念
知识点： 整体分析、杆件分析
力法解常见超静定结构
m AB 15kN m
mBC ql 2 9kN m 8
(3) 列杆端转角位移方程
MAB
EI
P
B MBA
MBC B
q
EI
设i
EI 6
M AB 2i B 15
M BC 3i B 9
M BA 4i B 15
(4) 位移法基本方程（平衡条件）
4I0 4m
B 5I0
3I0
3I0 F 4m
M
F BA
E 4m 5m
（1）基本未知量B、C （2）固端弯矩
F M BC
F M CB 41.7kN m
20kN/m
A 4I0 4m B 5I0 C 4I0
D
3I0
E 4m 5m F 4m
各杆刚度取相对值计算，设EI0=1，则
iBA iBE
Displacement Method
第 7 章 位移法
教学内容 7-1 等截面杆件的形常数和载常数 7-2 位移法的基本概念
7-3 无侧移刚架的计算
7-4 有侧移刚架的计算
7-5 对称结构的计算
7-1 等截面杆件的形常数和载常数
知识点：
等截面梁的形常数 等截面梁的载常数
（1）结构的独立结点位移
（2）结构拆成杆件，做杆件分析—荷载、变形
（3）平衡方程，求解
（4）回代，求杆端弯矩
小结
7-1 等截面杆件的形常数和载常数
知识点： 等截面梁的形常数
等截面梁的载常数 重点： 记忆等截面梁的形常数和载常数。
7-2 位移法的基本概念
知识点： 整体分析、杆件分析
力法解常见超静定结构
m AB 15kN m
mBC ql 2 9kN m 8
(3) 列杆端转角位移方程
MAB
EI
P
B MBA
MBC B
q
EI
设i
EI 6
M AB 2i B 15
M BC 3i B 9
M BA 4i B 15
(4) 位移法基本方程（平衡条件）
4I0 4m
B 5I0
3I0
3I0 F 4m
M
F BA
E 4m 5m
（1）基本未知量B、C （2）固端弯矩
F M BC
F M CB 41.7kN m
20kN/m
A 4I0 4m B 5I0 C 4I0
D
3I0
E 4m 5m F 4m
各杆刚度取相对值计算，设EI0=1，则
iBA iBE
结构力学 第七章 位移法
表示等截面直杆杆端力与杆端位移及杆上荷载间关系的表达式
B A
Δ
6i F M AB l 6i F M BA 2i A 4i B M BA l 6i 6i 12i F F QAB A B 2 FAB l l l M AB 4i A 2i B
B
4i
1
2i
6i l
12i
l
6i
3i
l
6i
0
l2
θ =1
B B
3i
3i l
l
2
1 θ =1
B
3i
i
l
0
A
－i
0
三 等截面直杆的载常数 由荷载作用所引起的杆端力（固端力）
单跨超静定梁简图
q A
↓↓↓↓↓↓ ↓↓↓↓↓↓ ↓↓
mAB
B
mBA
ql 2 12
Pl 8
ql 2 12
Pl 8
位移法方程实质上平衡方程
Z1
D i A 2i E
Z2
C 2i
i EI l
4m
EI
i B
A
B
4m
2m
2m
位移法基本体系
解：1 确定位移法基本体系 2 列位移法方程 k11Z1+ k12Z2+ F1P=0 k21Z1+ k22Z2+ F2P=0
３ 计算系数和自由项 Z1=1
4i 4i D i8i A 2i 8i 2i E 2i i B C
M AB 2i B
M BC ql 2 4i B 12
ql 2 ql 2 ql 2 4i 96i 12 24
结构力学形常数和载常数表
结构力学形常数和载常数表1. 形常数形常数是指描述材料在变形过程中的力学行为的常数。
在结构力学中，常见的形常数有弹性模量、剪切模量、泊松比等。
弹性模量是衡量材料抗弯曲和拉伸变形能力的常数。
它描述了材料在受力后产生的应力与应变之间的关系。
弹性模量越大，材料的刚度越高，抗弯曲和拉伸能力越强。
剪切模量是衡量材料抗剪切变形能力的常数。
它描述了材料在受到剪切力时产生的剪切应力与剪切应变之间的关系。
剪切模量越大，材料的刚度越高，抗剪切能力越强。
泊松比是衡量材料在受力时体积变化与横向应变之间的关系的常数。
它描述了材料在受到拉伸或压缩力时纵向应变与横向应变之间的比例关系。
泊松比的取值范围在0到0.5之间，常见材料的泊松比一般在0.25左右。
2. 载常数载常数是指结构在受到外部荷载时所产生的应力与应变之间的关系的常数。
在结构力学中，常见的载常数有抗弯强度、抗剪强度、抗压强度等。
抗弯强度是材料在受到弯曲力时能够抵抗变形和破坏的能力。
它描述了材料在弯曲过程中所能承受的最大应力。
抗弯强度越大，材料的抗弯能力越强。
抗剪强度是材料在受到剪切力时能够抵抗剪切变形和破坏的能力。
它描述了材料在剪切过程中所能承受的最大应力。
抗剪强度越大，材料的抗剪能力越强。
抗压强度是材料在受到压缩力时能够抵抗压缩变形和破坏的能力。
它描述了材料在压缩过程中所能承受的最大应力。
抗压强度越大，材料的抗压能力越强。
形常数和载常数是结构力学中非常重要的参数，它们直接影响着结构的性能和安全性。
在设计和分析结构时，我们需要准确地了解材料的形常数和载常数，以确保结构的稳定性和承载能力。
除了这些常见的形常数和载常数之外，还有许多其他的参数和常数在结构力学中起着重要的作用，如杨氏模量、体积模量、屈服强度等。
这些参数的取值与材料的性质和结构的要求有关，不同的材料和结构可能有不同的形常数和载常数。
形常数和载常数是结构力学中不可或缺的概念和参数。
它们描述了材料和结构在受力时的力学行为，对于结构的设计和分析起着重要的指导作用。
第07章位移法
22
2、结点转角 结点转角以顺时针方向为正，逆时针方向为负。 FP A D B C
B( )
C( )
3、杆件两端相对侧移 杆件两端相对侧移的正负号与弦转角的正负号 一致。而以顺时针方向为正，逆时针方向为负。 A
l
B
A
l
B
23
二、等截面直杆的刚度方程(形常数)
此时B结点产生固端弯矩。
12
q A B
q
B 0
F M BA 0
C B
F M BC
C
F M BC
ql 2 8
3、令B结点产生转角B( 单跨超静定梁。 A i A i
)。
此时AB、BC杆类似于B端为固端且产生转角B的 B i B
B
C
i
B 3i B
B
3i B
B
EI —线刚度 l
20
§7-2 等截面直杆的刚度方程
位移法计算的基础是：单跨超静定梁具有支座
移动和外荷载作用时的杆端力的计算。 位移法将整体结构拆成的杆件不外乎三种“单 跨超静定梁”：两端固定梁；一端固定、一端简支 梁；一端固定、一端滑动梁。 用到的数据是：形常数和载常数。 (1) 已知杆端位移求杆端弯矩——形常数；
D值法(广义反弯点法)。
2
§7-1 位移法基本概念
一、位移法的基本思路
将结构拆成杆件，再由杆件过渡到结构。即： 结构
拆成 搭接成 杆件 第二步 第一步
结构
第一步：杆件分析 找出杆件的杆端力与杆端位 移之间的关系。即：建立杆件的刚度方程。
第二步：结构分析 找出结构的结点力与结点位
移之间的关系。即：建立结构的位移法基本方程。
( a) B A C D E F G (b) B C D E F G
2、结点转角 结点转角以顺时针方向为正，逆时针方向为负。 FP A D B C
B( )
C( )
3、杆件两端相对侧移 杆件两端相对侧移的正负号与弦转角的正负号 一致。而以顺时针方向为正，逆时针方向为负。 A
l
B
A
l
B
23
二、等截面直杆的刚度方程(形常数)
此时B结点产生固端弯矩。
12
q A B
q
B 0
F M BA 0
C B
F M BC
C
F M BC
ql 2 8
3、令B结点产生转角B( 单跨超静定梁。 A i A i
)。
此时AB、BC杆类似于B端为固端且产生转角B的 B i B
B
C
i
B 3i B
B
3i B
B
EI —线刚度 l
20
§7-2 等截面直杆的刚度方程
位移法计算的基础是：单跨超静定梁具有支座
移动和外荷载作用时的杆端力的计算。 位移法将整体结构拆成的杆件不外乎三种“单 跨超静定梁”：两端固定梁；一端固定、一端简支 梁；一端固定、一端滑动梁。 用到的数据是：形常数和载常数。 (1) 已知杆端位移求杆端弯矩——形常数；
D值法(广义反弯点法)。
2
§7-1 位移法基本概念
一、位移法的基本思路
将结构拆成杆件，再由杆件过渡到结构。即： 结构
拆成 搭接成 杆件 第二步 第一步
结构
第一步：杆件分析 找出杆件的杆端力与杆端位 移之间的关系。即：建立杆件的刚度方程。
第二步：结构分析 找出结构的结点力与结点位
移之间的关系。即：建立结构的位移法基本方程。
( a) B A C D E F G (b) B C D E F G