02-1电阻等效变换
合集下载
电路理论_02_电阻电路的等效变换分析法
问题：
并联的计算方
R5
(1)如何计算?
法
R3
R4
(2)连接方式？
I
+
Us
R1
电桥电R路2 的关键：
△形Ｙ形
R1
R2
R5
R5
R3
R4
R3
R4
I
+
Us
2020/5/7
△形Ｙ形
I +
Us Ｙ形△形
22
Ｙ形和△形电阻网络
1 I1
1 I1’
R31
R12
I3 3
R23
I2 2
△形电路
R1
R2
I3’
R3
I2’
3
第2章 电阻电路的等效变换分析法
解永平 2007.10.30
2020/5/7
1
基本要求
理解单口网络等效概念 熟练计算等效电阻 掌握实际电源的两种模型及其等效变换 掌握简单电路的等效变换分析方法
2020/5/7
2
提纲
2.1 等效及等效变换的概念 2.2 不含独立源的单口网络的等效 2.3 Ｙ形和△形电阻网络的等效变换 2.4 含独立源单口网络的等效
解：以与ab垂直的直线cd为对称轴， 会发现电阻之间存在如下关系：
R1 ＝ R2 R4 R3
2 R1 R2
3
d R4 4
R5
10 R3
6 c
(R1R3=R2R4)
a
b
那么R1，R2，R3和R4组成平衡电桥，c，d两点电位相等，所以Ucd=0，cd之
间等效为短路；对R5应用欧姆定律，得Icd=0，所以cd之间又可等效为开路。
I1’ R1
I3’
电阻电路的等效变换习题及答案
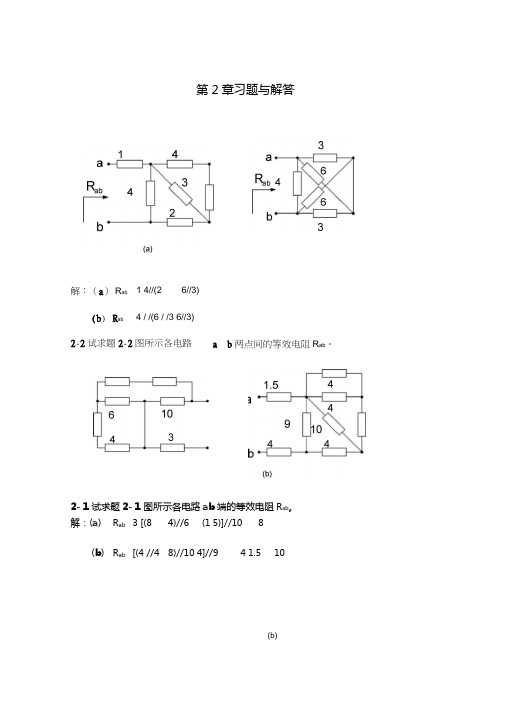
解：（a ） R ab 1 4//(26//3)(b ) R ab4 / /(6 / /3 6//3)2-2试求题2-2图所示各电路a 、b 两点间的等效电阻R ab 。
第2章习题与解答2- 1试求题2- 1图所示各电路ab 端的等效电阻R ab 。
解：(a ) R ab 3 [(84)//6(1 5)]//108(b ) R ab [(4 //4 8)//10 4]//94 1.510(b)2- 3试计算题2-3图所示电路在开关K打开和闭合两种状态时的等效电阻R ab⑻(b)解：(a)开关打开时(8 4)//4 3开关闭合时Rab4//4 2(b)开关打开时Rab(6 12)//(6 12) 9开关闭合时6//12 6//12 8题2-4图解：(a)从左往右流过1电阻的电流为l121/ (1 6//12 3//6) =21/ (1 4 2) 3A从上往下流过3电阻的电流为I3 63 2A3 6从上往下流过12电阻的电流为I 12所以I l3-l12=1A(b)从下往上流过6V电压源的电流为I(1+2) // ( 1+2) 1.5从上往下流过两条并联支路的电流分别为 2A 所以 U 2 2-1 2=2V2- 5试求题2-5图所示各电路ab 端的等效电阻 為，其中R R 211 11 )//(1 D 3 32(b )将图中的两个丫形变成△形，如图所示(b)题2-5图解：(a )如图,2.5I85即得40 21所以志 1.269 2-6计算题2-6图所示电路中a ]1I8888(a)解: 所以20 9题2- 6图(a )将图中的丫形变成△形，如图所示R ab 12//6 4(b )将图中的丫形变成△形，如图所示140 381、对-T~~110108A] I0Uab 532.5 { I—2612所以&b3//4 —2- 7对题2- 7图所示电路，应用Y—△等效变换求电路ab端的等效电阻角线电压U及总电压U ab。
电路基础02
电路基础
二、弥尔曼定理
一般地，电路为双节点电路，有多条支路，并 含有多个电压源和电流源时，节点间电压
u12=
GU u G
i Si i
Si
称为弥尔曼定理。含电压源的各项中，当电压源 支路的正极性端接到独立节点1时，USi取“+”号， 反之取“-”号。利用弥尔曼定理求出节点电压后， 再根据欧姆定律，就可求出各支路的电流。
电路基础
（2）对含有受控电源的线性有源二端网 络，求开路电压时按照叠加定理的方法求解。 求入端电阻时，设网络内所有独立电源为零， 将电路变为相应的无源二端网络，在端口处 施加电压u，计算或测量端口的电流i，由欧 姆定律求得入端电阻R0=u/i。
电路基础
（3）计算或测量二端网络的开路电压u0和短路 电流iSC，如下图所示，由戴维南等效电路图如图 （c）所示，当外电路短路时，电路中的电流等于 短路电流iSC，由欧姆定律求得入端电阻 R 0=
u0 iSC
电路基础
二、诺顿定理
诺顿定理表述为:任何一个有源线性二端网络， 就其对于外电路作用效果而言，总可以用一个电 流源与电阻的并联组合等效。电流源的电流等于 二端网络的端口短路电流，并联电阻等于该二端 网络中所有独立电源置零时的端口入端电阻。
电路基础
2.5 支路电流法
一、线性电路方程的独立性
k k
Sk
5. 联立求解上述b个独立方程，求出各支路电流。
6. 根据需要，求解各支路电压及功率等。
电路基础
2.6 网孔电流法
一、网孔电流法
i1=im1
i2=im1-im2
i3=-im2 i4=-im1+im3 i5=-im3 i6=-im2+im3
第02章电阻电路的等效变换(丘关源)
（1-29）
(6)恒压源并联任何元件其两端电压不变；
恒流源串联任何元件其流出电流不变；
a a
+ us
－
+ +
－
对外等效
us
－
b
c
b c
对外等效
is
+
－
d
is
d
（1-30）
例1 用电源等效变换法求i R5
R1 u1 + R2 R3 i
+
i=?
解：
-u3
R4
is
R5 u3 — R3 i
应 用 举 例
一、理想电压源的串联和并联
1、串联 + uS1_ _ uS2 +
+ 注意参考方向
º uS＝＋uS1 …－uS2 i + uS _ º
等效
+
uS _
º +
_ º
2、并联
条件：uS＝uS1＝uS2 方向相同 º 恒压源中的电流由外电路决定。相同的恒压源才能并联 。
（1-21）
uS1_
u S2
+ _
i
º
3、恒压源与任意支路(非恒压源)并联的等效 i i + + + + 任意 uS 对外等效 uS _ u _ u 元件 _ _ 4、实际电压源的串联等效
+ i +
uS1 _
R1
_ uS2 + u
R2 _
等效
uS _ R + i +
u
_
uS＝＋uS1－uS2
R＝R1 ＋ R2
（1-22）
二、理想电流源的串联和并联
(6)恒压源并联任何元件其两端电压不变；
恒流源串联任何元件其流出电流不变；
a a
+ us
－
+ +
－
对外等效
us
－
b
c
b c
对外等效
is
+
－
d
is
d
（1-30）
例1 用电源等效变换法求i R5
R1 u1 + R2 R3 i
+
i=?
解：
-u3
R4
is
R5 u3 — R3 i
应 用 举 例
一、理想电压源的串联和并联
1、串联 + uS1_ _ uS2 +
+ 注意参考方向
º uS＝＋uS1 …－uS2 i + uS _ º
等效
+
uS _
º +
_ º
2、并联
条件：uS＝uS1＝uS2 方向相同 º 恒压源中的电流由外电路决定。相同的恒压源才能并联 。
（1-21）
uS1_
u S2
+ _
i
º
3、恒压源与任意支路(非恒压源)并联的等效 i i + + + + 任意 uS 对外等效 uS _ u _ u 元件 _ _ 4、实际电压源的串联等效
+ i +
uS1 _
R1
_ uS2 + u
R2 _
等效
uS _ R + i +
u
_
uS＝＋uS1－uS2
R＝R1 ＋ R2
（1-22）
二、理想电流源的串联和并联
电路分析基础 张凤霞课件-第02章.电阻电路的等效变换
20 100 60
120 60
ab
20 100 60
40
2020/5/25
返回 上页 下 页
例5 求: Rab
5
15
6
a 20 b
7
6
缩短无 电阻支路
Rab＝10
4
ba
15
10
20
5
a
15 b
7 6 6 4 a
b
15 7 3
2020/5/25
返回 上页 下 页
例6 求: Rab
iR
对称电路 c、d等电位
变量之间无控制和被控的关系，则称 N1和 N2为 单口网络（二端网络）。
一个单口网络对电路其余部分的影响，决定于其 端口电流电压关系（VAR）。
2020/5/25
返回 上页 下 页
二. 等效单口网络
a
i +
b u-
N
u f (i)
a
i +
b u-
N'
u f(i)
若网络 N 与 N 的VAR相同，则称该两网络为
等效单口网络。
将电路中一个单口网络用其等效网络代替（称 为等效变换），电路其余部分的工作状态不会 改变。
2020/5/25
返回 上页 下 页
2.1.2 单口网络端口伏安关系(VAR)的求取
将单口网络从电路中分离出来，标 好其端口电流、电压的参考方向；
假定端电流i 已知（相当于在端口 接一电流源），求出 u = f (i) 。或 者，假定端电压 u 已知（相当于在 端口接一电压源），求出 i = g (u) 。
返回 上页 下 页
• 三端网络的端口VAR
端口独立电流（例如 i1、i2 ）与端口独立电压（例 如 u13 、u23 ）之间的关系。
120 60
ab
20 100 60
40
2020/5/25
返回 上页 下 页
例5 求: Rab
5
15
6
a 20 b
7
6
缩短无 电阻支路
Rab＝10
4
ba
15
10
20
5
a
15 b
7 6 6 4 a
b
15 7 3
2020/5/25
返回 上页 下 页
例6 求: Rab
iR
对称电路 c、d等电位
变量之间无控制和被控的关系，则称 N1和 N2为 单口网络（二端网络）。
一个单口网络对电路其余部分的影响，决定于其 端口电流电压关系（VAR）。
2020/5/25
返回 上页 下 页
二. 等效单口网络
a
i +
b u-
N
u f (i)
a
i +
b u-
N'
u f(i)
若网络 N 与 N 的VAR相同，则称该两网络为
等效单口网络。
将电路中一个单口网络用其等效网络代替（称 为等效变换），电路其余部分的工作状态不会 改变。
2020/5/25
返回 上页 下 页
2.1.2 单口网络端口伏安关系(VAR)的求取
将单口网络从电路中分离出来，标 好其端口电流、电压的参考方向；
假定端电流i 已知（相当于在端口 接一电流源），求出 u = f (i) 。或 者，假定端电压 u 已知（相当于在 端口接一电压源），求出 i = g (u) 。
返回 上页 下 页
• 三端网络的端口VAR
端口独立电流（例如 i1、i2 ）与端口独立电压（例 如 u13 、u23 ）之间的关系。
电阻电路的等效变换(电路分析基础课件)
03
02
01
等效变换的目的
等效变换的基本原则
电压和电流保持不变
在等效变换过程中，电路中的电压和电流值应保持不变。
元件参数相同
等效变换后的元件参数应与原电路中的元件参数相同。
功率平衡
等效变换后的电路应满足功率平衡条件，即电源提供的功率等于负载消耗的功率。
02
电阻的串并联等效变换
总结词
当多个电阻以串联方式连接时，总电阻值等于各电阻值之和。
详细描述
在并联电阻的等效变换中，总电阻倒数1/R_eq等于各个并联电阻倒数1/R1、1/R2、...、1/Rn之和。这种等效变换在电路分析中非常有用，因为它可以帮助我们简化电路模型。
01
02
03
04
电阻并联的等效变换
串并联电阻的等效变换
总结词：串并联电阻的等效变换是电路分析中的重要概念，它涉及到将复杂的串并联电路简化为易于分析的形式。
等效变换方法：对于非线性电阻电路，可以采用分段线性化方法，将非线性电阻的伏安特性曲线分段近似为直线，然后进行等效变换。
05
等效变换在电路分析中的应用
在计算电流和电压中的应用
总结词：简化计算
详细描述：通过等效变换，可以将复杂的电阻电路简化为简单的电路，从而更容易计算电流和电压。
总结词：提高精度
总结词：扩展应用范围
电阻串联的等效变换
总结词
当多个电阻以并联方式连接时，总电阻值倒数等于各电阻值倒数之和。
详细描述
在电路中，如果多个电阻以并联方式连接，则总电阻的倒数等于各电阻倒数之和。这是因为多个电阻并联时，它们共享相同的电压，因此总电流等于各支路电流之和。
总结词
并联电阻的等效变换可以通过公式1/R_eq = 1/R1 + 1/R2 + ... + 1/Rn表示。
02
01
等效变换的目的
等效变换的基本原则
电压和电流保持不变
在等效变换过程中，电路中的电压和电流值应保持不变。
元件参数相同
等效变换后的元件参数应与原电路中的元件参数相同。
功率平衡
等效变换后的电路应满足功率平衡条件，即电源提供的功率等于负载消耗的功率。
02
电阻的串并联等效变换
总结词
当多个电阻以串联方式连接时，总电阻值等于各电阻值之和。
详细描述
在并联电阻的等效变换中，总电阻倒数1/R_eq等于各个并联电阻倒数1/R1、1/R2、...、1/Rn之和。这种等效变换在电路分析中非常有用，因为它可以帮助我们简化电路模型。
01
02
03
04
电阻并联的等效变换
串并联电阻的等效变换
总结词：串并联电阻的等效变换是电路分析中的重要概念，它涉及到将复杂的串并联电路简化为易于分析的形式。
等效变换方法：对于非线性电阻电路，可以采用分段线性化方法，将非线性电阻的伏安特性曲线分段近似为直线，然后进行等效变换。
05
等效变换在电路分析中的应用
在计算电流和电压中的应用
总结词：简化计算
详细描述：通过等效变换，可以将复杂的电阻电路简化为简单的电路，从而更容易计算电流和电压。
总结词：提高精度
总结词：扩展应用范围
电阻串联的等效变换
总结词
当多个电阻以并联方式连接时，总电阻值倒数等于各电阻值倒数之和。
详细描述
在电路中，如果多个电阻以并联方式连接，则总电阻的倒数等于各电阻倒数之和。这是因为多个电阻并联时，它们共享相同的电压，因此总电流等于各支路电流之和。
总结词
并联电阻的等效变换可以通过公式1/R_eq = 1/R1 + 1/R2 + ... + 1/Rn表示。
习题02解答
习题二
2-1 如图题 2-1 所示电路中，Is = 16.5mA，Rs = 2kΩ，R1 = 40 kΩ，R2 = 10 kΩ，R3 = 25 kΩ。 求I1、I2和I3。
Rs +
I1
I2
I3
Is
U R1
R2
R3
–
题 2-1 图
解
U = Is (R1 // R2 // R3 ) = 16.5 × (40 //10 // 25) = 100V I1 = U R1 = 100 40k = 2.5mA I 2 = U R2 = 100 10k = 10mA I3 = U R3 = 100 25k = 4mA
R/3
2R/3
2R/3
R/3
R/3
2R/3
b
c
b
2R/9 R/3 b
c a R/3
2R/9 2R/9 R/3 c
a
5R/9
5R/9
5R/9
b
c
5
2-10 求如图 2-10 所示电路的等效电阻Rab。
a
4Ω
7Ω
a
4Ω
R
R
R
R
R
10Ω
10Ω
b
R
R
b
(b)
(a)
a 1Ω
1Ω 1Ω
Rc
R
R
1Ω
1Ω
R
R
R
b
图（b）：I =2A，U =4V P2A=2×(10-4)=12W，吸收功率，为负载。 P10V=2×10=20W，发出功率，为电源。 P2Ω=2×22=8W，吸收功率，为负载。
2-8 求如图题 2-8 所示电路中的电流 I。
4Ω I
2-1 如图题 2-1 所示电路中，Is = 16.5mA，Rs = 2kΩ，R1 = 40 kΩ，R2 = 10 kΩ，R3 = 25 kΩ。 求I1、I2和I3。
Rs +
I1
I2
I3
Is
U R1
R2
R3
–
题 2-1 图
解
U = Is (R1 // R2 // R3 ) = 16.5 × (40 //10 // 25) = 100V I1 = U R1 = 100 40k = 2.5mA I 2 = U R2 = 100 10k = 10mA I3 = U R3 = 100 25k = 4mA
R/3
2R/3
2R/3
R/3
R/3
2R/3
b
c
b
2R/9 R/3 b
c a R/3
2R/9 2R/9 R/3 c
a
5R/9
5R/9
5R/9
b
c
5
2-10 求如图 2-10 所示电路的等效电阻Rab。
a
4Ω
7Ω
a
4Ω
R
R
R
R
R
10Ω
10Ω
b
R
R
b
(b)
(a)
a 1Ω
1Ω 1Ω
Rc
R
R
1Ω
1Ω
R
R
R
b
图（b）：I =2A，U =4V P2A=2×(10-4)=12W，吸收功率，为负载。 P10V=2×10=20W，发出功率，为电源。 P2Ω=2×22=8W，吸收功率，为负载。
2-8 求如图题 2-8 所示电路中的电流 I。
4Ω I
电路分析实用第2章 电路的等效变换
2.分流公式 ik Gk u Gk
n
i Gk
Gk Geq
i
k 1
u
i
G1 G2 Gn
i
i
n
Gk
Geq
k 1
第k个电阻上的分流公式为 ik Gk u Gk
n
i Gk
Gk Geq
i
两个电阻并联，分流公式为
k 1
i1
R2 R1 R2
接在n节点的两电阻乘积
Rn
三个电阻之和
2. Y - Δ 变换
R1
1
R2
2
R12
1
2
R3
R13
R23
3
R12
R1R2
R2 R3 R3
R1R3
3
R23
R1R2
R2 R3 R1
R1R3
R13
R1R2
R2 R3 R2
R1R3
电阻两两乘积之和 Rmn 下标不为 m，n的电阻
例2: 求等效电阻 Rab
U0
R2 R1 R2
US
R3 R3 R4
US
输出电压随热敏电阻值变化
根据的变化值来确定温度的值
2.5 输入电阻
从(输入)端口两端看进去 的等效电阻。
Ri
Rab
u i
例3：求输入电阻Ri。
R1 I1 I a
解：I I2 I1
U U U
+
μU
I2 +
R2 U
Ri
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
0.5R
0.5R
2.1 二端网络与等效变换
例
试求a、b端的等效电阻。
2.8Ω
8 6 7 3 7 b 5 1 2
a 3 4
2.1 二端网络与等效变换
8 6
7
a 3 4
2、线性电路：
由线性无源元件、线性受控源和独立源组成的电路。 3、线性电阻电路： 如果构成线性电路的无源元件都是线性电阻。
2.1 二端网络与等效变换
4、二端（一端口）网络(one-port network)： 含两个引出端和外部电路相连的网络。 5、等效(equivalent)： 如果两个一端口网络A、B端口的伏安特性完 全一致，则称A、B等效。
1、运用等效变换法。 2、运用独立变量——建立电路方程的方法。
3、运用电路定理分析电路。
2.1 二端网络与等效变换
二、电阻的串联(Series connection of resistors)
I + R1 R2 U …… Rn + U _1 + U _2
1 U U1 U 2 2 R R1 R2 Rk 3 Uk U R 4 P P1 P2 RK 5 Pk P R
I A + U _ B I + U _
U f1 ( I )
= U f2 ( I )
2.1 二端网络与等效变换
6、等效变换(equivalent conversion) ： 若两个一端口网络A、B等效，则A、B 可以互换。这个互换过程就称为等效变换。 目的：简化电路。
注：分析线性电阻电路的三个途径
2.1 二端网络与等效变换
a
a a
R R c R c R d 0.5R R
字母标注法
1、在各节点处标上节点字母，短路线联 接的点或等位点用同一字母标注； 2、将接在同一对字母间的电阻用并联后 的等效电阻替代； 3、整理并简化电路，求出总的等效电阻。
R R b c
b
b a
0.5R
c
a
R
b
0.5R
d b
In Gn
Pn
2.1 二端网络与等效变换
四、电桥电路（Bridge Circuit）
R1 R3 平衡条件： R4
R5
R2
R1 R3 R2 R4 或 R1 R4 R2 R3
臂支路：R1、R2、R3、R4 桥支路：R5
2.1 二端网络与等效变换
四、电桥电路（Bridge Circuit）
R1 R3
R5
R2
R4
平衡时，R5所在的支路既可开路又可短路。
2.1 二端网络与等效变换
五、电阻的混联(Series and parallel connection of resistors
例1
求等效电阻Rab和Rcd。
c a 50Ω • 30Ω d •
50Ω
b
60Ω
30Ω
Rab 75, Rcd 21
第二章
简单 电路
电路的分析方法
基本定理——欧姆定理、基尔霍夫定理 基本方法——等效变换法 基尔霍夫定理 叠加原理 等效电源定理 KCL KVL 戴维宁定理 诺顿定理
电路 的分析 方法
基本定理
复杂 电路
一般方法
支路电流法 网孔电流பைடு நூலகம் 节点电压法
第二章
电路的分析方法
2.1 二端网络与等效变换
2.2 支路电流法
2.3 网孔电流法
2.4 节点电压法
2.5 叠加定理
2.6 等效电源定理
2.7 负载获得最大功率的条件
2.1 二端网络与等效变换
2.1
二端网络与等效变换
一、 名词解释 二、 电阻的串联 三、 电阻的并联 四、 电桥电路
五、 电阻的混联
2.1 二端网络与等效变换
一、名词解释
1、线性元件： 端口伏安关系为线性函数的元件。
Un Rn
_
+ Un _
Pn
2.1 二端网络与等效变换
三、电阻的并联(Parallel connection of resistors)
I + U _ I1 G1 I2 …… G2 In Gn
1 I I1 I 2 2 G G1 G2 Gk 3 Ik I G 4 P P1 P2 GK 5 Pk P G