Chapter 2 电阻电路的等效变换.
第二章 电阻电路的等效变换
i
+
… i
+ -
u
-
K=1,2 , i
+ -
u
Reg
u
G1
in Gn
u
-
Geg
分流公式: 分流公式:ik=Gku=Gk/Geg i n=2时,Reg=R1R2/(R1+R2) 时 ( i1=R2/(R1+R2), 2=R1/(R1+R2)×i ),i ( ( *混联:有串,又有并 混联:有串, 混联 1 R1 R2 R3 R4
对于△ 对于△形,各电阻中电流为:i12=u12/R12 i23=u23/R23 i31=u31/R31 各电阻中电流为:
i ′ =i12-i31=u12/R12-u31/R31 1
i ′2 =u23/R23-u12/R12
i ′3 =u31/R31-u23/R23
i1 + i 2 + i 3 = 0
③
2
2 i31 1 i12
④
2
⑤
i′2
1
1
R2
3
自已补充:R 自已补充 4与1串,R3与2串,然 串 串然 后再并 i2
R4 R3 2
3
i3 2
1
1
2-5
电压源和电流源的串联和并联
+
1、n个电压源串联:us=∑usk--------等效电压源 、 个电压源串联: 等效电压源 个电压源串联 + - + ○ ○ -○ us1 us2 usn。 。 注:正、负号取 。 。 。 2、n个电流源的并联: 个电流源的并联: 、 个电流源的并联 is1 is=is1+is2+…is=∑isk 。 。
αi
+ uS - i +
第2章电阻电路的等效变换

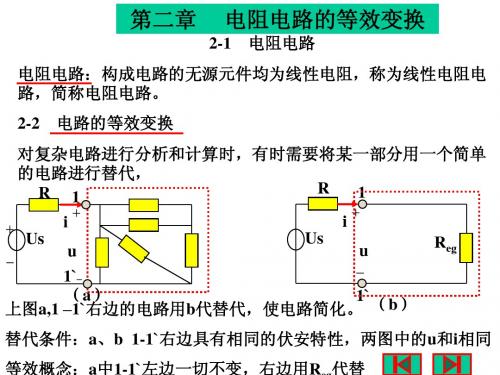
2.两端电路等效的概念
若两个两端电路,端口具有相同的电压与电 流关系,则称它们是等效的电路。
B
i
+ 等效 u
-
C
i
+ u
-
u=M i + N (VCR: Voltage – Current Relationship)
返回 上页 下页
明确
①电路等效变换的条件: 两电路具有相同的VCR;
返回 上页 下页
例1 桥 T 电路
1k
1k 1k
+
E
1k R
-
1/3k
+ E
-
1/3k
1/3k R
1k
1k
+ 3k
E
R
- 3k 3k
返回 上页 下页
例2 计算90电阻吸收的功率
1
10
1 +
20V
-
4 9 90
1
9 9
9
i+
i1
20V 90
-
1090
返回 上页 下页
例4 求: R a b
ab
R a b=70
20
100 10
40 80 60 50
ab
20 100 60
120 60
ab 20 100 100
ab
20 100 60
40
返回 上页 下页
例5 求: R a b
5 a 20
b
缩短无
20
5
a
返回
2.1 引言
电阻电路 分析方法
仅由电源和电阻构成的电路。
①欧姆定律和基尔霍夫定律是 分析电阻电路的依据;
二章电阻电路等效变换
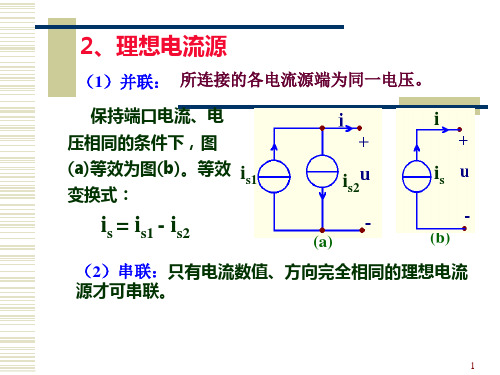
(1)并联: 所连接的各电流源端为同一电压。
保持端口电流、电 压相同的条件下,图
(a)等效为图(b)。等效 is1
变换式:
i
is2
is
is = is1 - is2
(a)
(b)
(2)串联:只有电流数值、方向完全相同的理想电流 源才可串联。
1
二、实际电源模型:
1、实际电压源模型
(1)伏安关系:
i=1.5A Uab=6(i-1)=3V R=Uab/1=3Ω
13
四、三个电阻的星形、三角形连接及等效变换 1、电阻的星形、三角形连接
(a) 星形连接(T形、Y形)
(b) 三角形连接(形、形)
14
2、从星形连接变换为三角形连接
R1
R3
R2
R31 R12 R23
变换式:R12
R1
R2
R1R2 R3
∴i3=i2/3 KCL: i2+i3=I
∴i3=i/4 ∴u=3i+2i = 5i
- 2i0 +
i0
i1 i2
i3
R= u/I=5Ω
21
二、含受控源简单电路的分析:
基本分析思想:运用等效概念将含受控源电路化简、 变换为只有一个单回路或一个独立节点的最简形式, 然后进行分析计算。 例1:求电压u、电流i。
R23
R2
R3
R2 R3 R1
15
3、从三角形连接变换为星形连接
R1
R3
R2
变换式:R1
R12
R12 R31 R23
R31
R31 R12 R23
R2
R12
R23 R23
R31
第2章电阻电路的等效变换

总电流
U S 18 I= = A = 6A R 3
由分流公式得
6 I1 = I = × 6A = 4A 4× 4 9 6 + (1 + ) 4+4
再分流得
6
1 I x = I 1 = 2A 2
返回
电路分析基础
第2章 电阻电路的等效变换
2.2.4 Y形电路和Δ形电路之间 的等效变换
返回
电路分析基础
如何等效化简电桥测温电路? 如何等效化简电桥测温电路?
返回
电路分析基础
第2章 电阻电路的等效变换
2.1 等效变换
电阻电路
线性电阻电路
非线性电阻电路
简化线性电阻电路的主要依据是等效变换
返回
电路分析基础
第2章 电阻电路的等效变换
2.1.1 一端口网络的定义
二端网络
一端口网络
流入一个端子的电流必定等于流出另一端子的电流
Ig =
Rp Rg + R p
× 10 × 10 −3 = 1 × 10 −3 mA
解之得应并联的电阻为
0.1RG 2 × 10 3 Rp = = Ω ≈ 222.22Ω 0.9 9
返回
电路分析基础
第2章 电阻电路的等效变换
2.2.3 电阻的混联
判别电路的串并联关系根据以下原则: 判别电路的串并联关系根据以下原则: (1)看电路的结构特点。 看电路的结构特点。 (2)看电压、电流关系。 看电压、电流关系。 (3)对电路作变形等效。 对电路作变形等效。 (4)找出等电位点。 找出等电位点。
R4 R5 R2(R3 + ) R4+R5 R = R1 + R4 R5 R2 + (R3 + ) R4 + R5
第二章 电阻电路等效变换

2、说明下图所示三个电路对端口而言,是否互 为等效电路。
§2-5 实际电源两种模型及其等效变换
一、实际电源的模型 实际电压源
u Us
理想电压源 实际电压源
理想电压源: 0 其特性仅由唯一参数 us来描述,且与外电路无关。
i
实际电压源:其端电压是随着输出电流 的改变而变化的。 原因:实际电压源内部存在电阻,即内 部有损耗。
R31 i3'
i'1 2
R23
i'2 3
2)形等效为Y形,有
R31 R12 R1 R12 R23 R31 R12 R23 R2 R12 R23 R31 R23 R31 R3 R R R 12 23 31
i1'
R12
R31
N1
2、等效电导
a
i i1 G1
+ u b
i2 G2
…
in Gn
a b
i + u Geq N2
N1
i = i1+ i2++ in = G1u+G2u++ Gnu =(G1+ G2+… +Gn)u 令 Geq= G1+ G2+… +Gn=Gk;则有: i = Geq u 可见: Geq= Gk —等效电导 或1 / Req=1/ Rk,Req R k
I
a Is b
I' Rs'
a
b
(3) 理想电压源和理想电流源不能等效互换 a I' a I + Uab' Us Is b b
Us Us IS (不存在) Rs 0
第二章 电阻电路的等效变换

4
Rab=10
15 10
a b
a b
7
20
15
3
返 回
上 页
下 页
例 2-8 求图 2-5电路 a b 端的等效电阻。
Req (2 // 2 (4 // 4 2) // 4) // 3 (1 4 // 4) // 3 1.5
21
复习
1、电阻的串联 等效电阻、分压
23
例2-4 图2-7所示电路每个电阻都是2Ω, 求a, b两端的等效电阻
解:
c
d
e
根据电路的对称性, 可知 c, d, e三点等电位, 故可用导线短接。
8 2 8 2 16 3 3 2 Req [(2//1) 2]// 2//1 2 // 2 8 2 3 3 15 3 3
26
R12 ( R23 + R31 ) R12 + R23 + R31
i1
i1
i3
i2
i3
i2
R12 R31 R12 + R23 + R31 R23 R12 R12 + R23 + R31 R31 R23 R12 + R23 + R31
27
同理,令i1=0, 可得: R23 ( R12 + R31 ) R2 + R3 = R12 + R23 + R31 同理,令i2=0, 可得:
25
二、 等效变换:保证伏安特性相同
对应端口电压、电流分别相等
i1
u12 = f1 ( i1 , i2 , i3 ) u23 = f 2 ( i1 , i2 , i3 ) u31 = f3 (i1 , i2 , i3 )
第2章 电阻电路的等效变换

i=iS – Gi u
Gi: 电源内电导,一般很小。
三 、电源的等效变换 本小节将说明实际电压源、实际电流源两种模型可 以进行等效变换,所谓的等效是指端口的电压、电流在 转换过程中保持不变。 i i + + uS iS + _ u Gi u Ri _ _
u=uS – Ri i
i = uS/Ri – u/Ri
并联: 可等效成一个理想电流源 i S( 注意参考方向). º iS1 iS2 iSk º
º iS º
i s i sk , i s i s1 i s 2 i sk
串联: 电流相同的理想电流源才能串联,并且每个电流
源的端电压不能确定。
例1:
us
例2:
is
us
us
例3:
1 / R1 R2 i i 1 / R1 1 / R2 R1 R2
º
4. 功率关系
1 / R2 R1 i2 i i 1 / R1 1 / R2 R1 R2
p1=G1u2, p2=G2u2,, pn=Gnu2 p1: p2 : : pn= G1 : G2 : :Gn
应用:利用电源转换可以简化电路计算。 例1. 5A 7
3
7 4
I
2A
例2. 5
+ 15v _ _ 8v +
I 7 I=0.5A
10V 5 6A
10V
+ U _
2A
6A
+ U _
5∥5 U=20V
例3.求图中所示电路中电流i。
2A i 2Ω 6A 2Ω 6V 2Ω 7Ω
3A 2Ω 6A 2Ω 2Ω 7Ω 2A i
第二章 电阻电路的等效变换

最后求得
10 10 i= = = 4A R 2.5
§ 2.5 电压源、电流源的串联和并联
一、理想电压源的串并联
+ uS1 _ + uSn _ º I + 5V _ + 5V _ º I º + 5V _ º º + uS _ º º
1.串联:
可等效成一个理想电压源uS
uS=us1+us2+…+usn=∑ uSk ( 注意参考方向) 2.并联:
§ 2. 3 电阻的串联、并联和串并联
一、电阻串联(Series Connection of Resistors) 1.电路特点:
R1 i + Rk Rn + un _ _
+ u1 _ + u k _ u
(a)各电阻顺序连接,流过同一电流(KCL); (b)总电压等于各串联电阻的电压之和 (KVL)。
§ 2.1 引言
时不变线性电路:由时不变线性无源元件、线性受 控源和独立电源组成的电路,简称线性电路。本书 大部分是线性电路。 线性电阻电路:电路的无源元件均为线性电阻构成 的电路,简称电阻电路。本书2、3、4章介绍电阻 电路分析。 直流电路:电路中的独立电源都是直流电源。
§ 2.2 电路的等效变换
3× 5 R1 = = 1.5Ω 3+ 2+ 5 3× 2 R2 = = 0.6Ω 3+ 2+ 5 2× 5 R3 = = 1Ω 3+ 2+5
再 用电阻串联和并联公式,求 出连 接到电压源两 端单口的等效电阻
(0.6 + 1.4)(1 + 1) R = 1.5 + = 2.5Ω 0.6 + 1.4 + 1 + 1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Chapter 2 电阻电路的等效变换
一、填空题
1. 电路中某一部分被等效变换后,未被等效部分的__ __与__ __仍然保持不变。
即电路的等效变换实质是__ __等效。
2. 当n 个电压源__ __联时,可以用一个电压源等效,且该电压源的电压值
∑==n
k k
S S u
u 1。
3. 当n 个电流源___ _联时,可以用一个电流源等效,且该电流源的电流值∑==n
i i k k
S
S 1。
4. 当把电阻为∆===R R R R 312312的三角形电路等效成星形电路时,其星形电阻为__
__。
5. 电阻串联电路中,阻值较大的电阻上分压较__ __,功率较_ ___。
6. 电阻并联电路中,阻值较大的电阻上分流较__ __,功率较_ ___。
7. 一个外特性为斜直线(不经过坐标原点)的实际电源,可用一个__ __源与_ ___并联等效。
8. 一个外特性为斜直线(不经过坐标原点)的实际电源,可用一个_ ___源与__ __串联等效。
9. 用电流源S I 与电阻i R 并联等效一个实际电源时,S I 为实际电源的__ __,i R 为实际电源的__ __与__ __之比。
10. 用电压源S U 与电阻i R 串联等效一个实际电源时,S U 为实际电源的__ __,i R 为实际电源
的__ __与__ __之比。
11. 电压源空载时应该__ _ _放置;电流源空载时应该__ __放置。
12. 只有电压值相等的电压源才允许__ __联结,只有电流值相等的电流源才允许___ _联结。
13. 从外特性来看,任何一条电阻支路与电压源S u __ __联,其结果可以用一个等效电压源替代,
该等效电压源电压为__ __。
14. 从外特性来看,任何一条电阻支路与电流源S i __ __联,其结果可以用一个等效电流源替代,
该等效电流源电流为_ ___。
15. n 个相同的电压源(其源电压为S U ,内阻为i R )
,将它们并联起来,其等效电压源与等效内
阻方分别为__ __与__ __。
16. n 个相同的电流源(其源电流为S I ,内阻为i R ),将它们串联起来,其等效电流源与等效内阻
方分别为_ _ __与__ __。
二、选择题
1. 设两个二端网络对外是等效的,则下列说法哪个是正确的?( ) A. 它们的外特性相同 B. 它们的内部特性相同 C. 它们的内部结构相同 D. 它们的内部电源相同
2. 图2-1所示电路中,当开关S 闭合后,电流表的读数将( )。
A. 减少
B. 增大
C. 不变
D. 不定
3. 图2-2所示电路中,当开关S 打开后,电压表的读数将( )。
A. 减少
B. 增大
C. 不变
D. 不定
4. 设
Y R 为对称Y 形电路中的一个电阻,则与其等效的△形电路中的每个电阻等于( )。
A. Y R 3
B. Y R 3
C. Y
R 31 D. Y R 31
5. 理想电压源的源电压为S U ,端口电路为I ,则其内阻为( )。
A. 0
B. ∞
C.
I U S D. S
U I
6. 理想电流源的源电流为S I ,端口电路为U ,则其内导为( )。
A. 0
B. ∞
C. S I U
D. U I S
7. 图2-3所示电路中,已知V
u S
28=,Ω=11R ,Ω==232R R ,Ω==454R R ,
图中电流=i
( )。
A. 1A
B. 2A
C. 2.5A
D. 4A
8. 图2-4所示电路中,已知Ω=101R ,Ω=52R ,a 、b 两端的等效电阻=R ( )。
A. Ω5
B. Ω6
C.
Ω320 D. Ω340
9. 如图2-5所示电路中,所有电阻均为Ω3,a 、b 两端的等效电阻
=ab R ( )。
A. Ω5.2
B. Ω3
C. Ω5.1
D. Ω2
10. 图2-6所示电路中,已知Ω==2021R R ,a 、b 两端的等效电阻=R ( )。
A. Ω4
B. Ω5
C. Ω10
D. Ω20
11. 图2-7所示电路中,已知Ω=201R ,Ω=52R ,a 、b 两端的等效电阻=R ( )。
A. Ω4
B. Ω15
C. Ω20
D. Ω25 12. 图2-8所示电路中,可简化等效为( )。
A. Ω8
B. Ω13
C. Ω3
D. 不能简化等效
13. 图2-9所示电路中,V u S 3=,A i S 1=,Ω=1R ,电流源发出(产生)的功率=P ( )
A. W 1
B. W 1-
C. W 4
D. W 4- 14. 图2-10所示电路中,V
u S
10=,Ω=101R ,Ω=202R ,电压源发出(产生)的功率
=P ( )
A. W 5.7
B. W 10
C. W 30
D. W 5.67
15. 图2-11所示电路中,V u S 2=,A i S 1=,求电阻Ω=3R 所消耗的功率=P ( )。
A.
W
34 B. W 3 C.
W 313 D. W 6
16. 图2-12所示电路中,Ω=4R ,A i S
3=,电流源发出(产生)的功率=P ( )。
A. W 108
B. W 36
C. W 72-
D. W 36-
17. 图2-13所示电路中,设R 为正电阻,则二端网络N 的功率是( )。
A. 吸收(即消耗)
B. 发出(即产生)
C. 时发时吸
D. 不发不吸
三、计算题
1. 图2-14所示电路中,画出其△形等效电路,并求各等效电阻。
2. 图2-15所示电路中,求电阻
1R 和2R 的阻值,并画出其Y 形等效电路。
3. 图2-16所示电路中,求
2i 和3u 的值。
4. 图2-17所示电路中,求电阻
1R 和2R 的阻值。
5.试用电源等效变换求出图2-18
a、b所示电路中的电流i。
6.图2-19所示电路中,已知
V
u6
=,试求电流=i?
7.图2-20所示电路中,已知
V
u3
=,试求电流=i?
8.图2-21所示电路中,已知
V
u6
1
=
,试求电流S
i
及电压
u。
u与电流i的关系式。
9.图2-22所示电路中,请写出电压
i。
10.图2-23所示电路中,求电流
11.利用电源电路等效变换,求图2-24所示电路的最简等效电路。
a、b所示所示电路的端口等效电路。
12.利用等效变换的概念,化简图2-25
13.试利用电源的等效变换,把图2-26所示电路化简为最简形式的等效电路。
U。
14.试利用电源的等效变换,求图2-27所示电路中的电压。
