同济大学朱慈勉-结构力学第8章矩阵位移法
同济大学朱慈勉位移法_结构力学
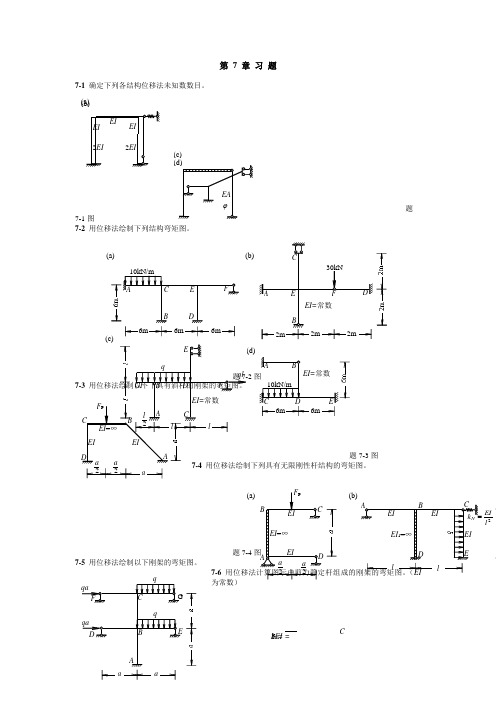
C 第 7 章 习 题7-1 确定下列各结构位移法未知数数目。
题7-1图7-2 用位移法绘制下列结构弯矩图。
用位移法绘制以下下具有斜杆的刚架的弯矩图。
题7-3图题7-47-5 用位移法绘制以下刚架的弯矩图。
7-6 用位移法计算图示由剪力静定杆组成的刚架的弯矩图。
(EI为常数)A 6m 6m 6m(a) D(b)GF C E D 常数 6m 6m a 22(a)EI 2lEI k l l (b)(a) (b) (c) aak N = =3EIl 3BAliiD题 7-5图题 7-6图7-7 利用对称性,用位移法求作下列结构的弯矩图。
题7-7图 7-8 试用位移法求作下列结构由于支座位移产生的弯矩。
7-9 用混合法求作弯矩图。
题 7-9图C E F 2m 2m A ′D ′B ′ EI 2EI4m 3EI A D C B l EI EIϕl Δ=ϕ题 7-8图(a) B 4m 4m DAC B 2kN/m16m (b) EI=常数第7章7-1 (a )一个角位移未知量。
(b )三个角位移未知量,一个线位移未知量。
(c )四个角位移未知量,三个线位移未知量。
(d )三个角位移未知量,一个线位移未知量。
(e )一个角位移未知量,一个线位移未知量;或两个线位移未知量。
(f )三个角位移未知量,两个线位移未知量。
(g )一个角位移未知量,一个线位移未知量。
(h )一个角位移未知量,一个线位移未知量。
(i )三个角位移未知量,一个线位移未知量。
7-5 (a )2472ql MDC-=,62qlMDB=,8Q ql F AD -=。
(b )m kN 26⋅=BA M (上边受拉),m kN 14⋅=BC M (左侧受拉)。
(c )P49F MAD=(左侧受拉)。
(d )P N 6.0F F BE =,P N 2.1F F CF =,a F M BA P 6.0=(上边受拉)。
(e )PN )21(2221F F DC ++=,PN )21(22F F AC +=。
结构力学-矩阵位移法-PPT

当p=l时才能相乘
a12 b11 a22 b21
a12 a22
共形
b11 a11 BA b21 a21
非共形
(2)不具有交换律,即 AB BA
6、转置矩阵 将一个阶矩阵的行和列依次互换,所得的阶矩 阵称之为原矩阵的转置矩阵,如:
任意矩阵与单位矩阵相乘仍等于原矩阵,即 AI =A IA =A
10、逆矩阵
在矩阵运算中,没有矩阵的直接除法,
除法运算由矩阵求逆来完成。例如,若
AB = C
则
B=A 1 C
-
此处A-1 称为矩阵A的逆矩阵。
一个矩阵的逆矩阵由以下关系式定义:A A 1 = A 1 A =I
矩阵求逆时必须满足两个条件: (1)矩阵是一个方阵。 (2)矩阵的行列式不为零,即矩阵是非奇异矩阵(行列 式为零的矩阵称为奇异矩阵)。
矩阵位移法(刚度法):
结点力
P
F
(物理条件)
结点位移
(几何条件)
(平衡条件)
杆端力
杆端位移
r11 z1 r12 z 2 L r1i zi R1p 0 r21 z1 r22 z 2 L r2i zi R2p 0 r31 z1 r32 z 2 L r3i zi R3p 0
结构力学
STRUCTURE MECHANICS
第十章
矩阵位移法
知识点:
• • • • 矩阵位移法的基本要点 常见单元单元刚度矩阵的建立 单元刚度矩阵的坐标变换 矩阵位移法计算连续梁和刚架
教学基本要求:
掌握矩阵位移法的基本要点;
理解各种常见单元杆端位移和杆端力的对应 关系,理解单刚矩阵的建立方法及过程,能正确 写出常见单元的单刚方程;理解坐标变化的意义 及方法。 掌握前处理法计算连续梁和不考虑轴线变形 的刚架,结合刚架理解后处理法的基本思想。
结构力学矩阵位移法

k jk 表示,k端弯矩用 k kk 表示,放在劲度矩阵第二列;
k(1)k(2)k(3) k kk jjj
k kk jk k 2 4ii
2i 4i
21
K1是 1 1自由度发生单1自 位由 转度 角引 在起的刚
位移法用结点的平衡
K1
1.位移法作结点位移引起的单位内力(弯矩、剪力) 图 矩阵位移法将结点位移引起的杆端力放在单元劲度 矩阵中。
2.位移法从结点位移引起的单位内力(弯矩、剪力) 图中取出结点作为脱离体,由脱离体的力平衡条件 求得附加约束反力,即整体劲度系数。
矩阵位移法由单元劲度矩阵集合成整体劲度矩阵。
10
位移法和矩阵位移法求自由项系数的方法有何不同?
11
背:位移法矩阵位移法整体结点位移正负号规定?
整体结点位移,矩阵位移法中与整体坐标方向一 致为正。位移法中角位移顺钟向为正,线位移无 规定。
12
第二专题: 只有转角未知量的连续梁的矩阵位移法
13
用位移法和矩阵位移法求图示连续梁的杆端弯矩
FP1 FP FP2 2FP ql FP
14
背:位移法和矩阵位移法的基本系-结点转角处附加刚臂
K21kk(2j) 2i
23
K12是2自由度发生单1自 位由 转度 角引 在起的刚
位移法用结点的平衡
K12的形成
矩阵位移法:与1和2自由度都 有关的单元单元只有(2)单 元,1自由度对应(2)单元的 j端,2自由度对应(2)单元 的k端,故:
K12k(j2k) 2i
24
K22是2自由度发生单2自 位由 转度 角引 在起的刚
5
背:为什么矩阵位移法比位移法可能有更多的独立的 结点线位移作为基本未知量?
结构力学十三讲(矩阵位移法)

1 i1 2i23
2 i2 2i22
2 i2
4i23 3
F1
4i1 2i1 0 1
F2 = 2i1 4i1+4i2 2i2 2
传统位移法 根据每个结点位移 对附加约束上的约束
F3
0 2i2 4i2 3
{F}=[K]{}
力{F}的贡献大小进 行叠加而计算所得。
7
一、 单元集成法的力学模型和基本概念
一、矩阵位移法的基本思路
矩阵位移法的两个基本步骤是 (1)结构的离散化;(2)单元分析;(3)整体分析,
单元 分析
整体 分析
任务
建立杆端力与杆端位移 间的刚度方程,形成单 元刚度矩阵
由变形条件和平衡条件 建立结点力与结点位移 间的刚度方程,形成整 体刚度矩阵
意义 用矩阵形式表示杆 件的转角位移方程
单元贡献矩阵是单元刚度矩阵,利用“单元定位向量”进行“换码重排位”。
单元
(1) (2)
1 (1)
[k] = (2)
4i1 2i1
2i1 4i1
1
=
1 2
12 3
1 40i1 20i1 0
1
[K] = 2
20i1
40 i1
0
30 0 0
单元
(1) (2)
2 (1)
[k] = (2)
2i1
0
2
[k] =
4i2 2i2 2i2 4i2
12 [K] =
00 0
0 4i2 2i2 0 2i2 4i2
2i1 44i1i+1 4i2 20i2 0 20i2 40i2
4i1 2i1 0
整体刚度矩阵: [K]= 2i1 4(i1+i2) 2i2
同济大学朱慈勉 结构力学 第8章 矩阵位移法习题答案

同济大学朱慈勉 结构力学 第8章 矩阵位移法习题答案8-1 试说出单元刚度矩阵的物理意义及其性质与特点。
8-2 试说出空间桁架和刚架单元刚度矩阵的阶数。
8-3 试分别采用后处理法和先处理法列出图示梁的结构刚度矩阵。
(a)解:(a )用后处理法计算 (1)结构标识(2)建立结点位移向量,结点力向量[]T44332211 θνθνθνθν=∆[]T y M F M F M F M F F 4y43y32y211 =θ(3)计算单元刚度矩阵⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡-=⎥⎥⎦⎤⎢⎢⎣⎡=2222322211211462661261226466126122EI 21 l l -l l l -l -l l -l l l l - l k k k k k ①①①①①⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡-=⎥⎥⎦⎤⎢⎢⎣⎡=222233332232223 33 6 3632336 362EI 21 l l - l l l - l -l l -l l l -l l k k k k k ②②②②②lll⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡-=⎥⎥⎦⎤⎢⎢⎣⎡=222234443343323 33 6 3632336 362EI 2 1 l l - l l l - l -l l -l l l -l l k k k k k ③③③③③(4)总刚度矩阵⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡++=222222222234443343333322322222112112 3300003 6 3 6 000 03403003601236000 0 3632600 363186120000 26460 0 0 06126122EI 0 0 00 0 0 4 3 2 1 4 3 2 1 l l -l l l - l - - l l -l l l l - l - - l l -l l -l l l l - -l -- l l -l l l l - l k k k k k k k k k k k k k ③③③③②②②②①①①①θ (5)建立结构刚度矩阵支座位移边界条件[][]00004311 θ θ θν=将总刚度矩阵中对应上述边界位移行列删除,得刚度结构矩阵。
结构力学应用-矩阵位移法

3、集成总刚
(6)定位向量法:对号入座,同号相加 定位向量法:对号入座,
4.综合结点荷载
综合结点荷载 {F}={FD}+{FE} }――直接结点荷载 ①{FD}――直接结点荷载 }――等效结点荷载 ②{FE}――等效结点荷载 (7-1)局部坐标系单元固端力 (7-2)整体坐标系单元固端力 (7-3)单元等效结点荷载。 单元等效结点荷载。
等效原则: 等效原则: ——两种荷载对基本体系产生相同的结点位移。 两种荷载对基本体系产生相同的结点位移 ——两种荷载对基本体系产生相同的结点位移。
矩阵位移法的计算步骤及示例
矩阵位移法计算平面刚架 计算机计算――程序化) 程序化) (计算机计算 程序化
1. 编码、整理原始数据 编码、
(1)整体与局部坐标系 ) (2)结点位移编码 ) 单元编码 (3)原始数据: )原始数据: E 、A i、I i、l i 定位向量{λ} 定位向量 e, αi([ T ]) ])
几点补充说明
1、结点位移分量编号,定位向量 、结点位移分量编号,
——引入支承条件:已知位移约束的方向,编码为零。 引入支承条件:已知位移约束的方向,编码为零。 引入支承条件
2、铰结点处理: 铰结点处理: 铰结点处理
铰结的各杆杆端的转角均为基本未知量 ——分别编码(统一单元,程序简单) 分别编码(统一单元,程序简单) 分别编码
矩阵位移法
矩阵位移法——基本原理与位移法相同 基本原理与位移法相同 矩阵位移法 *数学工具 —— 矩阵运算
1、矩阵知识 矩阵: (1)矩阵:A 方阵: 方阵: 阶方阵A相应的行列式 (2)行列式:n阶方阵 相应的行列式 )行列式: 阶方阵 相应的行列式D 若D=0,A为奇异矩阵 (3)矩阵运算 相等:加减:数乘: 相等:加减:数乘: l aik 乘法: 乘法:Cmn=Aml*Bln,则 cij =
结构力学答案(下册).

k 23 ② k33② + k 33③
0 k34 ③
⎥
⎢
⎥ 2EI ⎢6l
⎥= ⎥
l3
⎢⎢0
-6l 18 -3l -6 2l 2 -3l 6l 2 -3l 0 -6 -3l 12
3l l2 0
⎢⎣0 0
k 43③
k 44 ③
⎥ ⎦
⎢0
0 3l l 2 0 4l 2
⎢
⎢0 0 0 0 -6 -3l
⎢⎣0
① 1→2
l
cosα
1
sin α
0
② 3→4 ③ 1→3 ④ 2→4 ⑤ 2→3
⑥ 1→4
l
1
l
0
l
0
2l − 2
2
2l
2 2
0 -1 -1
−2 2
2 2
(2)建立结点位移向量,结点力向量
[ ] ∆ = µ1 ν 1 µ2 ν 2 µ3 ν 3 µ4 ν 4 T
[ ] F = Fx1 Fy1 0 -Fp Fx3 Fy3 0 0 T
1
⎥ ⎥
k⑥ = k⑤ =
⎢1
EA ⎢ 2
2l
⎢ ⎢-
1
1 2 -1
2 2⎥
⎢2 2
1 1⎥ ⎥
2 2⎦
⎢ ⎢-
1
-1
⎣2 2
4
-1 2
-
1 2
⎤ ⎥ ⎥
-1 2
-
1 2
⎥ ⎥
1
1
⎥ ⎥
2 2⎥
1 1⎥ ⎥
2 2⎦
(4)形成刚度矩阵,刚度方程
1
2
3
4
⎡4+ 2
⎢ ⎢
第八章矩阵位移法-135页PPT

Fyi Fxj
F4 Fyj
8-1 概述
31
刚架单元
结构坐标系
1 (e) ui (e)
2
v
i
δ (e)
δi (e)
δ
j
3 4
i u j
5
6
8-1 概述
10
3.结构坐标系(整体坐标系)
• 对整个结构建立统一的坐标系 • 在整体分析中,采用统一的坐标来
描述结构的结点和单元位置等。
8-1 概述
11
4.单元坐标系(局部坐标系)
• 针对每一单元的坐标系 x o y
• 以杆轴线的某方向作为 x 轴正向,在轴线
上以箭头作正方向标记,以垂直于杆件轴线 方向为 y 轴,本章采用右手坐标系
u 1v 1 1u 2v 2
2u 3v 3
3u 4v 4
T 4
8-1 概述
20
结点位移
若平面刚架有n个结点
Δ u 1v 11u 2v 22 u nv nn T
第i结点的位移为 Δ i ui vi iT
则n个结点的位移向量为
Δ Δ 1 Δ 2 Δ nT
F x 1F y 1M 1F x 2F y 2M 2F x 3F y 3M 3F x 4F y 4M 4T
8-1 概述
25
刚架的结点力向量
• 第i结点的结点力为 Fi = ( Fxi Fyi Mi )T
• 刚架的结点力向量为 F =(F1 F2 F3 … Fi … Fn )T
