结构力学第七章-位移法(一)
结构力学_位移法

1
1
1 B
1 B
B
1 C
1 C
C C
FP FP A A D D
D
Z2 Z2
C
Z3 Z3 C
B B
D
B
C C
A
A
Z1 Z1
B
B
C
D D
2
2
F F E E
G G
Z4 Z4
G
G
F E
F
G
G
E
A D
A D
nB Y= 4
Z6
Z5 C
Z5
B
C
Z6
F
G
3、结点独立线位移数 (1) 先简化结构
1)除特殊指明外,梁与刚架一般不考虑由于轴向变形引
b)一端固定 一端铰支
c) 一端固定 一端定向支承
由荷载或温度变化引起的杆端内力称为载常数。其中的杆端弯
F F 矩也常称为固端弯矩,用M BA 和 M AB 表示;杆端剪力也常称为 F F 固端剪力,用FQ 和 表示。 F AB QBA
常见荷载和温度作用下的载常数列入表中(书P5) 。
由杆端单位位移引起的杆端内力称为形常数,见书P279,7-7 式。表中引入记号i=EI/l,称为杆件的线刚度。
F 3i A 3i M AB l 0
3、一端固定另一端定向支承梁
FP B EI
A
A
MAB FQAB
A
B1
B
l
F M AB i A i B M AB F M BA i A i B M BA
(非独立线位移)
M
q
应用以上三组转角位移方程,即可求出三种基本的单跨超 静定梁的杆端弯矩表达式,汇总如下:
位移法与力法的比较
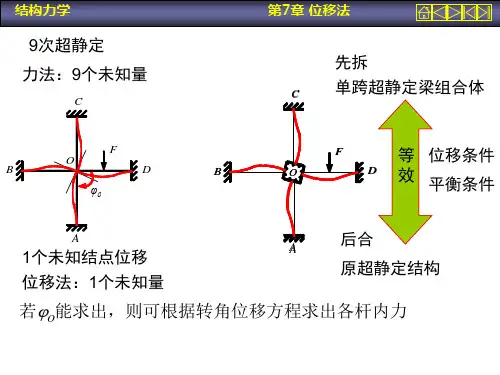
A l
F
l
l
结构力学
FR1
C 2i i A
l 2 l 2
第7章 位移法
F=ql
例题1 试用位移法求图示刚架内力,并绘内力图。
F=ql B
Δ2 FR2
4i B
r11
r12
B
φ1
l
C
r21
3(2i)=6i A D M1
6i l
6i l
C
r22
i D
q
q
基本体系
r12
B
6i l
r11
B 4i 6i
2i
FR1F F T R2F F F F FR F R1F R2F RnF 自由项列阵 FRnF
A A Z AF
结构力学
第7章 位移法
C
§7-3 位移法计算举例 例1:刚架内力计算,并绘内力图。 例2:排架内力计算,并绘内力图。
结构力学
第7章 位移法
四、推广到n个基本未知量
r11Z1 r12 Z 2 + +r1n Z n FR1F 0 r Z r Z + +r Z F 0 21 1 22 2 2n n R2F rn1Z1 rn 2 Z 2 + +rnn Z n FRnF 0
(2)位移法法典型方程 平衡 FR1 FR11 FR12 +FR1F 0 条件 FR2 FR21 FR22 +FR2F 0
典型 方程
r111 r12 2 +FR1F 0 r211 r22 2 +FR2F 0
结构力学-第7章-位移法习题答案
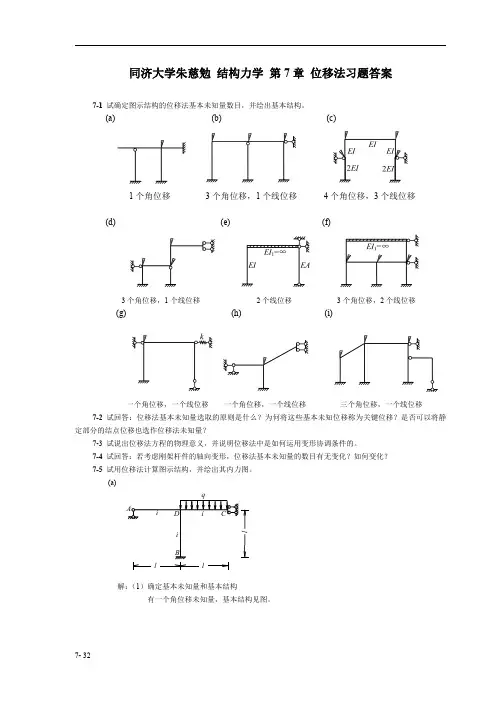
1 2
ql
1 12
ql 2
/ l
7 12
ql
由位移法方程得出:
r11Z1
R1 p
0
Z1
7ql 4 348EI
作出最终 M 图
7-9 试不经计算迅速画出图示结构的弯矩图形。
(a)
B
θA A
(b)
C B
yB
B′
A
C
题 7-9 图 7-10 试计算图示有剪力静定杆的刚架,并绘出 M 图。
13EI l
, r12
r21
3EI l2
r22
18EI l2
R1 p
1 16
ql 2 , R2 p
ql
代入,解得
Z1
66 3600
ql3 EI
,
Z2
211 3600
ql 4 EI
(4)求最终弯矩图
(e)
50kN·m
80kN·m 10kN·m 20kN
A 2EI B EI C
EI
(b)
B
3EI
C
EI
EI
A
D
Δ l
l
解:(1)求 M1, M 2 , M 3, M p 图。
(2)由图可知:
r11
16i, r12
r21
6i, r23
r32
6i l
, r22
16i, r33
24i l
R1 p
0, R2 p
结构力学 7.位移法

§7-1 位移法的基本概念
2 位移法计算刚架的基本思路
(1)基本未知量——A 和。
(2)建立位移法基本方程 ■刚架拆成杆件,得出杆件的刚度方程。 ■杆件合成刚架,利用刚架平衡条件,建立位移法基本方程。
§7 – 2 等截面直杆的刚度方程 正负号规定
结点转角 A 、 B 、弦转角( = / l ) 和杆端弯矩M AB
0
0
6
5ql
3ql
3l / 8
8
8
9ql2 / 128
(↑) (↑)
2ql
ql
7
5
10
(↑) (↑)
8
9ql
11ql
40
40
(↑) (↑)
§7-2 等截面杆件的刚度方程
表1:载常数表(续)
序号 计算图及挠度图
弯矩图及固端弯矩
9
10
5FPl / 32
11
12
固端剪力
FQAB
FQBA
FPb(3l 2 b2 ) 2l 3
M AB
4i A
2i B
6i
l
M BA
2i A
4i B
6i
l
(1)B端为固定支座 B 0
FQ AB FQ BA
6i l
A
6i l
B
12i l2
(2)B端为铰支座 MBA 0
M AB
4i A
6i
l
M BA
2i A
6i
l
M AB
3i A
3i
l
§7-2 等截面杆件的刚度方程
M AB
24
25
26
27
固端剪力
结构力学 位移法典型方程、计算举例
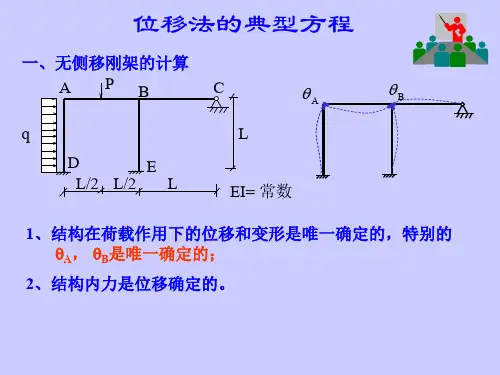
r21 B r22 CH R2
满足此方程,就消去了施加的2个约束
即,
r11 B r12 CH R1P 0 r21 B r22 CH R2 P 0
4)弯矩图的作法----消去最先附加的刚臂 P R1P R2P + MP图 R2
r
j 1
n
ij
Zj
,为消去该处的约束力,令: R iP
r
j 1
n
ij
Z j =0 即可。写成方程组的形式为:
r11 Z1 r12 Z 2 r1n Z n R1P 0 r Z r Z r Z R 0 21 1 22 2 2n n 2P rn1 Z1 rn 2 Z 2 rnn Z n RnP 0
R1P
R2P
+ +
r11 R A
1
r21R 2A
MP图 +
r12 B
r22 B
或
P
qL2/12
PL/8
4i
2i
q
R1P
R2P
+ A•
r11 8i r21 2i
2i
M 1图
MP图
4i
+
B•
4i r22 11i 2i r12 2i 3i 2i
M 2图
M M P M 1 A M 2 B
叠加右侧2个图,意味着结点B转动 及结点C侧移都发生。
叠加后B处的转角和C处的位移
分别为:B CH 则两处的约 束力必为R1,R2
r12 CH
结构力学位移法

R2
R1=0 R2=0
ql
C D
Z1 R1
l
四.位移法典型方程
ql
q
l/2 B
ql
C D
ql B
A r22
q
R2 Z1
R1=0
ql C D
Z2=1
l/2 A
EI=常数
R2=0 R1 R1 r11 Z1 r12 Z 2 R1 P 0
l
C
r21
R2 r21 Z1 r22 Z 2 R2 P 0
r11
3i 3i
EI
r
11
=6i
R1P
ql 2 / 8
R1P
q
R1 P ql 2 / 8
Z1 ql / 48i ql 2 8 MM Z M 1 1 P
2
MP
ql2 / 16
r11
3i
Z1=1 3i
M1
Z1
M
位移法求解过程:
1)确定基本体系和基本未知量 2)建立位移法方程 3)作单位弯矩图和荷载弯矩图 4)求系数和自由项 5)解方程 6)作弯矩图
A
Z1
B
Z1
q
B
C
=
A
B
+
B
ቤተ መጻሕፍቲ ባይዱ
C
Z1
q
A
EI
B
Z1
EI
C
----刚臂,限制转动的约束 R1=0 R1=r11 Z1+ R1P =0
R1
q
A
EI
B
EI
C
r11
3i
B B
ql 8
2
3i
r
结构力学位移法的计算
B t2=-30°C C t2=-30°C F
° t1=10°C
t1=10°C °
A
D l=6m
E
l=6m
a) 解:
B t2=-30°C C ° t1=10°C °
A l=6m D b)
取如图b)半边结构,未知量为B ( ) 。
62
1)各杆两端相对侧移
AB
杆AB缩短 t0h 40 杆CD伸长 t0h 40
FC
FP
i
2i
i1 A
i2 H
未知量 D ,F
51
FP D
C
FP E
i2
i1
i1
A
B
FP
C
D
2i2
i1
A
CL 0, CR 0,
CH 0,
(MCL MCR 0), CV 0。
未知量 D
52
2.反对称荷载:
对称结构在反对称荷载作用下,其内力和变形 均是反对称的。
选取基本体系如下图所示。 D i
E
Z1 D 0,
Z2 EH 0。
C
i/2
2i
基本体系
A
B
44
45
46
47
ii)求方程的系数和自由项:
r11= 5i, r12 = r21 = 0.75i,
r22= 0.75i,R1P = 14,R2P = 3。
4)回代入方程中,求解得:
3i(
4 i
)
12kN
m。
M DA
2i D
0.75i E
2i(
4 i
)
0.75i(
结构力学位移法01
位移法的概念 位移法基本体系的确定 位移法计算荷载引起的超静定结构内力 位移法计算温度改变引起的超静定结构内力 位移法计算支座位移引起的超静定结构内力 混合法
位移法是计算超静定结构的基本方法之一. 主要用于超静定梁和刚架的内力计算。
FP
力法计算,9个基本未知量
位移法计算, 1个基本未知量
§6-2 位移法基本概念
1
1
B EA D
FP
EI
EI
A
C
1
D
C
1
B
FP
FP
=
A
1
+
3i/l
3i/l 2
3FPl /16
3i/l 2 FP
内力计算的关键是
求结点位移Δ1
11FP /16 5FP /16
l/2 l/2
1
1
B EA D
FP
EI
EI
A
C
F1 0 F1 F11 F1P 0
k111 F1P 0
§6-1 单跨超静定梁的形常数与载常数
一.等截面梁的形常数 杆端位移引起的杆端内力称为形常数.
6i/l
6i/l
1
1
1
12i/l 2
12i/l 2
i=EI/l----线刚度
1
2i
4i
6i/l
6i/l
3i 3i/l
3i/l
3i/l 2
3i/l
3i/l 2
1
1
i
0
0
0
二.等截面梁的载常数
荷载引起的杆端内力称为载常数.
FPl
5 32 FPl
M图
Δ1
F1
《结构力学习题集》(下)-矩阵位移法习题及答案 (2)
第七章 矩阵位移法一、是非题1、单元刚度矩阵反映了该单元杆端位移与杆端力之间的关系。
2、单元刚度矩阵均具有对称性和奇异性。
3、局部坐标系与整体坐标系之间的坐标变换矩阵T 是正交矩阵。
4、结构刚度矩阵反映了结构结点位移与荷载之间的关系。
5、用 矩 阵 位 移 法 计 算 连 续 梁 时 无 需 对 单 元 刚 度 矩 阵 作 坐 标 变 换。
6、结 构 刚 度 矩 阵 是 对 称 矩 阵 ,即 有K i j = K j i ,这 可 由 位 移 互 等 定 理 得 到 证 明 。
7、结构刚度方程矩阵形式为:[]{}{}K P ∆=,它是整个结构所应满足的变形条件。
8、在直接刚度法的先处理法中,定位向量的物理意义是变形连续条件和位移边界条件。
9、等效结点荷载数值等于汇交于该结点所有固端力的代数和。
10、矩阵位移法中,等效结点荷载的“等效原则”是指与非结点荷载的结点位移相等。
11、矩阵位移法既能计算超静定结构,也能计算静定结构。
二、选择题1、已知图示刚架各杆EI = 常数,当只考虑弯曲变形,且各杆单元类型相同时,采用先处理法进行结点位移编号,其正确编号是:(0,1,2)(0,0,0)(0,0,0)(0,1,3)(0,0,0)(1,2,0)(0,0,0)(0,0,3)(1,0,2)(0,0,0)(0,0,0)(1,0,3)(0,0,0)(0,1,2)(0,0,0)(0,3,4)A.B.C.D.2134123412341234xy M , θ2、平面杆件结构一般情况下的单元刚度矩阵[]k 66⨯,就其性质而言,是: A .非对称、奇异矩阵; B .对称、奇异矩阵; C .对称、非奇异矩阵; D .非对称、非奇异矩阵。
3、单元i j 在图示两种坐标系中的刚度矩阵相比:A .完全相同;B .第2、3、5、6行(列)等值异号;C .第2、5行(列)等值异号;D .第3、6行(列)等值异号。
i jyxi jyxM , θM , θ4、矩阵位移法中,结构的原始刚度方程是表示下列两组量值之间的相互关系: A .杆端力与结点位移; B .杆端力与结点力; C .结点力与结点位移; D .结点位移与杆端力 。
龙驭球《结构力学Ⅰ》(第4版)笔记和课后习题(含考研真题)详解(中册)-第七章【圣才出品】
圣才电子书 十万种考研考证电子书、题库视频学习平台
(b)如图 7-2-3 所示。
图 7-2-2
图 7-2-3 ①当α≠0 时,结点 A、B、C、E、F、G 有转角,AB、FG 有水平位移,C、E 点有两个 水平位移,所以基本未知量有 10 个,分别是θA、θB、θC、θE、θF、θG、ΔA、ΔG、ΔC、ΔE。 ②当α=0 时,结点 A、B、C、E、F、G 有转角,AB、FG 有水平位移,CDE 有水平位 移,D 点有竖向位移,所以基本未知量有 10 个,分别是θA、θB、θC、θE、θF、θG、ΔA、Δ G、ΔC、ΔVD。 (c)如图 7-2-4 所示。 ①当不考虑轴向变形时,结点 A、B、C 有转角,整体有一个水平位移,所以基本未知 量有 4 个,分别是θA、θB、θC、Δ。
15 / 134
圣才电子书 十万种考研考证电子书、题库视频学习平台
②当考虑轴向变形时,A、B、C 三个结点都有独立的转角、竖向位移、水平位移,所 以基本未知量有 9 个,分别是θA、θB、θC、ΔA、ΔB、ΔC、ΔVA、ΔVB、ΔVC。
图 7-2-4 (d)如图 7-2-5 所示。 ①当α≠0 时,结点 B、C 有转角,D 结点有独立的竖向位移,所以基本未知量有θA、θ B、ΔV。 ②当α=0 时,结点 B、C 有转角,虽然 D 结点有位移,但不是独立的,所以基本未知 量有θA、θB。
图 7-1-8 反对称荷载作用下奇数跨对称结构的半结构选取方法 图 7-1-9 对称荷载作用下偶数跨对称结构的半结构选取方法
12 / 134
ቤተ መጻሕፍቲ ባይዱ
圣才电子书 十万种考研考证电子书、题库视频学习平台
图 7-1-10 反对称荷载作用下偶数跨对称结构的半结构选取方法 7.2 课后习题详解
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
由 M B = 0 同理可得,
FQAB 6i 6i 12i F A B 2 FQAB l l l
结构力学 第七章 位移法
2015年9月12日星期六
§7-2 等截面直杆的转角位移方程
等截面直杆的转角位移方程:
一端固端一端铰支的等截面直杆:
B端角位移不独立。
C
B A
AB:一端固定一端定向滑动 BC:一端固定一端定向滑动 BD:一端固定一端铰支
C
EI=c D B A
AB:两端固定 BC:一端固定一端定向滑动 BD:一端固定一端铰支
C
EI=c D B A
AB:两端固定 BC:两端固定 BD:一端固定一端铰支
C
EI=c D EI=c B A
AB:两端固定 BC:一端固定一端定向滑动 BD:两端固定
R1 = 0 R2 = 0 R3 = 0
R11 Z1
R21
R31
R12
R22 Z2
R32
R13
R23
R1P R33
R2P
P2
R3P
D EI=c A
E
F
D EI=c
E
F
D EI=c
E
F
P1
D EI=c A
E
F
B
C
A
B
C
A
B
C
B
C
(a)基本结构只发生 Z1
(b)基本结构只发生 Z 2
EI 1
B’ O
B
A’
EI
EI
EI
A EI
EI 1
不考虑杆件伸缩变形,AB 不能转动,无结点角位移
结构力学 第七章 位移法
刚杆AB绕O刚体转动,A、B结点转角相同, 1个结点角位移(且与结点线位移相关)
2015年9月12日星期六
§7-3 位移法基本未知量和基本结构
基本未知量数量的确定:
f A B D C
力法如何求解? 缺点:基本未知量多(3个) 基本结构不唯一
如何画结构的变形? 关键:B结点的转动 方向
若f求得,则AB、BC、BD三杆均为单跨超静定杆件, 内力可分别独立求出。
单跨超静定杆件的形式不外乎以下三种:⑴两端固端(如AB);⑵一端固定另 一端铰支(如BC);⑶一端固定另一端滑动支座(如BD)。有限种典型荷载作 用下的内力可用力法求出。故,可以作为位移法的基本结构。
由 M BA = 2iθ A + 4iθB - 6i 从而, M AB = 3iθ A FQAB FQAB
3i F + M AB l 3i 3i F = - θ A + 2 + FQAB l l 3i 3i F = - θ A + 2 + FQBA l l
Δ 1 3 Δ = 0 可得, θB = - θ A + l 2 2 l
§7-4 位移法原理与位移法方程
以图示结构为例,说明如何建立位移法典型方程。
P2
R1 Z1
D
P1
E
F
几个基本未知量? D结点角位移
3个基本未知量 E结点角位移 DEF水平线位移
R2 Z2
P2
R3
D
P1
E
F
Z3
EI=c A B
原结构
EI=c A B
基本结构 叠加原理 分解
C
C
当基本结构承受 与原结构相同外 荷载,且发生相 同结点位移时, 与原结构等效。 此时,附加约束 上的约束力均为 零,即
基本未知量数量的确定:
最少基本未知量数量: 。 A. 1; B. 2; C. 3; D. 4 C B A EI=c D 基本结构
【选择题】图示结构有位移法基本未知量数量是
由于位移法基本结构不唯一, 所以基本未知量的数量也不唯一, 但最少基本未知量的数量是唯一 的。 建议尽可能按最少基本未知量计 算。 最少基本未知量数量:把原结构 转化为基本结构所必需的最少附 加约束数量。
两端固端梁:编号1、2、3(a = b =
一端固定一端定向滑动梁可视为两端固端梁的对称半结构。 位移法分析中要养成勤于作结构位移(变形)图的习惯,杆端弯矩只记大小,不记
正负,弯矩方向根据变形图判别。
牢记弯矩,不必记剪力,杆端剪力可根据杆端弯矩利用平衡条件计算。
注意:载常数计算时有外荷载作用,杆端内力应与外荷载共同平衡,由杆端弯 矩计算杆端剪力时万不可漏掉外荷载。
记基本结构只发生 1 时, 附加约束的约束力为 r11 ,则
基本结构只发生结点位移f,不 承受外荷载。
基本结构只承受外荷载,不发 生结点位移。
R1P 可通过基本结构的荷载弯矩 图 M P 求得。
结构力学 第七章 位移法
2015年9月12日星期六
§7-1 位移法的基本概念
【法二】通过附加约束,利用叠加原理间接建立B结点的力矩平衡方程
线位移数量的确定:
线位移数量就是确定铰接体系所有结点位置所需要的附加链杆数量。 除特别说明外,一般不考虑杆件轴向变形。 弯曲变形微小,构件受弯后长度不变。
【例】 EI=c
1个结点线位移
EI=c
2个结点线位移
结构力学 第七章 位移法
2015年9月12日星期六
§7-3 位移法基本未知量和基本结构
结构力学 第七章 位移法
基本结构 静定结构 单跨超静定杆
基本方程 几何方程 静力平衡方程
2015年9月12日星期六
多余约束力 结点位移
§7-1 位移法的基本概念
力法与位移法的区别:
在给定的外部因素的作用下结构真实的解答是唯一的。 力(反力、内力) 二者之间有着确定的关系,且一一对应,知其一 变位(变形、位移)
式中, i =
EI F F 称为杆件的线刚度;M AB 和M BA 称为固端弯矩, l
表示由荷载引起的杆端弯矩。
杆端剪力:可根据杆端弯矩利用平衡条件计算。
由 M A = 0 可得,FQBA = M AB + M BA + M Pq (A)
l l F F M AB M BA M Pq (A) 6i 6i 12i A B 2 l l l l 6i 6i 12i F A B 2 FQBA 固端剪力:杆件只承受跨内荷载时的杆端剪力。 l l l
结构力学 第七章 位移法
2015年9月12日星期六
§7-3 位移法基本未知量和基本结构
位移法基本未知量: 结点位移
结点角位移 结点线位移 相互独立 三类单跨超静定杆 静定结构
位移法基本结构: 形常数和载常数已知的结构 基本未知量与基本结构是一一对应的。 原结构
附加刚臂约束结点角位移 附加链杆约束结点线位移
结构力学 第七章 位移法 2015年9月12日星期六
§7-3 位移法基本未知量和基本结构
基本未知量数量的确定:
角位移数量的确定:
一般情况下(弹性杆件),角位移数量就是刚结点的数量。 【例】 EI=c EI=c EI2 EI=c
3个角位移
EI1
1个角位移
1个角位移
2个角位移
特殊情况:如结构中含有刚杆,必定存在相关位移。 B 【例】 A
真实解答中, 必知其二。
力法:先求力(未知内力或约束力),再计算相应位移。 位移法:先确定位移,再求内力。
位移法需要解决的问题:
解出单跨超静定梁在常见外部因素作用下的内力。 (§7-2的内容) —— 用于基本结构的内力分析,作基本结构的单位内力图和荷载内力图。进而计算方程的 系数项和自由项。 确定以哪些结点的哪些位移作为基本未知量。(§7-3的内容)
QBA
正杆端位移示意图
A
A
B
A
B
AB
结构力学 第七章 位移法
2015年9月12日星期六
§7-2 等截面直杆的转角位移方程
等截面直杆的转角位移方程:
推导方法:力法,推导过程略。 两端固端的等截面直杆:
杆端弯矩: M AB = 4iθ A + 2iθB - 6i
M BA Δ F + M AB l Δ F = 2iθ A + 4iθB - 6i + M BA l
2015年9月12日星期六
§7-2 等截面直杆的转角位移方程
等截面直杆的形常数和载常数表及其应用:
形常数和载常数表:是位移法中作基本结构内力图的基础,详见Text Book P.187 表7-1。 应用要点:
要求熟练掌握的项:
l )、4项; 2 l a = b = )、10、13(b = 0 )项。 一端固定一端铰支梁:编号7、8、9( 2
第七章
Chapter 7
位移法
Displacement Method
同济大学土木工程学院
School of Civil Engineering,Tongji Univesity
2015年9月12日星期六
Contents
§7-1 位移法的基本概念 §7-2 等截面直杆的转角位移方程 §7-3 位移法基本未知量和基本结构 §7-4 位移法原理与位移法方程 §7-5 位移法解超静定结构 §7-6 对称性的利用 §7-7 广义荷载作用下的位移法计算
结构力学 第七章 位移法
2015年9月12日星期六
§7-2 等截面直杆的转角位移方程
几个概念:
可用于位移法基本结构的单跨超静定杆: 有几种基本形式? ⑴一端固定一端铰支 ⑵一端固定一端定向铰 ⑶两端固端 (一次超静定) (二次超静定) (三次超静定)
